On the Integral of the Fractional Brownian Motion and Some Pseudo-Fractional Gaussian Processes
Abstract
1. Introduction
1.1. The FBM Process and Its Integral
1.2. Neuronal Models and Pseudo-Fractional Gaussian Processes
1.3. A Fractional Ornstein–Uhlenbeck Process for Some Comparisons
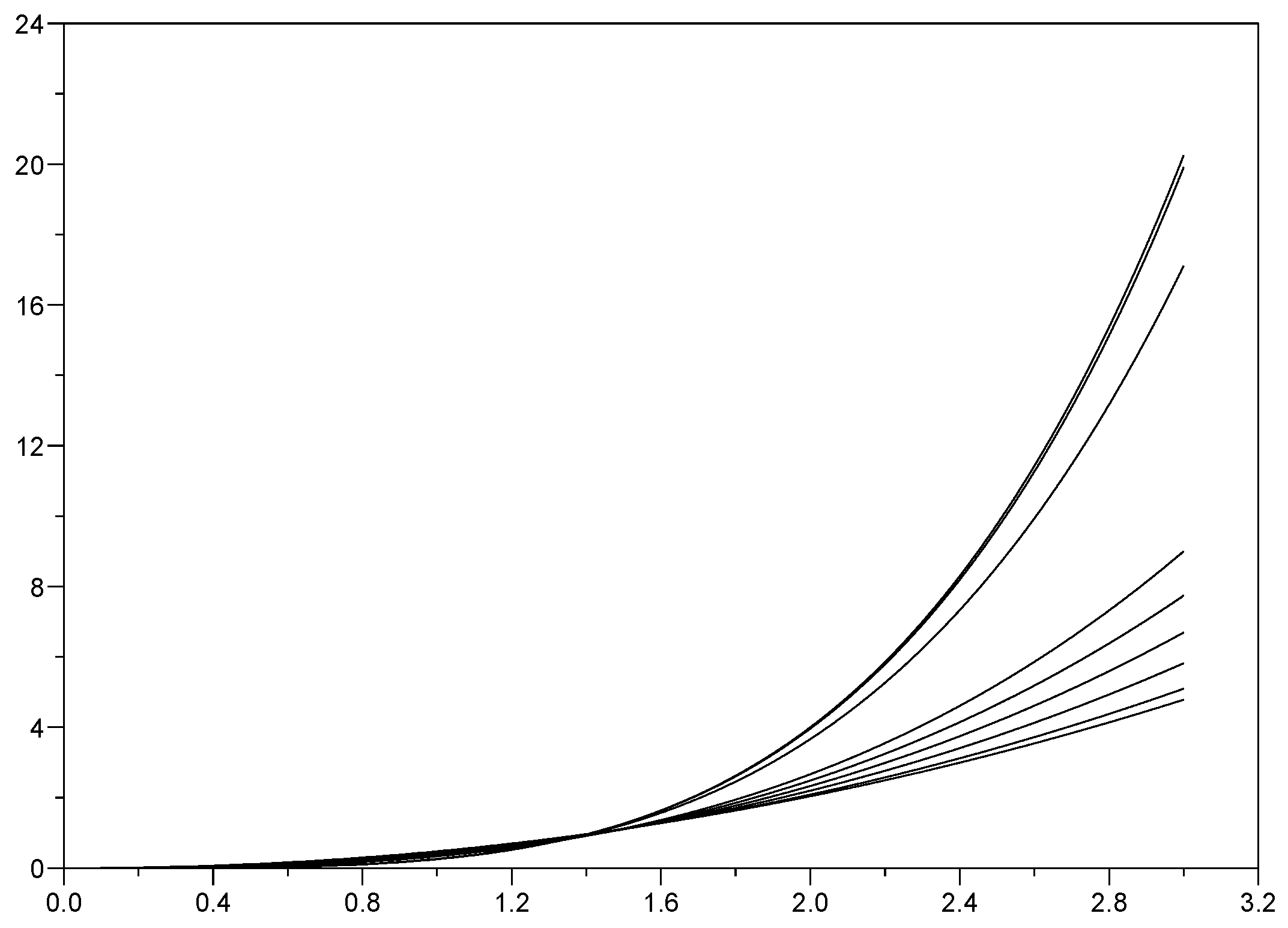
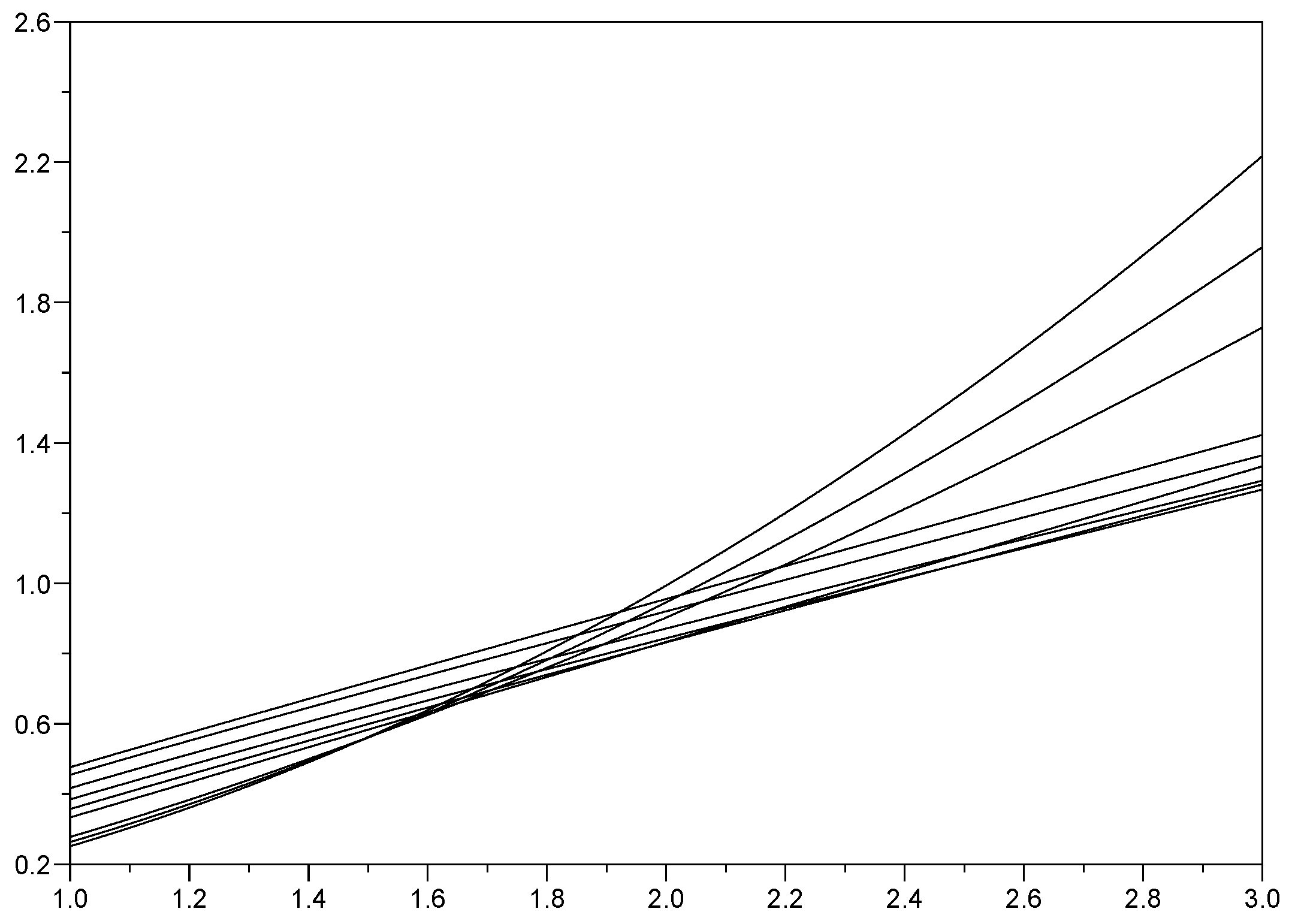
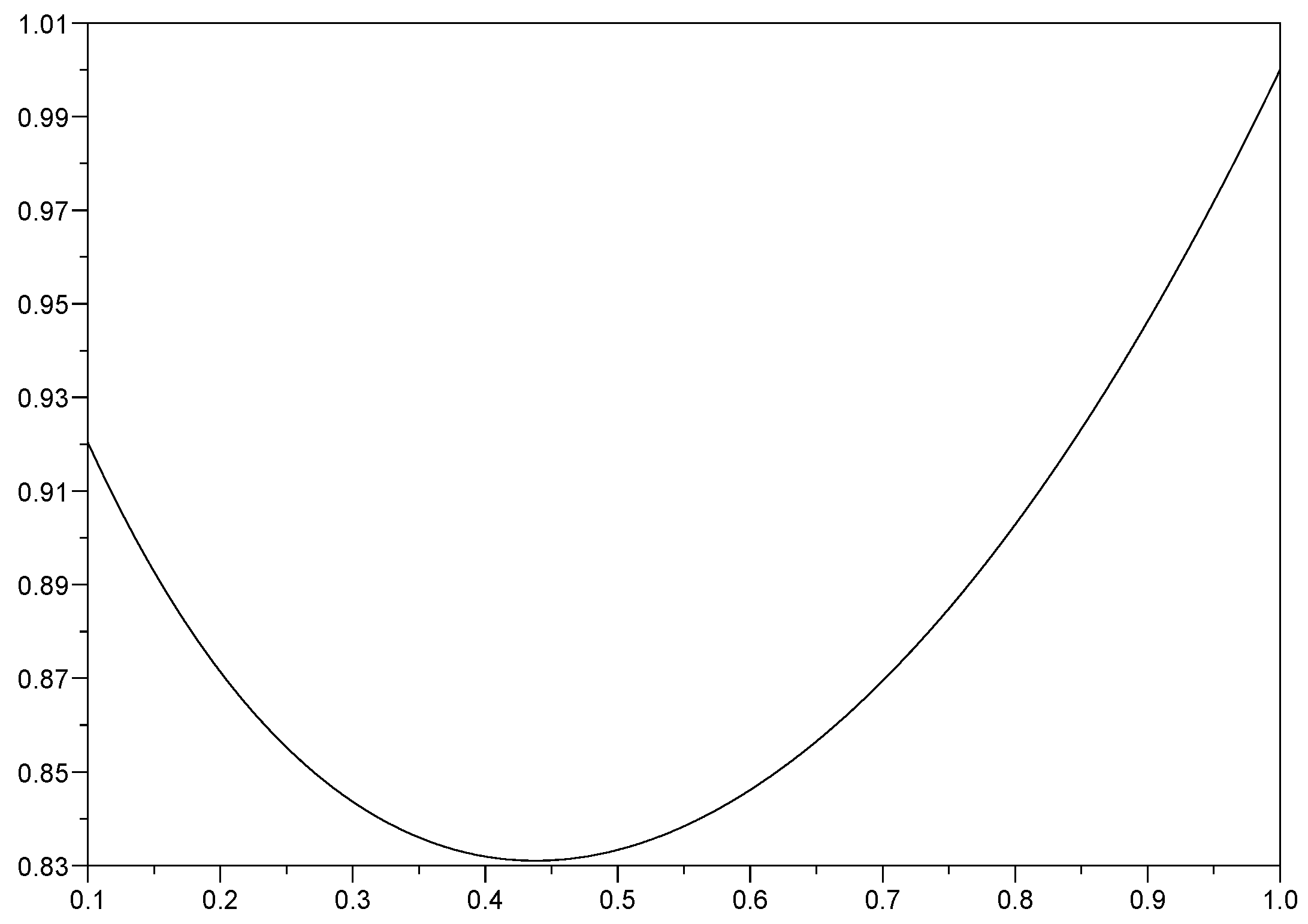
2. Integrated Fractional Gaussian Process
3. Comparisons with a Particular Fractional OU
4. Conclusions and Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mura, A.; Taqqu, M.S.; Mainardi, F. Non-Markovian diffusion equations and processes: Analysis and simulations. Phys. A Stat. Mech. Its Appl. 2008, 387, 5033–5064. [Google Scholar] [CrossRef]
- Sokolov, I.M. Solutions of a class of non-Markovian Fokker–Planck equations. Phys. Rev. 2002, E66, 041101. [Google Scholar] [CrossRef] [PubMed]
- Baldovin, F.; Bovina, D.; Camana, F.; Stella, A.L. Modeling the Non-Markovian, Non-stationary Scaling Dynamics of Financial Markets. In Econophysics of Order-Driven Markets; Abergel, F., Chakrabarti, B.K., Chakraborti, A., Mitra, M., Eds.; New Economic Windows Springer: Milano, Italy, 2011. [Google Scholar]
- Barndorff-Nielsen, O.E.; Shephard, N. Integrated OU Processes and Non-Gaussian OU-based Stochastic Volatility Models. Scand. J. Stat. 2003, 30, 277–295. [Google Scholar] [CrossRef]
- Buonocore, A.; Caputo, L.; Pirozzi, E.; Carfora, M.F. Gauss-diffusion processes for modeling the dynamics of a couple of interacting neurons. Math. Biosci. Eng. 2014, 11, 189–201. [Google Scholar] [PubMed]
- Mura, I.; Prandi, D.; Priami, C.; Romanel, A. Exploiting non-Markovian Bio-Processes. Electron. Notes Theor. Comput. Sci. 2009, 253, 83–98. [Google Scholar] [CrossRef]
- Buonocore, A.; Caputo, L.; Pirozzi, E.; Carfora, M.F. A leaky integrate-and-fire model with adaptation for the generation of a spike train. Math. Biosci. Eng. 2016, 13, 483–493. [Google Scholar] [PubMed]
- D’Onofrio, G.; Pirozzi, E. Successive spike times pblackicted by a stochastic neuronal model with a variable input signal. Math. Biosci. Eng. 2016, 13, 495–507. [Google Scholar] [CrossRef] [PubMed]
- Pirozzi, E. Coloblack noise and a stochastic fractional model for correlated inputs and adaptation in neuronal firing. Biol. Cybern. 2018, 1–2, 25–39. [Google Scholar] [CrossRef] [PubMed]
- Abundo, M. On the representation of an integrated Gauss–Markov process. Sci. Math. Jpn. Online 2013, 77, 719–723. [Google Scholar]
- Abundo, M.; Pirozzi, E. Integrated stationary Ornstein–Uhlenbeck Process, and double integral processes. Phys. A Stat. Mech. Its Appl. 2018, 494, 265–275. [Google Scholar] [CrossRef]
- Abundo, M. On the first-passage time of an integrated Gauss–Markov process. Sci. Math. Jpn. Online 2015, 28, 1–14. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; ISBN 978-981-4355-20-9. [Google Scholar] [CrossRef]
- Biagini, F.; Hu, Y.; Oksendal, B.; Zhang, T. Stochastic Calculus for Fractional Brownian Motion and Applications, Probability and Its Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Abundo, M.; Pirozzi, E. On the Fractional Riemann–Liouville Integral of Gauss–Markov processes and applications. arXiv 2019, arXiv:1905.08167. [Google Scholar]
- Mishura, Y. Stochastic Calculus for Fractional Brownian Motion and Related Processes; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1929. [Google Scholar]
- Abundo, M.; Ascione, G.; Carfora, M.F.; Pirozzi, E. A fractional PDE for first passage time of time-changed Brownian motion and its numerical solution. Appl. Numer. Math. 2019, in press. [Google Scholar] [CrossRef]
- Ascione, G.; Pirozzi, E. On a stochastic neuronal model integrating correlated inputs. Math. Biosci. Eng. 2019, 16, 5206–5225. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, A.N. Wienersche Spiralen und einige andere interessante Kurven im Hilbertschen Raum. Acad. Sci. URSS (NS) 1940, 26, 115–118. [Google Scholar]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motion, fractional noise and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Vardar, C. Results on the Supremum of Fractional Brownian Motion. arXiv 2012, arXiv:0910.5193v3. [Google Scholar]
- Ascione, G.; Mishura, Y.; Pirozzi, E. Fractional Ornstein–Uhlenbeck process with stochastic forcing, and its applications. 2019; submitted. [Google Scholar]
- Ascione, G.; Mishura, Y.; Pirozzi, E. Time-changed fractional Ornstein–Uhlenbeck process. arXiv 2019, arXiv:1907.04847. [Google Scholar]
- Kaarakka, T.; Salminen, P. On Fractional Ornstein–Uhlenbeck Processes. Commun. Stoch. Anal. 2011, 5, 121–133. [Google Scholar] [CrossRef]
- Cheridito, P.; Kowaguchi, H.; Maejima, M. Fractional Ornstein–Uhlenbeck processes. Electron. J. Probab. 2003, 8, 1–14. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abundo, M.; Pirozzi, E. On the Integral of the Fractional Brownian Motion and Some Pseudo-Fractional Gaussian Processes. Mathematics 2019, 7, 991. https://doi.org/10.3390/math7100991
Abundo M, Pirozzi E. On the Integral of the Fractional Brownian Motion and Some Pseudo-Fractional Gaussian Processes. Mathematics. 2019; 7(10):991. https://doi.org/10.3390/math7100991
Chicago/Turabian StyleAbundo, Mario, and Enrica Pirozzi. 2019. "On the Integral of the Fractional Brownian Motion and Some Pseudo-Fractional Gaussian Processes" Mathematics 7, no. 10: 991. https://doi.org/10.3390/math7100991
APA StyleAbundo, M., & Pirozzi, E. (2019). On the Integral of the Fractional Brownian Motion and Some Pseudo-Fractional Gaussian Processes. Mathematics, 7(10), 991. https://doi.org/10.3390/math7100991





