Fractional Order Unknown Inputs Fuzzy Observer for Takagi–Sugeno Systems with Unmeasurable Premise Variables
Abstract
1. Introduction
2. A Brief Introduction to Fractional Calculus
3. Fractional Order Takagi–Sugeno Model
4. Fractional Order Takagi–Sugeno Unknown Input Observer
4.1. First Approach
4.2. Second Approach
5. Unknown Inputs Estimation
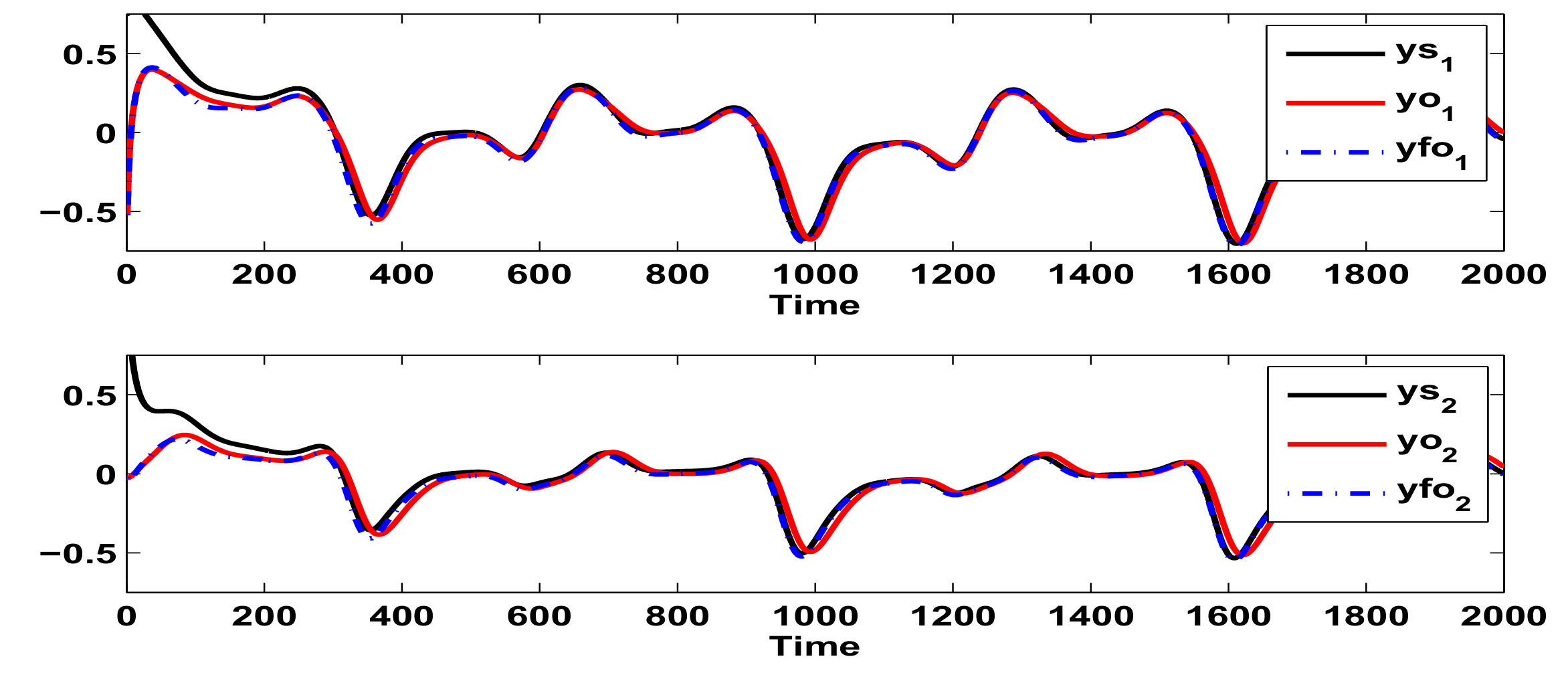
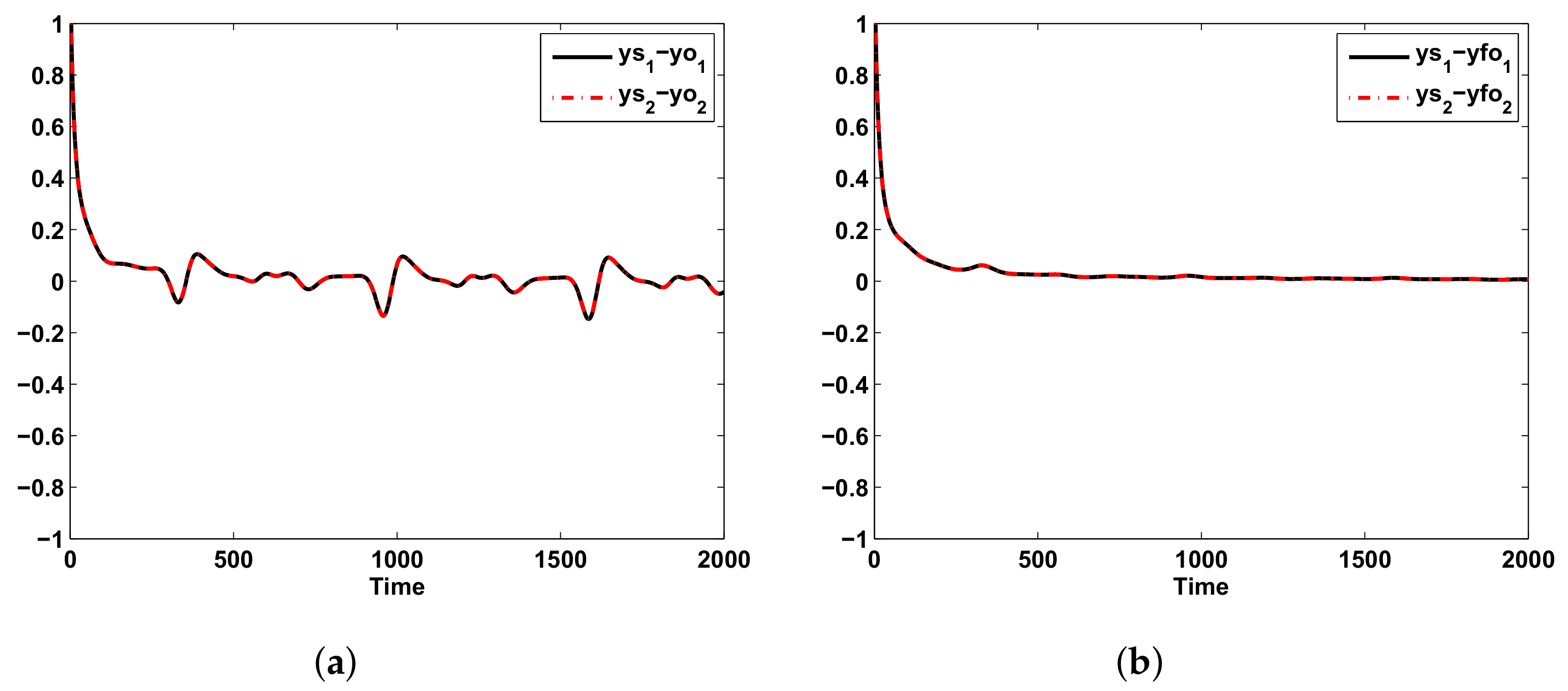
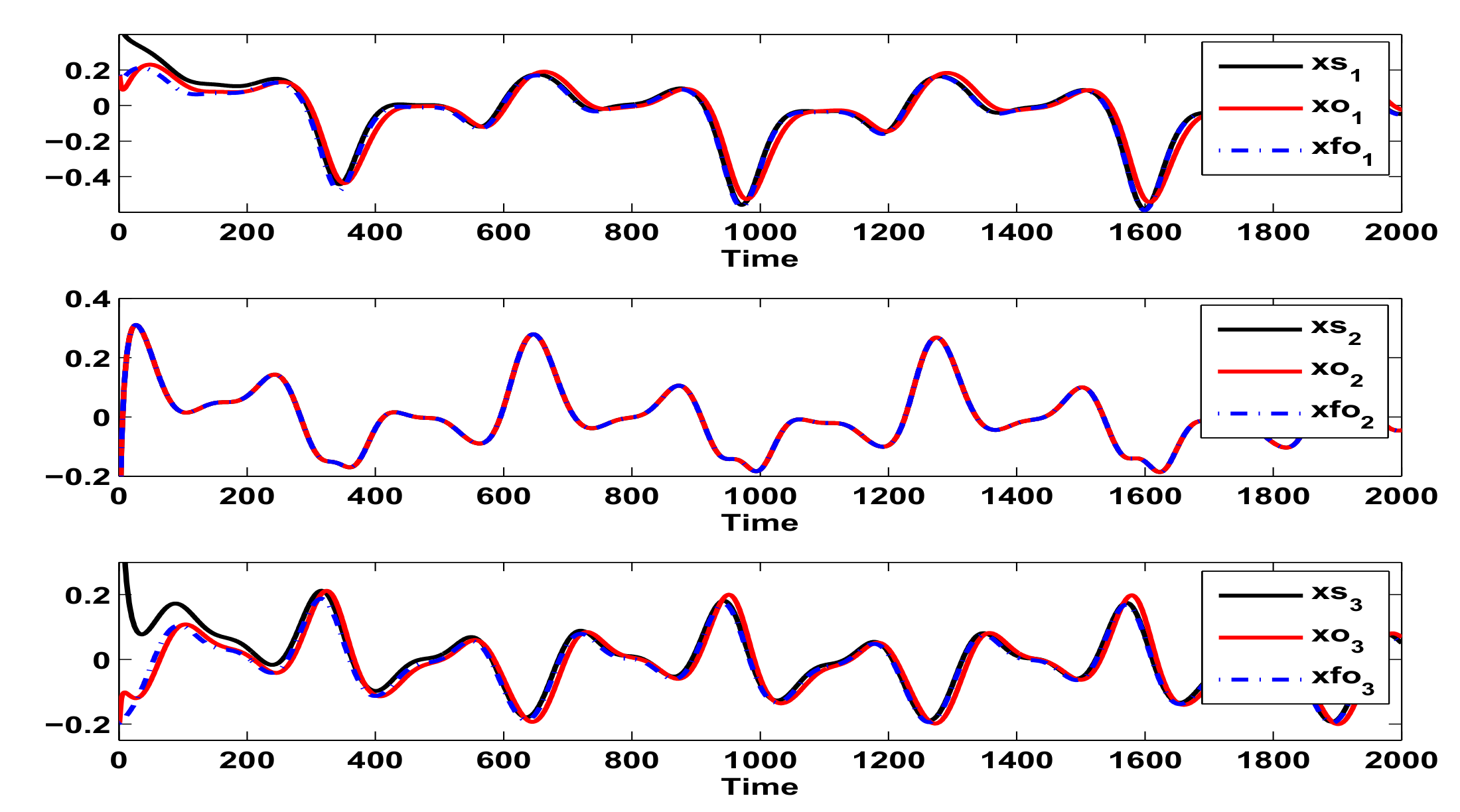
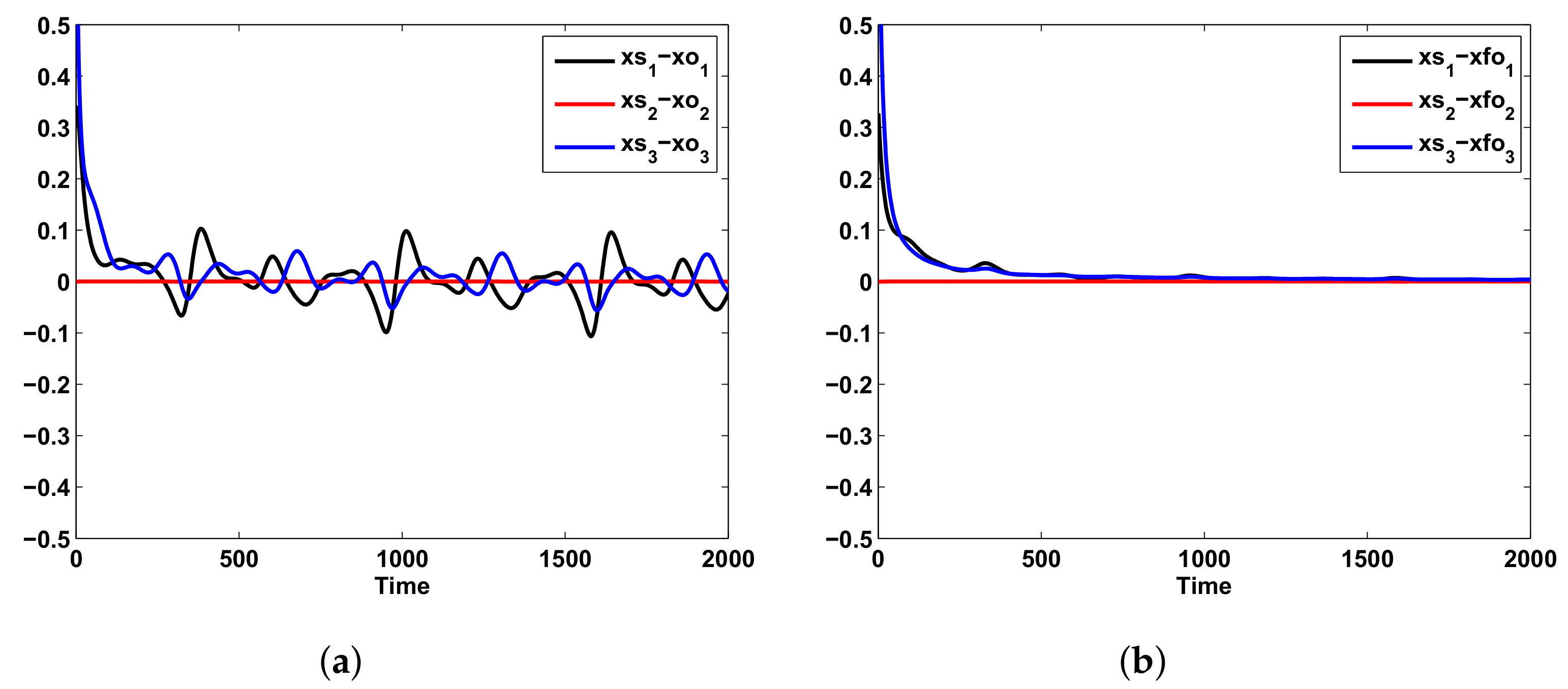
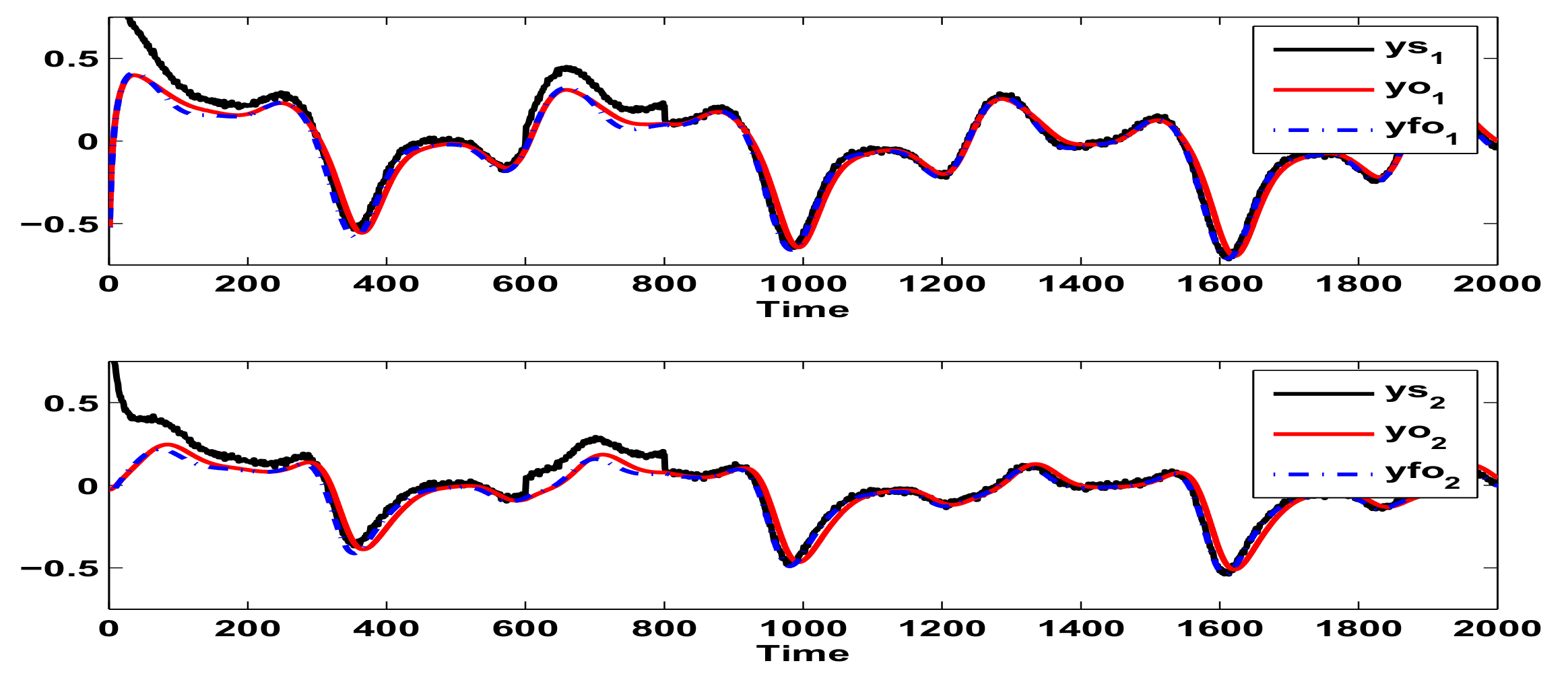
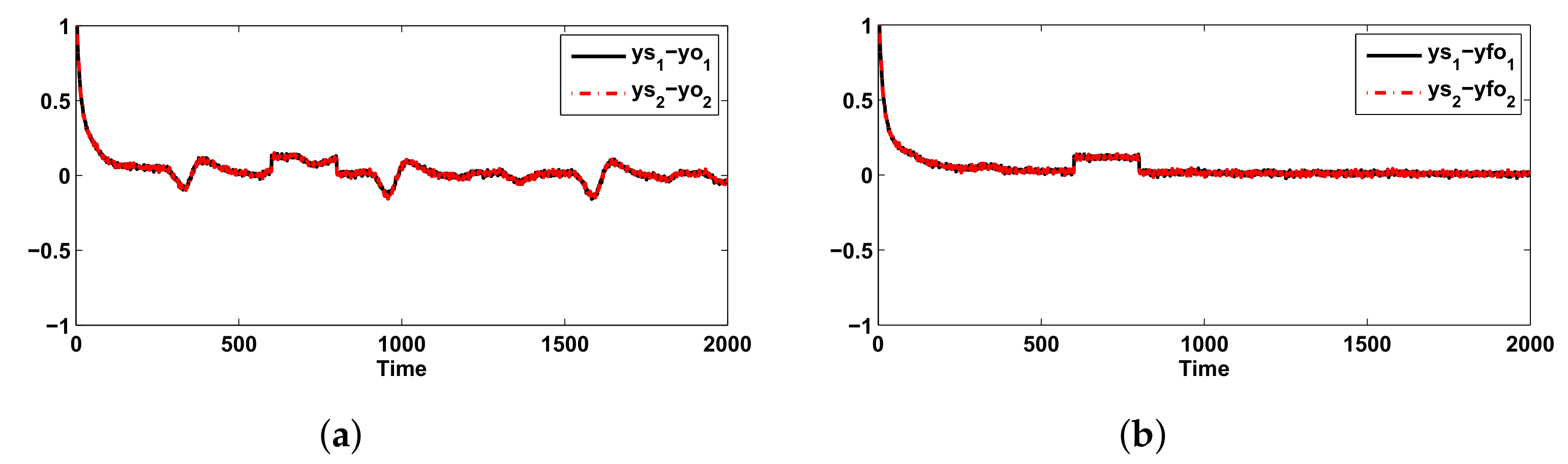
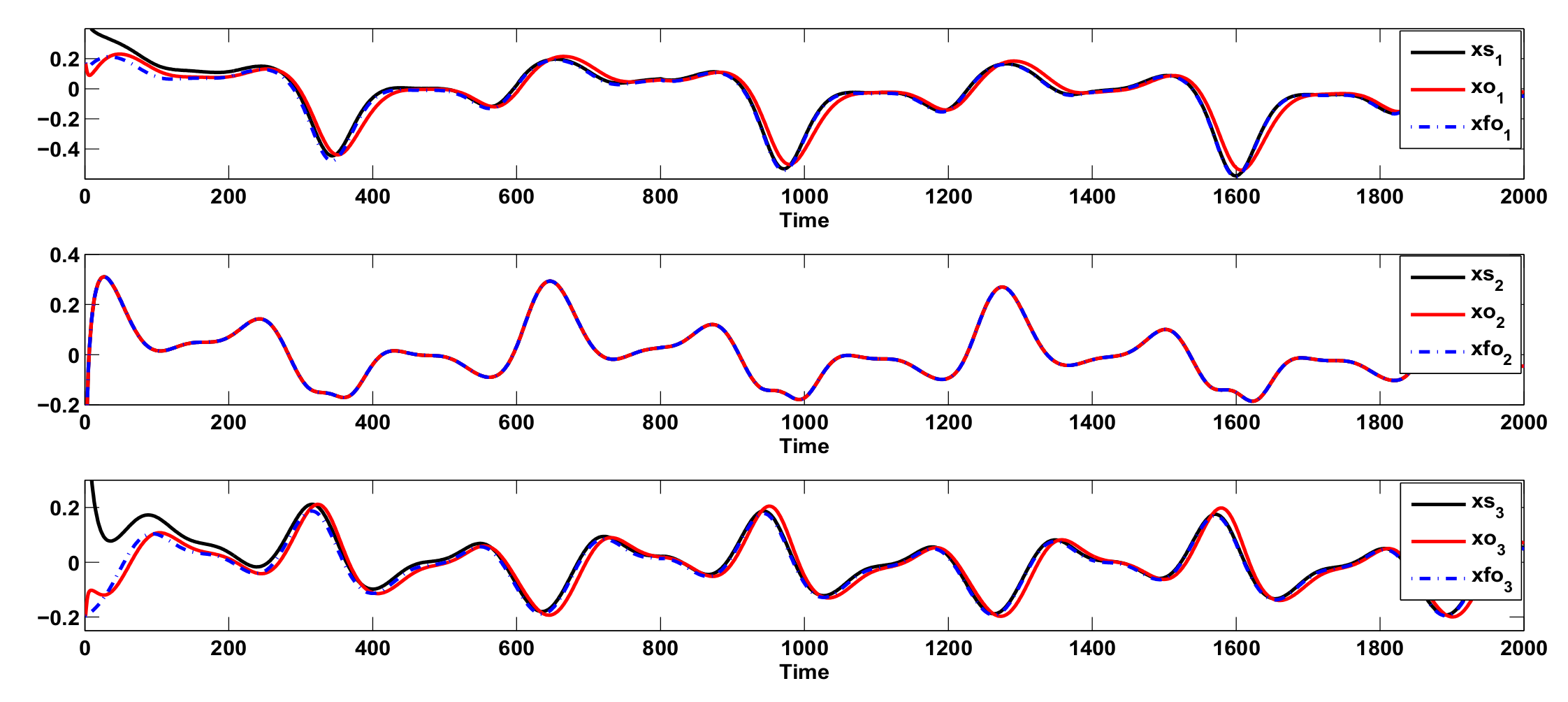
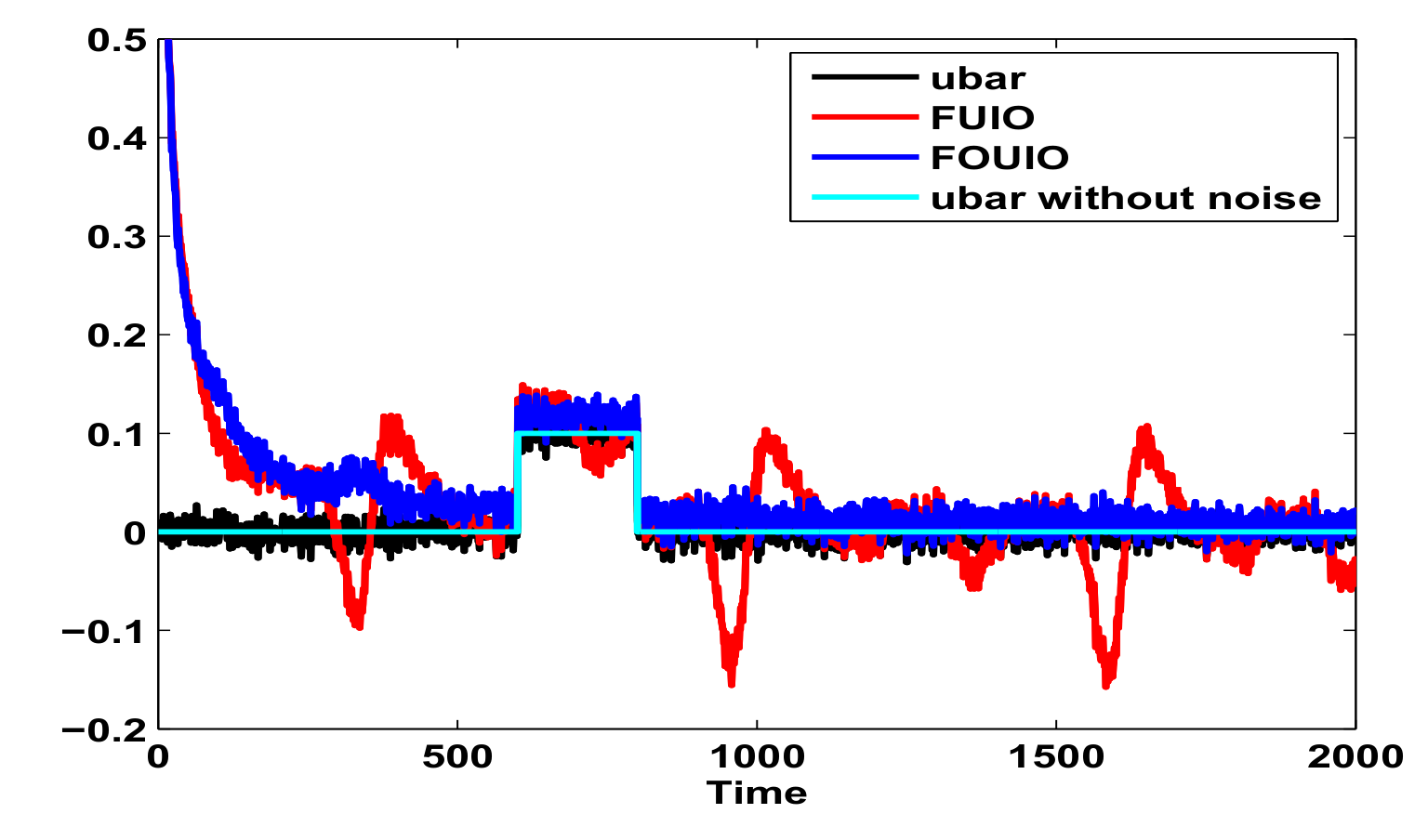
6. Example and Comparisons
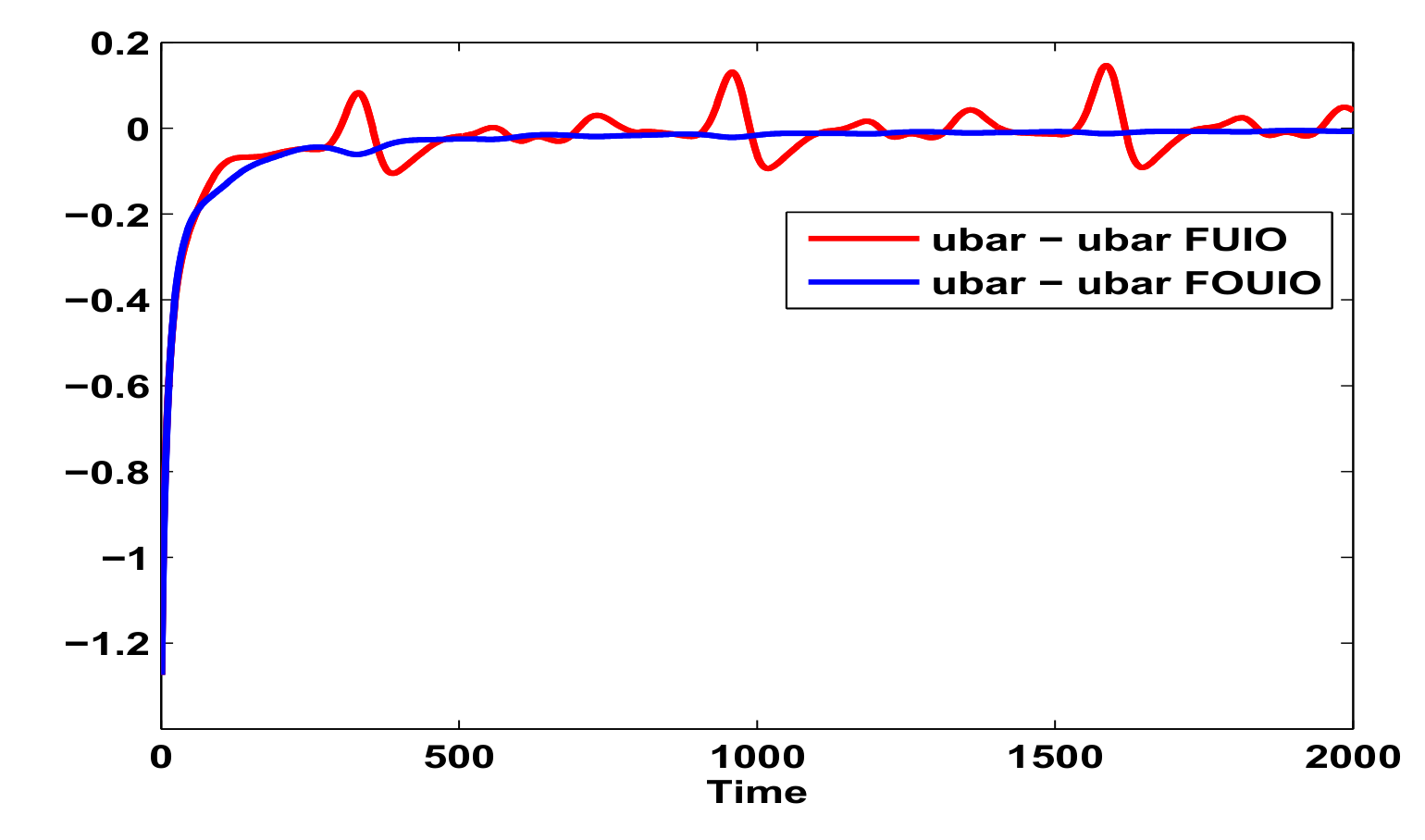
Example and Simulation Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FOTS | Fractional Order Takagi–Sugeno |
| FOS | Fractional Order Systems |
| FUIO | Fuzzy Unknown Input Observer |
| FOUIO | Fractional Order Unknown Input Observer |
| LMI | Linear Matrix Inequalities |
| UPV | Unmeasurable Premise Variables |
| MPV | Measurable Premise Variables |
References
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus, Theory and Applications of Differentiation and Integration of Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. The Fractional Calculus, an Introduction to the Fractional Calculus and Fractional Deferential Equations; John Wiley & Sons Inc.: New York, NY, USA, 1993. [Google Scholar]
- George, A.; Argyros, I.K. Intelligent Numerical Methods: Applications to Fractional Calculus; Springer International Publishing: Cham, Switzerland, 2016; Volume 624. [Google Scholar]
- Li, W.; Zhao, H.M. Rational function approximation for fractional order differential and integral operators. Acta Autom. Sin. 2011, 37, 999–1005. [Google Scholar]
- Xe, D.Y.; Zhao, C.N.; Chen, Y.Q. Robust control for fractional order four-wing hyperchaotic system using LMI. In Proceedings of the IEEE Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1043–1048. [Google Scholar]
- Li, C.L.; Su, K.L.; Zhang, J.; Wei, D.Q. Rational function approximation for fractional order differential and integral operators. Opt. Int. J. Light Electron Opt. 2013, 124, 5807–5810. [Google Scholar] [CrossRef]
- Yuan, J.; Shi, B.; Ji, W.Q. Adaptive sliding mode control of a novel class of fractional chaotic systems. Adv. Math. Phys. 2013, 2013, 6709. [Google Scholar] [CrossRef]
- Li, W.; Peng, C.; Wang, Y. Frequency domain subspace identification of commensurate fractional order input time delay systems. Int. J. Control. Autom. Syst. 2011, 9, 310–316. [Google Scholar]
- Vinagre, B.M.; Podlubny, I.; Dorcak, L.; Feliu, V. On fractional PID controllers: A frequency domain approach. In Proceedings of the IFAC Workshop on Digital Control: Past, Present and Future of PID Control, Terrasa, Spain, 5–7 April 2000; pp. 53–58. [Google Scholar]
- Aldair, A.A.; Wang, W.J. Design of fractional order controller based on evolutionary algorithm for a full vehicle nonlinear active suspension systems. Int. J. Control. Autom. 2010, 3, 33–46. [Google Scholar]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing. In Series in Computer Vision; World Scientific Publishing Co.: Singapore, 2016; Volume 4. [Google Scholar]
- Mozyrska, D.; Wyrwas, M. The Z-transform method and delta type fractional difference operators. Discret. Dyn. Nat. Soc. 2015, 2–3, 1–12. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus for System Identification and Controls; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ibrir, S. Robust state estimation with q-integral observers. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 3466–3471. [Google Scholar]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo-state feedback stabilization of commensurate fractional order systems. Automatica 2010, 46, 1730–1734. [Google Scholar] [CrossRef]
- Stanisławski, R.; Rydel, M.; Latawiec, K.J. Modeling of discrete-time fractional-order state space systems using the balanced truncation method. J. Frankl. Inst. 2017, 354, 3008–3020. [Google Scholar] [CrossRef]
- Doye, I.; Darouach, M.; Voos, H.; Zasadzinsk, M. Design of unknown input fractional-order observer for fractional-order systems. Int. J. Appl. Math. Comput. Sci. 2013, 23, 491–500. [Google Scholar] [CrossRef]
- Wei, Y.H.; Sun, Z.Y.; Hu, Y.S.; Wang, Y. On fractional order adaptive observer. Int. J. Autom. Comput. 2015, 12, 664–670. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C.; Merveillaut, M.; Feneteau, L. On Observability and Pseudo State Estimation of Fractional Order Systems. Eur. J. Control. 2012, 18, 260–271. [Google Scholar] [CrossRef]
- Safarinejadian, B.; Asad, M.; Sha Sadeghi, M. Simultaneous state estimation and parameter identification in linear fractional order systems using colored measurement noise. Int. J. Control. 2016, 89, 2277–2296. [Google Scholar] [CrossRef]
- Li, F.; Wu, R.; Liang, S. Observer-based state estimation for non-linear fractional systems. Int. J. Dyn. Syst. Differ. Equ. 2015, 5, 322–335. [Google Scholar] [CrossRef]
- Fuli, Z.; Hui, L.; Shouming, Z. State estimation based on fractional order sliding mode observer method for a class of uncertain fractional-order nonlinear systems. Signal Process. 2016, 127, 168–184. [Google Scholar]
- Kong, S.; Saif, M.; Liu, B. Observer design for a class of nonlinear fractional-order systems with unknown input. J. Frankl. Inst. 2017, 354, 5503–5518. [Google Scholar] [CrossRef]
- Djeghali, N.; Djennoune, S.; Bettayeb, M.; Ghanes, M.; Barbot, J.P. Observation and sliding mode observer for nonlinear fractional-order system with unknown input. ISA Trans. 2016, 63, 1–10. [Google Scholar] [CrossRef]
- Ding, B.; Sun, H.; Yang, P. Further studies on LMI based relaxed stabilization conditions for nonlinear systems in Takagi–Sugeno’s form. Automatica 2006, 42, 503–508. [Google Scholar] [CrossRef]
- Kruszewski, A.; Wang, R.; Guerra, T.M. Nonquadratic stabilization conditions for a class of uncertain nonlinear discrete time TS fuzzy models: A new approach. IEEE Trans. Autom. Control. 2008, 53, 606–611. [Google Scholar] [CrossRef]
- N’Doye, I.; Darouach, M.; Zasadzinski, M.; Radhy, N.E. Robust stabilization of uncertain descriptor fractional-order systems. Automatica 2013, 49, 1907–1913. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional-order interval systems with the fractional order α: The case 0 < α < 1. IEEE Trans. Autom. Control. 2010, 55, 152–158. [Google Scholar]
- Trigeassou, J.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process. 2011, 91, 437–445. [Google Scholar] [CrossRef]
- Yu, W.; Li, Y.; Wen, G.; Yu, X.; Cao, J. Observer design for tracking consensus in second-order multi-agent systems: Fractional order less than two. IEEE Trans. Autom. Control. 2017, 62, 894–900. [Google Scholar] [CrossRef]
- Park, J.H.; Park, T.S.; Kim, S.H. Approximation-Free Output-Feedback Non-Backstepping Controller for Uncertain SISO Nonautonomous Nonlinear Pure-Feedback Systems. Mathematics 2019, 7, 456. [Google Scholar] [CrossRef]
- Faieghi, M.; Mashhadi, S.K.M.; Baleanu, D. Sampled-data nonlinear observer design for chaos synchronization: A Lyapunov-based approach. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2444–2453. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F.; Xu, L.; Alsaedi, A.; Tasawar, H. A Hierarchical Approach for Joint Parameter and State Estimation of a Bilinear System with Autoregressive Noise. Mathematics 2019, 7, 356. [Google Scholar] [CrossRef]
- Ibrir, S.; Bettayeb, M. New sufficient conditions for observer-based control of fractional-order uncertain systems. Automatica 2015, 59, 216–223. [Google Scholar] [CrossRef]
- Song, C.; Fei, S.; Cao, J.; Huang, C. Robust Synchronization of Fractional-Order Uncertain Chaotic Systems Based on Output Feedback Sliding Mode Control. Mathematics 2019, 7, 599. [Google Scholar] [CrossRef]
- Liu, S.; Dong, X.; Zhang, Y. A New State of Charge Estimation Method for Lithium-Ion Battery Based on the Fractional Order Model. IEEE Access 2019, 7, 122949–122954. [Google Scholar] [CrossRef]
- Shi, S.L.; Li, J.X.; Fang, Y.M. Fractional-disturbance-observer-based Sliding Mode Control for Fractional Order System with Matched and Mismatched Disturbances. Int. J. Control. Autom. Syst. 2019, 17, 1184–1190. [Google Scholar] [CrossRef]
- Trinh, H.; Huong, D.C.; Nahavandi, S. Observer design for positive fractional-order interconnected time-delay systems. Trans. Inst. Meas. Control. Publ. 2018, 41, 378–391. [Google Scholar] [CrossRef]
- Dabiri, A.; Butcher, E. Optimal observer-based feedback control for linear fractional-order systems with periodic coefficients. J. Vib. Control. 2019, 25, 1379–1392. [Google Scholar] [CrossRef]
- Kong, S.; Saif, M.; Cui, G. Estimation and Fault Diagnosis of Lithium-Ion Batteries: A Fractional-Order System Approach. Math. Probl. Eng. 2018, 8705363, 1–12. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhu, D.; Sang, Y.; Jiang, L. Passivity-based fractional-order sliding-mode control design and implementation of grid-connected photovoltaic systems. J. Renew. Sustain. Energy 2018, 10, 43701. [Google Scholar] [CrossRef]
- Chadli, M.; Karimi, H.R. Robust observer design for unknown inputs Takagi–Sugeno models. IEEE Trans. Fuzzy Syst. 2013, 21, 158–164. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Wang, H.; Yan, J. Adaptive fault estimation for T-S fuzzy systems with unmeasurable premise variables. Adv. Differ. Equ. 2018, 105. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Krokavec, D.; Filasova, A. On observer design methods for a class of Takagi Sugeno fuzzy systems. In Proceedings of the Third International Conference on Advanced Information Technologies & Applications, Dubai, UAE, 7–8 November 2014; pp. 279–290. [Google Scholar]
- Djeddi, A.; Harkat, M.F.; Soufi, Y. A New Approach for State Estimation of Uncertain Multiple model with Unknown Inputs. Application to Sensor Fault Diagnosis. Mediterr. J. Meas. Control. 2016, 12, 537–545. [Google Scholar]
- Chadli, M.; Guerra, T.M. LMI solution for robust static output feedback control of Takagi–Sugeno fuzzy models. IEEE Trans. Fuzzy Syst. 2012, 20, 1060–1065. [Google Scholar] [CrossRef]
- Oukacine, S.; Djamah, T.; Djennoune, S.; Mansouri, R.; Bettayeb, M. Multi-model identification of a fractional nonlinear system. IFAC Proc. 2013, 46, 48–53. [Google Scholar] [CrossRef]
- Junmin, L.; Yuting, L. Robust Stability and Stabilization of Fractional Order Systems Based on Uncertain Takagi–Sugeno Fuzzy Model With the Fractional Order 1 ≤ ν < 2. ASME J. Comput. Nonlinear Dyn. 2013, 8, 41005. [Google Scholar]
- Gao, Z.; Liao, X. Observer-based fuzzy control for nonlinear fractional-order systems via fuzzy T-S models: The 1 < α < 2 case. In Proceedings of the 19th World Congress, The International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Ichalal, D.; Marx, B.; Mammar, S.; Maquin, D.; Ragot, J. How to cope with unmeasurable premise variables in Takagi–Sugeno observer design: Dynamic extension approach. Eng. Appl. Artif. Intell. 2018, 67, 430–435. [Google Scholar] [CrossRef]
- Shantanu, D. Functional Fractional Calculus, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Petras, I. Fractional-Order Nonlinear Systems Modeling, Analysis and Simulation; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Akhenak, A.; Chadli, M.; Ragot, J.; Maquin, D. Estimation of state and unknown inputs of a nonlinear system represented by a multiple model. IFAC Proc. Vol. 2004, 37, 385–390. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djeddi, A.; Dib, D.; Azar, A.T.; Abdelmalek, S. Fractional Order Unknown Inputs Fuzzy Observer for Takagi–Sugeno Systems with Unmeasurable Premise Variables. Mathematics 2019, 7, 984. https://doi.org/10.3390/math7100984
Djeddi A, Dib D, Azar AT, Abdelmalek S. Fractional Order Unknown Inputs Fuzzy Observer for Takagi–Sugeno Systems with Unmeasurable Premise Variables. Mathematics. 2019; 7(10):984. https://doi.org/10.3390/math7100984
Chicago/Turabian StyleDjeddi, Abdelghani, Djalel Dib, Ahmad Taher Azar, and Salem Abdelmalek. 2019. "Fractional Order Unknown Inputs Fuzzy Observer for Takagi–Sugeno Systems with Unmeasurable Premise Variables" Mathematics 7, no. 10: 984. https://doi.org/10.3390/math7100984
APA StyleDjeddi, A., Dib, D., Azar, A. T., & Abdelmalek, S. (2019). Fractional Order Unknown Inputs Fuzzy Observer for Takagi–Sugeno Systems with Unmeasurable Premise Variables. Mathematics, 7(10), 984. https://doi.org/10.3390/math7100984




