Optimal Control of a PDE Model of an Invasive Species in a River
Abstract
1. Introduction
2. Optimal Control Problem Formulation
| in | ||
| on | ||
| on | ||
| on | . |
3. Numerical Results
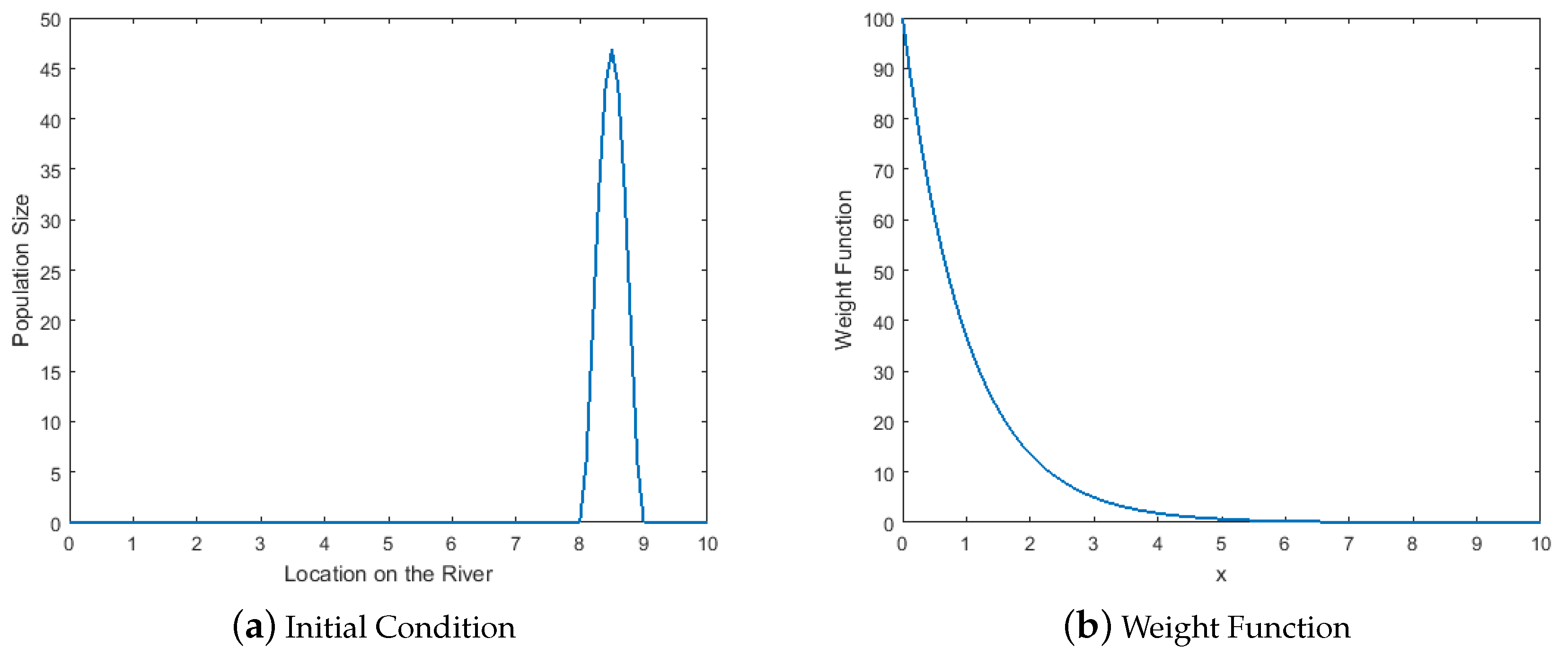
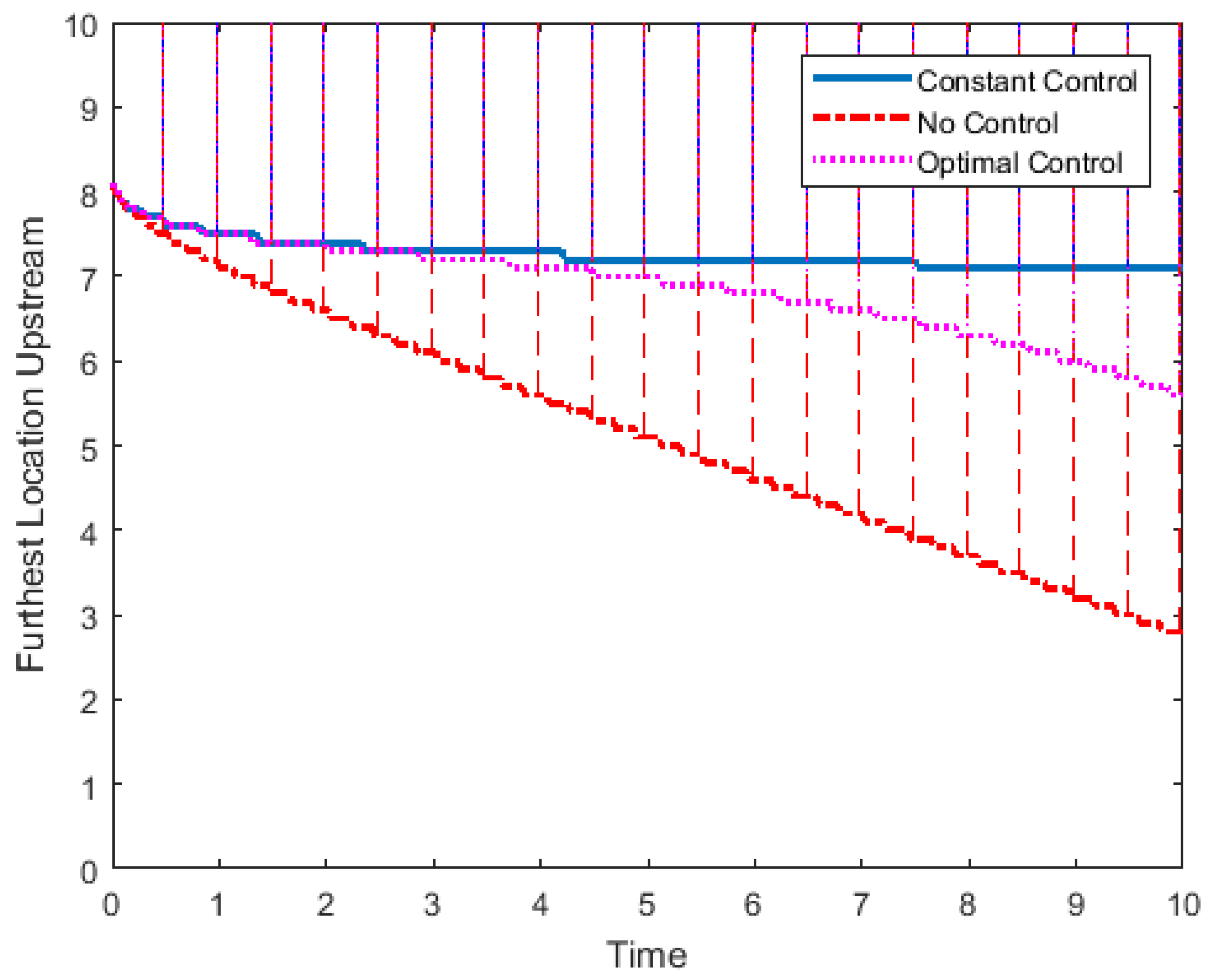
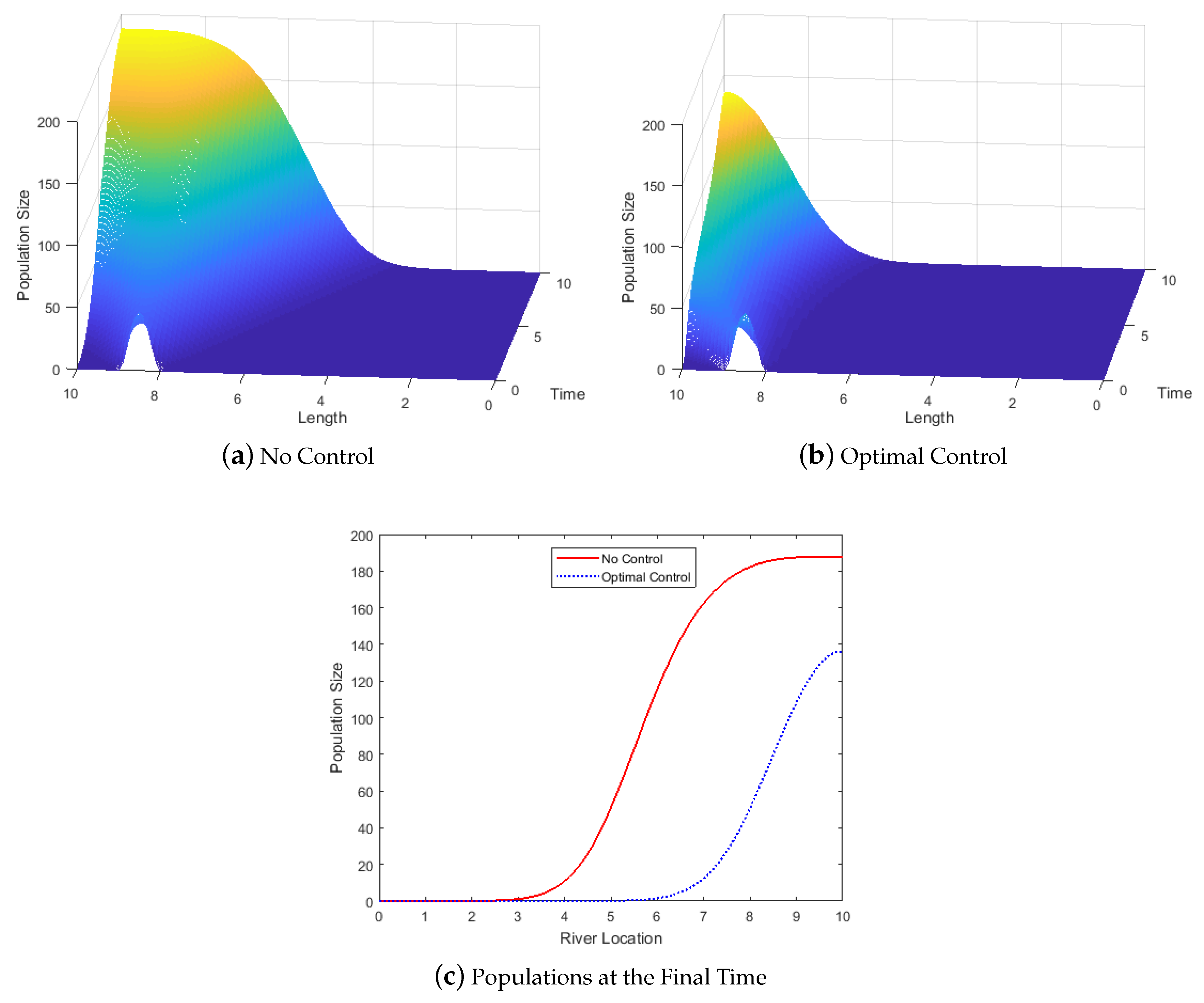
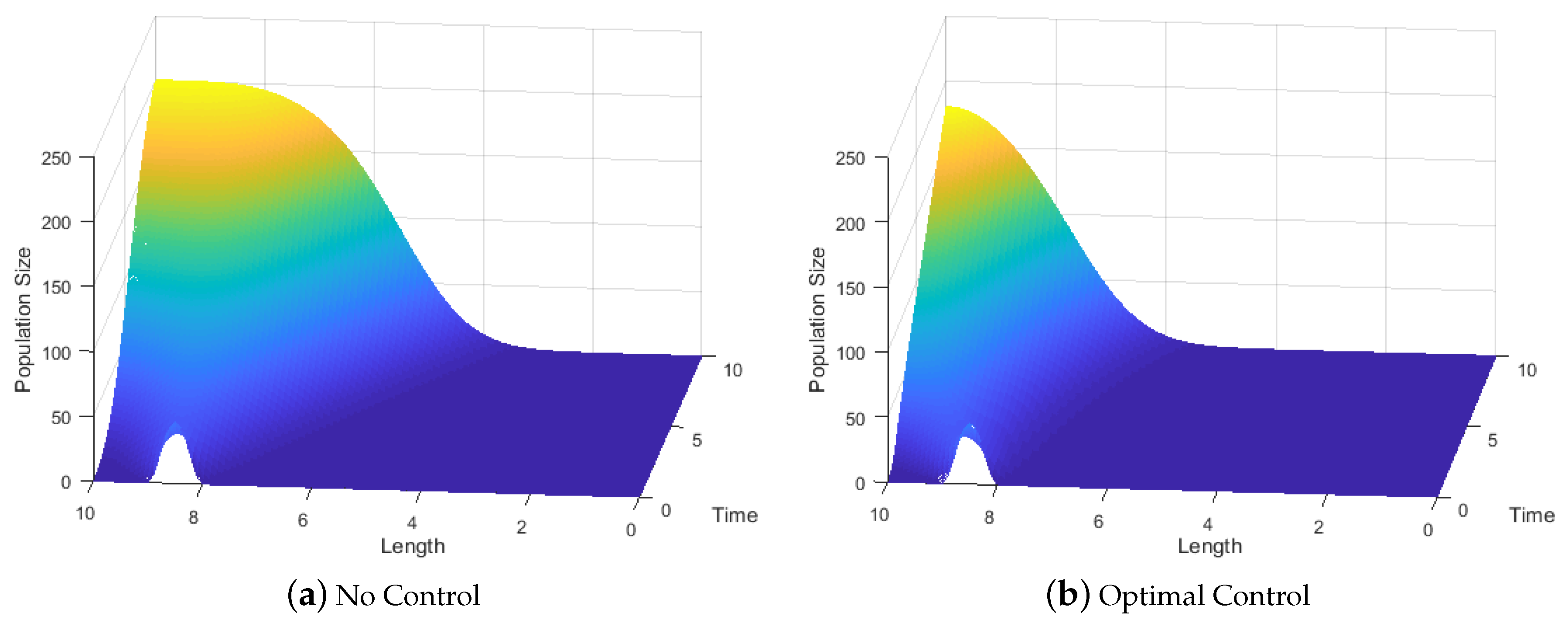
3.1. Cross-Sectional Area Is Constant
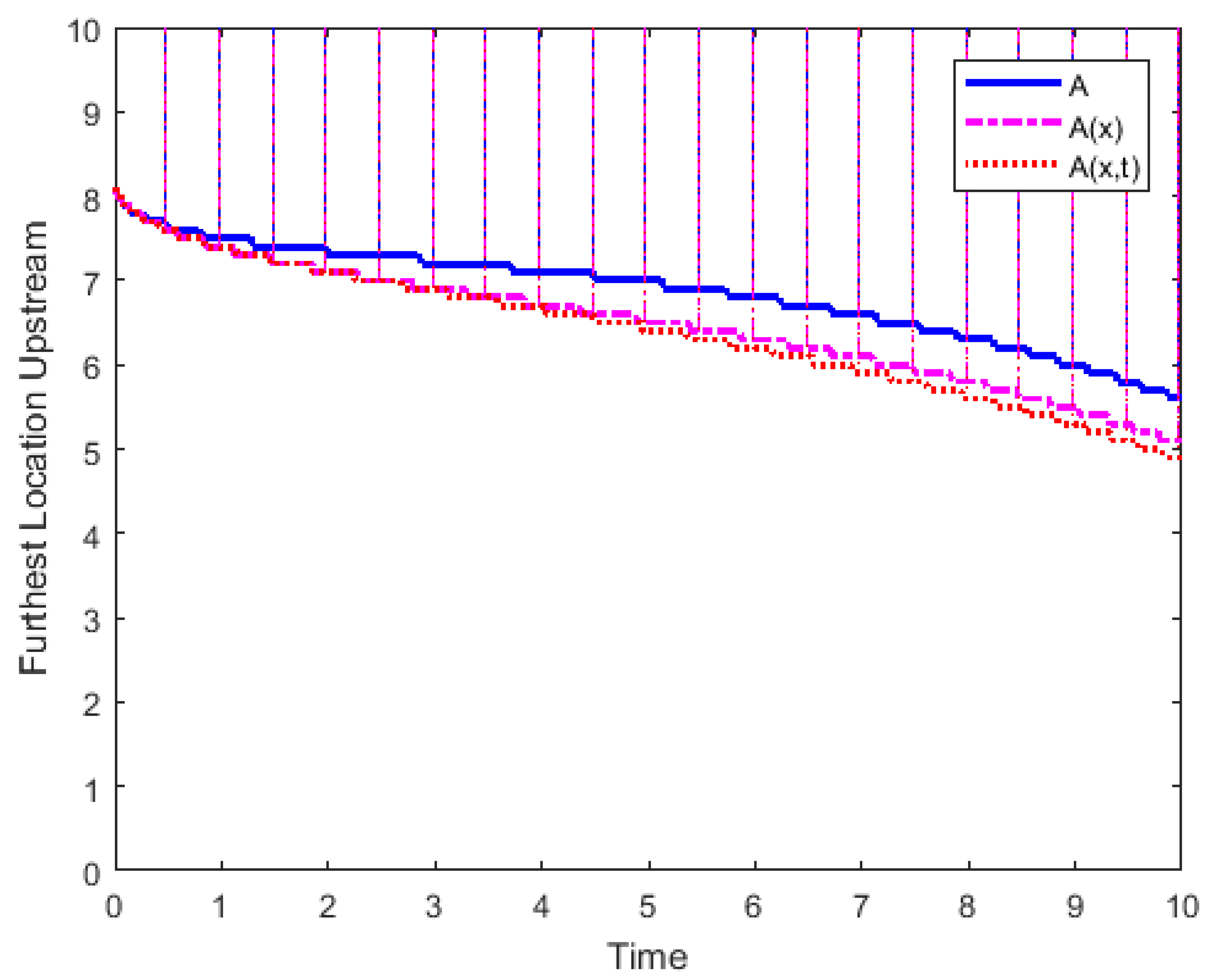
3.2. Cross-Sectional Area Is Not Constant
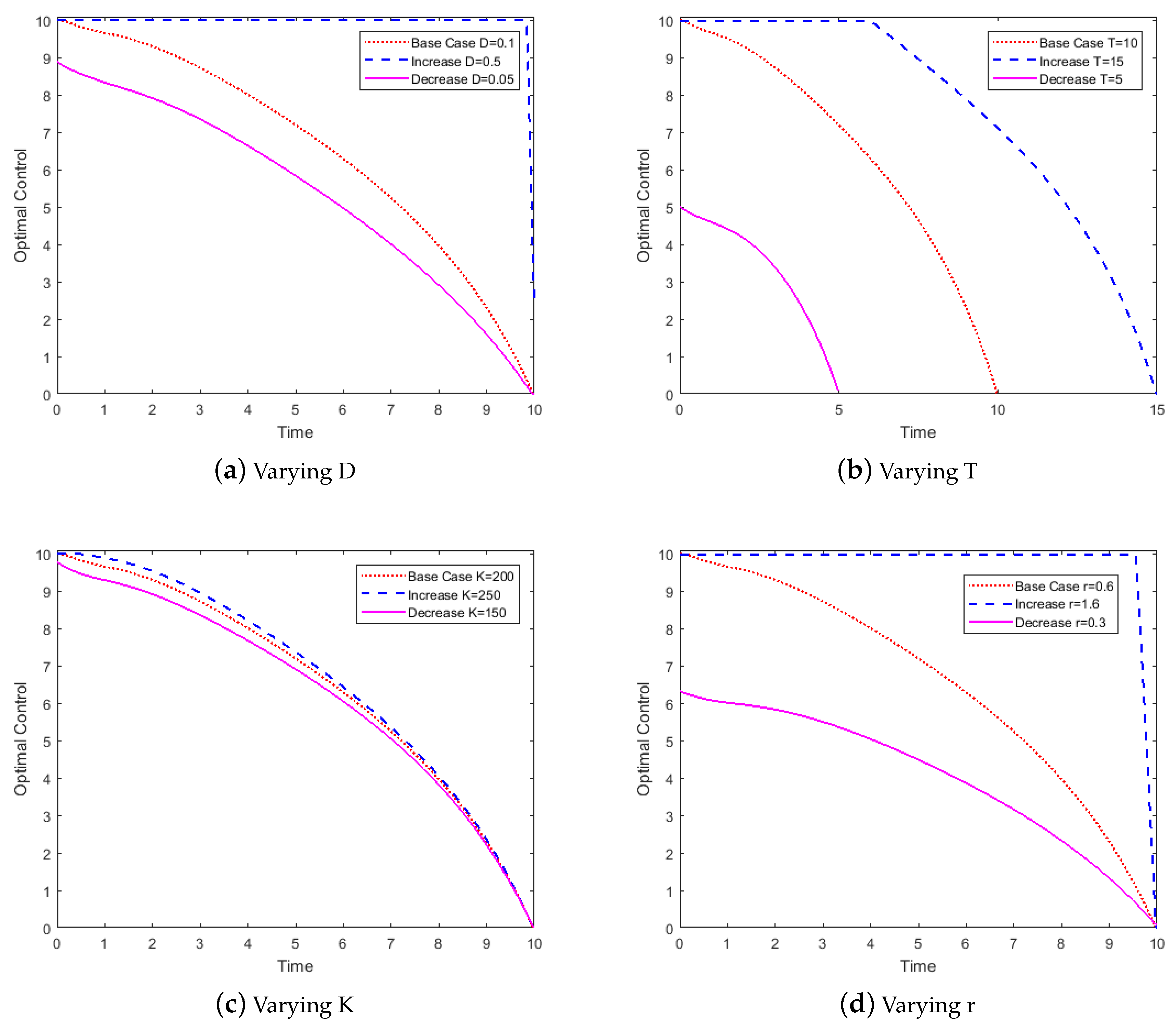
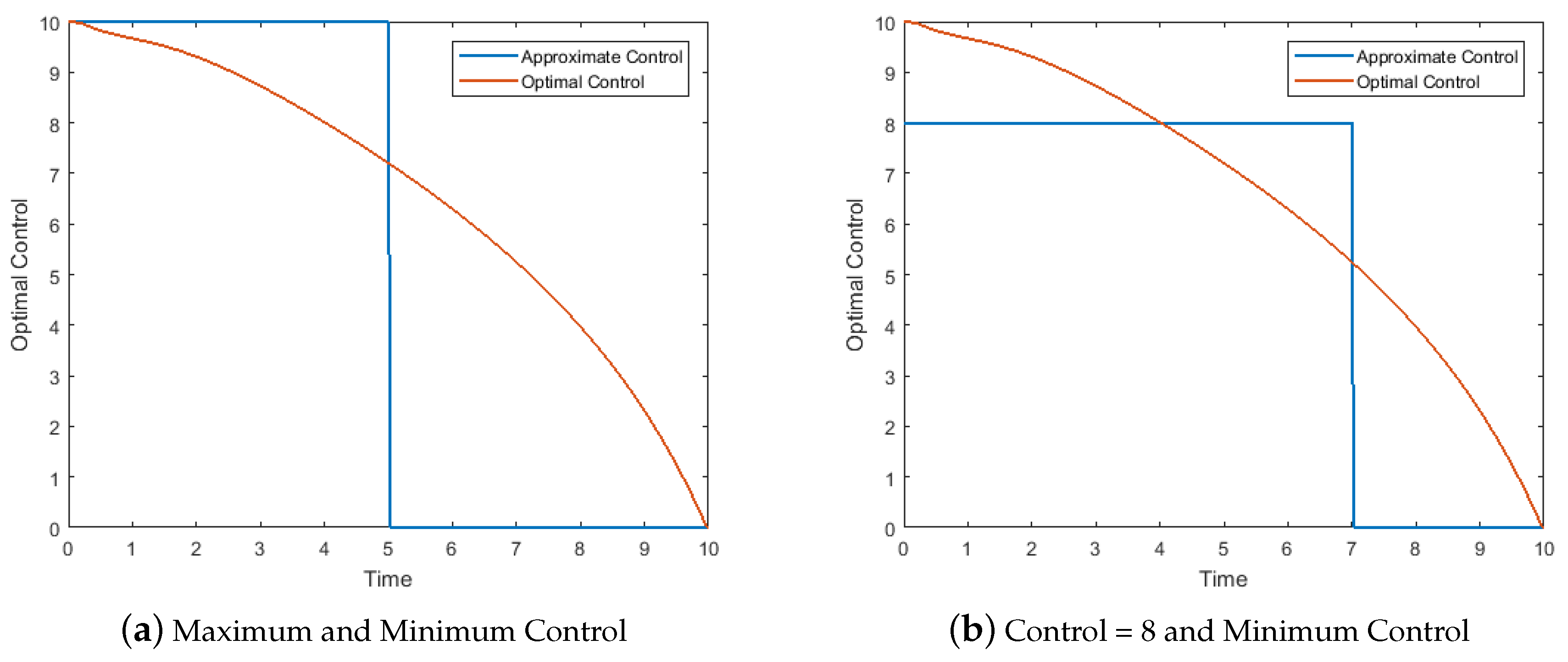
3.3. Approximate Controls
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kolar, C.S.; Chapman, D.C.; Courtenay, W.R.; Housel, C.M.; Williams, J.D.; Jennings, D.P. Bigheaded Carps: A Biological Synopsis and Environmental Risk Assessment; American Fisheries Society: Bethesda, MD, USA, 2007. [Google Scholar]
- Simberloff, D. Invasive Species: What Everyone Needs to Know; Oxford University Press: New York, NY, USA, 2013. [Google Scholar]
- Lockwood, J.L.; Hoopes, M.F.; Marchetti, M.P. Invasion Ecology; Blackwell Publishing: Malden, MA, USA, 2007. [Google Scholar]
- Jacobsen, J.; Jin, Y.; Lewis, M.A. Integrodifference models for persistence in temporally varying river environments. J. Math. Biol. 2015, 70, 549–590. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Lewis, M.A. Seasonal influences on population spread and persistence in streams: critical domain size. SIAM J. Appl. Math. 2011, 71, 1241–1262. [Google Scholar] [CrossRef]
- Jin, Y.; Lewis, M.A. Seasonal influences on population spread and persistence in streams: Spreading speeds. J. Math. Biol. 2012, 65, 403–439. [Google Scholar] [CrossRef]
- Gagnon, K.; Peacock, S.J.; Jin, Y.; Lewis, M.A. Modelling the spread of the invasive alga Codium fragile driven by long-distance dispersal of buoyant propagules. Ecol. Model. 2015, 316, 111–121. [Google Scholar] [CrossRef]
- Jin, Y.; Hilker, F.M.; Steffler, P.M.; Lewis, M.A. Seasonal Invasion Dynamics in a Spatially Heterogeneous River with Fluctuating Flows. Bull. Math. Biol. 2014, 76, 1522–1565. [Google Scholar] [CrossRef] [PubMed]
- Clifford, N.J.; Harmar, O.P.; Harvey, G.; Petts, G.E. Physical habitat, eco-hydraulics and river design: A review and re-evaluation of some popular concepts and methods. Aquat. Conserv. Mar. Freshw. Ecosyst. 2006, 16, 389–408. [Google Scholar] [CrossRef]
- Huang, Q.; Jin, Y.; Lewis, M.A. R0 analysis of a benthic-drift model for a stream population. SIAM J. Appl. Dyn. Syst. 2016, 15, 287–321. [Google Scholar] [CrossRef]
- Jin, Y.; Lutscher, F.; Pei, Y. Meandering rivers: How important is lateral variability for species persistence? Bull. Math. Biol. 2017, 79, 2954–2985. [Google Scholar] [CrossRef] [PubMed]
- Poff, N.L.; Zimmerman, J.K. Ecological responses to altered flow regimes: A literature review to inform the science and management of environmental flows. Freshw. Biol. 2010, 55, 194–205. [Google Scholar] [CrossRef]
- De Silva, K.R.; Phan, T.V.; Lenhart, S. Advection control in parabolic PDE systems for competitive populations. Discret. Contin. Dyn. Syst. Ser. B 2017, 22, 1049–1072. [Google Scholar] [CrossRef]
- Kelly, M.; Xing, Y.; Lenhart, S. Optimal fish harvesting for a population modeled by a nonlinear parabolic partial differential equation. Nat. Resour. Model. J. 2016, 29, 36–70. [Google Scholar] [CrossRef]
- Simon, J. Compact sets in the Lp(0,t:b). Ann. Mat. Pura Appl. 1987, 146, 65–96. [Google Scholar] [CrossRef]
- Lions, J.L. Equations Différentielles Opérationnelles et Problèmes aux Limites; Springer: Berlin, Germany, 1961. [Google Scholar]
- Friedman, A. Foundations of Modern Analysis; Dover Publications: New York, NY, USA, 1970. [Google Scholar]
- Evans, L. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Lenhart, S. Optimal Control of a Convective Diffusive Fluid Problem. Math. Models Methods Appl. Sci. 1995, 5, 225–237. [Google Scholar] [CrossRef]
- Ladyzenskaja, O.A.; Solonnikov, V.A.; Ural’ceva, N.N. Linear and Quasi-Linear Equations of Parabolic Type; American Mathematical Society: Providence, RI, USA, 1968. [Google Scholar]
- Li, X.; Yong, J. Optimal Control for Infinite Dimensional Systems; Birkhauser: Boston, MA, USA, 1995. [Google Scholar]
- Hackbush, W. A numerical method for solving parabolic equations with opposite orientations. Computing 1978, 20, 229–240. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Iserles, A. A First, Course in the Numerical Analysis of Differential Equations; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]

| Base Case | |||||
|---|---|---|---|---|---|
| No Control | 239.52 | 111.96 | 5485.3 | 17.13 | 2373 |
| Constant Control | 56.63 | 53.72 | 316.89 | 28.39 | 84.87 |
| Optimal Control | 40.12 | 29.40 | 316.56 | 12.31 | 68.17 |
| Base Case | |||||
|---|---|---|---|---|---|
| No Control | 239.52 | 204.28 | 269.14 | 55.18 | 3837.3 |
| Constant Control | 56.63 | 56.16 | 56.97 | 52.44 | 176.67 |
| Optimal Control | 40.12 | 37.96 | 41.13 | 20.29 | 176.55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pettit, R.; Lenhart, S. Optimal Control of a PDE Model of an Invasive Species in a River. Mathematics 2019, 7, 975. https://doi.org/10.3390/math7100975
Pettit R, Lenhart S. Optimal Control of a PDE Model of an Invasive Species in a River. Mathematics. 2019; 7(10):975. https://doi.org/10.3390/math7100975
Chicago/Turabian StylePettit, Rebecca, and Suzanne Lenhart. 2019. "Optimal Control of a PDE Model of an Invasive Species in a River" Mathematics 7, no. 10: 975. https://doi.org/10.3390/math7100975
APA StylePettit, R., & Lenhart, S. (2019). Optimal Control of a PDE Model of an Invasive Species in a River. Mathematics, 7(10), 975. https://doi.org/10.3390/math7100975





