Developing an ANFIS-PSO Model to Predict Mercury Emissions in Combustion Flue Gases
Abstract
1. Introduction
2. Literature Review
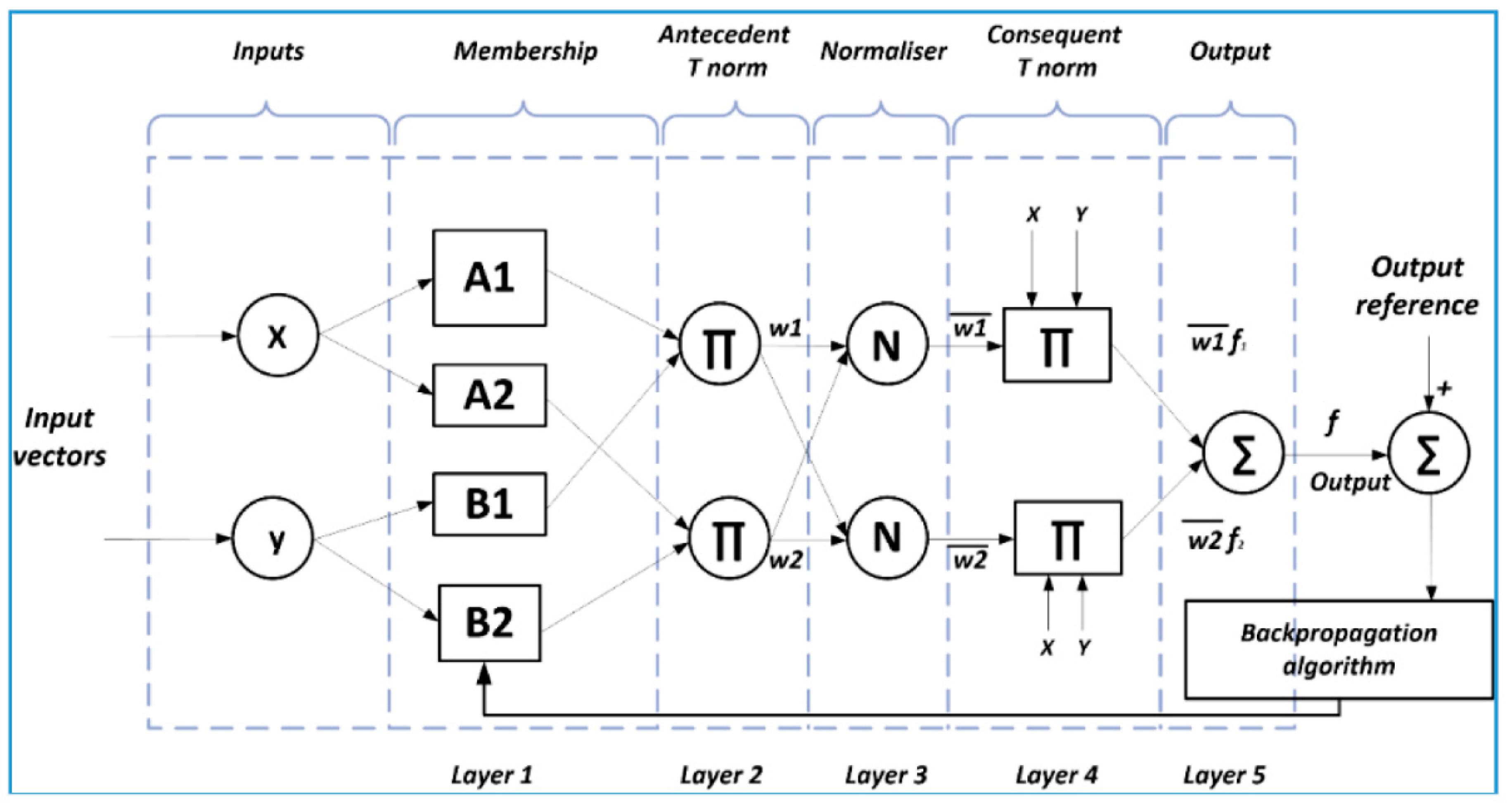
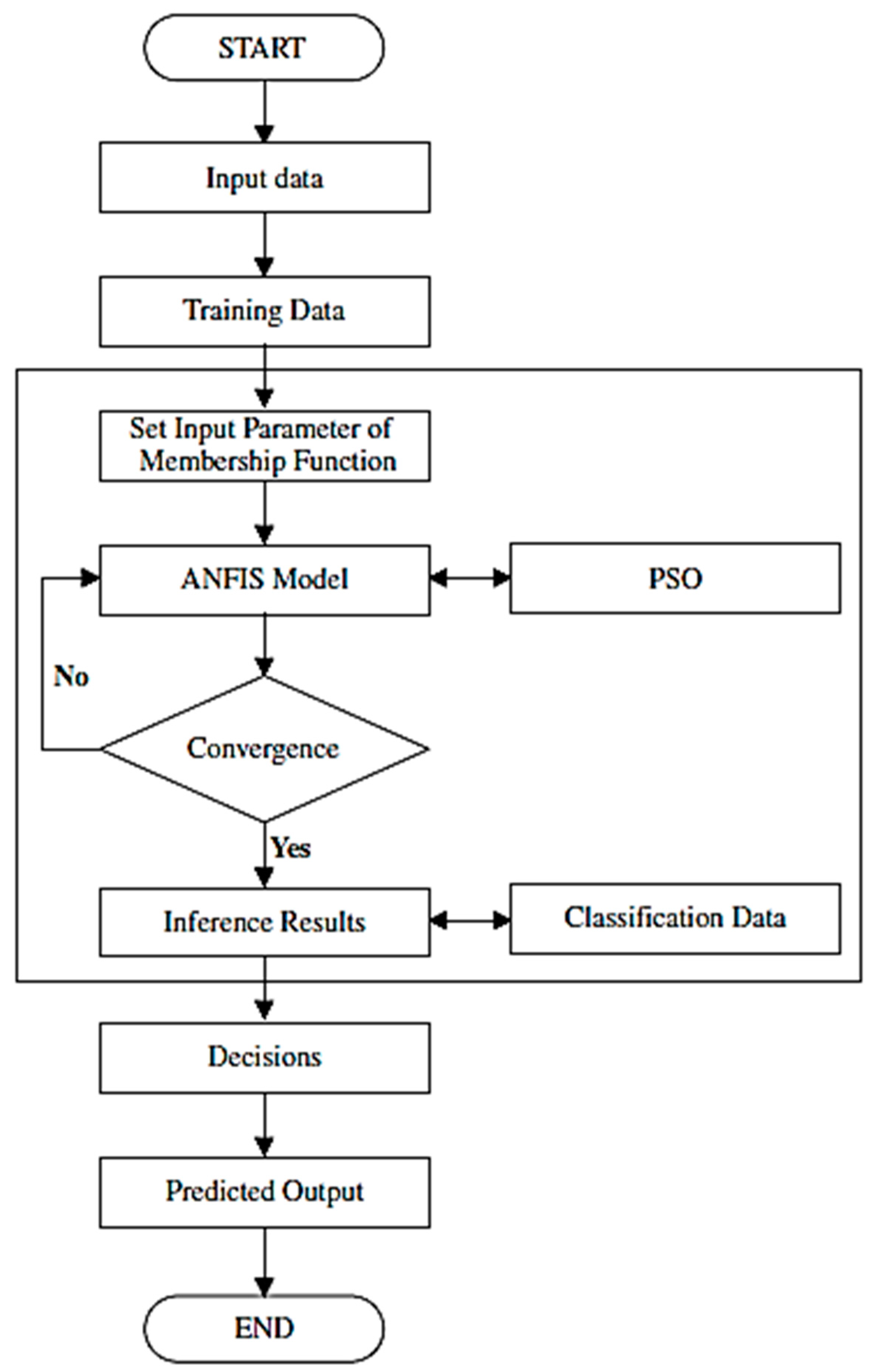
3. Model Development
- A dataset was partitioned into different clusters via kernel-based clustering approaches;
- The cluster centers obtained from clustering were applied to create the fuzzy rule base of the ANFIS;
- The resulting ANFIS model was trained using the PSO method.
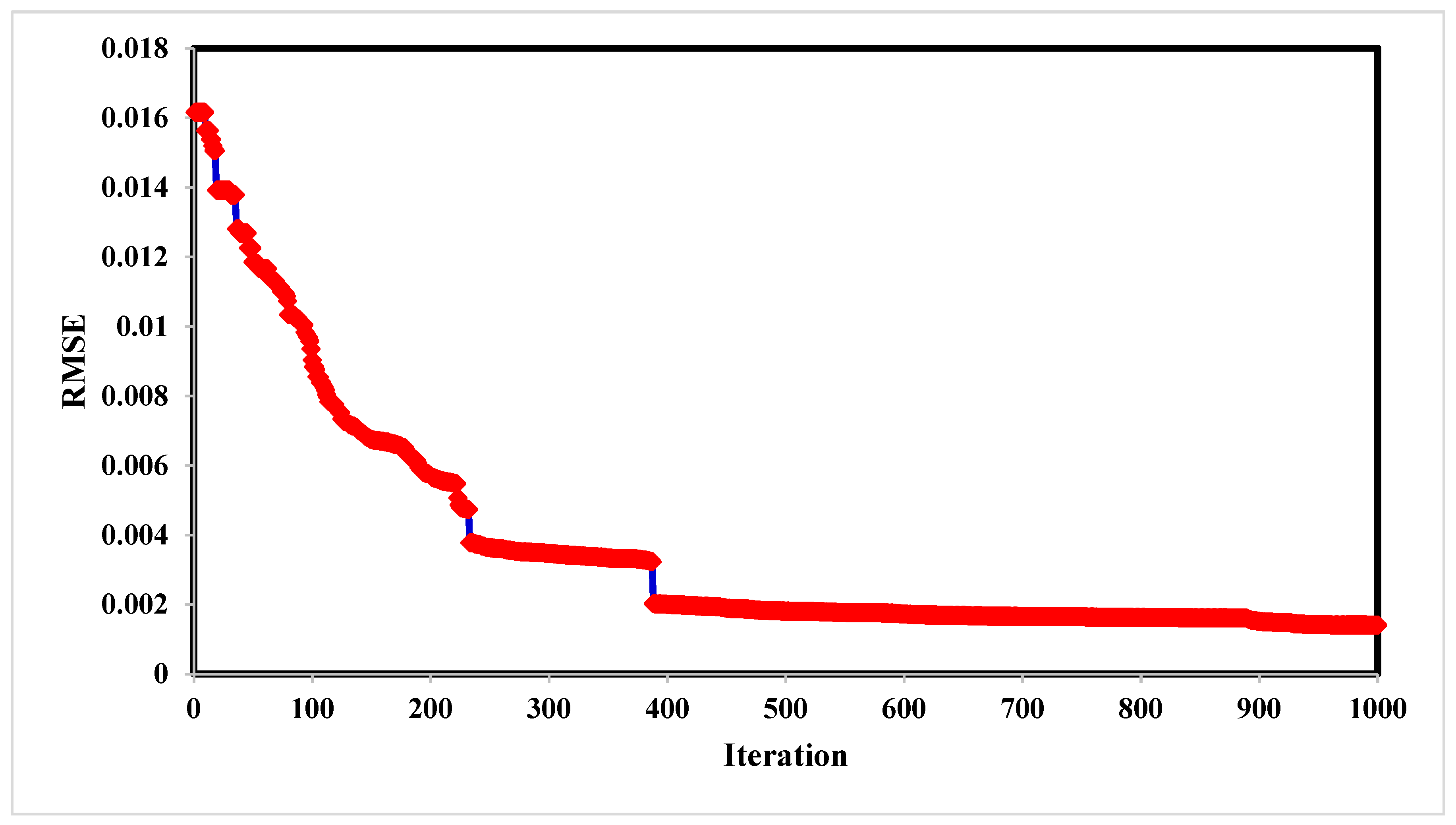
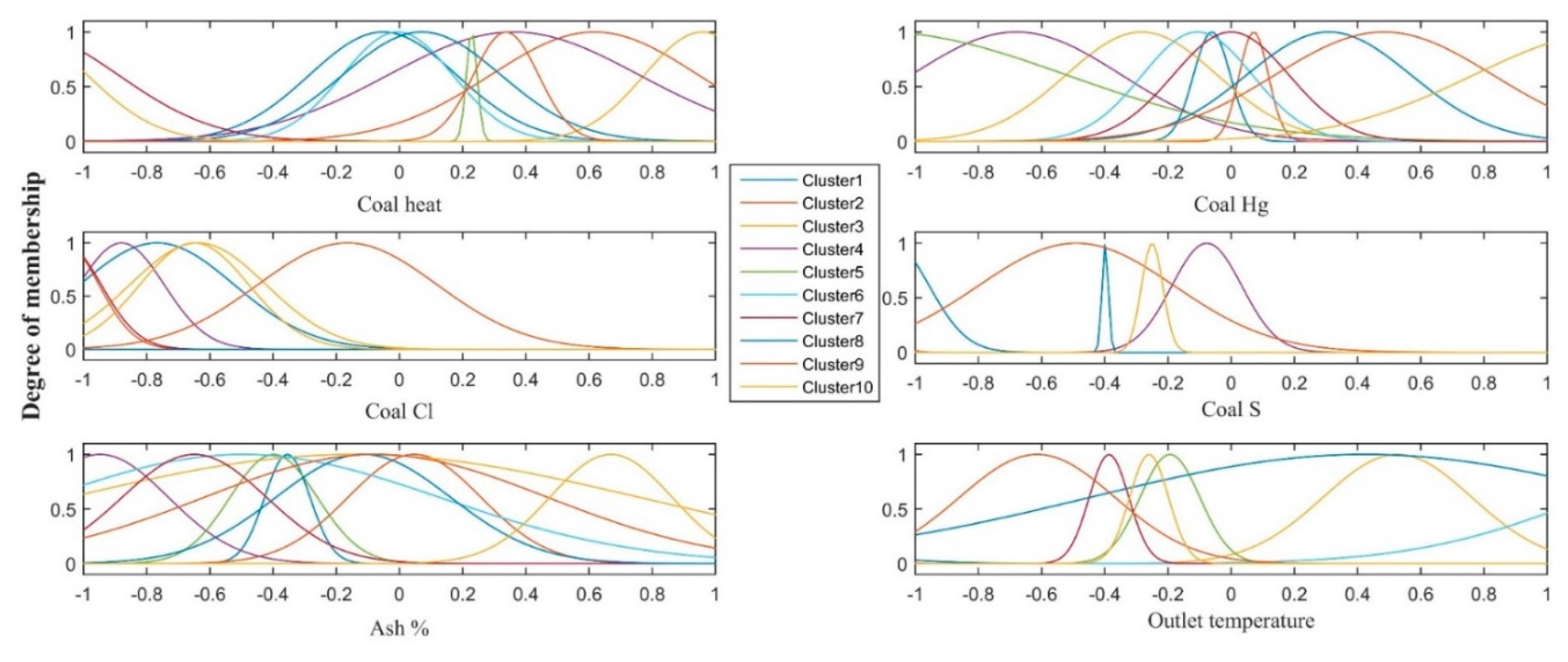
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, Y.; Wang, X.; Du, W.; Liu, J. Effects of air pollution control on urban development quality in Chinese cities based on spatial durbin model. Int. J. Environ. Res. Public Health 2018, 15, 2822. [Google Scholar] [CrossRef] [PubMed]
- Paramesh, H. Air Pollution and Allergic Airway Diseases: Social Determinantsand Sustainability in the Control and Prevention. Indian J. Pediatr. 2018, 85, 284–294. [Google Scholar] [CrossRef]
- Wang, J.; Fang, Y. Status, fiscal and taxation policy adjustment of air pollution in China. Nat. Environ. Pollut. Technol. 2018, 17, 917–924. [Google Scholar]
- Appiah, K.; Du, J.; Yeboah, M.; Appiah, R. Causal correlation between energy use and carbon emissions in selected emerging economies—Panel model approach. Environ. Sci. Pollut. Res. 2019, 26, 7896–7912. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Jiang, L.; Zhang, W.; Bao, H.; Geng, B.; He, Q.; Zhang, L.; Streets, D.G. Evaluation of China’s environmental pressures based on satellite NO2 observation and the extended STIRPAT model. Int. J. Environ. Res. Public Health 2019, 16, 1487. [Google Scholar] [CrossRef]
- Ye, L.; Ou, X. Spatial-temporal Analysis of Daily Air Quality Index in the Yangtze River Delta Region of China during 2014 and 2016. Chin. Geogr. Sci. 2019, 29, 382–393. [Google Scholar] [CrossRef]
- Moghim, S.; Garna, R.K. Countries’ classification by environmental resilience. J. Environ. Manag. 2019, 230, 345–354. [Google Scholar] [CrossRef]
- Xu, S.C.; Miao, Y.M.; Gao, C.; Long, R.Y.; Chen, H.; Zhao, B.; Wang, S.X. Regional differences in impacts of economic growth and urbanization on air pollutants in China based on provincial panel estimation. J. Clean. Prod. 2019, 208, 340–352. [Google Scholar] [CrossRef]
- Hong, E.; Lee, S.; Kim, G.B.; Kim, T.J.; Kim, H.W.; Lee, K.; Son, B.S. Effects of environmental air pollution on pulmonary function level of residents in Korean industrial complexes. Int. J. Environ. Res. Public Health 2018, 15, 834. [Google Scholar] [CrossRef]
- Jirik, V.; Brezna, B.; Machaczka, O.; Honkysova, S.; Miturova, H.; Janout, V. Associations between air pollution in the industrial and suburban parts of Ostrava city and their use. Environ. Monit. Assess. 2017, 189, 381. [Google Scholar] [CrossRef]
- Lyanguzova, I.V. Dynamic trends of heavy metal contents in plants and soil under different industrial air pollution regimes. Russ. J. Ecol. 2017, 48, 311–320. [Google Scholar] [CrossRef]
- Oyjinda, P.; Pochai, N. Numerical Simulation to Air Pollution Emission Control near an Industrial Zone. Adv. Math. Phys. 2017, 2017. [Google Scholar] [CrossRef]
- Gao, W.; Jiang, W.; Zhou, M. The spatial and temporal characteristics of mercury emission from coal combustion in China during the year 2015. Atmos. Pollut. Res. 2019, 10, 776–783. [Google Scholar] [CrossRef]
- Marczak, M.; Budzyń, S.; Szczurowski, J.; Kogut, K.; Burmistrz, P. Active methods of mercury removal from flue gases. Environ. Sci. Pollut. Res. 2019, 26, 8383–8392. [Google Scholar] [CrossRef] [PubMed]
- Sung, J.H.; Back, S.K.; Lee, E.S.; Jang, H.N.; Seo, Y.C.; Kang, Y.S.; Lee, M.H. Application of powdered activated carbon coating to fabrics in a hybrid filter to enhance mercury removal. J. Environ. Sci. (China) 2019, 80, 58–65. [Google Scholar] [CrossRef]
- Zhao, S.; Pudasainee, D.; Duan, Y.; Gupta, R.; Liu, M.; Lu, J. A review on mercury in coal combustion process: Content and occurrence forms in coal, transformation, sampling methods, emission and control technologies. Prog. Energy Combust. Sci. 2019, 73, 26–64. [Google Scholar] [CrossRef]
- Bourtsalas, A.C.; Themelis, N.J. Major sources of mercury emissions to the atmosphere: The U.S. case. Waste Manag. 2019, 85, 90–94. [Google Scholar] [CrossRef]
- Budnik, L.T.; Casteleyn, L. Mercury pollution in modern times and its socio-medical consequences. Sci. Total Environ. 2019, 654, 720–734. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Wu, T.; Chen, J.; Fu, C.; Zhang, L.; Feng, X.; Fu, X.; Tang, L.; Wang, Z.; et al. Atmospheric mercury emissions from two pre-calciner cement plants in Southwest China. Atmos. Environ. 2019, 199, 177–188. [Google Scholar] [CrossRef]
- Zhou, H.; Hopke, P.K.; Zhou, C.; Holsen, T.M. Ambient mercury source identification at a New York State urban site: Rochester, NY. Sci. Total Environ. 2019, 650, 1327–1337. [Google Scholar] [CrossRef]
- Zhao, S.; Duan, Y.; Chen, L.; Li, Y.; Yao, T.; Liu, S.; Liu, M.; Lu, J. Study on emission of hazardous trace elements in a 350 MW coal-fired power plant. Part 1. Mercury. Environ. Pollut. 2017, 229, 863–870. [Google Scholar] [CrossRef] [PubMed]
- Mahavong, K.; Pataranawat, P.; Chinwetkitvanich, S. Mercury contamination in environment surrounding coal-fired power plant. Int. J. Geomate 2017, 12, 71–77. [Google Scholar] [CrossRef]
- Amap/Unep. Technical Background Report for the Global Mercury Assessment 2013; Arctic Monitoring and Assessment Programme: Oslo, Norway; UNEP Chemicals Branch: Geneva, Switzerland, 2013. [Google Scholar]
- Burmistrz, P.; Kogut, K.; Marczak, M.; Zwoździak, J. Lignites and subbituminous coals combustion in Polish power plants as a source of anthropogenic mercury emission. Fuel Process. Technol. 2016, 152, 250–258. [Google Scholar] [CrossRef]
- Alto, P. Power Plants and Mercury, Environmental Issues; Electric Power Research Institute: Palo Alto, CA, USA, 2001. [Google Scholar]
- Carpi, A. Mercury from combustion sources: A review of the chemical species emitted and their transport in the atmosphere. Water Air Soil Pollut. 1997, 98, 241–254. [Google Scholar] [CrossRef]
- Srivastava, R.K.; Hutson, N.; Martin, B.; Princiotta, F.; Staudt, J.X. Control of mercury emissions from coal-fired electric utility boilers. Environ. Sci. Technol. 2006, 40, 1385–1393. [Google Scholar] [CrossRef]
- Zhang, L.; Zhuo, Y.; Chen, L.; Xu, X.; Chen, C. Mercury emissions from six coal-fired power plants in China. Fuel Process. Technol. 2008, 89, 1033–1040. [Google Scholar] [CrossRef]
- Streets, D.G.; Zhang, Q.; Wu, Y. Projections of global mercury emissions in 2050. Environ. Sci. Technol. 2009, 43, 2983–2988. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Y.; Cheng, K.; Qu, Y.; Hao, J.; Xue, Z.; Chai, F. Control strategies of atmospheric mercury emissions from coal-fired power plants in China. J. Air Waste Manag. Assoc. 2012, 62, 576–586. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Y.; Xue, Z.; Qu, Y.; Chai, F.; Hao, J. Atmospheric emissions estimation of Hg, As, and Se from coal-fired power plants in China, 2007. Sci. Total Environ. 2011, 409, 3078–3081. [Google Scholar] [CrossRef]
- You, C.F.; Xu, X.C. Coal combustion and its pollution control in China. Energy 2010, 35, 4467–4472. [Google Scholar] [CrossRef]
- Chen, Z.F.; Young, L.; Yu, C.H.; Shiao, S.P.K. A meta-prediction of Methylenetetrahydrofolate-reductase polymorphisms and air pollution increased the risk of ischemic heart diseases worldwide. Int. J. Environ. Res. Public Health 2018, 15, 1453. [Google Scholar] [CrossRef] [PubMed]
- Girguis, M.S.; Li, L.; Lurmann, F.; Wu, J.; Urman, R.; Rappaport, E.; Breton, C.; Gilliland, F.; Stram, D.; Habre, R. Exposure measurement error in air pollution studies: A framework for assessing shared, multiplicative measurement error in ensemble learning estimates of nitrogen oxides. Environ. Int. 2019, 125, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Kerckhoffs, J.; Hoek, G.; Portengen, L.; Brunekreef, B.; Vermeulen, R.C.H. Performance of Prediction Algorithms for Modeling Outdoor Air Pollution Spatial Surfaces. Environ. Sci. Technol. 2019, 53, 1413–1421. [Google Scholar] [CrossRef] [PubMed]
- Tao, Q.; Liu, F.; Li, Y.; Sidorov, D. Air Pollution Forecasting Using a Deep Learning Model Based on 1D Convnets and Bidirectional GRU. IEEE Access 2019, 7, 76690–76698. [Google Scholar] [CrossRef]
- Xiao, D.; Fang, F.; Zheng, J.; Pain, C.C.; Navon, I.M. Machine learning-based rapid response tools for regional air pollution modelling. Atmos. Environ. 2019, 199, 463–473. [Google Scholar] [CrossRef]
- Carlos, G.; Valeria, F.; Guillermo, V. Use of non-industrial environmental sensors and machine learning techniques in telemetry for indoor air pollution. ARPN J. Eng. Appl. Sci. 2018, 13, 2702–2712. [Google Scholar]
- Eldakhly, N.M.; Aboul-Ela, M.; Abdalla, A. A Novel Approach of Weighted Support Vector Machine with Applied Chance Theory for Forecasting Air Pollution Phenomenon in Egypt. Int. J. Comput. Intell. Appl. 2018, 17. [Google Scholar] [CrossRef]
- Martínez-España, R.; Bueno-Crespo, A.; Timón, I.; Soto, J.; Muñoz, A.; Cecilia, J.M. Air-pollution prediction in smart cities through machine learning methods: A case of study in Murcia, Spain. J. Univ. Comput. Sci. 2018, 24, 261–276. [Google Scholar]
- Xayasouk, T.; Lee, H. Air pollution prediction system using deep learning. WIT Trans. Ecol. Environ. 2018, 230, 71–79. [Google Scholar] [CrossRef]
- Choubin, B.; Borji, M.; Mosavi, A.; Sajedi-Hosseini, F.; Singh, V.P.; Shamshirband, S. Snow avalanche hazard prediction using machine learning methods. J. Hydrol. 2019, 577. [Google Scholar] [CrossRef]
- Dineva, A.; Mosavi, A.; Ardabili, S.; Vajda, I.; Shamshirband, S.; Rabczuk, T.; Chau, K.W. Review of soft computing models in design and control of rotating electrical machines. Energies 2019, 12, 49. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Mosavi, A.; Salimi, M.; Ardabili, S.F.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the art of machine learning models in energy systems, a systematic review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef]
- Mosavi, A.; Shamshirband, S.; Salwana, E.; Chau, K.W.; Tah, J.H.M. Prediction of multi-inputs bubble column reactor using a novel hybrid model of computational fluid dynamics and machine learning. Eng. Appl. Comput. Fluid Mech. 2019, 13, 482–492. [Google Scholar] [CrossRef]
- Qasem, S.N.; Samadianfard, S.; Nahand, H.S.; Mosavi, A.; Shamshirband, S.; Chau, K.W. Estimating daily dew point temperature using machine learning algorithms. Water 2019, 11, 582. [Google Scholar] [CrossRef]
- Torabi, M.; Hashemi, S.; Saybani, M.R.; Shamshirband, S.; Mosavi, A. A Hybrid clustering and classification technique for forecasting short-term energy consumption. Environ. Prog. Sustain. Energy 2019, 38, 66–76. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Ma, X.; Zhou, H.; Zhang, F. Hybrid support vector machines with heuristic algorithms for prediction of daily diffuse solar radiation in air-polluted regions. Renew. Energy 2020, 145, 2034–2045. [Google Scholar] [CrossRef]
- Kaimian, H.; Li, Q.; Wu, C.; Qi, Y.; Mo, Y.; Chen, G.; Zhang, X.; Sachdeva, S. Evaluation of different machine learning approaches to forecasting PM2.5 mass concentrations. Aerosol. Air Qual. Res. 2019, 19, 1400–1410. [Google Scholar] [CrossRef]
- Li, C.; Zhu, Z. Research and application of a novel hybrid air quality early-warning system: A case study in China. Sci. Total Environ. 2018, 626, 1421–1438. [Google Scholar] [CrossRef]
- Qi, X.; Luo, Y.; Wu, G.; Boriboonsomsin, K.; Barth, M. Deep reinforcement learning enabled self-learning control for energy efficient driving. Transp. Res. Part C Emerg. Technol. 2019, 99, 67–81. [Google Scholar] [CrossRef]
- Requia, W.J.; Coull, B.A.; Koutrakis, P. Evaluation of predictive capabilities of ordinary geostatistical interpolation, hybrid interpolation, and machine learning methods for estimating PM2.5 constituents over space. Environ. Res. 2019, 175, 421–433. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Wei, S.; Luo, H.; Yue, C.; Grunder, O. A novel hybrid model for air quality index forecasting based on two-phase decomposition technique and modified extreme learning machine. Sci. Total Environ. 2017, 580, 719–733. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.H.; Yien, J.M.; Chiang, C.H.; Tsai, P.C.; Tsai, F.S. Identifying key sources of city air quality: A hybrid MCDM model and improvement strategies. Appl. Sci. 2019, 9, 1414. [Google Scholar] [CrossRef]
- Li, Q.; Wu, J.; Wei, H. Reduction of elemental mercury in coal-fired boiler flue gas with computational intelligence approach. Energy 2018, 160, 753–762. [Google Scholar] [CrossRef]
- Metia, S.; Ha, Q.P.; Duc, H.N.; Azzi, M. Estimation of Power Plant Emissions with Unscented Kalman Filter. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2763–2772. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Q. Deep learning based fossil-fuel power plant monitoring in high resolution remote sensing images: A comparative study. Remote Sens. 2019, 11, 1117. [Google Scholar] [CrossRef]
- Baghban, A.; Ahmadi, M.A.; Shahraki, B.H. Prediction carbon dioxide solubility in presence of various ionic liquids using computational intelligence approaches. J. Supercrit. Fluids 2015, 98, 50–64. [Google Scholar] [CrossRef]
- Frontalini, F.; Greco, M.; Di Bella, L.; Lejzerowicz, F.; Reo, E.; Caruso, A.; Cosentino, C.; Maccotta, A.; Scopelliti, G.; Nardelli, M.P.; et al. Assessing the effect of mercury pollution on cultured benthic foraminifera community using morphological and eDNA metabarcoding approaches. Mar. Pollut. Bull. 2018, 129, 512–524. [Google Scholar] [CrossRef]
- Ahn, S.J.; Kim, L.; Kwon, O. Korea’s social dynamics towards power supply and air pollution caused by electric vehicle diffusion. J. Clean. Prod. 2018, 205, 1042–1068. [Google Scholar] [CrossRef]
- Dhammapala, R. Analysis of fine particle pollution data measured at 29 US diplomatic posts worldwide. Atmos. Environ. 2019, 213, 367–376. [Google Scholar] [CrossRef]
- Gong, J.W.; Li, Y.P.; Suo, C. Full-infinite interval two-stage credibility constrained programming for electric power system management by considering carbon emission trading. Int. J. Electr. Power Energy Syst. 2019, 105, 440–453. [Google Scholar] [CrossRef]
- Song, J.; Romero, C.E.; Yao, Z.; He, B. A globally enhanced general regression neural network for on-line multiple emissions prediction of utility boiler. Knowl. Based Syst. 2017, 118, 4–14. [Google Scholar] [CrossRef]
- Jha, S.K.; Bilalovikj, J. Short-term wind speed prediction at Bogdanci power plant in FYROM using an artificial neural network. Int. J. Sustain. Energy 2019, 38, 526–541. [Google Scholar] [CrossRef]
- Lee, C.Y.; Wang, K. Nash marginal abatement cost estimation of air pollutant emissions using the stochastic semi-nonparametric frontier. Eur. J. Oper. Res. 2019, 273, 390–400. [Google Scholar] [CrossRef]
- Leung, W.H.; Ma, W.M.; Chan, P.K.Y. Nuclear accident consequence assessment in Hong Kong using JRODOS. J. Environ. Radioact. 2018, 183, 27–36. [Google Scholar] [CrossRef]
- Liu, K.; Liu, T.Z.; Jian, P.; Lin, Y. The re-optimization strategy of multi-layer hybrid building’s cooling and heating load soft sensing technology research based on temperature interval and hierarchical modeling techniques. Sustain. Cities Soc. 2018, 38, 42–54. [Google Scholar] [CrossRef]
- Mlakar, P.; Božnar, M.Z.; Grašič, B.; Breznik, B. Integrated system for population dose calculation and decision making on protection measures in case of an accident with air emissions in a nuclear power plant. Sci. Total Environ. 2019, 666, 786–800. [Google Scholar] [CrossRef]
- Dragomir, E.G.; Oprea, M.J.I.P.V. A Multi-Agent System for Power Plants Air Pollution Monitoring. IFAC Proc. Vol. 2013, 46, 89–94. [Google Scholar] [CrossRef]
- Jensen, R.R.; Karki, S.; Salehfar, H. Artificial neural network-based estimation of mercury speciation in combustion flue gases. Fuel Process. Technol. 2004, 85, 451–462. [Google Scholar] [CrossRef]
- Antanasijević, D.Z.; Pocajt, V.V.; Povrenović, D.S.; Ristić, M.Đ.; Perić-Grujić, A.A. PM10 emission forecasting using artificial neural networks and genetic algorithm input variable optimization. J. Sci. Total Environ. 2013, 443, 511–519. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, Z.; Jin, J.; Pan, W.P. Modeling mercury speciation in combustion flue gases using support vector machine: Prediction and evaluation. J. Hazard. Mater. 2010, 174, 244–250. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Tian, G.; Wang, X.; Liu, Y.; Deng, S.; Wang, H.; Zhang, F. Application of genetic algorithm-back propagation for prediction of mercury speciation in combustion flue gas. Clean Technol. Environ. Policy 2016, 18, 1211–1218. [Google Scholar] [CrossRef]
- Choubin, B.; Abdolshahnejad, M.; Moradi, E.; Querol, X.; Mosavi, A.; Shamshirband, S.; Ghamisi, P. Spatial hazard assessment of the PM10 using machine learning models in Barcelona, Spain. Sci. Total Environ. 2019, 134474. [Google Scholar] [CrossRef]
- Ardabili, S.F.; Najafi, B.; Alizamir, M.; Mosavi, A.; Shamshirband, S.; Rabczuk, T. Using SVM-RSM and ELM-RSM approaches for optimizing the production process of methyl and ethyl esters. Energies 2018, 11, 2889. [Google Scholar] [CrossRef]
- Torabi, M.; Mosavi, A.; Ozturk, P.; Varkonyi-Koczy, A.; Istvan, V. A Hybrid Machine Learning Approach for Daily Prediction of Solar Radiation. In Lecture Notes in Networks and Systems; Springer: New York, NY, USA, 2019; Volume 53, pp. 266–274. [Google Scholar]
- Basser, H.; Karami, H.; Shamshirband, S.; Akib, S.; Amirmojahedi, M.; Ahmad, R.; Jahangirzadeh, A.; Javidnia, H. Hybrid ANFIS-PSO approach for predicting optimum parameters of a protective spur dike. Appl. Soft Comput. J. 2015, 30, 642–649. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Hybrid wavelet-PSO-ANFIS approach for short-term electricity prices forecasting. IEEE Trans. Power Syst. 2011, 26, 137–144. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Hybrid wavelet-PSO-ANFIS approach for short-term wind power forecasting in Portugal. IEEE Trans. Sustain. Energy 2011, 2, 50–59. [Google Scholar] [CrossRef]
- Anemangely, M.; Ramezanzadeh, A.; Tokhmechi, B. Shear wave travel time estimation from petrophysical logs using ANFIS-PSO algorithm: A case study from Ab-Teymour Oilfield. J. Nat. Gas Sci. Eng. 2017, 38, 373–387. [Google Scholar] [CrossRef]
- Atuahene, S.; Bao, Y.; Yevenyo Ziggah, Y.; Semwaah Gyan, P.; Li, F. Short-term electric power forecasting using dual-stage hierarchical wavelet-Particle swarm optimization-Adaptive neuro-fuzzy inference system pso-ANFIS approach based on climate change. Energies 2018, 11, 2822. [Google Scholar] [CrossRef]
- Banashooshtari, H.; Ashtari Larki, S.; Shokrollahzadeh Behbahani, H. A PSO-ANFIS framework for prediction of density of bitumen diluted with solvents. Pet. Sci. Technol. 2018, 36, 122–129. [Google Scholar] [CrossRef]
- Ceylan, Z.; Pekel, E.; Ceylan, S.; Bulkan, S. Biomass higher heating value prediction analysis by ANFIS, PSO-ANFIS and GA-ANFIS. Glob. Nest J. 2018, 20, 589–597. [Google Scholar] [CrossRef]
- Chu, Z.Q.; Sasanipour, J.; Saeedi, M.; Baghban, A.; Mansoori, H. Modeling of wax deposition produced in the pipelines using PSO-ANFIS approach. Pet. Sci. Technol. 2017, 35, 1974–1981. [Google Scholar] [CrossRef]
- Darvish, H.; Rahmani, S.; Maleki Sadeghi, A.; Emami Baghdadi, M.H. The ANFIS-PSO strategy as a novel method to predict interfacial tension of hydrocarbons and brine. Pet. Sci. Technol. 2018, 36, 654–659. [Google Scholar] [CrossRef]
- Djavareshkian, M.H.; Esmaeili, A. Heuristic optimization of submerged hydrofoil using ANFIS-PSO. Ocean Eng. 2014, 92, 55–63. [Google Scholar] [CrossRef]
- Esfandyari, M.; Esfandyari, M.; Jafari, D. Prediction of thiophene removal from diesel using [BMIM][AlCl4] in EDS Process: GA-ANFIS and PSO-ANFIS modeling. Pet. Sci. Technol. 2018, 36, 1305–1311. [Google Scholar] [CrossRef]
- Isazadeh, G.; Hooshmand, R.A.; Khodabakhshian, A. Modeling and optimization of an adaptive dynamic load shedding using the ANFIS-PSO algorithm. Simulation 2012, 88, 181–196. [Google Scholar] [CrossRef]
- Keybondorian, E.; Taherpour, A.; Bemani, A.; Hamule, T. Application of novel ANFIS-PSO approach to predict asphaltene precipitation. Pet. Sci. Technol. 2018, 36, 154–159. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, D.; Peng, W. A Novel ANFIS-PSO Network for forecasting oil flocculated asphaltene weight percentage at wide range of operation conditions. Pet. Sci. Technol. 2018, 36, 1044–1050. [Google Scholar] [CrossRef]
- Malmir, P.; Suleymani, M.; Bemani, A. Application of ANFIS-PSO as a novel method to estimate effect of inhibitors on Asphaltene precipitation. Pet. Sci. Technol. 2018, 36, 597–603. [Google Scholar] [CrossRef]
- Mir, M.; Kamyab, M.; Lariche, M.J.; Bemani, A.; Baghban, A. Applying ANFIS-PSO algorithm as a novel accurate approach for prediction of gas density. Pet. Sci. Technol. 2018, 36, 820–826. [Google Scholar] [CrossRef]
- Pousinho, H.M.I.; Mendes, V.M.F.; Catalão, J.P.S. Short-term electricity prices forecasting in a competitive market by a hybrid PSO-ANFIS approach. Int. J. Electr. Power Energy Syst. 2012, 39, 29–35. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Dashti, A.; Asghari, M.; Shirazian, S. H2-selective mixed matrix membranes modeling using ANFIS, PSO-ANFIS, GA-ANFIS. Int. J. Hydrog. Energy 2017, 42, 15211–15225. [Google Scholar] [CrossRef]
- Salisu, S.; Mustafa, M.W.; Mustapha, M.; Mohammed, O.O. Solar radiation forecasting in Nigeria based on hybrid PSO-ANFIS and WT-ANFIS approach. Int. J. Electr. Comput. Eng. 2019, 9, 3916–3926. [Google Scholar] [CrossRef]
- Suleymani, M.; Bemani, A. Application of ANFIS-PSO algorithm as a novel method for estimation of higher heating value of biomass. Energy Sources Recover. Util. Environ. Eff. 2018, 40, 288–293. [Google Scholar] [CrossRef]
- Roger, J.J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. ManCybern. 1993, 23, 665–685. [Google Scholar]
- Jang, J.S.R. Fuzzy Modeling Using Generalized Neural Networks and Kalman Filter Algorithm. AAAI 1991, 91, 762–767. [Google Scholar]
- Baghban, A. Application of the ANFIS strategy to estimate vaporization enthalpies of petroleum fractions and pure hydrocarbons. Pet. Sci. Technol. 2016, 34, 1359–1366. [Google Scholar] [CrossRef]
- Hamdan, H.; Garibaldi, J.M. Adaptive neuro-fuzzy inference system (ANFIS) in modelling breast cancer survival. In Proceedings of the International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Sugeno, M.; Kang, G.T. Structure identification of fuzzy model. Fuzzy Sets Syst. 1988, 28, 15–33. [Google Scholar] [CrossRef]
- Baghban, A.; Bahadori, M.; Ahmad, Z.; Kashiwao, T.; Bahadori, A. Modeling of true vapor pressure of petroleum products using ANFIS algorithm. Pet. Sci. Technol. 2016, 34, 933–939. [Google Scholar] [CrossRef]
- Walia, N.; Singh, H.; Sharma, A. ANFIS: Adaptive neuro-fuzzy inference system-a survey. Int. J. Comput. Appl. 2015, 123, 32–38. [Google Scholar] [CrossRef]
- Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.K.; Chau, K.W. Prediction of hydropower generation using Grey wolf optimization adaptive neuro-fuzzy inference system. Energies 2019, 12, 289. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Rezakazemi, M.; Mosavi, A.; Shirazian, S. ANFIS pattern for molecular membranes separation optimization. J. Mol. Liq. 2019, 274, 470–476. [Google Scholar] [CrossRef]
- Baghban, A.; Kashiwao, T.; Bahadori, M.; Ahmad, Z.; Bahadori, A. Estimation of natural gases water content using adaptive neuro-fuzzy inference system. Pet. Sci. Technol. 2016, 34, 891–897. [Google Scholar] [CrossRef]
- Chen, G.; Huang, X.; Jia, J.; Min, Z. Natural exponential inertia weight strategy in particle swarm optimization. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 3672–3675. [Google Scholar]
- El-Gallad, A.; El-Hawary, M.; Sallam, A.; Kalas, A. Enhancing the particle swarm optimizer via proper parameters selection. In Proceedings of the IEEE CCECE2002. Canadian Conference on Electrical and Computer Engineering: Conference Proceedings (Cat. No. 02CH37373), Winnipeg, MB, Canada, 12–15 May 2002; pp. 792–797. [Google Scholar]
- Meng, X.; Pian, Z. Intelligent Coordinated Control of Complex Uncertain Systems for Power Distribution and Network Reliability; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
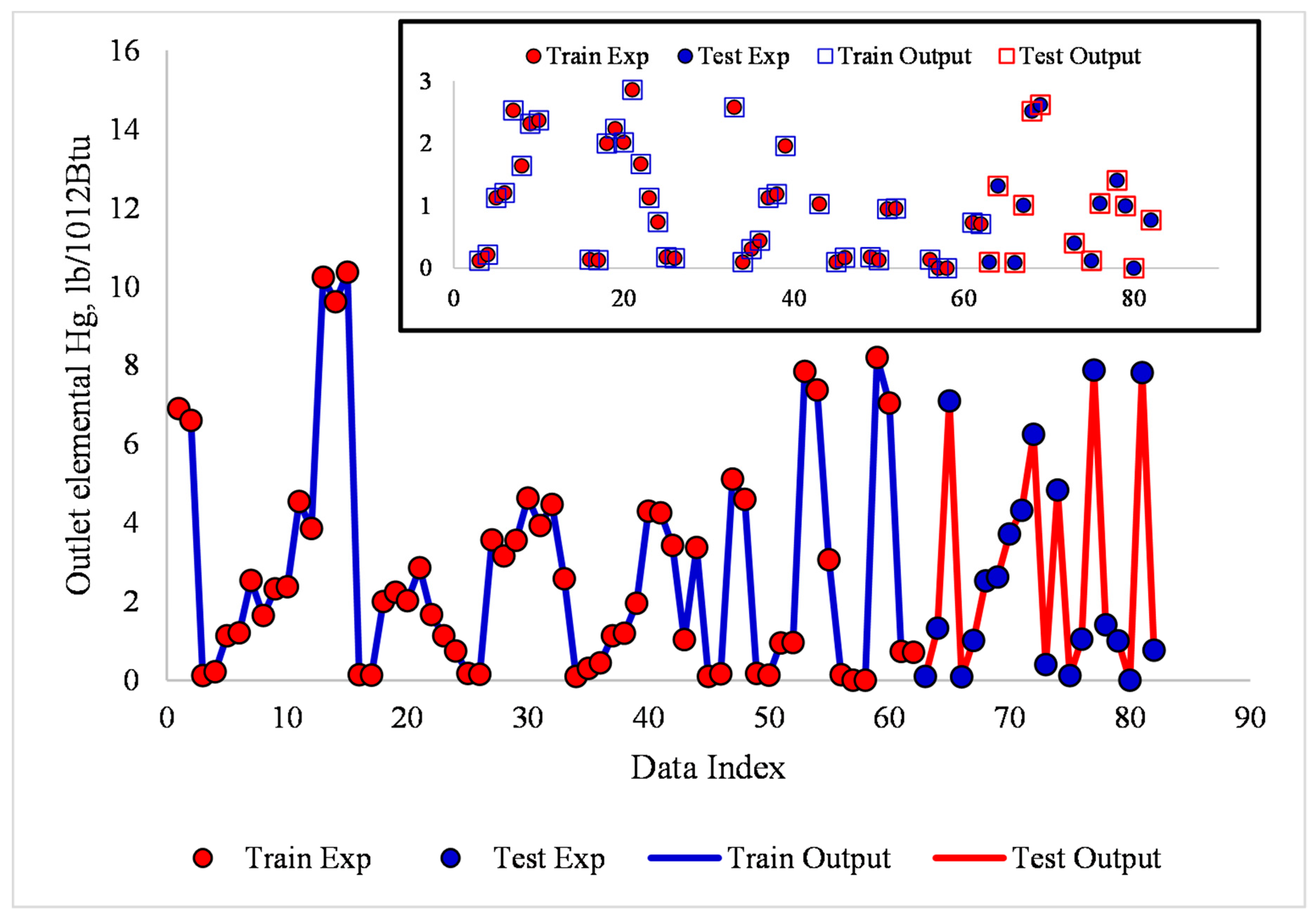
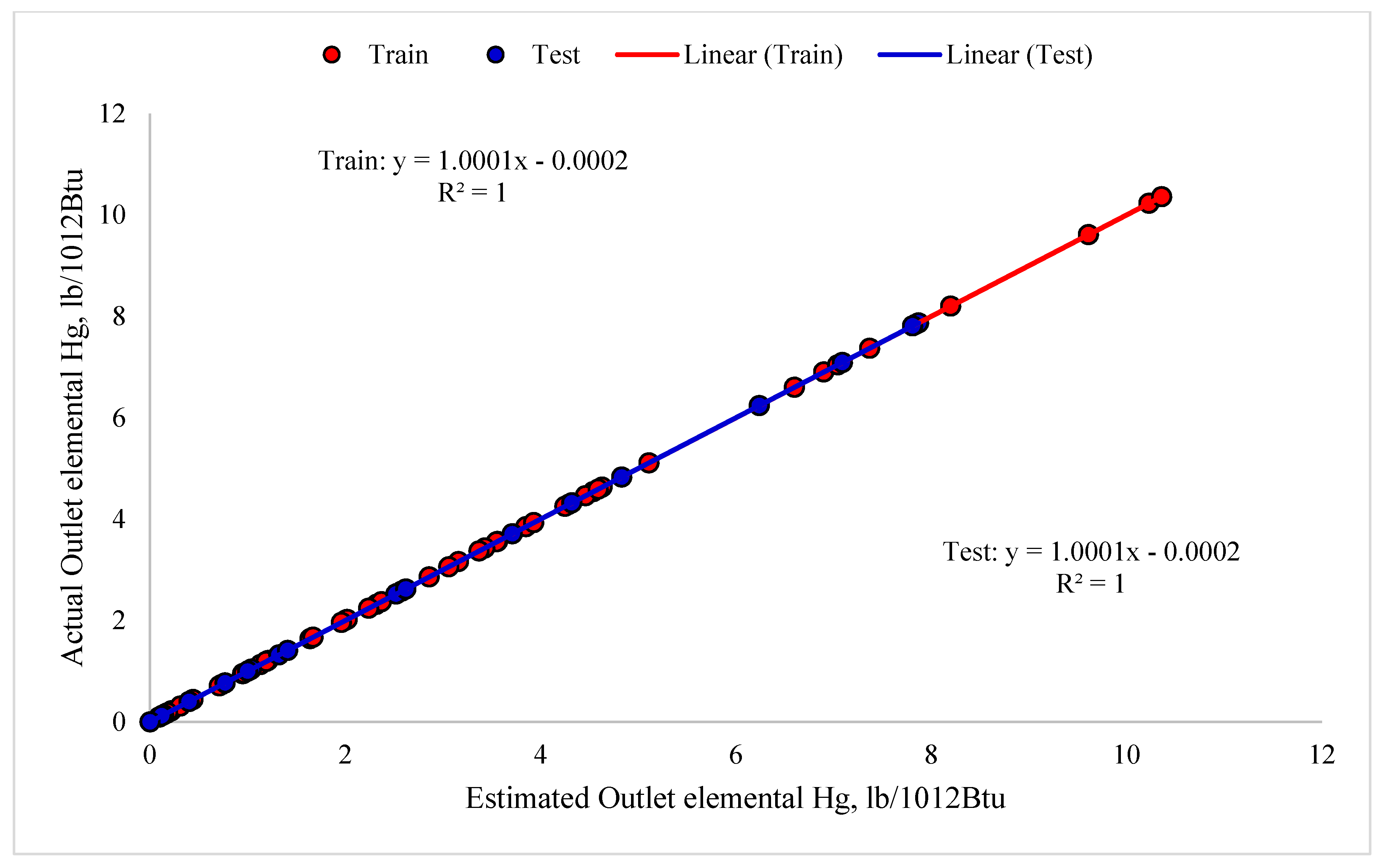
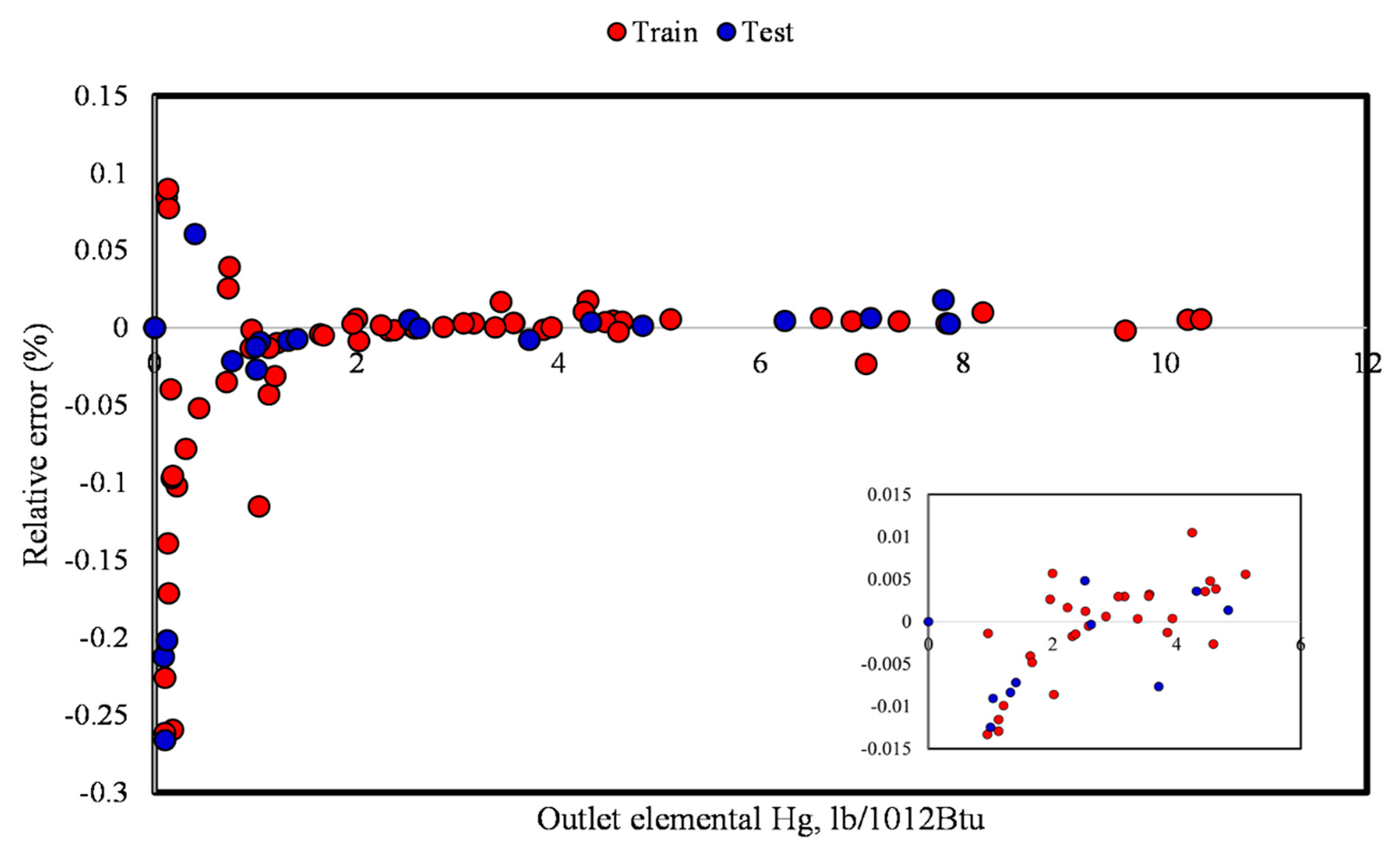
| Evaluation Metrics | Train | Test |
|---|---|---|
| R2 | 1.000 | 1.000 |
| MSE | 10−7 | 10−7 |
| MRE (%) | 0.037 | 0.044 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamshirband, S.; Hadipoor, M.; Baghban, A.; Mosavi, A.; Bukor, J.; Várkonyi-Kóczy, A.R. Developing an ANFIS-PSO Model to Predict Mercury Emissions in Combustion Flue Gases. Mathematics 2019, 7, 965. https://doi.org/10.3390/math7100965
Shamshirband S, Hadipoor M, Baghban A, Mosavi A, Bukor J, Várkonyi-Kóczy AR. Developing an ANFIS-PSO Model to Predict Mercury Emissions in Combustion Flue Gases. Mathematics. 2019; 7(10):965. https://doi.org/10.3390/math7100965
Chicago/Turabian StyleShamshirband, Shahaboddin, Masoud Hadipoor, Alireza Baghban, Amir Mosavi, Jozsef Bukor, and Annamária R. Várkonyi-Kóczy. 2019. "Developing an ANFIS-PSO Model to Predict Mercury Emissions in Combustion Flue Gases" Mathematics 7, no. 10: 965. https://doi.org/10.3390/math7100965
APA StyleShamshirband, S., Hadipoor, M., Baghban, A., Mosavi, A., Bukor, J., & Várkonyi-Kóczy, A. R. (2019). Developing an ANFIS-PSO Model to Predict Mercury Emissions in Combustion Flue Gases. Mathematics, 7(10), 965. https://doi.org/10.3390/math7100965







