A Multiscale RBF Collocation Method for the Numerical Solution of Partial Differential Equations
Abstract
1. Introduction
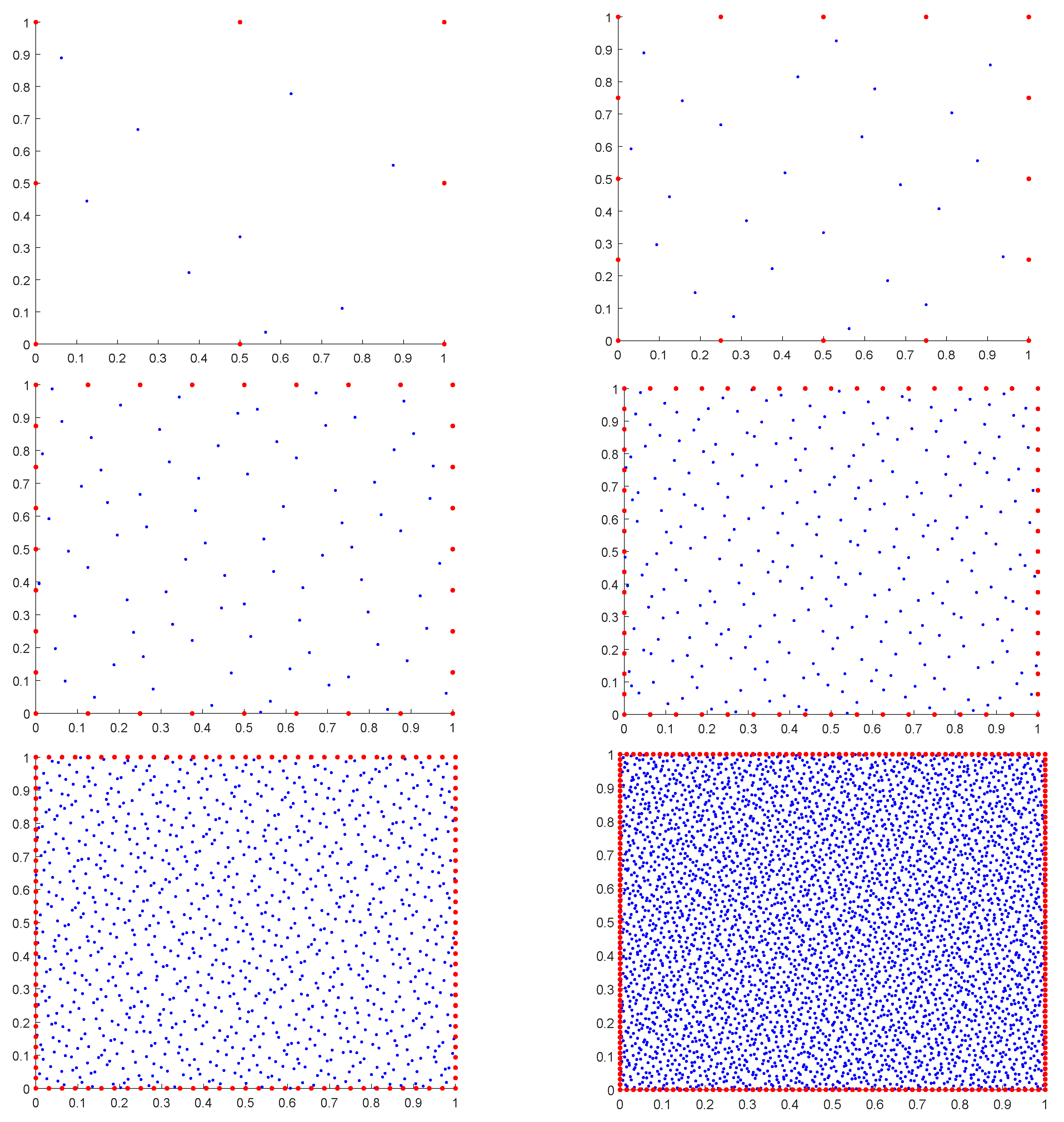
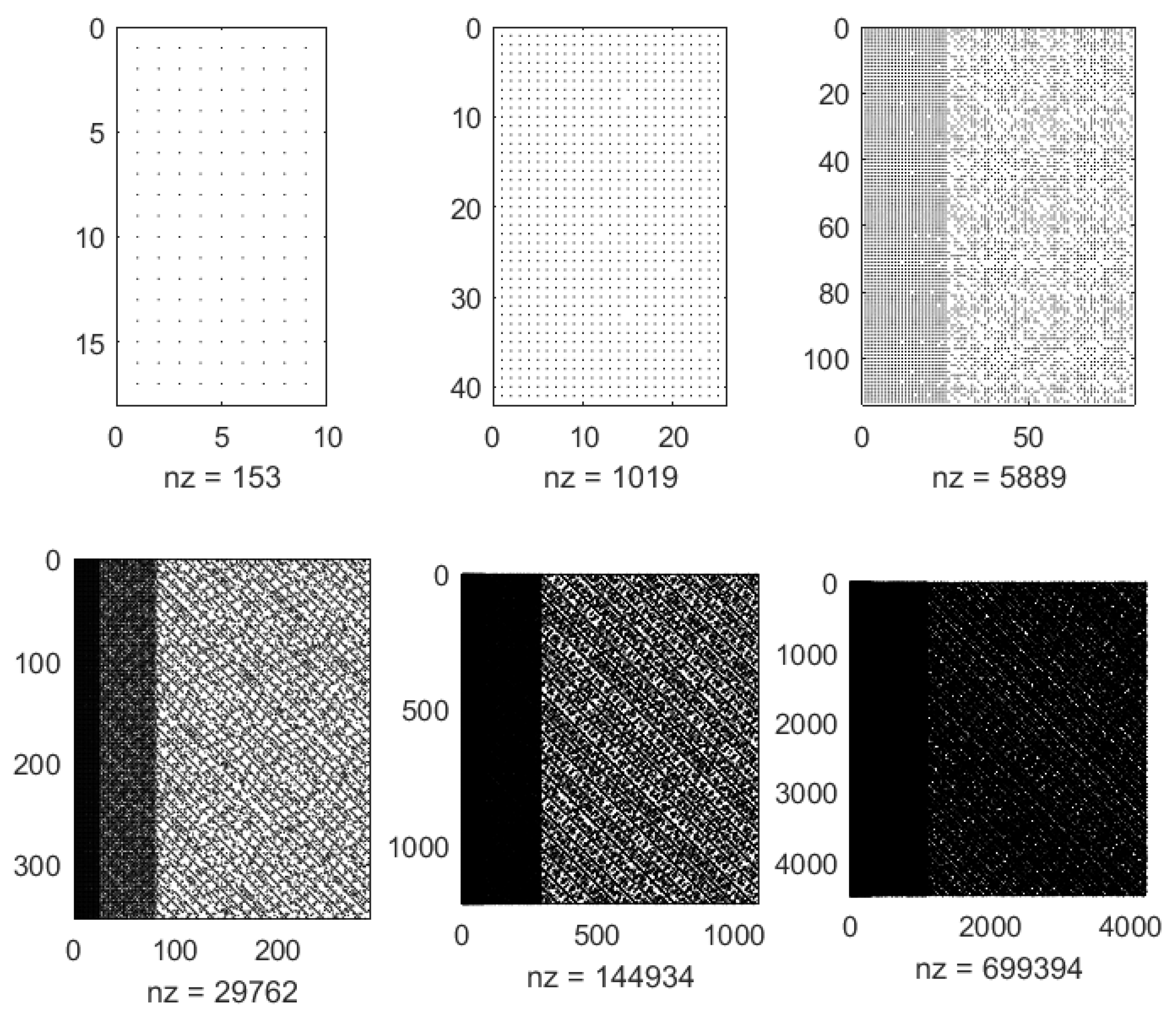
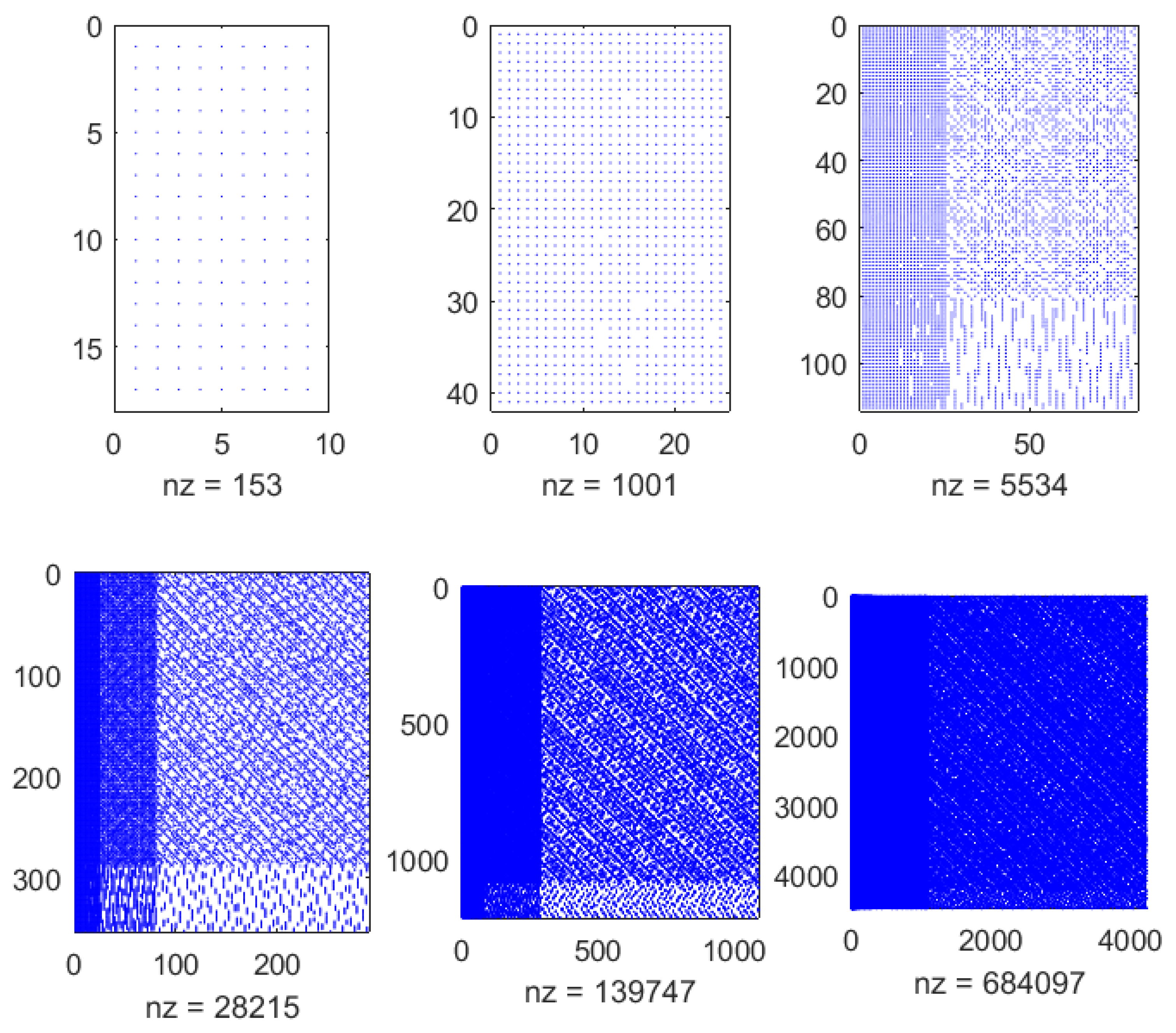
2. H-RBFs Trial Spaces
2.1. H-RBFs Trial Spaces
2.2. Norms of the Discrete Spaces
- (c1) is open and has a Lipschitz boundary
- (c2) with
- (c3)
- (c4) , ,

3. Interpolation via H-RBFs
4. Collocation via H-RBFs
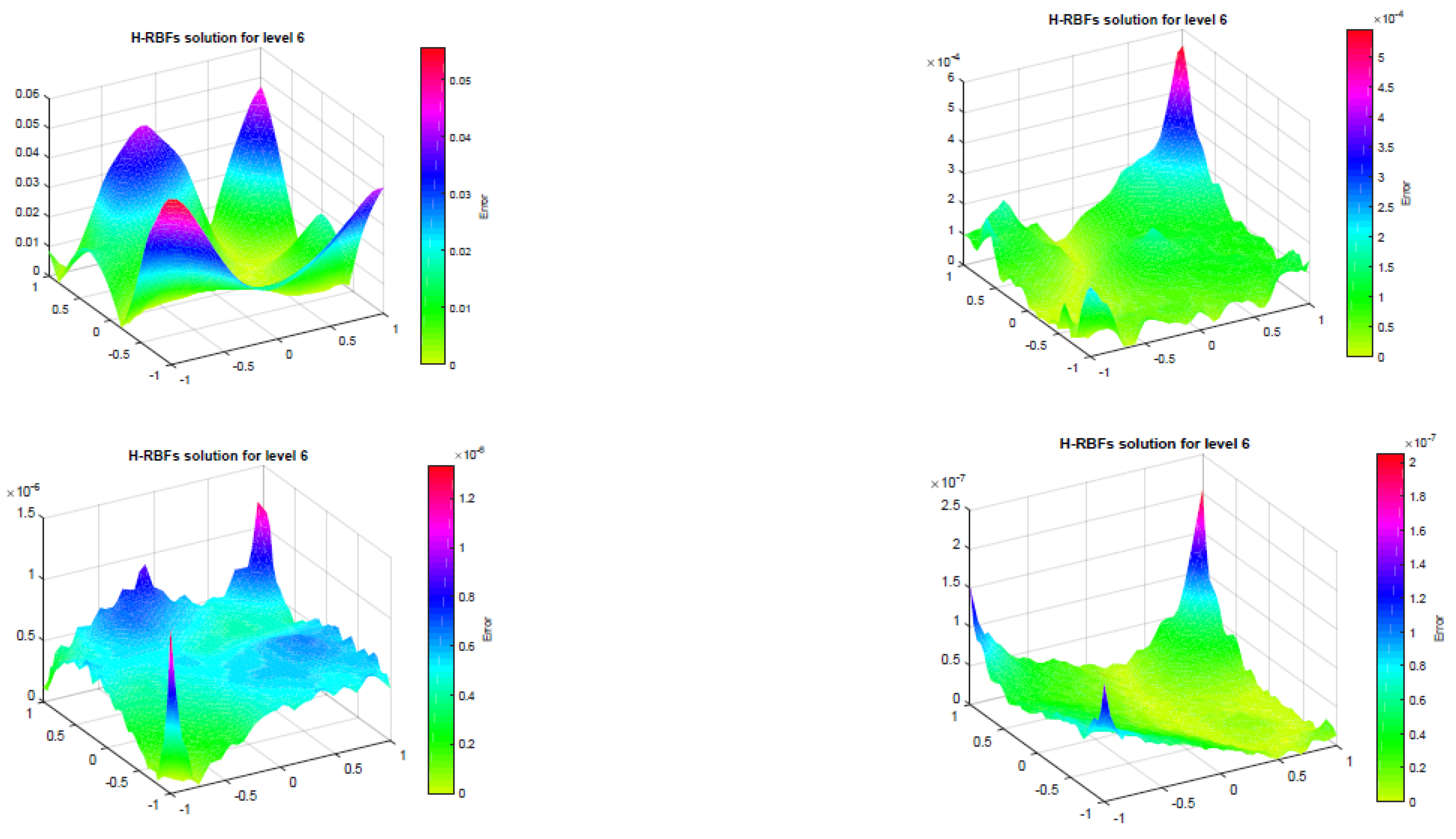
4.1. Example 1
4.2. Example 2
5. Conclusions
- (1)
- A convergence proof for H-RBFs collocation method will depend on the approximation of H-RBFs trial spaces, new inverse inequality (a frequently used inequality has been given in [24] for RBFs case), and sampling theorem.
- (2)
- This method can be used for solving well-posed nonlinear partial differential equations, and the convergence analysis of hierarchical radial basis function collocation method for nonlinear discretization will depend on Bhmer/Schaback theory [25].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yserentant, H. On the multi-level splitting of finite element spaces. Numer. Math. 1986, 49, 379–412. [Google Scholar] [CrossRef]
- Kansa, E.J. Application of Hardy’s multiquadric interpolation to hydrodynamics. In Proceedings of the 1986 Annual Simulations Conference, San Diego, CA, USA, 23 January 1986; Volume 4, pp. 111–117. [Google Scholar]
- Schaback, R. Error estimates and condition number for radial basis function interpolation. Adv. Comput. Math. 1995, 3, 251–264. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; McCourt, M. Kernel-Based Approximation Mthods Using MATLAB; World Scientific Publishers: Singapore, 2016. [Google Scholar]
- Fasshauer, G.E. Meshfree Approximation Methods with MATLAB; World Scientific Publishers: Singapore, 2007. [Google Scholar]
- Madych, W.R. Error estimates for interpolation by generalized splines. In Curves and Surfaces; Laurent, P.-J., Le Méhauté, A., Schumaker, L.L., Eds.; Academic Press: New York, NY, USA, 1991; pp. 297–306. [Google Scholar]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Wu, Z. Compactly supported positive definite radial functions. Adv. Comput. Math. 1995, 4, 283–292. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial functions on compact support. Proc. Edin. Math. Soc. II 1998, 41, 33–46. [Google Scholar] [CrossRef]
- Floater, M.S.; Iske, A. Multistep scattered data interpolation using compactly supported radial basis functions. J. Comput. Applied Math. 1996, 73, 65–78. [Google Scholar] [CrossRef]
- Le Gia, Q.T.; Sloan, I.H.; Wendland, H. Multiscale analysis in Sobolev spaces on the sphere. SIAM J. Numer. Anal. 2010, 48, 2065–2090. [Google Scholar] [CrossRef]
- Wendland, H. Multiscale analysis in Sobolev spaces on bounded domains. Numer. Math. 2010, 116, 493–517. [Google Scholar] [CrossRef]
- Le Gia, Q.T.; Sloan, I.H.; Wendland, H. Multiscale RBF collocation for solving PDEs on spheres. Numer. Math. 2012, 121, 99–125. [Google Scholar] [CrossRef]
- Chernih, A.; Le Gia, Q.T. Multiscale methods with compactly supported radial basis functions for Galerkin approximation of elliptic PDEs. IMA J. Numer. Anal. 2014, 34, 569–591. [Google Scholar] [CrossRef][Green Version]
- Chernih, A.; Le Gia, Q.T. Multiscale methods with compactly supported radial basis functions for the Stokes problem on bounded domains. Adv. Comput. Math. 2016, 42, 1187–1208. [Google Scholar] [CrossRef]
- Farrell, P.; Wendland, H. RBF multiscale collocation for second order elliptic boundary value problems. SIAM J. Numer. Anal. 2013, 51, 2403–2425. [Google Scholar] [CrossRef]
- Le Gia, Q.T.; Sloan, I.H.; Wendland, H. Zooming from global to local: A multiscale RBF approach. Adv. Comput. Math. 2017, 43, 581–606. [Google Scholar] [CrossRef]
- Liu, Z. Local multilevel scattered data interpolation. Eng. Anal. Bound. Elem. 2018, 92, 101–107. [Google Scholar] [CrossRef]
- Adams, R.A.; Fournier, P. Sobolev Spaces, Pure and Applied Mathematics, 2nd ed.; Academic Press: New York, NY, USA, 2003; Volume 65. [Google Scholar]
- Wendland, H. Scattered Data Approximation; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Schaback, R. Convergence of unsymmetric kernel-based meshless collocation methods. SIAM J. Numer. Anal. 2007, 45, 333–351. [Google Scholar] [CrossRef]
- Schaback, R. Unsymmetric meshless methods for operator equations. Numer. Math. 2010, 114, 629–651. [Google Scholar] [CrossRef]
- Fasshauer, G.E. Solving differential equations with radial basis functions: Multilevel methods and smoothing. Adv. Comput. Math. 1999, 11, 139–159. [Google Scholar] [CrossRef]
- Schaback, R.; Wendland, H. Inverse and saturation theroems for radial basis function interpolation. Math. Comput. 2001, 71, 669–681. [Google Scholar] [CrossRef]
- Böhmer, K.; Schaback, R. A nonlinear discretization theory. J. Comput. Appl. Math. 2013, 254, 204–219. [Google Scholar] [CrossRef]

| Centers | Rate | Rate | ||
|---|---|---|---|---|
| 9 | 1.113967 | 1.537637 | ||
| 25 | 6.950489 | 0.680520 | 8.362841 | 0.878650 |
| 81 | 7.783806 | 3.158567 | 8.430085 | 3.310374 |
| 289 | 4.849611 | 4.004535 | 3.210030 | 4.714889 |
| 1089 | 2.253331 | 4.427738 | 2.115728 | 3.923360 |
| 4225 | 1.128459 | 4.319634 | 3.572115 | 2.566304 |
| 4.42e+01(s) | 4.42e+01(s) |
| Centers | Rate | Rate | ||
|---|---|---|---|---|
| 9 | 1.113967 | 1.537637 | ||
| 25 | 4.205301 | 1.405425 | 6.950489 | 1.145528 |
| 81 | 2.288906 | 0.877551 | 9.036469 | 2.943283 |
| 289 | 2.330558 | −0.026018 | 5.143627 | 0.812973 |
| 1089 | 1.986107 | 0.230732 | 4.590088 | 0.164264 |
| 4225 | 2.010532 | −0.017633 | 4.395273 | 0.062569 |
| 1.46e+00(s) | 3.16e+00(s) |
| Centers | Initial ε = 0.5 | Rate | Initial ε = 0.25 | Rate |
|---|---|---|---|---|
| 9 | 1.113967 | 1.537637 | ||
| 25 | 5.321739 | 1.065737 | 7.271406 | 1.080408 |
| 81 | 8.346277 | 2.672693 | 5.457674 | 3.735876 |
| 289 | 3.142086 | 1.409410 | 9.231828 | 2.563598 |
| 1089 | 1.646392 | 0.932414 | 2.752895 | 1.745667 |
| 4225 | 9.882529 | 0.736356 | 1.053762 | 1.385401 |
| 2.08e+00(s) | 5.53e+00(s) |
| Centers | Initial ε = 0.5 | Rate | Initial ε = 0.25 | Rate |
|---|---|---|---|---|
| 9 | 8.715764 | 9.975067 | ||
| 25 | 4.380040 | 0.992683 | 5.449353 | 0.872242 |
| 81 | 8.765413 | 2.321050 | 2.426089 | 1.167453 |
| 289 | 1.146738 | 2.934287 | 8.471348 | 4.839897 |
| 1089 | 8.960631 | 3.677791 | 8.592933 | 6.623297 |
| 4225 | 9.886575 | 3.180058 | 1.835490 | 2.226986 |
| 4.42e+00(s) | 9.97e+00(s) |
| Centers | Rate | Rate | ||
|---|---|---|---|---|
| 9 | 5.154990 | 2.312114 | ||
| 25 | 2.523773 | 1.030387 | 2.501198 | 3.208521 |
| 81 | 5.129004 | 2.298832 | 8.196424 | 1.609552 |
| 289 | 1.169028 | 2.133369 | 1.976536 | 2.052021 |
| 1089 | 9.400882 | 3.636370 | 2.150290 | 3.200371 |
| 4225 | 7.877153 | 3.577050 | 4.789840 | 2.166482 |
| 5.61e+01(s) | 5.59e+01(s) |
| Centers | Initial ε = 0.5 | Rate | Initial ε = 0.25 | Rate |
|---|---|---|---|---|
| 9 | 5.154990 | 2.312114 | ||
| 25 | 1.880555 | 1.454811 | 2.523773 | −0.126370 |
| 81 | 1.845714 | 0.026979 | 2.415339 | 0.063357 |
| 289 | 3.232111 | −0.808298 | 1.619474 | 0.576701 |
| 1089 | 4.385499 | −0.440264 | 2.008842 | −0.310839 |
| 4225 | 4.782622 | −0.125061 | 2.480243 | −0.304117 |
| 2.11e+00(s) | 6.14e+00(s) |
| Centers | Initial ε = 0.5 | Rate | Initial ε = 0.25 | Rate |
|---|---|---|---|---|
| 9 | 5.154990 | 2.312114 | ||
| 25 | 5.196034 | −0.011441 | 1.827791 | 0.339111 |
| 81 | 5.185346 | 0.002970 | 1.886535 | −0.045637 |
| 289 | 5.185903 | −0.000155 | 1.890747 | −0.003218 |
| 1089 | 5.185993 | −0.000025 | 1.891628 | −0.000672 |
| 4225 | 5.186014 | −0.000006 | 1.891758 | −0.000099 |
| 3.19e+00(s) | 9.47e+00(s) |
| Centers | Initial ε = 0.125 | Rate | Initial ε = 0.0625 | Rate |
|---|---|---|---|---|
| 9 | 3.345335 | 2.877511 | ||
| 25 | 1.189874 | 1.491342 | 4.878530 | 2.560303 |
| 81 | 1.238221 | −0.057460 | 2.944292 | 0.728526 |
| 289 | 1.166663 | 0.085881 | 1.706502 | 0.786879 |
| 1089 | 1.158203 | 0.010500 | 7.585827 | 1.169664 |
| 4225 | 1.159396 | −0.001485 | 6.469642 | 0.229621 |
| 2.03e+01(s) | 4.21e+01(s) |
| Centers | Initial ε = 0.5 | Rate | Initial ε = 0.25 | Rate |
|---|---|---|---|---|
| 9 | 5.154990 | 2.312114 | ||
| 25 | 1.200069 | 2.102853 | 4.838983 | 2.256436 |
| 81 | 2.112357 | 2.506192 | 3.451755 | 3.809302 |
| 289 | 7.398191 | 1.513609 | 1.075014 | 5.004903 |
| 1089 | 2.440784 | 1.599828 | 5.835322 | 4.203399 |
| 4225 | 5.606710 | 2.122118 | 2.751613 | 4.406463 |
| 4.07e+00(s) | 9.69e+00(s) |
| Centers | Initial ε = 0.125 | Rate | Initial ε = 0.0625 | Rate |
|---|---|---|---|---|
| 9 | 3.345335 | 2.877511 | ||
| 25 | 1.060521 | 4.979305 | 6.205372 | 5.535160 |
| 81 | 1.898035 | 2.482195 | 1.655041 | 1.906651 |
| 289 | 2.565084 | 6.209357 | 2.628040 | 5.976736 |
| 1089 | 6.264679 | 5.355622 | 4.950454 | 5.730282 |
| 4225 | 2.553269 | 4.616823 | 1.102677 | 5.488478 |
| 1.97e+01(s) | 3.76e+01(s) |
| Centers | Initial ε = 0.5 | Rate | Initial ε = 0.25 | Rate |
|---|---|---|---|---|
| 9 | 3.117164 | 1.719666 | ||
| 25 | 2.035525 | 0.614833 | 8.951139 | 0.941985 |
| 81 | 1.837566 | 0.147605 | 8.238622 | 3.441596 |
| 289 | 1.749727 | 0.070666 | 3.459194 | 1.251967 |
| 1089 | 1.744016 | 0.004717 | 1.833905 | 0.915517 |
| 4225 | 1.787914 | −0.035864 | 1.024535 | 4.161878 |
| 1.94e+00(s) | 5.48e+00(s) |
| Centers | Initial ε = 0.125 | Rate | Initial ε = 0.0625 | Rate |
|---|---|---|---|---|
| 9 | 5.473827 | 3.289428 | ||
| 25 | 1.411404 | 5.277347 | 6.743427 | 2.286283 |
| 81 | 2.332565 | 2.597141 | 2.429136 | 4.794967 |
| 289 | 4.059524 | 2.522535 | 2.783964 | 3.125231 |
| 1089 | 1.776398 | 4.514284 | 1.239397 | 7.811358 |
| 4225 | 5.102425 | 5.121628 | 3.532572 | 5.132776 |
| 1.25e+01(s) | 2.62e+01(s) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Xu, Q. A Multiscale RBF Collocation Method for the Numerical Solution of Partial Differential Equations. Mathematics 2019, 7, 964. https://doi.org/10.3390/math7100964
Liu Z, Xu Q. A Multiscale RBF Collocation Method for the Numerical Solution of Partial Differential Equations. Mathematics. 2019; 7(10):964. https://doi.org/10.3390/math7100964
Chicago/Turabian StyleLiu, Zhiyong, and Qiuyan Xu. 2019. "A Multiscale RBF Collocation Method for the Numerical Solution of Partial Differential Equations" Mathematics 7, no. 10: 964. https://doi.org/10.3390/math7100964
APA StyleLiu, Z., & Xu, Q. (2019). A Multiscale RBF Collocation Method for the Numerical Solution of Partial Differential Equations. Mathematics, 7(10), 964. https://doi.org/10.3390/math7100964




