Existence and Iterative Method for Some Riemann Fractional Nonlinear Boundary Value Problems
Abstract
1. Introduction
2. Preliminary Results
2.1. Fractional Calculus
- For and
- if and only ifwhere m is the smallest integer greather than or equal to γ and are arbitrary constants.
- Assume that thenwhere m is the smallest integer greather than or equal to γ and are arbitrary constants.
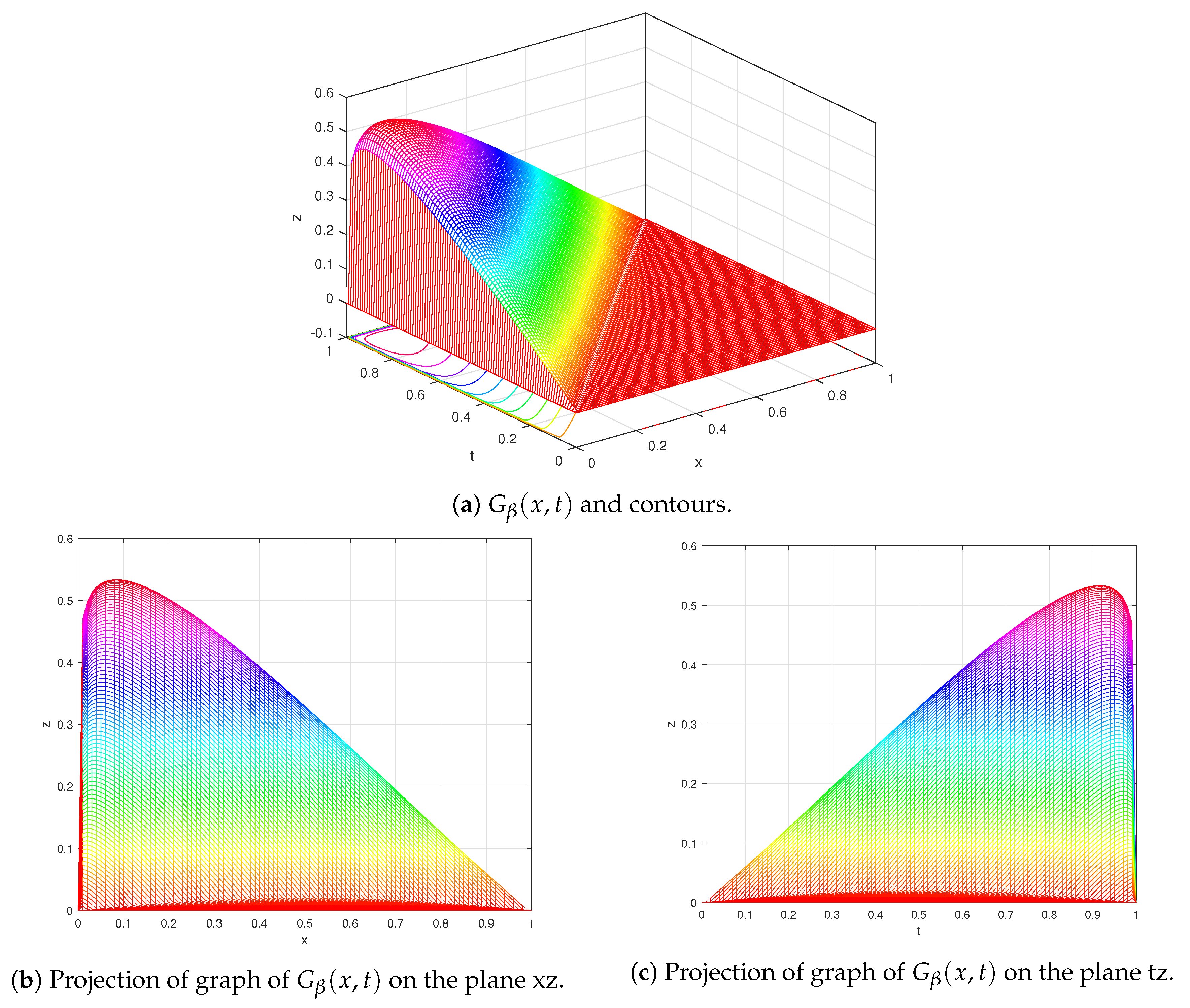
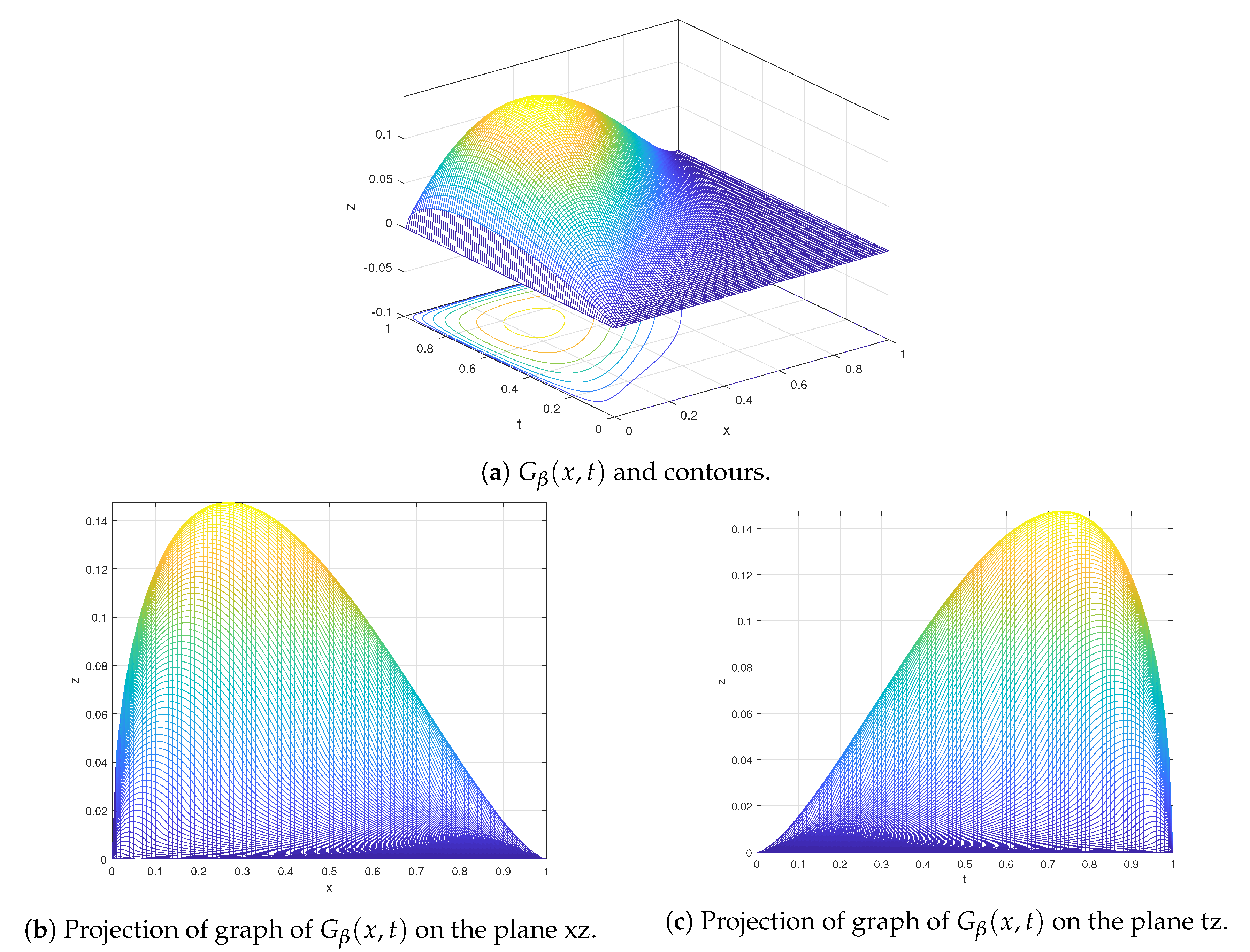
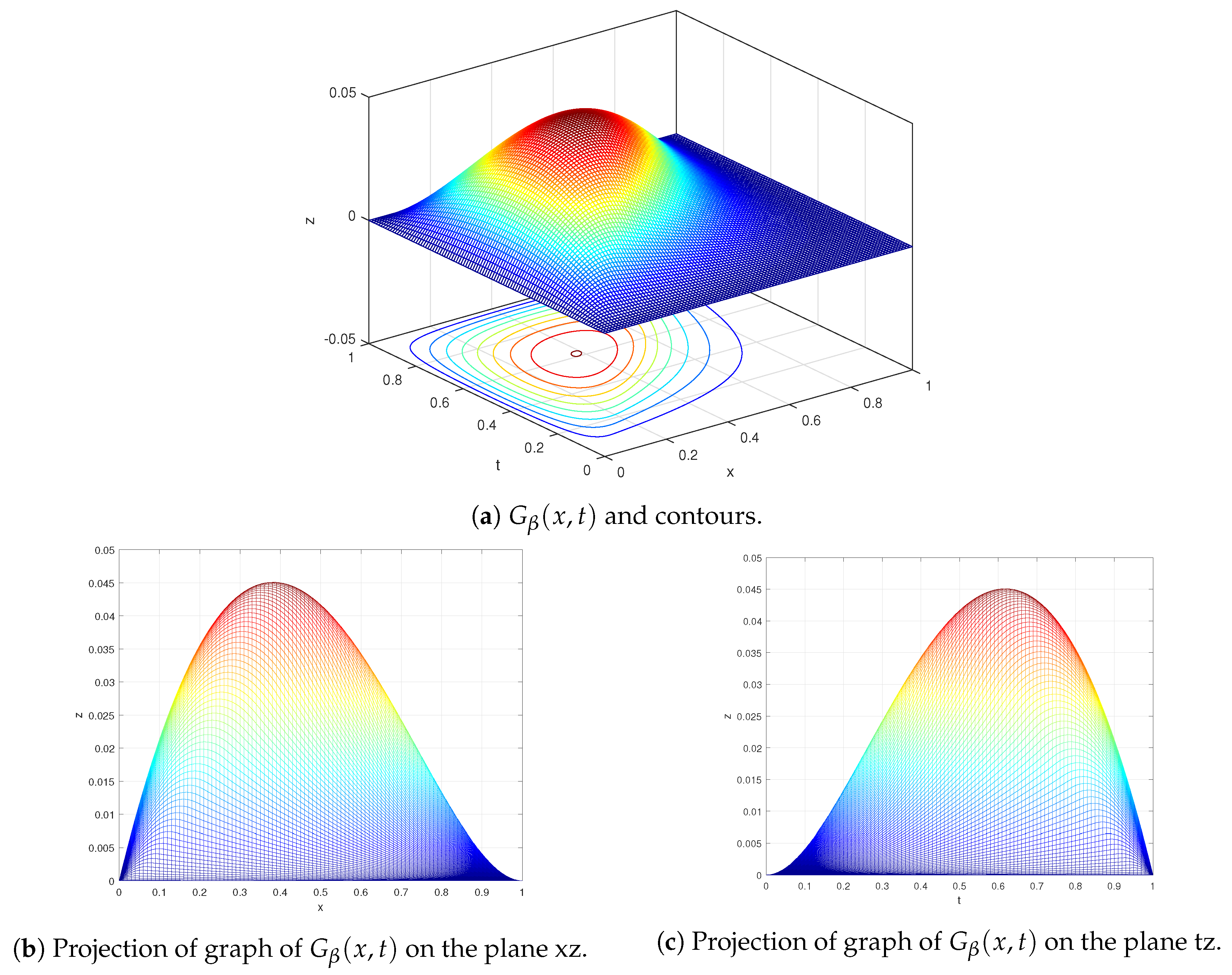
2.2. Estimates on the Green’s Function
- is continuous on
- For , we havewhere
- For , we havewhere
3. Main Results
3.1. Existence and Uniqueness of a Solution
- for any
- for any
- for any
- for any
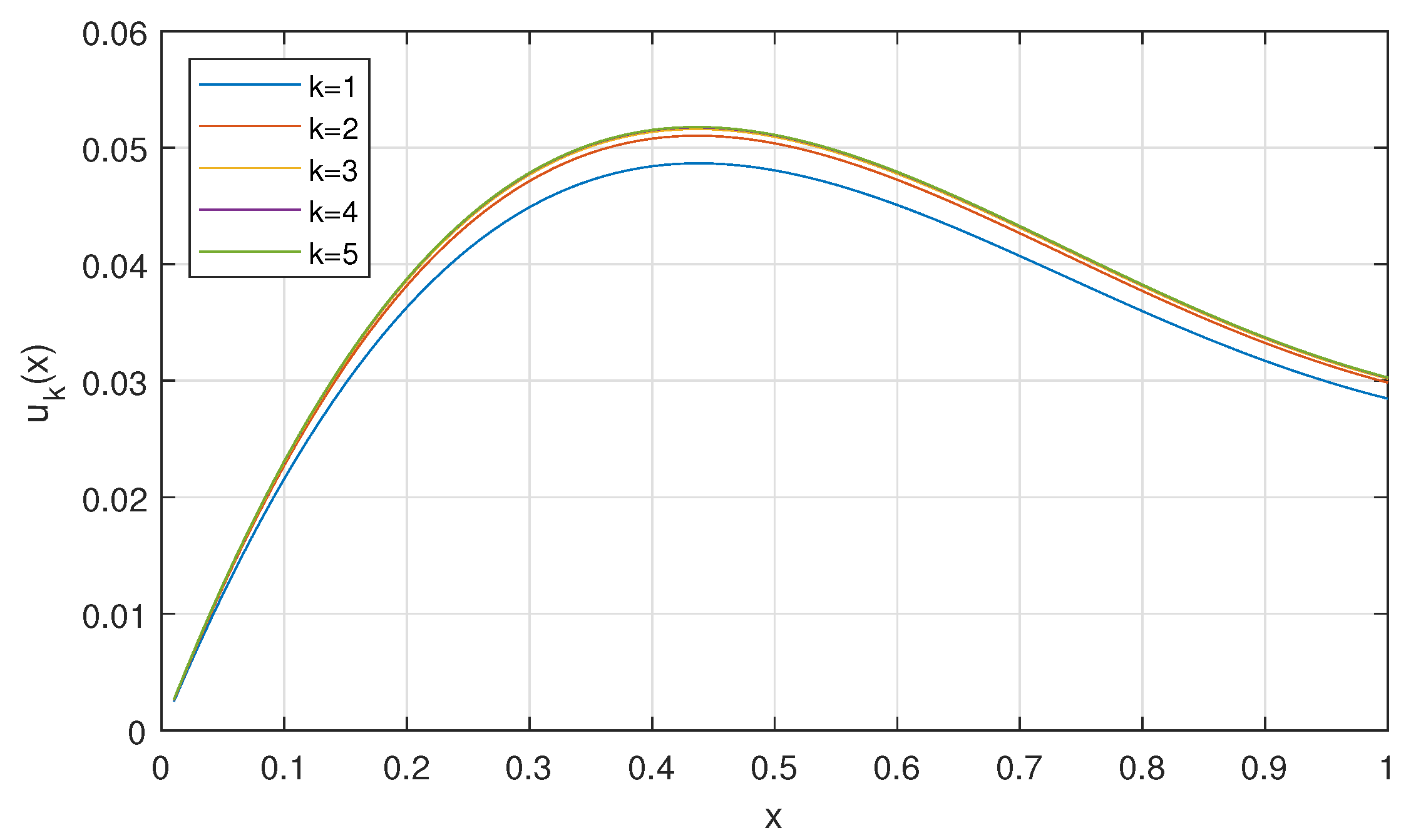
3.2. Iterative Method and Examples
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aftabizadeh, A.R. Existence and uniqueness theorems for fourth-order boundary value problems. J. Math. Anal. Appl. 1986, 116, 415–426. [Google Scholar] [CrossRef]
- Li, Y. Existence of positive solutions for the cantilever beam equations with fully nonlinear terms. Nonlinear Anal. 2016, 27, 221–237. [Google Scholar] [CrossRef]
- Alsaedi, R.S. Existence and global behavior of positive solutions for some fourth order boundary value problems. Abstr. Appl. Anal. 2014, 2014, 657926. [Google Scholar] [CrossRef][Green Version]
- Bai, Z. The method of lower and upper solutions for a bending of an elastic beam equation. J. Math. Anal. Appl. 2010, 248, 195–202. [Google Scholar] [CrossRef]
- Bai, Z. Positive solutions of some nonlocal fourth-order boundary value problem. Appl. Math. Comput. 2010, 215, 4191–4197. [Google Scholar] [CrossRef]
- Dang, Q.A. Iterative method for solving the Neumann boundary value problem for biharmonic type equation. J. Comput. Appl. Math. 2006, 196, 634–643. [Google Scholar] [CrossRef]
- Dang, Q.A.; Dang, Q.L.; Ngo, T.K.Q. A novel efficient method for nonlinear boundary value problems. Numer. Algorithms 2017, 76, 427–439. [Google Scholar]
- Li, Y. A monotone iterative technique for solving the bending elastic beam equations. Appl. Math. Comput. 2010, 2017, 2200–2208. [Google Scholar] [CrossRef]
- Ma, T.F.; da Silva, J. Iterative solutions for a beam equation with nonlinear boundary conditions of third order. Appl. Math. Comput. 2004, 159, 11–18. [Google Scholar] [CrossRef]
- Ma, R.; Tisdell, C.C. Positive solutions of singular sublinear fourth order boundary value problems. Appl. Anal. 2005, 12, 1199–1220. [Google Scholar] [CrossRef]
- Wei, Y.; Song, Q.; Bai, Z. Existence and iterative method for some fourth order nonlinear boundary value problems. Appl. Math. Lett. 2019, 87, 101–107. [Google Scholar] [CrossRef]
- Dang, Q.; Quy, N. Existence results and iterative method for solving the cantilever beam equation with fully nonlinear term. Nonlinear Anal. RWA 2017, 36, 56–68. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, O.; Staněk, S. Positive solutions for Dirichlet problems of singular nonlinear fractional differential equations. J. Math. Anal. Appl. 2010, 371, 57–68. [Google Scholar] [CrossRef]
- Bachar, I.; Mâagli, M.; Toumi, F.; Zine el Abidine, Z. Existence and Global Asymptotic Behavior of Positive Solutions for Sublinear and Superlinear Fractional Boundary Value Problems. Chin. Ann. Math. Ser. B 2016, 37, 1–28. [Google Scholar] [CrossRef]
- Bai, Z.; Lü, H. Positive solutions for boundary value problem of nonlinear fractional differential equation. J. Math. Anal. Appl. 2005, 311, 495–505. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. On the solution of nonlinear fractional order differential equations used in the modeling of viscoplasticity. In Scientific Computing in Chemical Engineering. II-Computational Fluid Dynamics, Reaction Engineering and Molecular Properties; Keil, F., Mackens, W., Voss, H., Werther, J., Eds.; Springer: Heidelberg, Germany, 1999; pp. 217–224. [Google Scholar]
- Gaul, L.; Klein, P.; Kempfle, S. Damping description involving fractional operators. Mech. Syst. Signal Process. 1991, 5, 81–88. [Google Scholar] [CrossRef]
- Glockle, W.G.; Nonnenmacher, T.F. A fractional calculus approach of self-similar protein dynamics. Biophys. J. 1995, 68, 46–53. [Google Scholar] [CrossRef]
- Graef, J.R.; Kong, L.; Kong, Q.; Wang, M. Existence and uniqueness of solutions for a fractional boundary value problem with Dirichlet boundary condition. Electron. J. Qual. Theory Differ. Equ. 2013, 55, 1–11. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kaufmann, E.R.; Mboumi, E. Positive solutions of a boundary value problem for a nonlinear fractional differential equation. Electron. J. Qual. Theory Differ. Equ. 2008, 3, 1–11. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, J. Positive solutions for boundary value problems of nonlinear fractional differential equation. Nonlinear Anal. 2009, 71, 5545–5550. [Google Scholar] [CrossRef]
- Mâagli, H.; Mhadhebi, N.; Zeddini, N. Existence and Estimates of Positive Solutions for Some Singular Fractional Boundary Value Problems. Abstr. Appl. Anal. 2009, 2009, 120781. [Google Scholar] [CrossRef]
- Mâagli, H.; Mhadhebi, N.; Zeddini, N. Existence and Exact Asymptotic Behavior of Positive Solutions for a Fractional Boundary Value Problem. Abstr. Appl. Anal. 2013, 2013, 420514. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B. 1975, 12, 2455–2477. [Google Scholar] [CrossRef]
- Timoshenko, S.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Xu, X.; Jiang, D.; Yuan, C. Multiple positive solutions for the boundary value problem of a nonlinear fractional differenteial equation. Nonlinear Anal. 2009, 71, 4676–4688. [Google Scholar] [CrossRef]
- Xu, X.; Jiang, D.; Yuan, C. Singular Positone and Semipositone Boundary Value Problems of Nonlinear Fractional Differential Equations. Math. Probl. Eng. 2009, 2009, 535209. [Google Scholar]
- Zhang, Y.; Liu, X.; Belić, M.R.; Zhong, W.; Zhang, Y.; Xiao, M. Propagation Dynamics of a Light Beam in a Fractional Schrödinger Equation. Phys. Rev. Lett. 2015, 115, 180403. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Wu, Y. Multiple positive solutions of a singular fractional differential equation with negatively perturbed term. Math. Comput. Model. 2012, 55, 1263–1274. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zhang, Z.; Ahmed, N.; Zhang, Y.; Li, F.; Belić, M.R.; Xiao, M. Unveiling the Link Between Fractional Schrödinger Equation and Light Propagation in Honeycomb Lattice. Ann. Phys. (Berlin) 2017, 529, 1700149. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, H.; Belić, M.R.; Zhu, Y.; Zhong, W.; Zhang, Y.; Christodoulides, D.N.; Xiao, M. PT symmetry in a fractional Schrödinger equation. Laser Photonics Rev. 2016, 10, 526–531. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations. In North-Holland Mathematics Studies Vol. 204; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivative. Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bachar, I.; Mâagli, H.; Eltayeb, H. Existence and Iterative Method for Some Riemann Fractional Nonlinear Boundary Value Problems. Mathematics 2019, 7, 961. https://doi.org/10.3390/math7100961
Bachar I, Mâagli H, Eltayeb H. Existence and Iterative Method for Some Riemann Fractional Nonlinear Boundary Value Problems. Mathematics. 2019; 7(10):961. https://doi.org/10.3390/math7100961
Chicago/Turabian StyleBachar, Imed, Habib Mâagli, and Hassan Eltayeb. 2019. "Existence and Iterative Method for Some Riemann Fractional Nonlinear Boundary Value Problems" Mathematics 7, no. 10: 961. https://doi.org/10.3390/math7100961
APA StyleBachar, I., Mâagli, H., & Eltayeb, H. (2019). Existence and Iterative Method for Some Riemann Fractional Nonlinear Boundary Value Problems. Mathematics, 7(10), 961. https://doi.org/10.3390/math7100961




