Remarks on the Preservation of the Almost Fixed Point Property Involving Several Types of Digitizations

Abstract

This paper explores a certain relationship between the almost fixed point property (AFPP for short) of a compact and n-dimensional Euclidean space and that of its digitized space. Based on several types of digitizations, we prove that the AFPP of a compact and n-dimensional Euclidean cube is preserved by each of the $U(k)$, the $L(k)$ and the Khalimsky digitizations, $k\in 3^n-1,n\in \mathbb{N}$.

1. Introduction

In order to study the fixed point property (FPP for brevity) and the almost (or approximate) fixed point property (AFPP for short) for Euclidean topological spaces and digital spaces, we need to recall some terminology from digital topology and fixed point theory. Hereafter, let $\mathbb{N}$, ${\mathbb{Z}}^n$ and $\mathbb{R}$ represent the sets of natural numbers, points in the Euclidean n-dimensional space with integer coordinates and real numbers, respectively. In addition, for distinct integers $a,b\in \mathbb{Z}$, we often use the notation ${[a,b]}_{\mathbb{Z}}:=\{t\in \mathbb{Z}|a\le t\le b\}$ called a digital interval [1]. We say that a digital image $(X,k)$ (see Equation (2)) is k-connected if, for any two points $x,y\in X$, there is a finite sequence $<x_i{>}_{i\in {[0,l]}_{\mathbb{Z}}}\subset X$ such that $x_0=x$ and $x_l=y$ and, furthermore, $x_i$ and $x_j$ are k-adjacent (see Equations (1) and (2) in Section 2) if $|i-j|=1,i,j\in {[0,l]}_{\mathbb{Z}}$ [1]. We say that a non-empty and k-connected digital image $(X,k)$ has the FPP [2] if every k-continuous map $f:(X,k)\to (X,k)$ has a point $x\in X$ such that $f(x)=x$ (see Section 2 for more details). In addition, we say that a non-empty digital image $(X,k)$ has the AFPP [2] if every k-continuous map $f:(X,k)\to (X,k)$ has a point $x\in X$ such that $f(x)=x$ or $f(x)$ is k-adjacent to x [2]. In general, a non-empty object Y of a category has the FPP if every morphism $h:Y\to Y$ has a point $y\in Y$ such that $h(y)=y$. It is obvious that the AFPP is weaker than the FPP [2].

Recently, many works relating to the FPP and the AFPP for digital spaces have been proceeded [2,3,4,5,6,7,8,9,10,11]. Furthermore, given a Euclidean subspace X, several types of digitizations of X were also developed [6,12,13]. These approaches indeed play important roles in applied topology and computer science, e.g., image processing, image analysis and so on. Hereafter, a compact and n-dimensional Euclidean space means a certain bounded and closed (or compact) n-dimensional Euclidean topological space $({\prod }_{i\in \{1,2,\cdots ,n\}}[-l_i,l_i]:=X,E_X^n)$,$l_i\in \mathbb{N}$. Then, we naturally wonder if there is a certain relationship between the AFPP of the above $(X,E_X^n)$ and the AFPP of a space obtained by its digitization (or a digitized space for short). Furthermore, based on the study of the AFPP of a finite digital picture, e.g., ${[a,b]}_{\mathbb{Z}}\times {[c,d]}_{\mathbb{Z}}$ with 8-adjacency [2], we may ask if the n-dimensional digital cube $({({[-1,1]}_{\mathbb{Z}})}^n:={[-1,1]}_{\mathbb{Z}}^n:=X,k)$ on ${\mathbb{Z}}^n$ has the AFPP. Regarding this issue, we need to recall the notion of a digital space. For a nonempty binary symmetric relation set $(X,\pi )$, we recall that X is π-connected [11] if for any two elements x and y of X there is a finite sequence $<x_i{>}_{i\in {[0,l]}_{\mathbb{Z}}}$ of elements in X such that $x=x_0$, $y=x_l$ and $(x_j,x_{j+1})\in \pi$ for $j\in {[0,l-1]}_{\mathbb{Z}}$. We say that a digital space is a nonempty, $\pi$-connected, symmetric relation set, denoted by $(X,\pi )$ [11]. It is well known that a digital space [11] includes a digital image $(X,k)$ with digital k-connectivity (i.e., Rosenfeld model) [2,14], a Khalimsky (K-, for brevity) topological space with Khalimsky adjacency [15], a Marcus-Wyse (M-, for short) topological space with Marcus-Wyse adjacency [16], and so forth [5,9,10] (see Section 2 in details).

Based on the several kinds of digitizations of a Euclidean space in [6,12,13], the present paper explores a certain relationship between the AFPP for Euclidean topological subspaces in ${\mathbb{R}}^n$ and that for their U-, L-, K-, or M-digitized spaces in ${\mathbb{Z}}^n$ from the viewpoint of digital topology, where U-, L-, K- and M- means the upper limit, the lower limit, Khalimsky and Marcus-Wyse topology, respectively.

In fixed point theory for digital spaces, we also assume that every digital space $(X,\pi )$ is $\pi$-connected and non-empty.

The rest of the paper is organized as follows: Section 2 provides basic notions from digital topology. Section 3 investigates some properties of digitizations in a K-, an M-, a U-, or an L-topological approach. Section 4 develops a link between the AFPP from the viewpoint of $ETC$ and the AFPP from the viewpoint of $DTC$, $KTC$, or $MTC$, where $ETC$, $DTC$, $KTC$ and $MTC$ are a Euclidean topological, a digital topological, a Khalimsky topological and a Marcus-Wyse topological category, respectively (for more details, see Section 2).

2. Several Kinds of Digital Topological Categories, DTC, KTC and MTC

To study the FPP or the AFPP for digital spaces from the viewpoint of digital topology, we first need to recall the k-adjacency relations of n-dimensional integer grids (see Equation (2)), a digital k-neighborhood, digital continuity, and so forth [2,14,17]. To study n-dimensional digital images, $n\in \mathbb{N}$, as a generalization of the k-adjacency relations of ${\mathbb{Z}}^n,n\in \{1,2,3\}$, we will take the following approach [17] (see also [18]).

For a natural number m, $1\le m\le n$, distinct points

$$p=(p_1,p_2,\cdots ,p_n)\mathrm{and}q=(q_1,q_2,\cdots ,q_n)\in {\mathbb{Z}}^n,$$

(1)

are $k(m,n)$-adjacent if at most m of their coordinates differ by ±1, and all others coincide.

According to the operator of Equation (1), the $k(m,n)$-adjacency relations of ${\mathbb{Z}}^n,n\in \mathbb{N}$, are obtained [17] (see also [18]) as follows:

$$\left\{\begin{array}{l}(\mathrm{a})k:=k(t,n)={\displaystyle \sum _{i=n-t}^{n-1}}{2}^{n-i}{C}_i^n,\mathrm{where}{C}_i^n=\frac{n!}{(n-i)!i!}\\ \mathrm{or},\mathrm{equivalently},\\ (\mathrm{b})k:=k(t,n)={\displaystyle \sum _{i=1}^t}{2}^i{C}_i^n,\mathrm{where}{C}_i^n=\frac{n!}{(n-i)!i!}.\end{array}\right\}$$

(2)

A. Rosenfeld [14] called a set $X(\subset {\mathbb{Z}}^n)$ with a k-adjacency a digital image, denoted by $(X,k)$. Indeed, to study digital images on ${\mathbb{Z}}^n$ in the graph-theoretical approach [2,14], using the k-adjacency relations of ${\mathbb{Z}}^n$ of Equation (2), we say that a digital k-neighborhood of p in ${\mathbb{Z}}^n$ is the set [14]

$$N_k(p):=\left\{q\right|p\mathrm{is}k\text{-}\mathrm{adjacent}\mathrm{to}q\}\cup \left\{p\right\}.$$

In addition, for a k-adjacency relation of ${\mathbb{Z}}^n$, a simple k-path with $l+1$ elements on $({\mathbb{Z}}^n,k)$ is assumed to be a finite sequence $<x_i{>}_{i\in {[0,l]}_{\mathbb{Z}}}\subset {\mathbb{Z}}^n$ (or k-path) such that $x_i$ and $x_j$ are k-adjacent if and only if $|i-j|=1$. If $x_0=x$ and $x_l=y$, then the length of the simple k-path, denoted by $l_k(x,y)$, is the number l. A simple closed k-curve with l elements on $({\mathbb{Z}}^n,k)$, denoted by $S{C}_k^{n,l}$ [17], is a simple k-path $<x_i{>}_{i\in {[0,l-1]}_{\mathbb{Z}}}$ on $({\mathbb{Z}}^n,k)$, where $x_i$ and $x_j$ are k-adjacent if and only if $|i-j|=\pm 1(modl)$.

For a digital image $(X,k)$, for $X\subset {\mathbb{Z}}^n$, we put [17]

$$N_k(x,1):=N_k(x)\cap X.$$

(3)

As a generalization of $N_k(x,1)$ of Equation (3), for a digital image $(X,k)$ let us recall a digital k-neighborhood [17]. Namely, the digital k-neighborhood of $x_0\in X$ with radius $\epsilon$ is defined in X to be the following subset of X [17]

$$N_k(x_0,\epsilon ):=\{x\in X|l_k(x_0,x)\le \epsilon \}\cup \left\{x_0\right\},$$

(4)

where $l_k(x_0,x)$ is the length of a shortest simple k-path from $x_0$ to x and $\epsilon \in \mathbb{N}$.

Given a digital image $(X,k)$ on ${\mathbb{Z}}^n$ and for two points $x,y\in X$, if there is no k-path connecting between these points, then we define $l_k(x,y)=\infty$. In addition, we may represent the notion of “k-connected” as follows: a digital image $(X,k)$ on ${\mathbb{Z}}^n$ is k-connected if, for any distinct points $x,y\in X$. there is a k-path connecting these two points.

Definition 1.

We say that a k-connected digital image $(X,k)$ on ${\mathbb{Z}}^n$ is bounded if for some point $x_0\in X$, there is an $N_k(x_0,\epsilon )$ that is equal to the set X, where $\epsilon ⪇\infty$.

In general, we say that a digital image $(X,k)$ on ${\mathbb{Z}}^n$ is bounded if there is a finite set $\{x_i\in X|i\in M:\mathrm{finite}\}$ such that $X={\cup }_{i\in M}{N}_k(x_i,{\epsilon }_i)$, where ${\epsilon }_i⪇\infty$.

The author in [2] established the notion of digital continuity of a map $f:(X,k_0)\to (Y,k_1)$ by saying that f maps every $k_0$-connected subset of $(X,k_0)$ into a $k_1$-connected subset of $(Y,k_1)$ (see Theorem 2.4 of [2]). Motivated by this approach, the digital continuity of maps between digital images was represented in terms of the neighborhood of Equation (3), as follows:

Proposition 1

([17]). Let $(X,k_0)$ and $(Y,k_1)$ be digital images in ${\mathbb{Z}}^{n_0}$ and ${\mathbb{Z}}^{n_1}$, respectively. A function $f:(X,k_0)\to (Y,k_1)$ is $(k_0,k_1)$-continuous if and only if for every $x\in X$, $f(N_{k_0}(x,1))\subset N_{k_1}(f(x),1)$.

In Proposition 1, in case $k_0=k_1$, the map f is called a $k_1$-continuous map. Using digitally continuous maps, we establish the category of digital images, denoted by DTC, consisting of the following two data [17] (see also [5]):

• The set of objects $(X,k)$, denoted by $Ob(DTC)$;
• For every ordered pair of objects $(X,k_1)$ and $(Y,k_2)$, the set of all $(k_1,k_2)$-continuous maps $f:(X,k_1)\to (Y,k_2)$ as morphisms.

In DTC, in case $k_0=k_1:=k$, we will particularly use the notation DTC(k).

The authors in [2] initiated the study of the FPP and the AFPP for digital pictures (see Proposition 2). Based on the approach, many works explored the properties for several types of digital spaces, such as Khalimsky, Marcus-Wyse topological spaces, and digital metric spaces associated with some typical fixed point theorems.

Proposition 2

([2]). Consider a bounded digital plane (or finite digital picture) $(X,k),k\in \{4,8\}$, i.e., $({[a,b]}_{\mathbb{Z}}\times {[c,d]}_{\mathbb{Z}}:=X,k)$.

Then, it does not have the FPP. However, $(X,8)$ has the AFPP.

Motivated by Proposition 2, we obtain the following:

Theorem 1.

For $n\in \mathbb{N}$, the n-dimensional digital cube with k-adjacency $({[-1,1]}_{\mathbb{Z}}^n:=X,k)$ on ${\mathbb{Z}}^n$ has the AFPP if and only if $k=3^n-1$.

Proof. 

Consider ${[-1,1]}_{\mathbb{Z}}^n:=X$ with a certain k-adjacency of ${\mathbb{Z}}^n$ (see Equation (2)), i.e., a digital image $(X,k)$. Motivated by Proposition 2, it is obvious that any k-adjacency of ${\mathbb{Z}}^n$$(X,k)$ does not have the FPP. With the given hypothesis, in case $(X,k)$ has the AFPP, for any k-continuous self-map of $(X,k)$, there is a point $x\in X$ such that $f(x)=x$ or $f(x)$ is k-adjacent to x. For any k-connectivity of $(X,k)$, since any k-continuity of f implies $(3^n-1)$-continuity of f (see Equations (1) and (2)), we may take the $(3^n-1)$-connectivity of X for supporting the given AFPP of $(X,k)$.

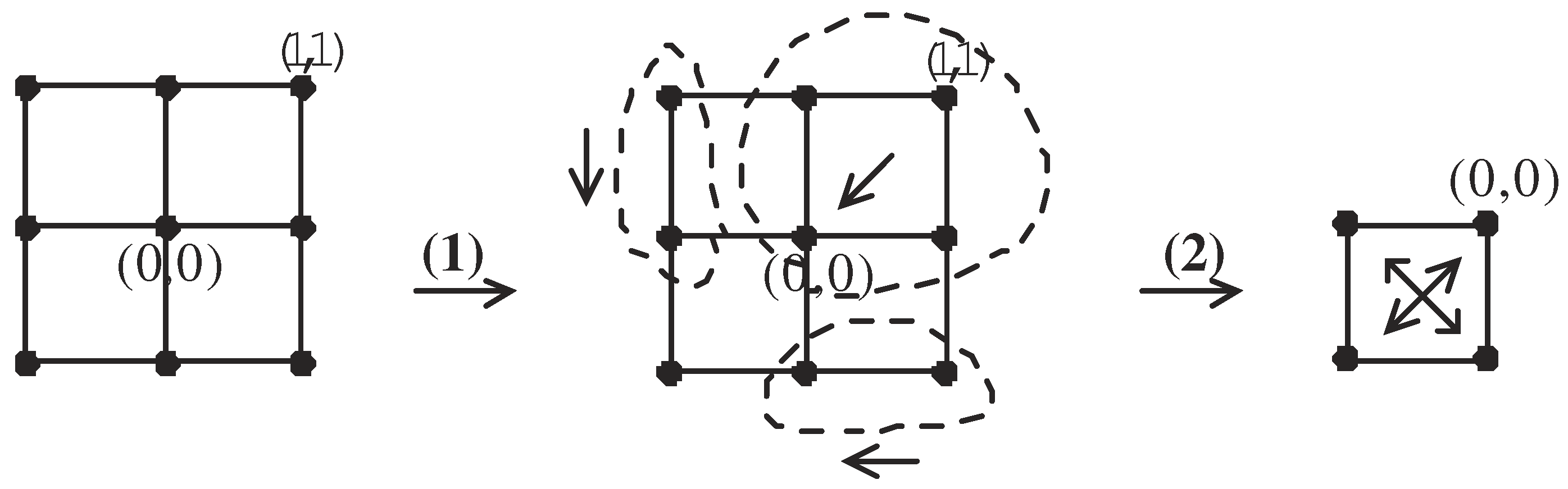
Conversely, if $k\ne 3^n-1$, then we first prove that $(X,k)$ does not have the AFPP. For instance, in ${\mathbb{Z}}^2$, consider the digital image $({[-1,1]}_{\mathbb{Z}}^2:=X,4)$ instead of $(X,8)$. Let us consider a self-map of $(X,4)$. To be precise, assume $f:(X,4)\to (X,4)$ as the composite of the following two 4-continuous maps $f_1$ and $f_2$ (see Figure 1(1)).

$$\left\{\begin{array}{l}{f}_1(X_1)=\left\{(0,-1)\right\},X_1=\{(0,-1),(1,-1)\},\\ f_1(X_2)=\left\{(0,0)\right\},X_2=\{(0,0),(1,0),(0,1),(1,1)\},\\ f_1(X_3)=\left\{(-1,0)\right\},X_3=\{(-1,0),(-1,1)\},\mathrm{and}\\ f_1((-1,-1))=(-1,-1).\end{array}\right\}$$

(5)

Then, we obtain $f_1(X)=\{(0,0),(0,-1),(-1,-1),(-1,0)\}$ (see Figure 1(2)). Let us further consider the map $f_2:f_1(X)\to f_1(X)$ such that

$$(0,0)\leftrightarrow (-1,-1),\mathrm{and}(0,-1)\leftrightarrow (-1,0).$$

(6)

Owing to the 4-continuous maps $f_1$ and $f_2$, the composite $f=f_2\circ f_1:(X,4)\to (X,4)$ is also a 4-continuous map. Although this map f is a 4-continuous self-map of $(X,4)$, it is not a map for supporting the AFPP of $(X,4)$.

As a generalization of the non-AFPP of $({[-1,1]}_{\mathbb{Z}}^2:=X,4)$, using a method similar to the Equations (5) and (6), we obtain that a digital image $(X:={[-1,1]}_{\mathbb{Z}}^n,k),k\ne 3^n-1$ does not have the AFPP either. For instance, on ${\mathbb{Z}}^3$, consider $(Y:={[-1,1]}_{\mathbb{Z}}^3,18:=k(2,3))$. Using the notion of 18-continuity of any self-map of $(Y,18)$ (see Proposition 1), we prove that the digital image $(Y,18)$ does not have the AFPP. To be precise, consider a self-map g of $(Y,18)$ in the following way: For $t\in {[-1,1]}_{\mathbb{Z}}$,

$$\left\{\begin{array}{l}g(1,1,t)=(-1,-1,t),\\ g(1,0,t)=(0,0,t)=g(0,1,t),\\ g(-1,1,t)=(-1,0,t),g(1,-1,t)=(0,-1,t),\mathrm{and}\\ g(Y_1)=1_{Y_1},\mathrm{where}{Y}_1={[-1,0]}_{\mathbb{Z}}^2\times {[-1,1]}_{\mathbb{Z}}.\end{array}\right\}$$

(7)

According to this map g, we obtain

$$g(Y)={[-1,0]}_{\mathbb{Z}}^2\times {[-1,1]}_{\mathbb{Z}}:=Z(\subset Y).$$

Let us now consider the self-map h of Z such that

$$\left\{\begin{array}{l}h(Z_1)=1_{Z_1},Z_1=\{(0,0),(-1,0),(0,-1),(-1,-1)\}\times {[0,1]}_{\mathbb{Z}},\\ h(s,-1)=(s,0),\mathrm{where}s\in \{(0,0),(-1,0),(0,-1),(-1,-1)\}.\end{array}\right\}$$

(8)

Then, we obtain

$$h(Z)={[-1,0]}_{\mathbb{Z}}^2\times {[0,1]}_{\mathbb{Z}}(\subset Y):=W.$$

Let us now further consider the self-map r of W such that

$$\left\{\begin{array}{l}(0,0,0)\leftrightarrow (-1,-1,1),(0,-1,0)\leftrightarrow (-1,0,1),\\ (-1,-1,0)\leftrightarrow (0,0,1),(-1,0,0)\leftrightarrow (0,-1,1).\end{array}\right\}$$

(9)

Then, it is obvious that each of the maps h and r is a 6-continuous map and the map g is an 18-continuous map (see Equations (7)–(9)). Hence, the composite $r\circ h\circ g:(Y,18)\to (Y,18)$ is an 18-continuous map. However, this composite does not have the AFPP of $(Y,18)$ (see the map r of Equation (9)).

Finally, in case of $(X:={[-1,1]}_{\mathbb{Z}}^n,3^n-1)$, according to the notion of $(3^n-1)$-continuity of any self-map of $(X,3^n-1)$ (see Proposition 1), it is obvious that the digital image $(X,3^n-1)$ has the AFPP. Indeed, to obtain a contradiction, suppose the digital image $(X,3^n-1)$ does not have the AFPP. Then, any self-map of $(X,3^n-1)$ is not a $(3^n-1)$-continuous map (see the point $0_3:=(0,0,0))$. □

Let us now briefly recall some basic facts and terminology involving the K-topology. The Khalimsky line topology on $\mathbb{Z}$, denoted by $(\mathbb{Z},\kappa )$, is induced by the set $\{{[2n-1,2n+1]}_{\mathbb{Z}}:n\in \mathbb{Z}\}$ as a subbase [15]. Furthermore, the product topology on ${\mathbb{Z}}^n$ induced by $(\mathbb{Z},\kappa )$ is called the Khalimsky product topology on ${\mathbb{Z}}^n$ (or Khalimsky n-dimensional space), which is denoted by $({\mathbb{Z}}^n,{\kappa }^n)$. Based on this approach, for a point p in $({\mathbb{Z}}^n,{\kappa }^n)$, its smallest open neighborhood $S{N}_K(p)$ is obtained [19].

Hereafter, for a subset $X\subseteq {\mathbb{Z}}^n,n\ge 1$, we will denote by $(X,{\kappa }_X^n)$ a subspace induced by $({\mathbb{Z}}^n,{\kappa }^n)$, and it is called a K-topological space. For a point x in $(X,{\kappa }_X^n)$, we often call $S{N}_K(x)$ the smallest open neighborhood of x in $(X,{\kappa }_X^n)$.

For $(X,{\kappa }_X^n)$, we say that distinct points x and y in X are K-adjacent in $(X,{\kappa }_X^n)$ if $y\in S{N}_K(x)$ or $x\in S{N}_K(y)$ [19]. According to this K-adjacency, it is obvious that a K-topological space $(X,{\kappa }_X^n)$ is a digital space.

A simple closed K-curve with l elements on $({\mathbb{Z}}^n,{\kappa }^n)$, denoted by $S{C}_K^{n,l}$, is defined as a finite sequence $<x_i){>}_{i\in {[0,l-1]}_{\mathbb{Z}}}$ in ${\mathbb{Z}}^n$ [20], where $x_i$ and $x_j$ are K-adjacent if and only if $|i-j|=\pm 1(modl)$.

Using the set of K-topological spaces $(X,{\kappa }_X^n)$ and that of K-continuous maps for every ordered pair objects of K-topological spaces, we obtain the category of K-topological spaces, denoted by KTC [4].

Let us now recall basic concepts on M-topology. The M-topology on ${\mathbb{Z}}^2$, denoted by $({\mathbb{Z}}^2,\gamma )$, is induced by the set $\left\{U(p)\right|p\in {\mathbb{Z}}^2\}$ in Equation (10) below as a base [16], where, for each point $p=(x,y)\in {\mathbb{Z}}^2$,

$$U(p):=\left\{\begin{array}{l}{N}_4(p)\mathrm{if}x+y\mathrm{is}\mathrm{even},\mathrm{and}\\ \left\{p\right\}:\mathrm{otherwise}.\end{array}\right\}$$

(10)

Owing to Equation (10), the set $U(p)$ is the smallest open neighborhood of the point p in ${\mathbb{Z}}^2$, denoted by $S{N}_M(p)$. Hereafter, for a subset $X\subseteq {\mathbb{Z}}^2$, we will denote by $(X,{\gamma }_X)$ a subspace induced by $({\mathbb{Z}}^2,\gamma )$, and it is called an M-topological space. For a point x in $(X,{\gamma }_X)$, we denote by $S{N}_M(x)$ the smallest open neighborhood of x in $(X,{\gamma }_X)$. For $(X,{\gamma }_X)$, we say that distinct points x and y in X are M-adjacent in $(X,{\gamma }_X)$ if $y\in S{N}_M(x)\mathrm{or}x\in S{N}_M(y)$ [10], where $S{N}_M(p)$ is the smallest open set containing the point p in $(X,{\gamma }_X)$. According to this M-adjacency, it turns out that an M-topological space $(X,{\gamma }_X)$ is a digital space [9].

A simple closed M-curve with l elements on $({\mathbb{Z}}^2,\gamma )$, denoted by $S{C}_M^{2,l}$, is defined as a finite sequence $<x_i{>}_{i\in {[0,l-1]}_{\mathbb{Z}}}$ in ${\mathbb{Z}}^2$ [8], where $x_i$ and $x_j$ are M-adjacent if and only if $|i-j|=\pm 1(modl)$.

Using the set of M-topological spaces $(X,{\gamma }_X)$ and that of M-continuous maps for every ordered pair of objects of M-topological spaces, we obtain the category of M-topological spaces, denoted by MTC [10].

Remark 1.

It is obvious that $S{C}_K^{n,l}$ [4], $S{C}_M^{2,l}$ [7] and $S{C}_k^{n,l}$ [3] do not have the AFPP in the categories $KTC$, $MTC$ and $DTC$, respectively. For instance, for $S{C}_K^{n,l}:={(x_i)}_{i\in {[0,l-1]}_{\mathbb{Z}}}$, consider a self-map of $S{C}_K^{n,l}$ such that $f(x_i)=x_{i+2(modl)}$. Whereas f is a K-continuous map, there is no point $x\in S{C}_K^{n,l}$ such that $f(x)=x$ or $f(x)$ is K-adjacent to x [5]. By using a method similar to this approach for $S{C}_K^{n,l}$, it is obvious that $S{C}_M^{2,l}$ and $S{C}_k^{n,l}$ do not have the AFPP in DTC and MTC, respectively (see also [7]).

3. Some Properties of a K-, an M-, a U- or an L-Digitization

Regarding several types of digitizations of $X(\subseteq {\mathbb{R}}^n)$ into a certain digital space, first of all we need to examine if given a digitization preserves the typical connectedness of X into the digital connectedness of the corresponding digitized space associated with a digital space structure. Indeed, the authors in [13] intensively studied this property. To combine this approach with the study of a preservation of the AFPP of a compact Euclidean topological space into that of its digitized space, we need to study a K-, an M-, a U- or an L-digitization [6,12,13]. Hence, this section recalls four types of local rules being used to formulate special kinds of neighborhoods of a given point $p\in {\mathbb{Z}}^n$.

Definition 2

([6]). In ${\mathbb{R}}^n$, for each point $p:={(p_i)}_{i\in {[1,n]}_{\mathbb{Z}}}\in {\mathbb{Z}}^n$, we define the set $N_K(p):=\left\{{(x_i)}_{i\in {[1,n]}_{\mathbb{Z}}}\right\}$, which is called the local K-neighborhood of p associated with $({\mathbb{Z}}^n,{\kappa }^n)$, where $t\in \mathbb{Z}$ and

$$\left\{\begin{array}{l}\mathit{if}{p}_i=2t,\mathit{then}{x}_i\in [2t-\frac{1}{2},2t+\frac{1}{2}],\\ \mathit{if}{p}_i=2t+1,\mathit{then}{x}_i\in (2t+\frac{1}{2},2t+\frac{3}{2}).\end{array}\right\}$$

It is obvious [6] that the set $\left\{N_K(p)\right|p\in {\mathbb{Z}}^n\}$ is a partition of ${\mathbb{R}}^n$.

Remark 2.

In view of Definition 2, for each point $p\in {\mathbb{Z}}^n$, $N_K(p)$ can be substantially used to digitize $({\mathbb{R}}^n,E^n)$ onto the K-topological space $({\mathbb{Z}}^n,{\kappa }^n)$ by using the following map [6]: For each $N_K(p),p\in {\mathbb{Z}}^n$

$$N_K(p)(\subset {\mathbb{R}}^n)\to p(\in {\mathbb{Z}}^n).$$

Using $N_K(p)$ of Definition 2 and the method given in Remark 2, let us recall the K-digitization of a non-empty space $(X,E_X^n)$.

Definition 3

([6]). For a nonempty space $(X,E_X^n)$, we define a K-digitization of X, denoted by $D_K(X)$, to be the space with K-topology

$$D_K(X):=\{p\in {\mathbb{Z}}^n|N_K(p)\cap X\ne \varnothing \}.$$

Let us now recall the M-digitization. For a point $p\in {\mathbb{Z}}^2$, the authors in [12,13] used an M-localized neighborhood of the given point p, denoted by $N_M(p)$, associated with $({\mathbb{Z}}^2,\gamma )$.

Definition 4

([12,13]). In ${\mathbb{R}}^2$, for a point $p:=(p_1,p_2)\in {\mathbb{Z}}^2$, we define the following neighborhood of p:

$$N_M(p):=\left\{\begin{array}{l}\left\{(t_1,t_2)\right|t_i\in [p_i-\frac{1}{2},p_i+\frac{1}{2}],i\in \{1,2\}\}\\ \mathit{if}p=(p_1,p_2)\in \left\{(2m,2n)\right|m,n\in \mathbb{Z}\};\\ \left\{(t_1,t_2)\right|t_i\in [p_i-\frac{1}{2},p_i+\frac{1}{2}],i\in \{1,2\}\}\backslash \left\{(p_1\pm \frac{1}{2},p_2\pm \frac{1}{2})\right\}\\ \mathit{if}p=(p_1,p_2)\in \left\{(2m+1,2n+1)\right|m,n\in \mathbb{Z}\}and;\\ \left\{(t_1,t_2)\right|t_i\in (p_i-\frac{1}{2},p_i+\frac{1}{2}),i\in \{1,2\}\}\\ \mathit{if}p=(p_1,p_2)\in \{(2m,2n+1),(2m+1,2n)|m,n\in \mathbb{Z}\},\end{array}\right\}$$

which is called an M-localized neighborhood of p associated with $({\mathbb{Z}}^2,\gamma )$.

It is obvious [12] that the set $\left\{N_M(p)\right|p\in {\mathbb{Z}}^2\}$ is a partition of ${\mathbb{R}}^2$.

Remark 3.

In view of Definition 4, for each point $p\in {\mathbb{Z}}^2$, $N_M(p)$ can be substantially used to digitized $({\mathbb{R}}^2,E^2)$ onto the M-topological space $({\mathbb{Z}}^2,\gamma )$ via the following map. For each $N_M(p),p\in {\mathbb{Z}}^2$

$$N_M(p)(\subset {\mathbb{R}}^2)\to p(\in {\mathbb{Z}}^2).$$

Using $N_K(p)$ of Definition 4 and the method given in Remark 3, we can define an M-digitization of a non-empty space $(X,E_X^2)$, as follows.

Definition 5

([12,13]). For a nonempty 2-dimensional Euclidean topological space $(X,E_X^2)$ in ${\mathbb{R}}^2$, we define an M-digitization of X, denoted by $D_M(X)$, to be the set in ${\mathbb{Z}}^2$ with M-topology

$$D_M(X):=\{p\in {\mathbb{Z}}^2|N_M(p)\cap X\ne \varnothing \}.$$

Remark 4.

In view of Definition 5, for each point $p\in {\mathbb{Z}}^2$, $N_M(p)$ can be substantially used to digitize the spaces $(X,E_X^2)$ in $Ob(ETC)$ into M-topological spaces $D_M(X)$ in $Ob(MTC)$.

Using Definitions 3 and 5 and Remarks 1, 2 and 3, for $X\subseteq {\mathbb{R}}^n$, we obtain the following:

Proposition 3.

For $X\subseteq {\mathbb{R}}^n$ and $Y\subseteq {\mathbb{R}}^2$, there are K- and M-digitizations

$$D_K:P({\mathbb{R}}^n)\to ({\mathbb{Z}}^n,{\kappa }^n)and{D}_M:P({\mathbb{R}}^2)\to ({\mathbb{Z}}^2,\gamma )$$

defined by

$$D_K(X)=(D_K(X),{\kappa }_{D_K(X)}^n)and{D}_M(Y)=(D_M(Y),{\gamma }_{D_M(Y)}).$$

In Proposition 3, $P(T)$ means the power set of the set T.

Let us now recall the so-called U-digitization of $(X,U_X)$. The upper limit topology (U-topology, for brevity) on $\mathbb{R}$, denoted by $(\mathbb{R},E_U)$, is induced by the set $\{(a,b]|a,b\in \mathbb{R}\mathrm{and}a<b\}$ as a base [21]. Based on the U-topology on $\mathbb{R}$, we obtain the product topology on ${\mathbb{R}}^n$, denoted by $({\mathbb{R}}^n,E_U^n)$, induced by $(\mathbb{R},E_U)$. Based on $({\mathbb{R}}^n,E_U^n)$, we use a U-local rule [13] that is used to digitize $({\mathbb{R}}^n,E_U^n)$ into $({\mathbb{Z}}^n,D^n)$, where $({\mathbb{Z}}^n,D^n)$ is a discrete topological space.

Definition 6

([13]). Under $({\mathbb{R}}^n,E_U^n)$, for a point $p:={(p_i)}_{i\in {[1,n]}_{\mathbb{Z}}}\in {\mathbb{Z}}^n$, we define $N_U(p):=\left\{{(x_i)}_{i\in {[1,n]}_{\mathbb{Z}}}\right|x_i\in (p_i-\frac{1}{2},p_i+\frac{1}{2}]\}$, and we call $N_U(p)$ the U-localized neighborhood of p associated with $({\mathbb{R}}^n,E_U^n)$.

Using the U-local rule of Definition 6, we define the following:

Definition 7

([13]). Let $D_{U(k)}:({\mathbb{R}}^n,E^n)\to ({\mathbb{Z}}^n,k)$ be the map defined by $D_{U(k)}(x)=p$, where $x\in N_U(p),p\in {\mathbb{Z}}^n$ and the k-adjacency is taken according to the situation. Then, we say that $D_{U(k)}$ is a $U(k)$-digitization operator.

Using the method similar to the establishment of $({\mathbb{R}}^n,E_U^n)$ and the above U-local rule, let us now consider the L-local rule associated with L-topology and its product topology, where the lower limit topology (L-topology, for brevity) on $\mathbb{R}$, denoted by $(\mathbb{R},E_L)$, is induced by the set $\{[a,b)|a,b\in \mathbb{R}\mathrm{and}a<b\}$ as a base [21].

Definition 8

([13]). Under $({\mathbb{R}}^n,E_L^n)$, for a point $p:={(p_i)}_{i\in {[1,n]}_{\mathbb{Z}}}\in {\mathbb{Z}}^n$, we define $N_L(p):=\{{(x_i)}_{i\in {[1,n]}_{\mathbb{Z}}}|x_i\in [p_i-\frac{1}{2},p_i+\frac{1}{2})\}$. We call $N_L(p)$ the L-localized neighborhood of p associated with $({\mathbb{R}}^n,E_L^n)$.

It is obvious [13] that the set $\left\{N_L(p)\right|p\in {\mathbb{Z}}^n\}$ is a partition of ${\mathbb{R}}^n$.

Using the L-local rule of Definition 8, we define the following:

Definition 9

([13]). Let $D_{L(k)}:({\mathbb{R}}^n,E^n)\to ({\mathbb{Z}}^n,k)$ be the map defined by $D_{L(k)}(x)=p$, where $x\in N_L(p),p\in {\mathbb{Z}}^n$ and the k-adjacency determined according to the situation. Then, we say that $D_{L(k)}$ is an $L(k)$-digitization operator.

For a non-empty set $X\subset {\mathbb{R}}^n$, let us now recall a $U(k)$- and an $L(k)$-digitization, as follows.

Definition 10

([13]). Let X be a subspace in $({\mathbb{R}}^n,E_U^n)$ (resp. $({\mathbb{R}}^n,E_L^n)$). The U- (resp. L-) digitization of X, denoted by $D_U(X)$ (resp. $D_L(X)$), is defined as follows:

$$\{\begin{array}{l}{D}_U(X)=\{p\in {\mathbb{Z}}^n|N_U(p)\cap X\ne \varnothing \};\\ D_L(X)=\{p\in {\mathbb{Z}}^n|N_L(p)\cap X\ne \varnothing \}\end{array}$$

with a k-adjacency of ${\mathbb{Z}}^n$ of (2) depending on the situation.

Using Definition 10, for $X\subseteq {\mathbb{R}}^n$, we obtain the following:

Proposition 4.

Given a k-adjacency of ${\mathbb{Z}}^n$ and $X\subseteq {\mathbb{R}}^n$, there are $U(k)$- and $L(k)$-digitizations

$$D_{U(k)},D_{L(k)}:P({\mathbb{R}}^n)\to ({\mathbb{Z}}^n,k)$$

defined by

$$D_{U(k)}(X)=(D_U(X),k)\mathit{and}{D}_{L(k)}(X)=(D_L(X),k).$$

In Proposition 4, $P({\mathbb{R}}^n)$ means the power set of of the set ${\mathbb{R}}^n$.

4. Explorations of the Preservation of the AFPP of a Compact Plane into theAFPP of a K-, an M-, a U(k)-, or an L(k)-Digitized Space

The author in [8,10] proved the FPP of the smallest open neighborhood of $({\mathbb{Z}}^n,{\kappa }^n)$ [10] and the non-FPP of a compact M-topological plane in $({\mathbb{Z}}^2,\gamma )$ [8]. Thus, we may now pose the following queries about the AFPP of compact M-topological plane X and the preservation of the AFPP of a compact n-dimensional Euclidean space (or cube) into that of each of K-, M-, U- and L-digitization, as follows:

Question 1

Let X be the set ${\prod }_{i\in \{1,2,\cdots ,n\}}{[-l_i,l_i]}_{\mathbb{Z}}$. How about the FPP or the AFPP of the K-topological space $(X,{\kappa }_X^n)$?

Question 2

Let Y be the set ${\prod }_{i\in \{1,2\}}{[-l_i,l_i]}_{\mathbb{Z}}$. What about the AFPP of the M-topological space $(Y,{\gamma }_Y)$?

Question 3

How about the preservation of the AFPP of a compact n-dimensional Euclidean cube into the AFPP of its $U(k)$-, or $L(k)$-digitized space?

To address these queries, we first compare the FPP among a compact n-dimensional Euclidean space, a compact and n-dimensional K-topological space and a compact M-topological plane as follows:

Lemma 1.

The smallest open neighborhood of $({\mathbb{Z}}^2,\gamma )$ has the FPP.

Proof. 

As the smallest open set $S{N}_M(p)$ of $({\mathbb{Z}}^2,\gamma ),p\in {\mathbb{Z}}^2$, we may consider $U(p)$ (see Equation (10)), where $p\in \{(2m,2n),(2m+1,2n+1)|m,n\in \mathbb{Z}\}$ or a singleton $\left\{p\right\}$, where $p\in \{(2m+1,2n)$, $(2m,2n+1)|m,n\in \mathbb{Z}\}$.

Case 1

Consider $U(p)$, where $p\in \{(2m,2n),(2m+1,2n+1)|m,n\in \mathbb{Z}\}$. Then, assume any M-continuous self-map f of $(U(p),{\gamma }_{U(p)})$. If p is mapped by f onto a point $q\in U(p)\backslash \left\{p\right\}$, then the map should be a constant map with $f(U(p))=\left\{q\right\}$ according to the M-continuity of f, which implies that $(U(p),{\gamma }_{U(p)})$ has the FPP with a fixed point q associated with the map f. In addition, in case $f(p)=p$, the assertion is trivial.

Case 2

Assume that $U(p)$ is a singleton. Then, it is obvious that $(U(p),{\gamma }_{U(p)})$ has the FPP.

□

In MTC, we say that an M-homeomorphic invariant is a property of an M-topological space which is invariable under M-homeomorphism [9].

Proposition 5

([9]). Each of the FPP and the AFPP from the viewpoint of MTC is an M-homeomorphic invariant.

Indeed, in Lemma 1, the shape of $U(p)(\ne \{p\})$ is a diamond. Then, we may pose a query about the FPP of another shape of a diamond, as follows:

Corollary 1.

Consider an M-topological space $(X,{\gamma }_X)$ which is M-homeomorphic to $(Y,{\gamma }_Y)$, where $Y=\{(0,1):=y_1,(1,1):=y_2,(0,2):=y_3,(-1,1):=y_4,(0,0):=y_5\}$. Then, $(X,{\gamma }_X)$ has the FPP.

Proof. 

According to Proposition 5, since the FPP in MTC is an M-topological invariant property [8], we may prove that $(Y,{\gamma }_Y)$ has the FPP. For any M-continuous self-map f of $(Y,{\gamma }_Y)$, we prove that there is always a point $y\in Y$ such that $f(y)=y$. To be precise, consider any M-continuous self-map f of $(Y,{\gamma }_Y)$. In case $f(y_1)=y_1$, $y_1$ is a fixed point of f. In case $f(y_1)\ne y_1$, i.e., we may assume $f(y_1)\in \{y_2,y_3,y_4,y_5\}$. Then, according to the M-continuity of f, f should have the fixed point $f(y_1)\in Y$, which implies that there is a point $y_i\in \{y_2,y_3,y_4,y_5\}$ satisfying $f(y_i)=y_i$. Thus, $(Y,{\gamma }_Y)$ is proved to have the FPP. □

The notion of an M-retract is used to study both the FPP and the AFPP of M-topological spaces [8]. Thus, let us recall it.

Definition 11

([8]). In MTC, we say that an M-continuous map $r:(X^{\prime },{\gamma }_{X^{\prime }})\to (X,{\gamma }_X)$ is an M-retraction if

(1) 

$(X,{\gamma }_X)$ is a subspace of $(X^{\prime },{\gamma }_{X^{\prime }}),$ and

(2) 

$r(a)=a$ for all $a\in (X,{\gamma }_X)$.

Then, we say that $(X,{\gamma }_X)$ is an M-retract of $(X^{\prime },{\gamma }_{X^{\prime }})$.

The author in [8] proved that a compact M-topological plane does not have the FPP. Hence, as a more generalized version, we need to study the following:

Lemma 2

([8]). For $(X,{\gamma }_X)$ let $(A,{\gamma }_A)$ be an M-retract of $(X,{\gamma }_X)$. If $(X,{\gamma }_X)$ has the AFPP, then $(A,{\gamma }_A)$ also has the AFPP.

Using this property, unlike the shape of a diamond in Lemma 1 and Corollary 1, as a generalization of the non-FPP of a compact M-topological plane [7], we now prove the non-AFPP of a compact M-topological plane, as follows:

Theorem 2.

A compact M-topological plane does not have the AFPP.

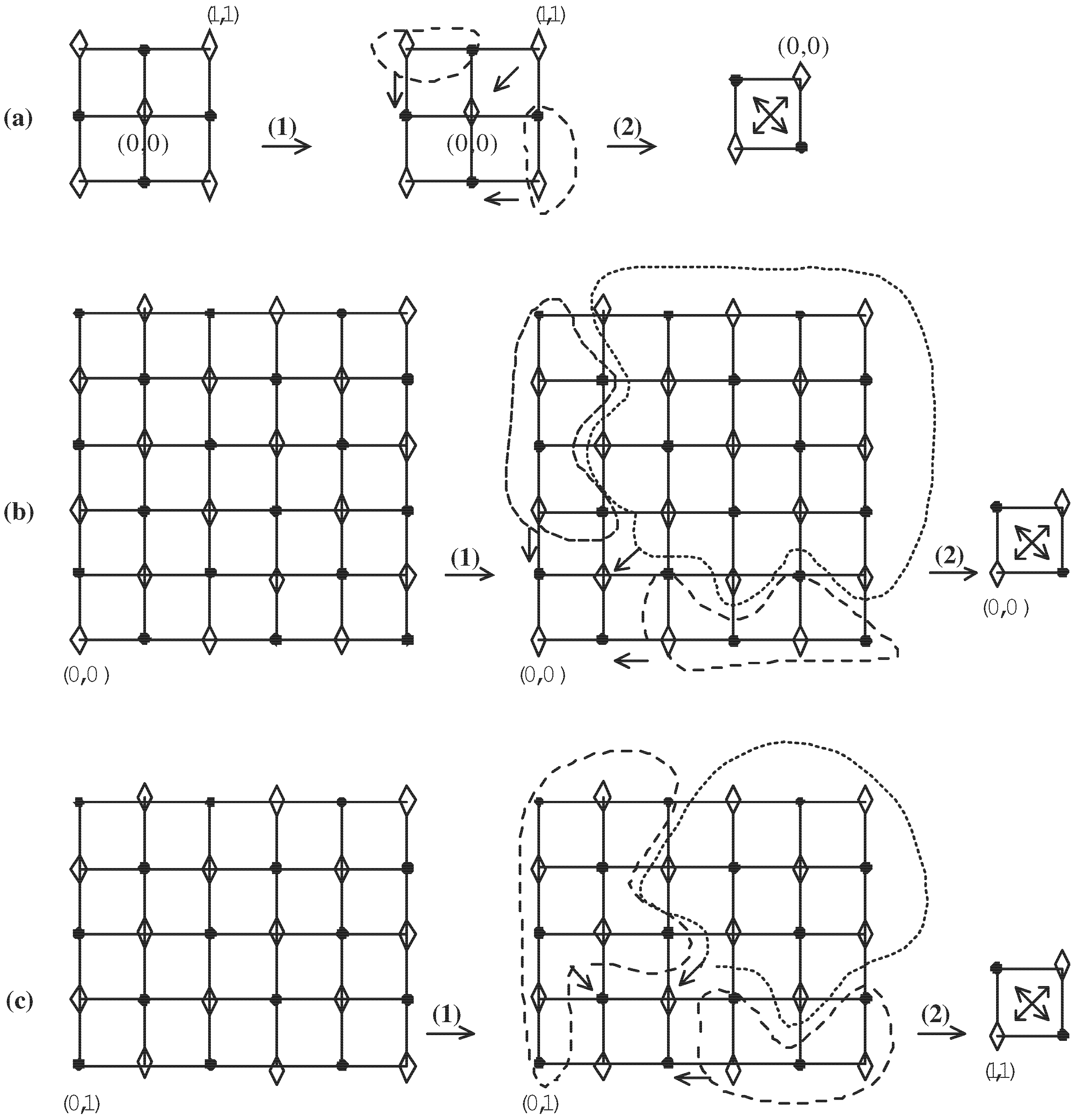
Proof. 

Consider a compact M-topological plane $(X,{\gamma }_X)$ containing the set $X_1\in \{{[2m,2m+1]}_{\mathbb{Z}}\times {[2n,2n+1]}_{\mathbb{Z}},{[2m+1,2m+2]}_{\mathbb{Z}}\times {[2n+1,2n+2]}_{\mathbb{Z}}|m,n\in \mathbb{Z}\}$. Then, we first prove that $(X_1,{\gamma }_{X_1})$ is an M-retract of $(X,{\gamma }_X)$. Furthermore, we second permutate $(X_1,{\gamma }_{X_1})$ as an M-continuous self-map of $(X_1,{\gamma }_{X_1})$. After combining these two processes, we obtain an M-continuous self-map of $(X,{\gamma }_X)$ which does not support the AFPP of $(X,{\gamma }_X)$.

For instance, let us consider the compact M-topological plane $({[-1,1]}_{\mathbb{Z}}^2:=X,{\gamma }_X)$. Then, further consider two self-maps $f_1$ (see Figure 2a(1)), $f_2$ (see Figure 2a(2)) of X such that

$$\left\{\begin{array}{l}{f}_1(X_1)=\left\{(-1,0)\right\},\mathrm{where}{X}_1=\{(-1,0),(-1,1),(0,1)\},\\ f_1(X_2)=\left\{(0,-1)\right\},\mathrm{where}{X}_2=\{(1,0),(1,-1),(0,-1)\},\\ f_1(X_3)=\left\{(0,0)\right\},\mathrm{where}{X}_3=\{(0,0),(1,1)\},\mathrm{and}\\ f_1((-1,-1))=(-1,-1).\end{array}\right\}$$

(11)

Furthermore, $f_2$ is defined as follows:

$$(0,0)\leftrightarrow (-1,-1)\mathrm{and}(-1,0)\leftrightarrow (0,-1).$$

(12)

Since the two maps $f_1$ and $f_2$ are M-continuous self-maps of X (see Equations (11) and (12)), the composite $f_2\circ f_1$ is also an M-continuous self-map of X. However, owing to this composite $f_2\circ f_1$, $(X,{\gamma }_X)$ does not have the AFPP.

In general, let us consider a compact M-topological plane $({[2m,2m+l_1]}_{\mathbb{Z}}\times {[2n,2m+l_2]}_{\mathbb{Z}}:=X,{\gamma }_X),l_i\in \mathbb{N},i\in \{1,2\}$ (see Figure 2b) or $({[2m,2m+l_1]}_{\mathbb{Z}}\times {[2n+1,2m+l_2]}_{\mathbb{Z}}:=X,{\gamma }_X),l_i\in \mathbb{N},i\in \{1,2\}$ (see Figure 2c). Without loss of generality, we may assume $X:={[0,5]}_{\mathbb{Z}}\times {[0,5]}_{\mathbb{Z}}$ (see Figure 2b) or $X:={[0,5]}_{\mathbb{Z}}\times {[1,5]}_{\mathbb{Z}}$ (see Figure 2c) because the other cases are obviously similar to these cases. Then, consider the following two M-continuous self-maps $g_1$ (see Figure 2b(1)), $g_2$ (see Figure 2b(2)) of $(X,{\gamma }_X)$ such that

$$\left\{\begin{array}{l}{g}_1(X_5)=\left\{(0,1)\right\},\mathrm{where}{X}_5=(\left\{0\right\}\times {[2,5]}_{\mathbb{Z}})\cup \{(1,2),(1,4)\},\\ g_1(X_6)=\left\{(1,1)\right\},\mathrm{where}{X}_6=({[2,5]}_{\mathbb{Z}}\times {[2,5]}_{\mathbb{Z}})\cup \{(1,3),(1,5),(3,1),(5,1)\},\\ g_1(X_7)=\left\{(1,0)\right\},\mathrm{where}{X}_7=({[2,5]}_{\mathbb{Z}}\times \left\{0\right\})\cup \{(2,1),(4,1)\},\mathrm{and}\\ g_1(X_8)=1_{X_8},\mathrm{where}{X}_8={[0,1]}_{\mathbb{Z}}\times {[0,1]}_{\mathbb{Z}}.\end{array}\right\}$$

(13)

Furthermore, $g_2$ is defined as follows:

$$(0,0)\leftrightarrow (1,1)\mathrm{and}(1,0)\leftrightarrow (0,1).$$

(14)

Then, the maps $g_1$ and $g_2$ are M-continuous maps (see Equations (13) and (14)) so that the composite $g_2\circ g_2$ is also an M-continuous map. However, there is no point in X supporting the AFPP of $(X,{\gamma }_X)$.

Similarly, let us consider another case such as $X:={[0,5]}_{\mathbb{Z}}\times {[1,5]}_{\mathbb{Z}}$ (see Figure 2c). Then, consider the following two M-continuous self-maps $h_1,h_2$ of $(X,{\gamma }_X)$ such that

$$\left\{\begin{array}{l}{h}_1(X_9)=\left\{(1,2)\right\},\mathrm{where}{X}_9=(\left\{0\right\}\times {[1,5]}_{\mathbb{Z}})\cup (\left\{1\right\}\times {[3,5]}_{\mathbb{Z}})\cup \{(2,3),(2,5)\},\\ h_1(X_{10})=\left\{(2,2)\right\},\mathrm{where}{X}_{10}=({[3,5]}_{\mathbb{Z}}\times {[3,5]}_{\mathbb{Z}})\cup \{(2,4),(4,2)\},\\ h_1(X_{11})=\left\{(2,1)\right\},\mathrm{where}{X}_{11}=({[3,5]}_{\mathbb{Z}}\times \left\{1\right\})\cup \{(3,2),(5,2)\},\mathrm{and}\\ h_1(X_{12})=1_{X_{12}},\mathrm{where}{X}_{12}={[1,2]}_{\mathbb{Z}}\times {[1,2]}_{\mathbb{Z}}.\end{array}\right\}$$

(15)

Furthermore, $h_2$ is defined as follows:

$$(1,1)\leftrightarrow (2,2)\mathrm{and}(2,1)\leftrightarrow (1,2).$$

(16)

Then, the maps $h_1$ and $h_2$ are M-continuous maps (see Equations (15) and (16)) so that the composite $h_2\circ h_2$ is also an M-continuous map. However, there is no point in X supporting the AFPP of $(X,{\gamma }_X)$. □

Based on Propositions 2 and 3, 4 and Theorem 1, we have the following:

Theorem 3.

Let X be a compact and two-dimensional Euclidean topological plane, i.e., $({\prod }_{i\in \{1,2\}}[-l_i,l_i]:=X,E_X^2)$, $l_i\in \mathbb{N}$. Then, we obtain the following:

(1) 

The functor $D_M$ does not preserve the AFPP,

(2) 

The functor $D_{U(k)}$ preserves the AFPP if $k=8$,

(3) 

The functor $D_{L(k)}$ preserves the AFPP if $k=8$

Let X be a compact and n-dimensional Euclidean topological cube, i.e., $({[-1,1]}^n:=X,E_X^n)$. Then, we obtain the following:

(4) 

The functor $D_{U(k)}$ preserves the AFPP if $k=3^n-1$,

(5) 

The functor $D_{L(k)}$ preserves the AFPP if $k=3^n-1$.

Proof. 

Based on Theorem 1 and Propositions 3 and 4, we consider the following digitizations:

$$\left\{\begin{array}{l}(1)D_M:ETC\to MTC,\\ (2)D_{U(k)}:ETC\to DTC\mathrm{in}\mathrm{terms}\mathrm{of}\mathrm{the}U\text{-}\mathrm{digitization},\mathrm{and}\\ (3)D_{L(k)}:ETC\to DTC\mathrm{via}\mathrm{an}L\text{-}\mathrm{digitization}.\end{array}\right\}$$

(1)

For $(X,E_X^2)(\subset ({\mathbb{R}}^2,E^2)$, since $D_M(X)$ is also M-connected [13] and furthermore that $(D_M(X),{\gamma }_{D_M(X)})$ is a compact M-topological plane, by Theorem 2, we obtain that $(D_M(X),{\gamma }_{D_M(X)})$ does not have the AFPP, which completes the proof.

(2)

Using Propositions 2 and 4, the proof is completed.

(3)

Using the method similar to the proof (2), we complete the proof.

(4)

For $(X:={[-1,1]}^n,E_X^n)(\subset ({\mathbb{R}}^n,E^n)$, it is obvious that $(D_{U(k)}(X),k)$ is k-connected, $k=3^n-1$. Hence, by Theorem 1, the digital image $(D_{U(k)}(X),k),k=3^n-1$ has the AFPP. Hence, $D_{U(k)}$ preserves the AFPP if $k=3^n-1$.

Indeed, in case $k\ne 3^n-1$, $(D_{U(k)}(X),k)$ does not have the AFPP. For instance, consider the compact Euclidean topological plane $([0,1]\times [0,1]:=X,E_X^2)$. Since $([0,1]\times [0,1]:=X,E_X^2)$ has the FPP [21], it obviously has the AFPP. Apparently, according to Theorem 1, the 4-connected digital image $(D_{U(4)}(X),4)$ does not have the AFPP because $D_{U(4)}(X)={[0,1]}_{\mathbb{Z}}^2$ is equal to $S{C}_4^{2,4}$. By Remark 1, $(D_{U(4)}(X),4)$ does not have the AFPP.

(5)

It is obvious that $(D_{L(k)}(X),k)$ is k-connected, $k=3^n-1$. Hence, by Theorem 1, the digital image $(D_{L(k)}(X),k),k=3^n-1$ has the AFPP.

Indeed, in case $k\ne 3^n-1$, by using a method similar to the case of (2) above, we prove that $(D_{L(k)}(X),k)$ does not have the AFPP. □

Regarding Questions 1 and 3, the author in [10] proved the FPP of $S{N}_K(p)$ in $({\mathbb{Z}}^n,{\kappa }^n)$. Moreover, the authors in [13] proved that the functor $D_K$ preserves the connectedness of $(X,{\kappa }_X^n)$ into its K-digitized space $(D_K(X),{\kappa }_{D_K(X)}^n)$. Based on this situation, we can conclude that $D_K:({[-1,1]}^n:=X,E_X^n)\to (D_K(X),{\kappa }_{D_K(X)}^n)$ preserves the FPP and furthermore the AFPP. As a general case of this case, we have the following conjecture.

The author in [10] proved that a smallest open set of $({\mathbb{Z}}^n,{\kappa }^n)$ has the FPP, and the authors in [22] proved that ${\prod }_{i\in \{1,2,\cdots ,n\}}{[-l_i,l_i]}_{\mathbb{Z}}:=Y,{\kappa }_Y^n)$ has the FPP, and, using these results, we obtain the following:

Remark 5.

Let X be the compact and n-dimensional Euclidean space ${\prod }_{i\in \{1,2,\cdots ,n\}}[-l_i,l_i]\subset {\mathbb{R}}^n,l_i\in \mathbb{N}$. Then, $(D_K(X),{\kappa }_{D_K(X)}^n)$ has the AFPP because it has the FPP.

5. Conclusions

We have studied the AFPP of an n-dimensional digital cube $(X,3^n-1)$ and also investigated the preservation of the AFPP via each of K-, $U(k)$- and $L(k)$-digitizations if $k=3^n-1$. In addition, based on the non-FPP of a compact M-topological plane, we also explored the non-preservation of the AFPP via an M-digitization. Furthermore, based on the FPP of $S{N}_K(p)$, we also proved the preservation of the FPP of $({[-1,1]}^n:=X,E_X^n)$ via a K-digitization. This approach can facilitate the study of applied sciences such as object classifications, image processing, pattern recognition, artificial intelligence, and so on.