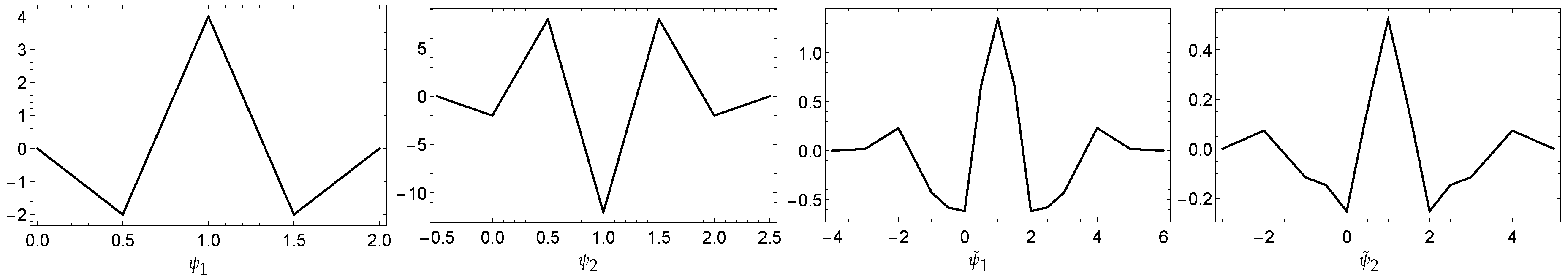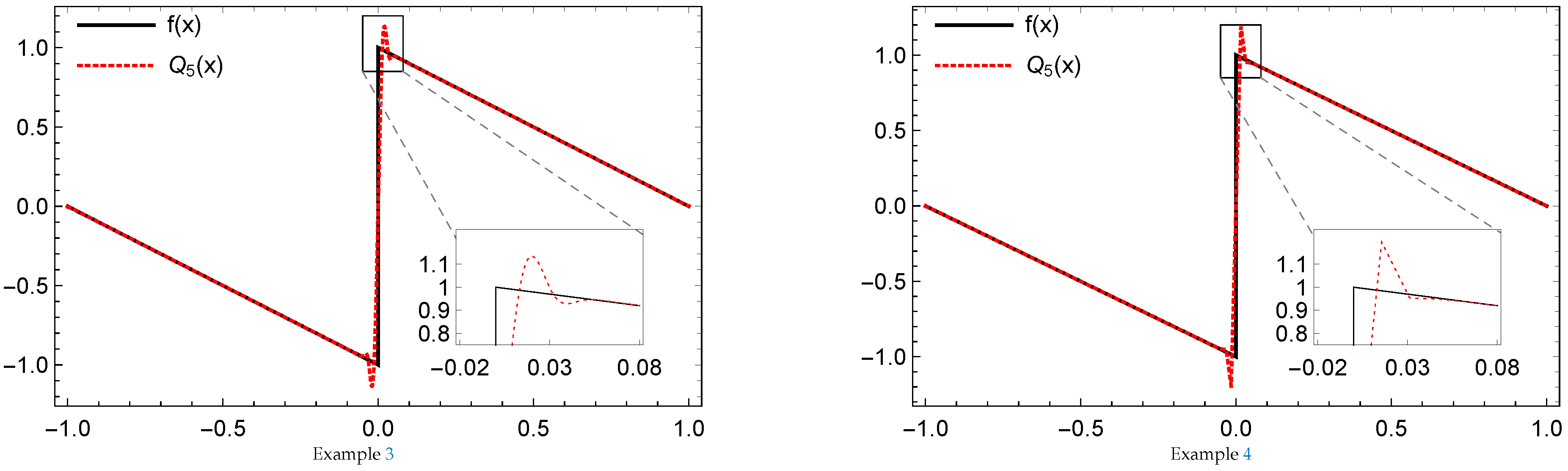1. Introduction
The Gibbs effect was first recognized over a century ago by Henry Wilbraham in 1848 (see Ref. [
1]). However, in 1898 Albert Michelson and Samuel Stratton (see Ref. [
2]) observed it via a mechanical machine that they used to calculate the Fourier partial sums of a square wave function. Soon after, Gibbs explained this effect in two publications [
3,
4]. In his first short paper, Gibbs failed to notice the phenomenon and the limits of the graphs of the Fourier partial sums was inaccurate. In the second paper, he published a correction and gave the description of overshoot at the point of jump discontinuity. In fact, Gibbs did not provide a proof for his argument but only in 1906 a detailed mathematical description of the effect was introduced and named after Gibbs phenomenon by Maxime (see Ref. [
5]) as he believed Gibbs to be the first person noticing it. This phenomenon has been studied extensively in Fourier series and many other situations such as the classical orthogonal expansions (see Refs. [
6,
7,
8]), spline expansion (see Refs. [
9,
10]), wavelets and framelets series (see Refs. [
11,
12,
13,
14,
15,
16,
17]), sampling approximations (see Ref. [
18]), and many other theoretical investigations (see Refs. [
19,
20,
21,
22,
23]). By considering Fourier series, it is impossible to recover accurate point values of a periodic function with many finitely jump discontinuities from its Fourier coefficients. Wavelets and their generalizations (framelets) have great success in coefficients recovering and have many applications in signal processing and numerical approximations (see Refs. [
24,
25,
26,
27]). However, many of these applications are represented by smooth functions that have jump discontinuities. However, expanding these functions will create (most often) unpleasant ringing effect near the gaps. It is the aim of this article to analyze the Gibbs effect of dual tight framelets using a different/higher order of vanishing moments.
Let us recall the preliminary background by introducing some notations (e.g., see Refs. [
28,
29,
30]). Let
denote the space of all square integrable functions over the space
, where
Definition 1 ([
31]).
Let . For , define the function byThen, we say the function ψ is a wavelet if the set forms an orthonormal basis for . Every square integrable function
has a wavelet representation and this requires an orthonormal basis. However, the existence of such complete orthonormal basis is in general hard to construct and their representation is too restrictive and rigid. Therefore, frames were defined by the idea of an additional lower bound of the Bessel sequence which does not constitute an orthonormal set and are not linearly independent. In this paper, we will use dual tight framelets constructed by the mixed oblique extension principle (MOEP) (see Ref. [
32]) which enables us to construct dual tight framelets for
of the form
. The MOEP provides an important method to construct dual framelets from refinable functions and gives us a better number of vanishing moments for
and therefore a better imation orders. In fact, using the unitary extension principle UEP (see Ref. [
32]), it is known that the approximation order of the system will not exceed 2, whereas the MOEP will give us a better approximation (see Ref. [
33]). Please note that the MOEP is a generalization of the UEP and the oblique extension principle OEP. extension principle OEP (see Ref. [
34]), which is again given to ensure that the system
forms a dual tight framelets for
. We refer the reader to Ref. [
34] for the general setup of the MOEP.
Definition 2 ([
31]).
A sequence of elements in is a framelet for if there exists constants such that The numbers are called frame bounds. If we can choose , then is called a tight framelet for .
Please note that we obtain a family of functions
such that
The family
is called dual (reciprocal) framelet of the framelet
. Equations (
1) and (
2) implies, respectively, the following equation
It follows directly from Equation (
3) that any function
has the following framelet representation
The framelet constructions of
and
require mother wavelets, called refinable functions
and
, where a compactly supported function
is said to be refinable if
for some finite supported sequence
. The sequence
is called the
low pass filter of
. For convenience, we define
and
. Therefore, Equation (
4) can be rewritten as
The above series expansion (
6) can be truncated as
which is typical in kernel-based system identification approaches (see Ref. [
35]).
Please note that
can be described by a reproducing kernel Hilbert space which is given by a linear combination of its frame and dual frame product.
where
is called the kernel of
.
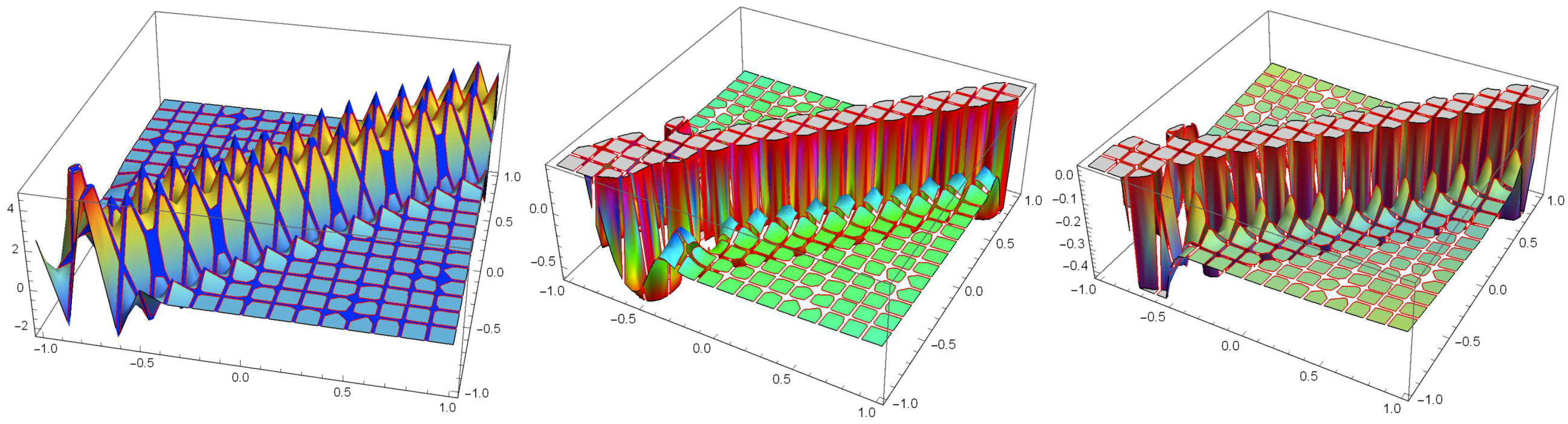
Figure 1 shows the graphs of the kernel
for different framelets.
It is known from the approximation theory, see e.g., Refs. ([
28,
35]), that the truncated expansion (
7) is equivalent to
The general setup is to construct a set of functions as the form of
, which can be summarized as follows: Let
be the closed space generated by
, i.e.,
, and
. Let
be the multiresolution analysis (MRA) generated by the function
and
such that
where
is a finitely supported sequence called
high pass filters of the system. Please note that from Equation (
7), the functions
and
are playing a great role. They are used for computing the coefficients of the expansion of the function
f in terms of
and
, and recovering the projection of
f onto
from the coefficients
. The Fourier transform of a function
is defined to be
and the Fourier series of a sequence
is defined by
2. Gibbs Effect in Quasi-Affine Dual Tight Framelet Expansions
In this section, we study the Gibbs effect by using dual tight framelet in the quasi-affine tight framelet expansions generated via the MOEP. In general, and by using the expansion in Equation (
7), we have
around
x, where
f is continuous except at many finite points. Hence, it is sufficient to study this effect by considering the following function
In fact, this function is useful in the sense that other functions that have the same type of gaps, can be represented as expansions in terms of
f plus a continuous function at
. Please note that if we define
as
then,
has a jump discontinuity at the point
and
. Thus, we have the following result.
Theorem 1. Any function with finitely many jump discontinuities can be written in terms of plus a continuous function at the origin.
Proof. Let
g be a discontinuous function with a jump discontinuity, say at
, of magnitude
D. We could put several of these together for
g but we would likely only be looking at one such function at a time. Suppose that
and
g are in the same direction of the needed jump (i.e., if
, then
, and similarly for
) or multiply
by (− or +)
D to create the needed jump in the same direction. Define
so that
d is a constant that makes the jump endpoints of
F and
g matched at
. Our continuous function in the neighborhood of the point
will then be
. □
The definition of the Gibbs effect under the quasi-projection approximation is defined as follows.
Definition 3. Suppose a function f is smooth and continuous everywhere except at , i.e., limits and exist, and that & . Define to be the truncated partial sum of Equation (7). We say that the framelet expansion of f exhibits the Gibbs effect at the right-hand side of if there is a sequence converging to , andSimilarly, we can define the Gibbs effect on the left-hand side of . Let
to be the system defined by Definition 2. Thus, the corresponding quasi-affine system
generated by
is defined by a collection of translations and dilation of the elements in
such that
where
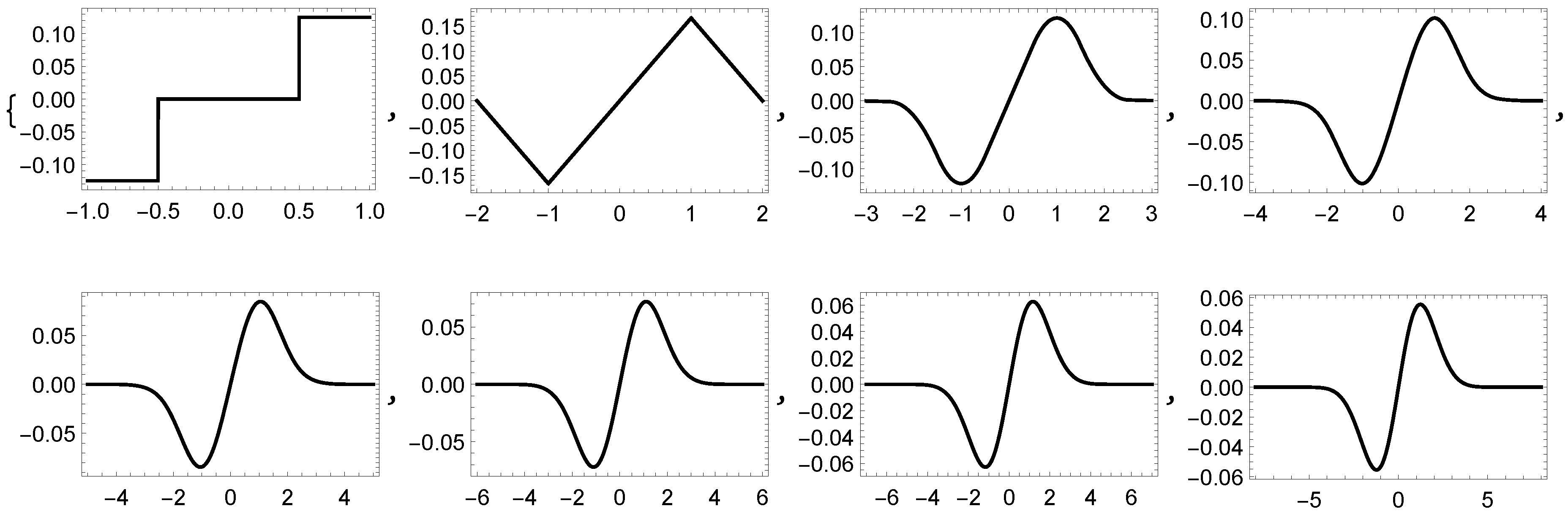
In the study of our expansion, we consider
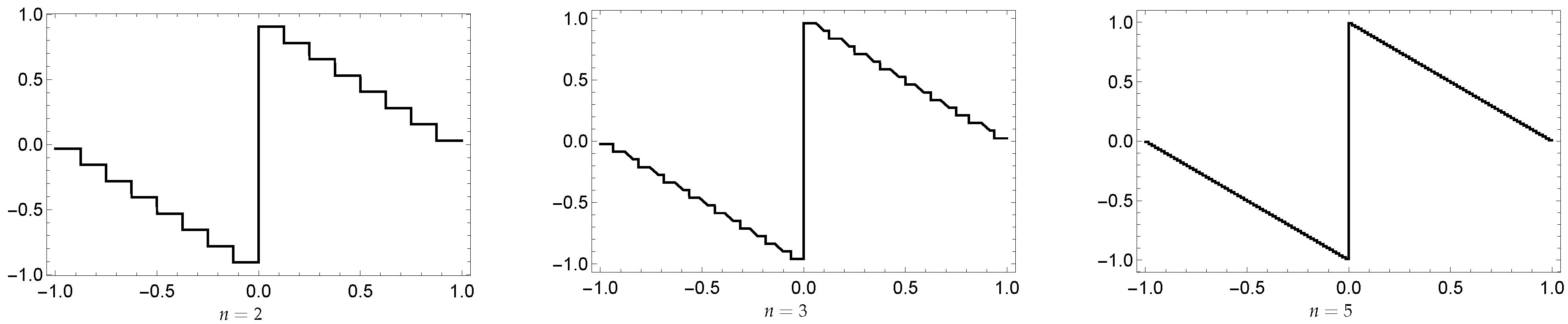
. Many applications in framelet and approximation theory are modeled by non-negative functions. One family of such important functions are the
B-splines, where the
B-spline
of order
m is defined by
where
Figure 2 shows the graphs of the
B-splines
for different order.
It is known that sparsity of the framelets representations is due to the vanishing moments of the underling refinable wavelet (see Ref. [
29]). We say
has
N vanishing moments if
which is equivalent to that
, for all
. This implies that the framelet
is orthogonal to the polynomials
. The following statement is well known in the literature [
13] for wavelets, but we present the proof for the reader’s convenience by considering the general quasi-affine dual framelet system.
Proposition 1. Assume that is a quasi-affine dual framelet system for and that ψ, where has a vanishing moment of order N. Then for any polynomial of degree at most , we havewhere is defined by Equation (9) for . Proof. From the definition of
, we know that all the generators must have a compact support. Therefore, we can find a positive integer
A such that the support of all these generators lie in the interval
. Define
Let
be a polynomial of degree at most
. Then, by the vanishing moment property of
we have
Now, the proof is completed by taking
and using Equations (
6) and (
13). Thus, we have
□
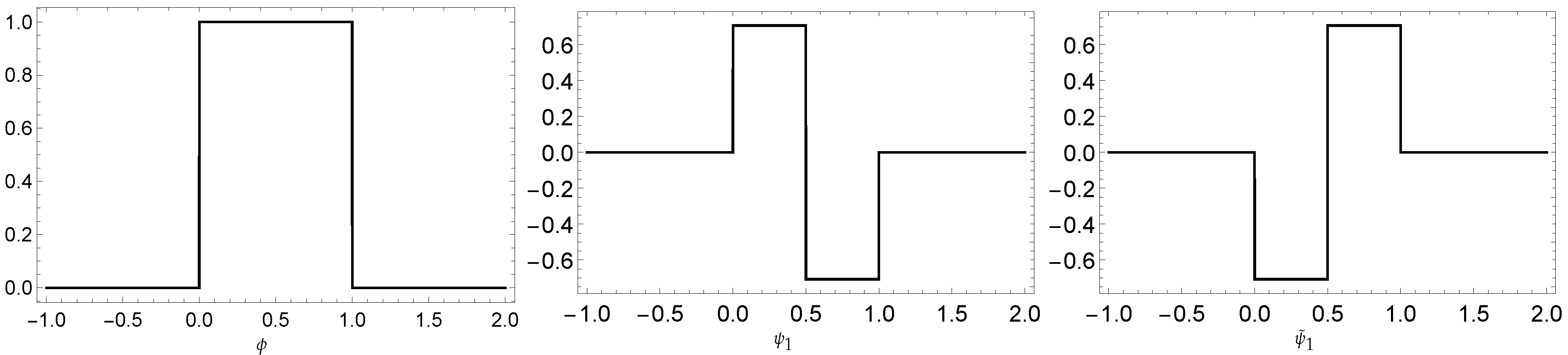
Now, we present some examples of dual tight framelets constructed by the MOEP in Ref. [
34].
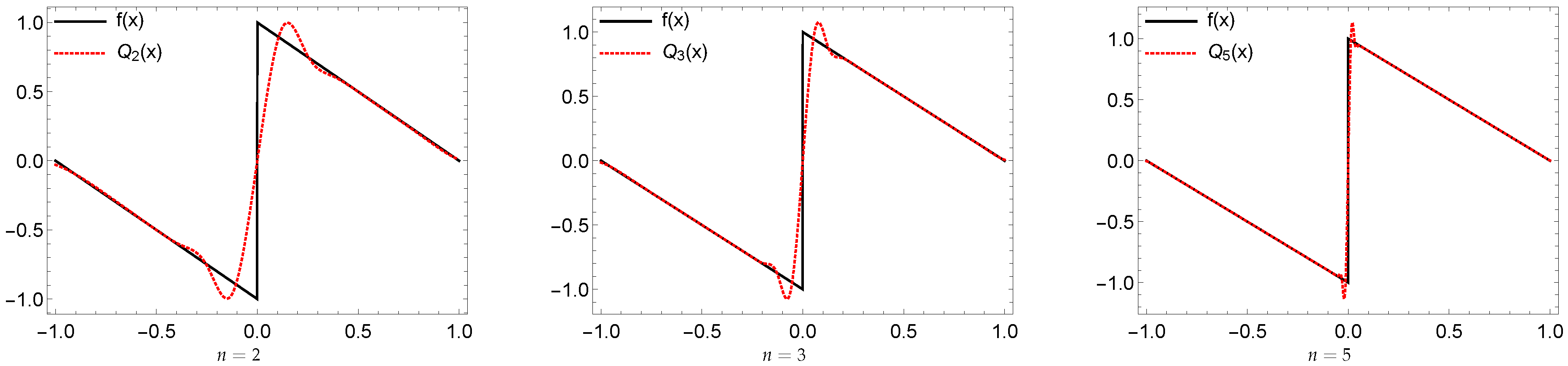
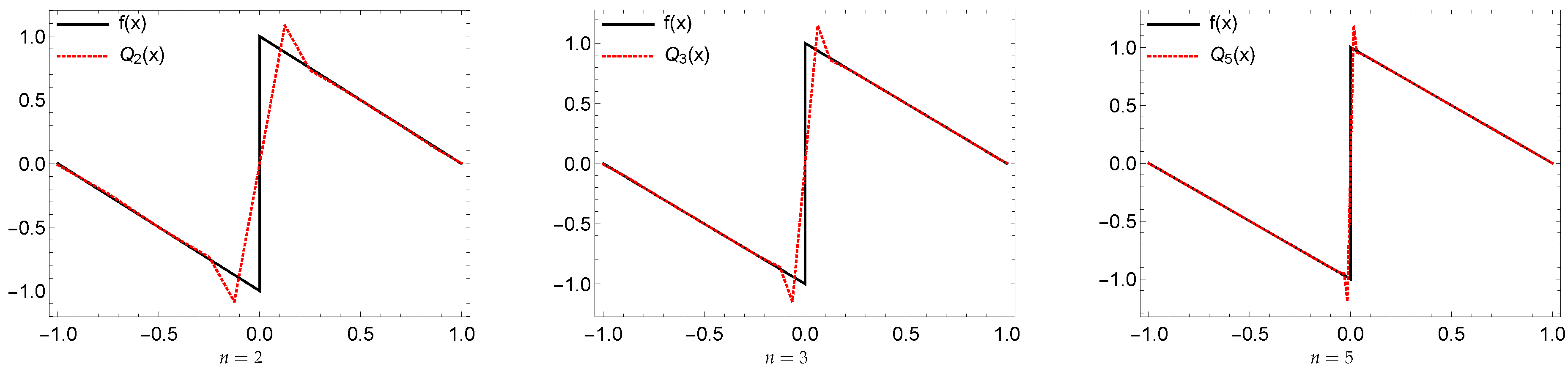
Example 1. Let . Define,Then, the resulting system generates a dual tight framelet for . We illustrate the framelet and its dual framelet generators in Figure 3. Example 2. Let . Then,Thus, by using the MOEP, one can find the following high pass filters,Then, forms a dual tight framelets for . These functions have vanishing moments (vm) as follows, while . See Figure 4 for their graphs. Example 3. Let . Then,We have the following high pass filters,The high pass filters for the dual framelets in , where , is given by
Then, forms a dual tight framelets for . Here we have . Their graphs are depicted in Figure 5. Example 4. Let , and . Thus, Then, we have the following tight framelets,and the high pass filters for its dual tight framelets in , where , are given by:Then, again forms a dual tight framelets for Here we have . Their graphs are depicted in Figure 6. We will use the framelet expansion defined by Equation (
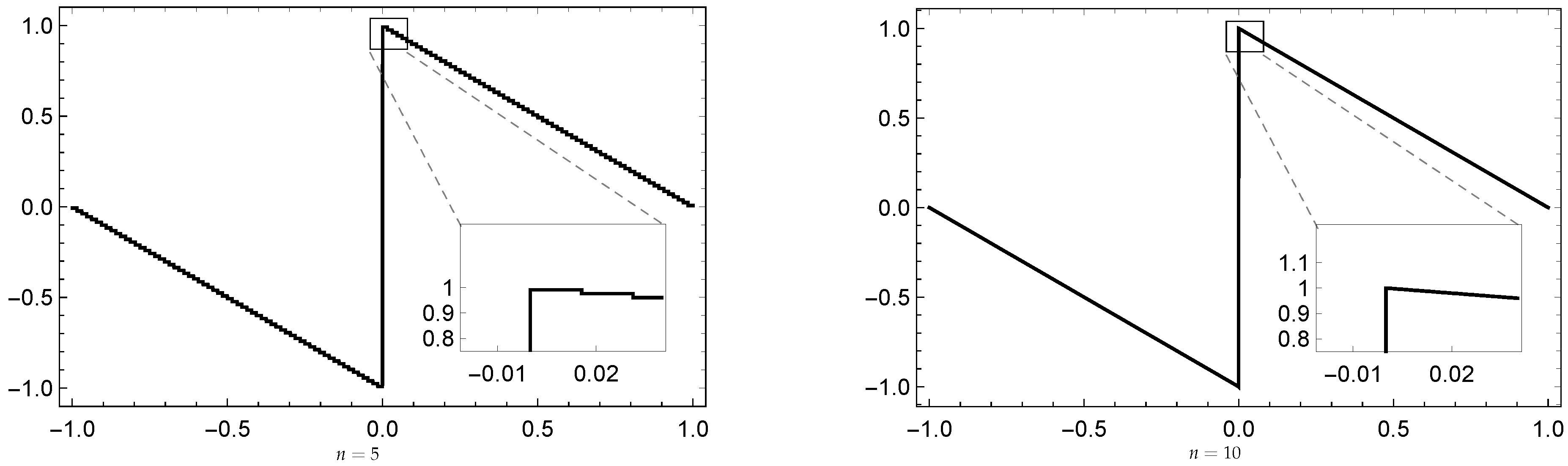
7) to present the numerical evidence of the Gibbs effect by determining the maximal overshoot and undershoot of the truncated expansion
near the origin. The behavior of the truncated functions
of a function with jump discontinuities is related to the existence of the Gibbs phenomenon, which is unpleasant in application, and not so easy to avoid. Therefore, examining a series of representations to avoid it or at least reduce it, is very important.
Proposition 2. For any two refinable compactly supported functions ϕ and in . Ifthen exhibits no Gibbs effect. Proof. Please note that for all . In particular, . Suppose that the truncated function do exhibit the Gibbs effect near . Thus, there exists an open interval such that . Therefore, such that . Define a sequence such that as (one can take such that as ). Hence, , a contradiction. Similarly, we can prove the case when in the same fashion. □
Please note that it is important to use non-negative functions in framelet analysis due to its use in a variety of applications. One of those functions is the B-splines. The following statement will require such non-negativity to avoid the Gibbs effect.
Theorem 2. Let ϕ and be any two non-negative refinable real valued compactly supported functions in such thatAssume further . If the vanishing moment of ϕ and is one, then exhibit no Gibbs effect. Proof. It suffices to show this for
as
on
. Please note that Proposition 1 is held for
, i.e.,
Now, for
, and since
by assumption, we have
The other side is analogue. Thus,
for all
. □