Group Geometrical Axioms for Magic States of Quantum Computing
Abstract
1. Introduction
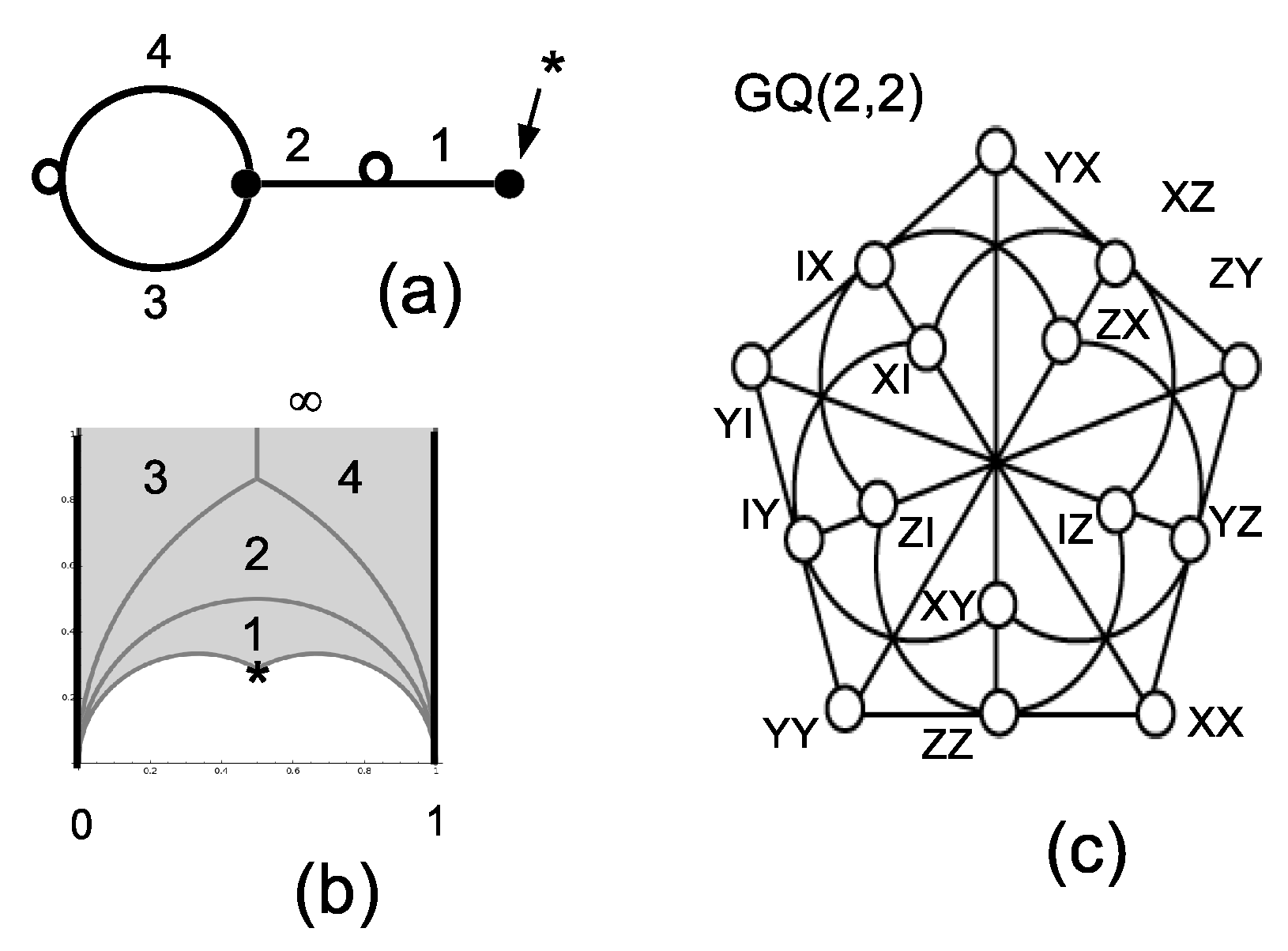
1.1. Finite Geometries from Cosets
The Kochen–Specker Theorem with a Mermin Square of Two-Qubit Observables
1.2. Magic States in Quantum Computing
Building a Two-Qubit MIC from a Subgroup of Index 4 of the Modular Group
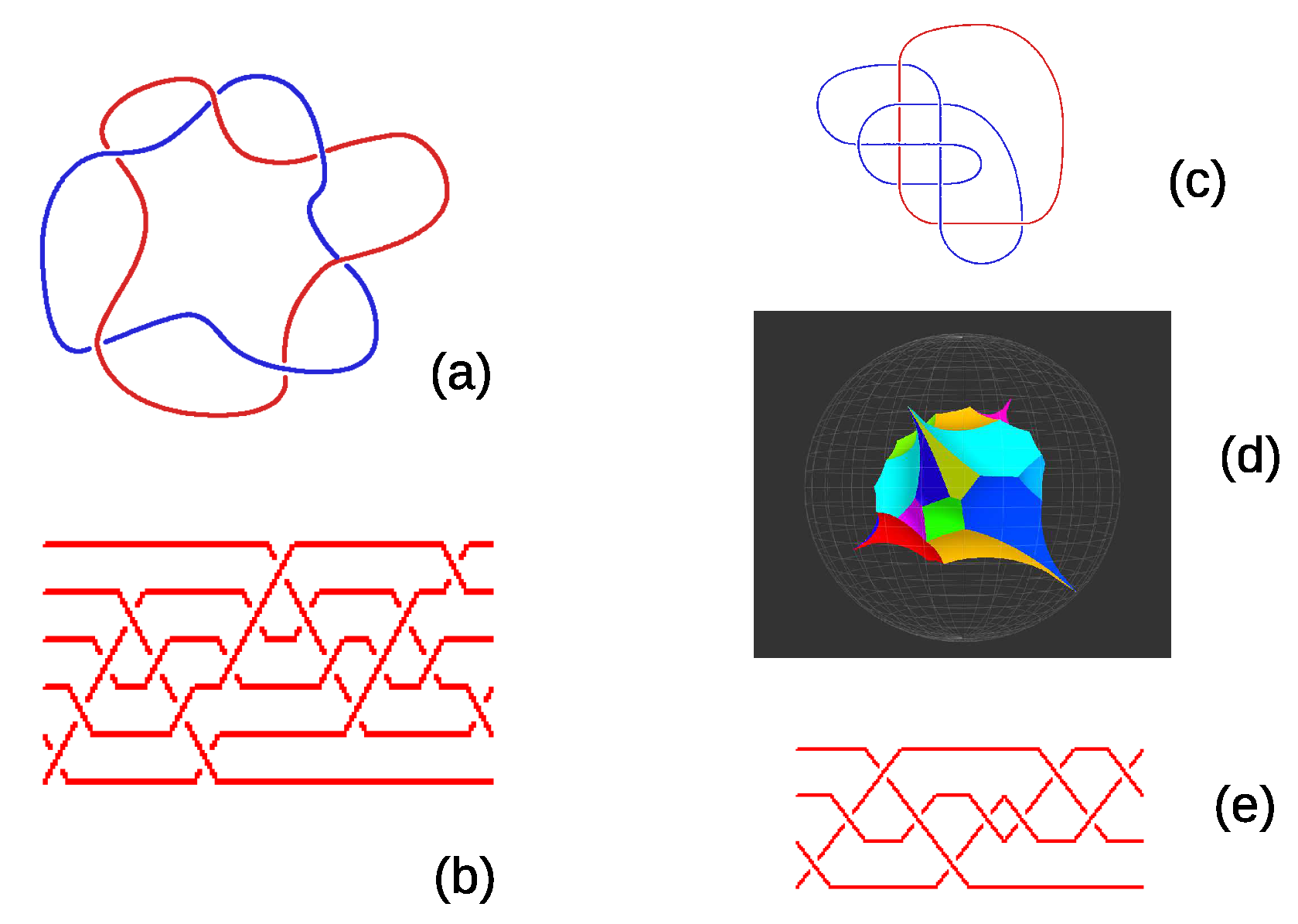
Constructing MICs Thanks to the Fundamental Group of a Knot or a Link
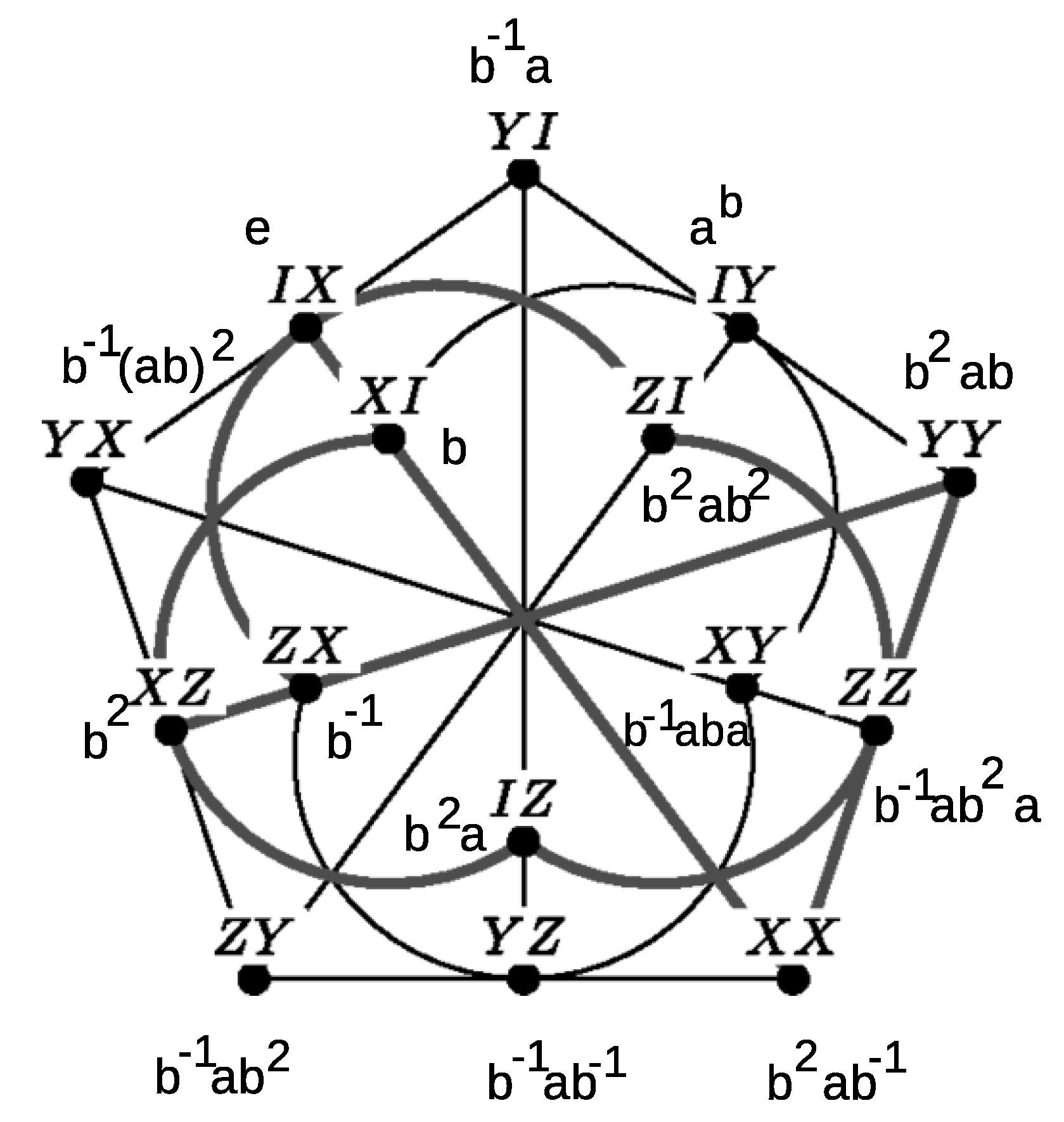
1.3. Coset Geometry of Magic States
2. MIC States Pertaining to the Figure-Eight Knot and Its 0-Surgery
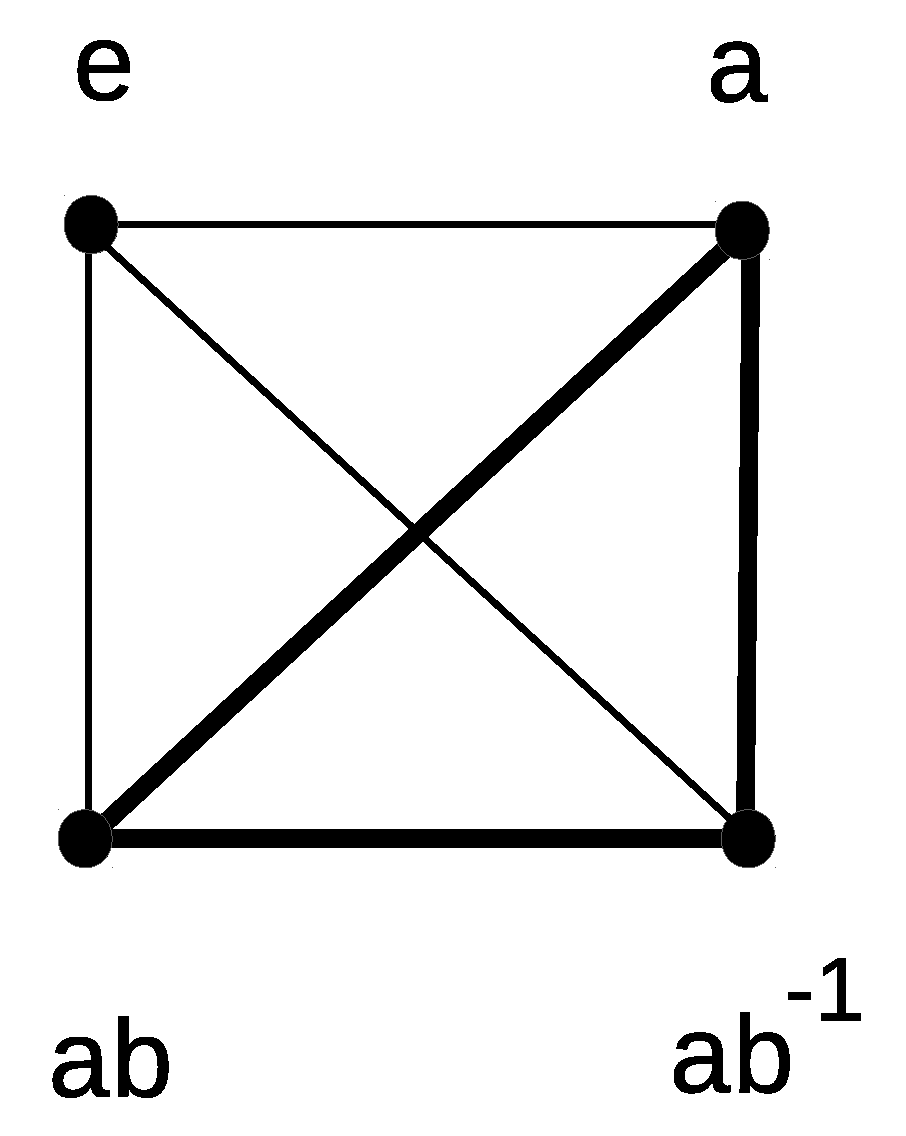
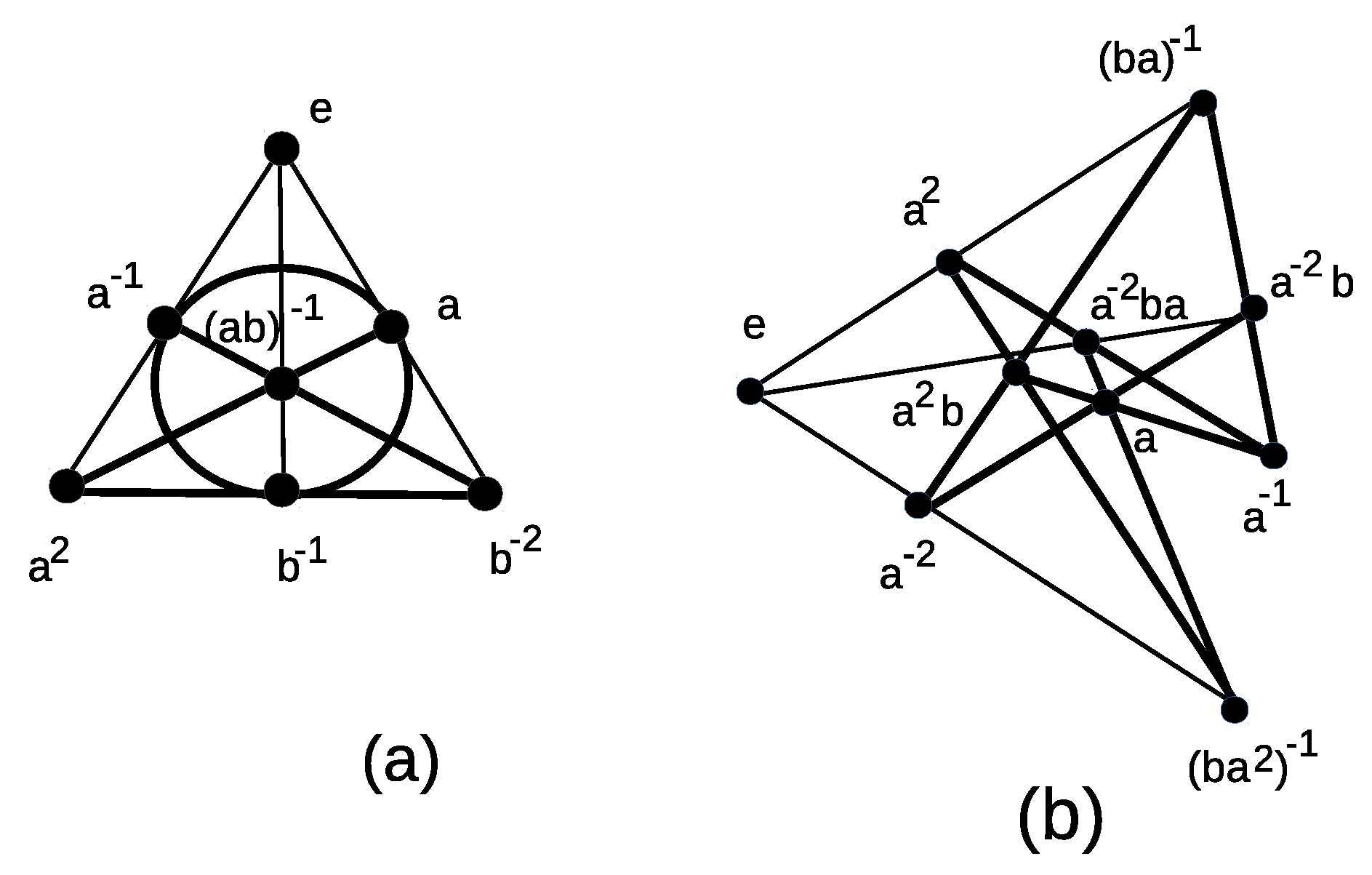
2.1. Group Geometrical Axioms Applied to the Fundamental Group
2.2. Group Geometrical Axioms Applied to the Fundamental Group
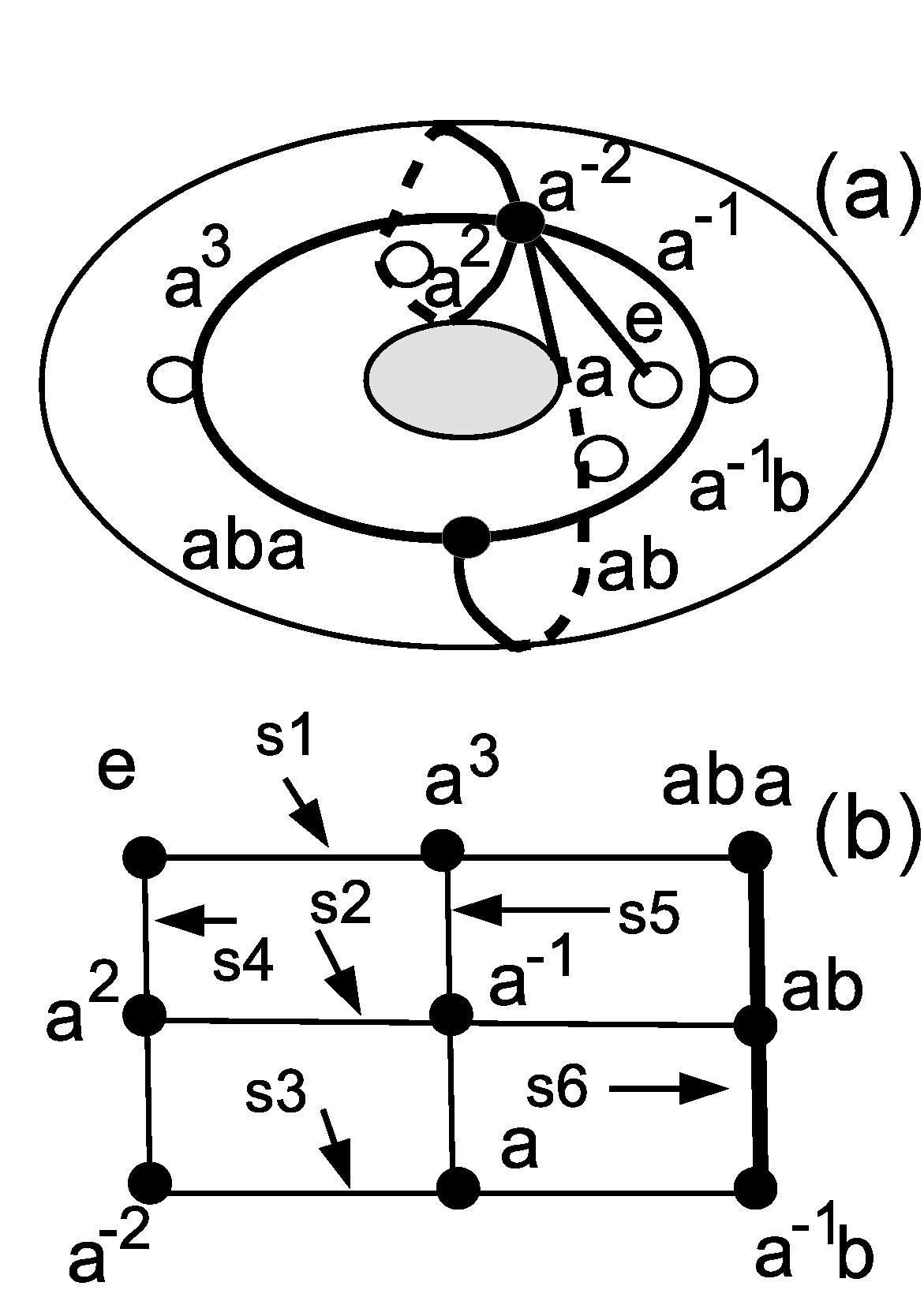
3. MIC States Pertaining to the Trefoil Knot and Its 0-Surgery
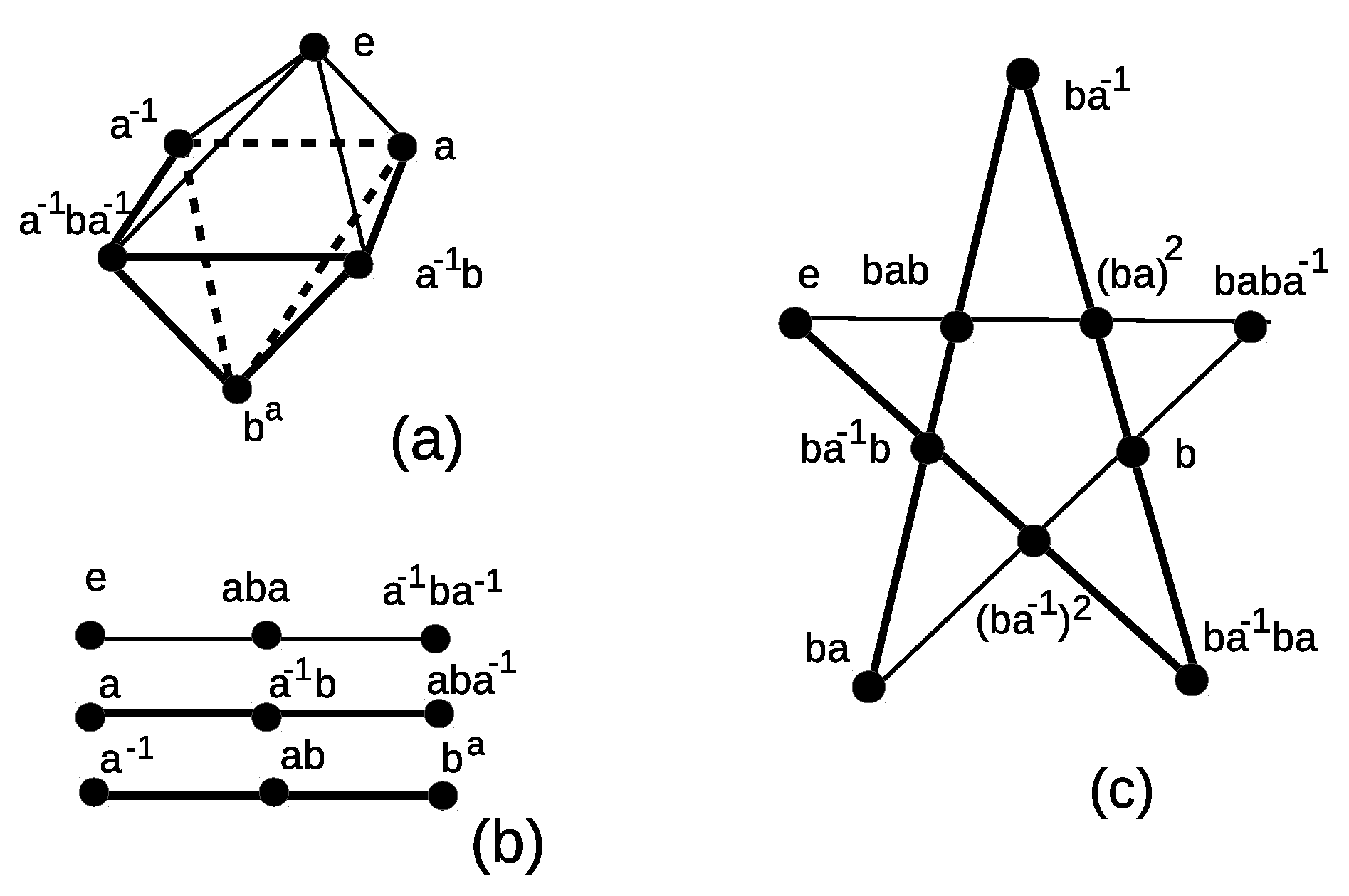
3.1. Group Geometrical Axioms Applied to the Fundamental Group
3.2. Group Geometrical Axioms Applied to the Fundamental Group
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Planat, M. Pauli graphs when the Hilbert space dimension contains a square: Why the Dedekind psi function? J. Phys. A Math. Theor. 2011, 44, 045301. [Google Scholar] [CrossRef]
- Thas, J.; van Maldeghem, H. Generalized polygons in finite projective spaces. In Proceedings of the 2004 Workshop on Distance-Regular Graphs and Finite Geometry, Busan, Korea, 19–23 July 2004. [Google Scholar]
- Planat, M.; Zainuddin, H. Zoology of Atlas-Groups: Dessins D’enfants, Finite Geometries and Quantum Commutation. Mathematics 2017, 5, 6. [Google Scholar] [CrossRef]
- Wilson, R.; Walsh, P.; Tripp, J.; Suleiman, I.; Parker, R.; Norton, S.; Nickerson, S.; Linton, S.; Bray, J.; Abbott, R. ATLAS of Finite Group Representations, Version 3. Available online: http://brauer.maths.qmul.ac.uk/Atlas/v3/exc/TF42/ (accessed on 22 June 2015).
- Mochon, C. Anyons from non-solvable finite groups are sufficient for universal quantum computation. Phys. Rev. A 2003, 67, 022315. [Google Scholar] [CrossRef]
- Planat, M.; Giorgetti, A.; Holweck, F.; Saniga, M. Quantum contextual finite geometries from dessins d’enfants. Int. J. Geom. Meth. Mod. Phys. 2015, 12, 1550067. [Google Scholar] [CrossRef]
- Planat, M. Geometry of contextuality from Grothendieck’s coset space. Quantum Inf. Process. 2015, 14, 2563–2575. [Google Scholar] [CrossRef]
- Bosma, W.; Cannon, J.J.; Fieker, C.; Steel, A. (Eds.) Handbook of Magma Functions; Edition 2.23; University of Sydney: Sydney, Australia, 2017; 5914p. [Google Scholar]
- Saniga, M.; Planat, M. Multiple qubits as symplectic polar spaces of order two. Adv. Stud. Theor. Phys. 2007, 1, 1. [Google Scholar]
- Planat, M. On small proofs of the Bell-Kochen–Specker theorem for two, three and four qubits. Eur. Phys. J. Plus 2012, 127, 86. [Google Scholar] [CrossRef]
- Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. 2005, A71, 022316. [Google Scholar] [CrossRef]
- Veitch, V.; Mousavian, S.A.; Gottesman, D.; Emerson, J. The resource theory of stabilizer quantum computation. New J. Phys. 2014, 16, 013009. [Google Scholar] [CrossRef]
- Planat, M.; Gedik, Z. Magic informationally complete POVMs with permutations. R. Soc. Open Sci. 2017, 4, 170387. [Google Scholar] [CrossRef] [PubMed]
- Planat, M. The Poincaré half-plane for informationally complete POVMs. Entropy 2018, 20, 16. [Google Scholar] [CrossRef]
- Sage Mathematics Software (Version 8.6), The Sage Development Team. 2019. Available online: http://www.sagemath.org (accessed on 1 January 2019).
- Cummins, C.; Pauli, S. Congruence Subgroups of PSL(2,Z) of Genus Less than or Equal to 24. Exp. Math. 2003, 12, 243–255. Available online: http://www.uncg.edu/mat/faculty/pauli/congruence/congruence.html#tables (accessed on 1 March 2019). [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Universal quantum computing and three-manifolds, Universal quantum computing and three-manifolds. Symmetry 2018, 10, 773. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum computing, Seifert surfaces and singular fibers. Quantum Rep. 2019, 1, 12–22. [Google Scholar] [CrossRef]
- Culler, M.; Dunfield, N.M.; Goerner, M.; Weeks, J.R. SnapPy, a Computer Program for Studying the Geometry and Topology of 3-Manifolds. Available online: http://snappy.computop.org (accessed on 1 January 2019).
- Grünbaum, B. Configurations of Points and Lines; Graduate Studies in Mathematics; AMS: Providence, RI, USA, 2009; Volume 103. [Google Scholar]
| d | P | (i) | pp | Geometry |
|---|---|---|---|---|
| 4 | yes | 2 | 2QB MIC, | |
| 5 | 10 | yes | ||
| 6 | no | 2 | 6-dit MIC, | |
| 9 | yes | 2 | 2QT MIC | |
| 11 | , | yes | 3 | 11-dit MIC |
| 16 | yes | |||
| 19 | yes | 3 | 19-dit MIC | |
| 20 | yes |
| d | ty | (or P) | cp | (i) | pp | Geometry |
|---|---|---|---|---|---|---|
| 2 | cyc | otet, | 1 | no | ||
| 3 | cyc | otet, | 1 | no | ||
| 4 | irr | otet, , | 2 | yes | 2 | 2QB MIC, |
| cyc | otet, | 1 | no | |||
| 5 | cyc | otet | 1 | no | ||
| irr | otet, | 3 | yes | |||
| irr | otet | 2 | yes | 1 | 5-dit MIC | |
| 6 | cyc | otet | 1 | no | ||
| irr | otet | 1 | no | |||
| irr | otet | 1 | yes | 10 | 6-dit MIC | |
| irr | otet | 2 | no | |||
| irr | otet | 2 | no | |||
| irr | otet | 2 | yes | 2 | 6-dit MIC | |
| 7 | cyc | otet | 1 | no | ||
| irr | otet, | 3 | yes | 2 | 7-dit MIC, | |
| irr | otet | 1 | yes | 2 | 7-dit MIC, | |
| 8 | cyc | otet | 1 | no | ||
| irr | otet | 1 | no | |||
| irr | otet | 2 | yes | fd | ||
| irr | otet | 2 | yes | fd | ||
| irr | otet | 2 | no | |||
| irr | otet | 2 | yes | 16-cell | ||
| irr | otet | 2 | no | |||
| 9 | yes | 2 | 2QT MIC | |||
| yes | 3 | 2QT MIC | ||||
| yes | 2 | 2QT MIC | ||||
| 10 | yes | 5 | 10-dit MIC | |||
| yes | 4 | 10-dit MIC, | ||||
| no | 7 | 10-dit MIC, 5-ortho | ||||
| yes | 5 | 10-dit MIC |
| d | P | (i) | pp | Geometry |
|---|---|---|---|---|
| 3 | 6 | yes | 1 | Hesse SIC, |
| 4 | yes | 2 | 2QB MIC, | |
| 6 | no | 2 | 6-dit MIC, | |
| 7 | yes | 2 | 7-dit MIC | |
| 9 | , | yes | ||
| 12 | yes | |||
| 13 | , | yes | 4 | 13-dit MIC |
| 15 | , | no | 6 | 15-dit MIC, |
| 16 | yes | |||
| 19 | yes | 3 | 19-dit MIC | |
| 21 | , | yes | 5 | 21-dit MIC, : K(3,3,3,3,3,3,3) |
| d | ty | cp | P | (i) | pp | Type in | Geometry |
|---|---|---|---|---|---|---|---|
| 2 | cyc | 1 | (2,1) ≡ 2 | no | |||
| 3 | cyc | 1 | (3,1) ≡ 3 | no | |||
| irr | 2 | (6,1) ≡ 6 | yes | 1 | Hesse SIC, , L7n1 | ||
| 4 | cyc | 1 | (4,1) ≡ 4 | no | |||
| irr | 2 | yes | 2 | 2QB MIC, , L6a3 | |||
| irr | 1 | yes | 2 | 2QB MIC | |||
| 5 | cyc | 2 | (5,1) ≡ 5 | no | |||
| irr | 3 | yes | 1 | 5-dit MIC | |||
| 6 | reg | 3 | (6,1) ≡ 6 | no | 2 | 6-dit MIC, [18] | |
| cyc | 3 | (6,2) = 3 | no | ||||
| irr | 2 | no | 2 | 6-dit MIC, K(2,2,2) | |||
| irr | 1 | no | |||||
| irr | 1 | no | |||||
| irr | 3 | yes | 2 | 6-dit MIC, | |||
| irr | 2 | yes | 2 | 6-dit MIC | |||
| irr | 2 | yes | 2 | 6-dit MIC, | |||
| 7 | cyc | 1 | (7,1) | no | |||
| irr () | 2 | yes | 2 | 7-dit MIC | |||
| irr | 1 | yes | 2 | 7-dit MIC | |||
| irr () | 2 | (order 5040) | yes | 7-dit MIC | |||
| 8 | cyc | 1 | no | ||||
| irr | 2 | (24,13) | no | ||||
| irr | 2 | no | |||||
| irr () | 2 | yes | 16-cell | ||||
| irr | 2 | yes | fd | ||||
| irr () | 1 | yes | fd | ||||
| irr () | 2 | yes | 16-cell | ||||
| 9 | no | ||||||
| 2 | (18,3) | no | 7 | 9-dit MIC, K(3,3,3) | |||
| 2 | no | 7 | 9-dit MIC, K(3,3,3) | ||||
| 1 | no | K(3,3,3), | |||||
| 3 | (54,5) | yes | 7 | 9-dit MIC | |||
| () | yes | K(3,3,3) | |||||
| () | 1 | yes | 3 | 2QT MIC | |||
| () | 2 | yes | 2 | 2QT MIC | |||
| 3 | yes | 2 | 2QT MIC, | ||||
| 10 | 1 | no | 5-ortho | ||||
| 2 | yes | 5 | 10-dit MIC, : MP | ||||
| () | 1 | yes | 9 | 10-dit MIC |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Group Geometrical Axioms for Magic States of Quantum Computing. Mathematics 2019, 7, 948. https://doi.org/10.3390/math7100948
Planat M, Aschheim R, Amaral MM, Irwin K. Group Geometrical Axioms for Magic States of Quantum Computing. Mathematics. 2019; 7(10):948. https://doi.org/10.3390/math7100948
Chicago/Turabian StylePlanat, Michel, Raymond Aschheim, Marcelo M. Amaral, and Klee Irwin. 2019. "Group Geometrical Axioms for Magic States of Quantum Computing" Mathematics 7, no. 10: 948. https://doi.org/10.3390/math7100948
APA StylePlanat, M., Aschheim, R., Amaral, M. M., & Irwin, K. (2019). Group Geometrical Axioms for Magic States of Quantum Computing. Mathematics, 7(10), 948. https://doi.org/10.3390/math7100948






