Hybrid Methods for a Countable Family of G-Nonexpansive Mappings in Hilbert Spaces Endowed with Graphs

Abstract

In this paper, we introduce the iterative scheme for finding a common fixed point of a countable family of G-nonexpansive mappings by the shrinking projection method which generalizes Takahashi Takeuchi and Kubota’s theorem in a Hilbert space with a directed graph. Simultaneously, we give examples and numerical results for supporting our main theorems and compare the rate of convergence of some examples under the same conditions.

1. Introduction

In this paper, we assume that H is a real Hilbert space with inner product $⟨·,·⟩$ and norm $\parallel ·\parallel$. Let C be a nonempty subset of H. Then, mapping $T:C\to C$ is called

1. contraction if there exists $\alpha \in (0,1)$ such that $\parallel Tx-Ty\parallel \le \alpha \parallel x-y\parallel$ for all $x,y\in C$;

2. nonexpansive if $\parallel Tx-Ty\parallel \le \parallel x-y\parallel$ for all $x,y\in C$.

An element $z\in C$ is called a fixed point of T if $z=Tz$. The fixed point set of T is denoted by $F(T)$. There are many iterative methods for approximating fixed points of nonexpansive mapping in a Hilbert space (see [1,2,3]) and references therein.

In 1953, Mann [2] introduced the iteration procedure as follows:

$$x_1\in C,x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)T{x}_n,\forall n\in \mathbb{N},$$

(1)

where $\left\{{\alpha }_n\right\}\subset [0,1]$ and $\mathbb{N}$ are the set of all positive integers. Recently, many mathematicians (see [4,5,6]) have used Mann’s iteration for obtaining a weak convergence theorem.

Let H be a Hilbert space and let C be a subset of H. Let $\left\{T_n\right\}$ and $\tau$ be two families of mappings of C into itself with $\varnothing \ne F(\tau )={\bigcap }_{n=1}^{\infty }F(T_n)$, where $F(T_n)$ is the set of all fixed points of $T_n$, $F(\tau )$ is the set of all common fixed points of $\tau$. $\left\{T_n\right\}$ is said to satisfy the $NST$-condition [7] with respect to $\tau$ if for each bounded sequence $\left\{z_n\right\}$ in C,

$$\underset{n\to \infty }{lim}\parallel z_n-T_n{z}_n\parallel =0\Rightarrow \underset{n\to \infty }{lim}\parallel z_n-T{z}_n\parallel =0,\forall T\in \tau .$$

To obtain a strong convergence theorem, Takahashi et al. [8] introduced the following modification of the Mann’s iteration method (1), which just involved one closed convex set for a countable family of nonexpansive mappings $\left\{T_n\right\}$, which is called the shrinking projection method:

Theorem 1.

Let H be a Hilbert space and C be a nonempty closed convex subset of H [8]. Let $\left\{T_n\right\}$ and τ be a family of nonexpansive mappings of C into H such that $F:={\cap }_{n=1}^{\infty }F(T_n)=F(\tau )\ne \varnothing$ and let $x_0\in H$. Suppose that $\left\{T_n\right\}$ satisfies the $NST$-condition with τ. For $C_1=C$ and $u_1=P_{C_1}{x}_0$, define a sequence $\left\{u_n\right\}$ in C as follows:

$$\left\{\begin{array}{c}{y}_n={\alpha }_n{u}_n+(1-{\alpha }_n)T_n{u}_n,\hfill \\ C_{n+1}=\{z\in C_n:\parallel y_n-z\parallel \le \parallel u_n-z\parallel \},\hfill \\ u_{n+1}=P_{C_{n+1}}{x}_0,\forall n\in \mathbb{N},\hfill \end{array}\right.$$

(2)

where $0\le {\alpha }_n\le a<1$ for all $n\in \mathbb{N}$. Then, the sequence $\left\{u_n\right\}$ converges strongly to a point $z_0=P_F{x}_0$.

This iteration is used to obtain strong convergence theorem (see, for example, [9,10]).

Let X be a Banach space and C be a nonempty subset of X. Let G be a directed graph with the set of vertices $V(G)=C$ and the set of edges $E(G)$ that contains the diagonal of $C\times C$, where an edge $(x,y)\in E(G)$ is the related pairs of vertices x and y. We suppose that G has no parallel edge.

Thus, we can identify the graph G with the pair $(V(G),E(G))$. A mapping $T:C\to C$ is said to be

• G-contraction if T satisfies the conditions:

  (i)

  T preserves edges of G, i.e.,

  $$(x,y)\in E(G)\Rightarrow (Tx,Ty)\in E(G),\forall (x,y)\in E(G);$$

  (ii)

  T decreases weights of edges of G in the following way: there exists $\alpha \in (0,1)$ such that

  $$(x,y)\in E(G)\Rightarrow \parallel Tx-Ty\parallel \le \alpha \parallel x-y\parallel ,\forall (x,y)\in E(G);$$

• G-nonexpansive if T satisfies the conditions:

  (i)

  T preserves edges of G, i.e.,

  $$(x,y)\in E(G)\Rightarrow (Tx,Ty)\in E(G),\forall (x,y)\in E(G);$$

  (ii)

  T non-increases weights of edges of G in the following way:

  $$(x,y)\in E(G)\Rightarrow \parallel Tx-Ty\parallel \le \parallel x-y\parallel ,\forall (x,y)\in E(G).$$

In 2008, Jachymski [11] proved some generalizations of the Banach’s contraction principle in complete metric spaces endowed with a graph. To be more precise, Jachymski proved the following result.

Theorem 2.

Let $(X,d)$ be a complete metric space, and a triple $(X,d,G)$ have the following property: for any sequence $\left\{x_n\right\}$ if $x_n\to x$ and $(x_n,x_{n+1})\in E(G)$ for $n\in \mathbb{N}$ and there is a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ with $(x_{n_k},x)\in E(G)$ for all $n\in \mathbb{N}$.

Let $T:X\to X$ be a G-contraction, and $X_T=\{x\in X:(x,Tx)\in E(G)\}$. Then, $F(T)\ne \varnothing$ if and only if $X_T\ne \varnothing$ [11].

In 2008, Tiammee et al. [12] and Alfuraidan [13] employed the above theorem to establish the existence and the convergence results for G-nonexpansive mappings with graphs. Recently, many mathematicians (see [14,15]) have introduced the iterative method for finding a fixed point of G-nonexpansive mappings in the framework of Hilbert spaces and Banach spaces.

Inspired by all aforementioned references, we introduce the iterative scheme for solving the fixed point problem of a countable family of G-nonexpansive mappings. We also obtain strong convergence theorems in a Hilbert space with a directed graph under suitable conditions. Furthermore, we demonstrate examples and numerical results for supporting our main results and compare the rate of convergence of some examples under the same conditions.

2. Preliminaries and Lemmas

We now provide some basic results for the proof. In a Hilbert space H, let C be a nonempty closed and convex subset of H. Letting $\left\{x_n\right\}$ be a sequence in H, we denote the weak convergence of $\left\{x_n\right\}$ to a point $x\in H$ by $x_n\rightharpoonup x$ and the strong convergence, that is, relative to a norm of $\left\{x_n\right\}$ to a point $x\in H$ by $x_n\to x$. For every point $x\in H$, there exists a unique nearest point of C, denoted by $P_{C}x$, such that $∥x-P_{C}x∥\le ∥x-y∥$ for all $y\in C$. Such a $P_C$ is called the metric projection from H onto C.

Lemma 1.

Let H be a real Hilbert space [16]. Then, for each $x,y$∈H and each $t\in [0,1],$

(a) 

${\parallel x-y\parallel }^2={\parallel x\parallel }^2-2⟨x,y⟩+{\parallel y\parallel }^2$,

(b) 

${\parallel tx+(1-t)y\parallel }^2={t\parallel x\parallel }^2+{(1-t)\parallel y\parallel }^2-t(1-t){\parallel x-y\parallel }^2$,

(c) 

If $\left\{x_n\right\}$ is a sequence in H weakly convergent to z, then ${lim\; sup}_{n\to \infty }\parallel x_n{-y\parallel }^2={lim\; sup}_{n\to \infty }\parallel x_n{-z\parallel }^2+{\parallel z-y\parallel }^2.$

Lemma 2.

Let C be a nonempty closed and convex subset of a real Hilbert space H [17]. For each x, y∈H and $a\in \mathbb{R}$, the set

$$D=\{v\in C:\parallel y-v{\parallel }^2\le \parallel x-v{\parallel }^2+⟨z,v⟩+a\}$$

is closed and convex.

Lemma 3.

Let C be a nonempty closed and convex subset of a real Hilbert space H and $P_C:H\to C$ be the metric projection from H onto C. Then, $\parallel y-P_c{x\parallel }^2+\parallel x-P_c{x\parallel }^2\le {\parallel x-y\parallel }^2$, for all $x\in H$ and $y\in C$ [18].

Lemma 4.

Let H be a real Hilbert space and let ${\left\{x_i\right\}}_{i=1}^m\subseteq H$ [19]. For ${\alpha }_i\in (0,1),i=1,2,\dots ,m$ such that ${\sum }_{i=1}^m{\alpha }_i=1$, the following identity holds:

$$\parallel \sum _{i=1}^m{\alpha }_i{x}_i{\parallel }^2=\sum _{i=1}^m{\alpha }_i\parallel x_i{\parallel }^2-\sum _{1\le i<j\le m}{\alpha }_i{\alpha }_j{\parallel x_i-x_j\parallel }^2.$$

Lemma 5.

[20] Let X be a Banach space. Then, X is strictly convex, if

$$\parallel x\parallel =\parallel y\parallel =\parallel \lambda x+(1-\lambda )y\parallel$$

for all $x,y\in X$ and $\lambda \in (0,1)$, which implies $x=y$.

Definition 1.

A directed graph G is transitive if, for any $x,y,z\in V(G)$ in which $(x,y)$ and $(y,z)$ are in $E(G)$, then we have $(x,z)\in E(G)$.

Definition 2.

Let $x_0\in V(G)$ and A be a subset of $V(G).$ We say that

(i) 

A is dominated by $x_0$ if $(x_0,x)\in E(G)$ for all $x\in A.$

(ii) 

A dominates $x_0$ if, for each $x\in A$, $(x,x_0)\in E(G).$

Definition 3.

Let $G=(V(G),E(G))$ be a directed graph. The set of edges $E(G)$ is said to be convex if $(x_i,y_i)\in E(G)$ for all $i=1,2,\dots ,N$ and ${\alpha }_i\in (0,1)$ such that ${\sum }_{i=1}^N{\alpha }_i=1$, then $({\sum }_{i=1}^N{\alpha }_i{x}_i,{\sum }_{i=1}^N{\alpha }_i{y}_i)\in E(G)$.

Lemma 6.

Let C be a nonempty, closed and convex subset of a Hilbert space H and $G=(V(G),E(G))$ a directed graph such that $V(G)=C$ [14]. Let $T:C\to C$ be a G-nonexpansive mapping and $\left\{x_n\right\}$ be a sequence in C such that $x_n\rightharpoonup x$ for some $x\in C$. If there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $(x_{n_k},x)\in E(G)$ for all $k\in \mathbb{N}$ and $\{x_n-T{x}_n\}\to y$ for some $y\in H$. Then, $(I-T)x=y$.

3. Main Results

In this section, we prove a strong convergence theorem by hybrid methods for families of G-nonexpansive mappings

Theorem 3.

Let H be a real Hilbert space and C be a nonempty, closed and convex subset of H. Let $G=(V(G),E(G))$ be a directed graph with $V(G)=C$ and $E(G)$ be also convex. Suppose that $\left\{T_n\right\}$ and τ are two families of G-nonexpansive mappings on C such that $F(\tau )={\bigcap }_{n=1}^{\infty }F(T_n)\ne \varnothing$ and $F(\tau )$ is closed. Assume that $F(T)\times F(T)\subseteq E(G)$ for all $T\in \tau$, $\left\{T_n\right\}$ satisfies the $NST$-condition with respect to τ and $0\le {\alpha }_n\le a<1$ for all $n\in \mathbb{N}$. For $x_0\in C$, $C_1=C$ and $x_1=P_{C_1}{x}_0$, define a sequence $\left\{x_n\right\}$ of C as follows:

$$\left\{\begin{array}{c}{y}_n={\alpha }_n{x}_n+(1-{\alpha }_n)T_n{x}_n,\hfill \\ C_{n+1}=\{z\in C_n:\parallel y_n-z\parallel \le \parallel x_n-z\parallel \},\hfill \\ x_{n+1}=P_{C_{n+1}}{x}_0,n\in \mathbb{N}.\hfill \end{array}\right.$$

If $\left\{x_n\right\}$ satisfies the following conditions:

(i) 

$\{x_n\}$ dominates p for all $p\in F(\tau )$;

(ii) 

if there exist a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that $x_{n_k}\rightharpoonup w\in C$, then $(x_{n_k},w)\in E(G)$.

Then, $\{x_n\}$ converges strongly to $w=P_{F(\tau )}{x}_0$.

Proof. 

We split the proof into five steps.

Step 1: Show that $P_{C_{n+1}}{x}_0$ is well-defined for every $x_0\in C$. We know that $F(T)$ is convex, if $F(T)\times F(T)\subseteq E(G)$ for all $T\in \tau$; see Theorem 3.2 of Tiammee et al. [12]. This implies that $F(\tau )$ is convex. It follows now from the assumption that $F(\tau )$ is closed. This implies that $P_{F(\tau )}{x}_0$ is well-defined. We first show, by induction, that $F(\tau )\subset C_n$ for all $n\in \mathbb{N}$. It is obvious that $F(\tau )\subset C_1$. Assume that $F(\tau )\subset C_k$ for some $k\in \mathbb{N}$. Then, by the fact that $\left\{x_n\right\}$ dominates p for all $p\in F(\tau )$, for $x\in F(\tau )\subset C_k$,

$$\begin{array}{ccc}\hfill \parallel y_k-x\parallel & =& \parallel {\alpha }_k{x}_k+(1-{\alpha }_k)T_k{x}_k-x\parallel \hfill \\ & \le & {\alpha }_k\parallel x_k-x\parallel +(1-{\alpha }_k)\parallel T_k{x}_k-x\parallel \hfill \\ & \le & {\alpha }_k\parallel x_k-x\parallel +(1-{\alpha }_k)\parallel x_k-x\parallel \hfill \\ & =& \parallel x_k-x\parallel \hfill \end{array}$$

and hence $x\in C_{k+1}$. This implies that $F(\tau )\subset C_n$ for all $n\in \mathbb{N}$. Next, we show that $C_n$ is closed and convex for all $n\in \mathbb{N}$. By the condition of $C_n$, $C_1=C$ is closed and convex. Assume that $C_k$ is closed and convex for some $k\in \mathbb{N}$. For $z\in C_k$, from Equation (6), we know that $\parallel y_k-z\parallel \le \parallel x_k-z\parallel$ is equivalent to $\parallel y_k-x_k{\parallel }^2+2⟨y_k-x_k,x_k-z⟩\ge 0$. Thus, $C_{k+1}$ is closed and convex. Then, for any $n\in \mathbb{N}$, $C_n$ is closed and convex. This implies that $\left\{x_n\right\}$ is well-defined.

Step 2: Show that ${lim}_{n\to \infty }\parallel x_n-x_0\parallel$ exists. From $x_n=P_{C_n}{x}_0$, we have $⟨x_0-x_n,x_n-y⟩\ge 0$ for all $y\in C_n$. As $F(\tau )\subset C_n$, we also have

$$\begin{array}{c}\hfill ⟨x_0-x_n,x_n-p⟩\ge 0\mathrm{for}\mathrm{all}p\in F(\tau )\mathrm{and}n\in \mathbb{N}.\end{array}$$

(3)

Thus, for $p\in F(\tau )$, we have

$$\begin{array}{c}\hfill 0\le ⟨x_0-x_n,x_n-p⟩=⟨x_0-x_n,x_n-x_0+x_0-p⟩\le -\parallel x_0-x_n{\parallel }^2+\parallel x_0-x_n\parallel \parallel x_0-p\parallel .\end{array}$$

This implies that

$$\parallel x_0-x_n\parallel \le \parallel x_0-x\parallel$$

(4)

for all $x\in F(\tau )$ and $n\in \mathbb{N}.$ From $x_n=P_{C_n}{x}_0$ and $x_{n+1}=P_{C_{n+1}}{x}_0\in C_{n+1}\subset C_n$, we also have

$$\begin{array}{c}\hfill 0\le ⟨x_0-x_n,x_n-x_{n+1}⟩.\end{array}$$

(5)

From (5), we have, for $n\in \mathbb{N}$,

$$\begin{array}{ccc}\hfill 0& \le & ⟨x_0-x_n,x_n-x_{n+1}⟩\hfill \\ & =& ⟨x_0-x_n,x_n-x_0+x_0-x_{n+1}⟩\hfill \\ & =& -\parallel x_0-x_n{\parallel }^2+⟨x_0-x_n,x_0-x_{n+1}⟩\hfill \\ & \le & -\parallel x_0-x_n{\parallel }^2+\parallel x_0-x_n\parallel \parallel x_0-x_{n+1}\parallel .\hfill \end{array}$$

Thus,

$$\begin{array}{c}\hfill \parallel x_0-x_n\parallel \le \parallel x_0-x_{n+1}\parallel .\end{array}$$

Since $\{\parallel x_n-x_0\parallel \}$ is bounded, ${lim}_{n\to \infty }\parallel x_n-x_0\parallel$ exists.

Step 3: Show that $x_n\to w\in C$ as $n\to \infty$. For $m>n$, by the definition of C, we see that $x_m=P_{C_m}{x}_0\in C_m\subset C_n$. Thus, we have

$$\begin{array}{c}\hfill \parallel x_n-x_m{\parallel }^2\le \parallel x_n-x_0{\parallel }^2-{\parallel x_m-x_0\parallel }^2.\end{array}$$

Since $\left\{x_n\right\}$ is a Cauchy sequence, there exists $w\in C$ such that $x_n\to w$ as $n\to \infty$. This implies that $(x_n,w)\in E(G)$ by condition (ii).

Step 4: Show that $w\in F(\tau )$. From Step 3, we have that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_n-x_{n+1}\parallel =0.\end{array}$$

On the other hand, $x_{n+1}\in C_{n+1}\subset C_n$ implies that

$$\begin{array}{c}\hfill \parallel y_n-x_{n+1}\parallel \le \parallel x_n-x_{n+1}\parallel .\end{array}$$

(6)

Furthermore, we have

$$\begin{array}{ccc}\hfill \parallel y_n-x_n\parallel & =& \parallel {\alpha }_n{x}_n+(1-{\alpha }_n)T_n{x}_n-x_n\parallel \hfill \\ & =& (1-{\alpha }_n)\parallel T_n{x}_n-x_n\parallel .\hfill \end{array}$$

From (6), we obtain

$$\begin{array}{ccc}\hfill \parallel T_n{x}_n-x_n\parallel & =& \frac{1}{1-{\alpha }_n}\parallel y_n-x_n\parallel \hfill \\ & \le & \frac{1}{1-a}\parallel y_n-x_n\parallel \hfill \\ & =& \frac{1}{1-a}\parallel y_n-x_{n+1}+x_{n+1}-x_n\parallel \hfill \\ & \le & \frac{2}{1-a}\parallel x_n-x_{n+1}\parallel .\hfill \end{array}$$

(7)

Hence, by (7), we have $\parallel T_n{x}_n-x_n\parallel \to 0$. Since $\left\{T_n\right\}$ satisfies the $NST$-condition with respect to $\tau$, we get

$$\begin{array}{c}\hfill \parallel T{x}_n-x_n\parallel \to 0\mathrm{for}\mathrm{all}T\in \tau .\end{array}$$

(8)

From Step 3, we know that $x_n\to w\in C$. From (ii) and (8), we obtain $w\in F(\tau )$ by Lemma 6.

Step 5: Show that $w=P_{F(\tau )}{x}_0$. Since $x_n=P_{C_n}{x}_0$ and $F(\tau )\subset C_n$, we obtain

$$⟨x_0-x_n,x_n-z⟩\ge 0,\forall z\in F(\tau ).$$

(9)

By taking the limit in (9), we obtain

$$⟨x_0-w,w-z⟩\ge 0,\forall z\in F(\tau ).$$

(10)

This shows that $w=P_{F(\tau )}{x}_0$.  □

We next give some examples of a family of G-nonexpansive mappings $\left\{T_n\right\}$, which satisfies the $NST$-condition.

Example 1.

Let $T\in \tau$. Define $T_n={\beta }_{n}I+(1-{\beta }_n)T$, where $0<b\le {\beta }_n\le c<1$ for all $n\in \mathbb{N}$. Then, $\left\{T_n\right\}$ is a family of G-nonexpansive mappings and satisfies the $NST$-condition.

Proof. 

We first prove that $T_n={\beta }_{n}I+(1-{\beta }_n)T$ is G-nonexpansive for all $n\in \mathbb{N}$.

Since $E(G)$ is convex and $(Tx,Ty)\in E(G)$ for all $(x,y)\in E(G)$, then

$$(T_{n}x,T_{n}y)=({\beta }_{n}x+(1-{\beta }_n)Tx,{\beta }_{n}y+(1-{\beta }_n)Ty)\in E(G).$$

Furthermore, we have

$$\begin{array}{ccc}\hfill \parallel T_{n}x-T_{n}y\parallel & =& \parallel {\beta }_{n}x+(1-{\beta }_n)Tx-{\beta }_{n}y-(1-{\beta }_n)Ty\parallel \hfill \\ & =& \parallel {\beta }_n(x-y)+(1-{\beta }_n)(Tx-Ty)\parallel \hfill \\ & \le & {\beta }_n\parallel x-y\parallel +(1-{\beta }_n)\parallel Tx-Ty\parallel \hfill \\ & \le & {\beta }_n\parallel x-y\parallel +(1-{\beta }_n)\parallel x-y\parallel \hfill \\ & =& \parallel x-y\parallel .\hfill \end{array}$$

(11)

Hence, $T_n={\beta }_{n}I+(1-{\beta }_n)T$ is G-nonexpansive for all $n\in \mathbb{N}$.

Next, we show that $\left\{T_n\right\}$ satisfies the $NST$-condition with respect to T. First, we show that $F(\tau )={\bigcap }_{n=1}^{\infty }F(T_n)$. It is obvious that $F(\tau )\subset {\bigcap }_{n=1}^{\infty }F(T_n)$. On the other hand, let $p\in {\bigcap }_{n=1}^{\infty }F(T_n)$. Then, we have

$$p=T_{n}p={\beta }_{n}p+(1-{\beta }_n)Tp={\beta }_{n}p+Tp-{\beta }_{n}Tp={\beta }_n(p-Tp)+Tp.$$

Then, $p-Tp={\beta }_n(p-Tp)$, which implies that $(1-{\beta }_n)\parallel p-Tp\parallel =0$. Hence, $p\in F(\tau )$ that is ${\bigcap }_{n=1}^{\infty }F(T_n)\subset F(\tau )$. This shows that $F(\tau )={\bigcap }_{n=1}^{\infty }F(T_n)$. Let $\left\{x_n\right\}$ be a sequence in C such that ${lim}_{n\to \infty }\parallel T_n{x}_n-x_n\parallel =0$; we have $\parallel x_n-T_n{x}_n\parallel =\parallel x_n-({\beta }_n{x}_n+(1-{\beta }_n)T{x}_n)\parallel =(1-{\beta }_n)\parallel x_n-T{x}_n\parallel .$ Since ${lim}_{n\to \infty }\parallel x_n-T_n{x}_n\parallel =0$, then

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_n-T{x}_n\parallel =0.\end{array}$$

(12)

From (11) and (12), we get that $\left\{T_n\right\}$ satisfies the $NST$-condition with respect to $\tau$.  □

Example 2.

Let $T,S\in \tau$. Define $T_n={\beta }_{n}I+{\gamma }_{n}S+(1-{\beta }_n-{\gamma }_n)T$, where $0<b\le {\beta }_n<1$, $0<c\le {\gamma }_n<1$ and $0<{\beta }_n+{\gamma }_n\le d<1$ for all $n\in \mathbb{N}$. If $Sz=Tz$ and $(x,z)\in E(G)$ for all $z\in {\bigcap }_{n=1}^{\infty }F(T_n)$ and $x\in C$, then $\left\{T_n\right\}$ is a family of G-nonexpansive mappings and satisfies the $NST$-condition.

Proof. 

We first prove that $T_n={\beta }_{n}I+{\gamma }_{n}S+(1-{\beta }_n-{\gamma }_n)T$ is G-nonexpansive for all $n\in \mathbb{N}$. Since $E(G)$ is convex and $(Sx,Sy),(Tx,Ty)\in E(G)$ for all $(x,y)\in E(G)$, then

$$\begin{array}{ccc}\hfill (T_{n}x,T_{n}y)& =& ({\beta }_{n}x+{\gamma }_{n}Sx+(1-{\beta }_n-{\gamma }_n)Tx,{\beta }_{n}y+{\gamma }_{n}Sy+(1-{\beta }_n-{\gamma }_n)Ty)\hfill \\ & \in & E(G).\hfill \end{array}$$

(13)

Furthermore, we have

$$\begin{array}{ccc}\hfill \parallel T_{n}x-T_{n}y\parallel & =& \parallel {\beta }_{n}x+{\gamma }_{n}Sx+(1-{\beta }_n-{\gamma }_n)Tx-{\beta }_{n}y-{\gamma }_{n}Sy-(1-{\beta }_n-{\gamma }_n)Ty)\parallel \hfill \\ & =& \parallel {\beta }_n(x-y)+{\gamma }_n(Sx-Sy)+(1-{\beta }_n-{\gamma }_n)(Tx-Ty)\parallel \hfill \\ & \le & {\beta }_n\parallel x-y\parallel +{\gamma }_n\parallel Sx-Sy\parallel +(1-{\beta }_n-{\gamma }_n)\parallel Tx-Ty\parallel \hfill \\ & \le & \parallel x-y\parallel .\hfill \end{array}$$

(14)

From (13) and (14), we have that $T_n$ is G-nonexpansive for all $n\in \mathbb{N}$. Next, we show that $\{T_n\}$ satisfies the $NST$-condition with respect to $\tau$. It is clear that $F(\tau )\subset {\bigcap }_{n=1}^{\infty }F(T_n)$. On the other hand, we let $p\in {\bigcap }_{n=1}^{\infty }F(T_n)$.

Consider

$$\begin{array}{ccc}\hfill \parallel p-Tp\parallel & \le & \parallel p-T_{n}p\parallel +\parallel T_{n}p-Tp\parallel \hfill \\ & =& \parallel {\beta }_{n}p+{\gamma }_{n}Sp+(1-{\beta }_n-{\gamma }_n)Tp-Tp\parallel \hfill \\ & =& \parallel {\beta }_n(p-Tp)+{\gamma }_n(Sp-Tp)\parallel \hfill \\ & \le & {\beta }_n\parallel p-Tp\parallel +{\gamma }_n\parallel Sp-Tp\parallel .\hfill \end{array}$$

(15)

By our assumption, we obtain $\parallel p-Tp\parallel =0$. Hence, $p=Tp=Sp$. Therefore, $F(\tau )={\bigcap }_{n=1}^{\infty }F(T_n)$. Next, we let $\left\{x_n\right\}$ be a sequence in C such that $\underset{n\to \infty }{lim}\parallel x_n-T_n{x}_n\parallel =0$ and $p\in F(\tau )$. We shall show that $\underset{n\to \infty }{lim}\parallel T{x}_n-x_n\parallel ={lim}_{n\to \infty }\parallel S{x}_n-x_n\parallel =0.$ Since $(x_n,p)\in E(G)$ for all $n\in \mathbb{N}$, we have

$$\begin{array}{ccc}\hfill \parallel T_n{x}_n{-p\parallel }^2& =& \parallel {\beta }_n{x}_n+{\gamma }_{n}S{x}_n+(1-{\beta }_n-{\gamma }_n)T{x}_n{-p\parallel }^2\hfill \\ & =& {\beta }_n\parallel x_n{-p\parallel }^2+{\gamma }_n{\parallel S{x}_n-p\parallel }^2\hfill \\ & & +(1-{\beta }_n-{\gamma }_n){\parallel T{x}_n-p\parallel }^2\hfill \\ & & -{\beta }_n{\gamma }_n\parallel S{x}_n-x_n{\parallel }^2-{\beta }_n(1-{\beta }_n-{\gamma }_n){\parallel T{x}_n-x_n\parallel }^2.\hfill \end{array}$$

Thus,

$$\begin{array}{c}\hfill {\beta }_n(1-{\beta }_n-{\gamma }_n)\parallel T{x}_n-x_n{\parallel }^2+{\beta }_n{\gamma }_n\parallel S{x}_n-x_n{\parallel }^2\le \parallel x_n{-p\parallel }^2-{\parallel T_n{x}_n-p\parallel }^2.\end{array}$$

ince $\parallel x_n-T_n{x}_n\parallel \to 0$ as $n\to \infty$, by our assumptions, we have $\parallel T{x}_n-x_n\parallel \to 0$ and $\parallel S{x}_n-x_n\parallel \to 0$ as $n\to \infty$. Hence, $\{T_n\}$ satisfies the $NST$-condition with respect to $\tau =\{S,T\}$. □

Example 3.

Let $T,S\in \tau$. Define $T_n={\gamma }_{n}I+(1-{\gamma }_n)S({\beta }_{n}I+(1-{\beta }_n)T)$, where $0<b\le {\beta }_n\le c<1$ and $0<d\le {\gamma }_n\le e<1$. If $(p,x^{*})\in E(G)$ for all $p\in {\bigcap }_{n=1}^{\infty }F(T_n)$, $x^{*}\in F(\tau )$ and $(x,Tx),(x,x^{*})\in E(G)$ for all $x\in C$ and $x^{*}\in F(\tau )$, then $\left\{T_n\right\}$ is a family of G-nonexpansive mappings and satisfies the $NST$-condition.

Proof. 

We first prove that $T_n$ is G-nonexpansive for all $n\in \mathbb{N}$. Let $(x,y)\in E(G)$, and we see that $(Tx,Ty)\in E(G)$. Setting $U_n={\beta }_n+(1-{\beta }_n)T$, by the convexity of $E(G)$, we have $(U_{n}x,U_{n}y)=({\beta }_{n}x+(1-{\beta }_n)Tx,{\beta }_{n}y+(1-{\beta }_n)Ty)\in E(G)$. This implies that $(S({\beta }_{n}x+(1-{\beta }_n)Tx),S({\beta }_{n}y+(1-{\beta }_n)Ty))\in E(G)$. Again by the convexity of $E(G)$, we have

$$\begin{array}{c}\hfill (T_{n}x,T_{n}y)=({\gamma }_{n}x+(1-{\gamma }_n)S({\beta }_{n}x+(1-{\beta }_n)Tx),{\gamma }_{n}y+(1-{\gamma }_n)S({\beta }_{n}y+(1-{\beta }_n)Ty))\in E(G).\end{array}$$

Then, we have

$$\begin{array}{ccc}\hfill \parallel U_{n}x-U_{n}y\parallel & =& \parallel {\beta }_{n}x+(1-{\beta }_n)Tx-{\beta }_{n}y-(1-{\beta }_n)Ty\parallel \hfill \\ & \le & {\beta }_n\parallel x-y\parallel +(1-{\beta }_n)\parallel Tx-Ty\parallel \hfill \\ & \le & \parallel x-y\parallel ,\hfill \end{array}$$

(16)

and hence

$$\begin{array}{ccc}\hfill \parallel T_{n}x-T_{n}y\parallel & =& \parallel {\gamma }_{n}x+(1-{\gamma }_n)S{U}_{n}x-{\gamma }_{n}y-(1-{\gamma }_n)S{U}_{n}y\parallel \hfill \\ & =& \parallel {\gamma }_n(x-y)+(1-{\gamma }_n)(S{U}_{n}x-S{U}_{n}y)\parallel \hfill \\ & \le & {\gamma }_n\parallel x-y\parallel +(1-{\gamma }_n)\parallel S{U}_{n}x-S{U}_{n}y\parallel \hfill \\ & \le & {\gamma }_n\parallel x-y\parallel +(1-{\gamma }_n)\parallel U_{n}x-U_{n}y\parallel \hfill \\ & \le & {\gamma }_n\parallel x-y\parallel +(1-{\gamma }_n)\parallel x-y\parallel \hfill \\ & =& \parallel x-y\parallel .\hfill \end{array}$$

Hence, $T_n$ is G-nonexpansive for all $n\in \mathbb{N}$. Next, we show that $\{T_n\}$ satisfies the $NST$-condition with respect to $\tau$. It is obvious that $F(\tau )\subset {\bigcap }_{n=1}^{\infty }F(T_n).$ Thus, it is enough to show that ${\bigcap }_{n=1}^{\infty }F(T_n)\subset F(\tau )$. Let $x^{*}\in F(\tau )$, $p\in {\bigcap }_{n=1}^{\infty }F(T_n)$ and $(p,x^{*})\in E(G)$. Then, we have $(U_{n}p,x^{*})\in E(G)$. It follows that

$$\begin{array}{ccc}\hfill \parallel p-x^{*}\parallel & =& \parallel T_{n}p-x^{*}\parallel \hfill \\ & =& \parallel r_{n}p+(1-{\gamma }_n)S{U}_{n}p-x^{*}\parallel \hfill \\ & \le & {\gamma }_n\parallel p-x^{*}\parallel +(1-{\gamma }_n)\parallel S{U}_{n}p-S{x}^{*}\parallel \hfill \\ & \le & {\gamma }_n\parallel p-x^{*}\parallel +(1-{\gamma }_n)\parallel U_{n}p-x^{*}\parallel \hfill \\ & \le & {\gamma }_n\parallel p-x^{*}\parallel +(1-{\gamma }_n)\parallel {\beta }_{n}p+(1-{\beta }_n)Tp-x^{*}\parallel \hfill \\ & \le & {\gamma }_n\parallel p-x^{*}\parallel +(1-{\gamma }_n)({\beta }_n\parallel p-x^{*}\parallel +(1-{\beta }_n)\parallel Tp-T{x}^{*}\parallel )\hfill \\ & \le & \parallel p-x^{*}\parallel .\hfill \end{array}$$

This implies that $\parallel p-x^{*}\parallel ={\gamma }_n\parallel p-x^{*}\parallel +(1-{\gamma }_n)\parallel U_{n}p-x^{*}\parallel$. Then, we have

$$\begin{array}{ccc}\hfill \parallel p-x^{*}\parallel & =& \parallel U_{n}p-x^{*}\parallel \hfill \\ & =& \parallel Tp-x^{*}\parallel \hfill \\ & =& \parallel {\beta }_{n}p+(1-{\beta }_n)Tp-x^{*}\parallel \hfill \\ & =& \parallel {\beta }_n(p-x^{*})+(1-{\beta }_n)(Tp-x^{*})\parallel .\hfill \end{array}$$

(17)

From Lemma 5, $Tp=p$. Consider

$$\begin{array}{ccc}\hfill \parallel p-Sp\parallel & \le & \parallel p-T_{n}p\parallel +\parallel T_{n}p-Sp\parallel \hfill \\ & =& \parallel {\gamma }_{n}p+(1-{\gamma }_n)S{U}_{n}p-Sp\parallel \hfill \\ & \le & {\gamma }_n\parallel p-Sp\parallel +(1-{\gamma }_n)\parallel S{U}_{n}p-Sp\parallel \hfill \\ & \le & {\gamma }_n\parallel p-Sp\parallel +(1-{\gamma }_n)\parallel U_{n}p-p\parallel .\hfill \\ & \le & {\gamma }_n\parallel p-Sp\parallel +(1-{\gamma }_n)(1-{\beta }_n)\parallel Tp-p\parallel .\hfill \end{array}$$

(18)

This implies that $Sp=p$. This shows that $F(\tau )={\bigcap }_{n=1}^{\infty }F({\tau }_n)$.

Let $\left\{x_n\right\}$ be a sequence in C such that ${lim}_{n\to 0}\parallel T_n{x}_n-x_n\parallel =0.$ Since $\left\{x_n\right\}$ dominates p, then $(U_n{x}_n,p)=({\beta }_n{x}_n+(1-{\beta }_n)T{x}_n,p)\in E(G)$. It follows that

$$\begin{array}{ccc}\hfill \parallel T_n{x}_n{-p\parallel }^2& =& \parallel {\gamma }_n{x}_n-(1-{\gamma }_n)S{U}_n{x}_n{-p\parallel }^2\hfill \\ & \le & {\gamma }_n\parallel x_n{-p\parallel }^2+(1-{\gamma }_n){\parallel S{U}_n{x}_n-p\parallel }^2\hfill \\ & \le & {\gamma }_n\parallel x_n{-p\parallel }^2+(1-{\gamma }_n){\parallel U_n{x}_n-p\parallel }^2\hfill \\ & =& {\gamma }_n\parallel x_n{-p\parallel }^2+(1-{\gamma }_n)({\beta }_n\parallel x_n{-p\parallel }^2+(1-{\beta }_n){\parallel T{x}_n-p\parallel }^2\hfill \\ & & -{\beta }_n(1-{\beta }_n){\parallel T{x}_n-x_n\parallel }^2)\hfill \\ & \le & \parallel x_n{-p\parallel }^2-(1-{\gamma }_n){\beta }_n(1-{\beta }_n){\parallel T{x}_n-x_n\parallel }^2.\hfill \end{array}$$

This implies that

$$(1-{\gamma }_n){\beta }_n(1-{\beta }_n)\parallel T{x}_n-x_n{\parallel }^2\le \parallel x_n{-p\parallel }^2-{\parallel T_n{x}_n-p\parallel }^2.$$

(19)

By our assumptions, we obtain

$$\underset{n\to \infty }{lim}\parallel T{x}_n-x_n\parallel =0.$$

(20)

It follows that

$$\parallel U_n{x}_n-x_n\parallel =(1-{\beta }_n)\parallel T{x}_n-x_n\parallel \to 0,$$

(21)

as $n\to \infty$. Since $(U_n{x}_n,p)\in E(G)$, it follows from (16) that

$$\begin{array}{ccc}\hfill \parallel T_n{x}_n{-p\parallel }^2& =& \parallel {\gamma }_n{x}_n-(1-{\gamma }_n)S{U}_n{x}_n{-p\parallel }^2\hfill \\ & =& {\gamma }_n\parallel x_n{-p\parallel }^2+(1-{\gamma }_n)\parallel S{U}_n{x}_n{-p\parallel }^2-{\gamma }_n(1-{\gamma }_n){\parallel S{U}_n{x}_n-x_n\parallel }^2\hfill \\ & \le & {\gamma }_n\parallel x_n{-p\parallel }^2+(1-{\gamma }_n)\parallel U_n{x}_n{-p\parallel }^2-{\gamma }_n(1-{\gamma }_n){\parallel S{U}_n{x}_n-x_n\parallel }^2\hfill \\ & \le & \parallel x_n{-p\parallel }^2-{\gamma }_n(1-{\gamma }_n){\parallel S{U}_n{x}_n-x_n\parallel }^2.\hfill \end{array}$$

(22)

This implies that

$${\gamma }_n(1-{\gamma }_n)\parallel S{U}_n{x}_n-x_n{\parallel }^2\le \parallel x_n{-p\parallel }^2-{\parallel T_n{x}_n-p\parallel }^2.$$

(23)

By our assumptions and (20), we have

$$\underset{n\to \infty }{lim}\parallel S{U}_n{x}_n-x_n\parallel =0.$$

(24)

It follows from (21) and (24) that

$$\begin{array}{ccc}\hfill \parallel T_n{x}_n-S{x}_n\parallel & =& \parallel {\gamma }_n{x}_n+(1-{\gamma }_n)S{U}_n{x}_n-S{x}_n\parallel \hfill \\ & =& \parallel {\gamma }_n(x_n-S{x}_n)+(1-{\gamma }_n)(S{U}_n{x}_n-S{x}_n)\parallel \hfill \\ & \le & {\gamma }_n\parallel x_n-S{x}_n\parallel +(1-{\gamma }_n)\parallel S{U}_n{x}_n-S{x}_n\parallel \hfill \\ & \le & {\gamma }_n(\parallel x_n-S{U}_n{x}_n\parallel +\parallel S{U}_n{x}_n-S{x}_n\parallel )+(1-{\gamma }_n)\parallel U_n{x}_n-x_n\parallel \hfill \\ & \le & {\gamma }_n\parallel x_n-S{U}_n{x}_n\parallel +{\gamma }_n\parallel U_n{x}_n-x_n\parallel +(1-{\gamma }_n)\parallel U_n{x}_n-x_n\parallel \hfill \\ & =& {\gamma }_n\parallel x_n-S{U}_n{x}_n\parallel +\parallel U_n{x}_n-x_n\parallel \to 0,\hfill \end{array}$$

as $n\to \infty$. This implies that $\parallel S{x}_n-x_n\parallel \le \parallel S{x}_n-T_n{x}_n\parallel +\parallel T_n{x}_n-x_n\parallel \to 0,$ as $n\to \infty .$ Hence, $\{T_n\}$ satisfies the $NST$-condition with respect to $\tau =\{S,T\}$.  □

4. Examples and Numerical Results

In this section, we provide some numerical examples to support our obtained result.

Example 4.

Let $H=\mathbb{R}$ and $C=[0,2]$. Assume that $(x,y)\in E(G)$ if and only if $0.4\le x,y\le 1.6$ or $x=y$, where $x,y\in \mathbb{R}$. Define mappings $T,S:C\to C$ by

$$\begin{array}{ccc}\hfill Tx& =& sin(\frac{\pi }{2})cos(tan(x-1)),\hfill \\ \hfill Sx& =& \frac{lnx}{3}+1,\hfill \end{array}$$

for all $x\in C$. It is easy to check that T and S are G-nonexpansive such that $F(S)=F(T)=\left\{1\right\}$. We have that T is not nonexpansive since for $x=1.6$ and $y=1.8$, then $\parallel Tx-Ty\parallel >0.21>\parallel x-y\parallel$. We also have that S is not nonexpansive since, for $x=0.1$ and $y=0.6$, then $\parallel Sx-Sy\parallel >0.58>\parallel x-y\parallel$.

We use the mappings in Example 4 and choose $x_0=0.4$. By computing, we obtain the sequences generated in Theorem 3 by using the mapping $T_n$ which, generated from Examples 1–3, converges to 1. We next show the following error plots of $\parallel x_{n+1}-x_n\parallel$:

(1) Choose ${\alpha }_n=\frac{n}{5n+2}$ and ${\beta }_n=\frac{n}{4n+3}$; then, the sequences $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ satisfy the conditions in Theorem 3 and Example 1.

(2) Choose ${\alpha }_n=\frac{n}{5n+2}$, ${\beta }_n=\frac{n}{4n+3}$ and ${\gamma }_n=\frac{n}{2n+1}$; then, the sequences $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ satisfy the conditions in Theorem 3 and Examples 2 and 3.

Example 5.

Let $H={\mathbb{R}}^3$ and $C={[0,\infty )}^3$. Assume that $(x,y)\in E(G)$ if and only if $0.4\le x_i,y_i\le 1.6$ or $x_i=y_i$ for all $i=1,2,3$, where $x=(x_1,x_2,x_3)$, $y=(y_1,y_2,y_3)\in {\mathbb{R}}^3$. Define mappings $T,S:C\to C$ by

$$Tx=\left(sin(\frac{\pi }{2})cos(tan(x_1-1)),tan\frac{(x_2-1)}{\sqrt{7.45}}+1,1\right),$$

$$Sx=\left(1,1,\frac{ln{x}_3}{3}+1\right)$$

for any $x=(x_1,x_2,x_3)\in C.$ It is easy to check that T and S are G-nonexpansive such that $F(S)=F(T)=\{(1,1,1)\}$. On the other hand, T is not nonexpansive since, for $x=(1.6,2,1)$ and $y=(1.8,2,1)$, then $\parallel Tx-Ty\parallel >0.21>\parallel x-y\parallel$. We also have that S is not nonexpansive since, for $x=(2,1,0.1)$ and $y=(2,1,0.6)$, then $\parallel Sx-Sy\parallel >0.58>\parallel x-y\parallel$.

We use the mappings in Example 5 and choose $x_0=(0.4,0.4,0.5)$. By computing, we obtain the sequences $\left\{x_n\right\}$ generated in Theorem 3 by using the mapping $T_n$, which generated from Examples 1–3, converge to $(1,1,1)$. We next show the following error plots of $\parallel x_{n+1}-x_n\parallel$.

(1) Choose ${\alpha }_n=\frac{n}{5n+2}$ and ${\beta }_n=\frac{n}{4n+3}$; then, the sequences $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ satisfy the conditions in Theorem 3 and Example 1.

(2) Choose ${\alpha }_n=\frac{n}{5n+2}$, ${\beta }_n=\frac{n}{4n+3}$ and ${\gamma }_n=\frac{n}{2n+1}$; then, the sequences $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ satisfy the conditions in Theorem 3 and Examples 2 and 3.

Remark 1.

According to the investigation of our numerical results under the same conditions, we see that the sequence in Theorem 3, which generated by using the mapping $T_n$ in Example 2, converges faster than the sequence of Example 3.

5. Conclusions

In this paper, we introduce the iterative scheme for approximating a common fixed point of a countable family of G-nonexpansive mappings by modifying the shrinking projection method. We then prove strong convergence theorems in a Hilbert space with a directed graph under some suitable conditions. We give some examples of some families of G-nonexpansive mappings $\left\{T_n\right\}$ that satisfy the $NST$-condition with respect to its $\tau$ (see in Examples 1–3). Finally, we give some numerical experiments for supporting our main results and compare the rate of convergence of some examples under the same conditions (see in Examples 4 and 5 and Figure 1, Figure 2, Figure 3 and Figure 4).

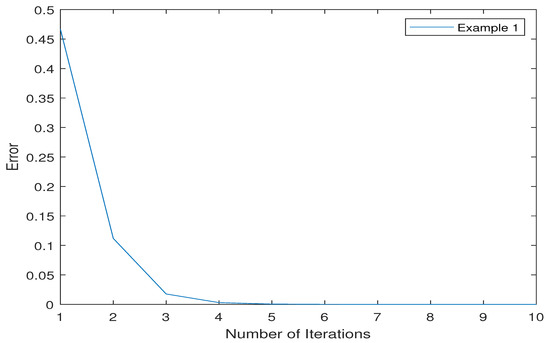
Figure 1. Error plots of the sequence $\left\{x_n\right\}$ in Theorem 3 by using the mapping $T_n$ in Example 1.

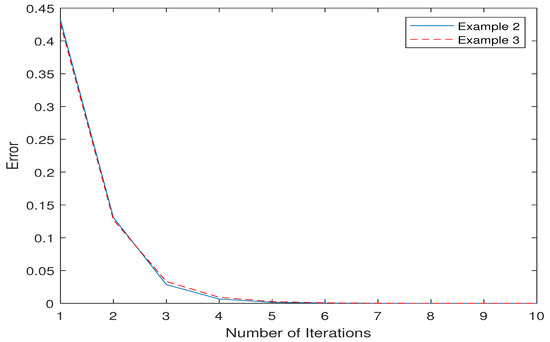
Figure 2. Error plots of the sequence $\left\{x_n\right\}$ in Theorem 3 by using the mapping $T_n$ in Examples 2 and 3.

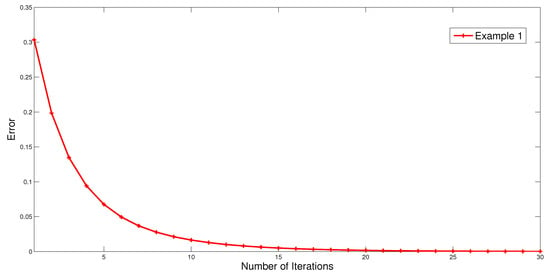
Figure 3. Error plots of the sequence $\left\{x_n\right\}$ in Theorem 3 by using the mapping $T_n$ in Example 1.

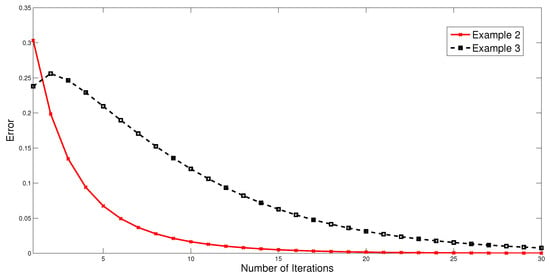
Figure 4. Error plots of the sequence $\left\{x_n\right\}$ in Theorem 3 by using the mapping $T_n$ in Examples 2 and 3.