Abstract
Unlike the study of the fixed point property (FPP, for brevity) of retractable topological spaces, the research of the FPP of non-retractable topological spaces remains. The present paper deals with the issue. Based on order-theoretic foundations and fixed point theory for Khalimsky (K-, for short) topological spaces, the present paper studies the product property of the FPP for K-topological spaces. Furthermore, the paper investigates the FPP of various types of connected K-topological spaces such as non-K-retractable spaces and some points deleted K-topological (finite) planes, and so on. To be specific, after proving that not every one point deleted subspace of a finite K-topological plane X is a K-retract of X, we study the FPP of a non-retractable topological space Y, such as one point deleted space .
MSC:
06A06; 54A10; 54C05; 55R15; 54C08; 54F65
1. Introduction
To make the paper self-contained, we recall that a mathematical object X has the FPP if every well-behaved mapping f from X to itself has a point such that . Reference [1] studied a certain fixed point Theorem in semimetric spaces and further, Reference [2] explored a coincidence point and common fixed point theorems in the product spaces of quasi-ordered metric spaces. Unlike the study of the fixed point property (FPP, for short) for retractable topological spaces, since the research of the FPP of non-retractable topological spaces still remains, the present paper addresses the issue.
A well-known connection exists between Alexandroff topology with -separation axiom and order theory via the so-called specialization order and the down-sets [3,4]. More precisely, Alexandroff topologies on X, denoted by which are induced by the preordered sets (for more details, see Section 3), are in one-to-one correspondence with preorders on X [3]. This approach is often used to describe a topological space on which every continuous mapping has a fixed point. But another approach is in order theory, where a partially ordered set (or a poset for brevity) P is said to have the FPP if every increasing function on P has a fixed point.
The paper will study the FPP from the viewpoints of both order theory and Alexandroff topology and adopt the results into the study of the FPP for Khalimsky topological spaces, which can play an important role in both pure and applied mathematics. In fixed point theory from the viewpoint of order theory, the well-known issue existed, as follows: If X and Y are ordered sets with the FPP, does have FPP? This was of interest in the theory of ordered sets [5]. It was conjectured for a long time (see Reference [5]) that the product of two finite ordered sets with the FPP has the FPP. This has been referred to as the Product Problem or the Product Conjecture. Motivated by the results in Reference [6], the conjecture was settled positively [7] if P is finite so that this became a theorem when Roddy [7] proved the conjecture true in 1994.
Let us recall the well-known theorem [8,9] that a lattice L has the FPP if and only if L is a complete lattice. Under this situation, for each order-preserving self-map g of L, the set is a complete lattice. Furthermore, motivated by the Tarski-Davis theorem [8,9] on a lattice and Kuratowski’s question [10,11] on the product property of the FPP on a peano continuum (or a compact, connected and locally connected metric space), many works dealt with the FPP for ordered sets and topological spaces. Some of these include References [3,10,12,13,14,15,16,17,18]. Rival [19] considered irreducible points in arbitrary ordered sets, as follows: For a poset , consider two distinct points . If and there is no such that , then y is said to be an upper cover of x and x is called a lower cover of y. Given a finite poset , a point in P is called irreducible if and only if it has exactly one upper cover or exactly one lower cover. Let be irreducible and assume that x has a unique lower cover. Then Rival [19] proved the following:
[Rival theorem] For a poset P and let be irreducible. Then P has the FPP if and only if has the FPP.
In poset theory, consider a poset P and two points . Then a is called retractable to b (see Definition 3.1 of Reference [20]) if and only if and and , where under the Hasse diagram of P, and mean the down set of a and the upper set of b in the poset P, respectively.
Besides, Schröder (see Theorem 3.3 of Reference [20]) proved the following:
[Schröder theorem] For a poset , assume that is retractable to . P has the FPP if and only if (1) has the FPP and (2) One of and has the FPP.
Motivated by these results, we can study the FPP for some Alexandroff (topological) spaces with -separation axiom (-A-space, for brevity if there is no danger of ambiguity) because a -A-space induces a poset and vice versa, as mentioned above. At the moment we have the following query.
[Question] How can we study the FPP of the poset (or the -A-space) in case a given poset (or a -A-space) is related to neither the Rival Theorem nor the Schröder theorem?
In Section 4, we will address the question (see Theorem 3). In topology, it is well known that in general the product property of the FPP does not hold [16,17,21]. Comparing with the FPP in References [5,16,17,21], its Khalimsky topological version has its own feature. Since the term “Khalimsky” will be often used in this paper, hereafter we will use the terminology -’ instead of “Khalimsky” if there is no danger of confusion. To study the product property of the FPP for K-topological spaces, we need to recall basic notions associated with both K-topology and fixed point theory.
Comparing a K-topological space with spaces dealt with in earlier papers [16,17,21], we can obtain a poset derived from the given K-topological space. Every two points of a poset need not be retractable point and further, each element of need not be irreducible either (see Property 1). Moreover, this poset need not be a lattice (see Lemma 1 in the present paper). Hence we cannot use the Tarski-Davis [8,9], Rival [19] and Schröder [20] theorems to study the FPP for K-topological spaces. Henceforth, we need to study fixed point theory for K-topological spaces in some different approaches from those of References [16,17,21] (see Theorem 3).
Let , and be the set of natural numbers, integers, and real numbers, respectively. Owing to Borsuk’s or Brouwer’s fixed point theorem [22], it is well known that a compact Euclidean n-dimensional cube has the FPP. However, in digital topology it is clear that any digital plane followed from the Rosenfeld model on does not have the FPP related to digitally k-continuous maps [23] (for more details, see References [24,25,26,27]). Besides, it turns out that not every -A-space has the FPP [28]. For instance, not every K-topological space has the FPP [28]. That is why in this paper we give particular attention to the FPP for K-topological spaces and its product property and further, to the further study of the FPP for some points deleted K-topological planes.
The rest of this paper is organized as follows. Section 2 provides some terminology from K-topology. Section 3 investigates a poset structure derived from an n-dimensional K-topological space and studies some properties of a K-continuous map from the viewpoint of order theory. Section 4 studies the product property of the FPP for K-topological spaces and further, investigates various properties of fixed points of K-continuous self-maps of a non-K-retractable space. Section 5 concludes the paper with summary and a further work.
2. Preliminaries
A poset consists of a set and a reflexive, antisymmetric and transitive binary relation ≤, denoted by . In this paper we will refer to the underlying set X as the ordered set and many notions are followed from References [29,30]. Subsets inherit the order relation from X in terms of a restriction to S. A homomorphism between ordered sets P and Q is an order-preserving map, that is, a map having the following property: (in P) implies (in Q). In addition, we say that an ordered set has the fixed point property if every order-preserving self-map f of X has a point such that and further, we denote . Besides, for a poset L, L is called a lattice if and only if any two elements of L have a supremum and an infimum. L is called a complete lattice if and only if any subset of L has a supremum and an infimum [3].
An Alexandroff (A-, for brevity) topological space is said to be a topological space of which each point has the smallest open neighborhood in [31]. As an example of an A-topological space is the Khalimsky (K-,for short) line topology. To be precise, K-line topology on , denoted by , is induced by the set as a subbase [31] (see also Reference [4]), where for , . Furthermore, the product topology on induced by is said to be the Khalimsky product topology on (or the Khalimsky n-dimensional space), denoted by . Hereafter, for a subset we will denote by , , a subspace induced by and it is called a K-topological space. The study of these spaces includes References [4,28,32,33,34,35,36,37,38,39].
Let us examine the structure of more precisely. A point is pure open if all coordinates are odd and pure closed if each of the coordinates is even [4] and the other points in is called mixed [4]. These points are showed like following symbols: The symbols ▪, a black jumbo dot, • mean a pure closed point, a pure open point and a mixed point (see Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5), respectively.
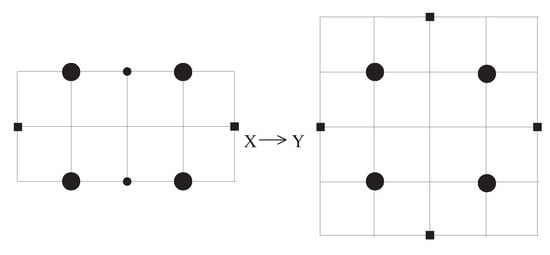
Figure 1.
Explanation of a K-homeomorphism with different numbers of pure closed points.
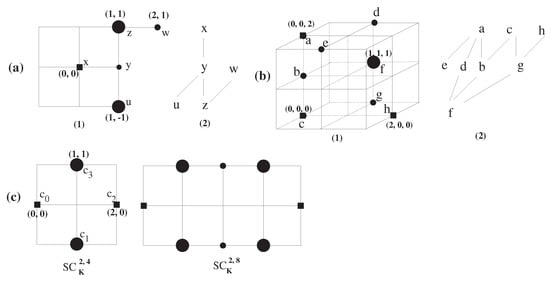
Figure 2.
(a) (1) , where ; (2) The Hasse diagram illustrating the poset derived from ; (b) (1) , where ; (2) The Hasse diagram representing the poset derived from and further, it is not a lattice; (c) Some examples for simple closed K-curves on [28].
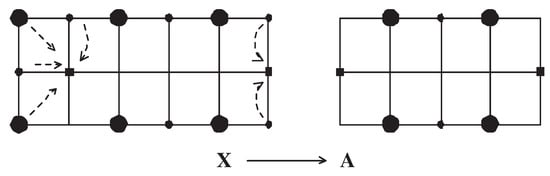
Figure 3.
Explanation of a K-retract of onto
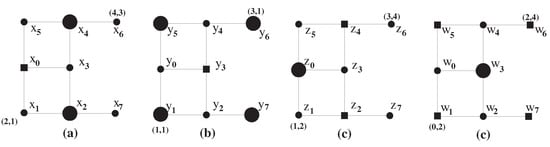
Figure 4.
(a) A non-K-retractable space from the given K-topological plane X; (b) A K-retractable space from the given K-topological plane Y; (c) A K-retractable space from the given K-topological plane Z; (d) A K-retractable space from the given K-topological plane W.
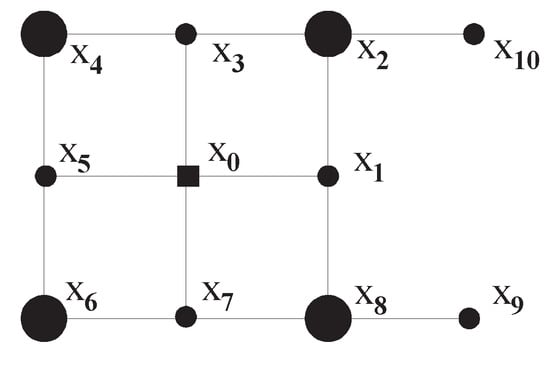
Figure 5.
Fixed Point Property (FPP) for a non-K-retractable space .
In relation to the further statement of a mixed point in , for the points (resp. ), we call the point p closed-open (resp. open-closed) [37]. In terms of this perspective, we clearly observe that the smallest (open) neighborhood of the point of , denoted by , is the following:
Similarly, for and , we can also consider in .
Definition 1
([4,33]). For , we say that two distinct points x and y in X are K-adjacent in if .
Let us recall the following terminology for studying K-topological spaces.
Definition 2
([33,40]). For we define the followings.
- (1)
- Two distinct pointsare called K-path connected (or K-connected) if there is the sequence (or a path)on X withsuch thatandare K-adjacent,. This sequence is called a K-path. Furthermore, the number l is called the length of this K-path.
- (2)
- A simple K-path in X is the K-pathin X such thatandare K-adjacent if and only if.
- (3)
- We say that a simple closed K-curve with l elementsin X, denoted by, is the K-path such thatandare K-adjacent if and only if.
Let us now recall the K-continuity of a map between two K-topological spaces [32] as follows: For two spaces and , a function is said to be K-continuous at a point if the following property holds
Furthermore, we say that a map is K-continuous if it is K-continuous at every point . This approach can be reasonable because each subspace of is an Alexandroff space.
In addition, we recall the notion of K-homeomorphism (see Figure 1) as follows: For two spaces and , a map is called a K-homeomorphism if h is a K-continuous bijection and further, is K-continuous.
Using the K-continuity of the map f, we obtain the K-topological category, denoted by KTC, consisting of the following two data [39]:
- The set of objects , denoted by ;
- For every ordered pair of objects and , the set of all K-continuous maps as morphisms.
Assume that has the FPP. If is a K-homeomorphism, then Y is also proved to have the FPP [28].
3. An Ordered Space Derived from a Khalimsky Topological Space
Recently, it turns out that not every K-topological space has the FPP such as () and [28]. Hereafter, we assume that a K-topological space is finite, K-connected and further, not a singleton. Besides, we will study the FPP of K-topological spaces by using an order-theoretical approach. In a Hasse diagram for a finite ordered set, elements x and y satisfy the relation if and only if or there is an upward path from x to y that may go through other elements of the set, but for which all segments are traversed in the upward direction (see Figure 2a,b). Let be a poset. For , put
as a down set of x in .
Using the set of (3), we develop an induced topology on X generated by the set as a base and we denoted by the topological space.
In this paper we say that an order-topological space (ordered space, for short) is a set which is both a topological space and a poset. In KTC, as special cases of the results in References [5,7,16,17,21], as follows:
Remark 1.
For two posetsand a function, f is an order-preserving map if and only if f is continuous between the induced Alexandroff topological spaces.
Proof.
Assume that f preserves order from to and let be an open base set, where means the down set of y in the given poset (for more details, see the property (3)). We need to show that is open in X. Let us now take any . In case , we have so that . Therefore . Hence, for any we have and further,
which implies that is open.
Conversely, assume that f is continuous between the induced Alexandroff topologies and let for some . Suppose . Let . Therefore but A is open, due to the continuity of f, we obtain that is open. Hence . But , so , which implies that so that it invokes a contradiction. □
For , we ask if the ordered space induced by is equal to the K-topological space . To be specific, based on the poset derived from , to establish the topology on X, we may have the following set as a subbase for the topology of (see the property (1))
where For instance, for , to establish the topology induced by the poset derived from , we have the set as a subbase. Hence it is clear that the topology on is equal to the K-topological space .
By using this approach, for an integral interval , the ordered space induced by is equal to the K-interval denoted by .
According to this approach, for we obtain the following:
Corollary 1.
For,is equal to, whereis a subspace for X relative to the topology.
Lemma 1.
A K-topological spaceis an ordered space which need not be a lattice.
Proof.
Under the Khalimsky n-dimensional space , we define a relation derived from , as follows:
For two points of we say that
Apart from this approach (4), we can also consider this relation ” in terms of the specialization order in Reference [4]. More precisely, we say that if and only if , where the notation “” means the closure operator. However, if we take the specialization order for establishing a relation “≤” for a poset, then this relation is different from the relation of (4). Since satisfies the -separation axiom, the relation “≤” of (4) is reflexive, antisymmetric(due to the -separation axiom) and transitive. Furthermore, it is clear that the subspace also induces a poset structure. However, the induced ordered space need not be a lattice. For instance, consider the K-topological spaces and in Figure 2a,b. Then, according to the property (4), we obtain their Hasse diagrams of which the induced posets and are not lattices (see Figure 2a,b(2)). □
The following is obtained by using the property of (3) and the relation of (4), which can be effectively used in studying the FPP of ordered spaces in Section 4.
Lemma 2.
The ordered spaceis a-A-space and further, a semi-space.
Proof.
Let us prove that the ordered space supports the -separation axiom. Consider any two distinct points . Note that, owing to the antisymmetric property of the relation ≤, we have or . Therefore or . Thus satisfies the -separation axiom because for every point we have .
Let us now prove that is Alexandroff. Indeed, we suffice to show that an arbitrary intersection of base open sets is open. So assume that is a subset of X such that and let . Then, owing to the transitive property of the relation ≤, it is clear that and thus
and therefore the intersection A is open, which implies that is an Alexandroff space. □
By using the notion of (4), Remark 1 and Lemma 2, we obtain the following:
Corollary 2.
A K-continuous map between two K-topological spaces is equivalent to an order preserving map between posets derived from the given K-topological spaces.
4. The FPP of Non--Retractable Spaces
There was the well-known conjecture [41] wondering if the fact that X and Y have the FPP implies that the product space has the property. This note contains an affirmative answer in the case that X and Y are compact ordered space (with the order topology) [7]. Besides, Cohen [29] rephrased the result as follows.
As referred to in the above, since the present paper deals with only finite and connected spaces which is not a singleton, in all spaces are assumed to be both compact and connected. Motivated by the property (5) (or an immediate consequence of Reference [7]), we have the following:
Remark 2.
Assume that bothandhave the FPP. Then the product spacehas the FPP.
Proof.
Under the hypothesis, it is clear that both and are compact (i.e., finite) connected ordered spaces. Owing to the results of Reference [7], since both and derived from the given K-topological spaces are finite posets, they have the FPP. Hence, by Corollary 1, the product space has the FPP because it is equal to the ordered space . By Corollary 1 and Lemma 1, the proof is completed (see the property (5)). □
Theorem 1
([28,37]). A simple K-path in has the FPP.
Owing to Theorem 1, it is clear that a K-interval obviously has the FPP because a simple K-path in is K-homeomorphic to a K-interval (see the last part of Section 2).
By Theorem 1, since the K-interval has the FPP and further, is compact and connected, we have the following:
Remark 3.
(1) References [35,37] dealt with the FPP of a K-interval and further, Reference [28] proved the FPP of a K-path. Besides, Reference [35] proved the FPP for finite K-topological plane in terms of an implicit function Theorem (see Theorem 9.2.4 on page 78 [35]).
(2) Letbe a finite n-dimensional cube as a K-topological subspace. Then, by Remark 2 and Theorem 1,has the FPP.
The notion of retraction in order theory has been used in studying the FPP [19]. More precisely, let be a poset. As mentioned in Section 1, a point is called retractable to [20] if and only if for all implies and implies [20]. In other words, for an ordered set, we say that an order-preserving self-map r of P is called a retraction [20] if and only if . We will say that is a retract of P if and only if there is a retraction with [20].
Based on the Schröder Theorem in Section 1, Reference [30] further studied the FPP for product spaces in terms of the retractability from an order theoretical view. Since an ordered space is both a poset and a topological space, we will use the K-retraction in Reference [27] for studying the FPP for K-topological spaces.
Definition 3
([27]). In KTC, a K-continuous map is a K-retraction if
- (1)
- is a K-topological subspace ofand
- (2)
- for all.
Then we call X a K-retract of.
Example 1.
As a special case of the Theorem in Reference [7], we see the following: Let be a K-topological space having the FPP. For , if a map is a K-retraction, then has the FPP.
In this paper a K-topological plane is defined, as follows:
Definition 4.
A spaceofis said to be a finite K-topological plane ifis K-homeomorphic to, wherefor some.
The following exploration involving a K-retract will be essentially used to prove main theorems of this paper.
Theorem 2.
Let X be a finite K-topological plane. Not every one pointdeleted subspace of X is a K-retract of X.
Proof.
We may consider for some such as
Based on this situation, we may examine the K-retract property of a spaces X with the following case according to the first case of (6).
Assume and in Figure 4a. Let us consider the K-topological spaces and . Then we observe that is not a K-retract of . □
Thus this example guarantees that not every one point deleted subspace of a finite K-topological plane X is a K-retract of X.
Using Remark 3(2), owing to the FPP of a retraction, we obtain the following:
Corollary 3.
Consider a K-topological spacecontained in a K-cubeas a subspace such thatis a K-retract of. Thenhas the FPP.
Example 2.
(1) As referred to in Theorem 2, since the spaceis K-retractable ontoin Figure 4b, owing to the K-retract property of the FPP (see Corollary 3), it turns out thathas the FPP. Hence we conclude thathas the FPP.
(2) As referred to in Theorem 2, since the spaceis K-retractable ontoin Figure 4c and further, owing to the K-retract property of the FPP, it turns out thathas the FPP. Hence we conclude thathas the FPP.
In relation to the two theorems initiated by Rival and Schröder referred to in Section 1, we can obviously have the following property.
Property 1.
Consider the setin Figure 4a with the K-topological structure denoted byor a posetinduced by the space. Then the pointin the posetis neither irreducible point nor retractable to any point.
Proof.
We first prove that the point is not irreducible in . Assume an element such that . Then we may take in , for example, . In case , there is an element such that , which implies that a is not irreducible in . Next, we prove that a is not retractable to any point . To be precise, in since , for any we obtain
which implies that a is not retractable to the point b. To be specific, for any element the set is not comparable with . In case , the element a is not retractable to b either because the points a and b also satisfies the property (7). □
In view of Property 1, we cannot address the question posed in Section 1 by using the two theorems in Section 1. Thus, by using the FPP for the K-topological category, let us now investigate the FPP for some points deleted K-topological spaces which are not K-retracts of some K-topological planes.
Theorem 3.
Consider the K-topological plane. Let, where p is a pure closed point in. While the spaceis not K-retractable onto,has the FPP.
Proof.
Without loss of generality, we may consider and in Figure 4a. As referred to in Theorem 2, the given space is not a K-retract of any K-topological plane such as . Thus we cannot adopt Corollary 3 into the study of the FPP of . Hence we need to prove the FPP for from the viewpoint of Khalimsky topological category. Let us consider any K-continuous self-map of . In particular, consider the point (see Figure 4a) and assume any K-continuous self-map f sending the point .
In case , the proof is completed.
In case is mapped into a pure open point in A such as . Then, owing to the K-continuity of f (see the property (2)), we have so that is a fixed point of f.
In case is mapped into a mixed point in A such as . Then, owing to the K-continuity of f, we should have or . If it happens to the former, the point t is a fixed point of f, and if it happens to the latter, the point or is a fixed point of f because . □
Example 3.
By using the method similar to the proof of Theorem 3, while the given K-topological spaceis not a K-retract of any K-topological plane such as, where, we observe thathas the FPP.
5. Summary and Future Work
Using both an order-theoretical and an Alexandroff topological approaches, we have studied the FPP of Khalimsky topological spaces. In particular, we developed the product property of the FPP for K-topological spaces. Furthermore, we studied the FPP of non-K-retractable spaces and some points deleted K-topological planes.
As an extension of the results in the present paper, we need to establish various types of -A-spaces. Besides, let ETC be the category of Euclidean topological space [22]. Then we need to develop a functor from ETC into KTC preserving the FPP of spaces in ETC into that of spaces in KTC. In addition, we can extend the results in this paper to the study of n-dimensional K-topological spaces.
Author Contributions
Conceptualization, S.-E.H. and J.M.K.; methodology, S.-E.H. and J.M.K.; validation, S.-E.H., J.M.K. and S.L.; formal analysis, S.-E.H., J.M.K. and S.L.; investigation, S.-E.H., J.M.K. and S.L.; writing—original draft preparation, S.-E.H. and J.M.K.; writing—review and editing, S.-E.H.; visualization, S.-E.H. and J.M.K.; supervision, S.-E.H.; funding acquisition, S.-E.H.
Funding
The second author was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology(2019R1I1A3A03059103).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Suzuki, W.T. Edelstein’s fixed point Theorem in semimetric spaces. J. Nonlinear Var. Anal. 2018, 2, 165–175. [Google Scholar]
- Wu, H.-C. Coincidence point and common fixed point theorems in the product spaces of quasi-ordered metric spaces. J. Nonlinear Var. Anal. 2017, 1, 175–199. [Google Scholar]
- Birkhoff, G. Lattice Theory; American Mathematical Society: Providence, RI, USA, 1961. [Google Scholar]
- Khalimsky, E.; Kopperman, R.; Meyer, P.R. Computer graphics and connected topologies on finite ordered sets. Topol. Appl. 1990, 36, 1–17. [Google Scholar] [CrossRef]
- Rival, I. Unsolved problems. Order 1984, 1, 103–105. [Google Scholar] [CrossRef]
- Ginsburg, S. Fixed points of products and ordered sums of simply ordered sets. Proc. Am. Math. Soc. 1954, 5, 554–565. [Google Scholar] [CrossRef]
- Roddy, M. Fixed points and products. Order 1994, 11, 11–14. [Google Scholar] [CrossRef]
- Davis, A.C. A characterization of complete lattices. Pac. J. Math. 1955, 5, 311–319. [Google Scholar] [CrossRef]
- Tarski, A. A lattice-theoretical fixpoint Theorem and its applications. Pac. J. Math. 1955, 5, 285–309. [Google Scholar] [CrossRef]
- Abian, S.; Brown, A.B. A Theorem on partially ordered sets with applications to fixed point theorems. Can. J. Math. 1961, 13, 78–82. [Google Scholar] [CrossRef]
- Kuratowski, K. Topology 2; Academic Press: New York, NY, USA; London, UK; Warszawa, Poland, 1968. [Google Scholar]
- Baclawski, K. A combinatorial proof of a fixed point property. J. Combin. Theory A 2012, 119, 994–1013. [Google Scholar] [CrossRef]
- Baclawski, K.; Bjorner, A. Fixed points in partially ordered sets. Adv. Math. 1979, 31, 263–287. [Google Scholar] [CrossRef][Green Version]
- Brown, R.F. The fixed point property and cartesian products. Am. Math. Mon. 1982, 89, 654–668. [Google Scholar] [CrossRef]
- Edelman, P. On a fixed point Theorem for partially ordered sets. Discret. Math. 1979, 15, 117–119. [Google Scholar] [CrossRef]
- Fadell, E. Recent results in fixed point results for continuous maps. Bull. Am. Math. Soc. 1970, 76, 10–29. [Google Scholar] [CrossRef]
- Fora, A. A fixed point Theorem for product spaces. Pacific J. Math. 1982, 99, 327–335. [Google Scholar] [CrossRef][Green Version]
- Kukiela, M. On homotopy types of Alexandroff spaces. Order 2010, 27, 9–21. [Google Scholar] [CrossRef]
- Rival, I. A fixed point Theorem for partially ordered sets. J. Combin. Theory A 1976, 21, 309–318. [Google Scholar] [CrossRef]
- Schrder, B. Fixed point property for 11-element sets. Order 1993, 10, 329–347. [Google Scholar]
- Kirk, W.A. Fixed point theorems in product spaces. In Operator Equations and Fixed Point Theorems; Singh, S.P., Sehgal, V.M., Burry, J.H.W., Eds.; MSRI Korea: Berkeley, CA, USA, 1986; pp. 27–35. [Google Scholar]
- Munkres, J.R. Topology; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Rosenfeld, A. Continuous functions on digital pictures. Patt. Recognit. Lett. 1986, 4, 177–184. [Google Scholar] [CrossRef]
- Han, S.-E. Banach fixed point Theorem from the viewpoint of digital topology. J. Nonlinear Sci. Appl. 2016, 9, 895–905. [Google Scholar] [CrossRef]
- Han, S.-E. The fixed point property of the smallest open neighborhood of the n-dimensional Khalimsky topological space. Filomat 2017, 31, 6165–6173. [Google Scholar] [CrossRef]
- Han, S.-E.; Yao, W. Euler characteristics for digital wedge sums and their applications. Topol. Methods Nonlinear Anal. 2017, 49, 183–203. [Google Scholar] [CrossRef]
- Han, S.-E. Fixed point theorems for digital images. Honam Math. J. 2015, 37, 595–608. [Google Scholar] [CrossRef]
- Han, S.-E. Contractibility and Fixed point property: The case of Khalimsky topological spaces. Fixed Point Theory Appl. 2016, 2016, 75. [Google Scholar] [CrossRef][Green Version]
- Cohen, H. Fixed points in products of ordered spaces. Proc. Am. Math. Soc. 1956, 7, 703–706. [Google Scholar] [CrossRef]
- Rutkowski, A.; Schrder, B. Retractability and the Fixed Point Property for Products. Order 1994, 11, 353–359. [Google Scholar] [CrossRef]
- Alexandorff, P. Diskrete Räume. Mat. Sb. 1937, 2, 501–518. [Google Scholar]
- Khalimsky, E.D. Applications of connected ordered topological spaces in topology. In Proceedings of the Conference of Mathematics Department of Provoia; 1970. [Google Scholar]
- Han, S.-E.; Sostak, A. A compression of digital images derived from a Khalimsky topological structure. Comput. Appl. Math. 2013, 32, 521–536. [Google Scholar] [CrossRef]
- Kang, J.M.; Han, S.-E. Compression of Khalimsky topological spaces. Filomat 2012, 26, 1101–1114. [Google Scholar] [CrossRef]
- Kiselman, C.O. Digital Geometry and Mathematical Morphology; Lecture Notes; Department of Mathematics, Uppsala University: Uppsala, Sweden, 2002. [Google Scholar]
- Melin, E. Continuous digitization in Khalimsky spaces. J. Approx. Theory 2008, 150, 96–116. [Google Scholar] [CrossRef][Green Version]
- Samieinia, S. The number of Khalimsky-continuous functions between two points. Comb. Image Anal. LNCS 2011, 6636, 96–106. [Google Scholar]
- Smyth, M.B.; Tsaur, R. AFPP vs FPP: The link between almost fixed point properties of discrete structures and fixed point properties of spaces. Appl. Categor. Struct. 2003, 11, 95–116. [Google Scholar] [CrossRef]
- Han, S.-E. Continuities and homeomorphisms in computer topology and their applications. J. Korean Math. Soc. 2008, 45, 923–952. [Google Scholar] [CrossRef]
- Han, S.-E. An extension problem of a connectedness preserving map between Khalimsky spaces. Filomat 2016, 30, 15–28. [Google Scholar] [CrossRef]
- Strother, W.L. On an open question concerning fixed points. Proc. Am. Math. Soc. 1953, 4, 988–993. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).