Exact Solutions for a Modified Schrödinger Equation
Abstract
1. Introduction
- V is a nonnegative potential belonging to the reverse Hölder class , that is, the class of all nonnegative locally integrable functions on , for which there exists such that the reverse Hölder inequality;holds for every , , denotes the ball centered at x with radius r and stands for the Lebesgue measure of the ball ;
- the source term f belongs to some suitable Morrey spaces associated to nonnegative potential V.
2. Main Results
3. Exact Solutions
- Reduction I:
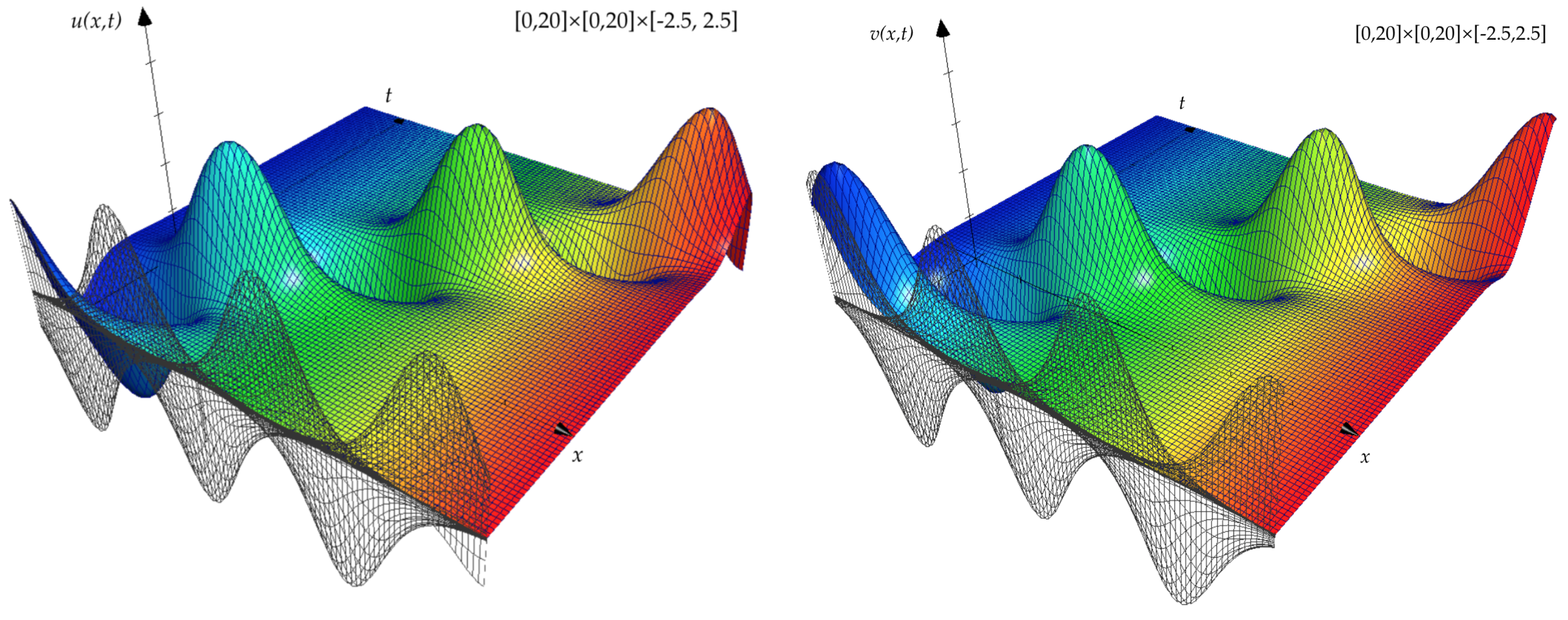
- In this case we consider the operator as a linear combination of the operators (10), namely:where and are real constants, which give the following similarity variable:and similarity solutions:where and satisfy the ODEs to which (2) and (3) are reduced by means of the operator (12):A solution to (16) and (17) isunder the condition , with the constant of integration normalized to one. When we return to the original variables, we obtain that the system (2) and (3) of PDEs admits a periodic wave solution:If, in particular, in (16) and (17), we have also the validity of the structural condition , the solution reads as:When and , the system admits a soliton solution of the form:
- Reduction II:
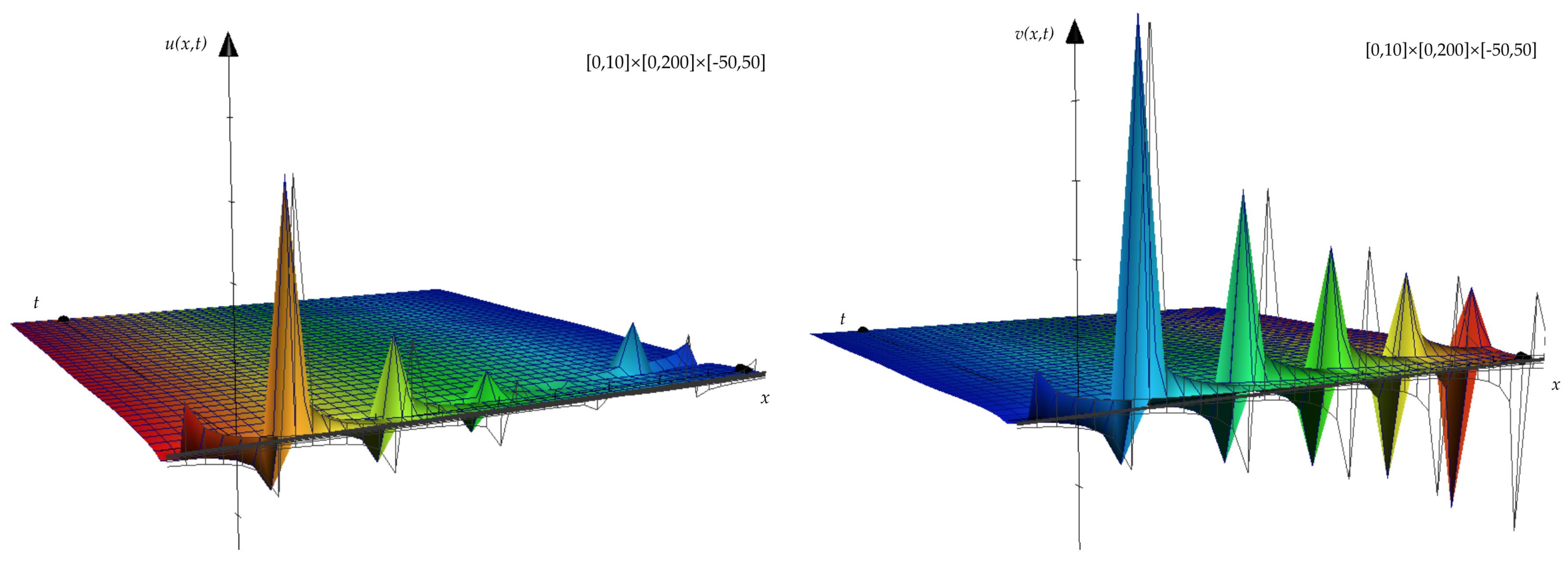
- Proceeding as in the previous case, through the operator (11)we obtain the similarity variable and solutions, respectively:Additionally, here, and satisfy the ODEs to which (2) and (3) are reduced by means of the operator (11), i.e.,In this case, we obtain a rational solution of (25) and (26) which reads as:under the condition .If, on the contrary, , a solution of (25) and (26) can be expressed in terms of Bessel functions:where we have set the Bessel functions as: , , and are arbitrary constants.
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NLS | Nonlinear Schrödinger |
| PDEs | Partial Differential Equations |
| ODEs | Ordinary Differential Equations |
References
- Davydov, A.S. The theory of contraction of proteins under their excitation. J. Theor. Biol. 1973, 38, 559–569. [Google Scholar] [CrossRef]
- Davydov, A.S.; Kislukha, N.I. Solitons in one-dimensional molecular chains. Phys. Status Solidi B 1976, 75, 735–742. [Google Scholar] [CrossRef]
- Davydov, A.S. Solitons in molecular systems. Phys. Scr. 1979, 20, 387–394. [Google Scholar] [CrossRef]
- Cisneros-Ake, L.A.; Brizhik, L.S. Charge and energy transport by Holstein solitons in anharmonic one-dimensional systems. Chaos Solitons Fractals 2019, 119, 343–354. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Glazebrook, J.F. On the quantum dynamics of Davydov solitons in protein α-helices. Phys. A Stat. Mech. Appl. 2019, 517, 257–269. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Glazebrook, J.F. Quantum tunneling of Davydov solitons through massive barriers. Chaos Solitons Fractals 2019, 123, 275–293. [Google Scholar] [CrossRef]
- Luo, J.; Piette, B.M.A.G. A generalized Davydov-Scott model for polarons in linear peptide chains. Eur. Phys. J. B 2017, 90, 1–21. [Google Scholar] [CrossRef]
- Brizhik, L.S.; Eremko, A.A.; Piette, B.; Zakrzewski, W.J.M. Solitons in α-helical proteins. Phys. Rev. E 2004, 70, 031914. [Google Scholar] [CrossRef] [PubMed]
- Daniel, M.; Latha, M.M. A generalized Davydov soliton model for energy transfer in alpha helical proteins. Phys. A 2001, 298, 351–370. [Google Scholar] [CrossRef]
- Komineas, S.; Kalosakas, G.; Bishop, A.R. Effects of intrinsic base-pair fluctuations on charge transport in DNA. Phys. Rev. E 2002, 65, 061905. [Google Scholar] [CrossRef]
- Mvogo, A.; Ben-Bolie, G.H.; Kofane, T.C. Energy transport in the three coupled α-polypeptide chains of collagen molecule with long-range interactions effect. Chaos 2015, 25, 063115. [Google Scholar] [CrossRef] [PubMed]
- Mvogo, A.; Ben-Bolie, G.H.; Kofane, T.C. Solitary waves in an inhomogeneous chain of α-helical proteins. Int. J. Mod. Phys. B 2014, 28, 1450109. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Takhtajan, L.A. Equivalence of a nonlinear Schrödinger equation and a Heisenberg ferromagnetic equation. Theor. Math. Phys. 1979, 37, 17–23. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focussing and one-dimensional self-modulating waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Hirota, R. Direct Methods in Soliton Theory; Springer: Berlin, Germany, 1980. [Google Scholar]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Liu, N.; Guo, B. Long-time asymptotics for the Sasa–Satsuma equation via nonlinear steepest descent method. J. Math. Phys. 2019, 60, 011504. [Google Scholar]
- Potasek, M.J.; Tabor, M. Exact solutions for an extended nonlinear Schrödinger equation. Phys. Lett. A 1991, 154, 449–452. [Google Scholar] [CrossRef]
- Kodama, Y. Optical solitons in a monomode fiber. J. Stat. Phys. 1985, 39, 597–614. [Google Scholar] [CrossRef]
- Di Fazio, G.; Ragusa, M.A. Commutators and Morrey Spaces. Boll. Unione Mat. Ital. 1991, 7, 321–332. [Google Scholar]
- Ragusa, M.A. Commutators of fractional integral operators on Vanishing-Morrey spaces. J. Glob. Optim. 2008, 40, 361–368. [Google Scholar] [CrossRef]
- Guliyev, V.S. Function spaces and integral operators associated with Schrödinger operators: An overview. Proc. Inst. Math. Mech. 2014, 40, 178–202. [Google Scholar]
- Akbulut, A.; Guliyev, R.V.; Celik, S.; Omarova, M.N. Fractional integral associated with Schrödinger operator on vanishing generalized Morrey spaces. J. Math. Inequal. 2018, 12, 789–805. [Google Scholar] [CrossRef]
- Guliyev, V.S.; Akbulut, A. Commutator of fractional integral with Lipschitz functions associated with Schrödinger operator on local generalized Morrey spaces. Bound. Value Probl. 2018, 80. [Google Scholar] [CrossRef]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1986. [Google Scholar]
- Biswas, B.; Mirzazadeh, M.; Savescu, M.; Milovic, D.; Khan, K.R.; Mahmood, M.F.; Belic, M. Singular solitons in optical metamaterials by ansatz method and simplest equation approach. J. Mod. Opt. 2014, 61, 1550–1555. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ma, W.X.; Huang, T.; Zhang, Y. A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 2010, 82, 065003. [Google Scholar] [CrossRef]
- Rogers, C.; Schief, W.K. Backlund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ibragimov, N.H. CRC Hanbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Ames, W.F.; Rogers, C. Nonlinear Equations in the Applied Sciences; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Fushchych, W.I.; Shtelen, W.M. Symmetry Analysis and Exact Solutions of Nonlinear Equations of Mathematical Physics; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Trippenbach, M.; Band, Y.B. Effects of self-steepening and self-frequency shifting on short-pulse splitting in dispersive nonlinear media. Phys. Rev. A 1998, 57, 4791–4803. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benia, Y.; Ruggieri, M.; Scapellato, A. Exact Solutions for a Modified Schrödinger Equation. Mathematics 2019, 7, 908. https://doi.org/10.3390/math7100908
Benia Y, Ruggieri M, Scapellato A. Exact Solutions for a Modified Schrödinger Equation. Mathematics. 2019; 7(10):908. https://doi.org/10.3390/math7100908
Chicago/Turabian StyleBenia, Yassine, Marianna Ruggieri, and Andrea Scapellato. 2019. "Exact Solutions for a Modified Schrödinger Equation" Mathematics 7, no. 10: 908. https://doi.org/10.3390/math7100908
APA StyleBenia, Y., Ruggieri, M., & Scapellato, A. (2019). Exact Solutions for a Modified Schrödinger Equation. Mathematics, 7(10), 908. https://doi.org/10.3390/math7100908





