Abstract
The aim of this paper was to propose a systematic study of a -dimensional higher order nonlinear Schrödinger equation, arising in two different contexts regarding the biological science and the nonlinear optics. We performed a Lie symmetry analysis and here present exact solutions of the equation.
1. Introduction
In the framework of biological phenomena, the Davydov model has been a theme of intensive studies and has attracted the attention of many researchers [1,2,3,4,5,6,7,8]. The nonlinear dynamics of DNA molecule has been investigated by several authors [9,10]; an interesting study concerning the Davydov’s model of -helical proteins can be found in [11,12]. Motivated by all these applications, the purpose of this paper is to make a complete study of a generalized Davydov model arising in literature in two different contexts regarding the biological science and the nonlinear optics. Working with the systematic analysis of Lie’s theory and without the restriction of the solitary wave ansatz, we showed that it admits some beautiful and most interesting reductions to ordinary differential equations; our results confirm that the equation can, in general, support periodic wave solutions, soliton solutions and interesting solutions expressed in terms of Bessel functions.
We consider the following higher order nonlinear Schrödinger equation:
where is a complex functions of x and t, is the complex conjugate of . In what follows, subscripts denote partial derivatives with respect to space and time coordinates.
When , the Equation (1) reduces to the completely integrable cubic nonlinear Schrödinger (NLS) equation, well studied in [13] and therefore we will not consider it further. Several interesting studies concerning NLS can be found in [14,15,16,17]; when it becomes the Hirota equation [16], while for the equation is referred to as the Sasa–Satsuma equation (see, e.g., [18] and references therein). The hyperbolic secant and hyperbolic tangent solutions of (1) have been studied in [19], while in [20] it is also shown that a higher-order nonlinear Schrödinger equation is solvable by means of the inverse scattering transform.
In the context of biological sciences, the Equation (1) was proposed in [9] as a generalized Davydov model. In this interpretation, the variable w represents the vibrational coordinate of the amide-I vibrations, the coefficient is a contribution related to self-steepening (also known as Kerr dispersion) and is linked to stimulated Raman scattering effects, while represents the lattice parameter. In addition, the second term represents a dispersion term linked to dipole-dipole coupling, the third term appears as the nonlinear coupling to hydrogen bonds, while the last term represents a term related to a global interaction due to molecular excitations.
In the framework of nonlinear optics, with a interchange of independent variables (), the equation characterizes the propagation of femtosecond pulses in nonlinear fibres, where w is the slowly-varying envelope of the electromagnetic field, the parameters are real coefficients linked to group velocity dispersion, self phase modulation, third-order dispersion, self steepening, and self-frequency shift due to stimulated Raman scattering, respectively.
We would like to point out that, today, a lot of problems related to regularity of solutions to Schrödinger equation in the framework of Morrey-type spaces (see, for instance, [21,22]) are studied. For an overview on Morrey spaces related on nonnegative potential, we refer the reader to [23] (and the references given there), where Guliyev collects some recently obtained results on Morrey classes and integral operators associated to Schrödinger operators and examines various versions of these spaces and the boundedness of some Schrödinger type operators on these spaces related to certain nonnegative potentials belonging to the reverse Hölder class. Furthermore, under the assumption that is an open set, in [23] are discussed some qualitative properties of solutions to the following Schrödinger equation:
where
- V is a nonnegative potential belonging to the reverse Hölder class , that is, the class of all nonnegative locally integrable functions on , for which there exists such that the reverse Hölder inequality;holds for every , , denotes the ball centered at x with radius r and stands for the Lebesgue measure of the ball ;
- the source term f belongs to some suitable Morrey spaces associated to nonnegative potential V.
We mention [24], where the authors recently studied fractional integrals associated with Schrödinger operators in the framework of vanishing generalized Morrey spaces and [25], where the authors investigated the action of commutator of fractional integral with Lipschitz functions with Schrödinger operator on local generalized Morrey space.
Despite to the general euclidean context in which the interesting regularity theory is currently studied, up to now, at our knowledge, in literature there are not regularity results, in the context of Morrey spaces, for higher order Schrödinger equation. For this reason, this paper seems to provide some basis for a potential subsequent study of qualitative properties of solutions to higher order Schrödinger equation in the context of Morrey spaces.
2. Main Results
It is convenient to rewrite the equation and after introducing , being and real smooth functions, we substitute the complex-valued function into (1) and then decomposing into real and imaginary parts yields two relations. The real and the imaginary parts gives the following system of real partial differential equations (PDEs):
The required theory, as well as the description of the method, can be found in the papers [26,27]; the symmetries of the system (2) and (3) will be generated by applying the third prolongation [26,27] of the infinitesimal operator, or generator
to Equations (2) and (3), by which we obtain the following results:
where are constants; from relation (9), we have the following two cases:
3. Exact Solutions
The study of exact solutions to nonlinear PDEs is an important point in the applied science. Many interesting methods have been elaborated, such as ansatz method, Hirota bilinear method, inverse scattering method, Darboux method, multiple-exp function method, etc. [28,29,30,31]. Lie theory gives an important contribution in almost all the scientific fields; Sophus Lie proved that a differential equation can be invariant with respect to the so-called “continuous transformation groups”. For the details, we suggest to the reader to see [26,27,32,33,34].
In this section, we use the symmetry group obtained in the Cases I and of Section 2 in order to determine the reductions of (2) and (3) from which we are able to construct exact solutions which carry important physical meanings. In the study we performed, we consider the case since, as already stated in the introduction of the paper, the case has been well studied in the literature [13].
- Reduction I:
- In this case we consider the operator as a linear combination of the operators (10), namely:where and are real constants, which give the following similarity variable:and similarity solutions:where and satisfy the ODEs to which (2) and (3) are reduced by means of the operator (12):A solution to (16) and (17) isunder the condition , with the constant of integration normalized to one. When we return to the original variables, we obtain that the system (2) and (3) of PDEs admits a periodic wave solution:If, in particular, in (16) and (17), we have also the validity of the structural condition , the solution reads as:When and , the system admits a soliton solution of the form:
- Reduction II:
- Proceeding as in the previous case, through the operator (11)we obtain the similarity variable and solutions, respectively:Additionally, here, and satisfy the ODEs to which (2) and (3) are reduced by means of the operator (11), i.e.,In this case, we obtain a rational solution of (25) and (26) which reads as:under the condition .If, on the contrary, , a solution of (25) and (26) can be expressed in terms of Bessel functions:where we have set the Bessel functions as: , , and are arbitrary constants.
4. Discussion and Conclusions
Usually, the nonlinear Schrödinger equation characterizes physical processes in which nonlinearity and dispersion cancel producing to solitons. The literature shows that the higher order nonlinear Schrödinger equation can, in general, support both soliton and periodic wave solutions. In this paper, we considered higher order nonlinear Schrödinger equation by using the Lie symmetry analysis in order to reduce it to ODEs; for each reduction exact solutions are obtained.
It is worth pointing out some details regarding the dimensionality of the parameters , and , which appear in the model. It is interesting to observe the meaning of parameter in two different contexts; in the framework of biological sciences, represents the lattice parameter and in the context of nonlinear optics can be interpreted as a dispersion parameter. Usually, in the applications, it expresses the size of atoms and molecules, the length of chemical bonds and the arrangement of atoms in crystals; commonly it is expressed in Ångström (Å). The coefficient is related to the Kerr effect that is a change in the refractive index of a given material in response to an applied electric field. Precisely, the induced index change by the Kerr effect is directly proportional to the square of the electric field. Finally, the parameter is related to the Raman scattering. Several optical processes involve the simultaneous (instantaneous) absorption of an incident photon and emission of another photon. These processes are usually called scattering processes and the emitted photon is called the scattered photon. Scattering process can be classified into two main classes: elastic scattering and inelastic scattering. In the case of elastic scattering, the incident and scattered photons have the same energy, but they could have different direction and/or polarization. In the case of inelastic scattering, the scattered photon is at a different energy from that of the incident photon. The Raman scattering is an inelastic scattering which involves transitions between the vibrational/rotational levels. Then, when we regard to the solution (22) and (23) without losing the generality, we have posed in Figure 1 the value .
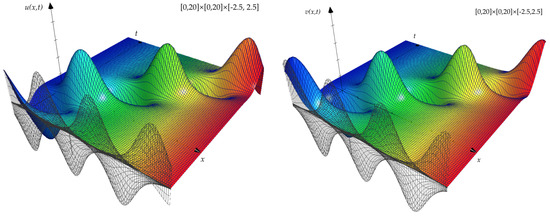
Figure 1.
Snapshots of 3D view of the solution (22) and (23), with a interchange of independent variables () and .
Remark 1.
In biological interpretation, as confirmed by Daniel [9], it turns out that the Equation (1), as well as variants of it, characterizes a protein chain where the nonlinear coupling, being liable to the development of solitons, derives from lightly different interaction. Futhermore, in two recent papers [5,6] the effects of anisotropy of left and right coupling between neighbouring peptide groups in proteins are studied in great details, and also moving solitons were illustrated.
On the other hand, looking solutions (22) and (23) from the point of view of nonlinear optics, as predicted by Trippenbach et al. [35], the higher order nonlinearities definitively influences the dynamics.
Looking at the class of solutions (24), we observe that it is obtained for then it is no longer valid in the limit of cubic nonlinear Schrödinger equation. This fact is perfectly justified by the dimensionality of the constant that we have clarified at the beginning of this section. From Figure 2, we see a plot of the solution (24) under the structural condition for the equation , when .

Figure 2.
Snapshot of 3D view of the solution (24), when , with and .
The novelty of this work lies in the fact that the application of Lie symmetry analysis is being made for the first time, to the best of our knowledge, in such systems that lend themselves to a double interpretation in two different contexts of the applied sciences. Moreover, our future aim is to study qualitative properties of solutions to differential problems driven by nonlinear Schrödinger equations as (1) in the context of suitable Morrey-type spaces. The results contained in this paper provide a satisfactory background because they give us a precise shape of the solutions. On the other hand, an a priori analysis in some new function spaces allows us to overcome the computational difficulties that arise directly using the representation formulae for the solutions.
Author Contributions
Y.B., M.R., and A.S. worked together in the derivation of the mathematical results. All the authors provided critical feedback and helped shape the research, analysis, and manuscript.
Funding
This research received no external funding.
Acknowledgments
The document was written during the stay of the first author Y.B. in Catania as part of the project DIRE-MED (Dialogue Interculturel, REseaux et Mobilité en MEDiterranée). M.R. is a member of the INdAM Research group GNFM (National Group for the Mathematical Physics). A.S. is a member of UMI (Italian Mathematical Union) and EMS (European Mathematical Society).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NLS | Nonlinear Schrödinger |
| PDEs | Partial Differential Equations |
| ODEs | Ordinary Differential Equations |
References
- Davydov, A.S. The theory of contraction of proteins under their excitation. J. Theor. Biol. 1973, 38, 559–569. [Google Scholar] [CrossRef]
- Davydov, A.S.; Kislukha, N.I. Solitons in one-dimensional molecular chains. Phys. Status Solidi B 1976, 75, 735–742. [Google Scholar] [CrossRef]
- Davydov, A.S. Solitons in molecular systems. Phys. Scr. 1979, 20, 387–394. [Google Scholar] [CrossRef]
- Cisneros-Ake, L.A.; Brizhik, L.S. Charge and energy transport by Holstein solitons in anharmonic one-dimensional systems. Chaos Solitons Fractals 2019, 119, 343–354. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Glazebrook, J.F. On the quantum dynamics of Davydov solitons in protein α-helices. Phys. A Stat. Mech. Appl. 2019, 517, 257–269. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Glazebrook, J.F. Quantum tunneling of Davydov solitons through massive barriers. Chaos Solitons Fractals 2019, 123, 275–293. [Google Scholar] [CrossRef]
- Luo, J.; Piette, B.M.A.G. A generalized Davydov-Scott model for polarons in linear peptide chains. Eur. Phys. J. B 2017, 90, 1–21. [Google Scholar] [CrossRef]
- Brizhik, L.S.; Eremko, A.A.; Piette, B.; Zakrzewski, W.J.M. Solitons in α-helical proteins. Phys. Rev. E 2004, 70, 031914. [Google Scholar] [CrossRef] [PubMed]
- Daniel, M.; Latha, M.M. A generalized Davydov soliton model for energy transfer in alpha helical proteins. Phys. A 2001, 298, 351–370. [Google Scholar] [CrossRef]
- Komineas, S.; Kalosakas, G.; Bishop, A.R. Effects of intrinsic base-pair fluctuations on charge transport in DNA. Phys. Rev. E 2002, 65, 061905. [Google Scholar] [CrossRef]
- Mvogo, A.; Ben-Bolie, G.H.; Kofane, T.C. Energy transport in the three coupled α-polypeptide chains of collagen molecule with long-range interactions effect. Chaos 2015, 25, 063115. [Google Scholar] [CrossRef] [PubMed]
- Mvogo, A.; Ben-Bolie, G.H.; Kofane, T.C. Solitary waves in an inhomogeneous chain of α-helical proteins. Int. J. Mod. Phys. B 2014, 28, 1450109. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Takhtajan, L.A. Equivalence of a nonlinear Schrödinger equation and a Heisenberg ferromagnetic equation. Theor. Math. Phys. 1979, 37, 17–23. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focussing and one-dimensional self-modulating waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Hirota, R. Direct Methods in Soliton Theory; Springer: Berlin, Germany, 1980. [Google Scholar]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Liu, N.; Guo, B. Long-time asymptotics for the Sasa–Satsuma equation via nonlinear steepest descent method. J. Math. Phys. 2019, 60, 011504. [Google Scholar]
- Potasek, M.J.; Tabor, M. Exact solutions for an extended nonlinear Schrödinger equation. Phys. Lett. A 1991, 154, 449–452. [Google Scholar] [CrossRef]
- Kodama, Y. Optical solitons in a monomode fiber. J. Stat. Phys. 1985, 39, 597–614. [Google Scholar] [CrossRef]
- Di Fazio, G.; Ragusa, M.A. Commutators and Morrey Spaces. Boll. Unione Mat. Ital. 1991, 7, 321–332. [Google Scholar]
- Ragusa, M.A. Commutators of fractional integral operators on Vanishing-Morrey spaces. J. Glob. Optim. 2008, 40, 361–368. [Google Scholar] [CrossRef]
- Guliyev, V.S. Function spaces and integral operators associated with Schrödinger operators: An overview. Proc. Inst. Math. Mech. 2014, 40, 178–202. [Google Scholar]
- Akbulut, A.; Guliyev, R.V.; Celik, S.; Omarova, M.N. Fractional integral associated with Schrödinger operator on vanishing generalized Morrey spaces. J. Math. Inequal. 2018, 12, 789–805. [Google Scholar] [CrossRef]
- Guliyev, V.S.; Akbulut, A. Commutator of fractional integral with Lipschitz functions associated with Schrödinger operator on local generalized Morrey spaces. Bound. Value Probl. 2018, 80. [Google Scholar] [CrossRef]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1986. [Google Scholar]
- Biswas, B.; Mirzazadeh, M.; Savescu, M.; Milovic, D.; Khan, K.R.; Mahmood, M.F.; Belic, M. Singular solitons in optical metamaterials by ansatz method and simplest equation approach. J. Mod. Opt. 2014, 61, 1550–1555. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ma, W.X.; Huang, T.; Zhang, Y. A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 2010, 82, 065003. [Google Scholar] [CrossRef]
- Rogers, C.; Schief, W.K. Backlund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ibragimov, N.H. CRC Hanbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Ames, W.F.; Rogers, C. Nonlinear Equations in the Applied Sciences; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Fushchych, W.I.; Shtelen, W.M. Symmetry Analysis and Exact Solutions of Nonlinear Equations of Mathematical Physics; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Trippenbach, M.; Band, Y.B. Effects of self-steepening and self-frequency shifting on short-pulse splitting in dispersive nonlinear media. Phys. Rev. A 1998, 57, 4791–4803. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).