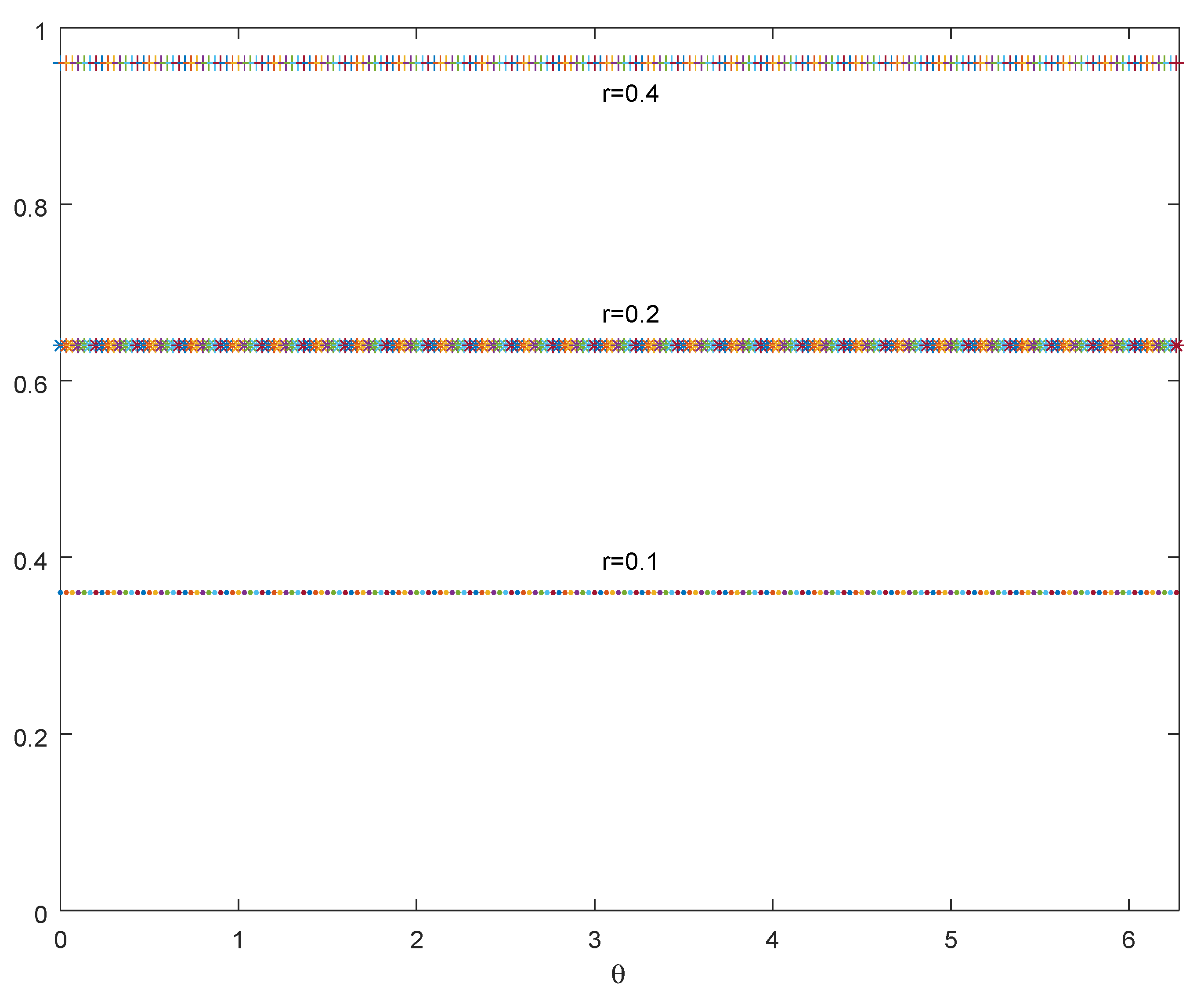1. Introduction
A complex fuzzy set [
1] (CFS) is an extension of the standard (i.e., type-1) fuzzy sets (FS) in which the range of the membership function was the unit disc of the complex plane. In the standard fuzzy sets and many other extensions of fuzzy sets, entropy measures are of high importance. Entropy measures of fuzzy sets [
2,
3,
4,
5,
6], type-2 fuzzy sets [
7,
8], interval-valued fuzzy sets [
9,
10], Atanassovs’s intuitionistic fuzzy sets [
11,
12,
13], hesitant fuzzy sets [
14,
15] and Pythagorean fuzzy sets [
16] have been investigated and successfully used in various fields.
In considering the applications of CFSs, some measures and concepts have been introduced for CFSs, such as distance measures [
17,
18], linguistic variables [
19], rotational invariance [
20], parallelity and orthogonality relations [
21,
22,
23]. However, for the entropy measures of complex fuzzy sets, as far as we know, no related research papers have been published yet. Generally speaking, complex fuzzy sets can be characterized by complex-valued membership functions containing an amplitude term and a phase term. While the amplitude term retains the traditional notion of “fuzziness”, the phase term is a completely novel parameter of membership function, that can essentially distinguish traditional fuzzy sets from complex fuzzy sets [
24]. In this paper, we present two kinds of entropy measures of complex fuzzy sets, one of which depends on the amplitude of the complex-valued membership functions, which is closely related to entropy of traditional fuzzy sets while ignoring the phase term, while the other depends on both the amplitude and phase terms.
The rest of this paper is organized as follows. In
Section 2, we first review some basic concepts of complex fuzzy sets.
Section 3 and
Section 4 define two classes of entropy measures of complex fuzzy sets, called type-A and type-B entropy measures, respectively. Conclusions are presented in
Section 5.
2. Preliminaries
Let
be a universe of discourse, a complex fuzzy set
A on
X may be represented as the set of ordered pairs
where membership function
is of the form
,
, the amplitude term
and the phase term
are both real-valued, and
. Because
is a periodic function whose periodicity law is
, we only consider
in this paper.
Several complex fuzzy complements of
A are specified by functions
where
. In this paper, the phase term is confined to the interval
, so the phase terms of above
and
are functions with modulo
.
3. Type-A Entropy Measures of Complex Fuzzy Sets
(1) A review of entropy of traditional fuzzy sets: The following axiomatic-based definition for the entropy of a traditional fuzzy set can be found in De Luca and Termini [
2], and is supported by many others (e.g., Refs. [
5,
9,
10,
11,
15]).
Definition 1. (De Luca and Termini [2]) Let A and B be two FSs. A mapping e: is called an entropy on if e satisfies the following axioms: - (a1)
if and only if A is a crisp set;
- (a2)
if for all ;
- (a3)
if A is less fuzzy than B, i.e., if when and when ;
- (a4)
, is the complement of A.
As mentioned in
Section 1, there are already many different real equations satisfying the axiomatic requirements of Definition 1. In this work, we takes the following two specific functions for discussion and comparison [
2,
5].
(2) Type-A entropy of complex fuzzy sets: Since the amplitude term retains the traditional notion of “fuzziness” [
24], the simpler method of defining the complex fuzzy sets entropy measure based on the amplitude term can be used to calculate the "fuzziness".
Definition 2. Let A and B be two CFSs. A mapping e: is called a type-A entropy on if e satisfies the following axioms:
- (a1’)
if and only if or for all ;
- (a2’)
if for all ;
- (a3’)
if when and when ;
- (a4’)
, is a complex fuzzy complement of A.
Specifically, this definition of entropy complex fuzzy sets reduces to its traditional counterpart (Definition 1) when a real-valued membership function, i.e., one with for all x, is used.
Two type-A entropy formulas respectively corresponding to (1), (2) are proposed as follows:
When for all x, then we have and .
Theorem 1. The mappings and , defined by formulas (3) and (4) respectively, are type-A entropy measures for CFSs.
Proof. In order for (3) to be qualified as an entropy measure for CFSs, it must satisfy the conditions (a1’)–(a4’) in Definition 2.
From , then , so we have .
(a1’) Suppose , it follows that for all . Thus or for all . On the other hand, let or for all . Then for all . Thus .
(a2’) Suppose , it follows that for all . Thus for all . On the other hand, let for all . Then for all . Thus .
(a3’) Suppose that when and when , then for all . Therefore, .
(a4’) For each , , we can easily obtain that .
For the mapping , the proof is similar to that of . ▯
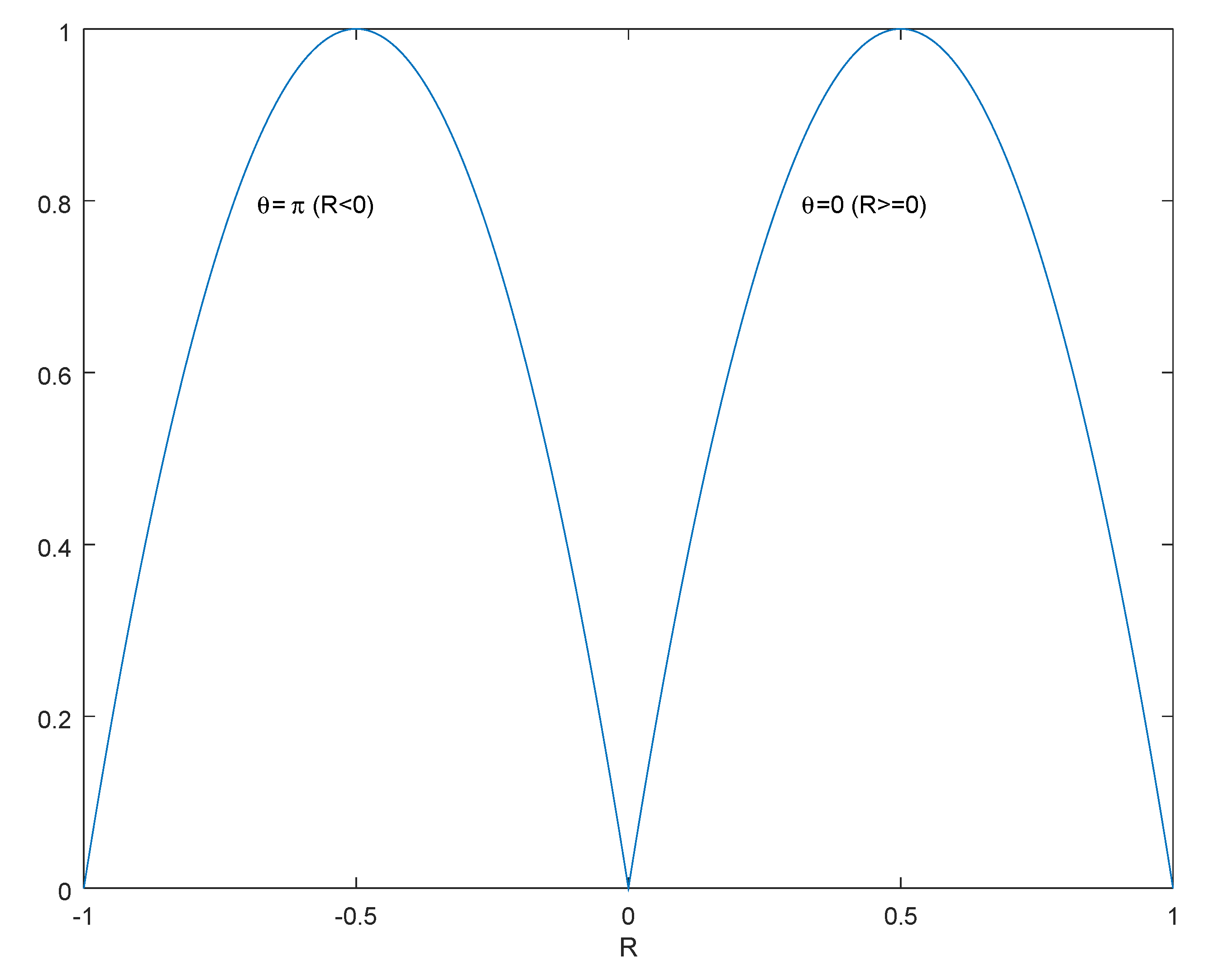
For convenience, we consider the case of
, where
A is a complex fuzzy set on
. The contour plot of
is depicted as in
Figure 1. The points whose moduli are 0.5 have the degree of fuzziness 100%. The points whose moduli are 0 or 1 have the degree of fuzziness 0%, as shown in
Figure 2.
The degree of fuzziness only relies on the modulus of a complex number, not its phase, as shown in
Figure 3. This property is called rotational invariance, which can be formally expressed as follows.
Rotational invariance, developed from Ref. [
20], is an intuitively appealing property of function application. After a simple rotation, if the entropy measure of a CFS is invariant, it will makes a great deal of sense.
Let
with membership function
. The rotation of
A by
radians [
24], denoted
, is defined as
The following is a definition of rotational invariance for entropy measures of complex fuzzy sets.
Definition 3. The entropy measure of CFSs is rotationally invariant, if and only iffor any θ and CFS . Theorem 2. The mappings and are rotationally invariant.
Proof. Since , we can easily obtain that and . ▯
Example 1. Assume a complex fuzzy sets A is given byThen we haveIt is easy to verify 4. Type-B Entropy Measures of Complex Fuzzy Sets
We notice that that type-A entropy measures of a CFS ignored the phase term of this CFS. The phase term distinguishes between traditional and complex fuzzy sets [
24]. Our new method is to define the entropy measures of complex fuzzy sets by combining the amplitude and phase terms.
Definition 4. Let A and B be two CFSs. A mapping e: is called a type-B entropy on if e satisfies the following axioms:
- (b1)
if and only if or , and for all ;
- (b2)
if and for all ;
- (b3)
if and for or and for ;
- (b4)
, is a complex fuzzy complement of A.
Unfortunately, this definition of entropy complex fuzzy sets does not reduce to Definition 1 when for all x.
Two type-B entropy formulas respectively corresponding to (1), (2) are proposed as follows:
Theorem 3. The mappings and , defined by formulas (5) and (6) respectively, are type-B entropy measures for CFSs.
Proof. Similar to Theorem 1. ▯
Remark 1. In the above Theorem 3, the condition (b4) is hold with respect to and , i.e., and , . It does not hold with respect to .
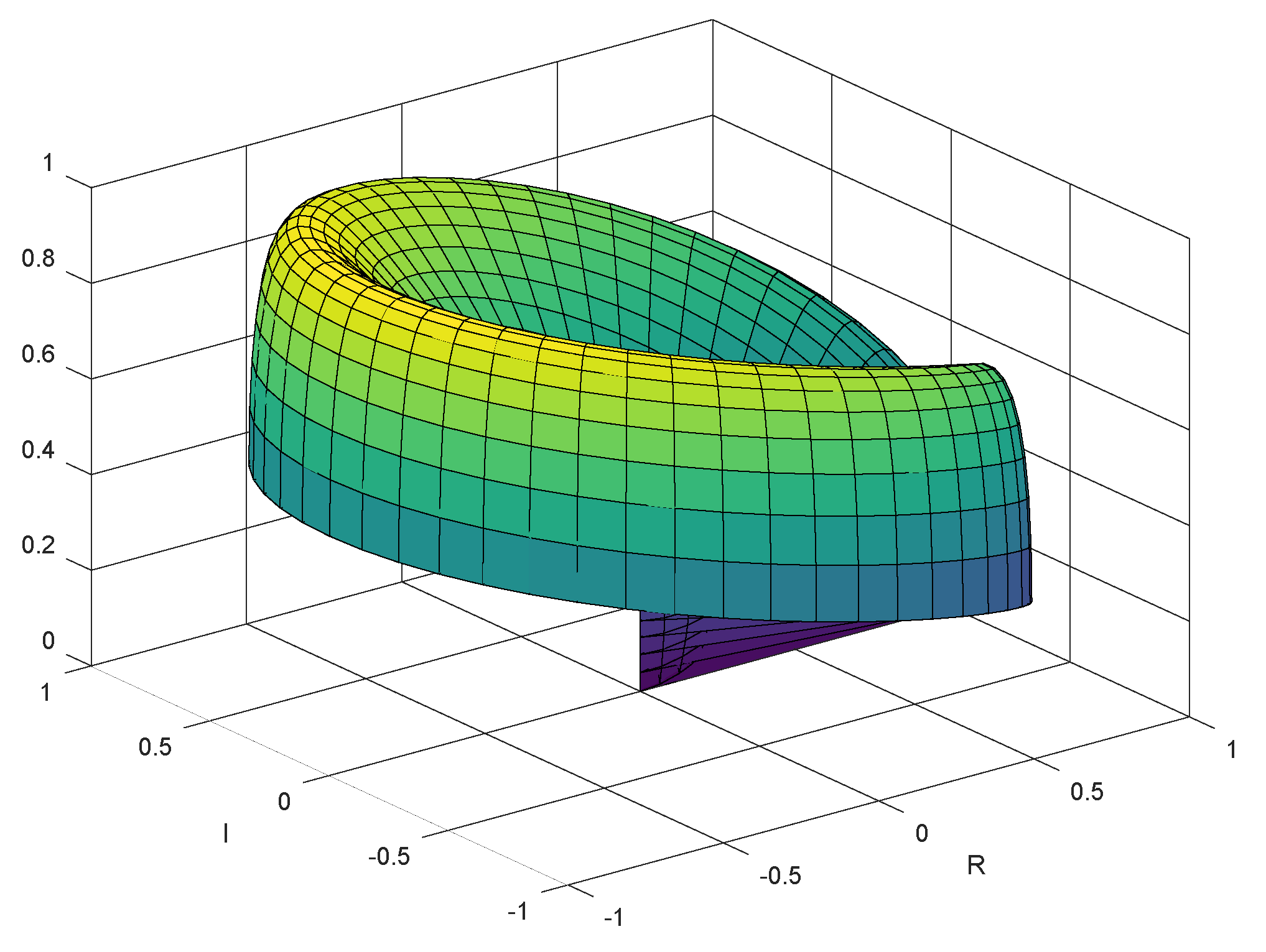
For convenience, we consider the case of
, where
A is a complex fuzzy set on
. The contour plot of
is depicted as in
Figure 4. The point whose modulus is 0.5 and phase is
has the degree of fuzziness 100%. The points whose modulus are 0 or whose phase is 0 have the degree of fuzziness 0%, as shown in
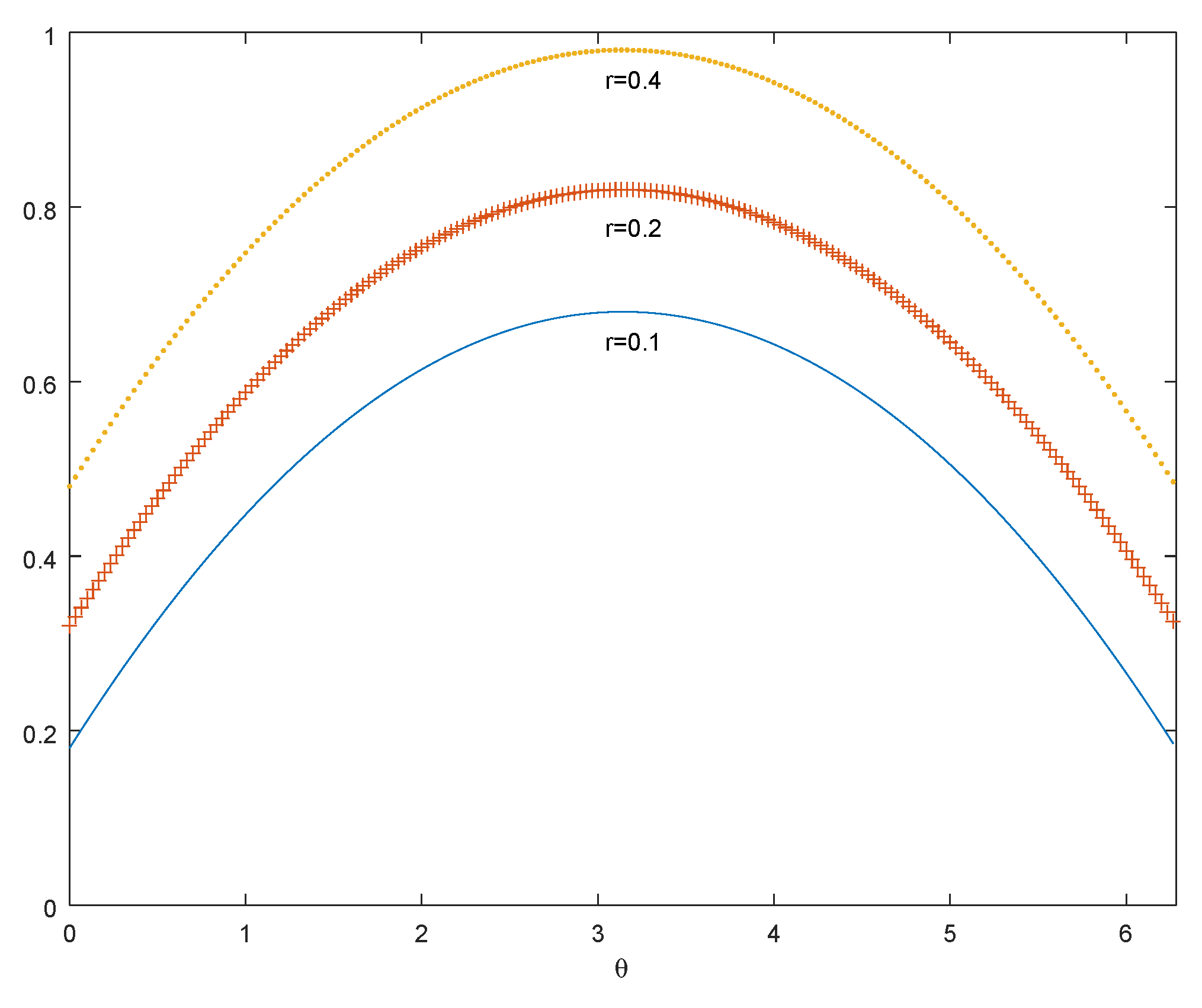
Figure 5. When we fix the modulus of a complex number, several relations between the phase term and the degree of fuzziness are given in
Figure 6.
The following results are obvious from
Figure 6.
Theorem 4. The mappings and are not rotationally invariant.
Example 2. Let A be a complex fuzzy set,then we haveIt is easy to verifyBut Several differences of the above four entropy measures can be summarized as in
Table 1. The symbol “×” means “dissatisfy the corresponding property”, “
√” means “satisfy the corresponding property”. Here,
means the property of rotational invariance.
Example 3. We consider a selection problem in complex fuzzy environment. Assume that there are five complex fuzzy values as followsThen we have the following orderThus we can choose or based on the modulus of complex numbers. However, as we can see, depending on the modulus of complex numbers used, the ordering of these two complex fuzzy values is the same. Moreover, we have , () based on two formulas of type-A entropy measures. So we can use the formulas of type-B entropy measures and get , (). Then we can choose based on minimum entropy criteria. Our definition of entropy measure gives a new index for the selection of complex fuzzy values. 5. Conclusions
In this paper, we propose two definitions of entropy measures for complex fuzzy sets: type-A and type-B. Among then, type-A depends on the amplitude of membership functions, and can reduce to its traditional counterpart, while type-B depends on both the amplitude and the phase of membership function. Their differences can refer to
Figure 1,
Figure 4 and
Table 1. In addition, the idea of rotational invariance for entropy measures of complex fuzzy sets was analyzed. It was proved that the two formulas of type-A entropy measures satisfy the property of rotational invariance.
In this paper, we only presented entropy measures of complex fuzzy sets and their properties. Naturally, a discussion of their practical applications in signal processing, decision making and image processing will be both necessary and interesting.
We should note that the entropy measures presented in this paper are conservative in a certain sense. Membership grades usually represent truth degrees in a “direct” way. However, in complex fuzzy sets, how to understand the membership degree of an object to a set is interpreted by a complex number. There are different understandings of complex fuzzy grade from different viewpoints. In the future, we will further study entropy measures for complex fuzzy sets with other interpretations of complex fuzzy sets. This will be useful for applying complex fuzzy sets.