Numerical Gradient Schemes for Heat Equations Based on the Collocation Polynomial and Hermite Interpolation
Abstract
:1. Introduction
2. One-Dimensional Numerical Gradient Schemes Based on the Local Hermite Interpolation and Collocation Polynomial
2.1. The High-Order Compact Difference Scheme in One-Dimension
2.2. One-Dimensional Numerical Gradient Scheme Based on Local Hermite Interpolation and the Collocation Polynomial
2.2.1. Local Hermite Interpolation and Refinement in the One-Dimensional Case
2.2.2. The Collocation Polynomial in the One-Dimensional Case
2.3. Richardson Extrapolation on the H-OCD Scheme in the One-Dimensional Case
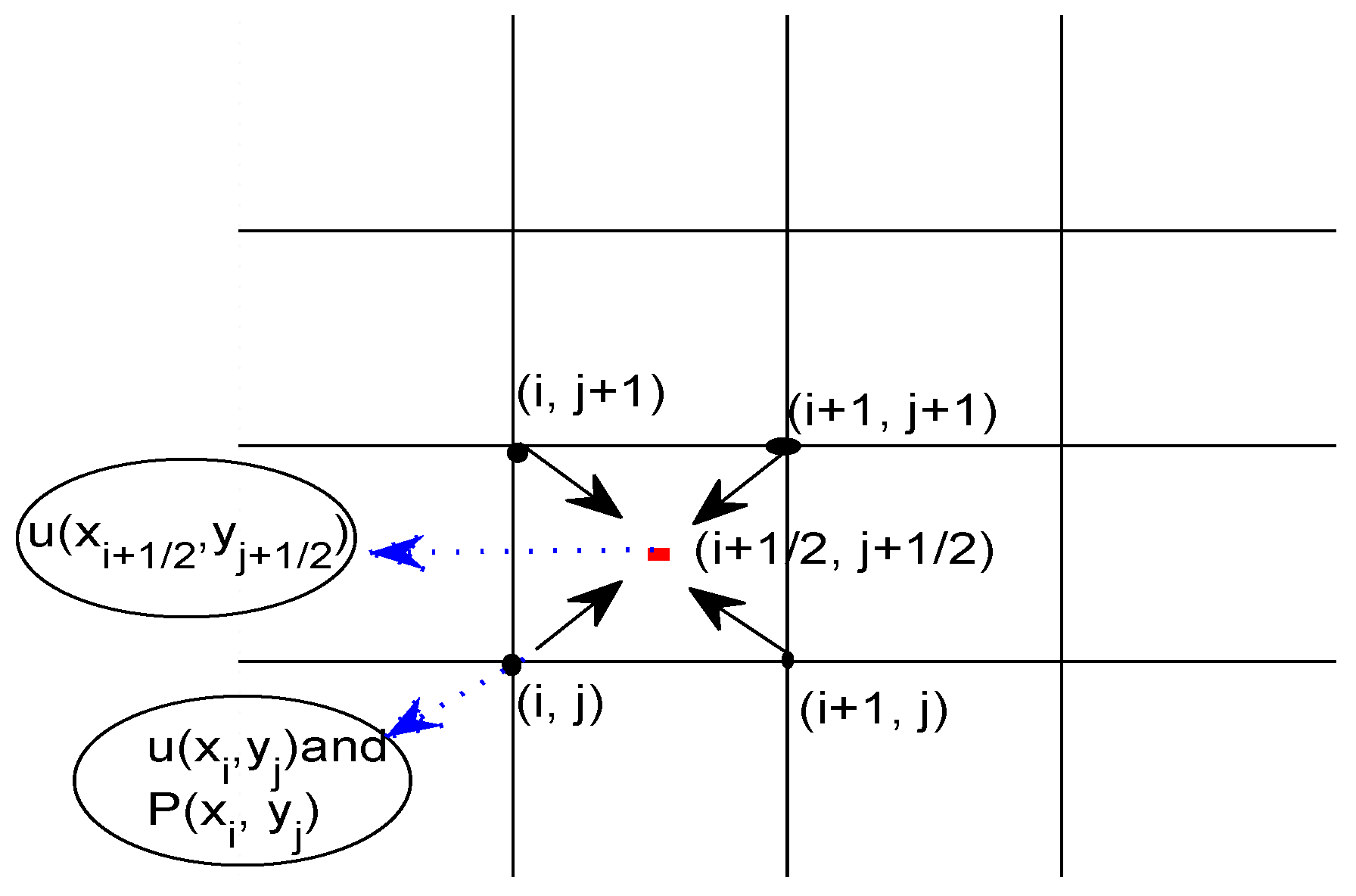
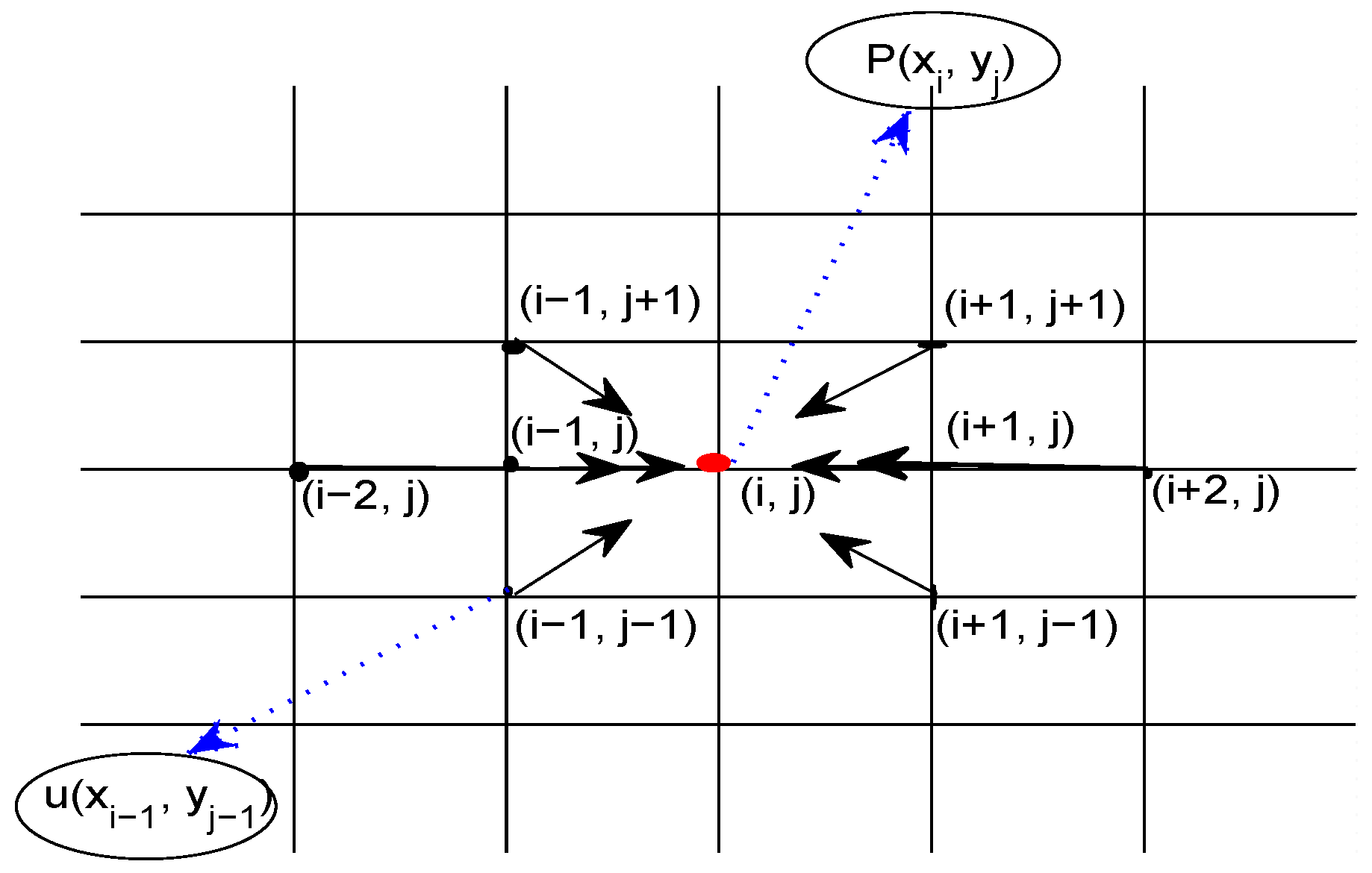
3. Two-Dimensional Numerical Gradient Scheme Based on Local Hermite Interpolation and the Collocation Polynomial
3.1. The High-Order Compact Difference Scheme in Two-Dimensions
3.2. Two-Dimensional Numerical Gradient Scheme
3.2.1. Local Hermite Interpolation and Refinement in the Two-Dimensional Case
3.2.2. The Collocation Polynomial in the Two-Dimensional Case
3.3. The Truncation Errors of the Numerical Gradient Scheme
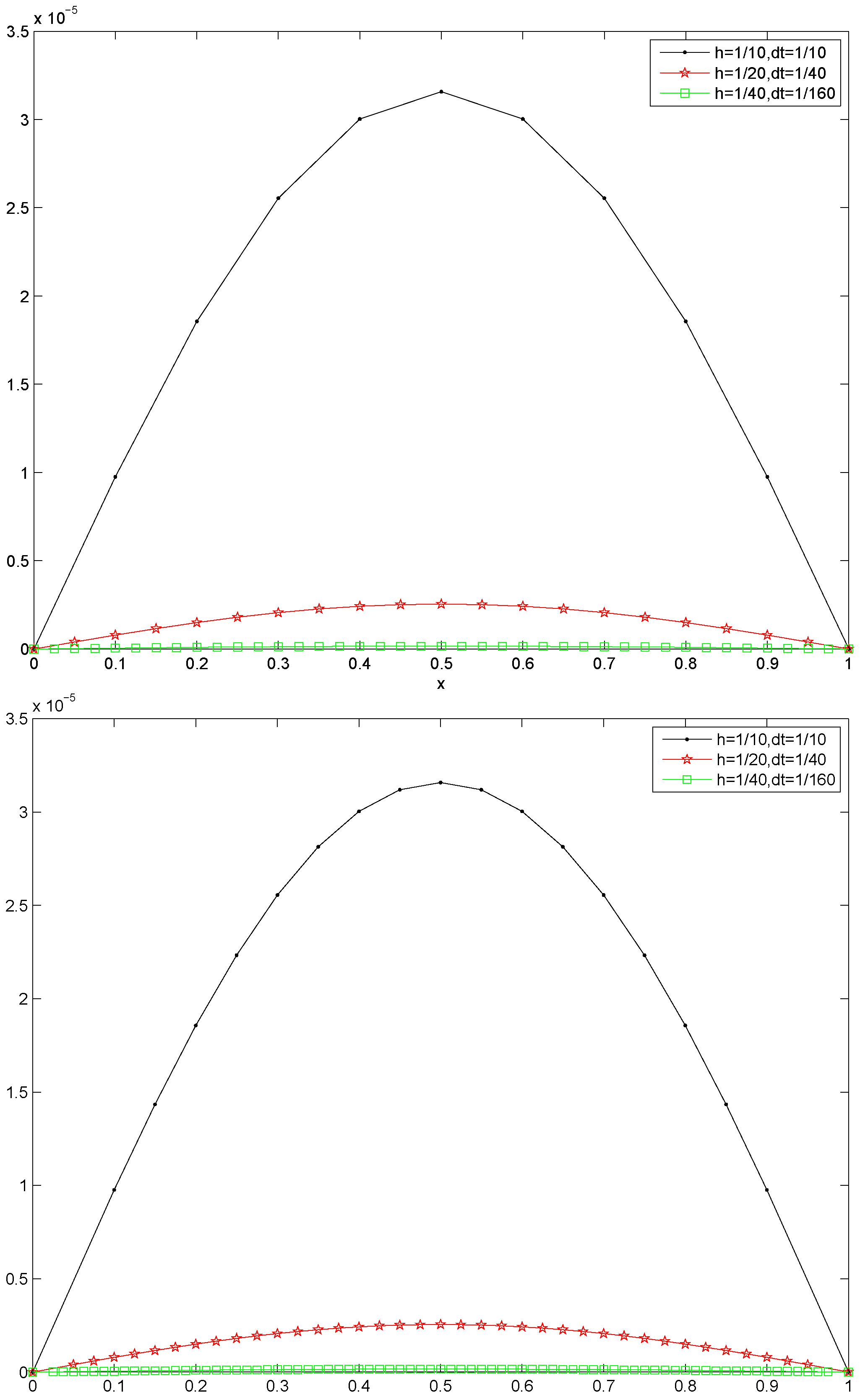
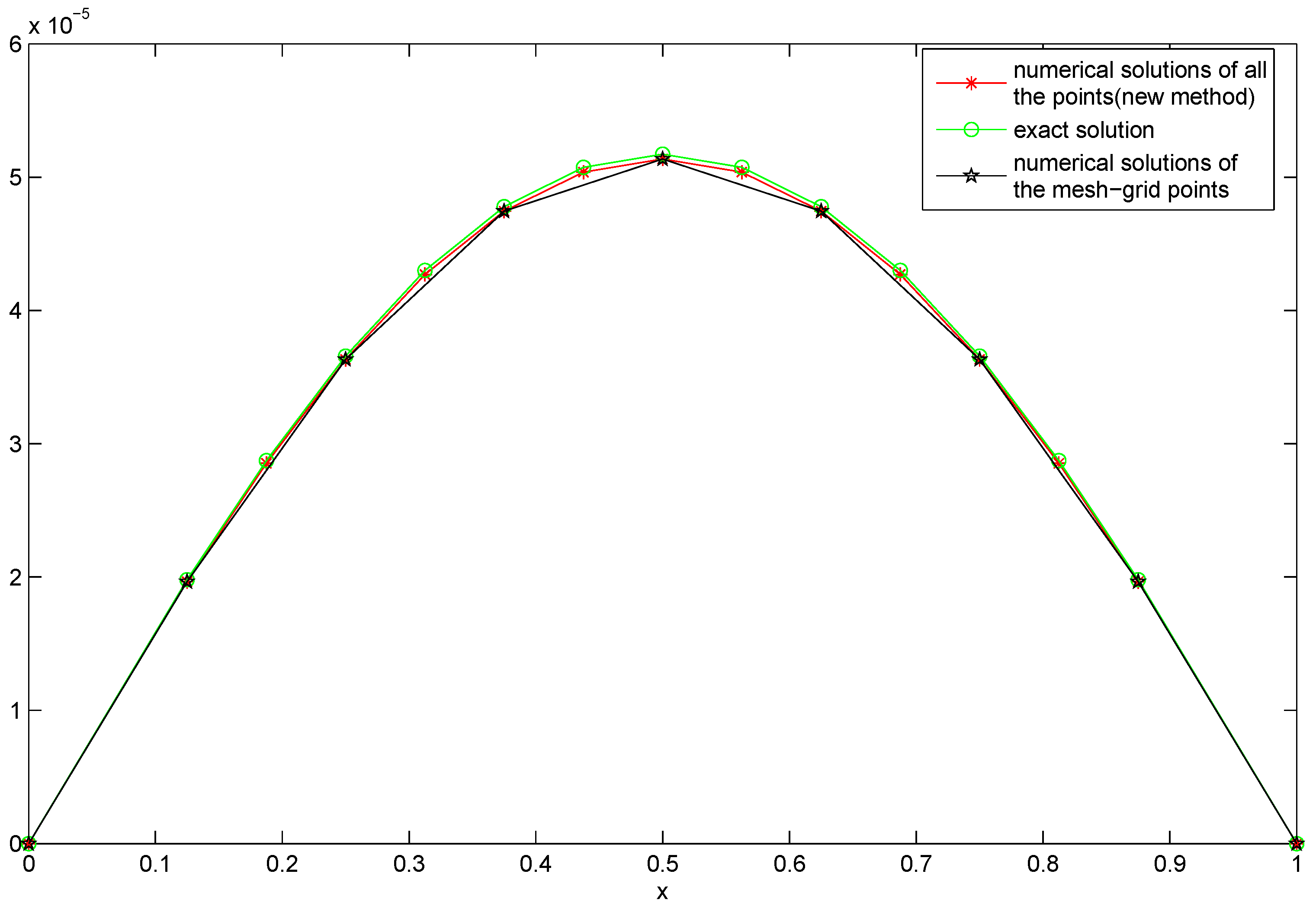
4. Numerical Experiments
4.1. Numerical Experiments for the One-Dimensional Case
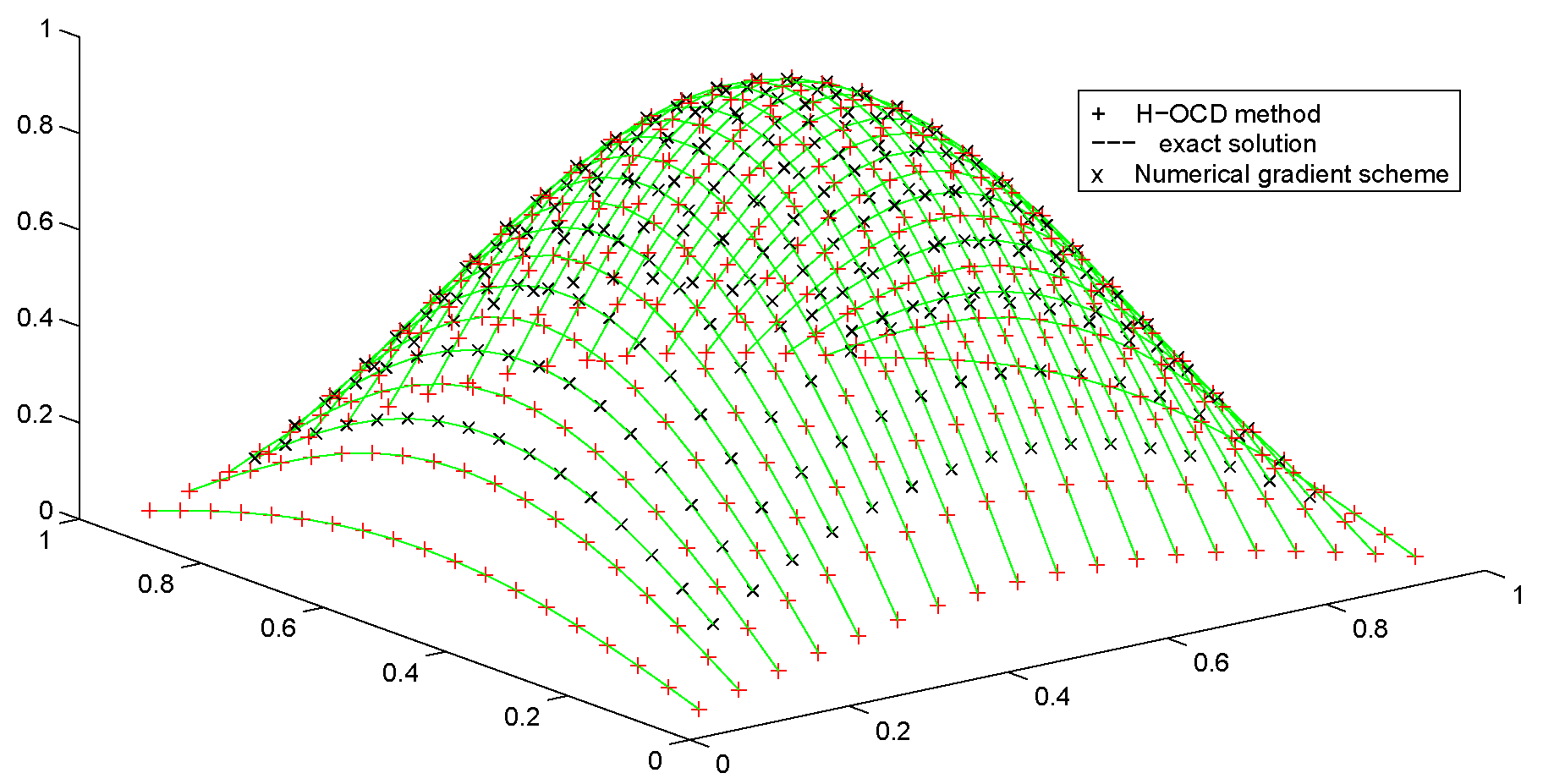
4.2. Numerical Experiments for the Two-Dimensional Case
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, J.W.; Tang, H.M. Numerical Methods of Differential Equations; Science Press: Berlin, Germany, 2007. [Google Scholar]
- Morton, K.W. Numerical Solutions of Partial Differential Equations, 2nd ed.; Posts and Telecom Press: Beijing, China, 2006. [Google Scholar]
- Sun, Z.Z. Compact Difference Schemes for Heat Equations with the Neumann Boundary Conditions. Numer. Method Partial Differ. Equ. 2009, 25, 1320–1341. [Google Scholar] [CrossRef]
- Zhang, W.S. Finite Difference Methods for Partial Difference Equations in Science Computation; Higher Education Press: Beijing, China, 2006. [Google Scholar]
- Sun, Z.Z.; Zhang, Z.B. A Linearized Compact Difference Schemes for a Class of Nonlinear Delay Partial Differential Equations. Appl. Math. Model. 2013, 37, 742–752. [Google Scholar] [CrossRef]
- Timothy, S. Numerical Analysis; Posts and Telecom Press: Beijing, China, 2010. [Google Scholar]
- Liao, H.L.; Sun, Z.Z.; Shi, H.S. Error Estimate of Fourth-order Compact Scheme for Linear Schromdinger Equations. SIAM Numer. Anal. 2010, 47, 4381–4401. [Google Scholar] [CrossRef]
- Richardson, L.F. The approximate arithmetical solution by finite differences of physical problems including differential equations, with an application to the stresses in a masonry dam. Philos. Trans. R. Soc. A 1911, 210, 307–357. [Google Scholar] [CrossRef]
- Liao, H.L.; Sun, Z.Z. Maxmum Norm Error Bounds of ADI and Compact ADI methods for Solving Parabolic Equations. Numer. Method Partial Differ. Equ. 2010, 26, 37–60. [Google Scholar] [CrossRef]
- Sun, Z.Z. Numerical Methods of Partial Differential Equations; Science Press: Berlin, Germany, 2012. [Google Scholar]
- Ikota, R.E. Yanagida. Stability of stationary interfaces of binary-tree type. Calc. Var. Partial Differ. Equ. 2004, 22, 375–389. [Google Scholar] [CrossRef]
- Dassios, I. Stability of basic steady states of networks in bounded domains. Comput. Math. Appl. 2015, 70, 2177–2196. [Google Scholar] [CrossRef]
- Dassios, I. Stability of Bounded Dynamical Networks with Symmetry. Symmetry 2018, 10, 121. [Google Scholar] [CrossRef]
- Xiaofeng, R.; Wei, J. A Double Bubble in a Ternary System with Inhibitory Long Range Interaction. Arch. Ration. Mech. Anal. 2013, 208, 201–253. [Google Scholar]
- Shang, Y. A Lie algebra approach to susceptible-infected-susceptible epidemics. Electron. J. Differ. Equ. 2012, 2012, 147–154. [Google Scholar]
- Shang, Y. Analytical Solution for an In-host Viral Infection Model with Time-inhomogeneous Rates. Acta Phys. Pol. Ser. B 2015, 46, 1567–1577. [Google Scholar] [CrossRef]

| h | Mesh Grid Points | Rate | Intermediate Points | Rate | P (i.e., ) | Rate |
|---|---|---|---|---|---|---|
| Error | Error | Error | ||||
| 1/4 | 4.0355 | 3.5729 | 3.7762 | |||
| 1/8 | 4.0073 | 3.9694 | 3.9370 | |||
| 1/16 | 4.0045 | 3.9952 | 3.9823 | |||
| 1/32 | 4.0466 | 4.0474 | 3.9715 | |||
| 1/64 | - | - | - |
| Grid Node Number | H-OCD Method | Time | Numerical Gradient Scheme | Time |
|---|---|---|---|---|
| Error | Error | |||
| N = 15 | 0.1544 | 0.0312 | ||
| N = 31 | 0.5725 | 0.1560 | ||
| N = 63 | 2.5389 | 0.5839 | ||
| N = 127 | 11.505 | 2.7233 | ||
| N = 255 | 142.64 | 12.8879 |
| h | Mesh-Grid Points | Rate | Intermediate Points | Rate | P (i.e., ) | Rate |
|---|---|---|---|---|---|---|
| Error | Error | Error | ||||
| 1/4 | 3.9974 | 3.8091 | 2.7543 | |||
| 1/8 | 3.9895 | 3.9099 | 2.8763 | |||
| 1/16 | 3.9993 | 3.9564 | 2.9379 | |||
| 1/32 | 4.0472 | 3.9787 | 2.9689 | |||
| 1/64 | - | - | - |
| Compact Difference | Rate | Intermediate Points | Rate | P (i.e., ) | Rate | |
|---|---|---|---|---|---|---|
| Error | Error | Error | ||||
| 1/10 | 1.9988 | 1.9988 | 1.9769 | |||
| 1/20 | 1.9998 | 1.9998 | 1.9887 | |||
| 1/40 | 1.9999 | 1.9999 | 1.9945 | |||
| 1/80 | 2.0005 | 2.0005 | 1.9987 | |||
| 1/160 | 2.0053 | 2.0053 | 2.0053 | |||
| 1/320 | 2.0246 | 2.0246 | 2.0259 | |||
| 1/640 | - | - | - |
| Grid Node Number | H-OCD Method | Time | Numerical Gradient Scheme | Time |
|---|---|---|---|---|
| Error | Error | |||
| N = 15 | 0.1248 | 0.0406 | ||
| N = 31 | 0.5725 | 0.1265 | ||
| N = 63 | 3.1590 | 0.5959 | ||
| N = 127 | 20.117 | 3.1844 | ||
| N = 255 | 128.44 | 21.542 |
| Example 1 | Example 2 | |||
|---|---|---|---|---|
| Error | Error | |||
| 1/8 | 14.2567 | 14.9661 | ||
| 1/16 | 15.6251 | 15.4867 | ||
| 1/32 | 15.9066 | 15.7438 | ||
| 1/64 | 15.9741 | 15.8711 | ||
| 1/128 | 15.9934 | 15.9209 | ||
| 1/256 | - | - |
| h | H-OCD Mesh-Grid Points | Rate | Intermediate Points (New Method) | Rate |
|---|---|---|---|---|
| Error | Error | |||
| 1/4 | 3.9403 | - | - | |
| 1/8 | 3.9878 | 3.9629 | ||
| 1/16 | 3.9805 | 3.9791 | ||
| 1/32 | - | - |
| N | H-OCD Method | Numerical Gradient | ||
|---|---|---|---|---|
| Error | Error | |||
| N = 5 | 9.7908 | 11.0802 | ||
| N = 10 | 15.6079 | 15.3196 | ||
| N = 20 | 15.9751 | 15.9015 | ||
| N = 40 | - | - |
| Grid Number | H-OCD Method | Grid Number | Numerical Gradient | ||
|---|---|---|---|---|---|
| Error | Time | Error | Time | ||
| n = 16 | 0.0374 | n = 17 | 0.0421 | ||
| n = 81 | 0.4563 | n = 117 | 0.5756 | ||
| n = 224 | 2.8782 | n = 433 | 2.8860 | ||
| n = 361 | 9.0527 | n = 745 | 10.8556 | ||
| n = 624 | 25.2347 | n = 1233 | 26.8556 | ||
| n = 899 | 63.2506 | n = 1783 | 66.8199 | ||
| n = 1599 | 422.8602 | n = 3183 | 424.2073 |
| h | H-OCD Method | Numerical Gradient | ||
|---|---|---|---|---|
| Error | Error | |||
| h = 1/5 | 14.1419 | 16.4508 | ||
| h = 1/10 | 15.9254 | 15.7474 | ||
| h = 1/20 | 15.9822 | 15.9392 | ||
| h = 1/40 | 15.9955 | 15.9848 | ||
| h = 1/40 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.-B.; Song, M.-Y.; Zhong, E.-J.; Gu, X.-M. Numerical Gradient Schemes for Heat Equations Based on the Collocation Polynomial and Hermite Interpolation. Mathematics 2019, 7, 93. https://doi.org/10.3390/math7010093
Li H-B, Song M-Y, Zhong E-J, Gu X-M. Numerical Gradient Schemes for Heat Equations Based on the Collocation Polynomial and Hermite Interpolation. Mathematics. 2019; 7(1):93. https://doi.org/10.3390/math7010093
Chicago/Turabian StyleLi, Hou-Biao, Ming-Yan Song, Er-Jie Zhong, and Xian-Ming Gu. 2019. "Numerical Gradient Schemes for Heat Equations Based on the Collocation Polynomial and Hermite Interpolation" Mathematics 7, no. 1: 93. https://doi.org/10.3390/math7010093
APA StyleLi, H.-B., Song, M.-Y., Zhong, E.-J., & Gu, X.-M. (2019). Numerical Gradient Schemes for Heat Equations Based on the Collocation Polynomial and Hermite Interpolation. Mathematics, 7(1), 93. https://doi.org/10.3390/math7010093





