q-Rung Orthopair Fuzzy Competition Graphs with Application in the Soil Ecosystem

Abstract

The q-rung orthopair fuzzy set is a powerful tool for depicting fuzziness and uncertainty, as compared to the Pythagorean fuzzy model. The aim of this paper is to present q-rung orthopair fuzzy competition graphs (q-ROFCGs) and their generalizations, including q-rung orthopair fuzzy k-competition graphs, p-competition q-rung orthopair fuzzy graphs and m-step q-rung orthopair fuzzy competition graphs with several important properties. The study proposes the novel concepts of q-rung orthopair fuzzy cliques and triangulated q-rung orthopair fuzzy graphs with real-life characterizations. In particular, the present work evolves the notion of competition number and m-step competition number of q-rung picture fuzzy graphs with algorithms and explores their bounds in connection with the size of the smallest q-rung orthopair fuzzy edge clique cover. In addition, an application is illustrated in the soil ecosystem with an algorithm to highlight the contributions of this research article in practical applications.

1. Introduction

Configurations of node connections take place in a wide diversity of applications. They may depict physical networks, such as electric circuits, roadways, and organic molecules. They are also employed in depicting fewer interactions as might arise in ecosystems, databases, sociological relationships, or in the flow of control in a computer program. Any mathematical object concerning points and connections between them is called a graph. The genesis of graph theory can be traced back to Euler’s work on the Königsberg bridges problem in $1736.$ Aristotle verbally outlined the first directed graph in a manner to organize logical arguments. In $1968,$ Cohen [1] formally introduced competition graphs in association with a problem in ecology. The competition graph is an undirected graph of a digraph $\overrightarrow{D}$, where the digraph corresponds to the food web of a group of predator and prey species in an ecosystem. In this regard, the digraph is usually acyclic. Cohen defined the competition graph of a digraph $\overrightarrow{D}=(V,\overrightarrow{E})$ as an undirected graph $C(\overrightarrow{D})$ with the same vertex set V and has an edge between two distinct vertices $u,v\in V$ if there exist a vertex $x\in V$ and arcs $ux,vx\in \overrightarrow{E}$ in $\overrightarrow{G}.$ Thus, the analogy of Cohen is based on the fact that if two species have common prey they will strive for the prey. After Cohen’s prologue on the competition graph, various variations of it are detected in the literature see [2,3,4,5,6,7]. In $2000,$ Cho et al. [8] introduced another generalization, named the m-step competition graph of a directed graph. Besides, in ecosystems, competition graphs have many applications in various fields, such as modeling market structures in the field of economics, communications over a noisy channel, energy systems, social interactions, channel assignments etc. After the primary motivation of food web models of ecosystems, a lot of work have been done on competition graphs, where it is assumed that vertices and edges are precisely defined. However, this assumption is not sufficient to describe competition in many real-world scenarios, such as in an ecosystem, where species may be weak, strong, vegetarian, non-vegetarian etc. and prey may be harmful, digestive, tasty etc. Due to the vagueness in description of species and prey, and their relationships, it is natural to design a fuzzy competition graph model.

Zadeh proposed the notion of fuzzy sets in his monumental paper [9] in 1965, to model uncertainty or vague ideas by nominating a degree of membership to each entity, ranging between 0 and $1.$ A fuzzy graph, originated by Kaufmann [10] in 1973 from the Zadeh’s fuzzy relations [11], can well express the uncertainty of plenty of networks. Rosenfeld [12] developed several theocratical concepts of fuzzy graphs in $1975.$ In $1983,$ intuitionistic fuzzy sets (IFSs), primarily proposed by Atanassov [13], offered many significant advantages in representing human knowledge by denoting fuzzy membership not only with a single value, but pairs of mutually orthogonal fuzzy sets, called orthopairs, which allow the incorporation of uncertainty. Since IFSs confine the selection of orthopairs to coming only from a triangular region, as shown in Figure 1, Pythagorean fuzzy sets (PFSs), proposed by Yager [14], as a new extension of IFSs, have emerged as an efficient tool for conducting uncertainty more properly in human analysis, as one can see in [14,15,16,17]. Although both IFSs and PFSs make use of orthopairs to narrate assessment objects, they still have visible differences. The membership function $\mu :X\to [0,1]$ and non-membership function $\nu :X\to [0,1]$ of IFSs are required to satisfy the constraint condition $\mu (x)+\nu (x)\le 1.$ However, these two functions in PFSs are needed to satisfy the condition $\mu {(x)}^2+\nu {(x)}^2\le 1,$ which shows that PFSs have expanded space to assign orthopairs, as compared to IFSs, displayed in Figure 1. Certain notions of Pythagorean fuzzy graphs have been discussed in [18,19,20,21].

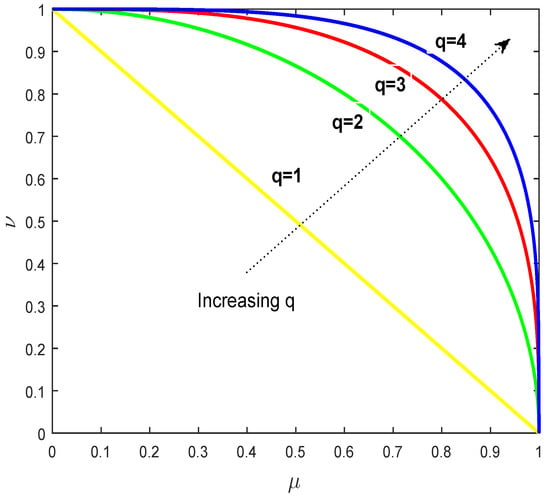
Figure 1. Spaces of acceptable q-rung orthopairs.

A q-rung orthopair fuzzy set (q-ROFS), originally proposed by Yager [22] in $2017,$ is a new generalization of orthopair fuzzy sets (e.g., IFSs, PFSs) which further relax the constraint of orthopair membership grades with $\mu {(x)}^q+\nu {(x)}^q\le 1(q\ge 1)$ [23]. As q increases, it is easy to see that the representation space of allowable orthopair membership grade increases. Figure 1 displays spaces of the most widely acceptable orthopairs for different q rungs. Ali [24] calculated the area of spaces with admissible orthopairs up to 10-rungs. Consider an example in the field of economics: in a market structure, a huge number of firms compete against each other with differentiated products with respect to branding or quality, which in nature are vague words. Since IFSs have the capability to explore both aspects of ambiguous words, for example, it assigns an orthopair membership grade to ‘quality’ i.e., support for quality and support for not-quality of an object with the condition that their sum is bounded by $1.$ This constraint clearly limits the selection of orthopairs. Moreover, in graph theocratical concepts, it is straightforward to observe the adaptations of predators towards their prey and fight of prey against predators. The IFS can translate the uncertainty associated with both phases of species at the same time with the restriction that their sum is less than or equal to one. To relax this condition and enhance one’s capability to express this knowledge more precisely, this paper defines q-ROFCGs to deal with competitions in many fields.

Fuzzy competition graphs, firstly defined by Samanta and Pal [25] with its generalizations [25,26,27], express the partialness of species and prey regarding their extent of competition. A lot of work has been done on fuzzy competition graphs. Recently, Sahoo and Pal [28] introduced the conception of intuitionistic fuzzy competition graphs to extend the capability to model human knowledge. Nasir et al. [29] discussed operations on intuitionistic fuzzy competition graphs. Moreover, Al-Shehrie and Akram [30] discussed bipolar fuzzy competition graphs. Sarwar and Akram further studied this concept in [31,32] by defining some operations. Akram and Nasir [33] discussed interval-valued neutrosophic competition graphs. Akram and Sarwar [34] analyzed m-polar fuzzy competition graphs. Recently, Sarwar et al. [35] introduced fuzzy competition hyper graphs. Furthermore, Suna et al. [36] defined fuzzy cliques. Furthermore, Suna et al. [36] defined fuzzy cliques. In the present study, an attempt is made to describe the novel concept of q-rung orthopair fuzzy competition graphs. We extend intuitionistic fuzzy k-competition graphs, p-competition intuitionistic fuzzy graphs and m-step intuitionistic fuzzy competition graphs and obtain analogous results under q-rung orthopair fuzzy environment. In particular, we propose a novel characterization towards q-rung orthopair fuzzy cliques and triangulated q-rung orthopair fuzzy graphs with several related results. On the other hand, in the literature of competition graphs, much attention has been focused on finding the competition number of a graph. Roberts [37] showed that after adding sufficient numbers of isolated vertices to an acyclic digraph, it leads to a competition graph. He defined competition number as the smallest such possible number. This parameter has been extensively studied by many researchers; see [38,39,40]. Previous work has underlined characterization, not only of the competition graphs but also m-step competition graphs. Cho et al. [8] introduced m-step competition number in this regard, which is analogous to the notion of competition number by Roberts [37]. Certain bounds on competition number was discussed in [38,40,41]. The contribution or this research article is not only restricted to q-ROFCGs but it introduces the concept of competition number and m-step competition number of q-rung orthopair fuzzy graphs along with two algorithms. The results show their connection with the size of smallest q-rung orthopair fuzzy edge clique cover as bounds. Finally, this work suggests a novel approach towards the soil ecosystem by exploring the strength of competition of bacteria with an algorithm.

2. Preliminaries

This section presents a brief review of competition graphs, fuzzy competition graphs and q-rung orthopair fuzzy sets. Meanwhile, we define cardinality, support, and height of q-rung orthopair fuzzy sets which will be used for further developments.

A graph $G=(V,E)$ consists of two sets V and $E.$ The elements of V and E are called vertices (or nodes) and edges respectively, where each edge has a set of one or two vertices associated with it. A digraph (or directed graph) $\overrightarrow{D}$ is a graph each of whose edges is directed, usually denoted by $\overrightarrow{D}=(V,\overrightarrow{E}),$ where $\overrightarrow{E}$ is the set of arcs $\overrightarrow{uv},$ for $u,v\in V.$ A walk in a graph G is an alternating sequence of vertices and edges, $W=v_0,e_1,v_1,e_2,\dots ,e_n,v_n$ such that for $j=1,2,\dots ,n,$ the vertices $v_{j-1}$ and $v_j$ are the end points of edge $e_j.$ If moreover, the edge $e_j$ is directed from $v_{j-1}$ to $v_j,$ then W is directed walk. A trail in a graph is a walk such that no edge occurs more than once. A path in a graph is a trail such that no internal vertex is repeated. A cycle is a closed path of length at least one. The out-neighborhood and in-neighborhood [42] of a vertex u in $\overrightarrow{D}$ can be defined by $N^{+}(u)=\{v\in V-\{u\}:\overrightarrow{uv}\in \overrightarrow{E}\}$ and $N^{-}(u)=\{v\in V-\{u\}:\overrightarrow{vu}\in \overrightarrow{E}\},$ respectively.

Definition 1 ([1]).

The competition graph $C(\overrightarrow{D})$ of a digraph $\overrightarrow{D}=(V,\overrightarrow{E})$ is an undirected graph $G=(V,E)$ which has the same vertex set V and has an edge between two distinct vertices $u,v\in V$ if there exist a vertex $x\in V$ and arcs $ux,vx\in \overrightarrow{E}$ in $\overrightarrow{G}.$

A clique in a graph G is a maximal set of mutually adjacent vertices of $G.$ The clique number, denoted by $w(G),$ is the number of vertices in a largest clique of $G.$ An edge clique cover of a graph G is any family $\theta (G)=\{C_1,C_2,\dots ,C_k\}$ of complete subgraphs of G such that every edge of G is in at least one of $E(C_1),E(C_2),\dots ,E(C_k).$

Competition number defined by Roberts in [37] states that, if G is any graph, we can obtain a competition graph by adding many isolated vertices. Add one isolated vertex $x_{\alpha }$ to $G,$ corresponding to every edge $\alpha$ in $G.$ Construct a food web F with vertex set $V(F)=V(G)\cup \{x_{\alpha }:\alpha \in E(G)\}$ with an arc from end points u and v of edge $\alpha$ to vertex $x_{\alpha }.$ Then F is a food web for the graph $G\cup I_r.$ Thus, the smallest r such that $G\cup I_r$ is a competition graph, is called competition number $k(G).$

Sometimes vertices and edges of graphs are not precisely defined. A fuzzy graph can well express such uncertainty. A fuzzy graph [10] on a non-empty set X is a pair $\mathcal{G}=(\sigma ,\mu ),$ where $\sigma :V\to [0,1]$ and $\mu :V\times V\to [0,1]$ such that for all $u,v\in V,\mu (u,v)\le \sigma (u)\wedge \sigma (v),$ where $\sigma (u)$ and $\mu (u,v)$ represent the membership values of the vertex u and edge $uv$ in $\mathcal{G},$ respectively. A fuzzy digraph [43] on a non-empty set X is a pair $\overrightarrow{\mathcal{D}}=(\mathcal{A},\overrightarrow{\mathcal{B}}),$ where ${\mu }_{\mathcal{A}}:V\to [0,1]$ and ${\mu }_{\overrightarrow{\mathcal{B}}}:V\times V\to [0,1]$ such that for all $u,v\in V,{\mu }_{\overrightarrow{\mathcal{B}}}(\overrightarrow{uv})\le {\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v),$ where ${\mu }_{\mathcal{A}}(u)$ and ${\mu }_{\overrightarrow{\mathcal{B}}}(\overrightarrow{uv})$ represent the membership values of the vertex u and edge $\overrightarrow{uv}$ in $\overrightarrow{\mathcal{D}},$ respectively. When we deal with a problem in ecology, species and prey may be fuzzy in nature and the relationship between them can be designed by fuzzy competition graphs. A lot of work has been done on fuzzy competition graphs and its variations which are designed as motivated by the fuzzy food web. A fuzzy out-neighborhood [25] of a vertex v of a directed fuzzy graph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ is a fuzzy set ${\mathcal{N}}^{+}(v)=(X_v^{+},{\mu }_{{\mathcal{P}}_v}^{+}),$ where $X_v^{+}=\{u:{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vu})\ge 0\}$ and ${\mu }_{{\mathcal{P}}_v}^{+}:X_v^{+}\to [0,1]$ defined by ${\mu }_{{\mathcal{P}}_v}^{+}(u)={\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vu}).$ A fuzzy in-neighborhood [25] of a vertex v of a directed fuzzy graph $\overrightarrow{\mathcal{D}}$ is a fuzzy set ${\mathcal{N}}^{-}(v)=(X_v^{-},{\mu }_{{\mathcal{P}}_v}^{-})$, where $X_v^{-}=\{u:{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{uv})\ge 0\}$ and ${\mu }_{{\mathcal{P}}_v}^{-}:X_v^{-}\to [0,1]$ defined by ${\mu }_{{\mathcal{P}}_v(u)}^{-}={\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{uv}).$

Definition 2 ([25]).

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed fuzzy graph. The fuzzy competition graph $\mathcal{C}(\overrightarrow{\mathcal{D}})$ of a fuzzy digraph $\overrightarrow{\mathcal{D}}$ is an undirected fuzzy graph $\mathcal{G}=(\mathcal{P},\mathcal{R})$ which has same fuzzy vertex set as in $\overrightarrow{\mathcal{D}}$ and has a fuzzy edge between two vertices $u,v\in {\mathcal{P}}^{*}$ in $\mathcal{C}(\overrightarrow{\mathcal{D}})$ if and only if ${\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)\ne \varphi$ in $\overrightarrow{\mathcal{D}}$ and the membership grade of edge $uv$ in $\mathcal{C}(\overrightarrow{\mathcal{D}})$ is

$${\mu }_{\mathcal{R}}(uv)=({\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v))h({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)).$$

Definition 3 ([25]).

Let k be a non-negative real number and $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed fuzzy graph. The fuzzy k-competition graph ${\mathcal{C}}_k(\overrightarrow{\mathcal{D}})$ of a fuzzy digraph $\overrightarrow{\mathcal{D}}$ is an undirected fuzzy graph $\mathcal{G}=(\mathcal{P},\mathcal{R})$ which has same fuzzy vertex set as in $\overrightarrow{\mathcal{D}}$ and has a fuzzy edge between two vertices $u,v\in {\mathcal{P}}^{*}$ in ${\mathcal{C}}_k(\overrightarrow{\mathcal{D}})$ if and only if $|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)|>k$ The membership grade of edge $uv$ in ${\mathcal{C}}_k(\overrightarrow{\mathcal{D}})$ is

$${\mu }_{\mathcal{R}}(uv)=\frac{k^{\prime }-k}{k^{\prime }}({\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v))h({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)),$$

where $k^{\prime }=|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)|.$

Definition 4 ([25]).

Let p be a positive integer and $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed fuzzy graph. The p-competition fuzzy graph ${\mathcal{C}}^p(\overrightarrow{\mathcal{D}})$ of a fuzzy digraph $\overrightarrow{\mathcal{D}}$ is an undirected fuzzy graph $\mathcal{G}=(\mathcal{P},\mathcal{R})$ which has same fuzzy vertex set as in $\overrightarrow{\mathcal{D}}$ and has a fuzzy edge between two vertices $u,v\in {\mathcal{P}}^{*}$ in ${\mathcal{C}}^p(\overrightarrow{\mathcal{D}})$ if and only if $|supp({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))|\ge p.$ The membership grade of edge $uv$ in ${\mathcal{C}}^p(\overrightarrow{\mathcal{D}})$ is

$${\mu }_{\mathcal{R}}(uv)=\frac{(n-p)+1}{n}({\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v))h({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)),$$

where $n=|supp({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))|.$

Before introducing m-step fuzzy competition graph, we define an m-step fuzzy digraph. An m-step fuzzy digraph $\overrightarrow{{\mathcal{D}}_m}=(\mathcal{A},\overrightarrow{\mathcal{C}})$ of a fuzzy digraph $\overrightarrow{\mathcal{D}}=(\mathcal{A},\overrightarrow{\mathcal{B}})$ has same fuzzy vertex set $\mathcal{A}$ and has a fuzzy edge between $u,v\in X$ if there exist a fuzzy directed path ${\overrightarrow{P}}_{uv}^m$ in $\overrightarrow{\mathcal{D}}$ of length m such that ${\mu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{uv})=min\{{\mu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{ab})|\overrightarrow{ab}isanedgeof{\overrightarrow{P}}_{uv}^m\},$ where m is positive integer. An m-step fuzzy out-neighborhood [27] of a vertex v of a directed fuzzy graph $\overrightarrow{\mathcal{D}}$ an m-step fuzzy set ${\mathcal{N}}_m^{+}(v)=(X_v^{+},{\mu }_{{\mathcal{P}}_v}^{+})$, where $X_v^{+}=\{u:{\overrightarrow{P}}_{vu}^{m}exists\}$ and ${\mu }_{{\mathcal{P}}_v}^{+}:X_v^{+}\to [0,1]$ defined by ${\mu }_{{\mathcal{P}}_v}^{+}(u)=min\{{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{xy}):\overrightarrow{xy}isanedgein{\overrightarrow{P}}_{vu}^m\}.$ An m-step fuzzy in-neighborhood [27] of a vertex v of a directed fuzzy graph $\overrightarrow{\mathcal{D}}$ is an m-step fuzzy set ${\mathcal{N}}_m^{-}(v)=(X_v^{-},{\mu }_{{\mathcal{P}}_v}^{-}),$ where $X_v^{-}=\{u:{\overrightarrow{P}}_{uv}^{m}exists\}$ and ${\mu }_{{\mathcal{P}}_v}^{-}:X_v^{-}\to [0,1]$ defined by ${\mu }_{{\mathcal{P}}_v}^{-}(u)=min\{{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ab}):\overrightarrow{ab}isanedgein{\overrightarrow{P}}_{uv}^m\}.$

Definition 5 ([27]).

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed fuzzy graph. An m-step fuzzy competition graph ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})$ of a fuzzy digraph $\overrightarrow{\mathcal{D}}$ is an undirected fuzzy graph $\mathcal{G}=(\mathcal{P},\mathcal{R})$ which has same fuzzy vertex set as in $\overrightarrow{\mathcal{D}}$ and has a fuzzy edge between two vertices $u,v\in {\mathcal{P}}^{*}$ in ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})$ if and only if ${\mathcal{N}}_m^{+}(u)\cap {\mathcal{N}}_m^{+}(v)\ne \varphi$ in $\overrightarrow{\mathcal{D}}$ and the membership grade of edge $uv$ in ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})$ is

$${\mu }_{\mathcal{R}}(uv)=({\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v))h({\mathcal{N}}_m^{+}(u)\cap {\mathcal{N}}_m^{+}(v)).$$

Definition 6 ([22]).

Let X be a universe of discourse, a q-rung orthopair fuzzy set(q-ROFS) $\mathcal{P}$ on X is given by

$$\mathcal{P}=\{⟨u,{\mu }_{\mathcal{P}}(u),{\nu }_{\mathcal{P}}(u)⟩|u\in X\},$$

characterized by a membership function ${\mu }_{\mathcal{P}}:X\to [0,1]$ and a non-membership function ${\nu }_{\mathcal{P}}:X\to [0,1]$ such that $0\le {\mu }_{\mathcal{P}}^q(u)+{\nu }_{\mathcal{P}}^q(u)\le 1\mathrm{for}\mathrm{all}u\in X.$ Moreover,  ${\pi }_{\mathcal{P}}(u)=\sqrt[q]{1-{\mu }_{\mathcal{P}}^q(u)-{\nu }_{\mathcal{P}}^q(u)}$ is called a q-rung orthopair fuzzy index or indeterminacy degree of u to the set $\mathcal{P}$.

Definition 7.

Let $\mathcal{P}=({\mu }_{\mathcal{P}}(u),{\nu }_{\mathcal{P}}(u))$ be a q-rung orthopair fuzzy set. Then the cardinality of $\mathcal{P}$ is denoted by Card($\mathcal{P}$), is defined as

$$Card(\mathcal{P})=(|\mathcal{P}{|}_{\mu },|\mathcal{P}{|}_{\nu })$$

such that

$$\begin{array}{ccc}\hfill {|\mathcal{P}|}_{\mu }& =& \sum _{u\in X}{\mu }_{\mathcal{P}}(u),\hfill \\ \hfill {|\mathcal{P}|}_{\nu }& =& \sum _{u\in X}{\nu }_{\mathcal{P}}(u).\hfill \end{array}$$

Definition 8.

Let $\mathcal{P}=({\mu }_{\mathcal{P}}(u),{\nu }_{\mathcal{P}}(u))$ be a q-rung orthopair fuzzy set. Then the support of $\mathcal{P}$ is denoted by Supp($\mathcal{P}$), is defined as

$$Supp(\mathcal{P})=Sup{p}_{\mu }(\mathcal{P})\cup Sup{p}_{\nu }(\mathcal{P})$$

such that

$$\begin{array}{ccc}\hfill Sup{p}_{\mu }(\mathcal{P})& =& \{u|{\mu }_{\mathcal{P}}(u)>0\},\hfill \\ \hfill Sup{p}_{\nu }(\mathcal{P})& =& \{u|{\nu }_{\mathcal{P}}(u)>0\}.\hfill \end{array}$$

Definition 9.

Let $\mathcal{P}=({\mu }_{\mathcal{P}}(u),{\nu }_{\mathcal{P}}(u))$ be a q-rung orthopair fuzzy set. Then the height of $\mathcal{P}$ is denoted by h($\mathcal{P}$), is defined as

$$h(\mathcal{P})=(h_{\mu }(\mathcal{P}),h_{\nu }(\mathcal{P}))$$

such that

$$\begin{array}{ccc}\hfill h_{\mu }(\mathcal{P})& =& \underset{u\in X}{sup}{\mu }_{\mathcal{P}}(u),\hfill \\ \hfill h_{\nu }(\mathcal{P})& =& \underset{u\in X}{inf}{\nu }_{\mathcal{P}}(u).\hfill \end{array}$$

The geometrical interpretation is shown in Figure 2.

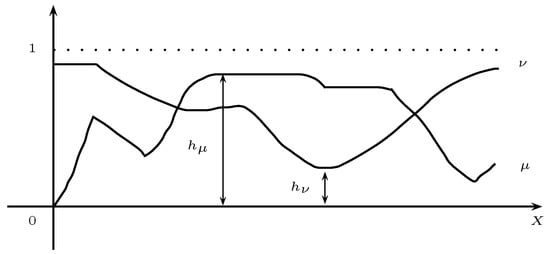
Figure 2. Geometric interpretation of height of q-ROFS (q-rung orthopair fuzzy set).

3. q-Rung Orthopair Fuzzy Graphs

The q-rung orthopair fuzzy sets (q-ROFSs) enhance the capability of decision-makers in assigning orthopairs by their own choice. We now define q-rung orthopair fuzzy graphs which can be extensively used in many practical problems.

Definition 10.

Let X be a non-empty set. A mapping $\mathcal{P}=({\mu }_{\mathcal{P}},{\nu }_{\mathcal{P}}):X\times X⟶[0,1]$ is called a q-rung orthopair fuzzy relation on X such that ${\mu }_{\mathcal{P}},{\nu }_{\mathcal{P}}\in [0,1],$ for all $u,v\in X.$

Definition 11.

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\nu }_{\mathcal{A}})$ and $\mathcal{B}=({\mu }_{\mathcal{B}},{\nu }_{\mathcal{B}})$ be q-rung orthopair fuzzy sets on a non-empty set X. If $\mathcal{B}=({\mu }_{\mathcal{B}},{\nu }_{\mathcal{B}})$ is a q-rung orthopair fuzzy relation on $X,$ then $\mathcal{B}$ is called a q-rung orthopair fuzzy relation on $\mathcal{A}$ if

$$\left\{\begin{array}{c}{\mu }_{\mathcal{B}}(uv)\le {\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v),\hfill \\ {\nu }_{\mathcal{B}}(uv)\le {\nu }_{\mathcal{A}}(u)\vee {\nu }_{\mathcal{A}}(v)forallu,v\in X\hfill \end{array}\right.$$

and $0\le {\mu }_{\mathcal{B}}^q(uv)+{\nu }_{\mathcal{B}}^q(uv)\le 1$ for all $u,v\in X.$

Definition 12.

A q-rung orthopair fuzzy graph on a non-empty set X is a pair $\mathcal{G}=(\mathcal{A},\mathcal{B})$ with $\mathcal{A}$ a q-rung orthopair fuzzy set on X and $\mathcal{B}$ a q-rung orthopair fuzzy relation on X such that

$$\left\{\begin{array}{c}{\mu }_{\mathcal{B}}(uv)\le {\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v),\hfill \\ {\nu }_{\mathcal{B}}(uv)\le {\nu }_{\mathcal{A}}(u)\vee {\nu }_{\mathcal{A}}(v)forallu,v\in X\hfill \end{array}\right.$$

and $0\le {\mu }_{\mathcal{B}}^q(uv)+{\nu }_{\mathcal{B}}^q(uv)\le 1$ for all $u,v\in X$, where, ${\mu }_{\mathcal{B}}:X\times X⟶[0,1]$ and ${\nu }_{\mathcal{B}}:X\times X⟶[0,1]$ represents the membership and non-membership functions of $\mathcal{B}$, respectively.

Example 1.

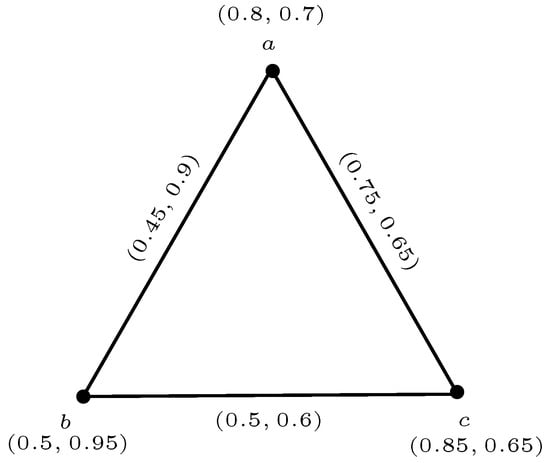
Figure 3 represents a 3-rung orthopair fuzzy graph $\mathcal{G}=(\mathcal{A},\mathcal{B})$ where$\mathcal{A}=⟨\left({\displaystyle \frac{a}{0.8}},{\displaystyle \frac{b}{0.5}},{\displaystyle \frac{c}{0.85}}\right),\left({\displaystyle \frac{a}{0.7}},{\displaystyle \frac{b}{0.95}},{\displaystyle \frac{c}{0.65}}\right)⟩$ and $\mathcal{B}=⟨\left({\displaystyle \frac{ab}{0.45}},{\displaystyle \frac{ac}{0.75}},{\displaystyle \frac{bc}{0.5}}\right),\left({\displaystyle \frac{ab}{0.9}},{\displaystyle \frac{ac}{0.65}},{\displaystyle \frac{bc}{0.6}}\right)⟩.$

Figure 3. A 3-rung orthopair fuzzy graph $\mathcal{G}$.

Definition 13.

A q-rung orthopair fuzzy digraph on a non-empty set X is a pair $\overrightarrow{\mathcal{D}}=(\mathcal{A},\overrightarrow{\mathcal{B}})$ with $\mathcal{A}$ a q-rung orthopair fuzzy set on X and $\overrightarrow{\mathcal{B}}$ a q-rung orthopair fuzzy relation on X such that

$$\left\{\begin{array}{c}{\mu }_{\overrightarrow{\mathcal{B}}}(\overrightarrow{uv})\le {\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v),\hfill \\ {\nu }_{\overrightarrow{\mathcal{B}}}(\overrightarrow{uv})\le {\nu }_{\mathcal{A}}(u)\vee {\nu }_{\mathcal{A}}(v)forallu,v\in X\hfill \end{array}\right.$$

and $0\le {\mu }_{\overrightarrow{\mathcal{B}}}^q(\overrightarrow{uv})+{\nu }_{\overrightarrow{\mathcal{B}}}^q(\overrightarrow{uv})\le 1$ for all $u,v\in X$, where, ${\mu }_{\overrightarrow{\mathcal{B}}}:X\times X⟶[0,1]$ and ${\nu }_{\overrightarrow{\mathcal{B}}}:X\times X⟶[0,1]$ represents the membership and non-membership functions of $\overrightarrow{\mathcal{B}}$, respectively.

Definition 14.

An m-step q-rung orthopair fuzzy digraph $\overrightarrow{{\mathcal{D}}_m}=(\mathcal{A},\overrightarrow{\mathcal{C}})$ of a q-ROF digraph $\overrightarrow{\mathcal{D}}=(\mathcal{A},\overrightarrow{\mathcal{B}})$ has same vertex set $\mathcal{A}$ and has a q-ROF edge between $u,v\in X$ if there exist a q-ROF directed path ${\overrightarrow{P}}_{uv}^m$ in $\overrightarrow{\mathcal{D}}$ of length m such that

$$\left\{\begin{array}{c}{\mu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{uv})=min\{{\mu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{ab})|\overrightarrow{ab}isanedgeof{\overrightarrow{P}}_{uv}^m\},\hfill \\ {\nu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{uv})=max\{{\nu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{ab})|\overrightarrow{ab}isanedgeof{\overrightarrow{P}}_{uv}^m\},\hfill \end{array}\right.$$

where m is positive integer.

Definition 15.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{A},\overrightarrow{\mathcal{C}})$ be a q-rung orthopair fuzzy digraph. The underlying q-rung orthopair fuzzy graph of $\overrightarrow{\mathcal{D}}$ is a q-ROFG $\mathcal{U}(\overrightarrow{\mathcal{D}})=(\mathcal{A},\mathcal{C})$ with same vertex set $\mathcal{A}$ and has a q-rung orthopair fuzzy edge between two distinct vertices $u,v\in X$ such that

$$({\mu }_{\mathcal{C}}(uv),{\nu }_{\mathcal{C}}(uv))=\left\{\begin{array}{cc}({\mu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{uv})\wedge {\mu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{vu}),{\nu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{uv})\vee {\nu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{vu}))& \mathrm{if}\overrightarrow{uv}\in \mathcal{C},\overrightarrow{vu}\in \mathcal{C},\\ ({\mu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{uv}),{\nu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{uv}))& \mathrm{if}\overrightarrow{uv}\in \mathcal{C},\overrightarrow{vu}\notin \mathcal{C},\\ ({\mu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{vu}),{\nu }_{\overrightarrow{\mathcal{C}}}(\overrightarrow{vu}))& \mathrm{if}\overrightarrow{vu}\in \mathcal{C},\overrightarrow{uv}\notin \mathcal{C}.\end{array}\right.$$

Definition 16.

Let $\mathcal{G}=({\mu }_{\mathcal{A}}(u),{\nu }_{\mathcal{B}}(u))$ be a q-rung orthopair fuzzy graph. An edge $uv$ of $\mathcal{G}$ is called strong if

$$\left\{\begin{array}{c}{\mu }_{\mathcal{B}}(u,v)\ge \frac{1}{2}({\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v)),\hfill \\ {\nu }_{\mathcal{B}}(u,v)\le \frac{1}{2}({\nu }_{\mathcal{A}}(u)\vee {\nu }_{\mathcal{A}}(v))\hfill \end{array}\right.$$

and weak otherwise.

Definition 17.

Let $\mathcal{G}=({\mu }_{\mathcal{A}}(u),{\nu }_{\mathcal{B}}(u))$ be a q-rung orthopair fuzzy graph. The strength of q-rung orthopair fuzzy edge $uv$ can be measured as

$$I_{uv}=({(I_{uv})}_{\mu },{(I_{uv})}_{\nu })$$

such that

$$\begin{array}{ccc}\hfill {(I_{uv})}_{\mu }& =& \frac{{\mu }_{\mathcal{B}}(uv)}{{\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v)},\hfill \\ \hfill {(I_{uv})}_{\nu }& =& \frac{{\nu }_{\mathcal{B}}(uv)}{{\nu }_{\mathcal{A}}(u)\vee {\nu }_{\mathcal{A}}(v)}.\hfill \end{array}$$

Definition 18.

A q-rung orthopair fuzzy graph $\mathcal{H}=(\mathcal{P},\mathcal{Q})$ is called a q-rung orthopair fuzzy subgraph of $\mathcal{G}=(\mathcal{A},\mathcal{B})$ if

$$\left\{\begin{array}{c}{\mu }_{\mathcal{P}}(u)\le {\mu }_{\mathcal{A}}(u),\hfill \\ {\nu }_{\mathcal{P}}(u)\ge {\nu }_{\mathcal{P}}(u)forallu\in X\hfill \end{array}\right.$$

$$\mathrm{and}\left\{\begin{array}{c}{\mu }_{\mathcal{Q}}(\mathrm{uv})\le {\mu }_{\mathcal{B}}(\mathrm{uv}),\hfill \\ {\nu }_{\mathcal{Q}}(\mathrm{uv})\ge {\nu }_{\mathcal{B}}(\mathrm{uv})forallu,v\in X\hfill \end{array}\right.$$

such that $0\le {\mu }_{\mathcal{Q}}(uv)+{\nu }_{\mathcal{Q}}(uv)\le 1$ for all $u,v\in X.$

Moreover, a q-rung orthopair fuzzy subgraph $\mathcal{H}=(\mathcal{P},\mathcal{Q})$ is said to be spanning q-rung orthopair fuzzy subgraph of $\mathcal{G}=(\mathcal{A},\mathcal{B})$ if

$$\left\{\begin{array}{c}{\mu }_{\mathcal{P}}(u)={\mu }_{\mathcal{A}}(u),\hfill \\ {\nu }_{\mathcal{P}}(u)={\nu }_{\mathcal{P}}(u)forallu\in X.\hfill \end{array}\right.$$

Example 2.

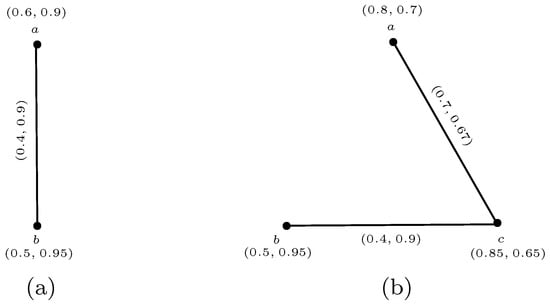
Consider a 3-rung orthopair fuzzy graph $\mathcal{G}=(\mathcal{A},\mathcal{B})$ as displayed in Figure 3. Figure 4a represents 3-rung orthopair fuzzy subgraph of $\mathcal{G}$ and Figure 4b represents spanning 3-rung orthopair fuzzy subgraph of $\mathcal{G}.$

Figure 4. (a) 3-Rung Orthopair Fuzzy Subgraph; (b) Spanning 3-Rung Orthopair Fuzzy Subgraph.

Definition 19.

In a q-rung orthopair fuzzy graph $\mathcal{G}=(\mathcal{A},\mathcal{B})$, a q-rung orthopair fuzzy subset $\mathcal{P}$ of $\mathcal{A}$ is called a q-rung orthopair fuzzy clique if q-rung orthopair fuzzy subgraph of $\mathcal{G}$ induced by $\mathcal{P}$ is complete.The size of largest q-ROF clique is called clique number of $\mathcal{G}.$

Example 3.

Figure 5 represents a 3-rung orthopair fuzzy graph $\mathcal{G}=(\mathcal{A},\mathcal{B}),$ where

$$\mathcal{A}=⟨\left({\displaystyle \frac{a}{0.8}},{\displaystyle \frac{b}{0.9}},{\displaystyle \frac{c}{0.7}},{\displaystyle \frac{d}{0.6}}\right),\left({\displaystyle \frac{a}{0.7}},{\displaystyle \frac{b}{0.6}},{\displaystyle \frac{c}{0.75}},{\displaystyle \frac{d}{0.85}}\right)⟩and$$

$$\mathcal{B}=⟨\left({\displaystyle \frac{ab}{0.8}},{\displaystyle \frac{ac}{0.65}},{\displaystyle \frac{bc}{0.65}},{\displaystyle \frac{ad}{0.6}},{\displaystyle \frac{bd}{0.5}}\right),\left({\displaystyle \frac{ab}{0.7}},{\displaystyle \frac{ac}{0.7}},{\displaystyle \frac{bc}{0.55}},{\displaystyle \frac{ad}{0.7}},{\displaystyle \frac{bd}{0.5}}\right)⟩.$$

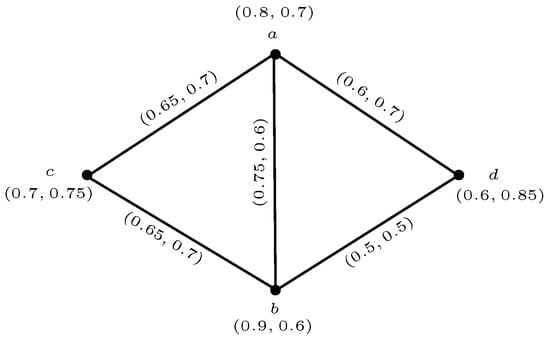
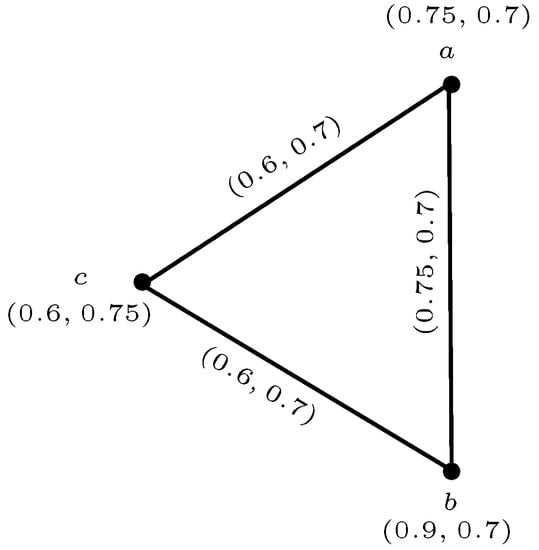
Figure 5. A 3-rung orthopair fuzzy graph $\mathcal{G}$.

Take $\mathcal{P}=\{(a,0.75,0.7),(b,0.9,0.7),(c,0.65,0.75)\}$ such that each pair of vertices is joined by an edge in $\mathcal{G}.$

A 3-rung orthopair fuzzy subgraph $\mathcal{H}=(\mathcal{P},\mathcal{Q})$ of $\mathcal{G}$ induced by $\mathcal{P}$ is given in Figure 6.

Figure 6. A 3-rung orthopair fuzzy induced subgraph $\mathcal{H}$.

We see that $\mathcal{H}=(\mathcal{P},\mathcal{Q})$ is complete 3-rung orthopair fuzzy graph. Hence, 3-rung orthopair fuzzy subset $\mathcal{P}$ is a 3-rung orthopair fuzzy clique.

Next we display an application of q-rung orthopair fuzzy clique.

Example 4.

A wholesaler must arrange a stall in an exhibition to display already existing brands and products. He must face a competition for higher manufacturing quality products. Many companies have turned to promotional tactics to recover their quality image. There are five well-known companies of different quality products as given in Table 1. The wholesaler must select some of them to display best product quality. If there is a big difference between qualities of products of some companies (i.e., more than 5%) then he cannot choose those companies. Clearly, the product quality of the stall is investigated by taking into account the lowest quality of their products.

Table 1. Quality of Products.

Company	Product Quality
$c_1$	70%
$c_2$	77%
$c_3$	65%
$c_4$	60%
$c_5$	73%

To understand the idea of q-rung orthopair fuzzy cliques, take companies as vertices. If the products of two companies are displayed in same stall, then there is an edge between them. The information to organize such a stall can be summarized by 6-rung orthopair fuzzy graph $\mathcal{G}=(\mathcal{A},\mathcal{B})$ given in Figure 7, where support for membership and non-membership of vertices for corresponding stall indicate their significant increase and not increase in product quality, respectively.

Figure 7. $\mathcal{G}=(\mathcal{A},\mathcal{B})$.

The membership grades of edges show the extent of both companies to be linked with same stall with respect to high quality products. The 6-rung orthopair fuzzy set

$$\mathcal{P}=\{(c_1,0.8,0.92),(c_2,0.75,0.95),(c_5,0.85,0.9)\}$$

is a 6-rung orthopair fuzzy clique of $\mathcal{G}$ as the 6-rung orthopair fuzzy graph induced by $\mathcal{P}$ is a complete subgraph of $\mathcal{G}.$ Which shows that the wholesaler can display the products of companies $c_1,c_2$ and $c_5$ as they all are linked with each other and their product qualities are matching to some extent. Hence the corresponding product quality of stall is $(0.75,0.95).$

Definition 20.

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be a q-rung orthopair fuzzy graph. The collection of q-rung orthopair fuzzy cliques which cover all the edges of $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is called a q-rung orthopair fuzzy edge clique cover(q-rung orthopair FECC) of $\mathcal{G}.$

The size of the smallest q-rung orthopair FECC is denoted by ${\theta }_e(\mathcal{G})$.

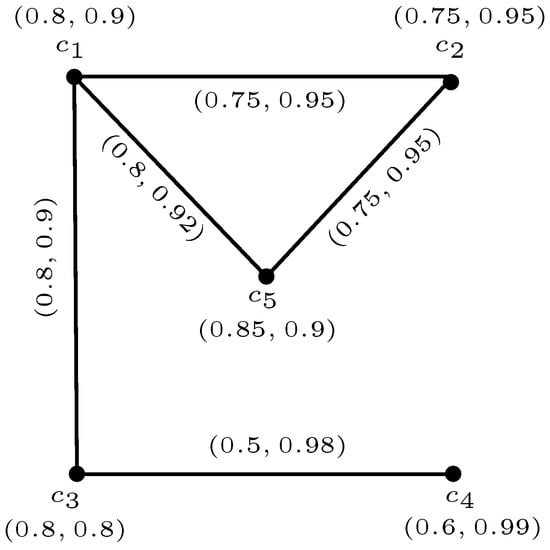
Example 5.

Consider a 4-rung orthopair fuzzy graph $\mathcal{G}=(\mathcal{A},\mathcal{B})$ where

$$\mathcal{A}=⟨\left({\displaystyle \frac{a}{0.8}},{\displaystyle \frac{b}{0.72}},{\displaystyle \frac{c}{0.65}},{\displaystyle \frac{d}{0.85}},{\displaystyle \frac{e}{0.4}}\right),\left({\displaystyle \frac{a}{0.8}},{\displaystyle \frac{b}{0.87}},{\displaystyle \frac{c}{0.9}},{\displaystyle \frac{d}{0.75}},{\displaystyle \frac{e}{0.99}}\right)⟩and$$

$$\mathcal{B}=⟨\left({\displaystyle \frac{ab}{0.7}},{\displaystyle \frac{ac}{0.6}},{\displaystyle \frac{bc}{0.6}},{\displaystyle \frac{cd}{0.65}},{\displaystyle \frac{bd}{0.6}},{\displaystyle \frac{be}{0.4}},{\displaystyle \frac{de}{0.4}}\right),\left({\displaystyle \frac{ab}{0.8}},{\displaystyle \frac{ac}{0.85}},{\displaystyle \frac{bc}{0.89}},{\displaystyle \frac{cd}{0.2}},{\displaystyle \frac{bd}{0.82}},{\displaystyle \frac{be}{0.99}},{\displaystyle \frac{de}{0.97}}\right)⟩,$$

as shown in Figure 8.

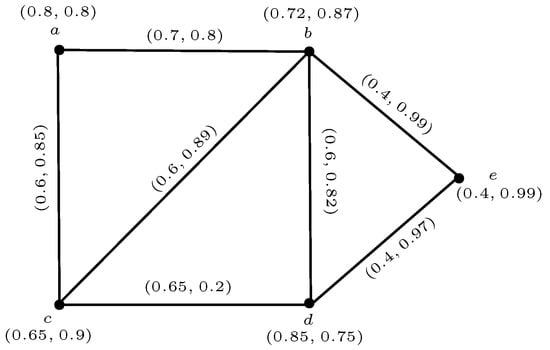
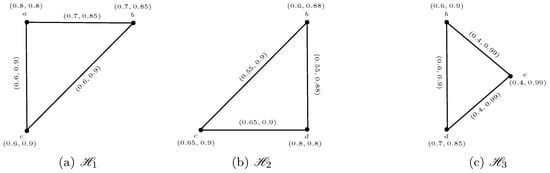
Figure 8. A 4-rung orthopair fuzzy graph $\mathcal{G}$.

Some 4-ROF cliques of $\mathcal{G}$ are given below

$$\begin{array}{ccc}\hfill {\mathcal{P}}_1& =& \{(a,0.8,0.8),(b,0.7,0.85),(c,0.6,0.9)\},\hfill \\ \hfill {\mathcal{P}}_1& =& \{(b,0.6,0.88),(c,0.65,0.9),(d,0.8,0.8)\},\hfill \\ \hfill {\mathcal{P}}_1& =& \{(b,0.6,0.9),(d,0.7,0.85),(e,0.4,0.99)\}.\hfill \end{array}$$

We see that 4-ROF subgraphs ${\mathcal{H}}_1=({\mathcal{P}}_1,{\mathcal{Q}}_1),{\mathcal{H}}_2=({\mathcal{P}}_2,{\mathcal{Q}}_2)$ and ${\mathcal{H}}_3=({\mathcal{P}}_3,{\mathcal{Q}}_3)$ of $\mathcal{G}$ induced by ${\mathcal{P}}_1,{\mathcal{P}}_2$ and ${\mathcal{P}}_3$ displayed in Figure 9 are complete. Also ${\mathcal{H}}_1,{\mathcal{H}}_2$ and ${\mathcal{H}}_3$ induced by ${\mathcal{P}}_1,{\mathcal{P}}_2$ and ${\mathcal{P}}_3$ covers all edges of $\mathcal{G}.$ Thus, the collection

$$\mathcal{F}=\{{\mathcal{P}}_1,{\mathcal{P}}_2,{\mathcal{P}}_3\}$$

is the 4-rung orthopair fuzzy edge clique cover. Moreover, it is the smallest 4-ROF edge clique cover as the size of all 4-ROF cliques other than ${\mathcal{P}}_1,{\mathcal{P}}_2$ and ${\mathcal{P}}_3$ must be less than $3.$ Hence, ${\theta }_e(\mathcal{G})=3.$

Figure 9. 4-rung orthopair fuzzy induced subgraphs. (a) ${\mathcal{H}}_1$; (b) ${\mathcal{H}}_2$; (c) ${\mathcal{H}}_3$.

Definition 21.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{A},\overrightarrow{\mathcal{B}})$ be a q-ROF acyclic digraph defined on $\overrightarrow{{\mathcal{D}}^{*}}=({\mathcal{A}}^{*},\overrightarrow{{\mathcal{B}}^{*}})$. The injective mapping $\pi :\mathcal{A}\to \{1,2,\dots ,|{\mathcal{A}}^{*}|\}$ is called vertex labeling of $\overrightarrow{\mathcal{D}}$ such that if D has a q-ROF arc $\overrightarrow{uv}$, then $\pi (u)<\pi (v)$ for all q-ROF vertices $u,v$ in $\overrightarrow{\mathcal{D}}.$ In other words, every q-ROF arc goes from lower integer to higher integer.

4. q-Rung Orthopair Fuzzy Competition Graphs

In realistic scenarios, sometimes the fuzzy vertices and edges of fuzzy competition graphs may not be enough to explore various types of species or prey. For example, animals have such adaptations that enhance their ability for being successful predators like built for speed; use jaws, sharp teeth, and claws to catch and kill prey; and can camouflage to hide themselves from prey. These qualities are vague in nature. Thus, there may exist some predators which use more than one adaptation towards it is prey, for instance, a lion can prey either with sharp teeth or claws or even jaws i.e., the ability of a lion towards its target to prey with claws as well as without claws is non-zero. On the contrary, several prey species fight against predators through chemicals, communal defense or by ejecting toxic substances. To overcome such cases, we need orthopairs of fuzzy sets. Sahoo and Pal [28] discussed this situation for Atanassov’s IFSs with restriction $\mu +\nu \le 1$ on support for membership $(\mu )$ and support for non-membership $(\nu )$ which allows the orthopairs to be in the triangular region shown in Figure 1. Since q-rung orthopair fuzzy sets relax the condition with ${\mu }^q+{\nu }^q\le 1$ (for sufficiently large q), results increase in the area of permissible orthopairs. They can translate the uncertainty associated with both phases of species at the same time in a more comprehensive manner. This motivates the necessity of q-rung orthopair fuzzy competition graphs.

Definition 22.

A q-rung orthopair fuzzy out-neighborhood of a vertex v of a directed q-ROFG $\overrightarrow{\mathcal{D}}$ is the q-ROFS ${\mathcal{N}}^{+}(v)=(X_v^{+},{\mu }_{{\mathcal{P}}_v}^{+},{\nu }_{{\mathcal{P}}_v}^{+})$, where $X_v^{+}=\{u:{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vu})\ge 0or{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vu})\ge 0\}$ and ${\mu }_{{\mathcal{P}}_v}^{+}:X_v^{+}\to [0,1]$ defined by ${\mu }_{{\mathcal{P}}_v}^{+}(u)={\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vu})$ and ${\nu }_{{\mathcal{P}}_v}^{+}:X_v^{+}\to [0,1]$ defined by ${\nu }_{{\mathcal{P}}_v}^{+}(u)={\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vu}).$ A q-rung orthopair fuzzy in-neighborhood of a vertex v of a directed q-ROFG $\overrightarrow{\mathcal{D}}$ is the q-ROFS ${\mathcal{N}}^{-}(v)=(X_v^{-},{\mu }_{{\mathcal{P}}_v}^{-},{\nu }_{{\mathcal{P}}_v}^{-})$, where $X_v^{-}=\{u:{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{uv})\ge 0or{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{uv})\ge 0\}$ and ${\mu }_{{\mathcal{P}}_v}^{-}:X_v^{-}\to [0,1]$ defined by ${\mu }_{{\mathcal{P}}_v(u)}^{-}={\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{uv})$ and ${\nu }_{{\mathcal{P}}_v}^{-}:X_v^{-}\to [0,1]$ defined by ${\nu }_{{\mathcal{P}}_v}^{-}(u)={\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{uv}).$

Definition 23.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed q-rung orthopair fuzzy graph. The q-rung orthopair fuzzy competition graph $\mathcal{C}(\overrightarrow{\mathcal{D}})$ of a q-rung orthopair fuzzy digraph $\overrightarrow{\mathcal{D}}$ is an undirected q-ROFG $\mathcal{G}=(\mathcal{P},\mathcal{R})$ which has same q-ROF vertex set as in $\overrightarrow{\mathcal{D}}$ and has a q-ROF edge between two vertices $u,v\in {\mathcal{P}}^{*}$ in $\mathcal{C}(\overrightarrow{\mathcal{D}})$ if and only if ${\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)\ne \varphi$ in $\overrightarrow{\mathcal{D}}$ and the support for membership and support for non-membership of edge $uv$ in $\mathcal{C}(\overrightarrow{\mathcal{D}})$ is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{\mathcal{R}}(uv)=({\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v)){\mathit{h}}_{\mu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)),\hfill \\ {\nu }_{\mathcal{R}}(uv)=({\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v)){\mathit{h}}_{\nu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)).\hfill \end{array}\right.\end{array}$$

such that ${\mu }_{\mathcal{R}}^q(uv)+{\nu }_{\mathcal{R}}^q(uv)\le 1,$ for all $u,v\in X.$

Example 6.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a 3-rung orthopair fuzzy digraph, given in Figure 10a, where,

$$\mathcal{P}=⟨\left({\displaystyle \frac{a}{0.8}},{\displaystyle \frac{b}{0.72}},{\displaystyle \frac{c}{0.63}},{\displaystyle \frac{d}{0.83}},{\displaystyle \frac{e}{0.4}}\right),\left({\displaystyle \frac{a}{0.75}},{\displaystyle \frac{b}{0.85}},{\displaystyle \frac{c}{0.9}},{\displaystyle \frac{d}{0.73}},{\displaystyle \frac{e}{0.95}}\right)⟩and$$

$$\overrightarrow{\mathcal{Q}}=⟨\left({\displaystyle \frac{\overrightarrow{ab}}{0.7}},{\displaystyle \frac{\overrightarrow{ac}}{0.6}},{\displaystyle \frac{\overrightarrow{bc}}{0.6}},{\displaystyle \frac{\overrightarrow{cd}}{0.63}},{\displaystyle \frac{\overrightarrow{bd}}{0.6}},{\displaystyle \frac{\overrightarrow{be}}{0.4}},{\displaystyle \frac{\overrightarrow{de}}{0.4}}\right),\left({\displaystyle \frac{\overrightarrow{ab}}{0.8}},{\displaystyle \frac{\overrightarrow{ac}}{0.85}},{\displaystyle \frac{\overrightarrow{bc}}{0.89}},{\displaystyle \frac{\overrightarrow{cd}}{0.2}},{\displaystyle \frac{\overrightarrow{bd}}{0.82}},{\displaystyle \frac{\overrightarrow{be}}{0.95}},{\displaystyle \frac{\overrightarrow{de}}{0.92}}\right)⟩.$$

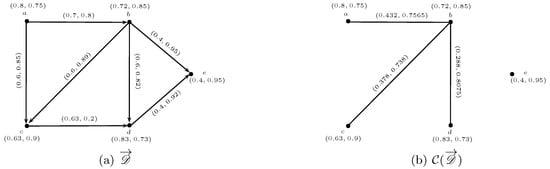
Figure 10. Competition graph of directed graph. (a) $\overrightarrow{\mathcal{D}}$; (b) $\mathcal{C}(\overrightarrow{\mathcal{D}})$.

The out-neighborhoods of q-ROF vertices are

$$\begin{array}{ccc}\hfill {\mathcal{N}}^{+}(a)& =& \{(b,0.7,0.8),(c,0.6,0.85)\},\hfill \\ \hfill {\mathcal{N}}^{+}(b)& =& \{(c,0.6,0.89),(d,0.6,0.82),(e,0.4,0.95)\},\hfill \\ \hfill {\mathcal{N}}^{+}(c)& =& \{(d,0.63,0.2)\},\hfill \\ \hfill {\mathcal{N}}^{+}(d)& =& \{(e,0.4,0.92)\},\hfill \\ \hfill {\mathcal{N}}^{+}(e)& =& \varphi .\hfill \end{array}$$

By using Definition 23, we get the corresponding 3-ROFCG $\mathcal{C}(\overrightarrow{\mathcal{D}})=(\mathcal{A},\mathcal{B})$ of $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ as displayed in Figure 10$b.$

Theorem 1.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed q-rung orthopair fuzzy graph. If ${\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)$ contains only one element of $\overrightarrow{\mathcal{D}},$ then the q-ROF edge of $\mathcal{C}(\overrightarrow{\mathcal{D}})$ is independent strong if and only if $|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}{(v)|}_{\mu }>0.5$ and $|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}{(v)|}_{\nu }<0.5.$

Theorem 2.

If all the edges of a q-rung orthopair fuzzy graph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ are independent strong, then $\frac{{\mu }_{\mathcal{R}}(uv)}{{\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v)}>0.5$ and $\frac{{\nu }_{\mathcal{R}}(uv)}{{\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v)}<0.5$ for all q-ROF edges $uv$ in $\mathcal{C}(\overrightarrow{\mathcal{D}})=(\mathcal{P},\mathcal{R}).$

Definition 24.

Let k be a non-negative real number and $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed q-rung orthopair fuzzy graph. The q-rung orthopair fuzzy k-competition graph ${\mathcal{C}}_k(\overrightarrow{\mathcal{D}})$ of a q-rung orthopair fuzzy digraph $\overrightarrow{\mathcal{D}}$ is an undirected q-ROFG $\mathcal{G}=(\mathcal{P},\mathcal{R})$ which has same q-ROF vertex set as in $\overrightarrow{\mathcal{D}}$ and has a q-ROF edge between two vertices $u,v\in {\mathcal{P}}^{*}$ in ${\mathcal{C}}_k(\overrightarrow{\mathcal{D}})$ if and only if $|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}{(v)|}_{\mu }>k$ and $|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}{(v)|}_{\nu }>k.$ The support for membership and support for non-membership of edge $uv$ in ${\mathcal{C}}_k(\overrightarrow{\mathcal{D}})$ is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{\mathcal{R}}(uv)=\frac{k_1-k}{k_1}({\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v)){\mathit{h}}_{\mu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)),\hfill \\ {\nu }_{\mathcal{R}}(uv)=\frac{k_2-k}{k_2}({\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v)){\mathit{h}}_{\nu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))\hfill \end{array}\right.\end{array}$$

such that ${\mu }_{\mathcal{R}}^q(uv)+{\nu }_{\mathcal{R}}^q(uv)\le 1,$ for all $u,v\in X,$ where $k_1=|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}{(v)|}_{\mu },k_2={|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)|}_{\nu }.$

Example 7.

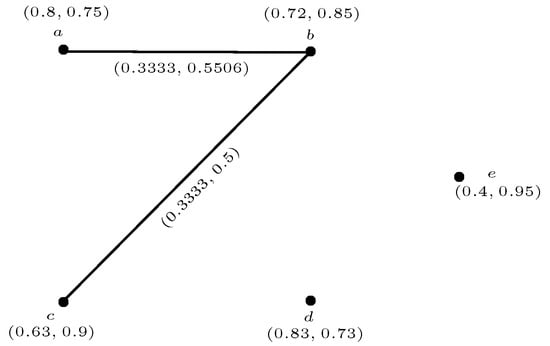
Consider a 3-rung orthopair fuzzy digraph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ given in Example 6, displayed in Figure 10$a.$ ${\mathcal{C}}_{0.4}(\overrightarrow{\mathcal{D}})$ has only two 3-ROF edges, since

$$|{\mathcal{N}}^{+}(a)\cap {\mathcal{N}}^{+}{(b)|}_{\mu }=0.6>0.4and{|{\mathcal{N}}^{+}(a)\cap {\mathcal{N}}^{+}(b)|}_{\nu }=0.89>0.4,$$

$$|{\mathcal{N}}^{+}(b)\cap {\mathcal{N}}^{+}{(c)|}_{\mu }=0.6>0.4and{|{\mathcal{N}}^{+}(b)\cap {\mathcal{N}}^{+}(c)|}_{\nu }=0.82>0.4.$$

Thus, by using Definition 24, we get the corresponding 3-rung orthopair fuzzy $0.4$-competition graph ${\mathcal{C}}_{0.4}(\overrightarrow{\mathcal{D}})=(\mathcal{A},\mathcal{B})$ of $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ as shown in Figure 11.

Figure 11. ${\mathcal{C}}_{0.4}(\overrightarrow{\mathcal{D}})$.

Theorem 3.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed q-rung orthopair fuzzy graph. If $h_{\mu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))=h_{\nu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))=1,{|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)|}_{\mu }>2k$ and $|{\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}{(v)|}_{\nu }<2k,$ then the q-ROF edge is independent strong in ${\mathcal{C}}_k(\overrightarrow{\mathcal{D}}).$

Definition 25.

Let p be a positive integer and $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed q-rung orthopair fuzzy graph. The p-competition q-rung orthopair fuzzy graph ${\mathcal{C}}^p(\overrightarrow{\mathcal{D}})$ of a q-rung orthopair fuzzy digraph $\overrightarrow{\mathcal{D}}$ is an undirected q-ROFG $\mathcal{G}=(\mathcal{P},\mathcal{R})$ which has same q-ROF vertex set as in $\overrightarrow{\mathcal{D}}$ and has a q-ROF edge between two vertices $u,v\in {\mathcal{P}}^{*}$ in ${\mathcal{C}}^p(\overrightarrow{\mathcal{D}})$ if and only if $|supp({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))|\ge p.$ The support for membership and support for non-membership of edge $uv$ in ${\mathcal{C}}^p(\overrightarrow{\mathcal{D}})$ is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{\mathcal{R}}(uv)=\frac{(n-p)+1}{n}({\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v)){\mathit{h}}_{\mu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)),\hfill \\ {\nu }_{\mathcal{R}}(uv)=\frac{(n-p)+1}{n}({\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v)){\mathit{h}}_{\nu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))\hfill \end{array}\right.\end{array}$$

such that ${\mu }_{\mathcal{R}}^q(uv)+{\nu }_{\mathcal{R}}^q(uv)\le 1,$ for all $u,v\in X,$ where $n=|supp({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))|.$

Example 8.

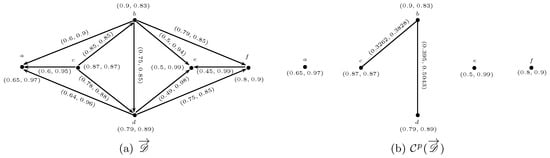
Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a 5-rung orthopair fuzzy digraph, given in Figure 12a, where

$$\mathcal{P}=⟨\left({\displaystyle \frac{a}{0.65}},{\displaystyle \frac{b}{0.9}},{\displaystyle \frac{c}{0.87}},{\displaystyle \frac{d}{0.79}},{\displaystyle \frac{e}{0.5}},{\displaystyle \frac{f}{0.8}}\right),\left({\displaystyle \frac{a}{0.97}},{\displaystyle \frac{b}{0.83}},{\displaystyle \frac{c}{0.87}},{\displaystyle \frac{d}{0.89}},{\displaystyle \frac{e}{0.99}},{\displaystyle \frac{f}{0.9}}\right)⟩and$$

$$\begin{array}{cc}\hfill \overrightarrow{\mathcal{Q}}=& ⟨\left({\displaystyle \frac{\overrightarrow{ba}}{0.6}},{\displaystyle \frac{\overrightarrow{ca}}{0.6}},{\displaystyle \frac{\overrightarrow{da}}{0.64}},{\displaystyle \frac{\overrightarrow{cb}}{0.85}},{\displaystyle \frac{\overrightarrow{cd}}{0.78}},{\displaystyle \frac{\overrightarrow{bd}}{0.75}},{\displaystyle \frac{\overrightarrow{be}}{0.5}},{\displaystyle \frac{\overrightarrow{de}}{0.49}},{\displaystyle \frac{\overrightarrow{bf}}{0.79}},{\displaystyle \frac{\overrightarrow{df}}{0.75}},{\displaystyle \frac{\overrightarrow{fe}}{0.45}}\right),\hfill \\ & \left({\displaystyle \frac{\overrightarrow{ba}}{0.9}},{\displaystyle \frac{\overrightarrow{ca}}{0.95}},{\displaystyle \frac{\overrightarrow{da}}{0.96}},{\displaystyle \frac{\overrightarrow{cb}}{0.85}},{\displaystyle \frac{\overrightarrow{cd}}{0.88}},{\displaystyle \frac{\overrightarrow{bd}}{0.85}},{\displaystyle \frac{\overrightarrow{be}}{0.94}},{\displaystyle \frac{\overrightarrow{de}}{0.98}},{\displaystyle \frac{\overrightarrow{bf}}{0.85}},{\displaystyle \frac{\overrightarrow{df}}{0.85}},{\displaystyle \frac{\overrightarrow{fe}}{0.99}}\right)⟩.\hfill \end{array}$$

${\mathcal{C}}^2(\overrightarrow{\mathcal{D}})$ has only two 5-ROF edges $bc$ and $bd$, since

$$|supp({\mathcal{N}}^{+}(b)\cap {\mathcal{N}}^{+}(c))|=2\ge 2,$$

$$|supp({\mathcal{N}}^{+}(b)\cap {\mathcal{N}}^{+}(d))|=3\ge 2.$$

Figure 12. p-Competition q-rung orthopair fuzzy graph. (a) $\overrightarrow{\mathcal{D}}$; (b) ${\mathcal{C}}^p(\overrightarrow{\mathcal{D}})$.

Thus, by using Definition 25, we get the corresponding 2-competition 5-rung orthopair fuzzy graph ${\mathcal{C}}^2(\overrightarrow{\mathcal{D}})=(\mathcal{A},\mathcal{B})$ of $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ as shown in Figure 12$b.$

Theorem 4.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed q-rung orthopair fuzzy graph. If $h_{\mu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))=1$ and $h_{\nu }({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))=0$ in ${\mathcal{C}}^{\lfloor \frac{n}{2}\rfloor }(\overrightarrow{\mathcal{D}})$, then the q-ROF edge is independent strong, where $n=|supp({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))|.$

Definition 26.

A q-rung orthopair fuzzy m-step out-neighborhood of a vertex v of a directed q-ROFG $\overrightarrow{\mathcal{D}}$ is the q-ROF m-step set ${\mathcal{N}}_m^{+}(v)=(X_v^{+},{\mu }_{{\mathcal{P}}_v}^{+},{\nu }_{{\mathcal{P}}_v}^{+})$, where $X_v^{+}=\{u:{\overrightarrow{P}}_{vu}^{m}exists\}$ and ${\mu }_{{\mathcal{P}}_v}^{+}:X_v^{+}\to [0,1]$ defined by ${\mu }_{{\mathcal{P}}_v}^{+}(u)=min\{{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{xy}):\overrightarrow{xy}isanedgein{\overrightarrow{P}}_{vu}^m\}$ and ${\nu }_{{\mathcal{P}}_v}^{+}:X_v^{+}\to [0,1]$ defined by ${\nu }_{{\mathcal{P}}_v}^{+}(u)=max\{{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{xy}):\overrightarrow{xy}isanedgein{\overrightarrow{P}}_{vu}^m\}.$ A q-rung orthopair fuzzy m-step in-neighborhood of a vertex v of a directed q-ROFG $\overrightarrow{\mathcal{D}}$ is the q-ROF m-step set ${\mathcal{N}}_m^{-}(v)=(X_v^{-},{\mu }_{{\mathcal{P}}_v}^{-},{\nu }_{{\mathcal{P}}_v}^{-})$, where $X_v^{-}=\{u:{\overrightarrow{P}}_{uv}^{m}exists\}$ and ${\mu }_{{\mathcal{P}}_v}^{-}:X_v^{-}\to [0,1]$ defined by ${\mu }_{{\mathcal{P}}_v}^{-}(u)=min\{{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ab}):\overrightarrow{ab}isanedgein{\overrightarrow{P}}_{uv}^m\}$ and ${\nu }_{{\mathcal{P}}_v}^{-}:X_v^{-}\to [0,1]$ defined by ${\nu }_{{\mathcal{P}}_v}^{-}(u)=max\{{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ab}):\overrightarrow{ab}isanedgein{\overrightarrow{P}}_{uv}^m\}.$

Definition 27.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed q-rung orthopair fuzzy graph. The m-step q-rung orthopair fuzzy competition graph ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})$ of a q-rung orthopair fuzzy digraph $\overrightarrow{\mathcal{D}}$ is an undirected q-ROFG $\mathcal{G}=(\mathcal{P},\mathcal{R})$ which has same q-ROF vertex set as in $\overrightarrow{\mathcal{D}}$ and has a q-ROF edge between two vertices $u,v\in {\mathcal{P}}^{*}$ in ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})$ if and only if ${\mathcal{N}}_m^{+}(u)\cap {\mathcal{N}}_m^{+}(v)\ne \varphi$ in $\overrightarrow{\mathcal{D}}$ and the support for membership and support for non-membership of edge $uv$ in ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})$ is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{\mathcal{R}}(uv)=({\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v)){\mathit{h}}_{\mu }({\mathcal{N}}_m^{+}(u)\cap {\mathcal{N}}_m^{+}(v)),\hfill \\ {\nu }_{\mathcal{R}}(uv)=({\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v)){\mathit{h}}_{\nu }({\mathcal{N}}_m^{+}(u)\cap {\mathcal{N}}_m^{+}(v))\hfill \end{array}\right.\end{array}$$

such that ${\mu }_{\mathcal{R}}^q(uv)+{\nu }_{\mathcal{R}}^q(uv)\le 1,$ for all $u,v\in X.$

Example 9.

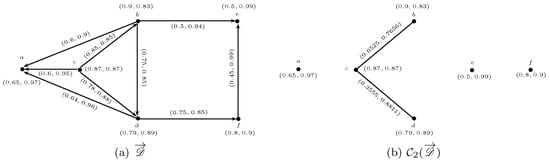
Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a 5-rung orthopair fuzzy digraph, given in Figure 13a, where

$$\mathcal{P}=⟨\left({\displaystyle \frac{a}{0.65}},{\displaystyle \frac{b}{0.9}},{\displaystyle \frac{c}{0.87}},{\displaystyle \frac{d}{0.79}},{\displaystyle \frac{e}{0.5}},{\displaystyle \frac{f}{0.8}}\right),\left({\displaystyle \frac{a}{0.97}},{\displaystyle \frac{b}{0.83}},{\displaystyle \frac{c}{0.87}},{\displaystyle \frac{d}{0.89}},{\displaystyle \frac{e}{0.99}},{\displaystyle \frac{f}{0.9}}\right)⟩and$$

$$\begin{array}{cc}\hfill \overrightarrow{\mathcal{Q}}=& ⟨\left({\displaystyle \frac{\overrightarrow{ba}}{0.6}},{\displaystyle \frac{\overrightarrow{ca}}{0.6}},{\displaystyle \frac{\overrightarrow{da}}{0.64}},{\displaystyle \frac{\overrightarrow{cb}}{0.85}},{\displaystyle \frac{\overrightarrow{cd}}{0.78}},{\displaystyle \frac{\overrightarrow{bd}}{0.75}},{\displaystyle \frac{\overrightarrow{be}}{0.5}},{\displaystyle \frac{\overrightarrow{df}}{0.75}},{\displaystyle \frac{\overrightarrow{fe}}{0.45}}\right),\hfill \\ & \left({\displaystyle \frac{\overrightarrow{ba}}{0.9}},{\displaystyle \frac{\overrightarrow{ca}}{0.95}},{\displaystyle \frac{\overrightarrow{da}}{0.96}},{\displaystyle \frac{\overrightarrow{cb}}{0.85}},{\displaystyle \frac{\overrightarrow{cd}}{0.88}},{\displaystyle \frac{\overrightarrow{bd}}{0.85}},{\displaystyle \frac{\overrightarrow{be}}{0.94}},{\displaystyle \frac{\overrightarrow{df}}{0.85}},{\displaystyle \frac{\overrightarrow{fe}}{0.99}}\right)⟩.\hfill \end{array}$$

${\mathcal{C}}_2(\overrightarrow{\mathcal{D}})$ has only two 5-ROF edges $bc$ and $cd$, since

$${\mathcal{N}}_2^{+}(b)\cap {\mathcal{N}}_2^{+}(c)=\{(f,0.75,0.88)\}\ne \varphi ,$$

$${\mathcal{N}}_2^{+}(c)\cap {\mathcal{N}}_2^{+}(d)=\{(e,0.45,0.99)\}\ne \varphi .$$

Figure 13. m-Step q-rung orthopair fuzzy competition graph. (a) $\overrightarrow{\mathcal{D}}$; (b) ${\mathcal{C}}_2(\overrightarrow{\mathcal{D}})$.

Thus, by using Definition 27, we get the corresponding 2-step 5-rung orthopair fuzzy competition graph ${\mathcal{C}}_2(\overrightarrow{\mathcal{D}})=(\mathcal{A},\mathcal{B})$ of $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ as shown in Figure 13$b.$

Theorem 5.

If all q-ROF edges of a q-rung orthopair fuzzy digraph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ are independent strong, then all the q-ROF edges of ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})$ are independent strong.

Theorem 6.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a q-rung orthopair fuzzy digraph defined on $\overrightarrow{D}=(P,\overrightarrow{Q}).$ If $m>|P|$, then ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})$ has no edges.

Theorem 7.

If $\overrightarrow{\mathcal{D}}$ be a q-rung orthopair fuzzy digraph and $\overrightarrow{{\mathcal{D}}_m}$ is the m-step q-rung orthopair fuzzy digraph of $\overrightarrow{\mathcal{D}},$ then ${\mathcal{C}}_m(\overrightarrow{\mathcal{D}})=\mathcal{C}({\overrightarrow{\mathcal{D}}}_m).$

Definition 28.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a directed q-rung orthopair fuzzy graph. Let z be a common q- ROF prey of m-step out-neighborhoods of q- ROF vertices $x_1,x_2,\dots ,x_k$. Also let ${\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_1{v}_1}),{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_2{v}_2}),\dots ,{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_k{v}_k})$ be minimum support for membership of q- ROF edges of the paths ${\overrightarrow{P}}_{x_{1}z}^m,{\overrightarrow{P}}_{x_{2}z}^m,\dots ,{\overrightarrow{P}}_{x_{k}z}^m$, respectively and ${\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_1{v}_1}),{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_2{v}_2}),\dots ,{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_k{v}_k})$ be maximum support for non-membership of q- ROF edges of the paths ${\overrightarrow{P}}_{x_{1}z}^m,{\overrightarrow{P}}_{x_{2}z}^m,\dots ,{\overrightarrow{P}}_{x_{k}z}^m$, respectively. The m-step q- ROF prey $z\in X$ is called independent strong q- ROF prey if for all $1\le i\le k,$

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{v}_i})>0.5,\hfill \\ {\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{v}_i})<0.5.\hfill \end{array}\right.\end{array}$$

The strength of q-ROF prey z measured by the mappings $s_1:X\to [0,1]$ and $s_2:X\to [0,1]$, is defined by $(s_1(z),s_2(z))$ such that

$$s_1(z)=\frac{{\sum }_{i=1}^k{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{v}_i})}{k}\mathrm{and}{s}_2(z)=\frac{{\sum }_{i=1}^k{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{v}_i})}{k}.$$

Example 10.

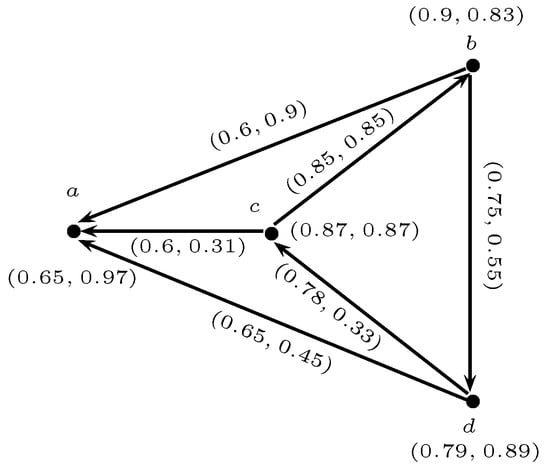
Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a 5-rung orthopair fuzzy digraph, given in Figure 14. We see that a is common 5-ROF prey of 2-step out-neighborhoods of 5-ROF vertices b and $d.$ ‘a’ is said to be strong 2-step 5-ROF prey, since there exist only two directed paths for a to be a common 5-ROF prey.

$${\overrightarrow{P}}_{ba}^2:{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{bd})\wedge {\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{da})=0.65>0.5\mathrm{and}{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{bd})\wedge {\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{da})=0.45<0.5$$

and

$${\overrightarrow{P}}_{da}^2:{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{dc})\wedge {\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ca})=0.60>0.5\mathrm{and}{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{dc})\wedge {\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ca})=0.33<0.5.$$

Figure 14. A strong 2-step 5-rung orthopair fuzzy prey.

Theorem 8.

If a q-rung orthopair fuzzy prey z of $\overrightarrow{\mathcal{D}}$ is independent strong then the strength of $z,$$s_1(z)>0.5$ and $s_2(z)<0.5$ but converse may not hold.

For the proofs of the above theorems, readers are referred to [28,29,30,31,32].

Theorem 9.

A q-rung orthopair fuzzy graph $\mathcal{G}$ is said to be a q-rung orthopair fuzzy competition graph of some q-rung orthopair fuzzy digraph if and only if ${\theta }_e(\mathcal{G})\le n,$ where $n=|V(\mathcal{G})|.$

Proof. 

Let $\overrightarrow{\mathcal{D}}=(\mathcal{A},\overrightarrow{\mathcal{B}})$ be a q-rung orthopair fuzzy digraph and $\mathcal{G}=\mathcal{C}(\overrightarrow{\mathcal{D}})=(\mathcal{A},\mathcal{P})$ be a q-rung orthopair fuzzy competition graph of $\overrightarrow{\mathcal{D}}$ such that $|V(\mathcal{G})|=n.$ Then by Definition 23

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{\mathcal{P}}(uv)=({\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v)){\mathit{h}}_{\mu }(N^{+}(u)\cap N^{+}(v)),\hfill \\ {\nu }_{\mathcal{P}}(uv)=({\nu }_{\mathcal{A}}(u)\vee {\nu }_{\mathcal{A}}(v)){\mathit{h}}_{\nu }(N^{+}(u)\cap N^{+}(v)),\hfill \end{array}\right.\end{array}$$

where $N^{+}(u)$ and $N^{+}(v)$ are q-rung orthopair fuzzy out-neighborhoods of vertices u and v, respectively. Consider the q-rung orthopair fuzzy cliques ${\mathcal{C}}_i=({\mathcal{H}}_i,{\mathcal{Q}}_i)$ of $\mathcal{G}$ such that

$$V({\mathcal{C}}_i)=\{u_j|\overrightarrow{u_j{v}_j}\in E(\overrightarrow{\mathcal{D}})\}$$

with

$$\left\{\begin{array}{c}{\mu }_{\mathcal{H}}(u_j)\le {\mu }_{\mathcal{A}}(u_j),\hfill \\ {\nu }_{\mathcal{H}}(u_j)\ge {\nu }_{\mathcal{A}}(u_j)forall{u}_j\in V({\mathcal{C}}_i).\hfill \end{array}\right.$$

Let ${\mathcal{S}}_i=({\mathcal{K}}_i,{\mathcal{R}}_i)$ are the q-rung orthopair fuzzy subgraphs of $\mathcal{G}=(\mathcal{A},\mathcal{P})$ induced by ${\mathcal{C}}_i$, respectively. Then by Definition of q-rung orthopair fuzzy clique, ${\mathcal{S}}_i$ are complete q-rung orthopair fuzzy subgraphs of $\mathcal{G}$ and every edge $uv$ of $\mathcal{G}$ must be in some ${\mathcal{S}}_i$ i.e., there exist a collection of cliques which cover all edges of $\mathcal{G}$ such that

$$\left\{\begin{array}{c}{\mu }_{\mathcal{R}}(uv)={\mu }_{\mathcal{P}}(uv),\hfill \\ {\nu }_{\mathcal{R}}(uv)={\nu }_{\mathcal{P}}(uv)forallu,v\in X,\hfill \end{array}\right.$$

called q-rung orthopair fuzzy edge clique cover. Then, clearly, the size of the smallest such q-rung orthopair FECC denoted by ${\theta }_e(\mathcal{G})$ cannot exceed the number of vertices of $\mathcal{G}$ i.e., $n.$ Hence ${\theta }_e(\mathcal{G})\le n.$

Conversely, let ${\theta }_e(\mathcal{G})=k\le n$ and let $\{{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_k\}$ be the collection of q-rung orthopair fuzzy cliques which covers all edges of $\mathcal{G}$ by complete q-rung orthopair fuzzy subgraphs. Construct q-rung orthopair fuzzy digraph $\overrightarrow{\mathcal{D}}=(\mathcal{A},\overrightarrow{\mathcal{B}})$ with $V(\overrightarrow{\mathcal{D}})=\{v_1,v_2,\dots ,v_n\}$ such that for all $v_i\in {\mathcal{C}}_i(1\le i\le k),$ the support for membership and non-membership of $v_i$ are same and $forall{v}_i,v_j\notin {\mathcal{C}}_i(1\le i\le k),$

$$\left\{\begin{array}{c}{\mu }_{\mathcal{A}}(v_{ij})={\mu }_{\mathcal{A}}(v_i)\wedge {\mu }_{\mathcal{A}}(v_j),\hfill \\ {\nu }_{\mathcal{A}}(v_{ij})={\nu }_{\mathcal{A}}(v_i)\vee {\nu }_{\mathcal{A}}(v_j),\hfill \end{array}\right.$$

where $v_{ij}$ are the isolated vertices, that is there exist arcs $\overrightarrow{v_i{v}_{ij}}$ and $\overrightarrow{v_j{v}_{ij}}$ in $\overrightarrow{\mathcal{D}}.$ Also, $\overrightarrow{v_i{v}_j}\in E(\overrightarrow{\mathcal{D}})$ if and only if $v_i\in C_j$ with

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{\overrightarrow{\mathcal{B}}}(\overrightarrow{v_i{v}_j})=\frac{{\mu }_{\mathcal{P}}(v_i{v}_j)}{{\mu }_{\mathcal{A}}(v_i)\wedge {\mu }_{\mathcal{A}}(v_j)},\hfill \\ {\nu }_{\overrightarrow{\mathcal{B}}}(\overrightarrow{v_i{v}_j})=\frac{{\nu }_{\mathcal{P}}(v_i{v}_j)}{{\nu }_{\mathcal{A}}(v_i)\vee {\nu }_{\mathcal{A}}(v_j)}.\hfill \end{array}\right.\end{array}$$

Then $\mathcal{G}=(\mathcal{A},\mathcal{P})$ is called q-rung orthopair fuzzy competition graph of D i.e., $\mathcal{G}=\mathcal{C}(\overrightarrow{\mathcal{D}}).$ This completes the proof. □

The notion of triangulated graphs also arises when we deal with competition graphs. As the terminological background of a competition graph based on predator-prey relationships, consider the ecosystem in which three predators $a,b$, and c, have a common prey x, which leads to the formation of a triangle in the graph. We now explore this situation for the q-rung orthopair fuzzy graph.

Definition 29.

A q-rung orthopair fuzzy graph $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is said to be triangulated if for every q-rung orthopair fuzzy cycle $\mathcal{C}$ of length $l>3$ there is a q-rung orthopair fuzzy edge of $\mathcal{G}$ joining two non-consecutive vertices of $\mathcal{C}.$ In other words, $\mathcal{G}$ does not have a cycle of length $l>3$ as induced q-rung orthopair fuzzy subgraph.

Theorem 10.

Let $\mathcal{G}$ is a q-rung orthopair fuzzy graph. If $\mathcal{G}$ has q-ROF clique number 3 and ${\theta }_e(\mathcal{G})\le |V(\mathcal{G})|,$ then $\mathcal{G}$ is the triangulated q-ROF competition graph.

Proof. 

Let $\mathcal{G}$ is a q-rung orthopair fuzzy graph with clique number 3. Let $\mathcal{P}$ be a largest q-rung orthopair fuzzy clique of $\mathcal{G}$ of size 3 and

$${\theta }_e(\mathcal{G})\le |V(\mathcal{G})|.$$

(1)

Then $\mathcal{P}$ induces a complete q-rung orthopair fuzzy subgraph $\mathcal{C}$ of $\mathcal{G}.$ Clearly, $\mathcal{C}$ is a q-ROF cycle of length 3 being a complete q-rung orthopair fuzzy generated subgraph. There is no q-ROF cycles of length $l>3$ in $\mathcal{G}$ as it is the largest possible set of q-ROF mutually adjacent vertices. Since $\mathcal{G}$ contains no induced q-ROF cycles of length greater than $3,$ $\mathcal{G}$ is triangulated. Also, since the size of smallest edge clique cover satisfies the relation 1, by Theorem 9, $\mathcal{G}$ is a q-ROF competition graph. Hence, $\mathcal{G}$ is triangulated q-ROF competition graph. □

Please note that if G is a triangulated graph then the vertex set of any induced cycle of length 3 must be a clique but this may not true for triangulated q-rung orthopair fuzzy graphs.

Theorem 11.

Let $\mathcal{G}$ is a q-rung orthopair fuzzy graph. If $\mathcal{G}$ is triangulated, then the vertex set of any induced q-ROF cycle of length 3 may not be a q-rung orthopair fuzzy clique of $\mathcal{G}.$

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be a triangulated q-ROFG. Then $\mathcal{G}$ has q-rung orthopair fuzzy cycle of length 3 as a generated subgraph. Let $\mathcal{C}=(\mathcal{P},\mathcal{Q})$ be such a q-ROF cycle of length 3 such that

$$\left\{\begin{array}{c}{\mu }_{\mathcal{P}}(u)\le {\mu }_{\mathcal{A}}(u),\hfill \\ {\nu }_{\mathcal{P}}(u)\ge {\nu }_{\mathcal{A}}(u)forallu\in {\mathcal{P}}^{*}\hfill \end{array}\right.$$

(2)

and

$$\left\{\begin{array}{c}{\mu }_{\mathcal{Q}}(uv)\le {\mu }_{\mathcal{B}}(uv),\hfill \\ {\nu }_{\mathcal{Q}}(uv)\ge {\nu }_{\mathcal{B}}(uv)forallu,v\in {\mathcal{P}}^{*}.\hfill \end{array}\right.$$

(3)

The set $\mathcal{P}=\{(u,{\mu }_{\mathcal{P}}(u),{\nu }_{\mathcal{P}}(u)):u\in {\mathcal{P}}^{*}\}$ is a q-ROF vertex set of $\mathcal{C}.$ Consider a complete q-ROFG $\mathcal{H}=(\mathcal{P},\mathcal{R})$ induced by $\mathcal{P}.$ Then

$$\left\{\begin{array}{c}{\mu }_{\mathcal{R}}(uv)={\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v),\hfill \\ {\nu }_{\mathcal{R}}(uv)={\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v)forallu,v\in {\mathcal{P}}^{*}.\hfill \end{array}\right.$$

(4)

Combining inequalities (3) and (4), we get

$$\begin{array}{ccc}\hfill {\mu }_{\mathcal{Q}}(uv)& =& {\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v)\hfill \\ & \le & {\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v).\hfill \end{array}$$

Also ${\mu }_{\mathcal{B}}(uv)\le {\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v).$ Which shows that ${\mu }_{\mathcal{Q}}(uv)$ may not always less than or equal to ${\mu }_{\mathcal{B}}(uv).$ Thus, the complete q-ROFG of $\mathcal{H}=(\mathcal{P},\mathcal{R})$ may not be a subgraph of triangulated q-ROFG $\mathcal{G}=(\mathcal{A},\mathcal{B}).$ Hence, $\mathcal{H}$ may not a q-rung orthopair fuzzy clique of $\mathcal{G}.$ □

Example 11.

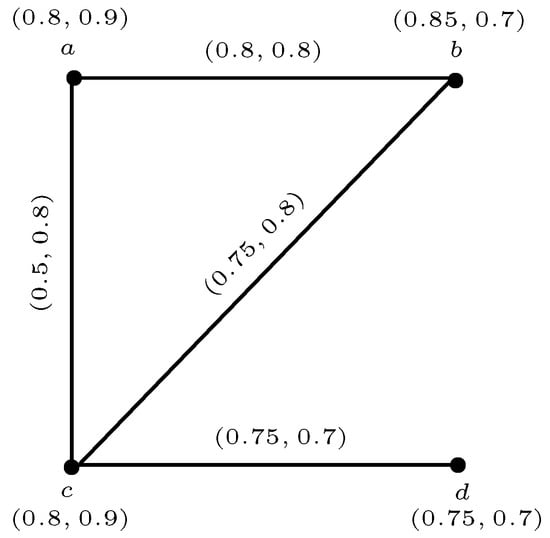
Consider a triangulated 3-rung orthopair fuzzy graph $\mathcal{G}=(\mathcal{A},\mathcal{B})$ as shown in Figure 15.

Figure 15. A triangulated q-rung orthopair fuzzy graph $\mathcal{G}$.

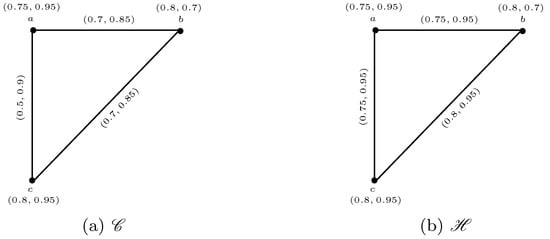
Let $\mathcal{C}$ be the q-ROF induced cycle of $\mathcal{G}$ of length 3 as shown in Figure 16a. Name the q-ROF vertex set of $\mathcal{C}$ as $\mathcal{P},$ given by

$$\mathcal{P}=\{(a,0.75,0.95),(b,0.8,0.7),(c,0.8,0.95)\}.$$

Figure 16. (a) $\mathcal{C}$; (b) $\mathcal{H}$.

Figure 16b represents a complete q-ROFG $\mathcal{H}=(\mathcal{P},\mathcal{R})$ induced by $\mathcal{P}.$ Clearly, $\mathcal{H}$ is not a subgraph of $\mathcal{G},$ since

$${\mu }_{\mathcal{Q}}(ac)=0.75\nleqq 0.5={\mu }_{\mathcal{B}}(ac).$$

Hence, $\mathcal{P}$ is not a q-rung orthopair fuzzy clique of $\mathcal{G}.$ One can see that the above result holds only when $\mathcal{C}$ is complete.

4.1. Competition Number of q-ROFGs

A basic ecological principle is that two species compete if and only if their ecological niches overlap. In crisp graph theory, we can obtain corresponding digraphs by the scheme proposed by Roberts in [37], which led him to introduce the concept of competition number. The competition number has been extensively studied by many researchers for crisp graphs. While dealing with uncertainties of competition in many practical scenarios, the competition number also plays a vital role. However, when we deal with fuzziness, the exact fuzzy digraphs cannot be obtained from fuzzy competition graphs.

To understand our adopted approach to define the competition number in q-rung orthopair fuzzy environment, consider an example in which two persons are competing for an object, where the ability to compete is given by their membership grades. Now the problem is to find the extent of competition of both persons towards the object.

Let $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a fuzzy directed graph. The out-neighborhoods of vertices are

$$\begin{array}{ccc}\hfill {\mathcal{N}}^{+}(u)& =& \{(x,{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ux}))\},\hfill \\ \hfill {\mathcal{N}}^{+}(v)& =& \{(x,{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vx}))\}.\hfill \end{array}$$

The height of common neighborhood ${\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v)=\{(x,{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ux})\wedge {\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vx}))\}$ is

$$\mathit{h}({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))={\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ux})\wedge {\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vx}).$$

By definition of fuzzy competition graph $\mathcal{G}=(\mathcal{A},\mathcal{B}),$

$${\mu }_{\mathcal{B}}(uv)=({\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v))\mathit{h}({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))$$

or

$$\mathit{h}({\mathcal{N}}^{+}(u)\cap {\mathcal{N}}^{+}(v))=\frac{{\mu }_{\mathcal{B}}(uv)}{{\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v)},$$

$${\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ux})\wedge {\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vx})=\frac{{\mu }_{\mathcal{R}}(uv)}{{\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v)}.$$

(5)

We know that

$${\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ux})\le {\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(x),{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vx})\le {\mu }_{\mathcal{P}}(v)\wedge {\mu }_{\mathcal{P}}(x).$$

(6)

Combining (5) and (6), we get

$${\mu }_{\mathcal{P}}(\overrightarrow{ux})\wedge {\mu }_{\mathcal{P}}(\overrightarrow{vx})\le {\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{ux})\le {\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(x),$$

$${\mu }_{\mathcal{P}}(\overrightarrow{ux})\wedge {\mu }_{\mathcal{P}}(\overrightarrow{vx})\le {\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{vx})\le {\mu }_{\mathcal{P}}(v)\wedge {\mu }_{\mathcal{P}}(x).$$

Thus, we can obtain the upper bounds and lower bounds of membership grades for edges in corresponding digraphs for the case when two species are competing for only one prey. However, when two species are competing for more than one prey, we cannot even find their bounds. Since the membership grade related to each directed edge of $\overrightarrow{\mathcal{D}}$ cannot be found exactly, we introduce the term ‘power of competition’, connected with each arc, to define the competition number of q-ROFGs. Also, we illustrate an algorithm in this context.

Theorem 12.

Let $\mathcal{G}$ be a q-rung orthopair fuzzy graph then adding sufficient number of r isolated q-ROF vertices ${\delta }_{u_i{v}_i},1\le i\le r,$ to $\mathcal{G}$ such that

$$\left\{\begin{array}{c}{\mu }_{\mathcal{P}}({\delta }_{u_i{v}_i})={\mu }_{\mathcal{A}}(u_i)\wedge {\mu }_{\mathcal{A}}(v_i),\hfill \\ {\nu }_{\mathcal{P}}({\delta }_{u_i{v}_i})={\nu }_{\mathcal{A}}(u_i)\vee {\nu }_{\mathcal{A}}(v_i),\hfill \end{array}\right.$$

produces a q-rung orthopair fuzzy competition graph $\mathcal{G}\cup {\mathcal{I}}_r$ of some digraph $\overrightarrow{\mathcal{D}}.$

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be a q-rung orthopair fuzzy graph where, $\mathcal{A}=({\mu }_{\mathcal{A}},{\nu }_{\mathcal{A}})$ is q-rung orthopair fuzzy set on X and $\mathcal{B}=({\mu }_{\mathcal{B}},{\nu }_{\mathcal{B}})$ is a q-rung orthopair fuzzy relation on $X.$ Construct a digraph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ as follows: Let $u,v\in X$ be any two q-ROF vertices of $\mathcal{G}$ such that ${\mu }_{\mathcal{P}}(uv)>0$ or ${\nu }_{\mathcal{P}}(uv)>0.$ Add a q-ROF vertex ${\delta }_{uv}$ such that

$$\left\{\begin{array}{c}{\mu }_{\mathcal{P}}({\delta }_{uv})={\mu }_{\mathcal{A}}(u)\wedge {\mu }_{\mathcal{A}}(v),\hfill \\ {\nu }_{\mathcal{P}}({\delta }_{uv})={\nu }_{\mathcal{A}}(u)\vee {\nu }_{\mathcal{A}}(v).\hfill \end{array}\right.$$

Remove the edge $uv$ and draw directed edges(arcs) from u and v to ${\delta }_{uv}$ such that the μ-power of competition and ν-power of competition of q-ROF vertices u and v towards the vertex ${\delta }_{uv}$ (i.e., power of competition associated with arcs $\overrightarrow{u{\delta }_{uv}}$ and $\overrightarrow{v{\delta }_{uv}}$) are

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{({\mathbb{P}}_{\overrightarrow{u{\delta }_{uv}}})}_{\mu }={({\mathbb{P}}_{\overrightarrow{v{\delta }_{uv}}})}_{\mu }=\frac{{\mu }_{\mathcal{B}}(uv)}{{\mu }_{\mathcal{P}}({\delta }_{uv})},\hfill \\ {({\mathbb{P}}_{\overrightarrow{u{\delta }_{uv}}})}_{\nu }={({\mathbb{P}}_{\overrightarrow{v{\delta }_{uv}}})}_{\nu }=\frac{{\nu }_{\mathcal{B}}(uv)}{{\nu }_{\mathcal{P}}({\delta }_{uv})}.\hfill \end{array}\right.\end{array}$$

(7)

Continuing the process, we get an acyclic digraph $\overrightarrow{\mathcal{D}}$ whose directed edges can be recognized by (7). This digraph $\overrightarrow{\mathcal{D}}$ gives a q-rung orthopair fuzzy competition graph $\mathcal{C}(\overrightarrow{\mathcal{D}})=\mathcal{G}\cup {\mathcal{I}}_r,$ where, ${\mathcal{I}}_r$ is q-rung orthopair fuzzy set of r isolated q-ROF vertices added to $\mathcal{G}.$ This completes the proof. □

The method of constructing the corresponding digraph $\overrightarrow{\mathcal{D}}$ of a q-ROFG is illustrated in Algorithm 1. The complexity of Algorithm 1 is $O(n^2).$

Algorithm 1.q-Rung orthopair fuzzy digraph INPUT: A q-ROFG $\mathcal{G}=(\mathcal{A},\mathcal{B}).$ OUTPUT: A q-ROF directed graph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}}).$   procedure Digraph$\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$   for$i:=1ton$do    for$j:=i+1ton$do     if${\mu }_{\mathcal{B}}(u_i{u}_j)>0$ or ${\nu }_{\mathcal{B}}(u_i{u}_j)>0$ then      add ${\delta }_{u_i{v}_j}$ such that      ${\mu }_{\mathcal{P}}({\delta }_{u_i{v}_j})={\mu }_{\mathcal{A}}(u_i)\wedge {\mu }_{\mathcal{A}}(u_j)$      ${\nu }_{\mathcal{P}}({\delta }_{u_i{v}_j})={\nu }_{\mathcal{A}}(u_i)\vee {\nu }_{\mathcal{A}}(u_j)$     end if    end for   end for   for$i:=1ton$do    for$j:=i+1ton$do     while${\mu }_{\mathcal{B}}(u_i{u}_j)>0$ or ${\nu }_{\mathcal{B}}(u_i{u}_j)>0$ do      remove $u_i{u}_j,$ draw $\overrightarrow{u_i{\delta }_{u_i{v}_j}}$ and $\overrightarrow{u_j{\delta }_{u_i{v}_j}}$ such that                          ${({\mathbb{P}}_{\overrightarrow{u_i{\delta }_{u_i{u}_j}}})}_{\mu }={({\mathbb{P}}_{\overrightarrow{u_j{\delta }_{u_i{u}_j}}})}_{\mu }=\frac{{\mu }_{\mathcal{B}}(u_i{u}_j)}{{\mu }_{\mathcal{P}}({\delta }_{u_i{u}_j})}$      ${({\mathbb{P}}_{\overrightarrow{u_i{\delta }_{u_i{u}_j}}})}_{\nu }={({\mathbb{P}}_{\overrightarrow{u_j{\delta }_{u_i{u}_j}}})}_{\nu }=\frac{{\nu }_{\mathcal{B}}(u_i{u}_j)}{{\nu }_{\mathcal{P}}({\delta }_{u_i{u}_j})}$     end while    end for   end for   end procedure

Remark 1.

In Algorithm 1, the only information about directed edges of $\overrightarrow{\mathcal{D}}$ are their power of competition towards common prey. Thus, q-rung orthopair fuzzy out-neighborhoods of vertices can be defined in a similar manner by taking into account the power of competition of edges instead of their membership grades.

The Theorem 12 naturally guide us to define competition number $k(\mathcal{G})$ of q-rung orthopair fuzzy graph $\mathcal{G}.$

Definition 30.

Let $\mathcal{G}$ be any q-rung orthopair fuzzy graph. The smallest possible number of isolated q-ROF vertices which when add in $\mathcal{G}$ leads a q-rung orthopair fuzzy competition graph of certain acyclic digraph(as constructed in Algorithm 1), is called competition number of $\mathcal{G}$.

Roberts proved in [37] that if $G=(V,E)$ is a connected graph without triangles, then $k(G)\ge |E|-|V|+2.$ We now generalize this result for q-rung orthopair fuzzy graph.

Theorem 13.

If $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is a connected q-rung orthopair fuzzy graph defined on $G=(A,B)$ without any q-ROF triangle, then $k(\mathcal{G})\ge |B|-|A|+2.$

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be a q-rung orthopair fuzzy graph defined on $G=(A,B).$ Suppose that $\mathcal{G}\cup {\mathcal{I}}_r$ is q-rung orthopair fuzzy competition graph constructed according to the Algorithm 1. Label the q-ROF vertices of $\mathcal{G}$ such that every q-ROF arc goes from lower integer to higher integer in $\overrightarrow{\mathcal{D}}$. For each q-ROF edge $uv$ of $\mathcal{G},$ there is a q-ROF vertex ${\delta }_{uv}$ such that ${\delta }_{uv}$ is common prey of u and v in $\mathcal{G}.$ Moreover, since $\mathcal{G}$ has no q-ROF triangles, the ${\delta }_{uv}$ are distinct. It follows that $\mathcal{G}\cup {\mathcal{I}}_r$ has at least $|B|$ q-ROF vertices ${\delta }_{uv}.$ Furthermore, since these $|B|$ q-ROF vertices all have at least two incoming q-ROF arcs in $\mathcal{G},$ therefore, at least two of the q-ROF vertices of $\mathcal{G}\cup {\mathcal{I}}_r$ are not ${\delta }_{uv}.$ These q-ROF vertices are labeled 1 and $2,$ where the q-ROF vertex labeled 1 has no incoming q-ROF arc and q-ROF vertex labeled 2 has only one incoming q-ROF arc. Hence,

$$k(\mathcal{G})+|A|-2\ge |B|$$

implies that

$$k(\mathcal{G})\ge |B|-|A|+2.$$

This completes the proof. □

The above result only gives the simple lower bounds of competition number of q-rung orthopair fuzzy graphs for the case when q-ROFGs are triangle-free. In crisp graph theory, Opsut [40] improved this result by defining both upper and lower bounds for any graph in connection with the size of smallest edge clique cover. It can be generalized for q-rung orthopair fuzzy graphs as follows:

Lemma 1.

If $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is a connected q-rung orthopair fuzzy graph defined on $G=(A,B)$ with no q-ROF triangle, then the size of smallest q-rung orthopair fuzzy edge clique cover of $\mathcal{G}$ is exactly equal to the number of edges in $\mathcal{G}.$

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be a connected q-rung orthopair fuzzy graph defined on $G=(A,B)$. Let ${\mathcal{P}}_i$ be the q-ROF cliques of $\mathcal{G}.$ Since $\mathcal{G}$ has no q-ROF triangle, therefore, each q-ROF clique ${\mathcal{P}}_i$ must have at most two q-ROF vertices $u_i$ and $v_i$ in order to get complete q-ROF induced subgraph of $\mathcal{G}.$ Thus, the smallest q-rung orthopair fuzzy edge clique cover has q-ROF cliques equal to the number of edges of $\mathcal{G}.$ Hence, the size of smallest q-ROF edge clique cover is $|B|,$ i.e., ${\theta }_e(\mathcal{G})=|B|.$ □

Theorem 14.

For any q-rung orthopair fuzzy graph $\mathcal{G},{\theta }_e(\mathcal{G})+|A|-2\le k(\mathcal{G})\le {\theta }_e(\mathcal{G}).$

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be a q-rung orthopair fuzzy graph defined on $G=(A,B).$ Suppose that $\mathcal{G}\cup {\mathcal{I}}_r$ is q-rung orthopair fuzzy competition graph constructed according to the Algorithm 1. Label the integers $1,2,\dots ,|A|+k(\mathcal{G})$ to q-ROF vertices of $\mathcal{G}$ so that every q-ROF arc goes from lower integer to higher integer in $\overrightarrow{\mathcal{D}}$. In particular, the q-ROF vertex labeled 1 has no incoming q-ROF arc and q-ROF vertex labeled 2 has only one incoming q-ROF arc. Consider the set $P=\{3,4,\dots ,|A|+k(\mathcal{G})\}$ and for each $i\in P$ the set ${\mathcal{P}}_i=\{(u,{\mu }_{\mathcal{A}}(u),{\nu }_{\mathcal{B}}(u)):\overrightarrow{ui}\in \mathcal{B}\}.$ Then, since $\mathcal{G}\cup {\mathcal{I}}_r$ is the competition graph for a digraph, each ${\mathcal{P}}_i$ is a q-ROF clique of $\mathcal{G}.$ Moreover, the subgraphs induced by each ${\mathcal{P}}_i$ must cover all q-ROF edges of $\mathcal{G}.$ If ${\theta }_e(\mathcal{G})$ denotes the size of smallest edge clique cover of $\mathcal{G}.$ Then,

$${\theta }_e(\mathcal{G})\le |P|=|A|+k(\mathcal{G})-2$$

or

$$k(\mathcal{G})\ge {\theta }_e(\mathcal{G})-|A|+2.$$

(8)

Which completes the proof of lower bounds of the competition number of $\mathcal{G}.$

To prove its upper bounds, consider the q-ROF cliques ${\mathcal{P}}_i(1\le i\le {\theta }_e(\mathcal{G}))$ belongs to smallest edge clique cover of $\mathcal{G}.$ Construct a digraph $\overrightarrow{\mathcal{D}}$ on the vertices q-ROFG of $\mathcal{G}\cup {\mathcal{I}}_r$ according to Algorithm 1, where the added isolated vertices are labeled $i,1\le i\le r.$ Then $\overrightarrow{\mathcal{D}}$ is acyclic and $\mathcal{G}\cup {\mathcal{I}}_r$ is q-ROF competition graph for $\overrightarrow{\mathcal{D}}.$ So by definition of competition number of q-ROF graph,

$$k(\mathcal{G})\le {\theta }_e(\mathcal{G}).$$

Hence, ${\theta }_e(\mathcal{G})+|A|-2\le k(\mathcal{G})\le {\theta }_e(\mathcal{G}).$ This completes the proof. □

4.2. m-Step Competition Number of q-ROFGs

Cho et al. in [8] use the notion of m-step competition number analogous to the competition number of Roberts [37]. They defined the m-step competition number of G as the smallest number r such that $\mathcal{G}$ together with r isolated vertices is m-step competition graph of an acyclic digraph. Analogous to this eminent concept, we now define it as orthopair membership grades.

Theorem 15.

Let $\mathcal{G}$ be a q-rung orthopair fuzzy graph and $m\ge 1$ is an integer, then adding a sufficient number of r isolated q-ROF vertices ${\delta }_{uv}^i(1\le i\le m),$ for each edge of $\mathcal{G}$ such that

$$\left\{\begin{array}{c}{\mu }_{\mathcal{P}}({\delta }_{uv}^1)={\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v),{\mu }_{\mathcal{P}}({\delta }_{uv}^i)={\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v)\wedge {\mu }_{\mathcal{P}}({\delta }_{uv}^1)\wedge \dots \wedge {\mu }_{\mathcal{P}}({\delta }_{uv}^{i-1}),\hfill \\ {\nu }_{\mathcal{P}}({\delta }_{uv}^1)={\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v),{\nu }_{\mathcal{P}}({\delta }_{uv}^i)={\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v)\vee {\mu }_{\mathcal{P}}({\delta }_{uv}^1)\vee \dots \vee {\nu }_{\mathcal{P}}({\delta }_{uv}^{i-1})\hfill \end{array}\right.$$

produces an m-step q-rung orthopair fuzzy competition graph $\mathcal{G}\cup {\mathcal{I}}_r$ of some acyclic digraph $\overrightarrow{\mathcal{D}}$ for all $2\le i\le m.$

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be a q-rung orthopair fuzzy graph where $\mathcal{A}=({\mu }_{\mathcal{A}},{\nu }_{\mathcal{A}})$ is q-rung orthopair fuzzy set on X and $\mathcal{B}=({\mu }_{\mathcal{B}},{\nu }_{\mathcal{B}})$ is a q-rung orthopair fuzzy relation on $X.$ Construct a digraph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ as follows: Let $u,v\in X$ be any two vertices of $\mathcal{G}$ such that ${\mu }_{\mathcal{P}}(uv)>0$ or ${\nu }_{\mathcal{P}}(uv)>0.$ For each edge $uv\in \mathcal{G},$ add vertices ${\delta }_{uv}^i,(1\le i\le m)$ remove the edge $uv$ and draw directed paths from u and v to ${\delta }_{uv}^m$ of length $m.$ The digraph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ whose q-ROF vertices consists of vertices of $\mathcal{G}$ plus m q-ROF isolated vertices ${\delta }_{uv}^i(1\le i\le m)$ for each edge $uv$ in $\mathcal{G},$ can be defined as

$$\mathcal{P}=\mathcal{A}\cup {\mathcal{I}}_r$$

such that for $2\le i\le m,$

$$\left\{\begin{array}{c}{\mu }_{\mathcal{P}}({\delta }_{uv}^1)={\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v),{\mu }_{\mathcal{P}}({\delta }_{uv}^i)={\mu }_{\mathcal{P}}(u)\wedge {\mu }_{\mathcal{P}}(v)\wedge {\mu }_{\mathcal{P}}({\delta }_{uv}^1)\wedge \dots \wedge {\mu }_{\mathcal{P}}({\delta }_{uv}^{i-1}),\hfill \\ {\nu }_{\mathcal{P}}({\delta }_{uv}^1)={\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v),{\nu }_{\mathcal{P}}({\delta }_{uv}^i)={\nu }_{\mathcal{P}}(u)\vee {\nu }_{\mathcal{P}}(v)\vee {\mu }_{\mathcal{P}}({\delta }_{uv}^1)\vee \dots \vee {\nu }_{\mathcal{P}}({\delta }_{uv}^{i-1})\hfill \end{array}\right.$$

and

$$\overrightarrow{\mathcal{Q}}=\bigcup _{\overrightarrow{uv}}\left[\left\{\overrightarrow{u{\delta }_{uv}^1},\overrightarrow{v{\delta }_{uv}^1}\right\}\cup \bigcup _{i=1}^{m-1}\left\{\overrightarrow{{\delta }_{uv}^i{\delta }_{uv}^{i+1}}\right\}\right]$$

such that power of competition of q-ROF vertices u and v towards the vertex ${\delta }_{uv}^1$ is

$$\left\{\begin{array}{c}{({\mathbb{P}}_{\overrightarrow{u{\delta }_{uv}^1}})}_{\mu }={({\mathbb{P}}_{\overrightarrow{v{\delta }_{uv}^1}})}_{\mu }=\frac{{\mu }_{\mathcal{B}}(uv)}{{\mu }_{\mathcal{P}}({\delta }_{uv}^1)},\hfill \\ {({\mathbb{P}}_{\overrightarrow{u{\delta }_{uv}^1}})}_{\nu }={({\mathbb{P}}_{\overrightarrow{v{\delta }_{uv}^1}})}_{\nu }=\frac{{\nu }_{\mathcal{B}}(uv)}{{\nu }_{\mathcal{P}}({\delta }_{uv}^1)}\hfill \end{array}\right.$$

and power of competition of q-ROF vertex ${\delta }_{uv}^i$ towards ${\delta }_{uv}^{i+1}$ are

$$\left\{\begin{array}{c}{({\mathbb{P}}_{\overrightarrow{{\delta }_{uv}^i{\delta }_{uv}^{i+1}}})}_{\mu }=\frac{{\mu }_{\mathcal{B}}(uv)}{{\mu }_{\mathcal{P}}({\delta }_{uv}^{i+1})},\hfill \\ {({\mathbb{P}}_{\overrightarrow{{\delta }_{uv}^i{\delta }_{uv}^{i+1}}})}_{\nu }=\frac{{\nu }_{\mathcal{B}}(uv)}{{\nu }_{\mathcal{P}}({\delta }_{uv}^{i+1})},\hfill \end{array}\right.$$

for all $2\le i\le m.$

Continuing the process, we get an acyclic digraph $\overrightarrow{\mathcal{D}}$ which gives an m-step q-rung orthopair fuzzy competition graph ${\mathcal{C}}^m(\overrightarrow{\mathcal{D}})=\mathcal{G}\cup {\mathcal{I}}_r,$ where ${\mathcal{I}}_r$ is q-rung orthopair fuzzy set of r isolated q-ROF vertices in $\mathcal{G}.$ This completes the proof. □

The method of constructing corresponding m-step digraph $\overrightarrow{\mathcal{D}}$ of a q-ROFG is demonstrated in Algorithm 2. The complexity of Algorithm 2 is $O(n^{2}m).$

Algorithm 2.q-RUNG ORTHOPAIR FUZZY DIGRAPH INPUT: A q-ROFG $\mathcal{G}=(\mathcal{A},\mathcal{B}).$ OUTPUT: A q-ROF directed graph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}}).$   procedure Digraph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$   for$i:=1ton$do    for$j:=i+1ton$do     if${\mu }_{\mathcal{B}}(u_i{u}_j)>0$ or ${\nu }_{\mathcal{B}}(u_i{u}_j)>0$ then      add ${\delta }_{u_i{v}_j}^t(1\le t\le m)$ such that      ${\mu }_{\mathcal{P}}({\delta }_{u_i{v}_j}^1)={\mu }_{\mathcal{P}}(u_i)\wedge {\mu }_{\mathcal{P}}(u_j)$      ${\nu }_{\mathcal{P}}({\delta }_{u_i{v}_j}^1)={\nu }_{\mathcal{P}}(u_i)\vee {\nu }_{\mathcal{P}}(u_j)$      $t:=1$      while$t\le m$do       ${\mu }_{\mathcal{P}}({\delta }_{u_i{u}_j}^t)={\mu }_{\mathcal{P}}(u_i)\wedge {\mu }_{\mathcal{P}}(u_j)\wedge {\mu }_{\mathcal{P}}({\delta }_{u_i{u}_j}^1)\wedge \dots \wedge {\mu }_{\mathcal{P}}({\delta }_{u_i{u}_j}^{t-1})$       ${\nu }_{\mathcal{P}}({\delta }_{u_i{u}_j}^t)={\nu }_{\mathcal{P}}(u_i)\vee {\nu }_{\mathcal{P}}(u_j)\vee {\mu }_{\mathcal{P}}({\delta }_{u_i{u}_j}^1)\vee \dots \vee {\nu }_{\mathcal{P}}({\delta }_{u_i{u}_j}^{t-1})$       $t:=t+1$      end while     end if    end for   end for   for$i:=1ton$do    for$j:=i+1ton$do     if${\mu }_{\mathcal{B}}(u_i{u}_j)>0$ or ${\nu }_{\mathcal{B}}(u_i{u}_j)>0$ then      remove $u_i{u}_j,$ draw directed paths $\overrightarrow{P_{u_i{\delta }_{u_i{v}_j}^m}^m}$ and $\overrightarrow{P_{u_j{\delta }_{u_i{u}_j}^m}^m}$ such that                ${({\mathbb{P}}_{\overrightarrow{u{\delta }_{uv}^1}})}_{\mu }={({\mathbb{P}}_{\overrightarrow{v{\delta }_{uv}^1}})}_{\mu }=\frac{{\mu }_{\mathcal{B}}(uv)}{{\mu }_{\mathcal{P}}({\delta }_{uv}^1)}$      ${({\mathbb{P}}_{\overrightarrow{u{\delta }_{uv}^1}})}_{\nu }={({\mathbb{P}}_{\overrightarrow{v{\delta }_{uv}^1}})}_{\nu }=\frac{{\nu }_{\mathcal{B}}(uv)}{{\nu }_{\mathcal{P}}({\delta }_{uv}^1)}$      $t:=1$      while$t\le m$do       ${({\mathbb{P}}_{\overrightarrow{{\delta }_{u_i{u}_j}^{t-1}{\delta }_{u_i{u}_j}^t}})}_{\mu }=\frac{{\mu }_{\mathcal{B}}(u_i{u}_j)}{{\mu }_{\mathcal{P}}({\delta }_{u_i{u}_j}^t)}$       ${({\mathbb{P}}_{\overrightarrow{{\delta }_{u_i{u}_j}^{t-1}{\delta }_{u_i{u}_j}^t}})}_{\nu }=\frac{{\nu }_{\mathcal{B}}(u_i{u}_j)}{{\nu }_{\mathcal{P}}({\delta }_{u_i{u}_j}^t)}$       $t:=t+1$      end while     end if    end for   end for   end procedure

Remark 2.

In Algorithm 2, the only information about q-ROF arcs of directed paths of $\overrightarrow{\mathcal{D}}$ are the power of competition of q-ROF vertices u and v towards m-step common q-ROF prey. Thus, q-rung orthopair fuzzy m-step out-neighborhoods of vertices can be defined in a similar manner by taking into account the power of competition of arcs of directed paths instead of their membership grades.

Theorem 15 naturally guides us to define m-step competition number $k^m(\mathcal{G})$ of q-rung orthopair fuzzy graph $\mathcal{G}.$

Definition 31.

Let $\mathcal{G}$ be any q-rung orthopair fuzzy graph. The smallest possible number of isolated q-ROF vertices which when add in $\mathcal{G}$ leads an m-step q-rung orthopair fuzzy competition graph of some acyclic digraph is called m-step competition number of $\mathcal{G}$, denoted by $k^m(\mathcal{G}).$

Cho et al. [8] proved a relation between m-step competition number and competition number of crisp graphs. We now generalize this relation for q-rung orthopair fuzzy graphs.

Theorem 16.

If $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is any q-rung orthopair fuzzy graph, then $k(\mathcal{G})\le k^m(\mathcal{G}),$ where m is a positive integer.

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is any q-rung orthopair fuzzy graph and $k^m(\mathcal{G})$ be the m-step competition number of $\mathcal{G}.$ Then there exists an acyclic q-ROF digraph $\overrightarrow{\mathcal{D}}$ such that ${\mathcal{C}}^m(\overrightarrow{\mathcal{D}})=\mathcal{C}(\overrightarrow{{\mathcal{D}}^m}).$ The q-ROF digraph $\overrightarrow{{\mathcal{D}}^m}$ is clearly acyclic and by the definition of competition number of q-ROFG $\mathcal{G},$ it follows that

$$k(\mathcal{G})\le k^m(\mathcal{G}).$$

This completes the proof. □

Theorem 17.

If $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is a q-rung orthopair fuzzy graph defined on $G=(A,B)$, then $k^m(\mathcal{G})\le m\times |B|,$ where m is a positive integer.

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be any q-rung orthopair fuzzy graph defined on $G=(A,B).$ By definition of m-step competition number of q-ROFG $\mathcal{G},$ we have to add m vertices for at most each q-ROF edge. Since there are $|B|$ edges in $\mathcal{G},$ therefore at most $m\times |B|$ vertices must add in $\mathcal{G}$ to make it q-ROF competition graph of acyclic digraph constructed according to Algorithm 2. Hence,

$$k^m(\mathcal{G})\le m\times |B|.$$

This completes the proof. □

Theorem 18.

If $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is a q-rung orthopair fuzzy graph without isolated q-ROF vertices, then $max\{m,{\theta }_e(\mathcal{G})+|A|-m+1\}\le k^m(\mathcal{G})\le m\times {\theta }_e(\mathcal{G}),$ where m is a positive integer.

Proof. 

Let $\mathcal{G}=(\mathcal{A},\mathcal{B})$ be any q-rung orthopair fuzzy graph defined on $G=(A,B),$ where $|A|=n.$ Let $\mathcal{C}=\{{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_l\}$ be a smallest q-ROF edge clique cover of $\mathcal{G}.$ Then ${\theta }_e(\mathcal{G})=l.$ Construct an acyclic directed graph $\overrightarrow{\mathcal{D}}$ as according to Algorithm 2. Then, it can easily be checked that $\overrightarrow{\mathcal{D}}$ is acyclic and ${\mathcal{C}}^m(\overrightarrow{\mathcal{D}})=\mathcal{G}\cup {\mathcal{I}}_{lm}.$ Thus,

$$k^m(\mathcal{G})\le m\times {\theta }_e(\mathcal{G}).$$

Now, consider an acyclic q-ROF digraph $\overrightarrow{\mathcal{D}}$ so that $\mathcal{G}$ along with $k^m(\mathcal{G})$ isolated q-ROF vertices defines ${\mathcal{C}}^m(\overrightarrow{\mathcal{D}}).$ We can assign an acyclic labeling to $\overrightarrow{\mathcal{D}}$ as $v_1,v_2,\dots ,v_{n+k}$ such that $v_{n+1},v_{n+2},\dots ,v_{n+k}$ are the k added isolated q-ROF vertices. Then $v_1,v_2,\dots ,v_{m+1}$ cannot be exerted as m-step q-ROF prey. Despite this, since two distinct q-ROF cliques in $\mathcal{C}$ should prey on different m-step common q-ROF prey, there should be at least ${\theta }_e(\mathcal{G})$ distinct q-ROF vertices operated as m-step common q-ROF prey. Therefore,

$$k^m(\mathcal{G})\ge {\theta }_e(\mathcal{G})+|A|-m+1.$$

To conclude the proof of first inequality, we notice that $v_n$ is adjacent to at least one q-ROF vertex of $\mathcal{G},$ as $\mathcal{G}$ has no isolated q-ROF vertices. Consequently, $v_n$ should have an m-step common q-ROF prey in $\overrightarrow{\mathcal{D}}.$ Since any q-ROF vertex possessing a label less than n cannot be an q-ROF out-neighbor of $v_n$ in $\overrightarrow{\mathcal{D}},$ it follows that $k^m(\mathcal{G})\ge m.$

Hence,

$$k^m(\mathcal{G})\ge max\{m,{\theta }_e(\mathcal{G})+|A|-m+1\}.$$

□

The special case of the above theorem (i.e., for $m=1$) is proved by Opsut [40] for any crisp graph $G.$

The next corollary is an instant consequence of the above theorem.

Corollary 1.

For any complete q-rung orthopair fuzzy graph ${\mathcal{K}}_n$ with $n\ge 2,k^m({\mathcal{K}}_n)=m.$

5. Application

Competition graphs are becoming increasingly significant as they can apply to many areas in which there occurs competition between entities. A general outlook of this fact as a source of an interesting graph theoretical idea that can be seen in the soil ecosystem. The q-rung orthopair fuzzy sets provide system modelers with more freedom and is less restrictive in permissible membership grades. To fully understand the concept of q-rung orthopair fuzzy competition graphs, we now display an important application of the competition graph under the Pythagorean fuzzy environment (taking $q=2$) to observe the strength of competition between plant-associated bacteria in the rhizosphere, or the soil ecosystem, with an algorithm.

5.1. Plant-Bacterial Interactions in Soil Ecosystem

The rhizosphere represents a nutrient-rich habitat for microorganisms. Soil is a hub of countless living organisms that account of the proper maintenance of balanced nutrients in the soil ecosystem as well as for better yield and growth of plants. These organisms include bacteria, fungi, soil algae or actinomycete. Among them, bacteria are of great importance with respect to soil fertility and plant health. They may be beneficial or hazardous for plants and the soil ecosystem. There are some bacteria commonly known as plant growth-promoting rhizobacteria (PGPR) which have growth-stimulating potential and enhance antioxidant enzymatic activity in plants, promote disease suppression and reduce stress susceptibility [44]. Contrary to this, pathogenic microorganisms affecting plant health are a major and chronic threat to food production and ecosystem stability worldwide. Thus, there are some bacteria which are reported as pathogenic for soil environment, plant growth, and development. These soil-borne bacteria inhibit plant growth due to the release of some toxic compounds in the rhizosphere. The inhibition in plant growth ultimately results in the lower yield of plants [45].

The Figure 17 explores competition among plant-associated bacteria in soil ecosystem.

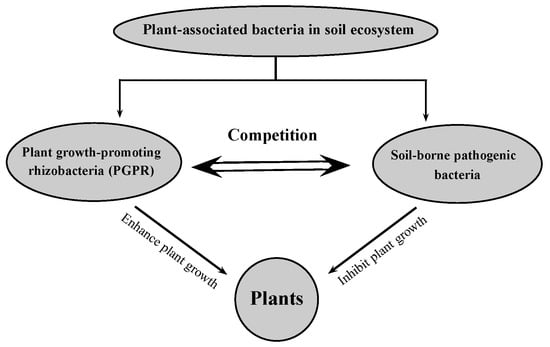
Figure 17. Potential role of plant-associated bacteria in soil ecosystem.

The ameliorating effects of PGPR and deleterious effects of phytopathogenic bacteria not only result in the promotion and retardation of growth parameters of plants, respectively, but also biochemical parameters such as chlorophyll content, proline content, carbohydrates, lipids, protein contents, and phenolic compounds. Hence, these facts employ the critiques made by several researchers that there is a competition between PGPR and soil-borne phytopathogenic bacteria which are present in soil ecosystem. These both types of bacteria compete to have their domination effect on plants. Side by side, there is also severe competition between all PGPR and in between all soil-borne phytopathogenic bacteria with each other to influence the growth of plants.

Consider an example of 12 bacteria in soil ecosystem. The set of PGPR {Bacillus pumulis, Bacillus atrophaeus, Staphylococcus lentus, Bacillus cereus, Achromobacter piechaudii, Azospirillum brasilense, Pseudomonas fluorescens} and phytopathogenic bacteria {Agrobacterium tumefaciens, Xanthomonas oryzae, Xylella fastidiosa, Pseudomonas syringae, Ralstonia solanacearum} are competing for following set of growth and biochemical parameters of plant {Shoot length, Root length, Plant biomass, Number of leaves, Chlorophyll content, Protein content, Proline content, Auxin content}. The estimated values for these growth and biochemical parameters with respect to selected bacterial species are given in Table 2.

Table 2. Impact of Bacterial Species on Plant Parameters.

Plant		Bacterial	Effectiveness of Bacterial Species
Parameters		Species	on Plant Parameters
Plant growth parameters	Shoot length	B. pumulis	$13.3$ inches
		A. brasilense	11.7 inches
		P. fluorescens	14.1 inches
		R. solanacearum	3.2 inches
	Root length	B. cereus	8.9 inches
		A. piechaudii	11.6 inches
	Plant biomass	B. atrophaeus	7.2 g
		S. lentus	9.6 g
		P. syringae	1.7 g
	No. of leaves	S. lentus	12
		A. brasilense	10
		P. fluorescens	15
Biochemical parameters	Proline content	A. tumefaciens	35 $\mathsf{\mu }$g/g
		X. oryzae	40 $\mathsf{\mu }$g/g
		X. fastidiosa	51 $\mathsf{\mu }$/g
	Protein content	X. fastidiosa	43 $\mathsf{\mu }$g/g
		P. syringae	59 $\mathsf{\mu }$g/g
	Auxin content	B. pumulis	266 $\mathsf{\mu }$g/g
		R. solanacearum	68 $\mathsf{\mu }$g/g
	Chlorophyll content	A. brasilense	6.7 $\mathsf{\mu }$g/g
		R. solanacearum	2.9 $\mathsf{\mu }$g/g

A Pythagorean fuzzy digraph presenting such a soil ecosystem, shown in Figure 18, displays bacterial competition for particular parameters resulting in plant’s growth.

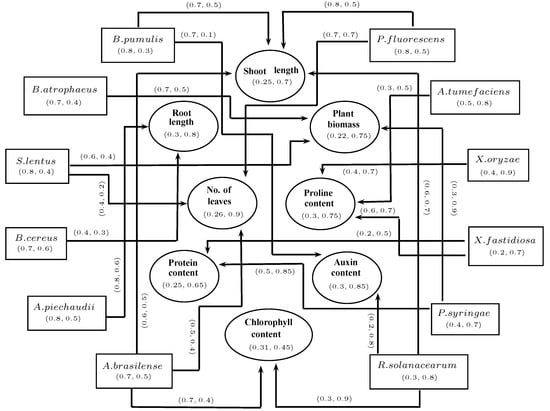
Figure 18. Pythagorean fuzzy soil ecosystem digraph.

The membership degree of each soil-borne phytopathogenic bacteria represents the extent of inhibition and non-membership degree represents the extent of non-inhibition in plant growth. The phytopathogenic bacteria can be represented by orthopair as:

(Inhibition in plant growth, Not inhibition in plant growth).

Moreover, the participation of plant parameters in the growth of a plant is shown by their membership values, and non-participation is represented by its non-membership values. For example, the orthopair corresponding to shoot length is $(0.25,0.7)$. The support for membership $‘0.25$’ shows that the role of shoot length is $6.25\%$ in growth of plant, $49\%$ of it does not take part in growth and there is hesitation of about $44.75\%$.

The arcs in the Pythagorean fuzzy digraph indicate the influence of bacteria on plant growth and biochemical parameters. For example, the bacteria ‘Bacillus pumulis’ has the influence on two parameters, namely shoot length and auxin content. It can influence both equally as the degree of membership $(\mu )$ is $0.7$ while having different degrees of non-membership $(\nu )$ and hesitation $(\pi =1-\mu -\nu ).$ Thus, the influential approach of bacteria towards plant parameters can be displayed in the form of an orthopair:

(Effectiveness of bacteria on plant parameters, Ineffectiveness of bacteria on plant parameters).

The Pythagorean fuzzy competition graph can be constructed to investigate the strength of competition between bacteria for growth of plant. The Pythagorean fuzzy out-neighborhoods of bacteria are displayed in Table 3.

Table 3. Pythagorean fuzzy out-neighborhoods of bacteria.

Bacteria	${\mathcal{N}}^{+}(\mathbf{Bacteria})$
Bacillus pumulis	{(Shoot length, 0.7, 0.5), (Auxin content, 0.7, 0.1)}
Bacillus atrophaeus	{(Plant biomass, 0.7, 0.5)}
Staphylococcus lentus	{(Plant biomass, 0.6, 0.4), (No. of leaves, 0.4, 0.2)}
Bacillus cereus	{(Root length, 0.4, 0.3)}
Achromobacter piechaudii	{(Root length, 0.8, 0.6)}
Azospirillum brasilense	{(Shoot length, 0.6, 0.5), (No. of leaves, 0.5, 0.4), (Chlorophyll content, 0.7, 0.4)}
Pseudomonas fluorescens	{(Shoot length, 0.8, 0.5), (No. of leaves, 0.7, 0.7)}
Agrobacterium tumefaciens	{(Proline content, 0.3, 0.5)}
Xanthomonas oryzae	{(Proline content, 0.4, 0.7)}
Xylella fastidiosa	{(Proline content, 0.6, 0.7), (Protein content, 0.2, 0.5)}
Pseudomonas syringae	{(Plant biomass, 0.3, 0.9), (Protein content, 0.5, 0.85)}
Ralstonia solanacearum	{(Shoot length, 0.6, 0.7), (Auxin content, 0.2, 0.8), (Chlorophyll content, 0.3, 0.9)}

This is an acyclic Pythagorean fuzzy digraph of the soil ecosystem/rhizosphere in which the orthopair assigned to each vertex and arc indicates its support for membership (membership degree) and support against membership (non-membership degree) under Pythagorean fuzzy environment. The membership degree of each PGPR represents the extent of amelioration and non-membership degree represents extent of non-amelioration in the growth of a plant. The PGPR can be represented by a pair of disjoint sets called orthopair:

(Amelioration in plant growth, Not amelioration in plant growth).

The corresponding competition graph of Pythagorean fuzzy soil ecosystem Figure 18 is displayed in Figure 19.

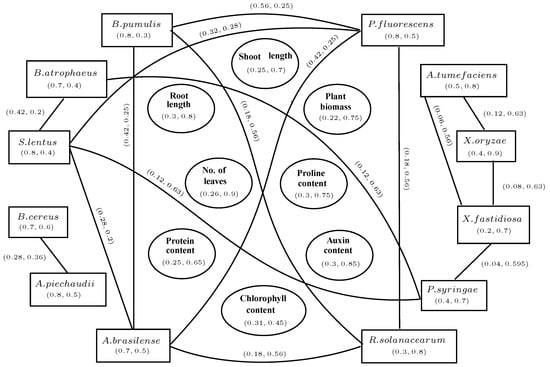
Figure 19. Pythagorean Fuzzy Competition Graph.

The edge connecting two bacteria in Pythagorean fuzzy competition graph highlights that both bacteria are competing for a particular biochemical or growth parameter of plant. Table 4 gives the strength of competition of each bacterium $‘b$’ for parameter $‘p$’ with respect to plant growth promotion. For instance, the bacteria B. atrophaeus, S. lentus and P. syringae are competing for the growth parameter “plant biomass” with strengths $1.685,1.685$ and $1.75$ respectively. We see that P. syringae has maximum strength of competition among these bacteria. Consequently, the bacterium “P. syringae” has more influential power on the growth parameter “plant biomass” as compared to bacteria B. atrophaeus and S. lentus and finally it inhibits the biomass of plant being a destructive phytopathogenic bacteria. In other words, the toxicity of phytopathogenic bacteria “P. syringae” is more effective/dominating than growth-promoting potential of PGPR B. atrophaeus and S. lentus.

Table 4. Strength of competition of bacteria for plant parameters.

Plant Parameters	Bacteria	Bacteria in Competition	R (Bacteria, Parameter)	S (Bacteria, Parameter)
Shoot length	B. pumulis	A. brasilense, P. fluorescens, R. solanacearum	(0.387, 0.353)	1.74
	A. brasilense	B. pumulis, P. fluorescens, R. solanacearum	(0.34, 0.353)	1.693
	P. fluorescens	B. pumulis, A. brasilense, R. solanacearum	(0.387, 0.353)	1.74
	R. solanacearum	B. pumulis, A. brasilense, P. fluorescens	(0.18, 0.56)	1.74
Root length	B. cereus	A. piechaudii	(0.28, 0.36)	1.64
	A. piechaudii	B. cereus	(0.28, 0.36)	1.64
Plant biomass	B. atrophaeus	S. lentus, P. syringae	(0.27, 0.415)	1.685
	S. lentus	B. atrophaeus, P. syringae	(0.27, 0.415)	1.685
	P. syringae	B. atrophaeus, S. lentus	(0.12, 0.63)	1.75
Number of leaves	S. lentus	A. brasilense, P. fluorescens	(0.3, 0.24)	1.54
	A. brasilense	S. lentus, P. fluorescens	(0.35, 0.225)	1.575
	P. fluorescens	S. lentus, A. brasilense	(0.37, 0.265)	1.635
Proline content	A. tumefaciens	X. oryzae, X. fastidiosa	(0.09, 0.595)	1.685
	X. oryzae	A. tumefaciens, X. fastidiosa	(0.1, 0.63)	1.73
	X. fastidiosa	A. tumefaciens, X. oryzae	(0.07, 0.595)	1.665
Protein content	X. fastidiosa	P. syringae	(0.4, 0.595)	1.995
	P. syringae	X. fastidiosa	(0.4, 0.595)	1.995
Auxin content	B. pumulis	R. solanacearum	(0.18, 0.56)	1.74
	R. solanacearum	B. pumulis	(0.18, 0.56)	1.74
Chlorophyll content	A. brasilense	R. solanacearum	(0.18, 0.56)	1.74
	R. solanacearum	A. brasilense	(0.18, 0.56)	1.74

In Table 4, some bacteria have equal maximum strength of competition for plant parameters. To assess which one has dominant influence on plant parameters, their support for amelioration or inhibition can be taken into account. For example, bacteria A. brasilense and R. solanacearum are competing for biochemical parameter “chlorophyll content” with same strength $1.74$. The support for amelioration of A. brasilense is $49\%$ which is more than its support for not amelioration i.e., $25\%$, while the bacterium R. solanacearum has $9\%$ support for inhibition and $64\%$ support for non-inhibition. Thus, we conclude that the bacterium “A. brasilense” is more effective to enhance the chlorophyll content in the plant as compared to R. solanacearum, which leads to inhibition of chlorophyll content.

The method for constructing a q-rung orthopair fuzzy competition graph of a digraph depicting plant-bacterial interactions in the soil ecosystem and to find strength of competition between bacteria is illustrated in Algorithm 3. The complexity of Algorithm 3 is $O(n^2+l{r}_k).$

Algorithm 3. STRENGTH OF COMPETITION OF BACTERIA INPUT: A q-ROF digraph $\overrightarrow{\mathcal{D}}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$, where $\mathcal{P}=\{(u_i,{\mu }_{\mathcal{P}}(u_i),{\nu }_{\mathcal{P}}(u_i)):1\le i\le n(=l+m)\},u_i^{\prime }s$ involve $‘m$’ bacteria and $‘l$’ plant parameters. OUTPUT: Strength of competition of bacteria $b_j,1\le j\le m$ for plant parameters $p_k,1\le k\le l.$   procedure Strength of competition $S(b,p)$   for$i:=1ton$do    for$j:=i+1ton$do     if${\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{u}_j})>0$ or ${\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{u}_j}>0$ then      $(u_j,{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{u}_j}),{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{u}_j}))\in {\mathcal{N}}_2^{+}(u_i)$     else      $(u_j,{\mu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{u}_j}),{\nu }_{\overrightarrow{\mathcal{Q}}}(\overrightarrow{u_i{u}_j}))\notin {\mathcal{N}}_2^{+}(u_i)$     end if    end for   end for   for$i:=1ton$do    for$j:=i+1ton$do     if${\mathcal{N}}_2^{+}(u_i)\cap {\mathcal{N}}_2^{+}(u_j)\ne \mathsf{\varnothing }$then      ${\mu }_{\mathcal{B}}(u_i{u}_j):=({\mu }_{\mathcal{P}}(u_i)\wedge {\mu }_{\mathcal{P}}(u_j))\times h_{\mu }({\mathcal{N}}_2^{+}(u_i)\cap {\mathcal{N}}_2^{+}(u_j))$      ${\nu }_{\mathcal{B}}(u_i{u}_j):=({\nu }_{\mathcal{P}}(u_i)\wedge {\nu }_{\mathcal{P}}(u_j))\times h_{\nu }({\mathcal{N}}_2^{+}(u_i)\cap {\mathcal{N}}_2^{+}(u_j))$     else      $({\mu }_{\mathcal{B}}(u_i{u}_j),{\nu }_{\mathcal{B}}(u_i{u}_j))=(0,0)$     end if    end for   end for   Number of bacteria ${b_j}_k$ competing for $p_k:=r_k$   for$k:=1tol$do    for$j:=1to{r}_k$do     $R_{\mu }({b_j}_k,p_k):={\mu }_{\mathcal{B}}({b_j}_k{b_1}_k)+{\mu }_{\mathcal{B}}({b_j}_k{b_2}_k)+\dots +{\mu }_{\mathcal{B}}({b_j}_k{b_{j-1}}_k)+{\mu }_{\mathcal{B}}({b_j}_k{b_{j+1}}_k)+{\mu }_{\mathcal{B}}({b_j}_k{b_{r_k}}_k)$     $R_{\nu }({b_j}_k,p_k):={\nu }_{\mathcal{B}}({b_j}_k{b_1}_k)+{\nu }_{\mathcal{B}}({b_2}_k)+\dots +{\nu }_{\mathcal{B}}({b_j}_k{b_{j-1}}_k)+{\nu }_{\mathcal{B}}({b_j}_k{b_{j+1}}_k)+{\nu }_{\mathcal{B}}({b_j}_k{b_{r_k}}_k)$     $R({b_j}_k,p_k):=\frac{(R_{\mu }({b_j}_k,p_k),R_{\nu }({b_j}_k,p_k))}{r_k-1}$     $S({b_j}_k,p_k):=R_{\mu }({b_j}_k,p_k)+1+R_{\nu }({b_j}_k,p_k)$    end for   end for   end procedure

6. Conclusions

One of the most important research directions is how to express uncertain information in human analysis. IFSs and PFSs are both a good way to deal with fuzzy information as pairs of disjoint sets, called orthopairs. The q-ROFSs, superior to IFSs and PFSs, broaden the space of vague information. Our current work has dealt with competition graphs under the q-rung orthopair fuzzy environment. The present investigation has provided more precision, pliability, and consistency for species and prey in a food web. Thus, a lot of competition in the real world can be designed by q-ROFCGs due to its notable characteristics $\mu {(x)}^q+\nu {(x)}^q\le 1(q\ge 1),$ which provides a substantial benefit in modeling human knowledge. The proposed concept of the q-rung orthopair fuzzy clique can well express several real-world problems. This paper has explored one example in this context. Moreover, the study has clearly analyzed the concept of competition number of q-ROFGs, which governs the altering of any q-ROFG into corresponding q-ROFCG of some digraph. In conclusion, we have explored the necessity of q-ROFCGs with an application in soil ecosystem and designed an algorithm to evaluate the strength of competition among bacteria. In future research, we will extend this work to (1) interval-valued q-rung orthopair fuzzy competition graphs; (2) q-rung orthopair fuzzy competition hypergraphs; and (3) q-rung picture fuzzy competition graphs.