Effect of Slip Surface’s Continuity on Slope Dynamic Stability Based on Infinite Slope Model
Abstract
:1. Introduction
2. Modeling and Solutions
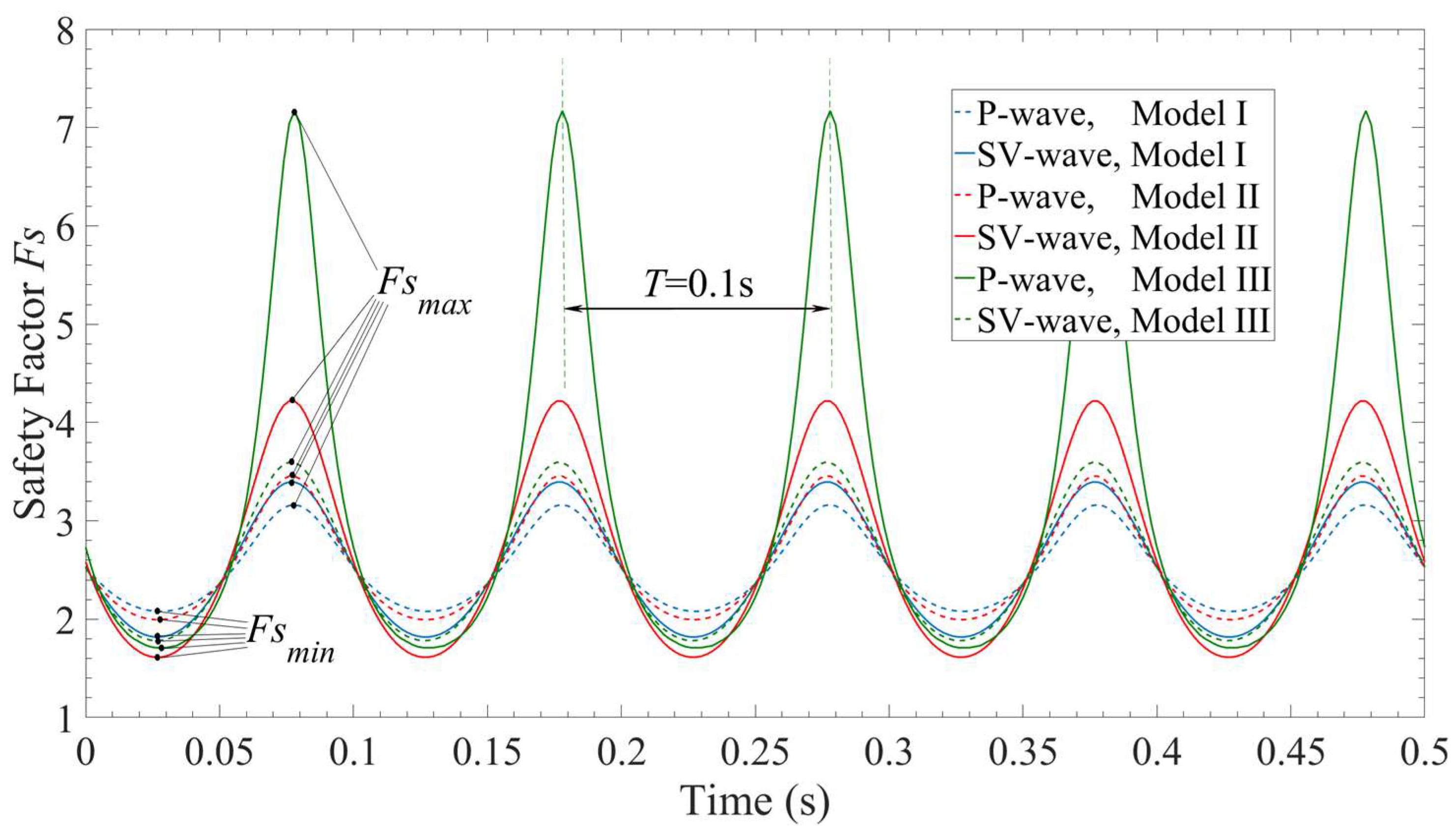
3. Dynamic Response of Instantaneous Safety Factor
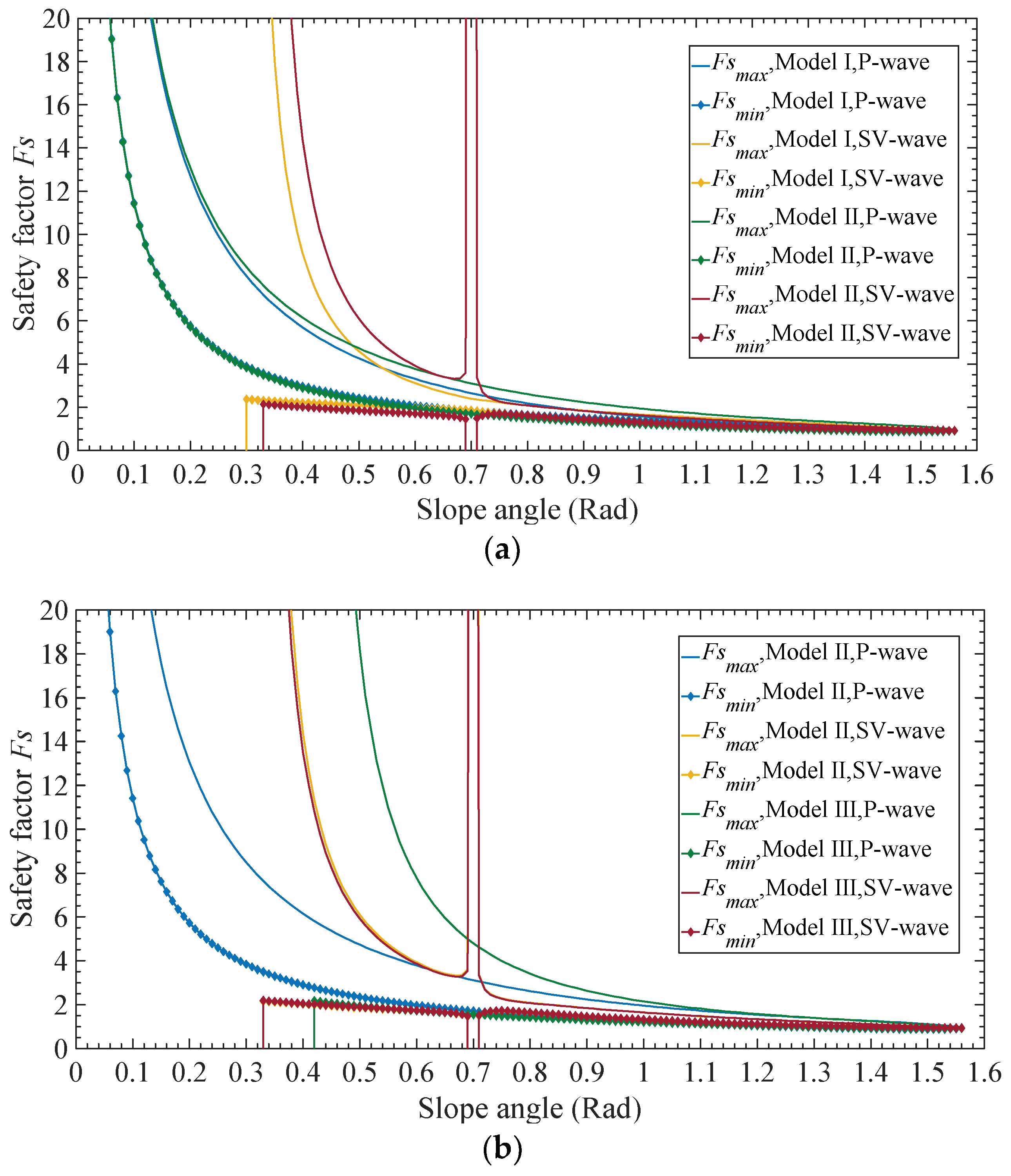
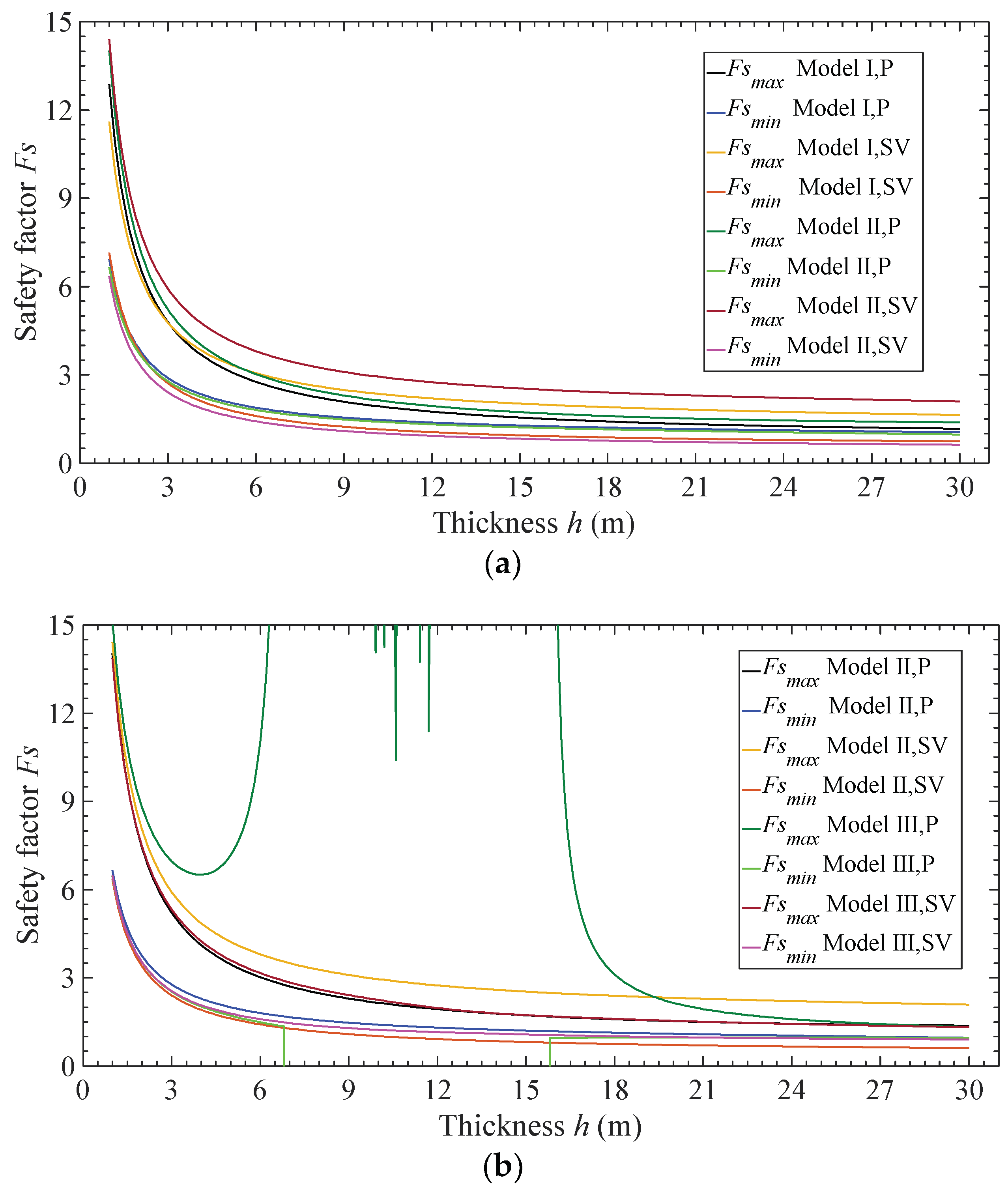
3.1. Effect of Slope Features
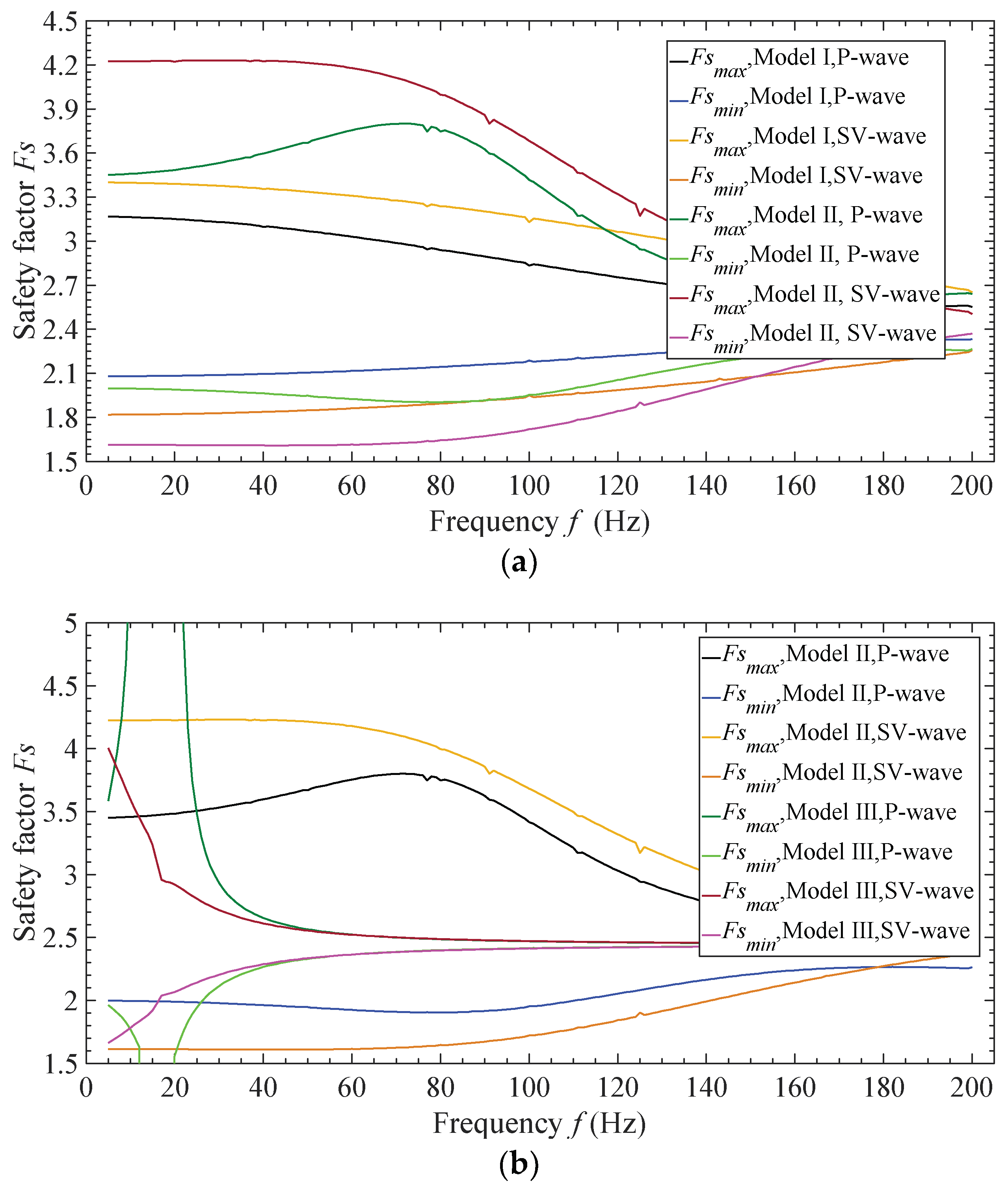
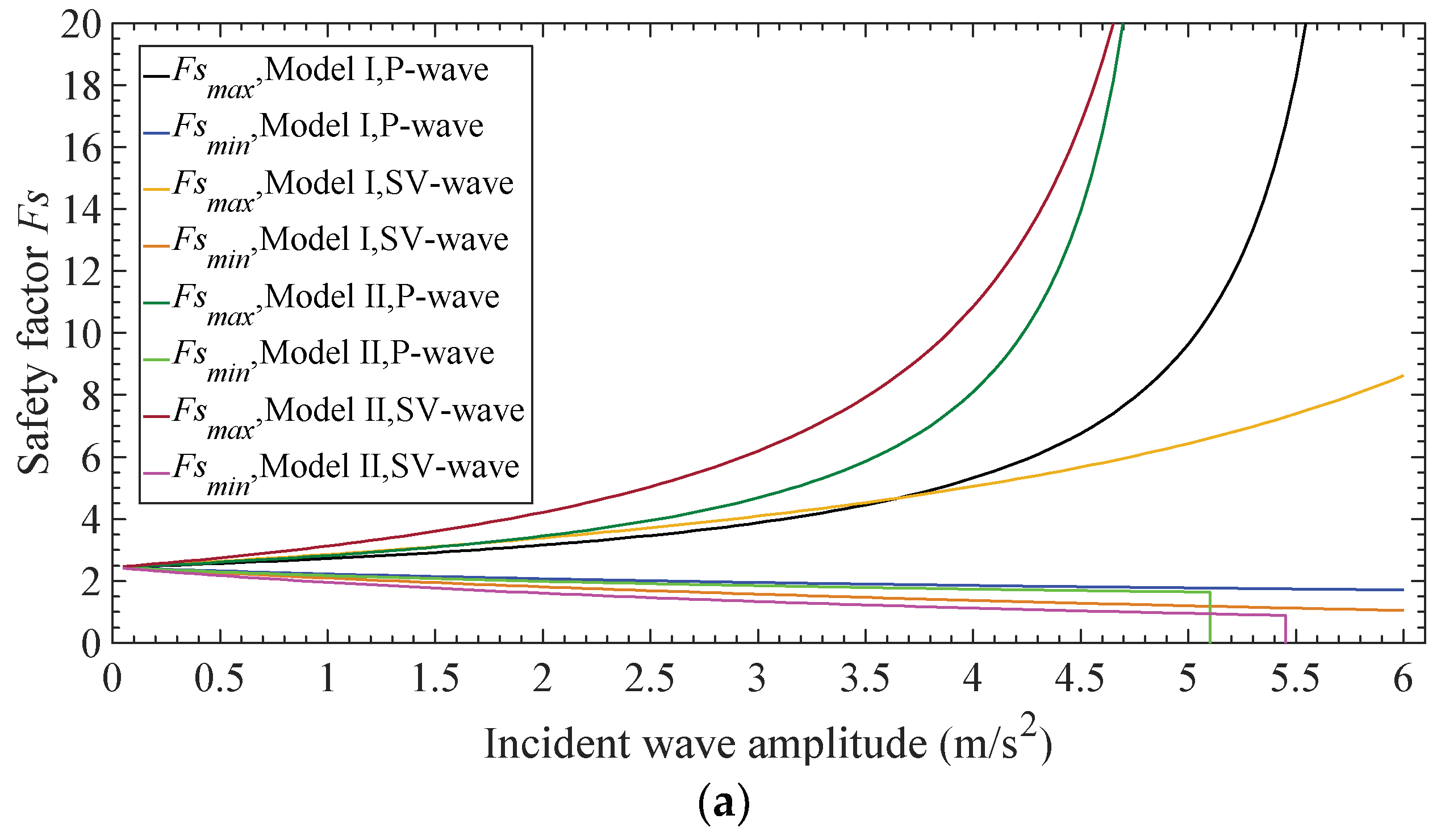
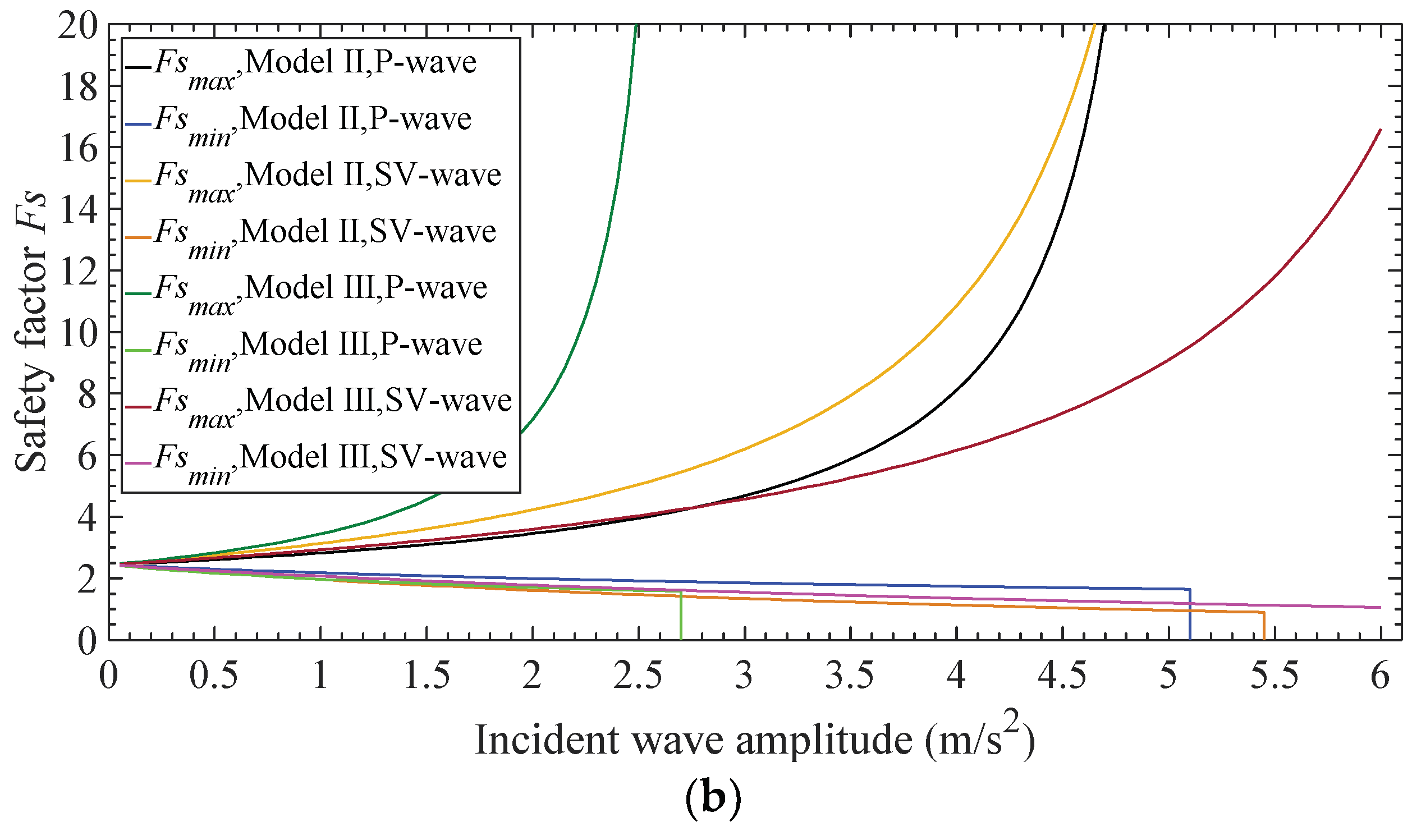
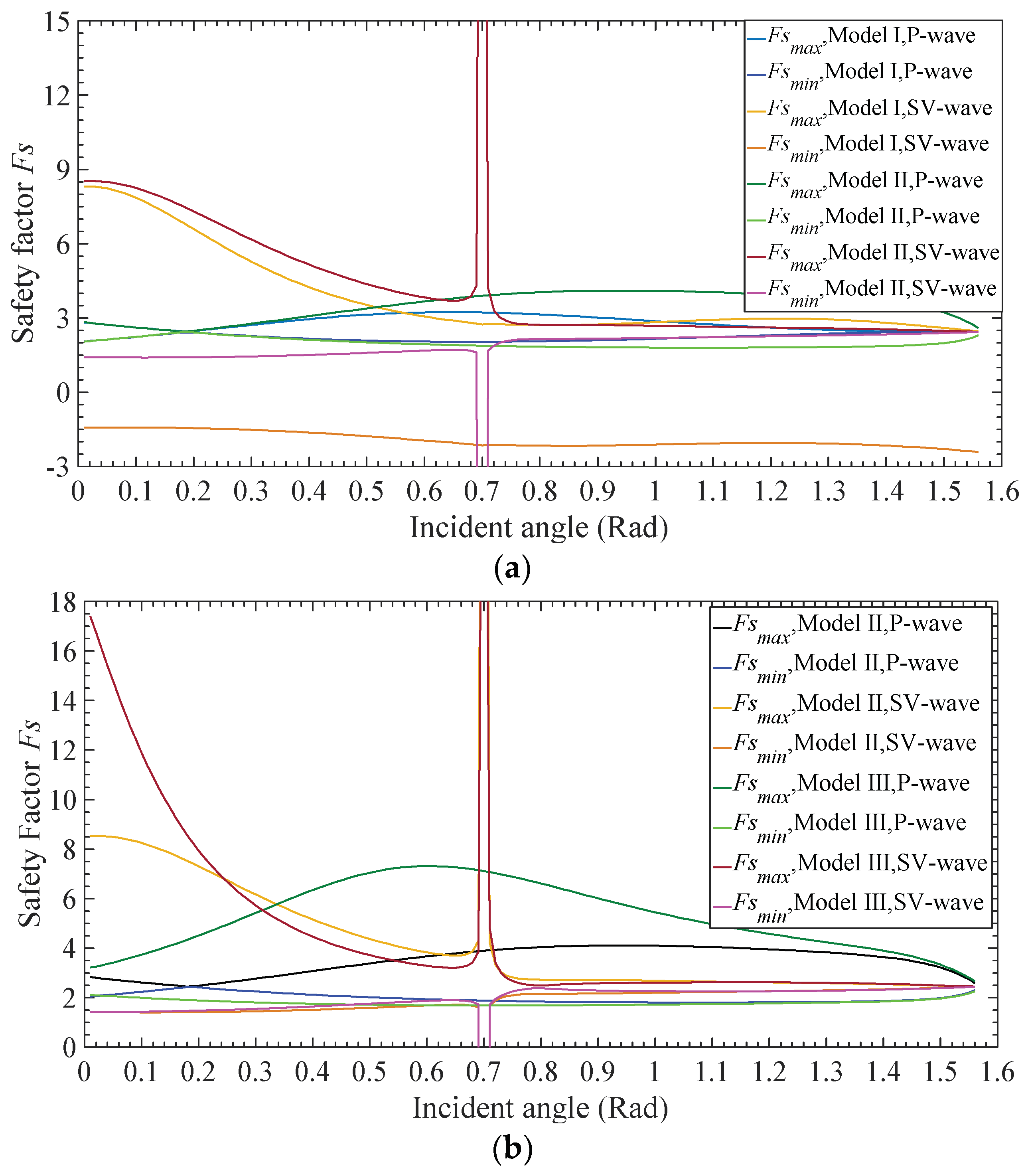
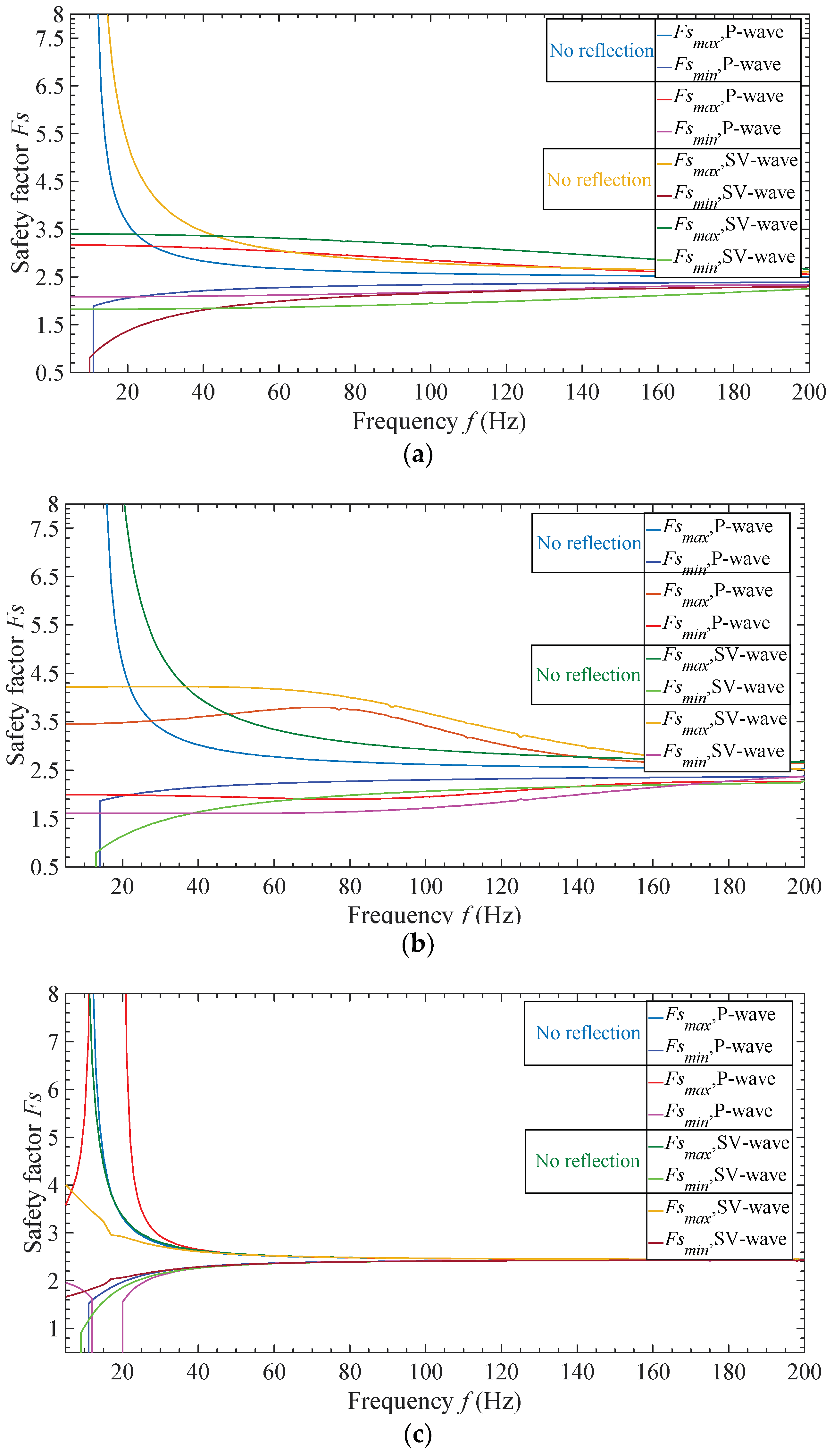
3.2. Effect of Incident Stress Wave
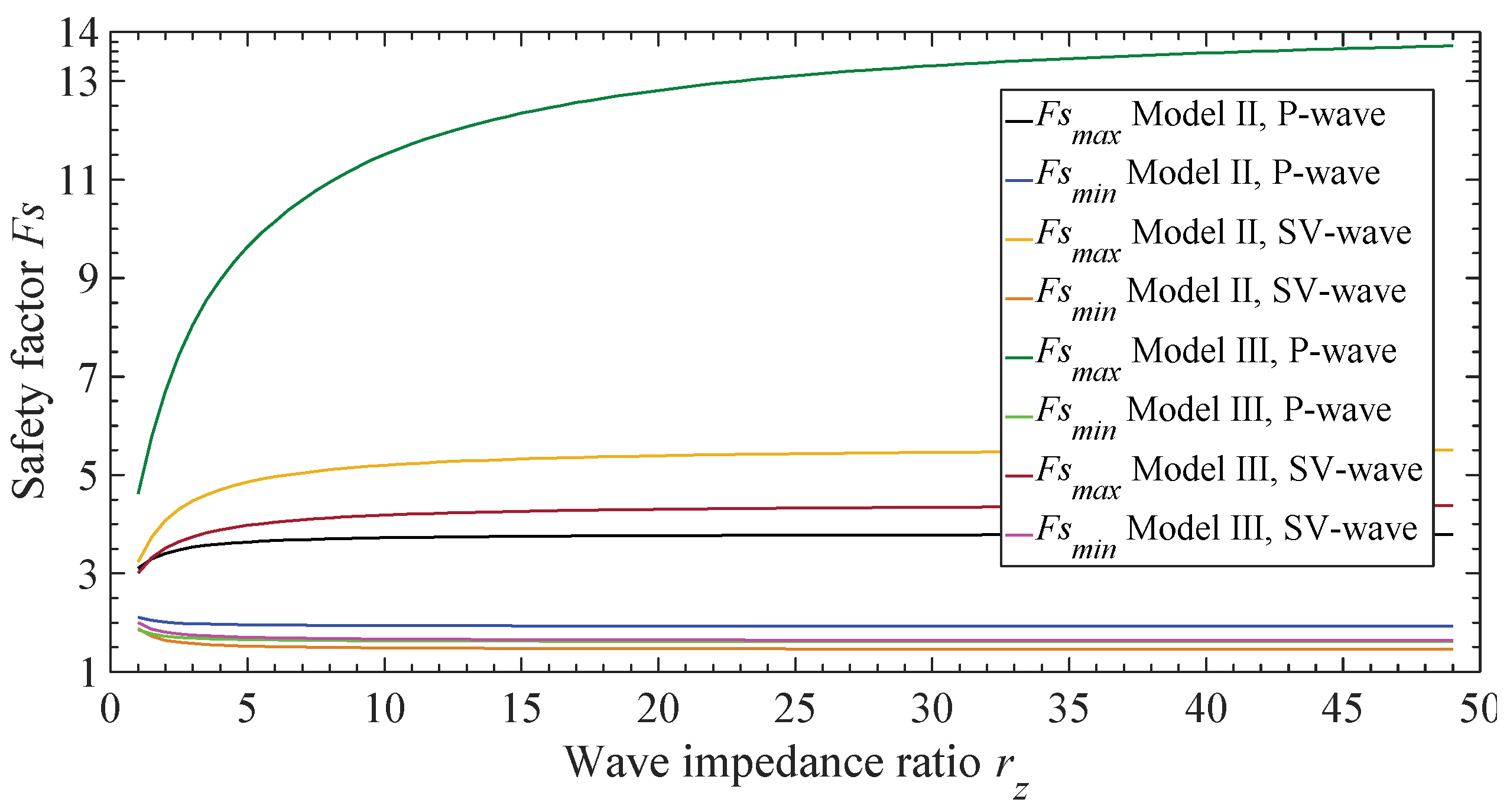
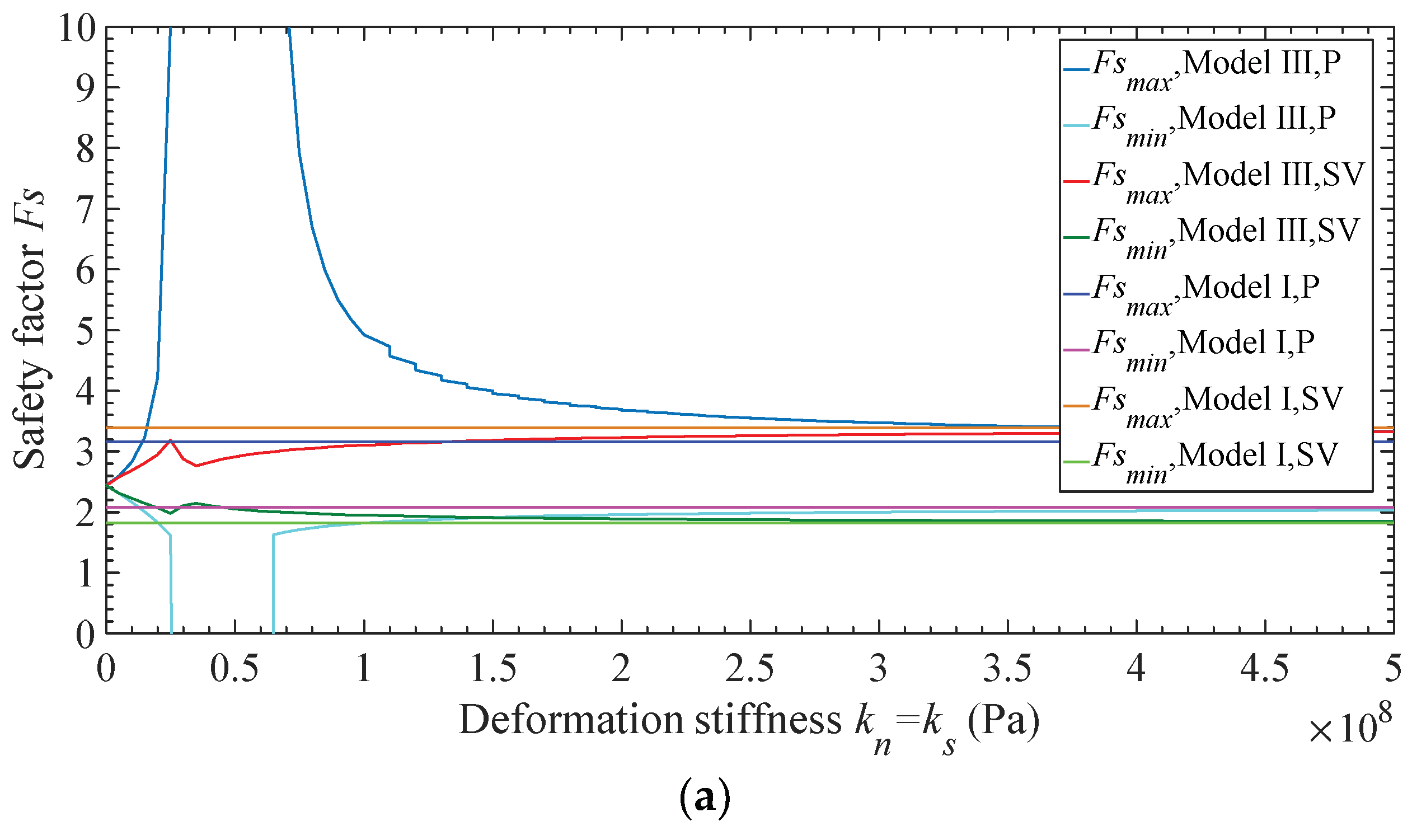
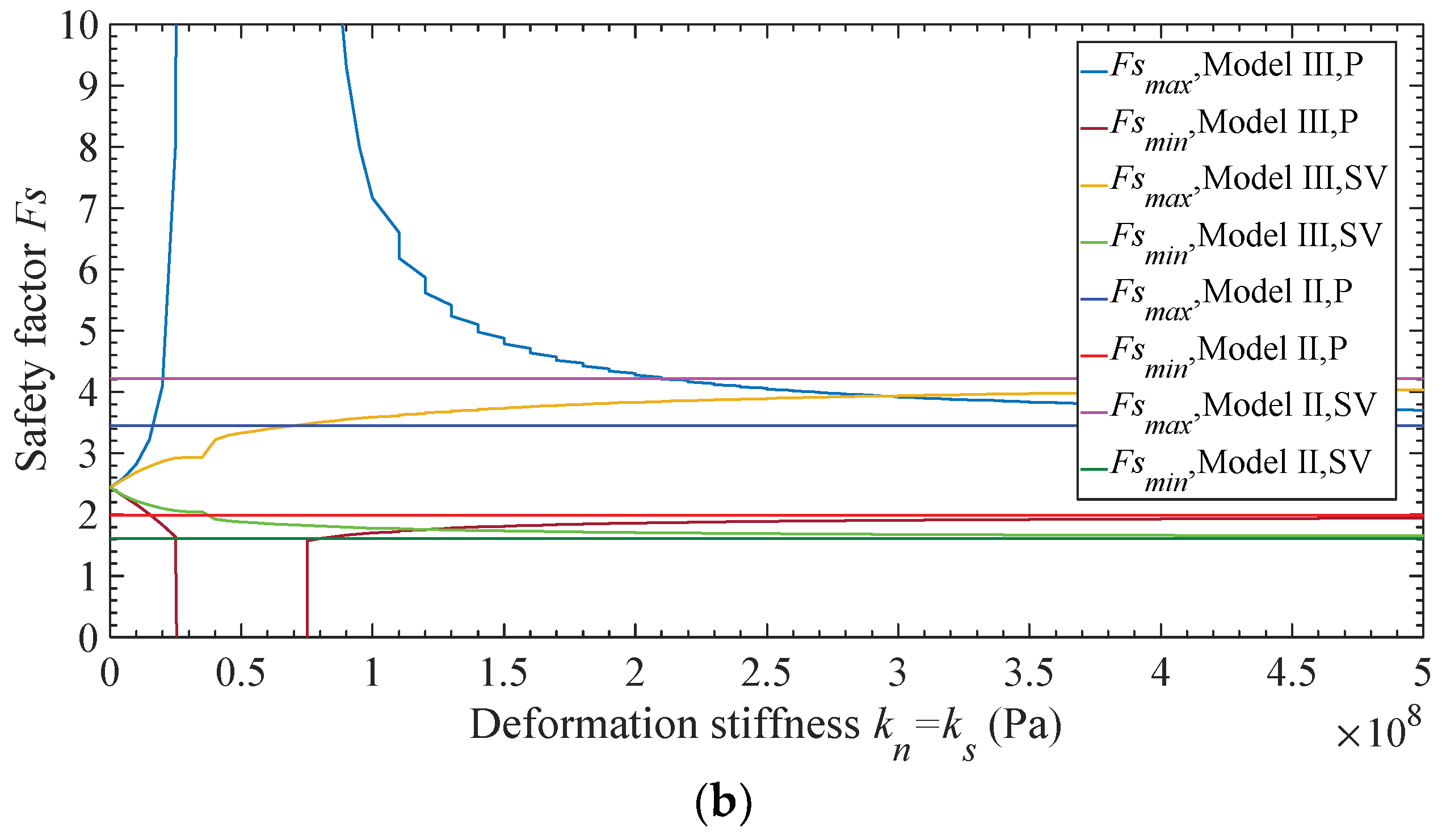
3.3. Effect of Deformation Stiffness of Slip Surface
4. Discussion
5. Conclusions
- The instantaneous safety factor of the slope does not simply increase or decrease with the decrease of the continuity of the slip surface, but significantly changes with the frequency of the incident wave, the incident angle and the deformation stiffness of the slip surface. However, in most cases, some significant regularities can be found:
- (a)
- When slip surface changes from the continuous surface to medium interface, it leads to the higher peak value of instantaneous safety factor, and the lower valley value;
- (b)
- When slip surface changes from the medium interface to displacement discontinuous surface, it leads to the higher peak value, and the lower valley value with the incident P-wave, and leads to the lower peak value lower, and the higher valley value with the incident SV-wave.
- Without the reflection of slope surface, the changing trend of peak value and valley value of instantaneous safety factor will become much simpler. Compared with instantaneous safety factor considering the reflection of slope surface, at lower frequencies, the peak value becomes higher and the valley value becomes lower; but at higher frequencies, the peak value becomes lower and the valley value becomes higher.
- Different from the static problem, as the slope angle and thickness of slip body increase, the instantaneous safety factor will not monotonically decrease.
- With the lower frequency and higher amplitude of incident wave, the valley value of instantaneous safety factor will be lower, and more unstable for the slope. Additionally, this kind of situation should be noticed in the engineering.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Wu, X.; Jiang, Y.; Guan, Z.; Wang, G. Estimating the support effect of the energy-absorbing rock bolt based on the mechanical work transfer ability. Int. J. Rock Mech. Min. Sci. 2018, 103, 168–178. [Google Scholar] [CrossRef]
- Li, X. Rock Dynamic Fundamentals and Applications; Science Press: Beijing, China, 2014. [Google Scholar]
- Knott, C.G. Reflexion and refraction of elastic waves, with seismological applications. Philos. Mag. 1924, 48, 64–97. [Google Scholar] [CrossRef]
- Zoeppritz, K. Erdbebenwellen VIII B, Uber Reflexion and Durchgang seismischer wellen durch Unstetigkeisflachen. Gott. Nachr 1919, 1, 66–84. [Google Scholar]
- Mindlin, R.D. Waves and vibrations in isotropic, elastic plates. In Structural Mechanics; Goodier, J.N., Hoff, N.J., Eds.; Pergamon Press: New York, NY, USA, 1960; pp. 199–232. [Google Scholar]
- Kendall, K.; Tabor, D. An Ultrasonic Study of the Area of Contact between Stationary and Sliding Surfaces. Proc. R. Soc. Lond. Part A 1971, 323, 321–340. [Google Scholar] [CrossRef]
- Schoenberg, M. Elastic wave behavior across linear slip interfaces. J. Acoust. Soc. Am. 1998, 68, 1516–1521. [Google Scholar] [CrossRef]
- Gu, B.; Suárez-Rivera, R.; Nihei, K.T.; Myer, L.R. Incidence of plane waves upon a fracture. J. Geophys. Res. Solid Earth 1996, 101, 25337–25346. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.; Cui, P. Reflection and refraction laws of low amplitude stress wave on a 3D rock joint surface. J. Vib. Shock 2018, 37, 68–77. [Google Scholar]
- Pyrak-Nolte, L.J.; Myer, L.R.; Cook, N.G.W. Transmission of seismic waves across single natural fractures. J. Geophys. Res. 1990, 95, 8617–8638. [Google Scholar] [CrossRef]
- Pyrak-Nolte, L.J. The seismic response of fractures and the interrelations among fracture properties. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 787–802. [Google Scholar] [CrossRef]
- Suarez-Rivera, F.R.; Cook, N.G.W.; Myer, L.R. Study on the transmission of shear waves across thin liquid films and thin clay layers. In Proceedings of the 33th U.S. Symposium on Rock Mechanics (USRMS), Santa Fe, NM, USA, 3–5 June 1992. [Google Scholar]
- Daehnke, A.; Rossmanith, H.P. Reflection and refraction of plane stress waves at interfaces modelling various rock joints. Fragblast 1997, 1, 111–231. [Google Scholar] [CrossRef]
- Funahashi, F.; Yoshioka, N. Effects of Contact Geometry of Faults on Transmission Waves. Pure Appl. Geophys. 2001, 158, 717–739. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, J.G. Transmission of Elastic P-waves across Single Fractures with a Nonlinear Normal Deformational Behavior. Rock Mech. Rock Eng. 2001, 34, 3–22. [Google Scholar] [CrossRef]
- Yu, J.; Song, X.; Qian, Q. Propagation of p-waves in dual nonlinear elastic medium for jointed rock mass. Chin. J. Rock Mech. Eng. 2011, 30, 2463–2473. [Google Scholar]
- Zheng, Y.; Hailin, Y.E.; Huang, R.; Li, H.; Xu, J. Study on the seismic stability analysis of a slope. J. Earthq. Eng. Eng. Vib. 2010, 30, 173–180. [Google Scholar]
- Ni, W.; Tang, H.; Liu, X.; Wu, Y. Dynamic stability analysis of rock slope considering vibration deterioration of structural planes under seismic loading. Chin. J. Rock Mech. Eng. 2013, 32, 492–500. [Google Scholar]
- Liu, X.; Liu, Y.; He, C.; Li, X. Dynamic stability analysis of the bedding rock slope considering the vibration deterioration effect of the structural plane. Bull. Eng. Geol. Environ. 2016, 77, 1–17. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, J.; Bi, J. Application of Hilbert-Huang Transform to the analysis of the landslides triggered by the Wenchuan earthquake. J. Mt. Sci. 2015, 12, 711–720. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, L.; Zhang, J.; Yang, C. Time-frequency analysis of instantaneous seismic safety of bedding rock slopes. Soil Dyn. Earthq. Eng. 2017, 94, 92–101. [Google Scholar] [CrossRef]
- Ali, A.; Huang, J.; Lyamin, A.V.; Sloan, S.W.; Griffiths, D.V.; Cassidy, M.J.; Li, J. Simplified quantitative risk assessment of rainfall-induced landslides modelled by infinite slopes. Eng. Geol. 2014, 179, 102–116. [Google Scholar] [CrossRef]
- Prisco, C.D.; Pastor, M.; Pisanò, F. Shear wave propagation along infinite slopes: A theoretically based numerical study. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 619–642. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. A performance-based method for the design of drainage trenches used to stabilize slopes. Eng. Geol. 2018, 239, 158–166. [Google Scholar] [CrossRef]
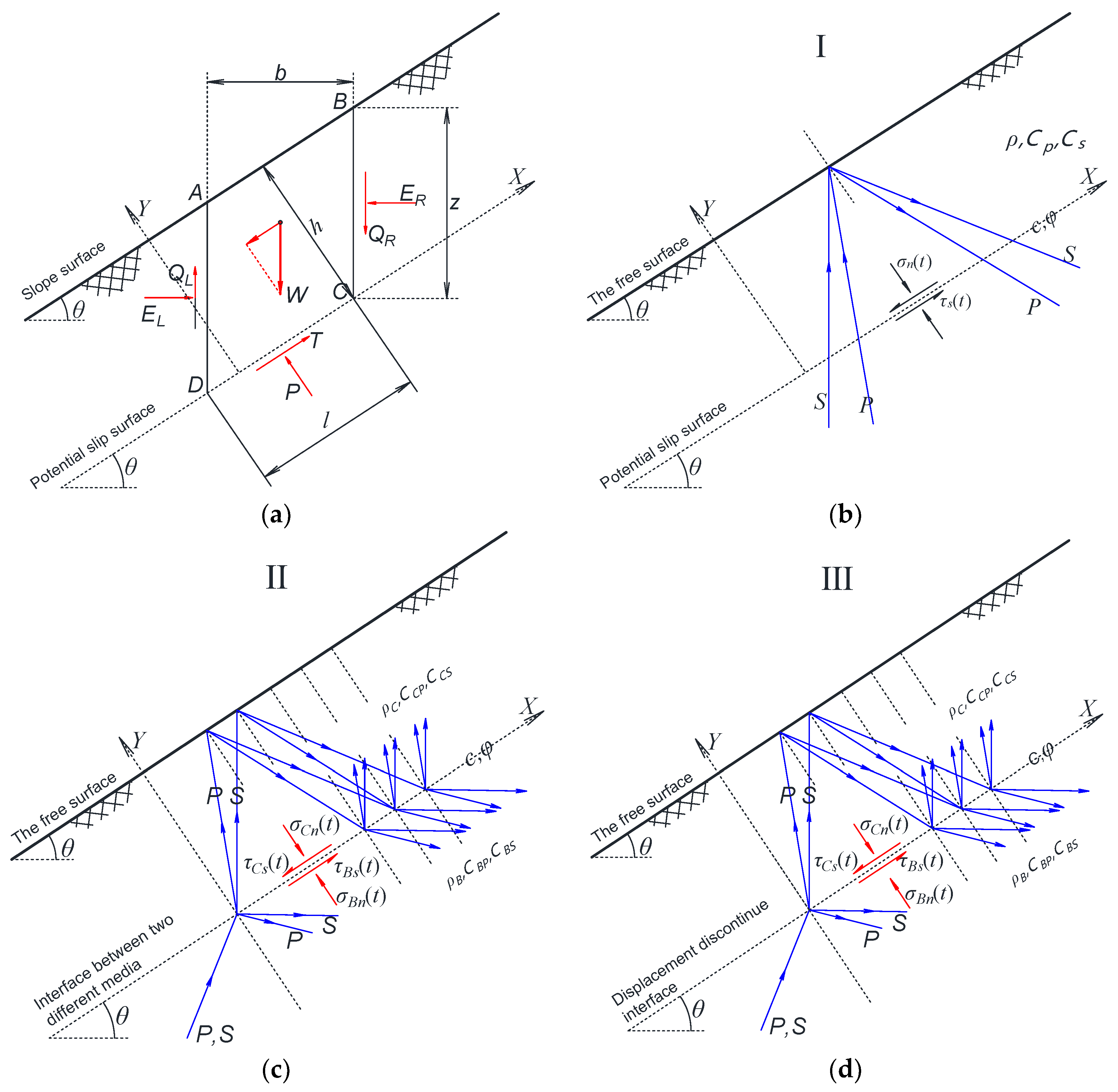


| Medium | Stress Wave | P-Wave | SV-Wave | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Amplitude | Wave Number | Wave Velocity | Angle | Amplitude | Wave Number | Wave Velocity | Angle | |||
| Model I | Incident wave | |||||||||
| Reflected wave | ||||||||||
| Model II, III | Basement layer | Incident wave | ||||||||
| Downward wave | ||||||||||
| Cover layer | Upward wave | |||||||||
| Downward wave | ||||||||||
| Cases | Analysis Variable | Slope Features | Model Type | Dynamic Properties | Incident Stress Wave Parameters | Mechanical Parameters of Slip Surface |
|---|---|---|---|---|---|---|
| 1 | Slope angle: θ = 0–90° | h = 5.0 m | I | , , and | Amplitude: 2.0 m/s2 Incident angle: 30° Frequency: f = 10 Hz | |
| II | , , , , , and | |||||
| III | ||||||
| 2 | Thickness of cover layer: h = 1.0–15.0 m | θ = 35.0° | I | , , and | ||
| II | , , , , , and | |||||
| III | ||||||
| 3 | Wave impedance ratio: rz = 1.0–49.0 | θ = 35.0° h = 5.0 m | II | , , , , , and | ||
| III |
| Cases | Analysis Variable | Wave Parameters | Model Type | Dynamic Properties | Slope Models’ Features | Mechanical Parameters of Slip Surface |
|---|---|---|---|---|---|---|
| 4 | Incident wave’s amplitude: 0.1–6.0 m/s2 | f = 10 Hz Incident angle: 30° | I | , , and | Cover layer’s thickness: Slope angle: | |
| II | , , , , , and | |||||
| III | ||||||
| 5 | Incident wave’s frequency: f = 5–200 Hz | Incident wave’s amplitude: 2.0 m/s2 Incident angle: 30° | I | , , and | ||
| II | , , , , , and | |||||
| III | ||||||
| 6 | Incident angle: 0–90° | Incident wave’s amplitude: 2.0 m/s2 f = 10 Hz | I | , , and | ||
| II | , , , , , and | |||||
| III |
| Cases | Analysis Variable | Model Type | Dynamic Properties | Stress Wave Parameters | Slope Models’ Features | Mechanical Parameters of Slip Surface |
|---|---|---|---|---|---|---|
| 7 | Integral stiffness coefficient: | III | , , , , , and , or , , and | Amplitude: 2.0 m/s2 Incident angle: 30° Frequency: f = 10 Hz | Cover layer’s thickness: Slope angle: |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Wang, G.; Han, W. Effect of Slip Surface’s Continuity on Slope Dynamic Stability Based on Infinite Slope Model. Mathematics 2019, 7, 58. https://doi.org/10.3390/math7010058
Liu C, Wang G, Han W. Effect of Slip Surface’s Continuity on Slope Dynamic Stability Based on Infinite Slope Model. Mathematics. 2019; 7(1):58. https://doi.org/10.3390/math7010058
Chicago/Turabian StyleLiu, Chuanzheng, Gang Wang, and Wei Han. 2019. "Effect of Slip Surface’s Continuity on Slope Dynamic Stability Based on Infinite Slope Model" Mathematics 7, no. 1: 58. https://doi.org/10.3390/math7010058
APA StyleLiu, C., Wang, G., & Han, W. (2019). Effect of Slip Surface’s Continuity on Slope Dynamic Stability Based on Infinite Slope Model. Mathematics, 7(1), 58. https://doi.org/10.3390/math7010058





