Abstract
Graph invariants are the properties of graphs that do not change under graph isomorphisms, the independent set decision problem, vertex covering problem, and matching number problem are known to be NP-Hard, and hence it is not believed that there are efficient algorithms for solving them. In this paper, the graph invariants matching number, vertex covering number, and independence number for the zero-divisor graph over the rings and are determined in terms of the sets and respectively. Accordingly, a formula in terms of and r, with , is provided.
1. Introduction
The independent set decision problem, vertex covering problem, and matching number problem are known to be classical optimization problems in computer science and are typical examples of NP-Hard problems [1,2,3], and hence it is not believed that there are efficient algorithms for solving them but rather have approximation algorithms. In this paper, the graph invariants matching number, vertex covering number, and independence number for the zero-divisor graph over the rings and are determined in terms of the sets and . Zero-divisor graphs were initially introduced by Beck [4]. Beck was mainly interested in graph coloring. He defined the vertices of the graph as the elements of a commutative ring R and two different vertices x and y are adjacent if . In later work, Anderson and Livingston introduced the zero-divisor graph of a commutative ring R [5]. They defined the set of vertices of the graph to be the nonzero zero-divisors of R and two different vertices x and y are adjacent if . The set of zero-divisors of R is usually denoted by and denotes the nonzero zero-divisors of R. The zero-divisor graph of R, denoted by , is written as usually. The most common definition in the literature of the zero-divisor graph is that given by Anderson and Livingston [5]. Zero-divisor graph has many applications in algebra, in fact it can be used to study many properties in ring and number theory. On the other side we can use ring theory to study many geometric properties of graph theory such as cliques, chromatic number, and the independence number, for example Akbari et al. [6] studied many properties of matrix algebra using graph theory and vice versa.
Anderson, Frazier, Lauve, Levy, Livingston, and Shapiro [5,7,8] have studied zero-divisor graph of a commutative ring extensively. Redmond [9] extended the idea of zero-divisor graph over commutative ring to non-commutative rings.
For a graph G with , denotes the induced subgraph by a set X. The neighborhood of a vertex is the set , and , for .
For any graph G, the graph theoretic invariant , , and are widely studied because of their importance in characterizing graphs. Our aim is to characterize these invariants for certain families of zero-divisor graphs.
Through this paper, we find the matching number, vertex covering number, and the independence number of zero-divisor graphs of , where the set . Let be a simple graph with and , then a set M of nonadjacent edges of G is called a matching and the matching number, denoted by , is the maximum size of a matching in G. We say that G contains a perfect matching, if . Moreover, for a graph G, is called vertex cover if every edge in G has an endpoint in S. The minimum cardinality of a vertex cover is called the vertex covering number, denoted by . According to the definition of vertex covering number, it is clear that .
An independent set in a graph G is a set of pairwise nonadjacent vertices. The independence number of G is the maximum size of an independent set in G and is denoted by .
2. Preliminaries
In this section we introduce some preliminary results and elaborate on some known algorithms that compute the zero-divisor graph of . Some of these algorithms have been developed by Joan Krone [10]. Moreover, the characterization of independence number in special cases was given in [11,12], we generalize their work.
For where p is some prime and k is positive integer, we can find the zero-divisors of by taking the numbers then multiplying those numbers by p. The zero-divisors can be divided into sets according to how many factors of p each divisor has. These sets are , where . To build the zero-divisor graph of , connect the vertices of the set to the vertices of the set when . Using the Euler’s phi-function we can get the sizes of the , that is .
For where p and q are distinct primes, k and r are positive integers. We can divide the zero-divisors into three families, , , and where , , similarly for . , , excluding the case when both and . Connect the vertices of to the vertices of if . Similarly, connect elements of to elements of if . Connect elements of elements of to elements of if and .
AbdAlJawad and Al-Ezeh [12] calculated the size of these sets as shown below.
Lemma 1.
[12] For ,
- 1.
- 2.
- 3.
The graph of is isomorphic to the complete graph . Hence, the independent number, the matching number, and the vertex covering number are presented in the following Lemma.
Lemma 2.
[12] For a graph , we have:
- 1.
- .
- 2.
- .
- 3.
- .
We omit the proof of previous Lemma, since it is clear. We can deduce that the zero-divisor graph has a perfect matching if p is odd.
Recall that a bipartite graph is a graph where its vertices can be divided into two disjoint sets of vertices such that every edge of the graph connects a vertex from one set to the other. Hall’s Theorem [13] guarantees that the maximum matching set could be saturated by X or Y.
Theorem 1.
(Hall 1935) [13]. Let be a bipartite graph. G has a matching saturating A if and only if for all .
From Hall’s Theorem, one can conclude that if is a complete bipartite graph, then .
3. Matching Number, Vertex Covering Number, and Independence Number of Zero-Divisor Graph , Where Is Prime and
In this section we compute the matching number, vertex covering number, and the independence number of , for .
First we give an example to clarify our calculations, consider , the zero divisor set of is . In , , , , and the graph is shown in Figure 1. The induced subgraph of over the set of vertices and are the empty graph and complete graph respectively, moreover for each vertex and , . Since , any edge in the induced subgraph of over the vertex set will form a maximum matching number of this subgraph. On the other hand the induced subgraph over the vertex set is the complete graph, so the maximum matching set of this subgraph is .
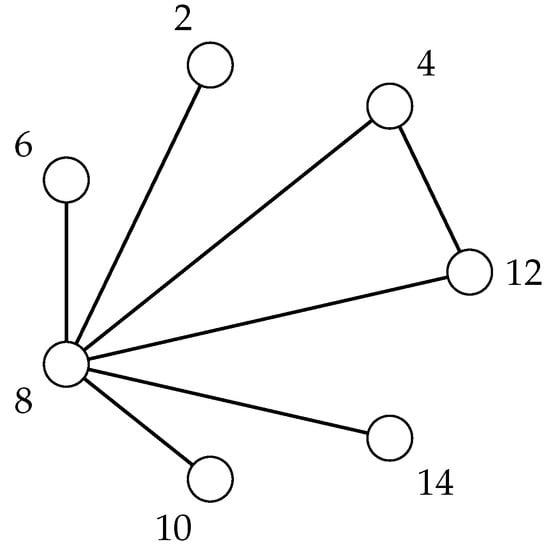
Figure 1.
.
Finally, since for each and , we have
For the vertex covering number, since for each vertex and , , the vertex set can be considered to be minimum vertex cover of the induced subgraph over the vertex set . On the other hand, the induced subgraph over the vertex set is the complete graph, so the vertex cover number of this subgraph is , therefore
Theorem 2.
For a graph , and p is a prime number, then:
- 1.
- 2.
Proof.
Consider the set , for some . Since we have , so we can define a one to one function Since we have for each and , , therefore
Moreover, since is one to one function, this guaranties that is a matching set.
Case 1.
k is odd number and .
Since , induces a complete subgraph, so for the induce subgraph over the vertex set , forms a maximum matching set, and hence form a maximum matching set of , therefore
Regarding the vertex covering number, observing that for every edge either or for some , we have form a vertex cover set, the minimality of this vertex cover set can be obtained from the fact that whenever we have .
Case 2.
k is even number In addition to scenario in case 1, induces a complete subgraph of , observing that the maximum matching set of a complete graph is we have
For this case of the vertex covering number, since the induced subgraph over the vertex set is the complete subgraph, the edges of this subgraph have no end points in . So, the vertex cover number of is
□
Using Lemma 1 and the above Theorem, we have:
Corollary 1.
If , for prime p and positive integer k:
- 1.
- 2.
In [12], the independence number of was calculated as follows:
Theorem 3.
[12] For a graph , and p is a prime number, then:
Using Lemma 1 and the above Theorem, we have:
Corollary 2.
If , for prime p and positive integer k:
4. , Where Are Prime Numbers and
Now, we will evaluate the matching number, covering vertex number, and the independence number, for with . We will divide our work into scenarios depending on the values of k and r.
Theorem 4.
If , where k and r are even, then the matching number of , is given by:
Proof.
- 1.
- For , and , whenever and we have .Since the cardinality of is less than the cardinality of we can define a one to one functionObserving that the induced subgraph of over the vertex set and the vertex set are the complete graph and the empty graph respectively, we haveform a maximum matching set for the induced subgraph over the vertex set , therefore form a maximum matching set for the induced subgraph over the vertex set
- 2.
- For and , the induced subgraph over the vertex set and the vertex set are the empty graphs, moreover for any and we have , so the induced subgraph over the vertex set is the complete bipartite graph, so using Hall’s theorem the matching number of the induced subgraph over the vertex set is
- 3.
- For and , the induced subgraph over is the complete graph, so the matching number of the induced subgraph over the vertex set is .Collecting the results in the above cases we get the result.
□
Using Lemma 1 and above Theorem, we have:
Corollary 3.
For , where k and r are even. Then:
Moreover, using analysis of Theorem 4, one can give the value of and the value of with k and r are even, where [12] gave a partial result of , as follows.
Corollary 4.
For , where k and r are even, then:
- 1.
- The covering number of , is equal to:.
- 2.
- The independence number of , is equal to:.
Using Lemma 1 and Corollary 4, we have:
Corollary 5.
For , where k and r are even. Then:
By similar approach with some minor differences, we get the following Theorems.
Theorem 5.
If , where k is even and r is odd, then the matching number of , is given by:
Using Lemma 1 and above Theorem, we have:
Corollary 6.
For , where k is even and r is odd. Then:
Theorem 6.
If , where k and r are odd, then the matching number of , is given by:
Using Lemma 1 and above Theorem, we have:
Corollary 7.
For , where k and r are odd. Then:
Corollary 8.
For , where k and r are odd or one of them is odd and one is even. Then the covering vertex number of , denoted by , is equal to .
Corollary 9.
For , where k is even and r is odd. Then the independence number of , denoted by , is equal to:
.
Corollary 10.
For , where k and r are odd. Then the independence number of , denoted by , is equal to:
.
Remark 1.
For , one can see that .
Further Works.
This work can be investigated further for any positive integer n.
5. Conclusions
Graph invariants are the properties of graphs that do not change under graph isomorphisms. In this paper, we provided a technique that can be used to find some graph invariants of the zero-divisor graphs of and . This technique can be used to calculate these graphs invariants of for any n depending on the factorization of n.
Author Contributions
These authors are contributed equally to this work.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Karp, R.M. Reducibility among combinatorial problems. In Complexity of Computer Computations; Springer: Boston, MA, USA, 1972; pp. 85–103. [Google Scholar]
- Ausiello, G.; Crescenzi, P.; Gambosi, G.; Kann, V.; Marchetti-Spaccamela, A.; Protasi, M. Complexity and Approximation: Combinatorial Optimization Problems and Their Approximability Properties; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Robson, J.M. Algorithms for maximum independent sets. J. Algorithms 1986, 7, 425–440. [Google Scholar] [CrossRef]
- Beck, I. Coloring of commutative rings. J. Algebra 1988, 116, 208–226. [Google Scholar] [CrossRef]
- Anderson, D.F.; Livingston, P.S. The zero-divisor graph of a commutative ring. J. Algebra 1999, 217, 434–447. [Google Scholar] [CrossRef]
- Akbari, S.; Kiani, D.; Ramezani, F. Commuting Graphs of Group Algebras. Commun. Algebra 2010, 38, 3532–3538. [Google Scholar] [CrossRef]
- Anderson, D.; Frazier, A.; Lauve, A.; Livingston, P.S. The zero-divisor graph of a commutative ring, II. Lect. Notes Pure Appl. Math. 2001, 220, 61–72. [Google Scholar]
- Anderson, D.; Levy, R.; Shapiro, J. Zero-divisor graphs, von Neumann regular rings, and Boolean algebras. J. Pure Appl. Algebra 2003, 180, 221–241. [Google Scholar] [CrossRef]
- Redmond, S. The zero-divisor graph of a non-commutative ring. Int. J. Commut. Rings 2002, 1, 203–211. [Google Scholar]
- Krone, J. Algorithms for Constructing Zero-Divisor Graphs of Commutative Rings. Available online: http://personal.denison.edu/~krone/docs/Zero-Divisor.pdf (accessed on 2 January 2019).
- AbdAlJawad, E. Some properties of the zero-divisor graph of the ring of dual numbers of a commutative ring. Ph.D. Thesis, Department of Mathematics, University of Jordan, Amman, Jordan, 2007. [Google Scholar]
- AbdAlJawad, E.; Al-Ezeh, H. Domination and independence numbers of Γ(Zn). Int. Math. Forum 2008, 11, 503–511. [Google Scholar]
- Gross, J.L.; Yellen, J.; Zhang, P. Handbook of Graph Theory; Chapman and Hall/CRC: New York, NY, USA, 2013. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).