Methods of Moment and Maximum Entropy for Solving Nonlinear Expectation
Abstract
:1. Introduction
2. Existence of Solutions for Moment Problems
3. Maximum Entropy for Moment Problems
4. Numerical Experiments
Author Contributions
Funding
Conflicts of Interest
References
- Peng, S.G. Filtration consistent nonlinear expectations and evaluations of contingent claims. Acta Math. Appl. Sin. 2004, 20, 191–214. [Google Scholar] [CrossRef]
- Peng, S.G. Nonlinear expectations and nonlinear Markov chains. Chin. Ann. Math. Ser. B 2005, 26, 159–184. [Google Scholar] [CrossRef]
- Peng, S.G. Survey on normal distributions, central limit theorem, Brownian motion and the related stochastic calculus under sublinear expectations. Sci. China 2009, 52, 1391–1411. [Google Scholar] [CrossRef]
- Peng, S.G. G-Expectation, G-Brownian motion and related stochastic calculus of Ito^ type. Stoch. Anal. Appl. 2007, 2, 541–567. [Google Scholar]
- Peng, S.G. Law of large numbers and central limit theorem under nonlinear expectations. arXiv, 2007; arXiv:math/0702358. [Google Scholar]
- Peng, S.G. G-Brownian motion and dynamic risk measure under volatility uncertainty. arXiv, 2007; arXiv:0711.2834. [Google Scholar]
- Peng, S.G. A new central limit theorem under sublinear expectations. Mathematics 2008, 53, 1989–1994. [Google Scholar]
- Peng, S.G. Multi-dimensional G-Brownian motion and related stochastic calculus under G-expectation. Stoch. Process. Their Appl. 2006, 118, 2223–2253. [Google Scholar] [CrossRef]
- Hu, M.S. Explicit solutions of G-heat equation with a class of initial conditions by G-Brownian motion. Nonlinear Anal. Theory Methods Appl. 2012, 75, 6588–6595. [Google Scholar] [CrossRef]
- Gong, X.S.; Yang, S.Z. The application of G-heat equation and numerical properties. arXiv, 2013; arXiv:1304.1599v2. [Google Scholar]
- Akihito, H.; Nobuaki, O. Quantum Probability and Spectral Analysis of Graphs; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Durrett, R. Probability: Theory and Examples; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Frontini, M.; Tagliani, A. Entropy convergence in Stieltjes and Hamburger moment problem. Appl. Math. Comput. 1997, 88, 39–51. [Google Scholar] [CrossRef]
- Schmu¨dgen, K. The Moment Problem; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
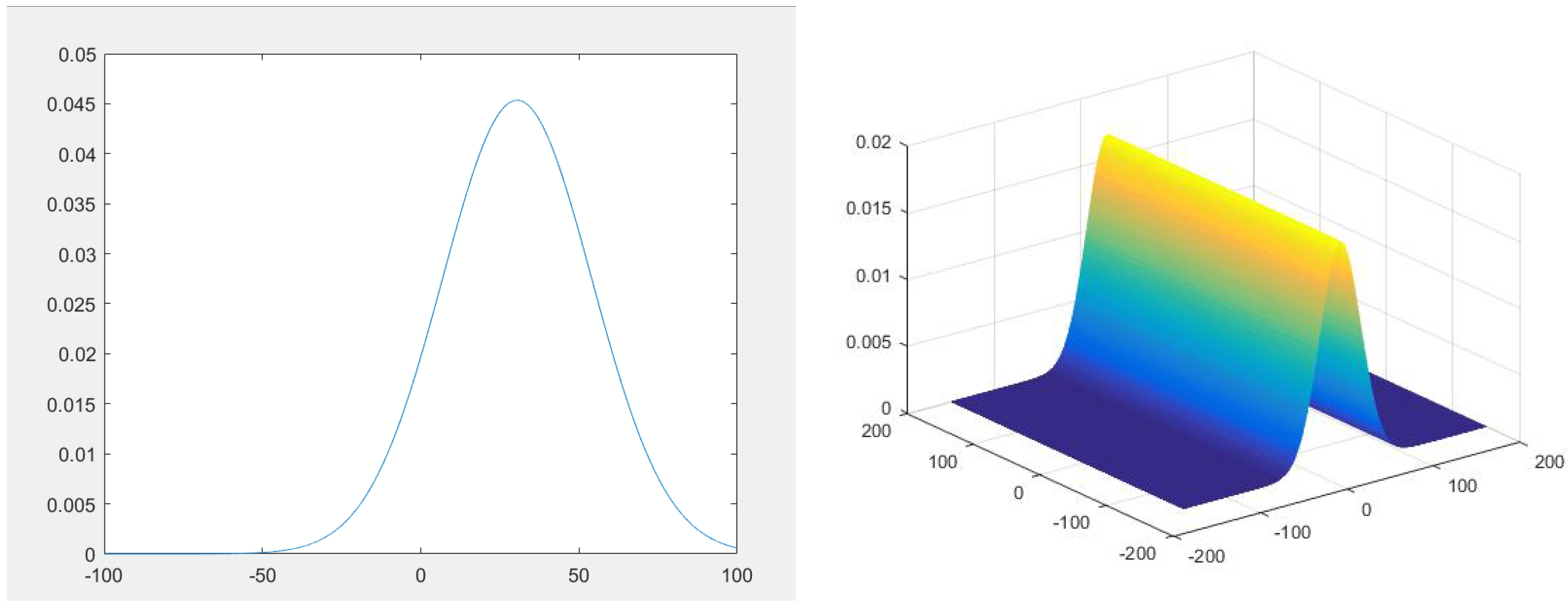
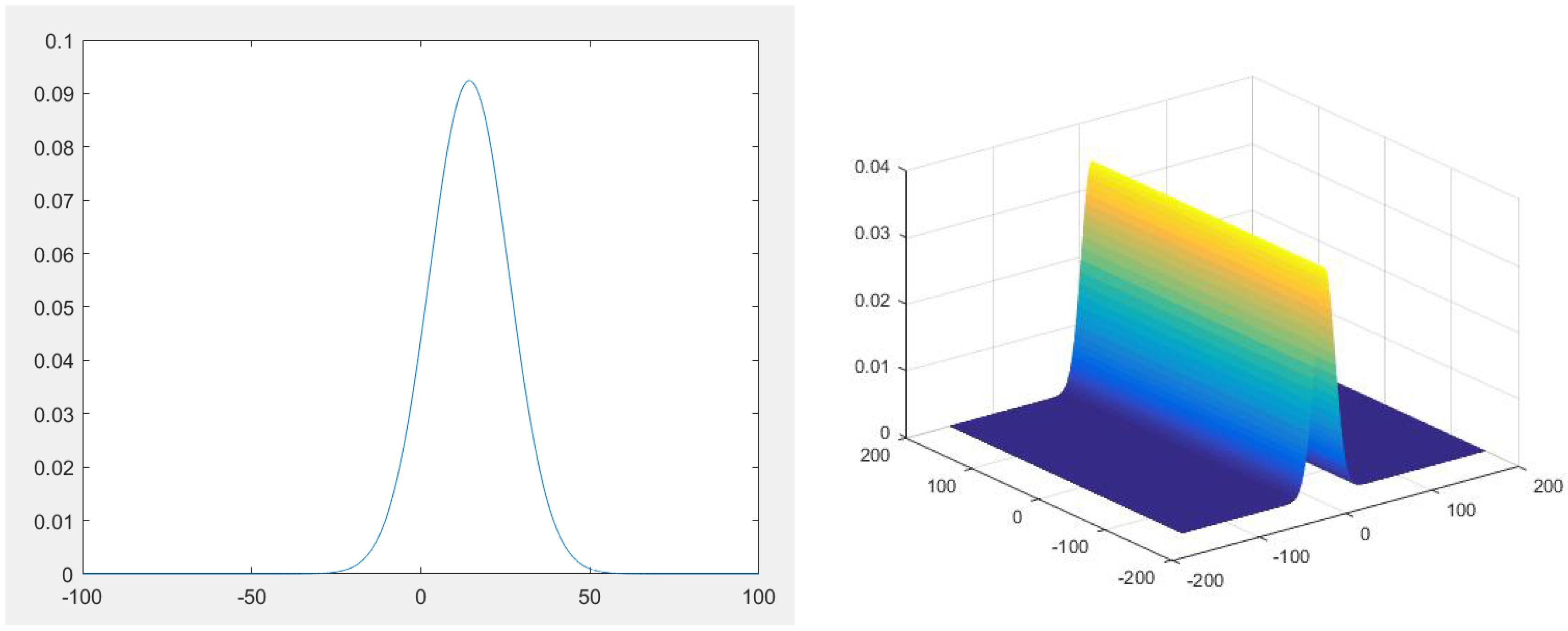
| Moments | ||||||
|---|---|---|---|---|---|---|
| Values | 1 | 30.781 | 1.5095 × 103 | 1.0158 | 0.033 | 0.0086 |
| Moments | ||||||
|---|---|---|---|---|---|---|
| Values | 1 | 14.311 | 343.1627 | −1.2451 | −0.087 | 0.0031 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Han, D. Methods of Moment and Maximum Entropy for Solving Nonlinear Expectation. Mathematics 2019, 7, 45. https://doi.org/10.3390/math7010045
Gao L, Han D. Methods of Moment and Maximum Entropy for Solving Nonlinear Expectation. Mathematics. 2019; 7(1):45. https://doi.org/10.3390/math7010045
Chicago/Turabian StyleGao, Lei, and Dong Han. 2019. "Methods of Moment and Maximum Entropy for Solving Nonlinear Expectation" Mathematics 7, no. 1: 45. https://doi.org/10.3390/math7010045
APA StyleGao, L., & Han, D. (2019). Methods of Moment and Maximum Entropy for Solving Nonlinear Expectation. Mathematics, 7(1), 45. https://doi.org/10.3390/math7010045




