Some Common Fixed Point Theorems for Generalized F-Contraction Involving w-Distance with Some Applications to Differential Equations

Abstract

In this paper, we introduce the Ćirić type generalized F-contraction and establish certain common fixed point results for such F-contraction in metric spaces with the w-distances. In addition, we give some examples to support our results. Finally, we apply our results to show the existence of solutions of the second order differential equation.

1. Introduction

In 1996, Kada, Suzuki and Takahashi [1] introduced the generalized metric, which is known as the w-distance and improved Caristi’s fixed point theorem, Ekeland’s variational principle and nonconvex minimization theorem using the results of Takahashi [2] (for more results on the w-distance, see [3,4,5,6,7]). Later, Shioji et al. [8] studied the relationship between weak contractions and weak Kannan’s contraction in metric spaces with the w-distance and the symmetric w-distance. In 2008, Ilić and Vladimir Rakočević [9] presented the unified approach to study common fixed point theorems in metric spaces with the w-distance.

On the other hand, in 2012, Wardoski [10] introduced a new contraction called F-contraction and proved a fixed point point result, which generalizes Banach’s contraction principal in many ways. Recently, Secelean [11], Piri and Kumam [12] and Singk et al. [13] purified the result of Wardoski [10] by launching some weaker conditions on the mapping F (for more results on the F-contraction, see [14,15,16,17,18,19]).

Motivated and inspired by the research mentioned above, in this paper, we prove some new common fixed point theorems for the Ćirić type generalized F-contraction in metric spaces with the w-distance, which enable us to show the existence of solutions of the second order differential equation arising in the oscillation of a spring.

2. Preliminaries

Now, we state some allied definitions and results which are needed for the main results of the present topic.

Definition 1.

Let X be an nonempty set and $f,g:X\to X$ be two mappings. A point $x\in X$ is called a fixed point of f if $fx=x$ and a point $x\in X$ is called a common fixed point of f and g if $fx=gx=x$.

Definition 2.

Let X be a nonempty set and $f,g:X\to X$ be two mappings. The pair $(f,g)$ is said to be commuting if $fgx=gfx$ for all $x\in X$ [20].

2.1. History of F-Contraction Mapping

In 2012, Wardowski [10] introduced the following concepts:

Definition 3.

We denote by $\mathcal{F}$ the family of all functions $F:{\mathbb{R}}^{+}\to \mathbb{R}$ with the following properties:

(F1) 

F is strictly increasing, which is that $s<t\mathit{implies}F\left(s\right)<F\left(t\right)$ for all $s,t\in {\mathbb{R}}^{+};$

(F2) 

for every sequence $\left\{s_n\right\}$ in ${\mathbb{R}}^{+}$, we have $\underset{n\to \infty }{\lim }{s}_n=0$ if only if $\underset{n\to \infty }{\lim }F\left(s_n\right)=-\infty ;$

(F3) 

there exists a number $k\in (0,1)$ such that $\underset{s\to 0^{+}}{\lim }{s}^{k}F\left(s\right)=0.$

Example 1.

The following functions $F_i:{\mathbb{R}}^{+}\to \mathbb{R}$ for each $i=1,2,3,4$ belong to $\mathcal{F}$ [10]:

(i) 

$F_1\left(t\right)=\ln t$ for all $t>0;$

(ii) 

$F_2\left(t\right)=\ln t+t$ for all $t>0;$

(iii) 

$F_3\left(t\right)=\ln (t^2+t)$ for all $t>0;$

(iv) 

$F_4\left(t\right)=-\frac{1}{\sqrt{t}}$ for all $t>0.$

Definition 4.

Let $(X,d)$ be a metric space [10]. A mapping $f:X\to X$ is called an F-contraction on X if there exist $F\in \mathcal{F}$ and $\tau >0$ such that, for all $x,y\in X$ with $d(fx,fy)>0,$

$$\tau +F\left(d\right(fx,fy\left)\right)\le F\left(d\right(x,y\left)\right).$$

(1)

Remark 1.

Let $F:{\mathbb{R}}^{+}\to R$ be given by the formula $F\left(\alpha \right)=\ln \alpha .$ It is clear that F satisfies (F1)–(F3) for any $k\in (0,1).$ Each mapping $f:X\to X$ satisfying (1) is an F-contraction such that

$$d(fx,fy)\le e^{-\tau }d(x,y)$$

for all $x,y\in X$ with $fx\ne fy$. It is clear that, for $x,y\in X$ such that $fx=fy$, the inequality $d(fx,fy)\le e^{-\tau }d(x,y)$ also holds, i.e., f is Banach’s contraction.

Remark 2.

Let $F:{\mathbb{R}}^{+}\to R$ be given by the formula $F\left(\alpha \right)=\ln ({\alpha }^2+\alpha ).$ It is clear that F satisfies (F1)–(F3) for any $k\in (0,1).$ Each mapping $f:X\to X$ satisfying (2.1) is an F-contraction such that

$$\frac{d(fx,fy)\left(d\right(fx,fy)+1)}{d(x,y)\left(d\right(x,y)+1)}\le e^{-\tau },forallx,y\in X,fx\ne fy.$$

(2)

Remark 3.

From (F1) and Label (1), it is easy to conclude that every F-contraction f is a contractive mapping, i.e.,

$$d(fx,fy)<d(x,y)$$

for all $x,y\in X$ with $fx\ne fy$. Thus, every F-contraction is a continuous mapping.

In 2013, Secelean [11] showed that the condition (F2) in Definition 3 can be replaced by an equivalent, but a more simple condition:

(F2′)

$\inf F=-\infty$

or, also, by the following condition:

(F2″)

there exists a sequence $\left\{s_n\right\}$ in ${\mathbb{R}}^{+}$ such that $\underset{n\to \infty }{\lim }F\left(s_n\right)=-\infty ,$

In 2014, Piri and Kumam [12] replaced the condition $\left(F3\right)$ by $\left(F{3}^{\prime }\right)$ due to Wardowski [10] as follows:

(F3′)

F is continuous on $(0,\infty )$

Thus, Piri and Kumam [12] re-established the result of Wordowski using the conditions $\left(F1\right)$, $\left(F{2}^{\prime }\right)$ and $\left(F{3}^{\prime }\right)$. Recently, Singk et al. [13] drop-out the condition $\left(F{2}^{\prime }\right)$ and named the contraction as the relaxed F-contraction as follows:

Definition 5.

${▵}_{\mathcal{F}}$ denotes the set of all functions $F:{\mathbb{R}}^{+}\to \mathbb{R}$ satisfying the following conditions:

(F1)

F is strictly increasing;

(F3′)

F is continuous on $(0,\infty ).$

2.2. w-Distance and Useful Lemmas

Definition 6.

Let $(X,d)$ be a metric space. A function $p:X\times X\to [0,\infty )$ is said to be the w-distance on X if the following are satisfied:

(a) 

$p(x,z)\le p(x,y)+p(y,z)$ for all $x,y,z\in X$;

(b) 

for any $x\in X,p(x,·):X\to [0,\infty )$ is lower semi-continuous (i.e., if $x\in X$ and $y_n\to y\in X$, then $p(x,y)\le {\lim \inf }_{n\to \infty }p(x,y_n)$;

(c) 

for any $\epsilon >0$, there exists $\delta >0$ such that $p(z,x)\le \delta$ and $p(z,y)\le \delta$ imply $d(x,y)\le \epsilon$.

Let $(X,d)$ be a metric space. The w-distance p on X is called symmetric if $p(x,y)=p(y,x)$ for all $x,y\in X$. Obviously, every metric d is a w-distance, but not conversely (for some more results, see [3,5,7]).

Next, we recall some examples in [21] to show that the w-distance is generalization of the metric d.

Example 2.

Let $(X,d)$ be a metric space. A function $p:X\times X\to [0,\infty )$ defined by $p(x,y)=c$ for every $x,y\in X$ is a w-distance on X, where c is a positive real number, but p is not a metric since $p(x,x)=c\ne 0$ for any $x\in X$.

Example 3.

Let $(X,\parallel ·\parallel )$ be a normed linear space. A function $p:X\times X\to [0,\infty )$ defined by $p(x,y)=\parallel x\parallel +\parallel y\parallel$ for all $x,y\in X$ is a w-distance on X.

Example 4.

Let D be a bounded and closed subset of a metric spaces X. Assume that D contain at least two points and c is a constant with $c\ge \delta \left(D\right)$, where $\delta \left(D\right)$ is the diameter of D. Then, a function $p:X\times X\to [0,\infty )$ defined by

$$p(x,y)=\left\{\begin{array}{c}d(x,y),ifx,y\in D,\hfill \\ c,ifx\notin Dory\notin D,\hfill \end{array}\right.$$

is the w-distance on X.

The following two lemmas are crucial for our results.

Lemma 1.

Let $(X,d)$ be a metric space with the w-distance p. Let $\left\{x_n\right\}$ and $\left\{y_n\right\}$ be sequences in X, where $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ are the sequences in $[0,\infty )$ converging to zero [1,21]. Then, the following conditions hold: for all $x,y,z\in X$,

(1) 

If $p(x_n,y)\le {\alpha }_n$ and $p(x_n,z)\le {\beta }_n$ for any $n\in N$, then $y=z$. In particular, if $p(x,y)=0$ and $p(x,z)=0$, then $y=z$;

(2) 

If $p(x_n,y_n)\le {\alpha }_n$ and $p(x_n,z)\le {\beta }_n$ for any $n\in N$, then $\left\{y_n\right\}$ converges to z;

(3) 

If $p(x_n,y_m)\le {\alpha }_n$ for any $n,m\in N$ with $m>n$, then $\left\{x_n\right\}$ is Cauchy sequence;

(4) 

If $p(y,x_n)\le {\alpha }_n$ for any $n\in N$, then $\left\{x_n\right\}$ is a Cauchy sequence.

Lemma 2.

Let $(X,d)$ be a metric space with the w-distance p. Let $\left\{x_n\right\}$ be a sequence in X such that, for each $\epsilon >0$, there exists $N_{\epsilon }\in \mathbb{N}$ such that $m>n>N_{\epsilon }$ implies $p(x_n,x_m)<\epsilon$ or $({\lim }_{m,n\to \infty }p(x_n,x_m)=0)$ [1]. Then, $\left\{x_n\right\}$ is a Cauchy sequence.

3. The Main Results

In this section, we establish some new existence theorems of common fixed points for the Ćirić type generalized F-contraction mapping in metric spaces with the w-distance. In addition, we give some examples to illustrate the obtained results.

First, we recall that a self mapping f defined on a metric space $(X,d)$ is called a quasi-contraction ([22]) if

$$d(fx,fy)\le \lambda \max \left\{d\right(x,y),d(x,fx),d(y,fy),d(x,fy),d(y,fx\left)\right\}$$

for all $x,y\in X$, where $0\le \lambda <1$.

Notice that the notion of quasi-contraction introduced by Ćirić [22] is known as one of the most general contractive type mappings—for more details, see, e.g., [4,23,24,25,26]).

Definition 7.

Let $(X,d)$ be a metric space equipped with a w-distance p. A mapping $f:X\to X$ is called theĆirić type generalized F-contraction (for short, the $CF$-contraction) if, for all $x,y\in X$, there exist $F\in {▵}_{\mathcal{F}}$ or $F\in \mathcal{F}$ and $\tau >0$ such that

$$p(fx,fy)>0\mathit{implies}\tau +F\left(p(fx,fy)\right)\le F\left(\lambda {\mathcal{M}}_p(x,y)\right)$$

(3)

for all $x,y\in X$, where $0\le \lambda <1$ and

$${\mathcal{M}}_p(x,y)=\max \{p(x,y),p(x,fx),p(y,fy),p(x,fy),p(y,fx)\}.$$

Definition 8.

Let $(X,d)$ be a metric space equipped with a w-distance p. A mapping $f:X\to X$ is called theĆirić-type generalized F-contraction with respect to g(for short, $C{F}_g$-contraction), where $g:X\to X$ is a mapping, if there exist $F\in {▵}_{\mathcal{F}}$ or $F\in \mathcal{F}$ and $\tau >0$ such that

$$p(fx,fy)>0\mathit{implies}\tau +F\left(p(fx,fy)\right)\le F\left(\lambda {\mathcal{M}}_p^g(x,y)\right)$$

(4)

for all $x,y\in X$, where $0\le \lambda <1$

$${\mathcal{M}}_p^g(x,y)=\max \{p(gx,gy),p(gx,fx),p(gy,fy),p(gx,fy),p(gy,fx)\}.$$

Remark 4.

Obviously, if g is the identity mapping, then Definition 8 reduces to Definition 7. Furthermore, in the case $p=d$ with $F\left(\alpha \right)=\ln \left(\alpha \right)$, Definition 7 becomes the Ćirić contraction [22].

Now, we recall the notion of ${\delta }_p$ and ${\mathcal{O}}_p^g$. Let $(X,d)$ be a metric space equipped with the w-distance p. For a subset $E\subseteq X$, we define

$${\delta }_p\left(E\right)=\sup \{p(x,y):x,y\in E\}.$$

If f and g satisfy (4), for any $x_0\in X$, we define a sequence $\left\{x_n\right\}$ in X by $f\left(x_n\right)=g\left(x_{n+1}\right)$ for each $n\ge 0$. Set $y_n=g\left(x_n\right)$, then we define the orbit

$${\mathcal{O}}^g(x_0,n)=\{y_1,y_2,y_3,\cdots ,y_n\},{\mathcal{O}}^g(x_0,\infty )=\{y_1,y_2,y_3,\cdots ,y_n,\dots \}$$

and ${\mathcal{O}}_p^g(x_0,n)$ is the orbit respected to the w-distance p.

Lemma 3.

Let $(X,d)$ be a metric space equipped with the w-distance p. Let $F\in {▵}_{\mathcal{F}}$ or $F\in \mathcal{F}$ and $f,g:X\to X$ be two mappings such that $f\left(X\right)\subseteq g\left(X\right)$ and g commutes with f. Assume that f and g satisfy (4). For any $x_0\in X$, define a sequence $\left\{x_n\right\}$ in X by $f\left(x_n\right)=g\left(x_{n+1}\right)$ for each $n\ge 0$. Then, we have the following:

(i) 

for each $x_0\in X$, $n\in \mathbb{N}$ and $i,j\in \mathbb{N}\cup \left\{0\right\}$ with $i,j\le n$,

$$\tau +F\left(p(f{x}_i,f{x}_j)\right)\le F\left(\lambda {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\right).$$

(ii) 

for each $x_0\in X$ and $n\in \mathbb{N}$, there exist $i,j\in \mathbb{N}$ with $i,j\le n$ such that

$${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)=\max \{p(g{x}_1,g{x}_1),p(g{x}_1,g{x}_i),p(g{x}_j,g{x}_1)\}.$$

(iii) 

for each $x_0\in X$,

$${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\le \frac{1}{1-\lambda }·\alpha \left(x_0\right),$$

where $\alpha \left(x_0\right):=p(g{x}_1,g{x}_1)$.

(iv) 

For each $n\in \mathbb{N}$,

$$\tau +F\left(p(f{x}_{n-1},f{x}_n)\right)\le F(\frac{{\lambda }^{n-1}}{1-\lambda }·\alpha \left(x_0\right)).$$

Furthermore,

$$\underset{n\to \infty }{\lim }p(f{x}_n,f{x}_{n+1})=0.$$

Proof. 

(i) Let $x_0\in X$, $n\in \mathbb{N}$ and $i,j\in \mathbb{N}\cup \left\{0\right\}$ with $i,j\le n$, then by (4), we have

$$\begin{array}{ccc}\hfill \tau +F\left(p(f{x}_i,f{x}_j)\right)& \le & F\left(\lambda {\mathcal{M}}_p^g(x_i,x_j)\right).\hfill \end{array}$$

(5)

Since

$$\begin{array}{ccc}\hfill {\mathcal{M}}_p^g(x_i,x_j)& =& \max \{p(g{x}_i,g{x}_j),p(g{x}_i,f{x}_i),p(g{x}_j,f{x}_j),p(g{x}_i,f{x}_j),p(g{x}_j,f{x}_i)\}\hfill \\ & \le & {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right),\hfill \end{array}$$

(6)

then, by (5), (6) and ($F1$), we get

$$\tau +F\left(p(f{x}_i,f{x}_j)\right)\le F\left(\lambda {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\right).$$

(ii) Clearly, from the definition of ${\delta }_p$, we get (ii).

(iii) Since

$${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)=\max \{p(g{x}_1,g{x}_1),p(g{x}_1,g{x}_i),p(g{x}_j,g{x}_1)\},$$

for some $1\le i,j\le n$. If ${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)=p(g{x}_1,g{x}_1)$,

$${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)-\lambda {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\le {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)=p(g{x}_1,g{x}_1).$$

Then, we get

$${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\le \frac{1}{1-\lambda }p(g{x}_1,g{x}_1).$$

If ${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)=p(g{x}_1,g{x}_i)$, then

$$\begin{array}{ccc}\hfill {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)=p(g{x}_1,g{x}_i)\le & p(g{x}_1,g{x}_1)+p(g{x}_1,g{x}_i)\le & p(g{x}_1,g{x}_1)+\lambda {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right).\hfill \end{array}$$

It follows that

$${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\le \frac{1}{1-\lambda }p(g{x}_1,g{x}_1).$$

If ${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)=p(g{x}_j,g{x}_1)$, then

$$\begin{array}{ccc}\hfill {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)=p(g{x}_j,g{x}_1)\le & p(g{x}_j,g{x}_1)+p(g{x}_1,g{x}_1)\le & p(g{x}_1,g{x}_1)+\lambda {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\hfill \end{array}$$

and hence

$${\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\le \frac{1}{1-\lambda }p(g{x}_1,g{x}_1).$$

Therefore, for all the cases, we get

$$\begin{array}{c}\hfill {\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\le \frac{1}{1-\lambda }p(g{x}_1,g{x}_1)=\frac{1}{1-\lambda }·\alpha \left(x_0\right).\end{array}$$

(iv) For each $n\in \mathbb{N}$, by (4), we have

$$\begin{array}{ccc}\hfill \tau +F\left(p(g{x}_n,g{x}_{n+1})\right)& =& \tau +F\left(p(f{x}_{n-1},f{x}_n)\right)\hfill \\ & \le & F\left(\lambda {\mathcal{M}}_p^g(x_{n-1},x_n)\right).\hfill \end{array}$$

(7)

Note that

$$\begin{array}{ccc}\hfill {\mathcal{M}}_p^g(x_{n-1},x_n)& =& \max \{p(g{x}_{n-1},g{x}_n),p(g{x}_{n-1},f{x}_{n-1}),p(g{x}_n,f{x}_n),p(g{x}_{n-1},f{x}_n),p(g{x}_n,f{x}_{n-1})\}\hfill \\ & =& \max \{p(g{x}_{n-1},g{x}_n),p(g{x}_n,g{x}_{n+1}),p(g{x}_{n-1},g{x}_{n+1}),p(g{x}_n,g{x}_n)\}.\hfill \end{array}$$

(8)

By (F1), (7) and (8), we have

$$p(g{x}_n,g{x}_{n+1})\le \lambda \max \{p(g{x}_{n-1},g{x}_n),p(g{x}_n,g{x}_{n+1}),p(g{x}_{n-1},g{x}_{n+1}),p(g{x}_n,g{x}_n)\}.$$

(9)

Furthermore, for any $n\in \mathbb{N}$, we have

$$\begin{array}{ccc}\hfill \tau +F\left(p(g{x}_{n-1},g{x}_{n+1})\right)& =& \tau +F\left(p(f{x}_{n-2},f{x}_n)\right)\hfill \\ & \le & F\left(\lambda {\mathcal{M}}_p^g(x_{n-2},x_n)\right),\hfill \end{array}$$

(10)

and

$$\begin{array}{ccc}\hfill \tau +F\left(p(g{x}_n,g{x}_n)\right)& =& \tau +F\left(p(f{x}_{n-1},f{x}_{n-1})\right)\hfill \\ & \le & F\left(\lambda {\mathcal{M}}_p^g(x_{n-1},x_{n-1})\right),\hfill \end{array}$$

(11)

with

$$\begin{array}{ccc}\hfill {\mathcal{M}}_p^g(x_{n-2},x_n)& =& \max \{p(g{x}_{n-2},g{x}_n),p(g{x}_{n-2},f{x}_{n-2}),p(g{x}_n,f{x}_n),p(g{x}_{n-2},f{x}_n),p(g{x}_n,f{x}_{n-2})\}\hfill \\ & =& \max \{p(g{x}_{n-2},g{x}_n),p(g{x}_{n-2},g{x}_{n-1}),p(g{x}_n,g{x}_{n+1}),p(g{x}_{n-2},g{x}_{n+1}),p(g{x}_n,g{x}_{n-1})\}\hfill \end{array}$$

(12)

and

$$\begin{array}{ccc}\hfill {\mathcal{M}}_p^g(x_{n-1},x_{n-1})& =& \max \{p(g{x}_{n-1},g{x}_{n-1}),p(g{x}_{n-1},f{x}_{n-1})\}\hfill \\ & =& \max \{p(g{x}_{n-1},g{x}_{n-1}),p(g{x}_{n-1},g{x}_n)\}.\hfill \end{array}$$

(13)

By ($F1$), (10) and (12), we have

$$\begin{array}{ccc}\hfill p(g{x}_{n-1},g{x}_{n+1})& \le & \lambda \max \{p(g{x}_{n-2},g{x}_n),p(g{x}_{n-2},g{x}_{n-1}),p(g{x}_n,g{x}_{n+1}),p(g{x}_{n-2},g{x}_{n+1}),p(g{x}_n,g{x}_{n-1})\}.\hfill \end{array}$$

(14)

Similarly, by ($F1$), (11) and (13),

$$\begin{array}{ccc}\hfill p(g{x}_n,g{x}_n)& \le & \lambda \max \{p(g{x}_{n-1},g{x}_n),p(g{x}_{n-1},g{x}_n)\}.\hfill \end{array}$$

(15)

Therefore, by (7), (9), (14) and (15), we get

$$\begin{array}{ccc}\hfill \tau +F\left(p(f{x}_{n-1},f{x}_n)\right)& \le & F\left(\lambda {\mathcal{M}}_p^g(x_{n-1},x_n)\right)\hfill \\ & \le & F\left({\lambda }^2\max \{{\mathcal{M}}_p^g(x_i,x_j):n-2\le i\le n,n-1\le j\le n\}\right)\hfill \\ & =& F\left({\lambda }^2\max \{p(g{x}_i,g{x}_j):n-2\le i\le n,n-1\le j\le n+1\}\right).\hfill \end{array}$$

By ($F1$), we get

$$p(f{x}_{n-1},f{x}_n)\le {\lambda }^2\max \{p(g{x}_i,g{x}_j):n-2\le i\le n,n-1\le j\le n+1\}.$$

Continuing this prosses and using ($F1$), we have

$$\begin{array}{ccc}\hfill \tau +F(p(f{x}_{n-1},f{x}_n)& \le & F\left({\lambda }^2\max \{p(g{x}_i,g{x}_j):n-2\le i\le n,n-1\le j\le n+1\}\right)\hfill \\ & \le & F\left({\lambda }^3\max \{{\mathcal{M}}_p^g(x_i,x_j):n-3\le i\le n,n-2\le j\le n\}\right)\hfill \\ & \le & F\left({\lambda }^3\max \{p(g{x}_i,g{x}_j):n-3\le i\le n,n-2\le j\le n+1\}\right)\hfill \\ & \le & \cdots \hfill \\ & \le & F\left({\lambda }^{n-1}\max \{p(g{x}_i,g{x}_j):1\le i\le n,2\le j\le n+1\}\right)\hfill \\ & \le & F\left({\lambda }^{n-1}{\delta }_p\left({\mathcal{O}}_p^g(x_0,n+1)\right)\right)\hfill \\ & \le & F\left(\frac{{\lambda }^{n-1}}{1-\lambda }·\alpha \left(x_0\right)\right)\hfill \end{array}$$

(16)

and hence

$$p(f{x}_{n-1},f{x}_n)\le \frac{{\lambda }^{n-1}}{1-\lambda }·\alpha \left(x_0\right).$$

Therefore, by $0\le \lambda <1$, we obtain that

$$\underset{n\to \infty }{\lim }p(f{x}_n,f{x}_{n+1})=0.$$

This completes the proof. □

Theorem 1.

Let $(X,d)$ be a complete metric space equipped with the w-distance p. Let $F\in {▵}_{\mathcal{F}}$ and $f,g:X\to X$ be two mappings such that $f\left(X\right)\subseteq g\left(X\right)$ and g is commuted with f. Assume that the following hold:

(i) 

f and g satisfy (4);

(ii) 

for all $y\in X$ with $gy\ne fy$,

$$\inf \left\{p\right(gx,y)+p(gx,fx\left)\right\}>0.$$

(17)

Then, f and g have a unique common fixed point $u_{★}$ in X and $p(u_{★},u_{★})=0$. Furthermore, if $\left\{g{x}_n\right\}$ converges to $u_{★}\in X$, then

$$\underset{n\to \infty }{\lim }p(gf{x}_n,f{u}_{★})=0=\underset{n\to \infty }{\lim }p(fg{x}_n,g{u}_{★}).$$

Proof. 

If we have $g\left(x_0\right)=f\left(x_0\right)=x_0$ for some $x_0\in X$, then there is nothing to prove. Suppose that $x_0\in X$ such that $g\left(x_0\right)\ne f\left(x_0\right)$. Since $f\left(X\right)\subseteq g\left(X\right)$, then there exists $x_1\in X$ such that $f\left(x_0\right)=g\left(x_1\right)$. Again, since $f\left(X\right)\subseteq g\left(X\right)$, then there exists $x_2\in X$ such that $f\left(x_1\right)=g\left(x_2\right)$. Continuing this way, we have a sequence $\left\{g{x}_n\right\}$ such that $f\left(x_n\right)=g\left(x_{n+1}\right)$ with $x_{n+1}\in X.$ Now, we will show that

$$\underset{m,n\to \infty }{\lim }p(f{x}_n,f{x}_m)=0.$$

(18)

Let $m>n$ and from Lemma 3(iv), we have

$$p(f{x}_n,f{x}_{n+1})\le \frac{{\lambda }^n}{1-\lambda }·\alpha \left(x_0\right).$$

Hence,

$$\begin{array}{cc}\hfill p(f{x}_n,f{x}_m)& \le p(f{x}_n,f{x}_{n+1})+p(f{x}_{n+1},f{x}_{n+2})+\cdots +p(f{x}_{m-1},f{x}_m)\hfill \\ & \le \left(\frac{{\lambda }^n}{1-\lambda }+\frac{{\lambda }^{n+1}}{1-\lambda }+\cdots +\frac{{\lambda }^{m-1}}{1-\lambda }\right)·\alpha \left(x_0\right)\hfill \\ & \le \frac{{\lambda }^n}{{(1-\lambda )}^2}·\alpha \left(x_0\right).\hfill \end{array}$$

which, on taking $m,n\to \infty ,$ we obtain (18). By Lemma 2, the sequence $\left\{f{x}_n\right\}$ is a Cauchy sequence. Consequently, the sequence $\left\{g{x}_n\right\}$ is also a Cauchy sequence. Since X is complete metric space, the sequence $\left\{g{x}_n\right\}$ converges to some element $x_{★}\in X$, and $p(x,·)$ is lower semi-continuous, we have

$$\begin{array}{ccc}\hfill p(g{x}_n,x_{★})& \le & \underset{m\to \infty }{\lim \inf }p(g{x}_n,g{x}_m)\hfill \\ & \le & \frac{{\lambda }^n}{{(1-\lambda )}^2}·\alpha \left(x_0\right).\hfill \end{array}$$

(19)

Now, we will prove that $f{x}_{★}=g{x}_{★}.$ Suppose $f{x}_{★}\ne g{x}_{★};$ then, by (19) and Lemma 3(iv) with $\left(F1\right),$ we imply

$$\begin{array}{cc}\hfill 0& <\inf \{p(g{x}_n,x_{★})+p(g{x}_n,f{x}_n):n\in \mathbb{N}\}\hfill \\ & \le \inf \{\frac{{\lambda }^n}{{(1-\lambda )}^2}·\alpha \left(x_0\right)+p(f{x}_{n-1},f{x}_n):n\in \mathbb{N}\}\hfill \\ & \le \inf \{\frac{{\lambda }^{n-1}}{{(1-\lambda )}^2}·\alpha \left(x_0\right)+\frac{{\lambda }^{n-1}}{(1-\lambda )}·\alpha \left(x_0\right):n\in \mathbb{N}\}\hfill \\ & =\inf \{\frac{(2-\lambda ){\lambda }^{n-1}}{{(1-\lambda )}^2}·\alpha \left(x_0\right):n\in \mathbb{N}\}\hfill \\ & =\frac{(2-\lambda )}{{(1-\lambda )}^2}·\alpha \left(x_0\right)·\inf \{{\lambda }^{n-1}:n\in \mathbb{N}\}\hfill \\ & =0,\hfill \end{array}$$

which is a contradiction and hence $f{x}_{★}=g{x}_{★}.$ If $p(g{x}_{★},g{x}_{★})\ne 0$, then we can write

$$\begin{array}{cc}\hfill \tau +F\left(p(g{x}_{★},g{x}_{★})\right)& =\tau +F\left(p(f{x}_{★},f{x}_{★})\right)\hfill \\ & \le F\left(\lambda {\mathcal{M}}_p^g(x_{★},x_{★})\right)\hfill \\ & =F\left(\lambda \max \{p(g{x}_{★},g{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g{x}_{★},f{x}_{★})\}\right)\hfill \\ & =F\left(\lambda p(g{x}_{★},g{x}_{★})\right).\hfill \end{array}$$

Using ($F1$), we get $p(g{x}_{★},g{x}_{★})<\lambda p(g{x}_{★},g{x}_{★})$ which is a contradiction, and thus $p(g{x}_{★},g{x}_{★})=0$. Furthermore, if $p(g^2{x}_{★},g^2{x}_{★})\ne 0$ and since g commutes with f,

$$\begin{array}{cc}\hfill \tau +F\left(p(g^2{x}_{★},g^2{x}_{★})\right)& =\tau +F(p(f\left(g{x}_{★}\right),f\left(g\left(x_{★}\right)\right))\hfill \\ & \le F\left(\lambda {\mathcal{M}}_p^g(g{x}_{★},g{x}_{★})\right)\hfill \\ & =F\left(\lambda \max \{p(g^2{x}_{★},g^2{x}_{★}),p(g^2{x}_{★},fg{x}_{★})\}\right)\hfill \\ & =F\left(\lambda \max \left\{p(g^2{x}_{★},g^2{x}_{★})\right\}\right)\hfill \\ & =F\left(\lambda p(g^2{x}_{★},g^2{x}_{★})\right).\hfill \end{array}$$

By a similar argument as above, $p(g^2{x}_{★},g^2{x}_{★})<\lambda p(g^2{x}_{★},g^2{x}_{★}),$ which is a contradiction, then we must have $p(g^2{x}_{★},g^2{x}_{★})=0$. Now, we will show that $p(g^2{x}_{★},g{x}_{★})=p(g{x}_{★},g^2{x}_{★})=0$. Suppose that $p(g^2{x}_{★},g{x}_{★})\ne 0$ and $p(g{x}_{★},g^2{x}_{★})\ne 0$, then

$$\begin{array}{cc}\hfill \tau +F\left(p(g^2{x}_{★},g{x}_{★})\right)& =\tau +F\left(p(fg{x}_{★},f{x}_{★})\right)\hfill \\ & \le F\left(\lambda {\mathcal{M}}_p^g(g{x}_{★},x_{★})\right)\hfill \\ & =F\left(\lambda \max \{p(g^2{x}_{★},g{x}_{★}),p(g^2{x}_{★},fg{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g^2{x}_{★},f{x}_{★}),p(g{x}_{★},fg{x}_{★})\}\right)\hfill \\ & =F\left(\lambda \max \{p(g^2{x}_{★},g{x}_{★}),p(g^2{x}_{★},g^2{x}_{★}),p(g{x}_{★},g{x}_{★}),p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}\right)\hfill \\ & =F\left(\lambda \max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \tau +F\left(p(g{x}_{★},g^2{x}_{★})\right)& =\tau +F\left(p(f{x}_{★},gf{x}_{★})\right)\hfill \\ & \le F\left(\lambda {\mathcal{M}}_p^g(x_{★},g{x}_{★})\right)\hfill \\ & =F\left(\lambda \max \{p(g{x}_{★},g^2{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g^2{x}_{★},fg{x}_{★}),p(g{x}_{★},fg{x}_{★}),p(g^2{x}_{★},f{x}_{★})\}\right)\hfill \\ & =F\left(\lambda \max \{p(g{x}_{★},g^2{x}_{★}),p(g{x}_{★},g{x}_{★}),p(g^2{x}_{★},g^2{x}_{★}),p(g{x}_{★},g^2{x}_{★}),p(g^2{x}_{★},g{x}_{★})\}\right)\hfill \\ & =F\left(\lambda \max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}\right).\hfill \end{array}$$

On utilizing ($F1$), we get

$$p(g^2{x}_{★},g{x}_{★})<\lambda \max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}$$

(20)

and

$$p(g{x}_{★},g^2{x}_{★})<\lambda \max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}.$$

(21)

Therefore, by (20) and (21), we have

$$\max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}<\lambda \max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\},$$

which implies that $\max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}=0$. Thus, $p(g^2{x}_{★},g{x}_{★})=p(g{x}_{★},g^2{x}_{★})=0$, by applying Lemma 1(i), we get $g^2{x}_{★}=g{x}_{★}$. Furthermore,

$$fg{x}_{★}=gf{x}_{★}=g^2{x}_{★}=g{x}_{★}.$$

Putting $u_{★}=g{x}_{★}$, then we have $f{u}_{★}=g{u}_{★}=u_{★}.$ That is, $u_{★}$ is a common fixed point of f and g. To prove the uniqueness part, suppose that there exists $v_{★}\in X$ such that $f{v}_{★}=g{v}_{★}=v_{★}$ with $p(f{u}_{★},f{v}_{★})>0$. By a similar argument as above, we can see that $p(v_{★},v_{★})=0$ since

$$\begin{array}{ccc}\hfill \tau +F\left(p(u_{★},v_{★})\right)& =& \tau +F\left(p(f{u}_{★},f{v}_{★})\right)\hfill \\ & \le & F\left(\lambda {\mathcal{M}}_p^g(u_{★},v_{★})\right)\hfill \\ & =& F\left(\lambda \max \{p(g{u}_{★},g{v}_{★}),p(g{u}_{★},f{u}_{★}),p(g{v}_{★},f{v}_{★}),p(g{u}_{★},f{v}_{★}),p(g{v}_{★},f{u}_{★})\}\right)\hfill \\ & =& F\left(\lambda \max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}\right)\hfill \end{array}$$

(22)

and

$$\begin{array}{ccc}\hfill \tau +F\left(p(v_{★},u_{★})\right)& =& \tau +F\left(p(f{v}_{★},f{u}_{★})\right)\hfill \\ & \le & F\left(\lambda {\mathcal{M}}_p^g(v_{★},u_{★})\right)\hfill \\ & =& F\left(\lambda \max \{p(g{v}_{★},g{u}_{★}),p(g{v}_{★},f{v}_{★}),p(g{u}_{★},f{u}_{★}),p(g{v}_{★},f{u}_{★}),p(g{u}_{★},f{v}_{★})\}\right)\hfill \\ & =& F\left(\lambda \max \{p(v_{★},u_{★}),p(u_{★},v_{★})\}\right).\hfill \end{array}$$

(23)

By (22), (23) and ($F1$), we have

$$p(u_{★},v_{★})<\lambda \max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}$$

and

$$p(v_{★},u_{★})<\lambda \max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}.$$

Hence, we have

$$\max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}<\lambda \max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}.$$

It follows that $p(u_{★},v_{★})=p(v_{★},u_{★})=0$. From $p(v_{★},u_{★})=p(v_{★},v_{★})=0$ and Lemma 1(i), we get $v_{★}=u_{★}$. This completes the proof.  □

If g is the identity mapping in Theorem 1, then the following holds:

Corollary 1.

Let $(X,d)$ be a complete metric space equipped with the w-distance p. Let $F\in {▵}_{\mathcal{F}}$ and suppose that the following holds:

(i) 

f satisfies (3);

(ii) 

for all $y\in X$ with $y\ne fy$,

$$\inf \left\{p\right(x,y)+p(x,fx\left)\right\}>0.$$

(24)

Then, f has a unique fixed point $u_{★}$ in X and $p(u_{★},u_{★})=0$. Furthermore, if $\left\{x_n\right\}$ converges to $u_{★}\in X$, then $\underset{n\to \infty }{\lim }p(f{x}_n,u_{★})=0.$

If we take $F\left(\alpha \right)=\ln \alpha$ in Theorem 1, then we obtain the following:

Corollary 2.

Let $(X,d)$ be a complete metric space equipped with the w-distance p. Let $f,g:X\to X$ be two mappings such that $f\left(X\right)\subseteq g\left(X\right)$ and g commutes with f. Assume that f and g satisfy

$$p(fx,fy)\le k\max \left\{p\right(gx,gy),p(gx,fx),p(gy,fy),p(gx,fy),p(gy,fx)$$

for some $0\le k\le \lambda e^{-\tau }$, $\tau >0,$ for all $x,y\in X$, and, for all $y\in X$ with $gy\ne fy$,

$$\inf \left\{p\right(gx,y)+p(gx,fx\left)\right\}>0.$$

(25)

Then, f and g have a unique common fixed point $u_{★}$ in X and $p(u_{★},u_{★})=0$. Furthermore, if $\left\{g{x}_n\right\}$ converges to $u_{★}\in X$, then

$$\underset{n\to \infty }{\lim }p(gf{x}_n,f{u}_{★})=0=\underset{n\to \infty }{\lim }p(fg{x}_n,g{u}_{★}).$$

The following example illustrates Theorem 1:

Example 5.

Let $X=\{\frac{1}{n};n\in \mathbb{N}\}\cup \left\{0\right\}$ with usual metric $d(x,y)=|x-y|$ and the w-distance p on X defined by $p(x,y)=\max \{x,y\}$ for all $x,y\in X$. For any $n\in \mathbb{N}$, define the mapping $f,g:X\to X$ by

$$f\left(x\right)=\left\{\begin{array}{cc}\frac{1}{n^4},\hfill & ifx=\frac{1}{n},n\ge 2;\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

$$g\left(x\right)=\left\{\begin{array}{cc}\frac{1}{n^2},\hfill & ifx=\frac{1}{n},n\ge 2;\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

Then, we have $f\left(X\right)\subseteq g\left(X\right)$. Furthermore, g commutes with f and $\inf \left\{p\right(gx,y)+p(gx,fx\left)\right\}>0$ when $gy\ne fy$. Now, we will show that the mapping f and g satisfy (4) with $\lambda =0.8$, $\tau =0.75>0$ and $F\left(\alpha \right)=\frac{1}{1-e^{\alpha }}$. Clearly, $F\in {▵}_{\mathcal{F}}$, we distinguish two cases.

Case ILet $x=0$ (or x = 1) and $y=\frac{1}{n}$, when n ≥ 2. Then,

$$p(fx,fy)=\max \left\{0,\frac{1}{n^4}\right\}=\frac{1}{n^4}>0$$

and

$$\begin{array}{ccc}\hfill {\mathcal{M}}_p^g(x,y)& =& \max \left\{p\right(gx,gy),p(gx,fx),p(gy,fy),p(gx,fy),p(gy,fx\left)\right\}\hfill \\ & =& \max \{gy,0,fy\}\hfill \\ & =& \frac{1}{n^2}.\hfill \end{array}$$

(26)

Hence, the L.H.S. (the left hand side) of (4),

$$\tau +F\left(p(fx,fy)\right)=0.75+\frac{1}{1-e^{\frac{1}{n^4}}}$$

and the R.H.S. (the right hand side) of (4),

$$F\left(\lambda {\mathcal{M}}_p^g(fx,fy)\right)=\frac{1}{1-e^{0.8·\frac{1}{n^2}}}.$$

Following figures (Figure 1 and Figure 2), we compare R.H.S. and L.H.S. in 2D, 3D views.

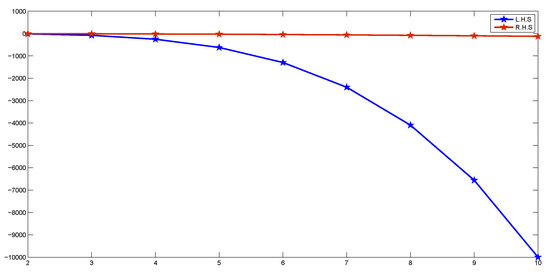
Figure 1. The value of comparison of L.H.S. and R.H.S. of (4) in 2D view.

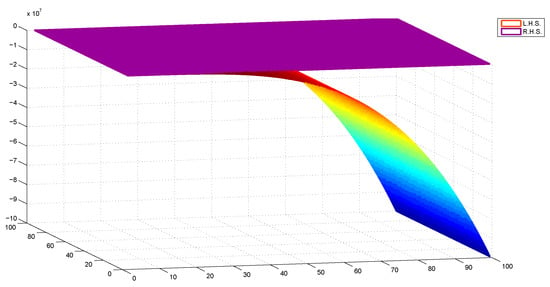
Figure 2. The value of comparison of L.H.S. and R.H.S. of (4) in 3D view.

Now, we give numerical comparisons of L.H.S. and R.H.S. of (4) as follows (Table 1):

Table 1. The numerical comparison of L.H.S. and R.H.S. of (4).

n	$\mathit{\tau }+\mathit{F}\left(\mathit{p}({\mathit{fx}}_{\mathit{n}},{\mathit{fx}}_{\mathit{m}})\right)$	$\mathit{F}\left(\mathit{\lambda }{\mathcal{M}}_{\mathit{p}}^{\mathit{g}}({\mathit{x}}_{\mathit{n}},{\mathit{x}}_{\mathit{m}})\right)$
2	−14.755208	−4.5166556
3	−79.751029	−10.7574064
4	−254.750326	−19.5041665
5	−623.750133	−30.7526666
6	−1294.750064	−44.5018518
7	−2399.750035	−60.7513605
8	−4094.750020	−79.5010417
9	−6559.750013	−100.7508230
10	−9998.750008	−124.5006667
20	−159,998.750002	−499.5001667
30	−809,998.750009	−1124.5000741
50	−6,249,998.750220	−3124.5000267
100	−99,999,999.857747	−12,499.5000067
⋮	⋮	⋮

Therefore, $\tau +F\left(p(fx,fy)\right)\le F\left(\lambda {\mathcal{M}}_p^g(x,y)\right)$.

Case IILet $x=\frac{1}{n}$ and $y=\frac{1}{m}$, when n, m ≥ 2. We can assume that $n\le m$; then,

$$p(fx,fy)=\max \left\{\frac{1}{n^4},\frac{1}{m^4}\right\}=\frac{1}{n^4}>0$$

and

$$\begin{array}{ccc}\hfill {\mathcal{M}}_p^g(x,y)& =& \max \left\{p\right(gx,gy),p(gx,fx),p(gy,fy),p(gx,fy),p(gy,fx\left)\right\}\hfill \\ & =& \max \{\frac{1}{n^2},\frac{1}{m^2}\}\hfill \\ & =& \frac{1}{n^2}.\hfill \end{array}$$

(27)

Similar to case I, we can see that $\tau +F\left(p(fx,fy)\right)\le F\left(\lambda {\mathcal{M}}_p^g(x,y)\right)$.

Case IIILet $x=\frac{1}{n}$, when n ≥ 2 and $y=0$ (or y = 1). Then,

$$p(fx,fy)=\max \left\{\frac{1}{n^4},0\right\}=\frac{1}{n^4}>0$$

and

$$\begin{array}{ccc}\hfill {\mathcal{M}}_p^g(x,y)& =& \max \left\{p\right(gx,gy),p(gx,fx),p(gy,fy),p(gx,fy),p(gy,fx\left)\right\}\hfill \\ & =& \max \{gx,0,fx\}\hfill \\ & =& \frac{1}{n^2}.\hfill \end{array}$$

(28)

Hence, the L.H.S. of (4),

$$\tau +F\left(p(fx,fy)\right)=0.75+\frac{1}{1-e^{\frac{1}{n^4}}}$$

and the R.H.S. of (4),

$$F\left(\lambda {\mathcal{M}}_p^g(fx,fy)\right)=\frac{1}{1-e^{0.8·\frac{1}{n^2}}}.$$

Similar to case I, we can see that $\tau +F\left(p(fx,fy)\right)\le F\left(\lambda {\mathcal{M}}_p^g(x,y)\right)$.

Thus, all the conditions of Theorem 1 are satisfied and $x=0$ is unique common fixed point of f and g. Moreover, $p(0,0)=0$. For any $x_0\in X,$ define $f{x}_n=g{x}_{n+1}$. Then, $\left\{g{x}_n\right\}$ converges to $0\in X$ and

$$\underset{n\to \infty }{\lim }p(gf{x}_n,f\left(0\right))=0=\underset{n\to \infty }{\lim }p(fg{x}_n,g\left(0\right)).$$

Next, we improve the $C{F}_g$-contraction mapping by removing the constant $\lambda$ in (4) and prove new common fixed point theorems as follows:

Theorem 2.

Let $(X,d)$ be a complete metric space equipped with a w-distance p and $f:X\to X$ and $g:X\to X$ be two mappings such that $f\left(X\right)\subseteq g\left(X\right)$ and g commutes with f. Assume that there exist $F\in \mathcal{F}$ and the following holds:

(i) 

for any $x,y\in X$, with $fx\ne fy,$ there exits $\tau >0$ such that

$$p(fx,fy)>0\mathit{implies}\tau +F\left(p(fx,fy)\right)\le F\left({\mathcal{M}}_p^g(x,y)\right);$$

(29)

(ii) 

${\lim }_{n\to \infty }F\left({\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\right)$ exits;

(iii) 

for all $y\in X$ with $gy\ne fy$,

$$\inf \left\{p\right(gx,y)+p(gx,fx\left)\right\}>0.$$

(30)

Then, f and g have a unique common fixed point $u_{★}$ in X and $p(u_{★},u_{★})=0$. Furthermore, if $\left\{g{x}_n\right\}$ converges to $u_{★}\in X$, then

$$\underset{n\to \infty }{\lim }p(gf{x}_n,f{u}_{★})=0=\underset{n\to \infty }{\lim }p(fg{x}_n,g{u}_{★}).$$

Proof. 

By (7), (9), (14) and (15), we get

$$\begin{array}{ccc}\hfill F(p(f{x}_{n-1},f{x}_n)& \le & F\left({\mathcal{M}}_p^g(x_{n-1},x_n)\right)-\tau \hfill \\ & \le & F\left(\max \{{\mathcal{M}}_p^g(x_i,x_j):n-2\le i\le n-1,n-1\le j\le n\}\right)-\tau \hfill \\ & =& F\left(\max \{p(g{x}_i,g{x}_j):n-2\le i\le n,n-1\le j\le n+1\}\right)-\tau .\hfill \end{array}$$

Continuing this process and using (F1), we have

$$\begin{array}{ccc}\hfill F(p(f{x}_{n-1},f{x}_n)& \le & F\left(\max \{p(g{x}_i,g{x}_j):n-2\le i\le n,n-1\le j\le n+1\}\right)-\tau \hfill \\ & \le & F\left(\max \{{\mathcal{M}}_p^g(x_i,x_j):n-3\le i\le n-1,n-2\le j\le n\}\right)-2\tau \hfill \\ & \le & F\left(\max \{p(g{x}_i,g{x}_j):n-3\le i\le n,n-2\le j\le n+1\}\right)-2\tau \hfill \\ & \le & \cdots \hfill \\ & \le & F\left(\max \{p(g{x}_i,g{x}_j):1\le i\le n,2\le j\le n+1\}\right)-(n-1)\tau \hfill \\ & \le & F\left({\delta }_p\left({\mathcal{O}}_p^g(x_0,n+1)\right)\right)-(n-1)\tau .\hfill \end{array}$$

(31)

Using hypothesis $\left(ii\right)$, we get ${\lim }_{n\to \infty }F\left(p(f{x}_{n-1},f{x}_n)\right)=-\infty .$ Hence, ${\lim }_{n\to \infty }p(f{x}_{n-1},f{x}_n)=0$, and then

$$\begin{array}{ccc}\hfill p(f{x}_{n-1},f{x}_n)& \le & {\gamma }_n\hfill \end{array}$$

(32)

for a sequence $\left\{{\gamma }_n\right\}$ converging to zero. Using the same argument as the proof of Theorem 1, the sequence $\left\{g{x}_n\right\}$ is a Cauchy sequence and converges to some element $x_{★}\in X$. Furthermore, by $p(x,·)$ being lower semi-continuous, we have

$$\begin{array}{ccc}\hfill p(g{x}_n,x_{★})& \le & \underset{m\to \infty }{\lim \inf }p(g{x}_n,g{x}_m)\hfill \\ & \le & {\beta }_n\hfill \end{array}$$

(33)

for a sequence $\left\{{\beta }_n\right\}$ converges to zero. Now, we will prove that $f{x}_{★}=g{x}_{★}.$ Suppose $f{x}_{★}\ne g{x}_{★};$ then, by (6), (32), (33) and Lemma 3(iv) with $\left(F1\right)$, imply

$$\begin{array}{cc}\hfill 0& \le \inf \{p(g{x}_n,x_{★})+p(g{x}_n,f{x}_n):n\in \mathbb{N}\}\hfill \\ & \le \inf \{{\beta }_n+p(f{x}_{n-1},f{x}_n):n\in \mathbb{N}\}\hfill \\ & \le \inf \{{\beta }_n+{\gamma }_n:n\in \mathbb{N}\},\hfill \\ & =0\hfill \end{array}$$

which is a contradiction and hence $f{x}_{★}=g{x}_{★}.$ If $p(g{x}_{★},g{x}_{★})\ne 0$, then we can write

$$\begin{array}{cc}\hfill \tau +F\left(p(g{x}_{★},g{x}_{★})\right)& =\tau +F\left(p(f{x}_{★},f{x}_{★})\right)\hfill \\ & \le F\left({\mathcal{M}}_p^g(x_{★},x_{★})\right)\hfill \\ & =F\left(\max \{p(g{x}_{★},g{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g{x}_{★},f{x}_{★})\}\right)\hfill \\ & =F\left(p(g{x}_{★},g{x}_{★})\right),\hfill \end{array}$$

which is a contradiction because $\tau >0$, and thus $p(g{x}_{★},g{x}_{★})=0$. Moreover, if $p(g^2{x}_{★},g^2{x}_{★})\ne 0$, then as g commutes with f, we have

$$\begin{array}{cc}\hfill \tau +F\left(p(g^2{x}_{★},g^2{x}_{★})\right)& =\tau +F(p(f\left(g{x}_{★}\right),f\left(g\left(x_{★}\right)\right))\hfill \\ & \le F\left({\mathcal{M}}_p^g(g{x}_{★},g{x}_{★})\right)\hfill \\ & =F\left(\max \{p(g^2{x}_{★},g^2{x}_{★}),p(g^2{x}_{★},fg{x}_{★})\}\right)\hfill \\ & =F\left(\max \left\{p(g^2{x}_{★},g^2{x}_{★})\right\}\right)\hfill \\ & =F\left(p(g^2{x}_{★},g^2{x}_{★})\right).\hfill \end{array}$$

By a similar argument as above, then we must have $p(g^2{x}_{★},g^2{x}_{★})=0$. Now, we will show that $p(g^2{x}_{★},g{x}_{★})=p(g{x}_{★},g^2{x}_{★})=0$. Suppose that $p(g^2{x}_{★},g{x}_{★})\ne 0$ and $p(g{x}_{★},g^2{x}_{★})\ne 0$, then

$$\begin{array}{cc}\hfill \tau +F\left(p(g^2{x}_{★},g{x}_{★})\right)& =\tau +F\left(p(fg{x}_{★},f{x}_{★})\right)\hfill \\ & \le F\left({\mathcal{M}}_p^g(g{x}_{★},x_{★})\right)\hfill \\ & =F\left(\max \{p(g^2{x}_{★},g{x}_{★}),p(g^2{x}_{★},fg{x}_{★}),p(g^2{x}_{★},f{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g{x}_{★},fg{x}_{★})\}\right)\hfill \\ & =F\left(\max \{p(g^2{x}_{★},g{x}_{★}),p(g^2{x}_{★},g^2{x}_{★}),p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}\right)\hfill \\ & =F\left(\max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \tau +F\left(p(g{x}_{★},g^2{x}_{★})\right)& =\tau +F\left(p(f{x}_{★},gf{x}_{★})\right)\hfill \\ & \le F\left({\mathcal{M}}_p^g(x_{★},g{x}_{★})\right)\hfill \\ & =F\left(\max \{p(g{x}_{★},g^2{x}_{★}),p(g{x}_{★},f{x}_{★}),p(g{x}_{★},fg{x}_{★}),p(g^2{x}_{★},f{x}_{★}),p(g{x}_{★},f{x}_{★})\}\right)\hfill \\ & =F\left(\max \{p(g{x}_{★},g^2{x}_{★}),p(g{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★}),p(g^2{x}_{★},g{x}_{★}),p(g^2{x}_{★},g{x}_{★})\}\right)\hfill \\ & =F\left(\max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}\right).\hfill \end{array}$$

On utilizing (F1), we get

$$p(g^2{x}_{★},g{x}_{★})<\max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}$$

(34)

and

$$p(g{x}_{★},g^2{x}_{★})<\max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}.$$

(35)

Therefore, by (34) and (35), we have

$$\max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\}<\max \{p(g^2{x}_{★},g{x}_{★}),p(g{x}_{★},g^2{x}_{★})\},$$

which is a contradiction. Thus $p(g^2{x}_{★},g{x}_{★})=p(g{x}_{★},g^2{x}_{★})=0$, by applying Lemma 1(i), we get $g^2{x}_{★}=g{x}_{★}$. Furthermore,

$$fg{x}_{★}=gf{x}_{★}=g^2{x}_{★}=g{x}_{★}.$$

Putting $u_{★}=g{x}_{★}$, then we have $f{u}_{★}=g{u}_{★}=u_{★}.$ That is, $u_{★}$ is a common fixed point of f and g. To prove the uniqueness part, suppose that there exists $v_{★}\in X$ such that $f{v}_{★}=g{v}_{★}=v_{★}$ with $p(f{u}_{★},f{v}_{★})>0$. By a similar argument as above, we can see that $p(v_{★},v_{★})=0$ since

$$\begin{array}{ccc}\hfill \tau +F\left(p(u_{★},v_{★})\right)& =& \tau +F\left(p(f{u}_{★},f{v}_{★})\right)\hfill \\ & \le & F\left({\mathcal{M}}_p^g(u_{★},v_{★})\right)\hfill \\ & =& F\left(\max \{p(g{u}_{★},g{v}_{★}),p(g{u}_{★},f{u}_{★}),p(g{u}_{★},f{v}_{★}),p(g{v}_{★},f{v}_{★}),p(g{v}_{★},f{u}_{★})\}\right)\hfill \\ & =& F\left(\max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}\right)\hfill \end{array}$$

(36)

and

$$\begin{array}{ccc}\hfill \tau +F\left(p(v_{★},u_{★})\right)& =& \tau +F\left(p(f{v}_{★},f{u}_{★})\right)\hfill \\ & \le & F\left({\mathcal{M}}_p^g(v_{★},u_{★})\right)\hfill \\ & =& F\left(\max \{p(g{v}_{★},g{u}_{★}),p(g{v}_{★},f{v}_{★}),p(g{v}_{★},f{u}_{★}),p(g{u}_{★},f{u}_{★}),p(g{u}_{★},f{v}_{★})\}\right)\hfill \\ & =& F\left(\max \{p(v_{★},u_{★}),p(u_{★},v_{★})\}\right).\hfill \end{array}$$

(37)

By (37) and ($F1$), we have

$$p(u_{★},v_{★})<\max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}$$

and

$$p(v_{★},u_{★})<\max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}.$$

Hence,

$$\max \{p(u_{★},v_{★}),p(v_{★},u_{★})\}<\max \{p(u_{★},v_{★}),p(v_{★},u_{★})\},$$

which is a contradiction, and hence $p(u_{★},v_{★})=p(v_{★},u_{★})=0$. From $p(v_{★},u_{★})=p(v_{★},v_{★})=0$, by Lemma 1(i), we get $v_{★}=u_{★}$. This completes the proof.  □

If g is the identity mapping in Theorem 2, then the following holds:

Corollary 3.

Let $(X,d)$ be a complete metric space equipped with the w-distance p and $f:X\to X$ be a mapping. Assume that there exist $F\in \mathcal{F}$ and the following holds:

(i) 

for any $x,y\in X$ with $fx\ne fy,$ there exits $\tau >0$ such that

$$p(fx,fy)>0\mathit{implies}\tau +F\left(p(fx,fy)\right)\le F\left({\mathcal{M}}_p(x,y)\right);$$

(38)

(ii) 

${\lim }_{n\to \infty }F\left({\delta }_p\left({\mathcal{O}}_p(x_0,n)\right)\right)$ exits;

(iii) 

for all $y\in X$ with $y\ne fy$,

$$\inf \left\{p\right(x,y)+p(x,fx\left)\right\}>0.$$

(39)

Then, f has a unique common fixed point $u_{★}$ in X and $p(u_{★},u_{★})=0$. Furthermore, if $\left\{x_n\right\}$ converges to $u_{★}\in X$, then $\underset{n\to \infty }{\lim }p(f{x}_n,u_{★})=0.$

Theorem 3.

Let $(X,d)$ be a complete metric space equipped with the w-distance p and $f:X\to X$ and $g:X\to X$ be two mappings such that $f\left(X\right)\subseteq g\left(X\right)$ and g commutes with f. Assume that there exist $F\in \mathcal{F}$, f and g satisfy (29), ${\lim }_{n\to \infty }F\left({\delta }_p\left({\mathcal{O}}_p^g(x_0,n)\right)\right)$ exits and one of the following conditions holds:

(i) 

for all $y\in X$ with $gy\ne fy$,

$$\inf \left\{p\right(gx,y)+p(gx,fx):x\in X\}>0;$$

(ii) 

if both $\left\{g{x}_n\right\}$ and $\left\{f{x}_n\right\}$ converge to $u_{★}\in X$, then $g{u}_{★}=f{u}_{★}$;

(iii) 

g and f are continuous on X.

Then, f and g have a unique common fixed point $u_{★}$ in X and $p(u_{★},u_{★})=0$. Furthermore, If $\left\{g{x}_n\right\}$ converges to $u_{★}\in X$, then

$$\underset{n\to \infty }{\lim }p(gf{x}_n,f{u}_{★})=0=\underset{n\to \infty }{\lim }p(fg{x}_n,g{u}_{★}).$$

Proof. 

By Theorem 2, we get the conclusion of (i). Now, we prove that (ii) ⟹ (i). Suppose that there exist $y\in X$ with $gy\ne fy$, such that

$$\inf \left\{p\right(gx,y)+p(gx,fx):x\in X\}=0.$$

Then, we can find a sequence $\left\{u_n\right\}$ in X such that

$$\inf \{p(g{u}_n,y)+p(g{u}_n,f{u}_n)\}=0.$$

Hence, we have

$$\underset{n\to \infty }{\lim }p(g{u}_n,y)=\underset{n\to \infty }{\lim }p(g{u}_n,f{u}_n)=0.$$

By Lemma 1, we have ${\lim }_{n\to \infty }f{u}_n=y.$ In fact, by the similar argument in Theorem 1, $\left\{g{u}_n\right\}$ is Cauchy sequences and thus $\underset{m,n\to \infty }{\lim }p(g{u}_m,g{u}_n)=0.$ It follow from Lemma 1, we also have ${\lim }_{n\to \infty }g{u}_n=y.$ Hence, by the assumption (ii), implies that $gy=Ty$. Therefore (ii) ⟹ (i). Next, we will prove (iii) ⟹ (ii). Let $\left\{g{x}_n\right\}$ and $\left\{f{x}_n\right\}$ converge to $u_{★}\in X$. By assumption $\left(iii\right)$, then we have

$$g{u}_{★}=\underset{n\to \infty }{\lim }g{u}_n=\underset{n\to \infty }{\lim }f{u}_n=f{u}_{★}.$$

This completes the proof.  □

If g is the identity mapping in Theorem 3, then we obtain the following:

Corollary 4.

Let $(X,d)$ be a complete metric space equipped with the w-distance p and $f:X\to X$ be a mappings such that f satisfy (38) and ${\lim }_{n\to \infty }F\left({\delta }_p\left({\mathcal{O}}_p(x_0,n)\right)\right)$ exits. Assume that one of the following conditions holds:

(i) 

for all $y\in X$ with $y\ne fy$,

$$\inf \left\{p\right(x,y)+p(x,fx):x\in X\}>0;$$

(ii) 

if both $\left\{x_n\right\}$ and $\left\{f{x}_n\right\}$ converge to $u_{★}\in X$, then $u_{★}=f{u}_{★}$;

(iii) 

f are continuous on X.

Then, f has a unique fixed point $u_{★}$ in X and $p(u_{★},u_{★})=0$. Furthermore, if $\left\{x_n\right\}$ converges to $u_{★}\in X$, then $\underset{n\to \infty }{\lim }p(f{x}_n,u_{★})=0$

4. Applications

Application to the Second Order Differential Equation

In this section, we present an application of our fixed point result to prove an existence theorem for the solution of second order differential equation.

Consider the following boundary value problem for second order differential equation of the form:

$$\left\{\begin{array}{c}\frac{d^{2}u}{d{t}^2}+\frac{c}{m}\frac{du}{dt}=K(t,u\left(t\right));\hfill \\ u\left(0\right)=0,u^{\prime }\left(0\right)=a,\hfill \end{array}\right.$$

(40)

where $K:[0,I]\times {\mathbb{R}}^{+}\to \mathbb{R}$, $I>0$ is a continuous function.

The above differential equation exhibits the engineering problem of activation of spring that is affected by an exterior force.

It is well known and easy to check that the problem (41) is equivalent to the following integral equation:

$$\begin{array}{c}\hfill u\left(t\right)={\int }_0^{t}G(t,s)K(s,u\left(s\right))ds,t\in [0,I],\end{array}$$

(41)

where $G(t,s)$ are the green functions given by

$$G(t,s)=\left\{\begin{array}{c}(t-s)e^{\tau (t-s)},\mathrm{if}0\le s\le t\le I,\hfill \\ 0,\mathrm{if}0\le t\le s\le I,\hfill \end{array}\right.$$

(42)

with $\tau >0$ being a constant, calculated in terms of c and m in (40).

Let $X:=C([0,I],{\mathbb{R}}^{+})$ be the set of all continuous functions from $[0,I]$ into ${\mathbb{R}}^{+}$. For an arbitrary $u\in X$, we define

$${\parallel u\parallel }_{\tau }=\underset{t\in [0,I]}{\sup }\left\{\right|u\left(t\right)|e^{-2\tau t}\}\mathrm{where}\tau >0.$$

Define the w-distance $p:X\times X\to [0,\infty )$ by

$$p(x,y)=\max \{\parallel x{\parallel }_{\tau },\parallel y{\parallel }_{\tau }\}$$

for all $x,y\in X.$ Consider a function $f:X\to X$ defined as follows:

$$f\left(u\left(t\right)\right)={\int }_0^{t}G(t,s)K(s,u\left(s\right))ds$$

(43)

for all $x\in X$ and $t\in [0,I]$.

Obviously, the existence of a solution to the Equation $\left(41\right)$ is equivalent to the existence of a fixed point of the mapping f.

Now, we prove the subsequent theorem to guarantee the existence of the fixed point of f.

Theorem 4.

Consider the nonlinear integral Equation $\left(41\right)$ and suppose that the following conditions hold:

(A) K is increasing function;

(B) there exists $\tau >0$ such that

$$\left|K(s,u)\right|\le \lambda {\tau }^2{e}^{-\tau }u,$$

where $0\le \lambda <1$, $s\in [0,I]$ and $u\in {\mathbb{R}}^{+}.$

(C) $f:X\to X$ is Ćirić type generalized F-contraction

Then, the integral Equation $\left(41\right)$ has a solution.

Proof. 

Now, we show that the function f defined as (43) satisfies (3). For this, we have

$$\begin{array}{ccc}\hfill \left|f\right(u\left(s\right)\left)\right|& =& {\int }_0^{t}G(t,s)\left|K(s,u\left(s\right))\right|ds\hfill \\ & \le & {\int }_0^{t}G(t,s)\lambda {\tau }^2{e}^{-\tau }\left|u\left(s\right)\right|ds(\mathrm{from}\mathrm{the}\mathrm{conditions}\left(\mathrm{A}\right) \& \left(\mathrm{B}\right))\hfill \\ & =& {\int }_0^{t}G(t,s)\lambda {\tau }^2{e}^{-\tau }{e}^{2\tau s}{e}^{-2\tau s}\left|u\left(s\right)\right|ds\hfill \\ & =& {\int }_0^t\lambda {\tau }^2{e}^{-\tau }(t-s)e^{\tau (t-s)}{e}^{2\tau s}{\parallel u\parallel }_{\tau }ds\hfill \\ & =& \lambda {\tau }^2{e}^{-\tau +\tau t}{\parallel u\parallel }_{\tau }{\int }_0^t(t-s)e^{\tau s}ds\hfill \\ & =& \lambda {\tau }^2{e}^{-\tau +\tau t}{\parallel u\parallel }_{\tau }[\frac{-t}{\tau }-\frac{1}{{\tau }^2}+\frac{e^{\tau t}}{{\tau }^2}]\hfill \\ & =& \lambda e^{-\tau }{\parallel u\parallel }_{\tau }{e}^{2\tau t}\left[1-\tau t{e}^{-\tau t}-e^{-\tau t}\right].\hfill \end{array}$$

Since $\left[1-\tau t{e}^{-\tau t}-e^{-\tau t}\right]\le 1$, then

$$\parallel f(u\left(s\right){\parallel }_{\tau }\le \lambda e^{-\tau }\parallel u{\parallel }_{\tau }.$$

Similarly, we can see that

$$\begin{array}{c}\hfill {\parallel f\left(v\left(s\right)\right)\parallel }_{\tau }\le \lambda e^{-\tau }{\parallel v\parallel }_{\tau }.\end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill p(fu,fv)& =& \max \{\parallel fu{\parallel }_{\tau },\parallel fv{\parallel }_{\tau }\}\hfill \\ & \le & \lambda e^{-\tau }{\max \{\parallel u\parallel }_{\tau }{,\parallel v\parallel }_{\tau }\}\hfill \\ & \le & e^{-\tau }\left(\lambda {\mathcal{M}}_p(u,v)\right)\hfill \end{array}$$

for all $u,v\in X$.

By passing to the logarithm, we write

$$\ln \left(p(fu,fv)\right)\le \ln \left(e^{-\tau }\lambda {\mathcal{M}}_p(u,v)\right)$$

and hence

$$\tau +\ln \left(p(fu,fv)\right)\le \ln \left(\lambda {\mathcal{M}}_p(u,v)\right).$$

Now, consider the function $F\in {▵}_{\mathcal{F}}$ defined by $F\left(\alpha \right)=\ln \alpha$; then, for each $\tau >0$, we have

$$\tau +F\left(p(fx,fy)\right)\le F\left(\lambda {\mathcal{M}}_p(x,y)\right),$$

which implies that $f:X\to X$ is Ćirić type generalized F-contraction. Thus, all the conditions of Corollary 1 are satisfied. Hence, from Corollary 1, the integral Equation (41) admits a solution.

This completes the proof.  □