1. Introduction
Graph theory is a powerful tool in exploring various network types, and in many areas of application, such as communication, biology, and chemistry. A key limit of graphs is that edges can only model the pairwise relations among the objects. This limitation stands out in many real complex systems. For example, in scientific collaboration networks, if one paper has more than two authors and another paper has two of the authors among these authors in the first paper, then such relationship can no longer be modeled by a graph. A hypergraph is a family of non-empty subsets (hyperedges) from a fixed set of vertices. It is a natural extension of a graph. It thus captures multivariate relationships in complex networks [
1,
2,
3,
4,
5]. Examples include communities and collaboration teams in social networks, cliques in communication networks, and molecules in chemistry.
Trees are among the most essential, useful, and understandable objects in all of graph theory, which is also common sense in hypergraph theory. In this paper, we generalize the concept of trees for hypergraphs and prove bounds on the edge numbers of such hypergraphs.
The concept of a tree in graph theory has many equivalent descriptions which can reflect different properties of the tree from different perspectives [
6]. The analogous situation for hypergraphs is unclear, because the descriptions of the corresponding concept of a tree in hypergraph theory is more complicated.
In 1989, Berge [
7] proposed the concept of an arboreal hypergraph based on a property of hypergraphs and one of concepts of cycles in hypergraph theory. In 1999, Nieminen et al. [
8] introduced two of generalizations of a tree into hypergraphs known as hypertrees and weak hypertrees, respectively. Recently, Katona et al. [
9] discussed bounds on the edge number in another interesting generalization of trees also called hypertrees.
It is well-known from elementary graph theory that any two vertices in a tree are connected by a unique path. This description of the definition of a tree can easily reflect the edge-connectivity property of the tree and means that the tree would be disconnected if any edge is deleted from the tree. Owing to the definition of a tree in graph theory, it has exactly two components by deleting any edge
from the tree
, i.e.,
,
. On the one hand, it is meaningful to define the similar structures in hypergraphs by this kind of method. On the other hand, the concept of the hypertree we usually consider (as the same in this paper) is a special case of the concept of the hypertree defined by Nieminen. A connected hypergraph
is a hypertree if the removal of any of its edges
results in a disconnected hypergraph
and the number of components of the hypergraph
is
. This concept of the generalization of a tree to hypergraphs has been introduced and studied in the literature, which can be regarded as a continuation of the classical generalization effort. For more details, see [
8,
10,
11].
In the following, we further develop the concept proposed by Nieminen into the generalized hypertrees (). Our main concern is that the number of components of is exactly 2 for any edge of the . After introducing the nomenclature and definitions in hypergraphs, we discuss lower and upper bounds on the edge number of .
Now, we want to clarify some basic terms and results in hypergraphs about our research object. The undefined concepts in this paper can be found in [
7,
12] for hypergraphs and [
6] for graphs.
Nomenclature and Definitions
A hypergraph is a pair where is the vertex set of and is a collection of the nonempty subsets of . An element in is a hyperedge, and it is also called an edge of . Note that we do not allow a hypergraph to have isolated vertices which are not included in any edge. The order of the hypergraph is the cardinality of , i.e., ; its size is the cardinality of , i.e., .
The degree of a vertex in , denoted by or , is the number of edges in containing . Let , the cardinality of an edge is . A hypergraph is simple if implies that for any with . We consider only simple hypergraphs, unless specified otherwise. A hypergraph is linear if it is simple and for any with . Two vertices in a hypergraph are adjacent if there is an edge which contains both vertices. Two edges in a hypergraph are adjacent if their intersection is not empty. A hypergraph is -uniform if for all with . Thus, a simple graph is a simple 2-uniform hypergraph, and vice versa.
Let
be a hypergraph, and let
be an integer. An
-walk in
is a finite vertex-edge alternative sequence
, such that
, for any
with
. The integer
is the length of the walk
. The shortest length of
-walk is the distance (also called path length) between
and
, which is denoted by
. If
are distinct vertices,
are distinct edges, and
, the walk is called a cycle of length
in
. A hypergraph is connected if for any pair of vertices, there is a walk which connects both vertices; it is disconnected otherwise. It means that a connected hypergraph has exactly one component and a disconnected hypergraph has more than one component. We denote the number of components of the hypergraph
by
. In
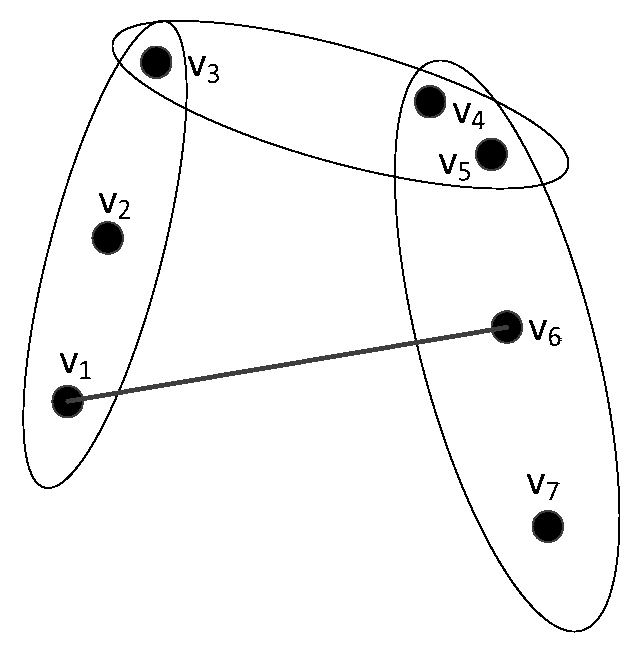
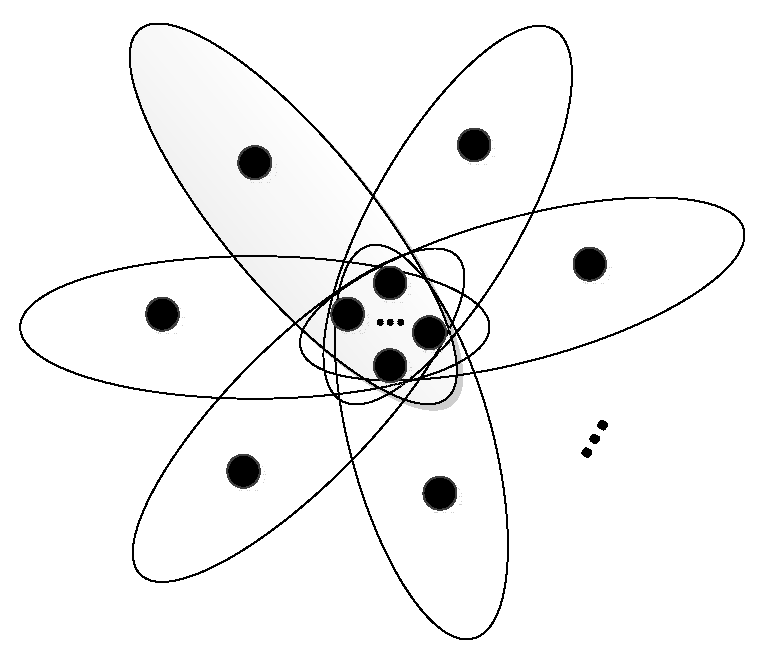
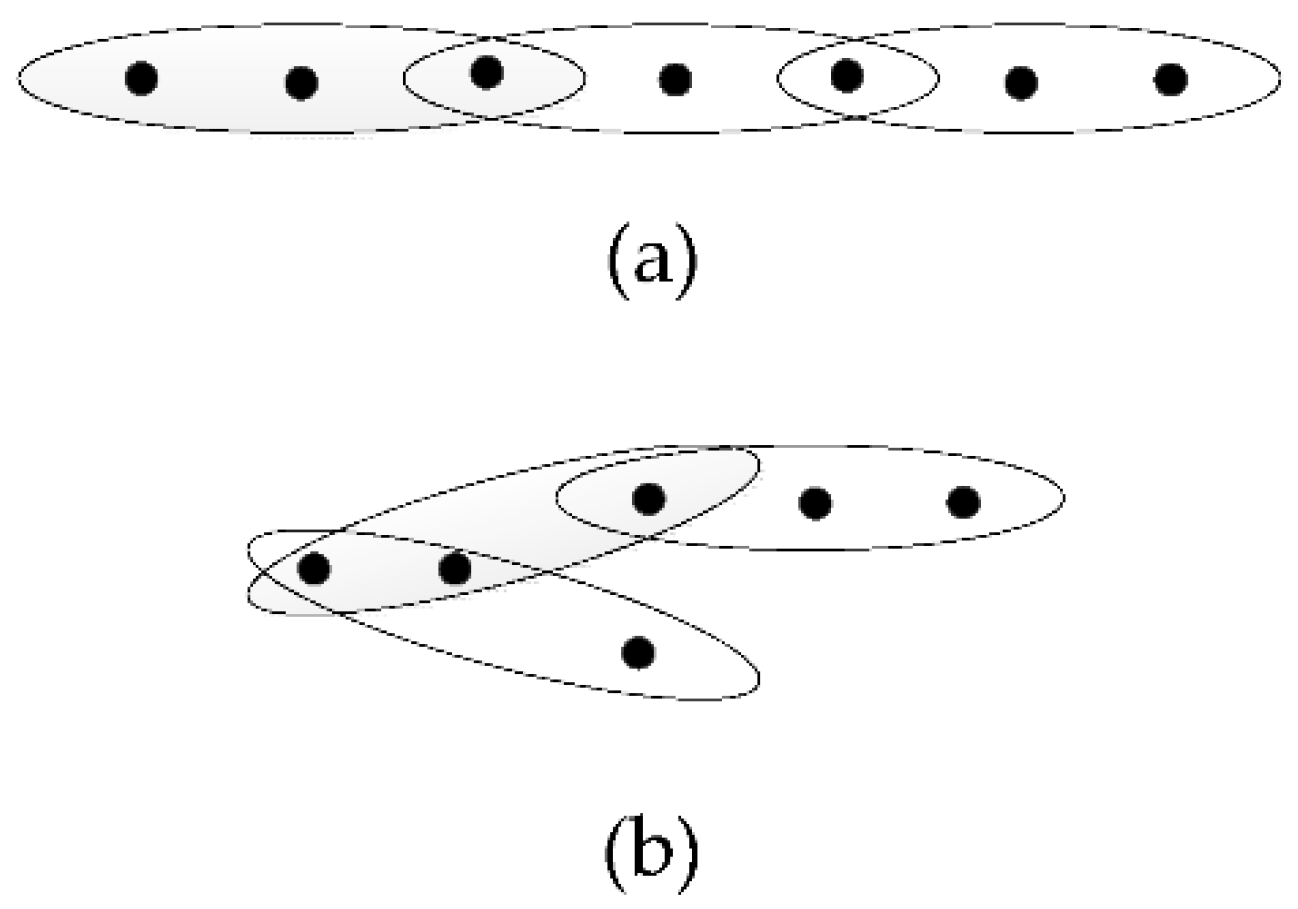
Figure 1, we show an illustrative example of a hypergraph with seven vertices where the vertices are connected by four edges.
The notion of edge-connectivity
of a graph
, defined as the minimum number of edges whose removal renders
disconnected, has attracted much attention [
13,
14]. The definition of edge-connectivity of graphs extends to hypergraphs in a natural way [
15].
The following Theorem 1 is the basic conclusion of describing hypertrees from the perspective on edge-connectivity. By the definitions of a tree and a hypertree, it is also true for the tree in graph theory.
Theorem 1. Letbe a connected hypergraph onvertices. Ifis a hypertree then[10].
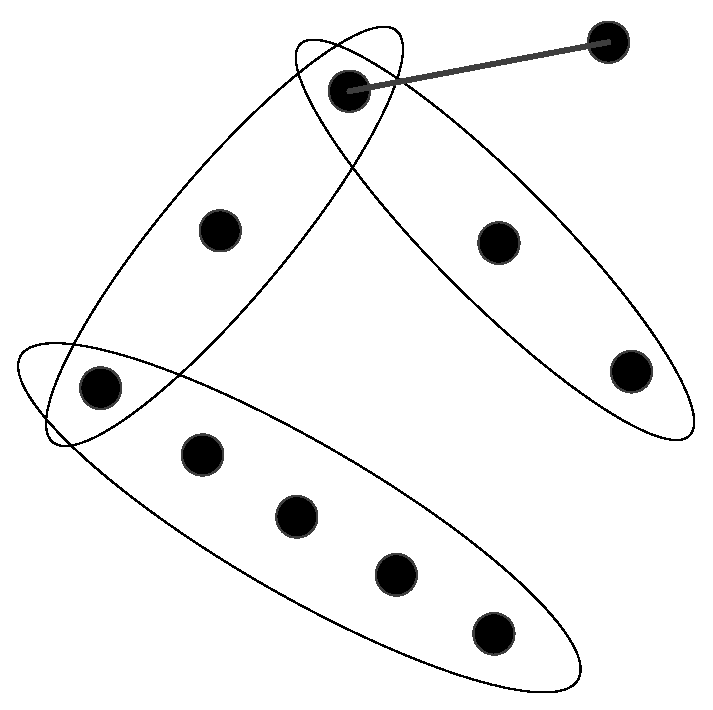
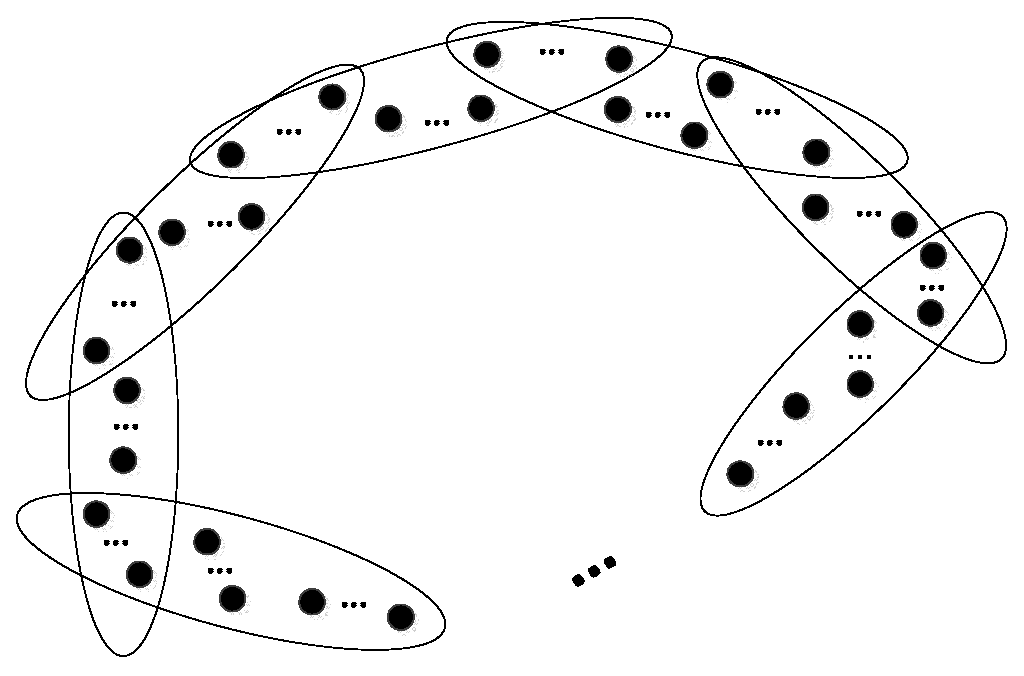
By the concept of a hypertree
, the number of components in the hypergraph
is
after deleting any edge
from
, i.e.,
,
, and vice versa (see
Figure 2).
For the
-uniform hypergraph, Lai et al. obtained another related result in [
16] as follows:
Theorem 2. Letbe an-uniform hypergraph onvertices. Ifis connected, then. Moreover, the equality holds if and only if for any edge,hascomponents.
It gives the lower bound of the edge number of connected
-uniform hypergraphs and it describes the class of hypergraphs when the equality holds. These hypergraphs, commonly known as hypertrees, have results of deep studies because they have special structures [
11]. However, it does not mean that this concept is the analogous situation of a tree in hypergraphs. In this paper, we call an analogous concept a generalized hypertree which attempts to give an in-depth description of the tree structure in hypergraphs.
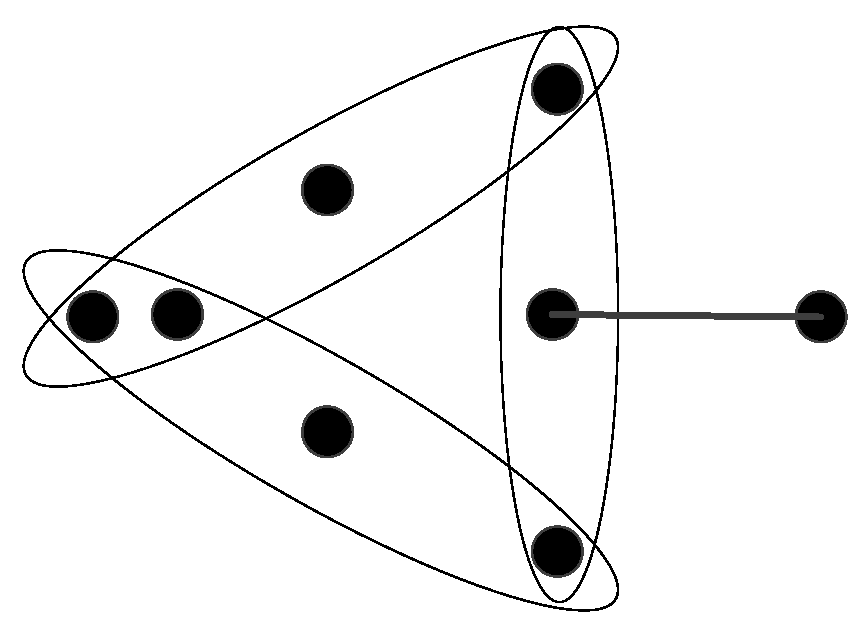
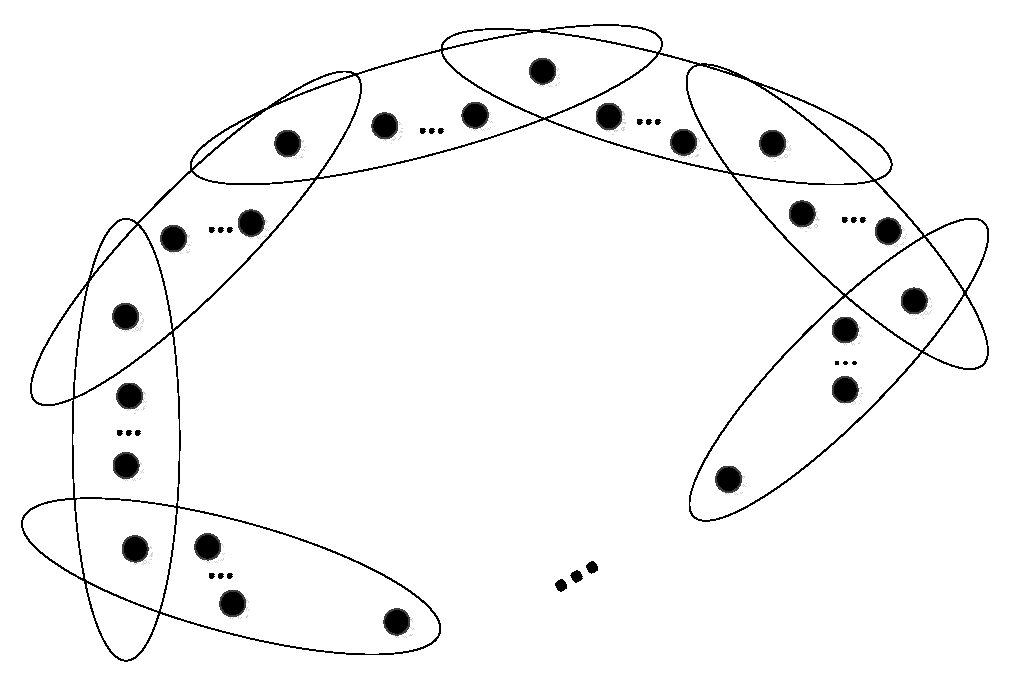
Definition 1. (Generalized hypertree). A connected hypergraph is a generalized hypertree if the removal of its any edge results in a disconnected hypergraph and the number of components of is exactly .
From a certain perspective, this definition is also a continuation of the common trees in hypergraphs. This definition is illustrated
Figure 3.
Our main results are the lower and upper bounds on the edge number of
. Theorem 3 in
Section 2 generalizes the well-known fact that a tree
on
vertices has
edges. It is the most important result in this paper. It turns out that the lower bound in Theorem 3 can be improved for
which has exactly
components for any edge
if
. The corresponding result is Theorem 4 whose discussion and proof are presented in
Section 2. Based on the notion of generalized hypertree, Theorem 5 and Corollary 2 in
Section 3, modify Theorems 1 and 2, respectively. When the lower bound holds in Corollary 2, we consider the relationship between generalized hypertrees and hypertrees, as shown in
Section 4.
2. The Bounds of the Edge Number of r-Uniform GHTs
In this section, we mainly research the bounds (lower bound and upper bound) on edge number of -uniform and the number of components in hypergraph is exactly 2.
Theorem 3. Let be a connected -uniform hypergraph on vertices ( ). If has exactly two components for any edge , then . Moreover, the lower and upper bounds are sharp.
In order to prove Theorem 3, we need the following preliminaries.
A classical result for a graph with and states that . Its parallel generalization in hypergraph theory is as follows.
Proposition 1. Let be a hypergraph, we have [12]when is an -uniform hypergraph, the above equation can be simplified to The characterization of the connected
-uniform hypergraphic sequences was given by Tusyadej [
7]. The following generalization of this result was proposed by Lai at al [
16].
Proposition 2. A -tuple is the degree sequence of a -edge connected -uniform hypergraph if and only if
- (1)
for
- (2)
if.
Lemmas 1 and 2 show us some of the characteristics about the -uniform whose component number exactly equals 2 after deleting any edge.
Lemma 1. Letbe a connected-uniform hypergraph onvertices (). Ifhas exactly two components for any edge, then there must exist an edge containing exactly one vertex of degree 1 in .
Proof. If the edge containing vertex with degree 1 does not exist in , then the degree of all vertices of is equal or greater than 2. By Proposition 2, is at least 2-edge connected. Therefore, is connected for any edge . Therefore, there exists an edge containing one vertex with degree 1 in . Additionally, if contains more than two vertices with degree 1, then the number of components is more than 2 after deleting . □
Lemma 2. Let be a connected -uniform hypergraph on vertices ( ). If has exactly two components for any edge , then , where is the number of edges containing exactly one vertex with degree 1 (the same below).
Proof. Obviously, . The main effort is the proof for . By Lemma 1, we only need to prove . Let us suppose that . If , then we can conclude that the result is not correct, because the component number of is (). If , let us assume is the unique edge containing exact one vertex with degree 1. For , the degree of vertex which contained in edge , is not less than 2. By Proposition 2, we can deduce that is connected. It is contrary with the condition. □
Now we are ready to prove Theorem 3.
Proof of Theorem 3. In order to interpret clearly, we divide the bounds into lower bound and upper bound.
Case 1. The proof on lower bound of the edge number in Theorem 3.
By Proposition 1, Proposition 2 and Lemma 2, we conclude that
For a fixed value
, we minimize the value on the right side of the above equation. All degrees of vertices bigger than 1 are taken as 2 for this purpose. That is,
for all
with
. At the same time, we must maximize the number of vertices with degree 1, namely
. Additionally, we have
So far, we have completed the proof on lower bound of the edge number in Theorem 3.
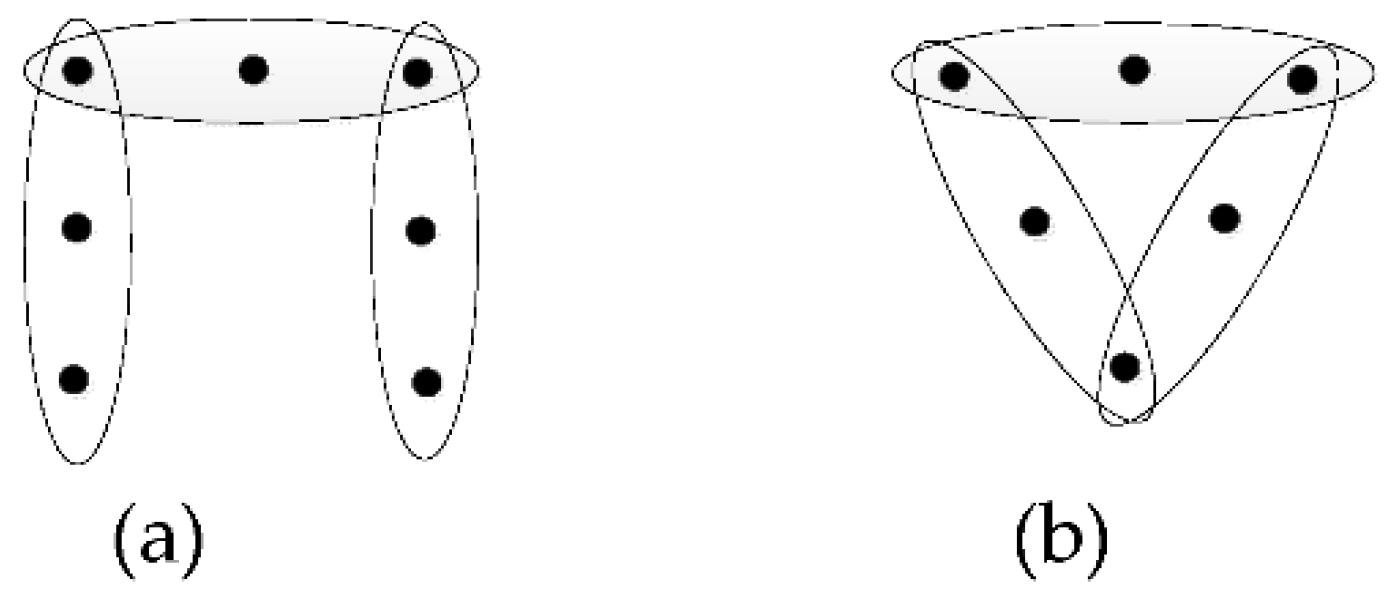
Figure 4 is an
-uniform
example that the lower bound of edge number holds.
Case 2. The proof on upper bound of the edge number in Theorem 3.
If , and , then we argue by induction on .
The base case of this induction is . Since the connected -uniform hypergraph has two components by deleting any edge, it is easy to see that the edge number of this hypergraph is 2.
Now we assume that the result is a true statement, for the vertex number is equal or less than , then we consider this case that the vertex number equals . Let be a connected -uniform hypergraph on vertices. If two components are , after deleting an edge from , and their edge numbers are and , and their vertex numbers are and , respectively, where , then we discuss the following three cases. By the inductive hypothesis
- (i)
If
, then we have
- (ii)
If
, then we have
- (iii)
If
, then we have
According to (i), (ii) and (iii), for on vertices, the result is also true. Based on the proof above, Theorem 3 holds. □
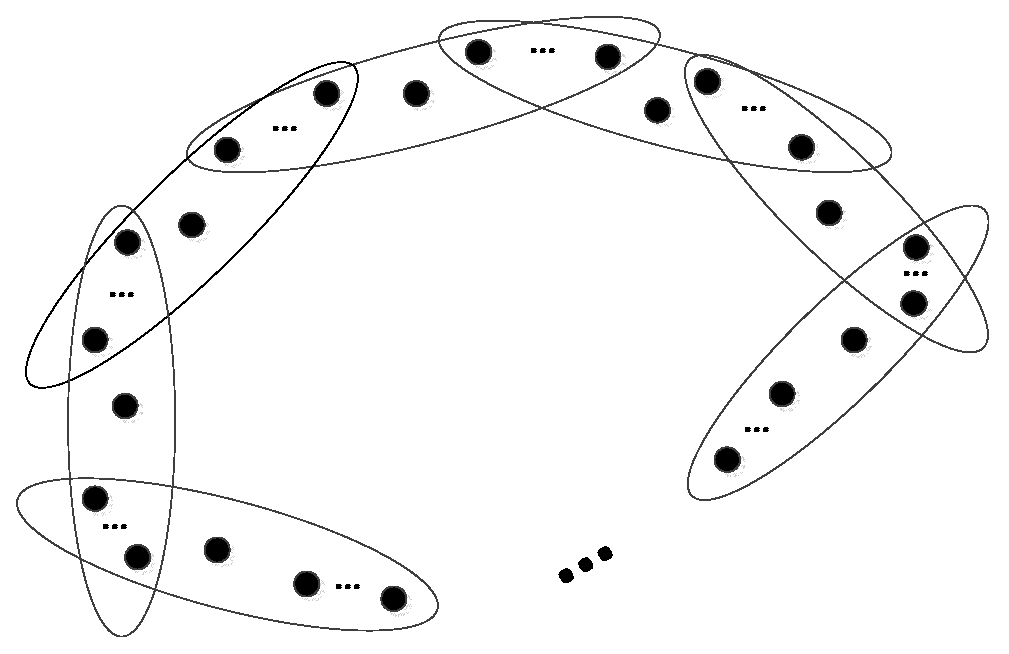
Figure 5 is an
-uniform
example that the upper bound of edge number holds.
We call the
-uniform hypergraph shown in
Figure 5 a sunflower which is denoted by
.
In order to compare with the edge number of a tree in graph theory, we consider another structure in
. If
, then we have that the number of edges (i.e., edge
), which made none of the two components of
containing an isolated vertex, is
by Lemma 1. To make
as small as possible, we need to make the degree of each vertex is not greater than 2. Hence
. Then, we have by Proposition 1,
For each
with
,
Therefore, under the premise of for any edge of the , the edge number of this kind of is not the smallest.
The
Figure 6 is an
-uniform
example that the edge number is
.
In the previous part, we have discussed the bounds of edge number of a connected -uniform , whose component number exactly equals 2 by deleting any edge. Theorem 4 gives the bounds of edge number of connected -uniform except hypertrees. Theorem 4 below, generalizes Theorem 3.
Theorem 4. Letbe a connected-uniform hypergraph onvertices (). Ifhas exactlycomponents for any edge, then. Moreover, the lower and upper bounds are sharp, and the upper bound holds if and only ifis a.
Proof. According to the definition of a connected -uniform , the maximum number of edges decreases with the increment of . Therefore, the upper bound is true.
The proof of the lower bound in Theorem 4 is similar to the proof of the lower bound in Theorem 3. To obtain the minimum value of
, each edge of
contains
vertices with degree 1 and
vertices with degrees 2. It follows that
which implies
□
According to the result of Theorem 4, if and , then we find that the hypergraph is , the cycle on vertices.
When the lower bound holds, the hypergraph is not unique. One of such structures is shown in
Figure 7, where each edge contains
vertices with degree 1.
Since when , gets the maximum value . Theorem 4 yields the following Corollary 1.
Corollary 1. Letbe a connected-uniform hypergraph onvertices. Ifis a, then.
5. Conclusions
Many structures in the real world can be modeled with hypergraphs. For example, authors and papers are supposed to vertices and edges in the scientific collaboration hypernetworks based on the hypergraph theory. The hypergraph theory provides us with effective approach to depict relationships among various objects accurately.
A generalized hypertree is the generalization of the concept of a tree in graph theory. The main result of this paper is to obtain the bounds of the edge number in generalized hypertrees, inspiring further study in the direction of edge-minimal and edge-maximal generalizations of trees. Another class of hard questions involve various generalizations which seem to be closely related to hypernetwork reliability. We believe that the challenging open problems in the topic makes it worthy of future study.
The number of components of a tree happens to be two after deleting an arbitrary edge, and the edge number of trees is . However, the description of the corresponding concepts of a tree in hypergraph theory is much more complicated. The reason why we focus on the generalized hypertree whose component number is exactly 2 after deleting any edge, is that it has broad application prospects in real-life network design and network fault detection.
In graph theory, the star
and the path
are two classes of graphs with special properties. For example,
is the most reliable structure in
(set of trees on
vertices), and
is the worst reliable structure in
under the situation of vertex failure. For another example,
is the tree of the smallest average path length in
, and
is the largest one. In this paper, two extreme hypergraphs whose component number is exactly 2 after deleting an arbitrary edge, are not the correspondence hypergraphs of
and
in
. Thus, the corresponding structures and properties in graph theory are not necessarily established in hypergraph theory, even if it is a natural generalization of some basic concepts in graph theory. As mentioned in many references [
1,
12], the properties of the hypergraph cannot be simply transformed into corresponding graphs to study and analyze, such as the two-section graph, the associated graph and the line graph, etc. Therefore, we should have to pay more attention to study of the hypergraph theory itself.