An Application of Multicriteria Decision-making for the Evaluation of Alternative Monorail Routes

Abstract

Urban transportation planning is important for a metropolitan city. Route selection, which is among the decisions of urban transportation planning, is also important in terms of developing the urban transportation. This study contains the route selection for the planned monorail transport system that is a new system in Ankara. The most suitable monorail route was selected among the determined eight alternative monorail routes. In this decision process, we used the Analytic Network Process (ANP) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method, which is one of the multi-criteria decision-making methods. Finally, we provided the most suitable ranking and planning with the selection process for the development of urban transportation.

1. Introduction

Transport systems are complex socio-technical systems that affect the social, economic, and environmental dimensions of a community [1]. In this context, transport planning is typically a decision-making process that based on rationality, aimed at defining and implementing transport system operations [2]. Transportation planning is now a fundamental support to a rational and sustainable development of the territorial system due to the increase of environmental issues and constraints, the worldwide financial crisis, and the numerous interactions of the transportation system with the social and economic contexts [3]. Strategic planning involves decisions on long-term nearly 10-20 years, capital investment programs for the realization of new infrastructures such as roads, railways, and ports, and the acquisition of vehicles and technologies [4]. So, the route selection problem is important in the metropolitan city for urban transportation planning processes, involving decisions on a medium- or long-term basis.

On the other hand, transportation development plays an essential role in a society’s economy and has long-lasting effects on the financial, social, and political life of individuals and the community. It is essential to develop a transportation network that best suits the public’s needs, to build a contemporary city [5]. Public transportation is one of the most important systems in transportation, especially in metropolis cities. So, evaluation of public transportation systems is a strategic decision-making problem for urban area [6]. At the same time, public transport is an essential element of urban life since it reduces car traffic and gives mobility to city residents. In addition, more use of public transport reduces emissions such as carbon dioxide. This feature has become more important due to the Kyoto Protocol came into effect [7]. It is important to consider the multifactorial evaluation of transportation projects due to these reasons.

The assessment of projects, meant here as capital investments that create transport infrastructure, supports the activity of decision makers. The assessment is deal with achieving social objectives, such as improvement of economic efficiency, reduction of the damage on the environment, improvement of safety. In the case of public decision makers, the assessment is used as a tool to assist the process of planning transport infrastructure. Multicriteria analysis are widely used due to the simplicity it’s in taking into account nonmarketable effects and qualitative criteria for these aims [8]. Multicriteria decision-making methods (MCDM) are widely used in transport planning to include in a comparative assessment of alternative projects their contributions to different evaluation criteria [9]. MCDM has gained importance as an evaluation method for transport projects and use of these methods increase day by day to evaluating transport projects such as passenger and freight transport, infrastructure investments, location decisions, etc. [10,11]. MCDM methodologies are rapidly growing in the various transportation problems [12,13,14]. At the same time, there are some studies using multi-objective optimization about transportation subjects [15] and solving multicriteria transportation-location problems [16]. Besides, these methods also have been applied in various area such as supply chain management and supply chain performance measurement [17,18].

Route selection is one of the most important activity for the planning of the urban traffic that needs MCDM process. Because constructing a new structure or installing new systems are big investments and require large budget, there should be good planning. Briefly, route selection is a process in which selection or ranking are carried out among the alternative routes. At the same time, the route selection is named by some names such as “investment project selection” [19], “project selection” [20], “transportation planning” [21], “infrastructure projects selection” [22] or “corridor selection” [23]. The aim of route selection is to provide maximum benefit for traffic and the developing urban transportation. So, it will provide livable urban environment and city center. These investments need big resources such as large budget. Planned investments should be addressed in a wide range by the executives. Otherwise, it will be inevitable that the investment will become a waste. Therefore, this process is dependent on lot of criteria such as social effect, environmental effect, cost, demand level etc.

The monorail, which is one of the rail system investments, is also one of the major investment projects. The monorail is one of the urban public transportation systems that acts on its own line. This new system for Turkey is used in various countries such as Japan and China. But Turkey does not have this technology yet. However, this system is planned for various cities in Turkey and studies on this subject are still ongoing. Monorail has a lot of advantages such as to be independent of vehicle traffic, to be safe, to be fast, to be comfortable, to use low area, to be environmentally friendly and to have its own road among the other rail systems. Therefore, monorails have been becoming common day by day in the urban transportation worldwide. In terms of environment, it is environmentally friendly because of quietness and usage of energy. This system is alternative to the other rail systems and public mass transportation vehicles due to all these reasons. But it also has some negative aspects, such as high initial investment costs and the electric is not free. This system has high visual impact. This situation can be developed with high construction cost. It is important to select this technology, but the planning process is the most important of all. Therefore, selecting the best or the most suitable route is needed as the first step. This process is difficult due to the effects of many factors.

Selecting a route and a new system are complex problems which involve and effect the development of urban areas, use of land, future of the city or various other criteria and sub-criteria. There are various transportation types used for urban transportation such as bus, metro, private vehicle, taxi, subway, tramway and monorail etc. Monorail has been being applied in the European countries, the USA, in Asia (especially Japan and Chine) and Middle East countries such as Saudi Arabia and United Arab Emirates (UAE).

There are various studies about monorail in the literature. Kuwabara et al. [24] mentioned that monorail is an effective vehicle for urban transportation due to the short construction time and low-cost advantages. Wang [25] also talked about the short construction processes of monorail projects, the cost and the quality of the transportation. Kato et al. [26] talked about the advantages of a saddle-type monorail system and pointed out that in the coming years, driverless monorail systems would be used more and more and system costs would be even lower. With simulation application, Sadatugu et al. [27] talked about alternative policies and scenarios for monorail. Sekitani et al. [28] mentioned a thrust-type monorail system for the solution of rugged roads, traffic congestion and air pollution, and they also described the technical characteristics of the line. Considering the rapid transportation of monorail, Kennedy [29] defined and mentioned their types and features. Kimijima et al. [30] gave information about the monorail by mentioning its active use in the place where the monorail was installed. Ghafooripour et al. [31] examined the countries with metro and monorail applications for developing countries and evaluated them in terms of cost-effectiveness. By evaluating its effectiveness in terms of user satisfaction, Das et al. [32] offered suggestions for the monorail transportation systems. Marathe and Hajian [33] pointed out that the monorail was ideal for the use in urban transportation in terms of economy, security and environmental sensitivity. Parekh et al. [34] discussed the features of the monorails which are popular in urban areas. Liu et al. [35] compared the conventional rail transport systems with the monorail system and discussed the advantages and disadvantages of monorail systems. Hussien [36] made a comparison between the monorail system and other public transportation vehicles. Li et al. [37] made a technical feasibility of suspended monorail type by analyzing the urban adaptation, capacity, specifications and construction costs. Timan [38] emphasized that monorail systems would be a suitable solution for the traffic problems in metropolitan cities. In his study, He [39] mentioned about the features of straddle-type monorail and noted the increase in its popularity day by day.

In the literature, related to this subject, there are a lot of studies focusing on route planning, route selection, local selection, station site selection, project selection and transportation planning. These studies have been carried out in various area and they examined different vehicle types. At the same time, authors of this research have conducted some studies related to this subject and they have contributed the literature with those studies. Hamurcu and Eren [40] proposed the monorail mass transportation for Turkey as first. Hamurcu and Eren [41] used multicriteria decision-making methods for monorail route selection in Ankara. Hamurcu et al. [42] used analytic hierarchy process (AHP) and 0-1 goal programming (GP) in the monorail project selection under the capacity constraints. Gür et al. [20] carried out monorail project selection for different route alternatives by using AHP and goal programming methods. Hamurcu and Eren [43], in their conference paper, used Analytic Network Process (ANP) and Similarity to Ideal Solution (TOPSIS) in order to carry out the monorail route selection in Ankara. Besides, selection of monorail technology [44], rail system projects selection in Istanbul [45], prioritization of high-speed rail projects [46], transportation planning [21] and decision-making for rail systems projects with MCDM and GP [47] are some of the studies of the authors of this article. So, multicriteria decision-making methods are today widely used in transport project studies commissioned by public bodies and city ad transportation planners.

Decision-making processes in transportation can be grouped different topic in terms of subject. Some of them and study areas are route planning for tramway [48], high-speed rail [49], [50], railway [51], for highway [52]; route selection for light rail system [53,54,55], metro line [56,57], and bicycle [14]; location selection for metro [58]; station location selection for rail system network [59]; project selection for rail systems network [11]; transportation planning for transport network [60,61,62,63,64,65].

These studies show that transportation planning decisions are very important processes for planners and managers, are need analytic methods. Transportation planning is the process of identifying and incorporating stakeholder concerns, needs and values in the transport decision-making process. MCDM makes it possible to incorporate, account and quantify human opinion and preferences; solve decision problems taking into account tangible and intangible aspects; provide a methodology to calibrate the numeric scale for the measurement of quantitative as well as qualitative performances. In this study, using the analytic network process and TOPSIS from MCDMs, the challenges faced by planners in route design these decision processes were eliminated in this study. Use of ANP and TOPSIS hybrid from multi-criteria decision-making methods which are effective in terms of analysis, selection and ranking, are effective tools for quantitatively considering qualitative concepts.

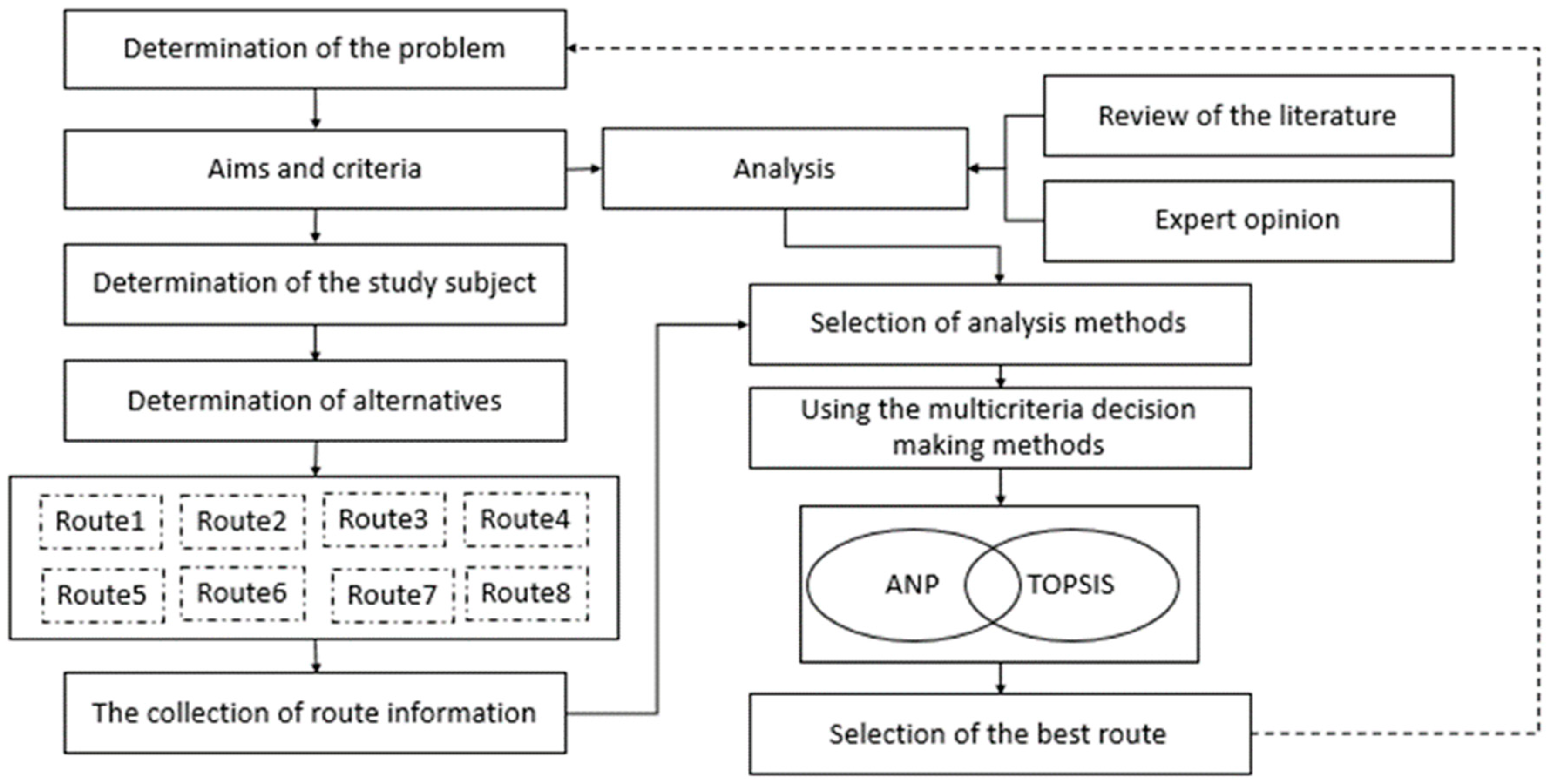
In this study, we focus on the selection of monorail route. Sections of this study are as follows: In Section 2, research methodology is shown. In Section 3, the multi-criteria decision-making methods used in this study are explained. In Section 4, application of the route selection in Ankara is presented. Finally, the ranking of the best route selection is shown in Section 5.

2. Materials and Methods

Multicriteria decision analysis has seen frequently used the last several decades. Its application in different areas has increased significantly, especially as new methods develop and as old methods improve.it has allowed for more complex decision analysis methods with technology advancement over the past couple of decades to be developed in addition to applying single MCDM methods to real-world decisions. This process with hybrid multi-criteria decision-making methods and their application has provided a whole new approach to decision analysis [66].

In this study, the research was carried out on eight monorail routes in Ankara, the capital city of Turkey. This study involved two methods related to the multi-criteria decision-making. These methods were ANP and TOPSIS which were used for the determination of the criteria and alternative routes for urban public transportation in Ankara. Ankara hasn’t got a monorail technology for urban transportation yet. Considered monorail projects were selected from expert opinions for urban transport planning. In the implementation of this research, there were four main parts (Figure 1), which were;

-

Identification of the goal and criteria

-

Use of the multi-criteria decision-making methods

-

Determination of alternative eight route

-

Selection of the best route and evaluation at the end of the selection

This process was used in order to select the best monorail route. The alternative route characteristics were taken from Ankara metropolitan municipality and the criteria were determined by expert opinions and literature research.

The contribution of this study to the state-of-the-art can be summarized as follows: This study presents new example application and proposes a comprehensive multicriteria decision-making model for the route selection problem, which accounts for the criterion components reported in the literature. The proposed work is one of the first few works to investigate application of ANP and TOPSIS for evaluation of monorail projects under various criteria. Besides, this new system for Ankara will be first. Thus, selection of the best alternative route by using MCDM play an important role for sustainability and public transportation in Ankara metropolitan area.

2.1. Analytic Network Process (ANP)

There ANP can improve communication and resolve conflicts, help diffusion of responsibility, and assist decision makers in understanding other members’ viewpoints. These characteristics are attractive when a good decision calls for actions that may not be well-liked, such as outsourcing. The ANP can evaluate a wide range of criteria including tangible and intangible factors related to the outcome. Because ANP allows for complex interactions and influences among the various components of the decision problem, it can be seen as a better choice for studying more complex decision problems [67]. ANP brings all the decision objectives, criteria, alternatives and actors (such as decision makers, stakeholder, and influencers) into a single unified framework, and it facilitates interaction and feedback of elements (alternatives, criteria and actors) within groups (inner dependence) and between groups (outer dependence) [68]. Briefly, ANP is more concerned with network structure. In terms of advantages, it allows for dependence and includes independence and has the ability to prioritize groups or clusters of elements. Besides, it can support complex, networked decision-making with various intangible criteria [69]. ANP is often utilized in project selection, product planning, green supply chain management, and optimal scheduling problems and also transportation.

Most of the complex real-world decision problems have numerous inter-dependent elements that can be captured and processed by utilizing the feedback and interaction capabilities of an ANP model. In this regard, the ANP method was used directly or indirectly by Lee and Kim [70] in the information system project, by Meade and Presley [71] for the selection of research and development projects, by Ravi et al. [72] for the selection of the reverse logistics projects, by Büyüközkan and Öztürkcan [73] in six sigma projects selection, by Wey and Wu [74] for the selection of projects among transportation systems, by Begičević et al. [75] for the selection of projects at higher education institutions, by El-Abbasy et al. [76] for the selection of highway projects and by Tuzkaya and Yolver [77] for the selection of research and development projects.

To derive the global priorities of the criteria by using ANP, it is necessary first to carry out the pairwise comparison of the criteria with respect to the node representing their category and to all other criteria with which they interact or on which they have effect. Next, the principal right eigenvector of each comparison matrix is computed to obtain the local priority of every criterion [78]. In the last step, a super-matrix consisting of all the local-limiting matrices is formed for overall criteria prioritization and alternative ranking. The weighted super matrix is taken to the limit for the results.

2.2. TOPSIS

This technique, developed by Hwang and Yoon [79], is based on the selection of the shortest distance from the positive ideal solution and the longest distance alternative from the negative ideal solution. The positive-ideal solution is the best possible combination of the criteria. The negative ideal solution consists of the worst criterion values that can be reached. The only assumption in this method is the assumption that each measure is either a monotone increasing or monotonously decreasing one-way benefit. The steps of the TOPSIS method will be shown on the handling problem.

TOPSIS is an approach for identifying an alternative that is closest to the ideal solution and farthest to the negative ideal solution [80]. It has numerous advantages such as a simple process and easy to use and programmable. The number of steps remains the same regardless of the number of alternatives and criteria [81]. This method has a wide range of application areas such as multi-criteria inventory planning [82], freight transport selection [83], selection of the scholarship with the AHP [84], selection of the service providers [85], performance evaluation [86], personnel selection [87], reverse logistics supplier selection [88].

In addition, ANP and TOPSIS methods have been used together in some studies. Ersoz and his colleagues determined the weights of the criteria that were effective in the course selection of graduate students by the ANP method and alternative courses were ranked by using the TOPSIS method [89]. ANP and TOPSIS methods have been used together to evaluate the supplier’s selection process [90] and to rank strategies in the mining industry [91].

3. Using the ANP and TOPSIS Approach for Route Selection

Firstly, the criteria and alternatives were identified for selection. Then, the interdependence between criteria, sub-criteria and alternatives was determined. The pairwise comparisons were carried out between these criteria and sub-criteria by using Super Decision program. The pairwise comparisons were made by expert opinions. By this way, weights of the criteria were found for TOPSIS method. In the other step, TOPSIS method were applied by using ANP weights. Then the negative and positive ideal solution and separation were calculated in the TOPSIS steps. At the end of the solution process, the best ranking was created among the alternative routes. This process:

Step_1.

Identify criteria and alternatives

Step_2.

Determination interdependence relationship between criteria and sub-criteria. Then finding the criteria weight with ANP.

Step_3.

Using the ANP weights for TOPSIS method

Step_4.

Calculate the negative-positive ideal solution and separation.

Step_5.

The best ranking for among the alternative route

4. An Application in ANKARA

In this study, a route selection was applied for Ankara. Monorail is a new urban mass transportation system. It will be the first example of this system in urban transportation in Turkey with its implementation in Ankara. Ankara is a region covered with plains formed by confined the Kızılırmak and Sakarya rivers in the north-western part of Central Anatolia. The population of Ankara is 5,045,083 according to the results of the 2013 census using Address-Based Population Registration System. The largest districts of Ankara in terms of population are Cankaya, Keciören, Yenimahalle, Mamak, Sincan, Etimesgut, Altındag, Pursaklar and Polatli. The largest district in terms of surface area is Polatli. The main determinant of Ankara’s socio-economic structure is the fact that the city of Ankara is the administrative center of the country at the same time. For this reason, the public service sector has an important place in Ankara’s economic life. Economical, technological and political developments have initiated the population migration to Ankara from other settlements.

Due to the increasing population and migration, public transportation systems have to be used for urban transportation in Ankara. Public transportation services are provided municipal buses, private buses, minibuses, subways and suburban in this city. Efforts are continuing to establish the monorail system in Ankara.

4.1. Determination of the Alternatives

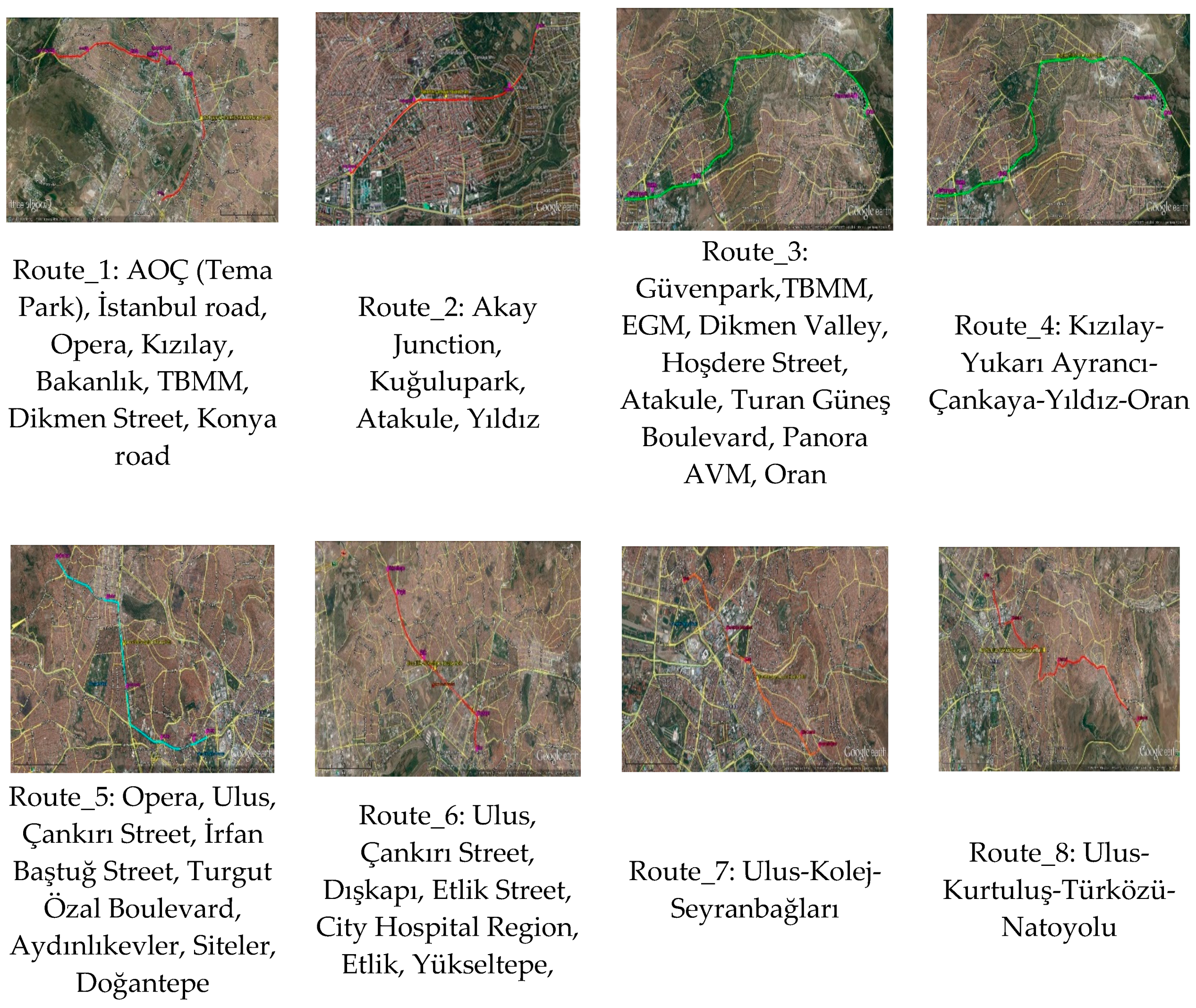
Ankara is a big city and its population density is very high. For this reason, it has traffic problems. Therefore, municipal administrators have been producing projects for the solution of traffic problems. The first of their projects is urban mass transportation projects. Therefore, monorail technology, one of the types of public transportation, was considered. And 8 alternative routes were identified within the scope of this study.

Table 1. Characteristic features of the routes.

Route	Distance (m)	Number of Stations	Number of Vehicles	Number of Series	Total Number of Vehicles	Approximate Total Cost ($)
Route_1	11140	11	4	20	80	412,180,000
Route_2	5020	5	4	10	40	185,740,000
Route_3	8076	8	4	15	60	298,812,000
Route_4	7763	7	4	15	60	287,231,000
Route_5	11596	10	4	22	88	429,052,000
Route_6	11426	10	4	22	88	422,762,000
Route_7	4069	4	4	8	32	150,553,000
Route_8	19168	18	4	36	144	709,216,000

shows characteristic of the routes in terms of distance, number of stations, number of vehicles, number of series, total number of vehicles and approximate total cost of the routes. In this study eight monorail routes were used to determine the best route. These routes and their pictures are shown in Figure 2.

4.2. Determination of the Criteria

Criteria and sub-criteria were determined by taking the expert opinions and as a result of the literature review. Some of the experts were personnel of Ankara Metropolitan Municipality and they were working in urban planning and traffic planning sections. Other experts were academicians studying in the related field. The determined criteria, sub-criteria and their explanations are shown in

Table 2. Criteria for the route selection.

Criteria	Sub-Criteria	Explanation
Economic	(K1) Construction cost	Refers to the use of monetary resources such as implementation costs, infrastructure investments, operational costs, maintenance costs, infrastructure and others
	(K2) Expropriation
Social impact	(K3) Access to shopping and residential areas	This type of criteria refers to the effects on the society because of decisions made regarding the transportation system.
	(K4) Access to employment and education
	(K5) Aesthetic and visual impact
	(K6) Population density
	(K7) Public mobility
	(K8) Accessibility
Engineering	(K9) Ability to develop and to improve	These criteria are related to the issues regarding technical requirements and prudential situations of the city. They were not explicitly computed like monetary functions and they are possible predictions about the city.
	(K10) The total travel time
	(K11) The integration of transport
	(K12) Traffic capacity
	(K13) Demand level
Environmental impact	(K14) Sensitive area	This set of criteria is associated to the impact(s) on the natural environment and sensitive areas such as cultural and historical or other.
	(K15) Land structure

.

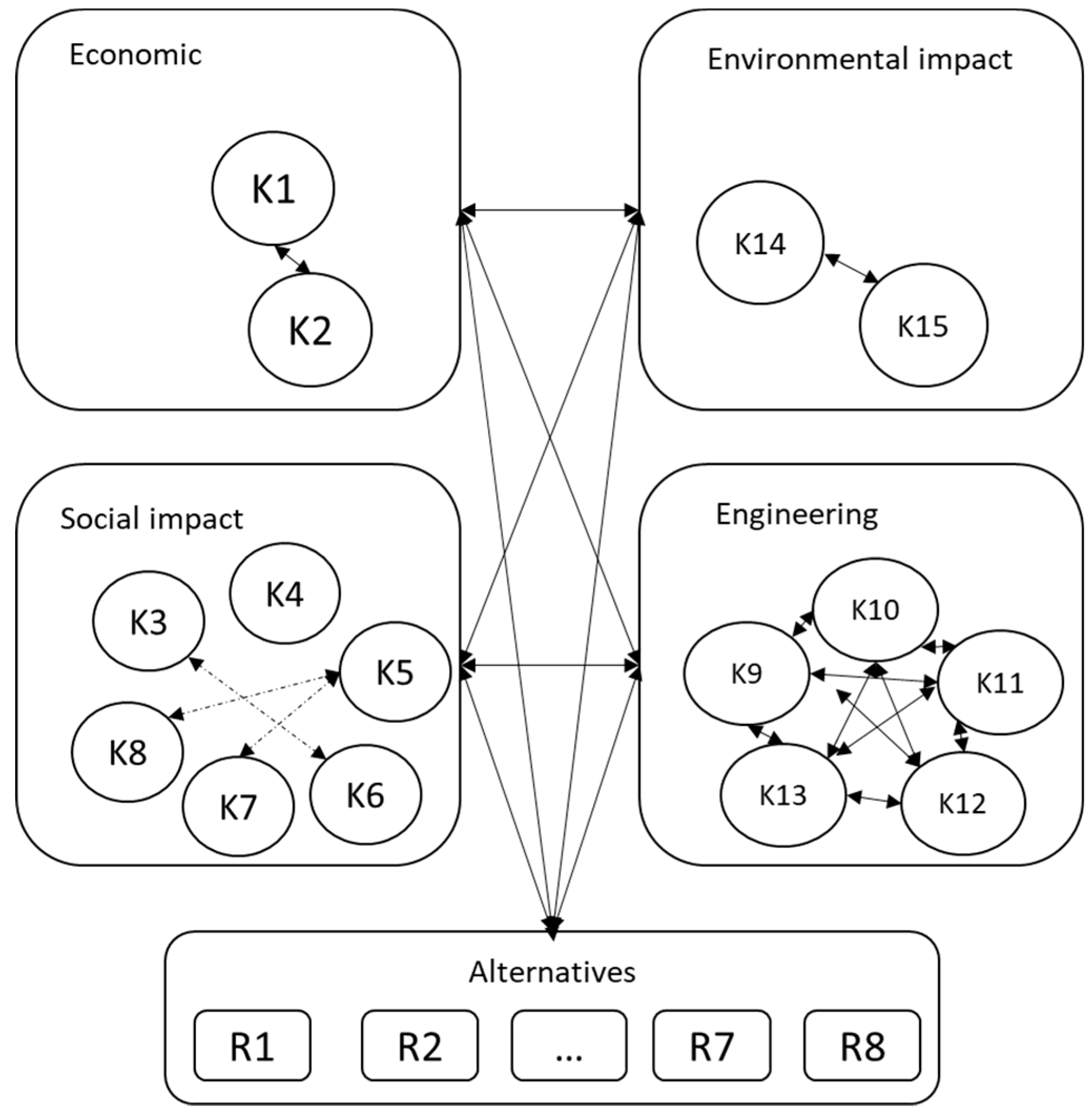
Economic: Refers to the use of monetary resources. This criterion deal with construction costs, infrastructure investment, fuel costs. Social impact: This type of criteria refers to both benefits and negative impacts on society because of decisions made regarding the transport system such as the access to shopping-employment-resistant. In addition, the criterion deal with mobility, population density and visual impact for urban area. Engineering: These criteria are related with issues technical of transportation planning such as travel time, demand, accessibility, traffic capacity, ability to develop and to improve, the integration of transport. Environmental impact: This set of criteria is associated to the impacts on the natural environment and historical-cultural area. In this category, we find the sensitive areas and use of land. The attribute of criteria K14 influences criteria K15, the attribute of criteria K9 influences criteria K10, K11, K12 and K13, and criteria K3 influences criteria K4, K5, K7, K1, K2, K14, K15 and sub-criteria of engineering.

4.3. Determination of the Weights of the Criteria by ANP Technique

One of the most important parts is to determine the criteria and measuring indicators in decision-making models. To be determined criteria and their interdependence for this purpose that the important aspects and characteristics of alternatives being measured. Therefore, the design for decision-making model has a direct impact on model efficiency. The criteria and sub-criteria affecting on selection processes differ based on objectives, in this study, we used expert opinion (academic and engineer planners) in order to identify criteria, with regard to municipality strategic goals. For evaluation of the monorail projects, we need quantitative data on environmental impact, engineering, economic and social impact main criteria. Since these projects are new and implemented for the first time in Ankara context, there is very limited quantitative data available, thereby making the evaluation process difficult. At the same time, these projects have yet been considered and have in the process of being planned. To address this situation, a decision-making committee comprising of subject matter experts (4 academic researchers from industrial engineering and civil engineering, 2 transportation experts as rail system planner and transportation planner from Ankara Metropolitan Municipality) made qualitative ratings by using Saaty’s 1–9 importance scale for assessing the alternatives and the criteria. In the TOPSIS method, the criterion values of the alternatives were found by using ANP with this scale according to expert opinions.

In this research, to be able to identify the relationship and degree of interdependency among the criteria, opinions of the experts from academia and from metropolitan municipality staff were consulted. Those experts were working and studying in the urban planning and traffic planning area. The relationship having interdependence among the four essential criteria and fifteen sub-criteria taken in this research is shown in Figure 3. There is an interdependence relationship among these criteria in the route selection problem. For example, population density criterion would result in an increase in public mobility and increase the demand level for the selection of alternative routes. All the criteria are linearly related to each other under the engineering criterion. And these criteria also related to the other essential 3 criteria. Likewise, sensitive areas increase the construction cost and these areas affect the current situation such as traffic capacity, ability to develop and to improve, the total travel time, the integration of transport. Thus, there is an interdependency among these criteria and sub-criteria, economy, environmental impact, social impact and engineering.

Comparing the structure of AHP hierarchy, there is the same level relationship among factors in the solution of ANP. At the same time, “Super Decision” program was used in this study.

In order to create pairwise comparisons in the direction of determining the relationships between criteria and alternatives and present them to the user, this program was used. In

Table 3. Comparisons between population density and social impact.

Comparisons wrt “Population density” Node in “Social impact” Cluster
1	Access to employment and educ…	9	8	7	6	5	4	3	2	1	2	3	4	5	6	7	8	9	Access to shopping and res…
2	Access to employment and educ…	9	8	7	6	5	4	3	2	1	2	3	4	5	6	7	8	9	Accessibility
3	Access to employment and educ…	9	8	7	6	5	4	3	2	1	2	3	4	5	6	7	8	9	Public mobility
4	Access to shopping and residen…	9	8	7	6	5	4	3	2	1	2	3	4	5	6	7	8	9	Accessibility
5	Access to shopping and residen…	9	8	7	6	5	4	3	2	1	2	3	4	5	6	7	8	9	Public mobility
6	Accessibility	9	8	7	6	5	4	3	2	1	2	3	4	5	6	7	8	9	Public mobility

, the pairwise comparison of sub-criteria under the engineering factor is shown. This process was carried out for other criteria and sub-criteria. The interrelated criteria is made with ANP using 1–9 Saaty’scale to compare two alterative with respect to attribute.

This decision process is done for every pair of among the each other as shown in Table 3. A basic questionnaire has been prepared and feedback has been taken from academics and planner experts to find out the relative importance of the selected criteria. The pairwise comparison for population density is also shown in this table.

Then, for each criterion, comparisons were carried out with each alternative. Prioritization of the weight of the criteria is ranked in

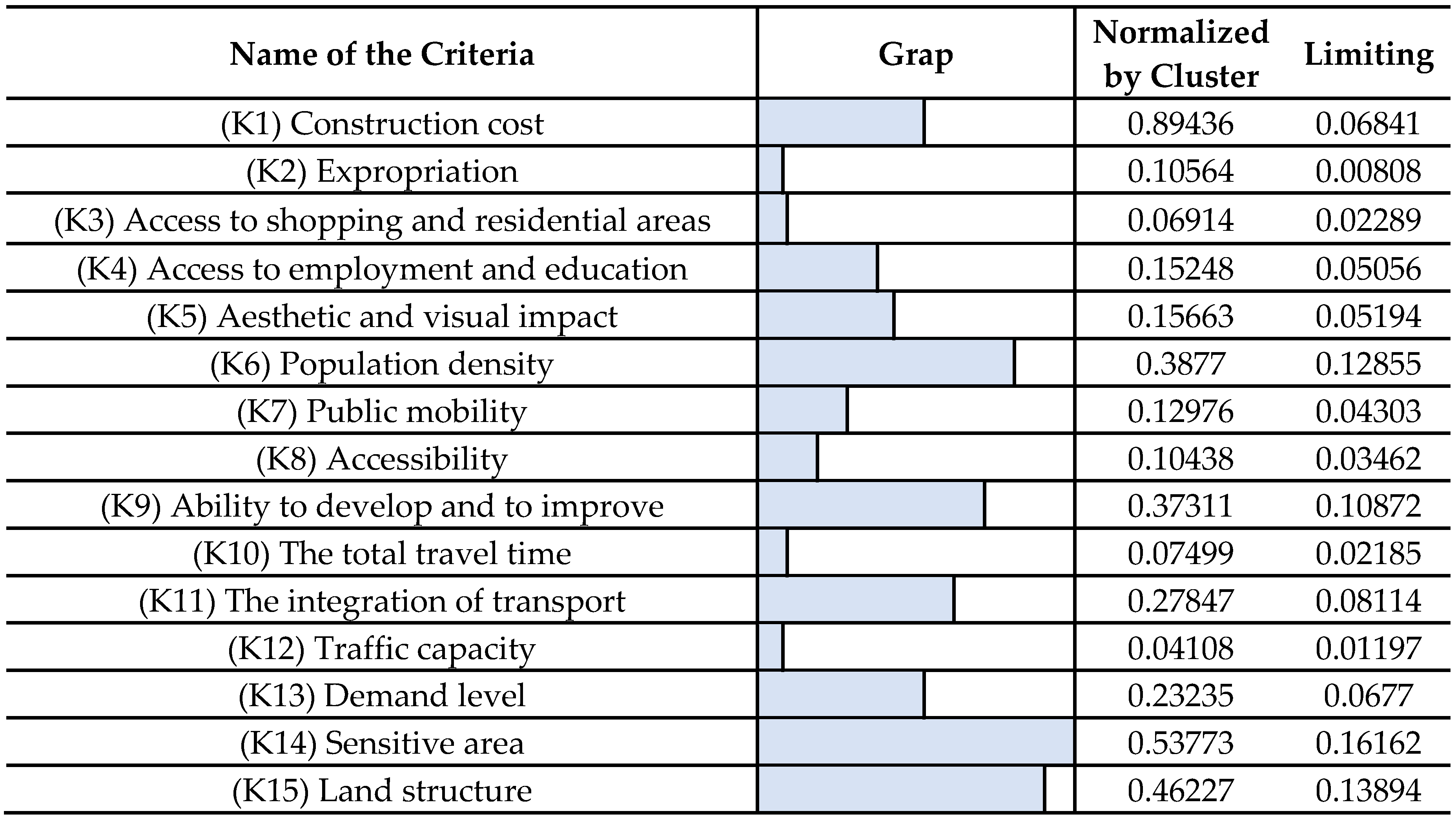
Table 4. Weights of the criteria.

. In the table, weights of the criteria found with ANP are seen. The criteria having the highest weight values are construction cost, sensitive area, land structure, population density, and ability to develop and to improve, respectively.

4.4. Ranking Monorail Route Alternatives by Using TOPSIS

The In this step, TOPSIS technique played role for ranking the routes. The weights were obtained by the ANP technique using Equations (1) and (2).

Table 5. Normalized weighted matrix.

Alternatives	K1	K2	K3	K4	…	K12	K13	K14	K15
R1	0.014	0.184	0.224	0.426	…	0.031	0.331	0.26	0.042
R2	0.363	0.092	0.107	0.018	…	0.155	0.03	0.127	0.153
R3	0.037	0.148	0.216	0.056	…	0.144	0.11	0.132	0.141
R4	0.036	0.101	0.228	0.11	…	0.132	0.157	0.17	0.134
R5	0.109	0.139	0.072	0.059	…	0.119	0.071	0.066	0.139
R6	0.126	0.102	0.059	0.144	…	0.188	0.114	0.066	0.149
R7	0.252	0.121	0.042	0.114	…	0.091	0.046	0.068	0.155
R8	0.041	0.114	0.053	0.073	…	0.142	0.141	0.113	0.086

shows the normalized weighted matrix by using Equations (1).

TOPSIS method was applied by using weights of the criteria that are results of the ANP method in the ANP-TOPSIS combine model. The used standard decision matrix in TOPSIS is found at the end of the comparisons of the alternatives with each criterion.

The weights of the evaluation criteria using ANP is shown in

Table 6. The weights of the evaluation criteria using ANP.

Important Weight	Criteria
	K1	K2	K3	K4	K5	K6	K7	K8
	0.8944	0.1056	0.0691	0.1525	0.1566	0.3877	0.1298	0.1044
	K9	K10	K11	K12	K13	K14	K15
	0.3731	0.75	0.2785	0.0411	0.2324	0.5377	0.4623

. In addition, the weighted normalized decision matrix by TOPSIS is shown in

Table 7. The weighted normalized decision matrix.

Alternatives	K1	K2	K3	K4	…	K12	K13	K14	K15
R1	0.013	0.019	0.015	0.065	…	0.001	0.077	0.14	0.02
R2	0.325	0.01	0.007	0.003	…	0.006	0.007	0.068	0.071
R3	0.033	0.016	0.015	0.009	…	0.006	0.026	0.071	0.065
R4	0.032	0.011	0.016	0.017	…	0.005	0.036	0.091	0.062
R5	0.117	0.015	0.005	0.009	…	0.005	0.016	0.035	0.064
R6	0.113	0.011	0.004	0.022	…	0.008	0.026	0.035	0.069
R7	0.225	0.013	0.003	0.017	…	0.004	0.011	0.036	0.072
R8	0.037	0.012	0.004	0.011	…	0.006	0.033	0.061	0.04

. The vector normalization technique is used for computing the element (a_ij) of the normalized decision matrix, which is given as:

$$a_{ij}=\frac{r_{ij}}{\sqrt{{\sum }_{i=1}^m{r}_{ij}}}$$

(1)

The weighted normalized decision matrix can be calculated by multiplying each row (r_ij) of the normalized decision matrix with its associated attribute weight N_D. The weighted normalized value v_ij is calculated as below:

$$V_{ij}=N_D\ast r_{ij}\mathrm{where}j=1,2,\dots ,n;i=1,2,\dots ,m.$$

(2)

Then, using Equations (3) and (4) positive and negative ideal solutions were obtained. The obtained results are shown in

Table 8. The ideal solution and negative solution.

Criteria	K1	K2	K3	K4	K5	K6	K7	K8
A+	0.013	0.01	0.016	0.065	0.027	0.057	0.031	0.043
A−	0.325	0.019	0.003	0.003	0.013	0.035	0.007	0.002
Criteria	K9	K10	K11	K12	K13	K14	K15
A+	0.129	0.002	0.069	0.008	0.077	0.035	0.02
A−	0.015	0.025	0.011	0.001	0.007	0.14	0.072

. Compute the positive ideal solution (PIS/A⁺) and the negative ideal solution (NIS/A⁻) for each criterion:

$$A^{+}=\left\{\left(max{X}_{ij}|j\in J^{\ast }\right),\left(min{X}_{ij}|j\in J^{-}\right)\right\}=\{X_1^{+},X_2^{+},\dots .,X_n^{+}\}$$

(3)

$$A^{-}=\left\{\left(min{X}_{ij}|j\in J^{\ast }\right),\left(max{X}_{ij}|j\in J^{-}\right)\right\}=\{X_1^{-},X_2^{-},\dots .,X_n^{-}\}$$

(4)

where J* is the set of benefit attributes and J⁻ is the set of cost attributes.

The ideal solution which maximizes the benefit criteria (criteria of K3, K4, K5, K6, K7, K8, K9, K11 and K12 in this study) and minimizes the cost criteria (criteria of K1, K2, K10, K14 and K15 in this study), whereas the negative ideal solution criteria in this study maximizes the cost criteria/attributes and minimizes the benefit criteria/attributes. The negative ideal solution consists of the worst performance values whereas the best alternative is the one that is nearest to the ideal solution.

The next step of TOPSIS technique is to calculate the Euclidean distance of each alternative. For the positive and negative ideals, the Euclidean distance of each alternative was calculated by using Equations (5) and (6). The distance (di⁺, di⁻) of each weighted alternative i = 1, 2 …, m from the PIS($d_i^{+})$ and the NIS($d_i^{-})$ is computed as follows:

$$d_i^{+}={\left\{{{\displaystyle \sum }}_{j=1}^n{(X_{ij}-X_j^{+})}^2\right\}}^{0.5}i=1,2,\dots ,m;j=1,2,\dots ,n$$

(5)

$$d_i^{-}={\left\{{{\displaystyle \sum }}_{j=1}^n{(X_{ij}-X_j^{-})}^2\right\}}^{0.5}i=1,2,\dots ,m;j=1,2,\dots ,n$$

(6)

In the final stage, relative closeness of suppliers to ideal solution was obtained by using Equation (7) and the results were ranked in terms of relative approximately descending order of routes.

Table 9. Final ranking in two-phase ANP-TOPSIS approaches.

Route	A+	A−	Ci(S-/S-+S*)	Ranking
R1	0.1061	0.3585	0.7716	1
R2	0.3476	0.0897	0.2052	8
R3	0.1438	0.305	0.6796	4
R4	0.1366	0.3035	0.6897	3
R5	0.1885	0.2353	0.5553	6
R6	0.1744	0.2404	0.5795	5
R7	0.2713	0.1454	0.349	7
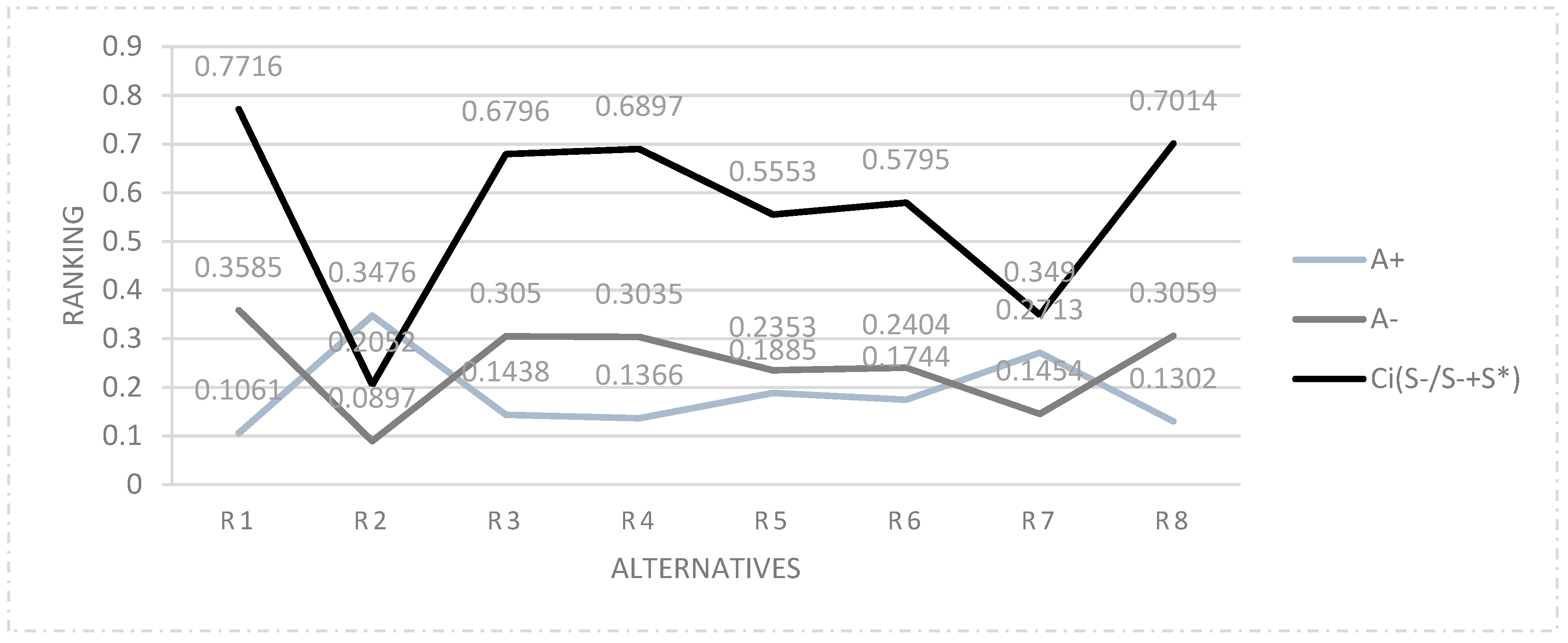
R8	0.1302	0.3059	0.7014	2

presents the ranking of alternative routes based on combination of ANP and TOPSIS techniques. The closeness coefficient ${CL}_i^{+}$ represents the distances to the positive ideal solution (A⁺) and the negative ideal solution (A⁻) simultaneously. The closeness coefficient of each alternative is calculated as:

$${CL}_i^{+}=\frac{d_i^{-}}{(d_i^{+}+d_i^{-})},0\le {CL}_i^{+}\le 1,i=1,2,\dots ..,m$$

(7)

As it is shown in Table 9, route R1 can give the best score among all alternative routes. The order of alternative monorail routes according to the obtained closeness coefficients is R1 > R8 > R4 > R3 > R6 > R5 > R7 > R2. According to this ranking, the best monorail route is "Route_1(R1): AOÇ (Tema Park), İstanbul road, Opera, Kızılay" which has the highest closeness coefficient. The results are also shown graphically in Figure 4.

In the study, the criteria with the highest importance levels are sensitive areas, land structure, population density, ability to expand and develop, and construction cost. As a result, this line, which was selected first, became the foreground in terms of being the longest route and having high population.

5. Results

Route selection and evaluation are very important in terms of the success of metropolitan municipality and urban planning. The objective of this paper is to present an integrated different approach for effective route decisions and determination of the suitable route. Therefore, an integrated approach of ANP- TOPSIS is proposed in order to select the best route and define the relation among the criteria used to select the best route. Urban transportation planning is an important decision for planners and it is the most important activity for managers. Therefore, there are a lot of criteria effecting this selection process. All this criterion should be evaluated with various dimensions. In this study, for 8 route alternatives, four criteria and 15 sub-criteria were evaluated, and the model solution was established with multi-criteria decision-making. Finally, the most suitable routes were ranked. Results show that application of the ANP-TOPSIS methods together provide some important advantages such as the establishing relationship, evaluation of the various factors at the same time and use of tangible and intangible criteria.

In other studies, for the transportation planners and other public institutes in other decision process, the ANP-TOPSIS integrated model can help transport infrastructure project or project selection/ranking. The other MCDM methods such as analytic hierarchy process (AHP), VIKOR (Vise Kriterijumska Optimizacija I Kompromisno Resenje), AHP-TOPSIS, or fuzzy methods can be used, and this model can be also used in the other urban planning processes related to decision-making. In addition, group decision-making approaches can be developed using various MCDM techniques such as AHP or PROMETHEE for selection of transportation projects or route selection in public institutions. Besides, this study can be extended via a mathematical programming-decision model for transport infrastructure projects with resource constraints such as budget.

Public participation in transport planning is important factor for society and it is, therefore, emerging as a basic component in the decision process for rationality [4]. We don’t deal with public participation factors in this study. So, in future studies, alternative projects or routes can be evaluated to take account of factors and criteria such as public participation and "community acceptance". The community acceptance can be researched with surveys. Survey-based MCDM techniques can be used to reproduce a participatory process where territorial communities acts as key stakeholders.