Stability Analysis of Quaternion-Valued Neutral-Type Neural Networks with Time-Varying Delay
Abstract
1. Introduction
2. Definition of Quaternion
3. Problem Statement and Preliminaries
- (1)
- : is an injective mapping,
- (2)
- while , then ,
4. Main Results
5. Numerical Example
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Birx, D.L.; Pipenberg, S.J. A complex mapping network for phase sensitive classification. IEEE Trans. Neural Netw. 1993, 4, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Forster, B. Five Good Reasons for Complex-Valued Transforms in Image Processing; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Arima, Y. Envelope-detection Millimeter-wave Active Imaging System using Complex-Valued Self-Organizing Map Image Processing. Water Resour. Res. 2015, 50, 1846. [Google Scholar]
- Filliat, D.; Battesti, E.; Bazeille, S. RGBD object recognition and visual texture classification for indoor semantic mapping. In Proceedings of the IEEE International Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 23–24 April 2012. [Google Scholar]
- Hirose, A.; Eckmiller, R. Behavior control of coherent-type neural networks by carrier-frequency modulation. IEEE Trans. Neural Netw. 1996, 7, 1032–1034. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.S.; Tan, M.C. Delay-independent stability criteria for complex-valued BAM neutral-type neural networks with time delays. Nonlinear Dyn. 2017, 89, 819–832. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, Z.; Liu, X.; Lin, C. Existence, uniqueness, and exponential stability analysis for complex-valued memristor-based BAM neural networks with time delays. Appl. Math. Comput. 2017, 311, 100–117. [Google Scholar] [CrossRef]
- Liu, D.; Zhu, S.; Ye, E. Synchronization stability of memristor-based complex-valued neural networks with time delays. Neural Netw. 2017, 96, 115–127. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, X.Y. Complex projective synchronization of complex-valued neural network with structure identification. J. Frankl. Inst. 2017, 354, 5011–5025. [Google Scholar] [CrossRef]
- Ali, M.S.; Yogambigai, J. Extended dissipative synchronization of complex dynamical networks with additive time-varying delay and discrete-time information. J. Comput. Appl. Math. 2019, 348, 28–341. [Google Scholar]
- Zhang, L.; Yang, X.; Xu, C. Exponential synchronization of complex-valued complex networks with time-varying delays and stochastic perturbations via time-delayed impulsive control. Appl. Math. Comput. 2017, 306, 22–30. [Google Scholar] [CrossRef]
- Wang, J.F.; Tian, L.X. Global Lagrange stability for inertial neural networks with mixed time-varying delays. Neurocomputing 2017, 235, 140–146. [Google Scholar] [CrossRef]
- Tang, Q.; Jian, J.G. Matrix measure based exponential stabilization for complex-valued inertial neural networks with time-varying delays using impulsive control. Neurocomputing 2018, 273, 251–259. [Google Scholar] [CrossRef]
- Li, X.F.; Fang, J.A.; Li, H.Y. Master-slave exponential synchronization of delayed complex-valued memristor-based neural networks via impulsive control. Neural Netw. 2017, 93, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.K.; Zhao, Z.J.; Liu, Y.R. Impulsive effects on stability of discrete-time complex-valued neural networks with both discrete and distributed time-varying delays. Neurocomputing 2015, 168, 1044–1050. [Google Scholar] [CrossRef]
- Jian, J.G.; Wan, P. Global exponential convergence of fuzzy complex-valued neural networks with time-varying delays and impulsive effects. Fuzzy Sets Syst. 2018, 338, 23–39. [Google Scholar] [CrossRef]
- Huang, C.D.; Cao, J.D.; Xiao, M.; Alsaedi, A.; Haya, T. Bifurcations in a delayed fractional complex-valued neural network. Appl. Math. Comput. 2017, 292, 210–227. [Google Scholar] [CrossRef]
- Miron, S.; Le Bihan, N.; Mars, J.I. Quaternion-music for vector-sensor array processing. IEEE Trans. Signal Process. 2006, 54, 1218–1229. [Google Scholar] [CrossRef]
- Ell, T.; Sangwine, S.J. Hypercomplex fourier transforms of color images. IEEE Trans. Image Process. 2007, 16, 22–35. [Google Scholar] [CrossRef]
- Took, C.C.; Strbac, G.; Aihara, K.; Mandic, D.P. Quaternion-valued short-term joint forecasting of three-dimensional wind and atmospheric parameters. Renew. Energy 2011, 36, 1754–1760. [Google Scholar] [CrossRef]
- Isokawa, T.; Kusakabe, T.; Matsui, N.; Peper, F. Quaternion Neural Network and It’s Application. In Knowledge-Based Intelligent Information and Engineering Systems; Springer: Berlin/Heidelberg, Germany, 2003; pp. 318–324. [Google Scholar]
- Mandic, D.P.; Jahanchahi, C.; Took, C.C. A quaternion gradient operator and it is applications. IEEE Trans. Signal Process. Lett. 2011, 18, 47–50. [Google Scholar] [CrossRef]
- Sudbery, A. Quaternionic analysis. Math. Proc. Camb. Philos. Soc. 1979, 85, 199–225. [Google Scholar] [CrossRef]
- Bihan, N.L.; Sangwine, S.J. Quaternion principal component analysis of color images. In Proceeding of the IEEE International Conference on Image Processing, Barcelona, Spain, 14–17 September 2003. [Google Scholar]
- Mandic, D.P.; Goh, V.S.L. Complex Valued Nonlinear Adaptive Filters: Noncircularity; Widely Linear and Neural Models; Wiley Publishing: Hoboken, NJ, USA, 2009. [Google Scholar]
- Liu, Y.; Zhang, D.D.; Lu, J.Q. Global μ-stability criteria for quaternion-valued neural networks with unbounded time-varying delays. Inf. Sci. 2016, 360, 273–288. [Google Scholar] [CrossRef]
- Chen, X.; Li, Z.; Song, Q. Robust stability analysis of quaternion-valued neural networks with time delays and parameter uncertainties. Neural Netw. 2017, 91, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, B.; Yao, S. The global exponential pseudo almost periodic synchronization of quaternion-valued cellular neural networks with time-varying delays. Neurocomputing 2018, 303, 75–87. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.D.; Lou, J.Q.; Cao, J.D. Stability analysis of quaternion-valued neural networks: decomposition and direct approaches. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4201–4211. [Google Scholar] [PubMed]
- Ali, M.S.; Saravanakumar, R.; Cao, J. New passivity criteria for memristor-based neutral-type stochastic BAM neural networks with mixed time-varying delays. Neurocomputing 2016, 171, 1533–1547. [Google Scholar]
- Zhou, H.; Zhou, Z.; Jiang, W. Almost periodic solutions for neutral type BAM neural networks with distributed leakage delays on time scales. Neurocomputing 2015, 157, 223–230. [Google Scholar] [CrossRef]
- Lakshmanan, S.; Lim, C.P.; Prakash, M.; Nahavandi, S.; Balasubramaniam, P. Neutral-type of delayed inertial neural networks and their stability analysis using the LMI Approach. Neurocomputing 2016, 230, 243–250. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Zhang, X. Neutral-delay-range-dependent absolute stability criteria for neutral-type Lur’e systems with time-varying delays. J. Frankl. Inst. 2016, 353, 5025–5039. [Google Scholar] [CrossRef]
- Wu, T.; Xiong, L.L.; Cao, J.D.; Liu, Z.X.; Zhang, H.Y. New stability and stabilization conditions for stochastic neural networks of neutral type with Markovian jumping parameters. J. Frankl. Inst. 2018, 355, 8462–8483. [Google Scholar] [CrossRef]
- Xiong, L.L.; Zhang, H.Y.; Li, Y.K.; Liu, Z.X. Improved stability and H∞ performance for neutral systems with uncertain Markovian jump. Nonlinear Anal. Hybrid Syst. 2016, 19, 13–25. [Google Scholar] [CrossRef]
- Xiong, L.L.; Tian, J.K.; Liu, X.Z. Stability analysis for neutral Markovian jump systems with partially unknown transition probabilities. J. Frankl. Inst. 2012, 349, 2193–2214. [Google Scholar] [CrossRef]
- Wu, T.; Cao, J.D.; Xiong, L.L.; Ahmad, B. Exponential passivity conditions on neutral stochastic neural networks with leakage delay and partially unknown transition probabilities in Markovian jump. Adv. Differ. Eq. 2018, 2018, 317. [Google Scholar] [CrossRef]
- Xiong, L.L.; Cheng, J.; Liu, X.Z.; Wu, T. Improved conditions for neutral delay systems with novel inequalities. J. Nonlinear Sci. Appl. 2017, 10, 2309–2317. [Google Scholar] [CrossRef]
- Ghadiri, H.; Motlagh, M.R.J.; Yazdi, M.B. Robust stabilization for uncertain switched neutral systems with interval time-varying mixed delays. Nonlinear Anal. Hybrid Syst. 2014, 13, 2–21. [Google Scholar] [CrossRef]
- Salamon, D. Control and Observation of Neutral Systems; Pitman Advanced Publishing Program: Boston, MA, USA, 1984. [Google Scholar]
- Xiong, W.J.; Liang, J.L. Novel stability criteria for neutral systems with multiple time-delays. Chaos Solitons Fractals 2007, 32, 1735–1741. [Google Scholar] [CrossRef]
- Xu, S.; Lam, J.; Ho, D.W.C.; Zou, Y. Delay-dependent exponential stability for a class of neural networks with time delays. J. Comput. Appl. Math. 2005, 183, 16–28. [Google Scholar] [CrossRef]
- Zuo, Z.Q.; Wang, Y. Novel Delay-Dependent Exponential Stability Analysis for a Class of Delayed Neural Networks. In Proceedings of the International Conference on Intelligent Computing, Kunming, China, 16–19 August 2006; pp. 216–226. [Google Scholar]
- Hale, J.K. The Theory of Functional Differential Equations; Applied Mathematical Sciences; Springer-Verlag: New York, NY, USA, 1977. [Google Scholar]
- Velmurugan, G.; Rakkiyappan, R.; Cao, J. Further analysis of global μ-stability of complex-valued neural networks with unbounded time-varying delays. Neural Netw. 2015, 67, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Song, Q. Global stability of complex-valued neural networks with both leakage time delay and discrete time delay on time scales. Neurocomputing 2013, 121, 254–264. [Google Scholar] [CrossRef]
- Li, J.D.; Huang, N.J. Asymptotical Stability for a Class of Complex-Valued Projective Neural Network. J. Optim. Theory Appl. 2018, 177, 261–270. [Google Scholar] [CrossRef]
- Xiao, N.; Jia, Y. New approaches on stability criteria for neural networks with two additive time-varying delay components. Neurocomputing 2013, 118, 150–156. [Google Scholar] [CrossRef]
- Forti, M. New condition for global stability of neural networks with application to linear and quadratic programming problems. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1995, 42, 354–366. [Google Scholar] [CrossRef]
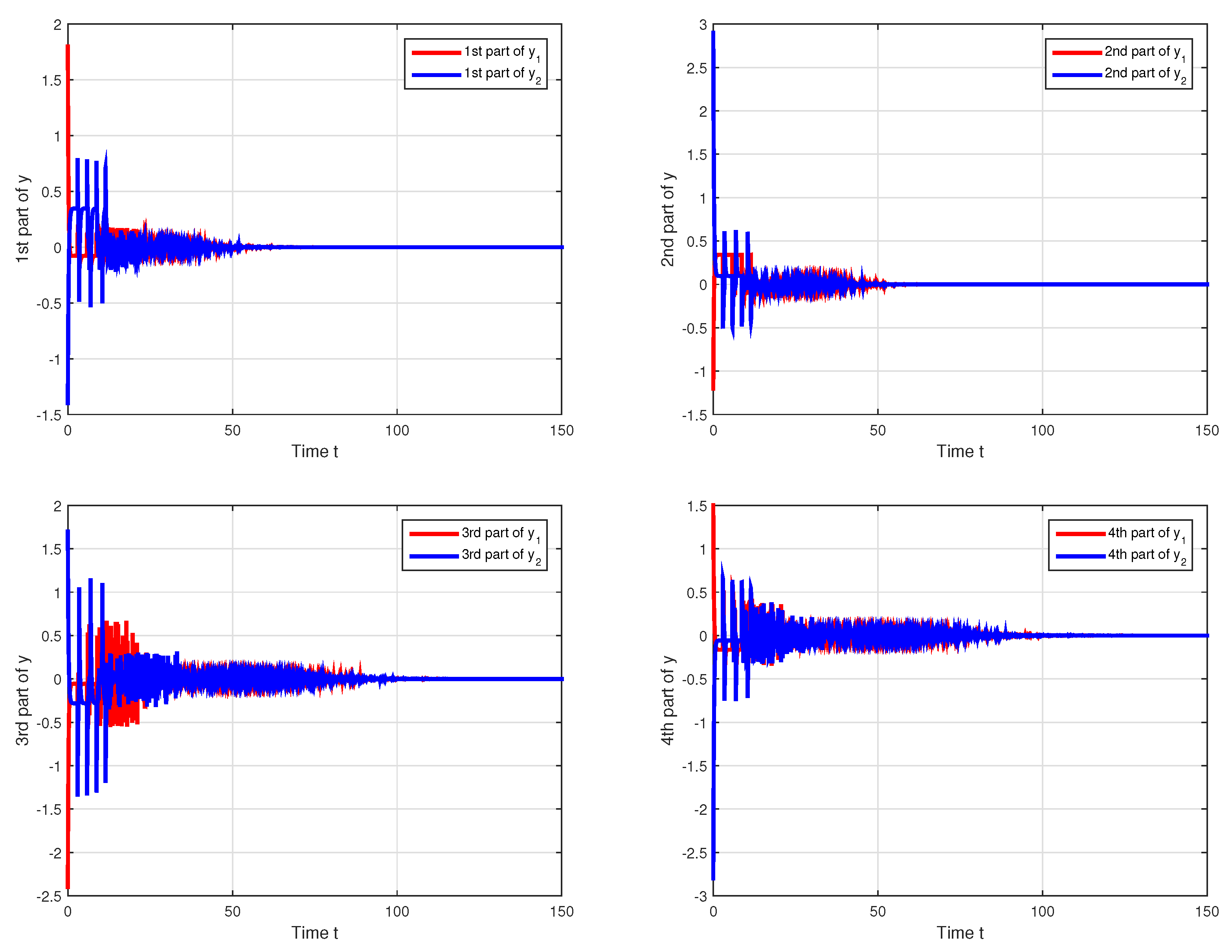
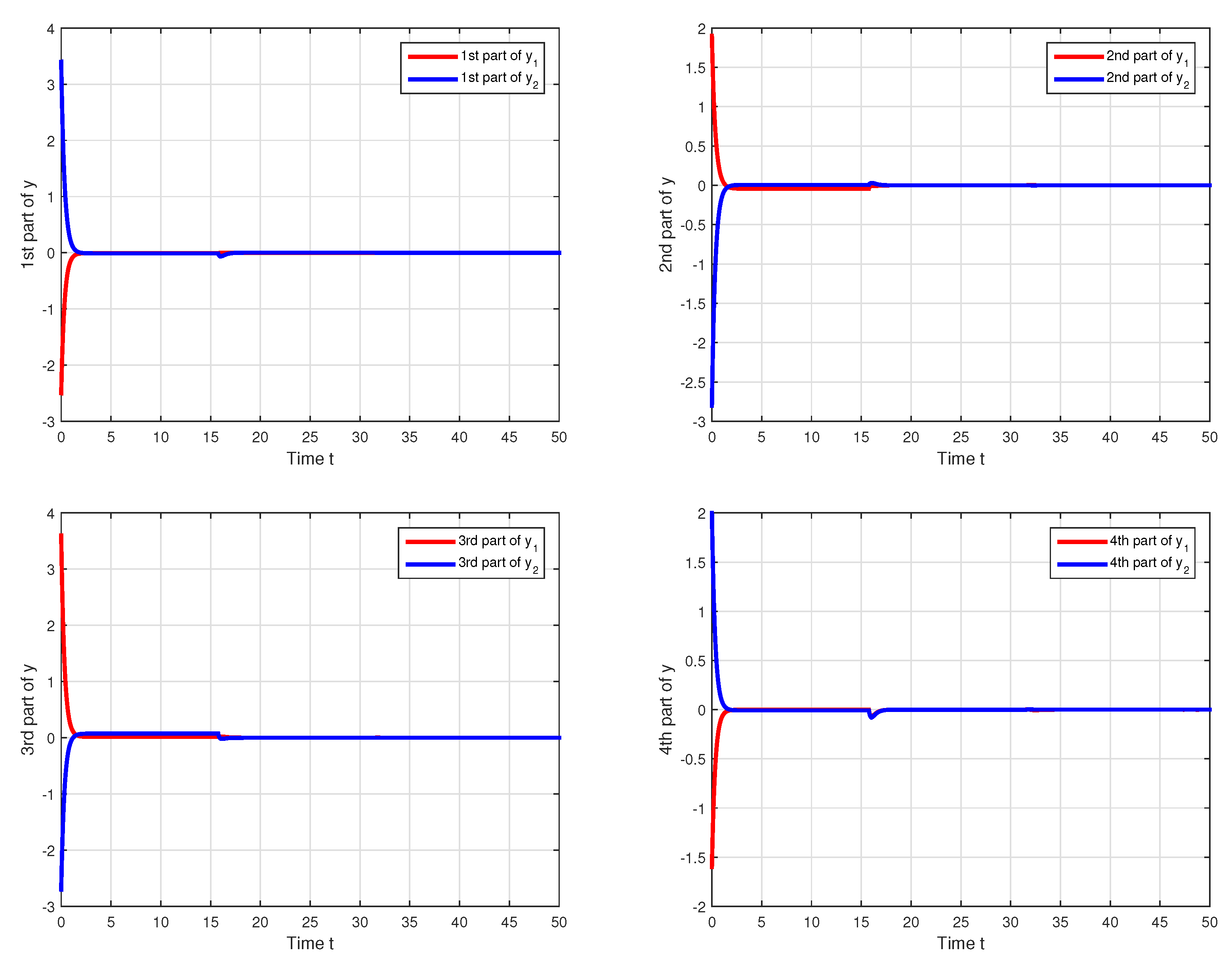
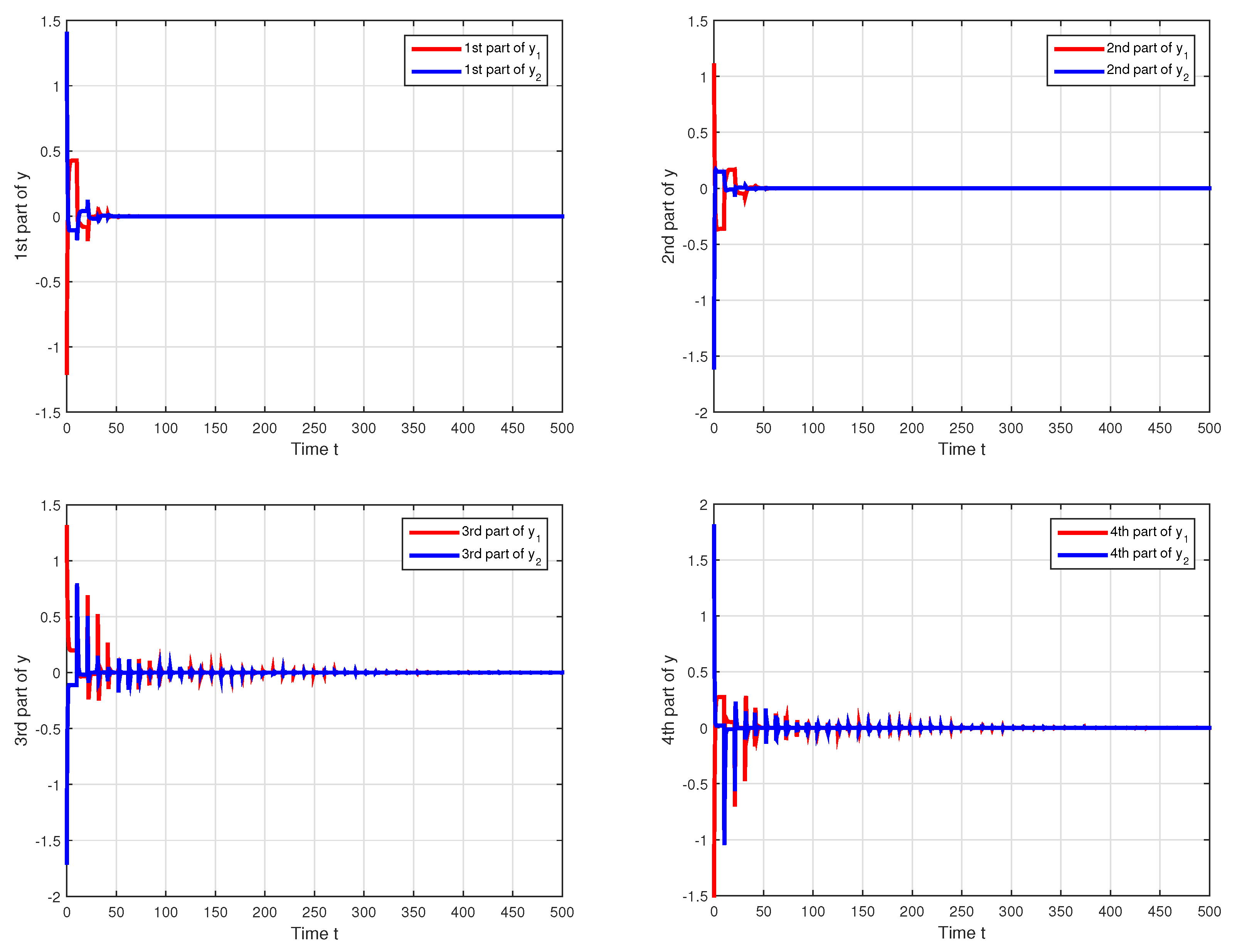
| Condition | QVNTNN | |
|---|---|---|
| global exponential stability | ||
| global power-stability | ||
| global log-stability |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, J.; Xiong, L.; Wu, T.; Liu, Z. Stability Analysis of Quaternion-Valued Neutral-Type Neural Networks with Time-Varying Delay. Mathematics 2019, 7, 101. https://doi.org/10.3390/math7010101
Shu J, Xiong L, Wu T, Liu Z. Stability Analysis of Quaternion-Valued Neutral-Type Neural Networks with Time-Varying Delay. Mathematics. 2019; 7(1):101. https://doi.org/10.3390/math7010101
Chicago/Turabian StyleShu, Jinlong, Lianglin Xiong, Tao Wu, and Zixin Liu. 2019. "Stability Analysis of Quaternion-Valued Neutral-Type Neural Networks with Time-Varying Delay" Mathematics 7, no. 1: 101. https://doi.org/10.3390/math7010101
APA StyleShu, J., Xiong, L., Wu, T., & Liu, Z. (2019). Stability Analysis of Quaternion-Valued Neutral-Type Neural Networks with Time-Varying Delay. Mathematics, 7(1), 101. https://doi.org/10.3390/math7010101




