A Nonlinear Systems Framework for Cyberattack Prevention for Chemical Process Control Systems †
Abstract
:1. Introduction
2. Preliminaries
2.1. Notation
2.2. Class of Systems
2.3. Model Predictive Control
2.4. Lyapunov-Based Model Predictive Control
3. A Nonlinear Dynamic Systems Perspective on Cyberattacks
4. Defining Cyberattack Resilience Against Specific Attack Types: Sensor Measurement Falsification in Feedback Control Loops
5. Control Design Concepts for Deterring Sensor Measurement Falsification Cyberattacks on Safety: Benefits, Limitations, and Perspectives
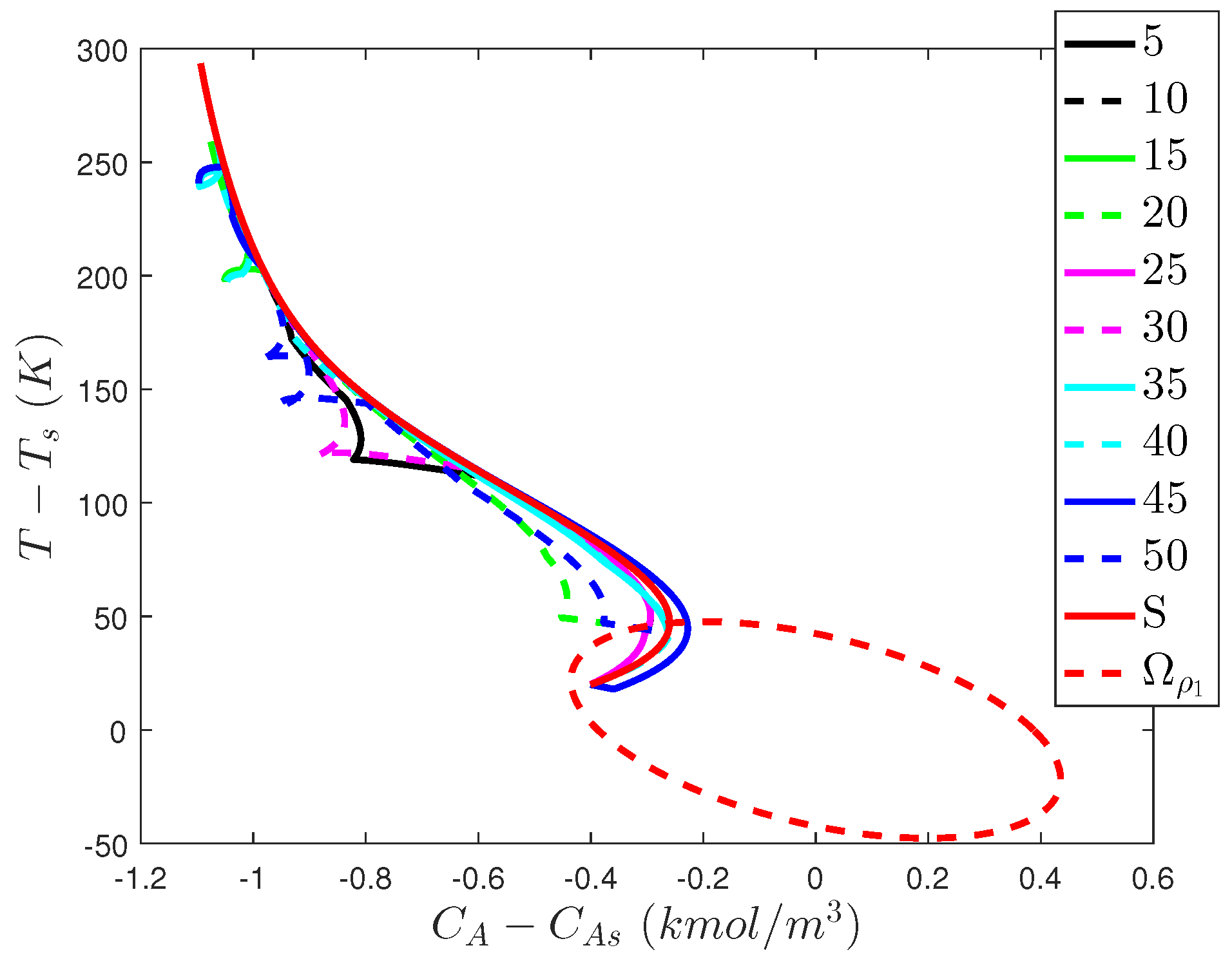
5.1. Motivating Example: The Need for Cyberattack-Resilient Control Designs
5.2. Deterring Sensor Measurement Falsification Cyberattacks on Safety: Creating Non-Intuitive Controller Outputs
5.2.1. Problems with Creating Non-Intuitive Controller Outputs
5.3. Deterring Sensor Measurement Falsification Cyberattacks on Safety: Creating Unpredictable Controller Outputs
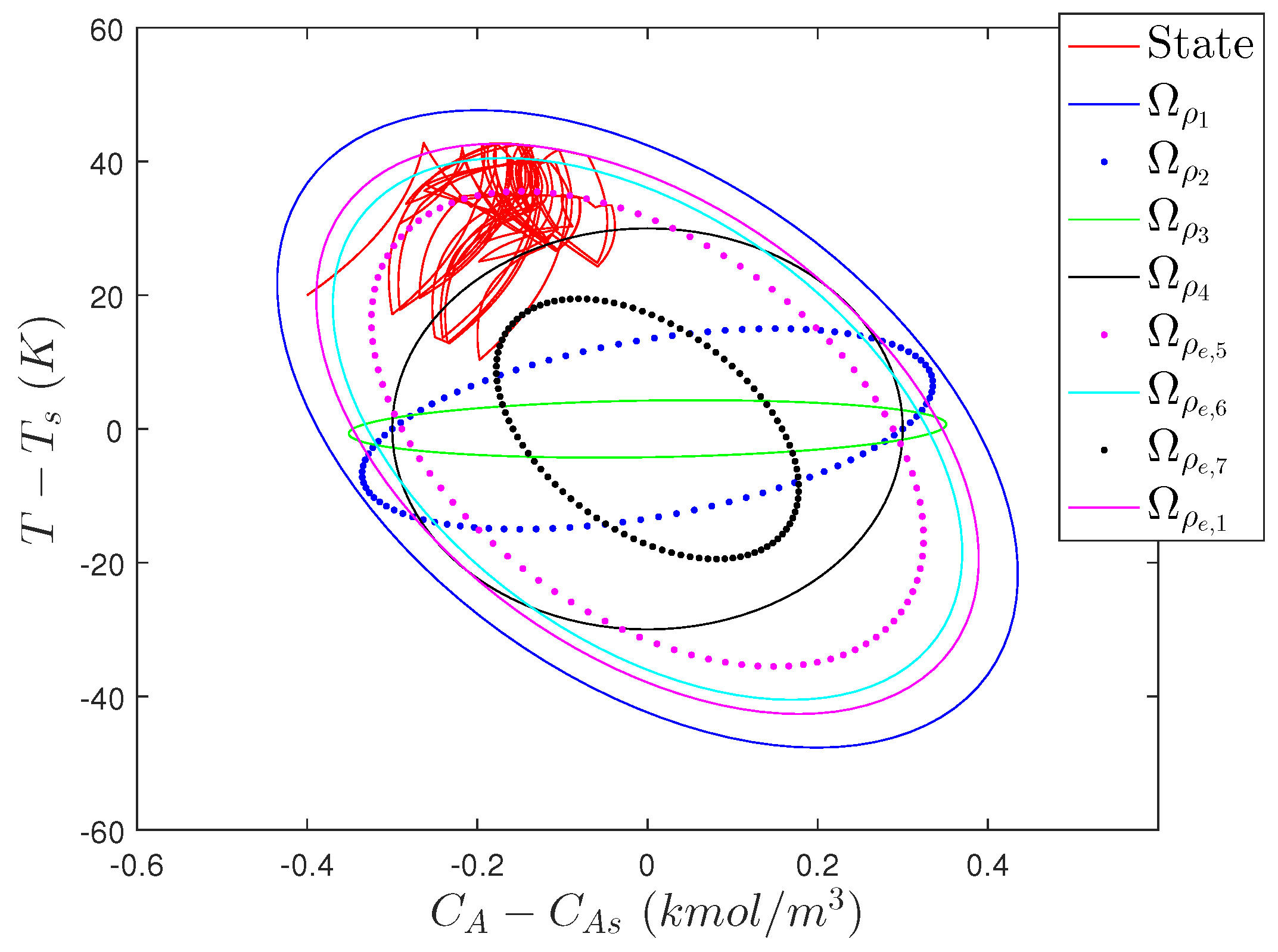
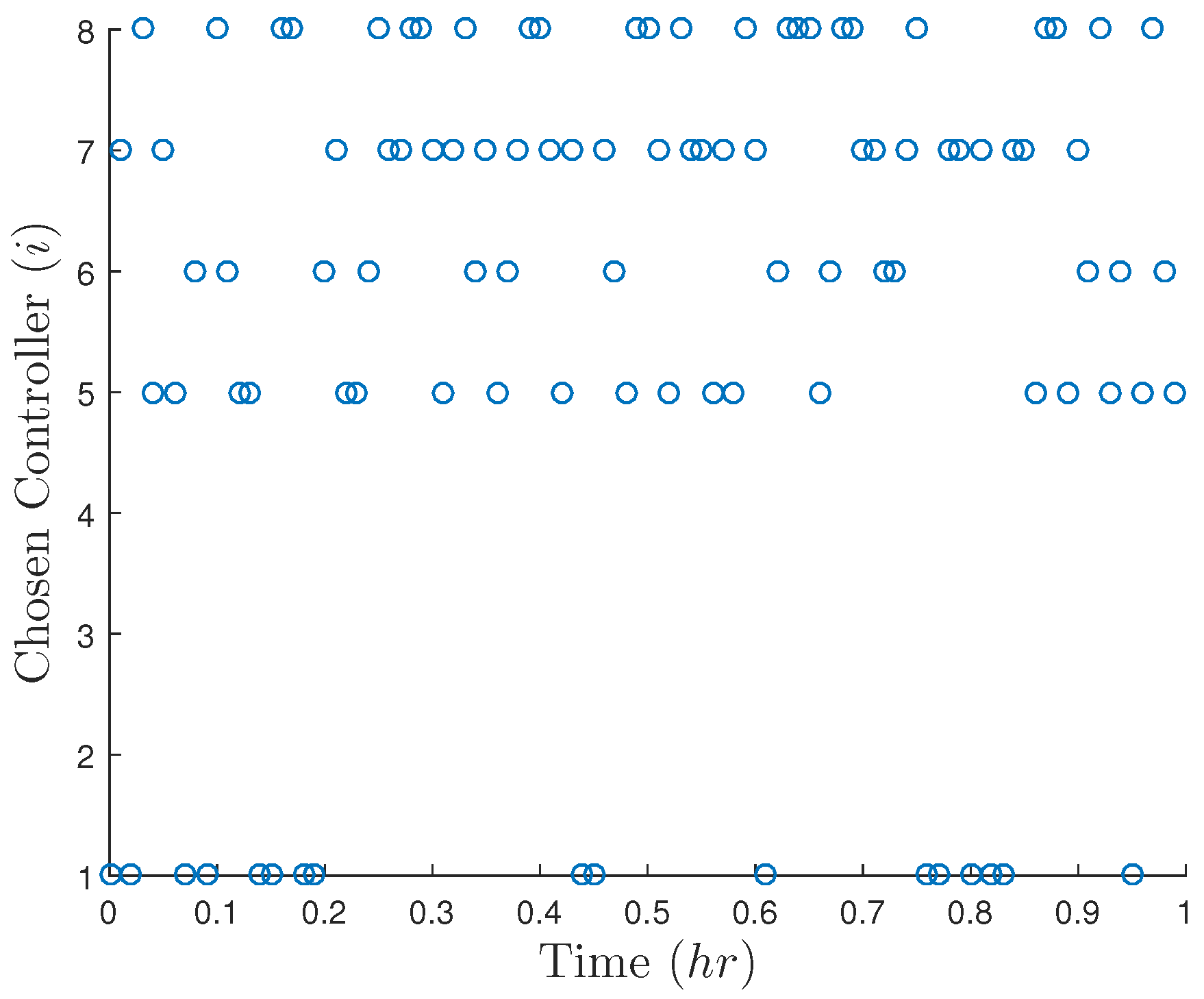
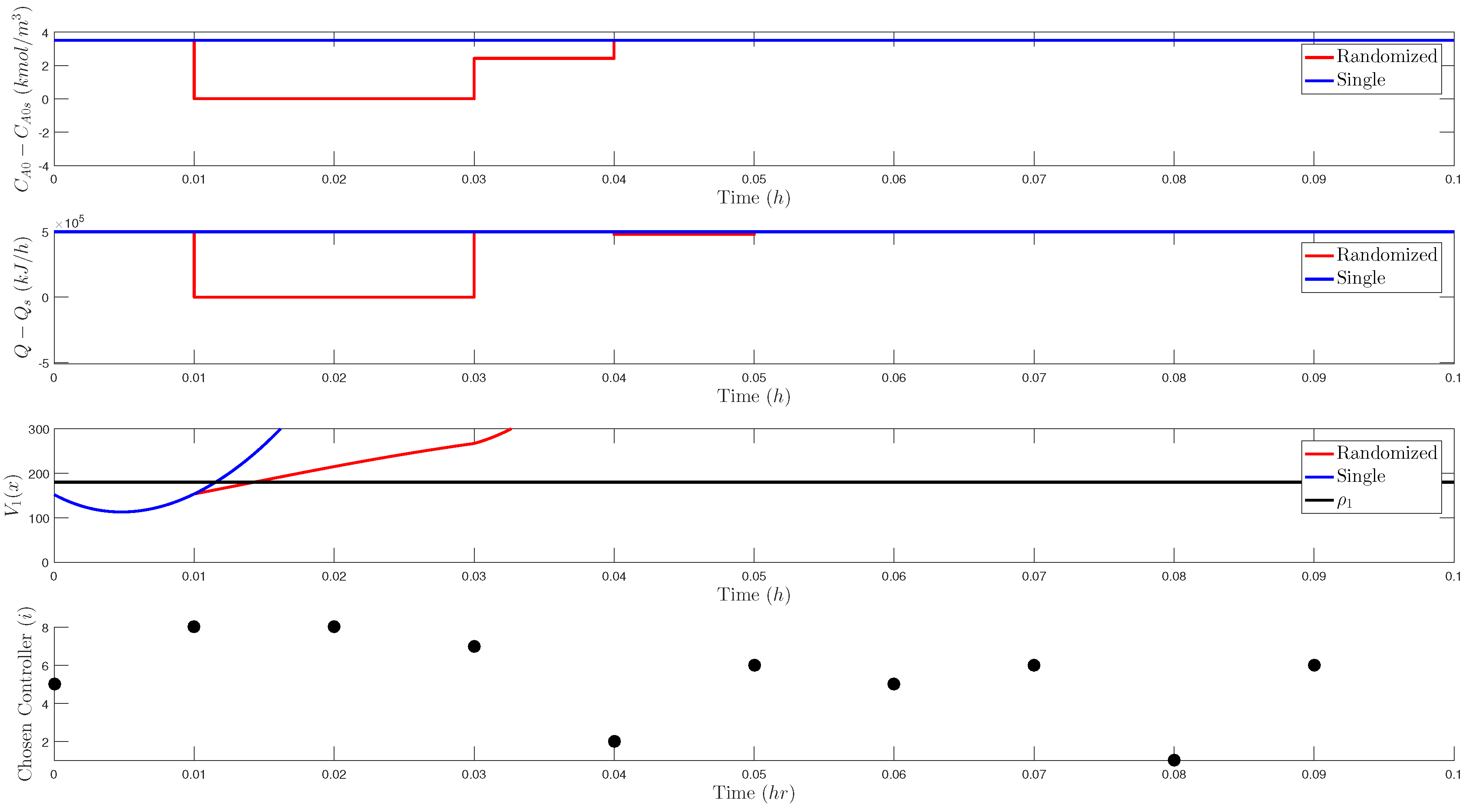
5.3.1. Creating Unpredictable Controller Outputs: Incorporating Randomness in LMPC Design
5.3.1.1. Stability Analysis of Randomized LMPC
5.3.2. Problems with Incorporating Randomness in LMPC Design
5.3.3. Creating Unpredictable Controller Outputs: Other Types of Randomness in MPC Design
5.4. Deterring Sensor Measurement Falsification Cyberattacks on Safety: Using Open-Loop Controller Outputs
5.4.1. Using Open-Loop Controller Outputs: Integration with LMPC
Stability Analysis of Open-Loop Control Integrated with LMPC
5.4.2. Problems with Integrating Open-Loop Control and LMPC
5.5. Deterring Sensor Measurement Falsification Cyberattacks on Safety: Perspectives
6. Conclusions
Funding
Conflicts of Interest
References
- Leveson, N.G.; Stephanopoulos, G. A system-theoretic, control-inspired view and approach to process safety. AIChE J. 2014, 60, 2–14. [Google Scholar]
- Mannan, M.S.; Sachdeva, S.; Chen, H.; Reyes-Valdes, O.; Liu, Y.; Laboureur, D.M. Trends and challenges in process safety. AIChE J. 2015, 61, 3558–3569. [Google Scholar]
- Venkatasubramanian, V. Systemic failures: Challenges and opportunities in risk management in complex systems. AIChE J. 2011, 57, 2–9. [Google Scholar]
- Albalawi, F.; Durand, H.; Christofides, P.D. Process operational safety via model predictive control: Recent results and future research directions. Comput. Chem. Eng. 2018, 114, 171–190. [Google Scholar]
- Albalawi, F.; Durand, H.; Alanqar, A.; Christofides, P.D. Achieving operational process safety via model predictive control. J. Loss Prev. Process Ind. 2018, 53, 74–88. [Google Scholar]
- Albalawi, F.; Durand, H.; Christofides, P.D. Process operational safety using model predictive control based on a process Safeness Index. Comput. Chem. Eng. 2017, 104, 76–88. [Google Scholar]
- Zhang, Z.; Wu, Z.; Durand, H.; Albalawi, F.; Christofides, P.D. On integration of feedback control and safety systems: Analyzing two chemical process applications. Chem. Eng. Res. Des. 2018, 132, 616–626. [Google Scholar] [Green Version]
- Carson, J.M.; Açıkmeşe, B.; Murray, R.M.; MacMartin, D.G. A robust model predictive control algorithm augmented with a reactive safety mode. Automatica 2013, 49, 1251–1260. [Google Scholar]
- Wu, Z.; Durand, H.; Christofides, P.D. Safe economic model predictive control of nonlinear systems. Syst. Control Lett. 2018, 118, 69–76. [Google Scholar]
- Wieland, P.; Allgöwer, F. Constructive Safety Using Control Barrier Functions. IFAC Proc. Vol. 2007, 40, 462–467. [Google Scholar]
- Braun, P.; Kellett, C.M. On (the existence of) Control Lyapunov Barrier Functions. 2017. Available online: https://epub.uni-bayreuth.de/3522/ (accessed on 10 August 2018).
- Shahnazari, H.; Mhaskar, P. Distributed fault diagnosis for networked nonlinear uncertain systems. Comput. Chem. Eng. 2018, 115, 22–33. [Google Scholar]
- Shahnazari, H.; Mhaskar, P. Actuator and sensor fault detection and isolation for nonlinear systems subject to uncertainty. Int. J. Robust Nonlinear Control 2018, 28, 1996–2013. [Google Scholar]
- Yin, X.; Liu, J. Distributed output-feedback fault detection and isolation of cascade process networks. AIChE J. 2017, 63, 4329–4342. [Google Scholar]
- Alanqar, A.; Durand, H.; Christofides, P.D. Fault-Tolerant Economic Model Predictive Control Using Error-Triggered Online Model Identification. Ind. Eng. Chem. Res. 2017, 56, 5652–5667. [Google Scholar]
- Demetriou, M.A.; Armaou, A. Dynamic online nonlinear robust detection and accommodation of incipient component faults for nonlinear dissipative distributed processes. Int. J. Robust Nonlinear Control 2012, 22, 3–23. [Google Scholar]
- Xue, D.; El-Farra, N.H. Resource-aware fault accommodation in spatially-distributed processes with sampled-data networked control systems. In Proceedings of the American Control Conference, Seattle, WA, USA, 24–26 May 2017; pp. 1809–1814. [Google Scholar]
- Xue, D.; El-Farra, N.H. Actuator fault-tolerant control of networked distributed processes with event-triggered sensor-controller communication. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 1661–1666. [Google Scholar]
- Smith, R.E. Elementary Information Security; Jones & Bartlett Learning, LLC: Burlington, MA, USA, 2016. [Google Scholar]
- Cárdenas, A.A.; Amin, S.; Lin, Z.S.; Huang, Y.L.; Huang, C.Y.; Sastry, S. Attacks against process control systems: Risk assessment, detection, and response. In Proceedings of the ACM Asia Conference on Computer & Communications Security, Hong Kong, China, 22–24 March 2011. [Google Scholar]
- Greenberg, A. How an Entire Nation Became Russia’s Test Lab for Cyberwar. 2017. Available online: https://www.wired.com/story/russian-hackers-attack-ukraine/ (accessed on 11 July 2018).
- Clark, R.M.; Panguluri, S.; Nelson, T.D.; Wyman, R.P. Protecting drinking water utilities from cyberthreats. J. Am. Water Works Assoc. 2017, 109, 50–58. [Google Scholar]
- Langner, R. Stuxnet: Dissecting a Cyberwarfare Weapon. IEEE Secur. Priv. 2011, 9, 49–51. [Google Scholar]
- Perlroth, N.; Krauss, C.; A Cyberattack in Saudi Arabia Had a Deadly Goal. Experts Fear Another Try. 2018. Available online: https://www.nytimes.com/2018/03/15/technology/saudi-arabia-hacks-cyberattacks.html (accessed on 11 March 2018).
- Groll, E. Cyberattack Targets Safety System at Saudi Aramco. 2017. Available online: https://foreignpolicy.com/2017/12/21/cyber-attack-targets-safety-system-at-saudi-aramco/ (accessed on 11 July 2018).
- Liu, Y.; Sarabi, A.; Zhang, J.; Naghizadeh, P.; Karir, M.; Bailey, M.; Liu, M. Cloudy with a Chance of Breach: Forecasting Cyber Security Incidents. In Proceedings of the USENIX Security Symposium, Washington, DC, USA, 12–14 August 2015; pp. 1009–1024. [Google Scholar]
- Solomon, M.G.; Kim, D.; Carrell, J.L. Fundamentals of Communications and Networking; Jones & Bartlett Publishers: Burlington, MA, USA, 2014. [Google Scholar]
- McLaughlin, S.; Konstantinou, C.; Wang, X.; Davi, L.; Sadeghi, A.R.; Maniatakos, M.; Karri, R. The Cybersecurity Landscape in Industrial Control Systems. Proc. IEEE 2016, 104, 1039–1057. [Google Scholar]
- Hull, J.; Khurana, H.; Markham, T.; Staggs, K. Staying in control: Cybersecurity and the modern electric grid. IEEE Power Energy Mag. 2012, 10, 41–48. [Google Scholar]
- Ginter, A. Unidirectional Security Gateways: Stronger than Firewalls. In Proceedings of the ICALEPCS, San Francisco, CA, USA, 6–11 October 2013; pp. 1412–1414. [Google Scholar]
- Khorrami, F.; Krishnamurthy, P.; Karri, R. Cybersecurity for Control Systems: A Process-Aware Perspective. IEEE Des. Test 2016, 33, 75–83. [Google Scholar]
- He, D.; Chan, S.; Zhang, Y.; Wu, C.; Wang, B. How Effective Are the Prevailing Attack-Defense Models for Cybersecurity Anyway? IEEE Intel. Syst. 2014, 29, 14–21. [Google Scholar]
- Ten, C.W.; Liu, C.C.; Manimaran, G. Vulnerability Assessment of Cybersecurity for SCADA Systems. IEEE Trans. Power Syst. 2008, 23, 1836–1846. [Google Scholar]
- Pang, Z.H.; Liu, G.P. Design and implementation of secure networked predictive control systems under deception attacks. IEEE Trans. Control Syst. Technol. 2012, 20, 1334–1342. [Google Scholar]
- Rieger, C.; Zhu, Q.; Başar, T. Agent-based cyber control strategy design for resilient control systems: Concepts, architecture and methodologies. In Proceedings of the 5th International Symposium on Resilient Control Systems, Salt Lake City, UT, USA, 14–16 August 2012; pp. 40–47. [Google Scholar]
- Chavez, A.R.; Stout, W.M.S.; Peisert, S. Techniques for the dynamic randomization of network attributes. In Proceedings of the IEEE International Carnahan Conference on Security Technology, Taipei, Taiwan, 21–24 September 2015; pp. 1–6. [Google Scholar]
- Linda, O.; Manic, M.; McQueen, M. Improving control system cyber-state awareness using known secure sensor measurements. In Critical Information Infrastructures Security. CIRITIS 2012; Hämmerli, B.M., Kalstad Svendsen, N., Lopez, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7722, pp. 46–58. [Google Scholar]
- Plosz, S.; Farshad, A.; Tauber, M.; Lesjak, C.; Ruprechter, T.; Pereira, N. Security vulnerabilities and risks in industrial usage of wireless communication. In Proceedings of the IEEE International Conference on Emerging Technology and Factory Automation, Barcelona, Spain, 6–19 September 2014; pp. 1–8. [Google Scholar]
- Lopez, J.; Zhou, J. (Eds.) Wireless Sensor Network Security; IOS Press: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Xu, L.D.; He, W.; Li, S. Internet of Things in Industries: A Survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar]
- Almorsy, M.; Grundy, J.; Müller, I. An analysis of the cloud computing security problem. arXiv, 2016; arXiv:1609.01107. [Google Scholar]
- Rieger, C.G. Notional examples and benchmark aspects of a resilient control system. In Proceedings of the 2010 3rd International Symposium on Resilient Control Systems, Idaho Falls, ID, USA, 10–12 August 2010; pp. 64–71. [Google Scholar]
- Rieger, C.G.; Gertman, D.I.; McQueen, M.A. Resilient control systems: Next generation design research. In Proceedings of the 2009 2nd Conference on Human System Interactions, Catania, Italy, 21–23 May 2009; pp. 632–636. [Google Scholar]
- Wakaiki, M.; Tabuada, P.; Hespanha, J.P. Supervisory control of discrete-event systems under attacks. arXiv, 2017; arXiv:1701.00881. [Google Scholar]
- Bopardikar, S.D.; Speranzon, A.; Hespanha, J.P. An H-infinity approach to stealth-resilient control design. In Proceedings of the 2016 Resilience Week, Chicago, IL, USA, 16–18 August 2016; pp. 56–61. [Google Scholar]
- Amin, S.; Cárdenas, A.A.; Sastry, S.S. Safe and secure networked control systems under denial-of-service attacks. In Hybrid Systems: Computation and Control. HSCC 2009; Majumdar, R., Tabuada, P., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5469, pp. 31–45. [Google Scholar]
- Fawzi, H.; Tabuada, P.; Diggavi, S. Secure Estimation and Control for Cyber-Physical Systems Under Adversarial Attacks. IEEE Trans. Autom. Control 2014, 59, 1454–1467. [Google Scholar] [Green Version]
- Zhu, Q.; Başar, T. Game-Theoretic Methods for Robustness, Security, and Resilience of Cyberphysical Control Systems: Games-in-Games Principle for Optimal Cross-Layer Resilient Control Systems. IEEE Control Syst. 2015, 35, 46–65. [Google Scholar]
- Zhu, Q.; Başar, T. Robust and resilient control design for cyber-physical systems with an application to power systems. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 4066–4071. [Google Scholar]
- Zhu, Q.; Bushnell, L.; Başar, T. Resilient distributed control of multi-agent cyber-physical systems. In Control of Cyber-Physical Systems; Tarraf, D., Ed.; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 449, pp. 301–316. [Google Scholar]
- Zonouz, S.; Rogers, K.M.; Berthier, R.; Bobba, R.B.; Sanders, W.H.; Overbye, T.J. SCPSE: Security-Oriented Cyber-Physical State Estimation for Power Grid Critical Infrastructures. IEEE Trans. Smart Grid 2012, 3, 1790–1799. [Google Scholar]
- Zheng, S.; Jiang, T.; Baras, J.S. Robust State Estimation under False Data Injection in Distributed Sensor Networks. In Proceedings of the 2010 IEEE Global Telecommunications Conference, Miami, FL, USA, 6–10 December 2010; pp. 1–5. [Google Scholar]
- Pasqualetti, F.; Dorfler, F.; Bullo, F. Control-Theoretic Methods for Cyberphysical Security: Geometric Principles for Optimal Cross-Layer Resilient Control Systems. IEEE Control Syst. 2015, 35, 110–127. [Google Scholar]
- Pasqualetti, F.; Dörfler, F.; Bullo, F. Attack Detection and Identification in Cyber-Physical Systems. IEEE Trans. Autom. Control 2013, 58, 2715–2729. [Google Scholar] [Green Version]
- McLaughlin, S. CPS: Stateful policy enforcement for control system device usage. In Proceedings of the 29th Annual Computer Security Applications Conference, New Orleans, LA, USA, 9–13 December 2013; pp. 109–118. [Google Scholar]
- Melin, A.; Kisner, R.; Fugate, D.; McIntyre, T. Minimum state awareness for resilient control systems under cyber-attack. In Proceedings of the 2012 Future of Instrumentation International Workshop, Gatlinburg, TN, USA, 8–9 October 2012; pp. 1–4. [Google Scholar]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [Green Version]
- Rawlings, J.B. Tutorial overview of model predictive control. IEEE Control Syst. 2000, 20, 38–52. [Google Scholar] [Green Version]
- Durand, H. State Measurement Spoofing Prevention through Model Predictive Control Design. In Proceedings of the IFAC NMPC-2018, Madison, WI, USA, 19–22 August 2018; pp. 643–648. [Google Scholar]
- Heidarinejad, M.; Liu, J.; Christofides, P.D. Economic model predictive control of nonlinear process systems using Lyapunov techniques. AIChE J. 2012, 58, 855–870. [Google Scholar]
- Mhaskar, P.; El-Farra, N.H.; Christofides, P.D. Stabilization of nonlinear systems with state and control constraints using Lyapunov-based predictive control. Syst. Control Lett. 2006, 55, 650–659. [Google Scholar]
- Muñoz de la Peña, D.; Christofides, P.D. Lyapunov-Based Model Predictive Control of Nonlinear Systems Subject to Data Losses. IEEE Trans. Autom. Control 2008, 53, 2076–2089. [Google Scholar] [Green Version]
- Zhu, B.; Joseph, A.; Sastry, S. A taxonomy of cyber attacks on SCADA systems. In Proceedings of the 2011 IEEE International Conferences on Internet of Things, and Cyber, Physical and Social Computing, Dalian, China, 19–22 October 2011; pp. 380–388. [Google Scholar]
- Krotofil, M.; Cárdenas, A.A. Resilience of process control systems to cyber-physical attacks. In Proceedings of the Nordic Conference on Secure IT Systems, Ilulissat, Greenland, 18–21 October 2013; pp. 166–182. [Google Scholar]
- Gentile, M.; Rogers, W.J.; Mannan, M.S. Development of an inherent safety index based on fuzzy logic. AIChE J. 2003, 49, 959–968. [Google Scholar]
- Heikkilä, A.M.; Hurme, M.; Järveläinen, M. Safety considerations in process synthesis. Comput. Chem. Eng. 1996, 20, S115–S120. [Google Scholar]
- Khan, F.I.; Amyotte, P.R. How to Make Inherent Safety Practice a Reality. Can. J. Chem. Eng. 2003, 81, 2–16. [Google Scholar]
- Gupta, J.P.; Edwards, D.W. Inherently Safer Design—Present and Future. Process Saf. Environ. Prot. 2002, 80, 115–125. [Google Scholar]
- Kletz, T.A. Inherently safer plants. Plant/Oper. Prog. 1985, 4, 164–167. [Google Scholar]
- Li, L.; Hu, B.; Lemmon, M. Resilient event triggered systems with limited communication. In Proceedings of the 2012 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 6577–6582. [Google Scholar]
- Melin, A.M.; Ferragut, E.M.; Laska, J.A.; Fugate, D.L.; Kisner, R. A mathematical framework for the analysis of cyber-resilient control systems. In Proceedings of the 2013 6th International Symposium on Resilient Control Systems, San Francisco, CA, USA, 13–15 August 2013; pp. 13–18. [Google Scholar]
- Chandy, S.E.; Rasekh, A.; Barker, Z.A.; Shafiee, M.E. Cyberattack Detection using Deep Generative Models with Variational Inference. arXiv, 2018; arXiv:1805.12511. [Google Scholar]
- Rosich, A.; Voos, H.; Li, Y.; Darouach, M. A model predictive approach for cyber-attack detection and mitigation in control systems. In Proceedings of the IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 6621–6626. [Google Scholar]
- Tajer, A.; Kar, S.; Poor, H.V.; Cui, S. Distributed joint cyber attack detection and state recovery in smart grids. In Proceedings of the IEEE International Conference on Smart Grid Communications, Brussels, Belgium, 17–20 October 2011; pp. 202–207. [Google Scholar]
- Kiss, I.; Genge, B.; Haller, P. A clustering-based approach to detect cyber attacks in process control systems. In Proceedings of the IEEE 13th International Conference on Industrial Informatics, Cambridge, UK, 22–24 July 2015; pp. 142–148. [Google Scholar]
- Valdes, A.; Cheung, S. Intrusion Monitoring in Process Control Systems. In Proceedings of the 42nd Hawaii International Conference on System Sciences, Big Island, HI, USA, 5–8 January 2009; pp. 1–7. [Google Scholar]
- Wu, Z.; Albalawi, F.; Zhang, J.; Zhang, Z.; Durand, H.; Christofides, P.D. Detecting and Handling Cyber-attacks in Model Predictive Control of Chemical Processes. Mathematics 2018, accepted. [Google Scholar]
- Ricker, N.L. Model predictive control of a continuous, nonlinear, two-phase reactor. J. Process Control 1993, 3, 109–123. [Google Scholar]
- Alanqar, A.; Ellis, M.; Christofides, P.D. Economic model predictive control of nonlinear process systems using empirical models. AIChE J. 2015, 61, 816–830. [Google Scholar]
- Lin, Y.; Sontag, E.D. A universal formula for stabilization with bounded controls. Syst. Control Lett. 1991, 16, 393–397. [Google Scholar] [Green Version]
- Grossmann, I.E. Review of nonlinear mixed-integer and disjunctive programming techniques. Optim. Eng. 2002, 3, 227–252. [Google Scholar]
- Mhaskar, P.; Liu, J.; Christofides, P.D. Fault-Tolerant Process Control: Methods and Applications; Springer: London, UK, 2013. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar]
- Mo, Y.; Sinopoli, B. Secure control against replay attacks. In Proceedings of the 2009 47th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 30 September–2 October 2009; pp. 911–918. [Google Scholar]
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive control methods. J. Process Control 2014, 24, 1156–1178. [Google Scholar]
- Rawlings, J.B.; Angeli, D.; Bates, C.N. Fundamentals of economic model predictive control. In Proceedings of the Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 3851–3861. [Google Scholar]
- Faulwasser, T.; Korda, M.; Jones, C.N.; Bonvin, D. Turnpike and dissipativity properties in dynamic real-time optimization and economic MPC. In Proceedings of the IEEE 53rd Annual Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 2734–2739. [Google Scholar]
- Müller, M.A.; Grüne, L.; Allgöwer, F. On the role of dissipativity in economic model predictive control. IFAC-PapersOnLine 2015, 48, 110–116. [Google Scholar] [Green Version]
- Huang, R.; Harinath, E.; Biegler, L.T. Lyapunov stability of economically oriented NMPC for cyclic processes. J. Process Control 2011, 21, 501–509. [Google Scholar]
- Omell, B.P.; Chmielewski, D.J. IGCC power plant dispatch using infinite-horizon economic model predictive control. Ind. Eng. Chem. Res. 2013, 52, 3151–3164. [Google Scholar]
- Amini-Rankouhi, A.; Huang, Y. Prediction of maximum recoverable mechanical energy via work integration: A thermodynamic modeling and analysis approach. AIChE J. 2017, 63, 4814–4826. [Google Scholar]
- Tula, A.K.; Babi, D.K.; Bottlaender, J.; Eden, M.R.; Gani, R. A computer-aided software-tool for sustainable process synthesis-intensification. Comput. Chem. Eng. 2017, 105, 74–95. [Google Scholar]
- Limon, D.; Alamo, T.; Salas, F.; Camacho, E. Input to state stability of min–max MPC controllers for nonlinear systems with bounded uncertainties. Automatica 2006, 42, 797–803. [Google Scholar] [Green Version]
- Campo, P.J.; Morari, M. Robust Model Predictive Control. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 10–12 June 1987; pp. 1021–1026. [Google Scholar]
- Pannocchia, G.; Gabiccini, M.; Artoni, A. Offset-free MPC explained: Novelties, subtleties, and applications. IFAC-PapersOnLine 2015, 48, 342–351. [Google Scholar] [CrossRef]
- Ellis, M.; Zhang, J.; Liu, J.; Christofides, P.D. Robust moving horizon estimation based output feedback economic model predictive control. Syst. Control Lett. 2014, 68, 101–109. [Google Scholar]
- Das, B.; Mhaskar, P. Lyapunov-based offset-free model predictive control of nonlinear process systems. Can. J. Chem. Eng. 2015, 93, 471–478. [Google Scholar]
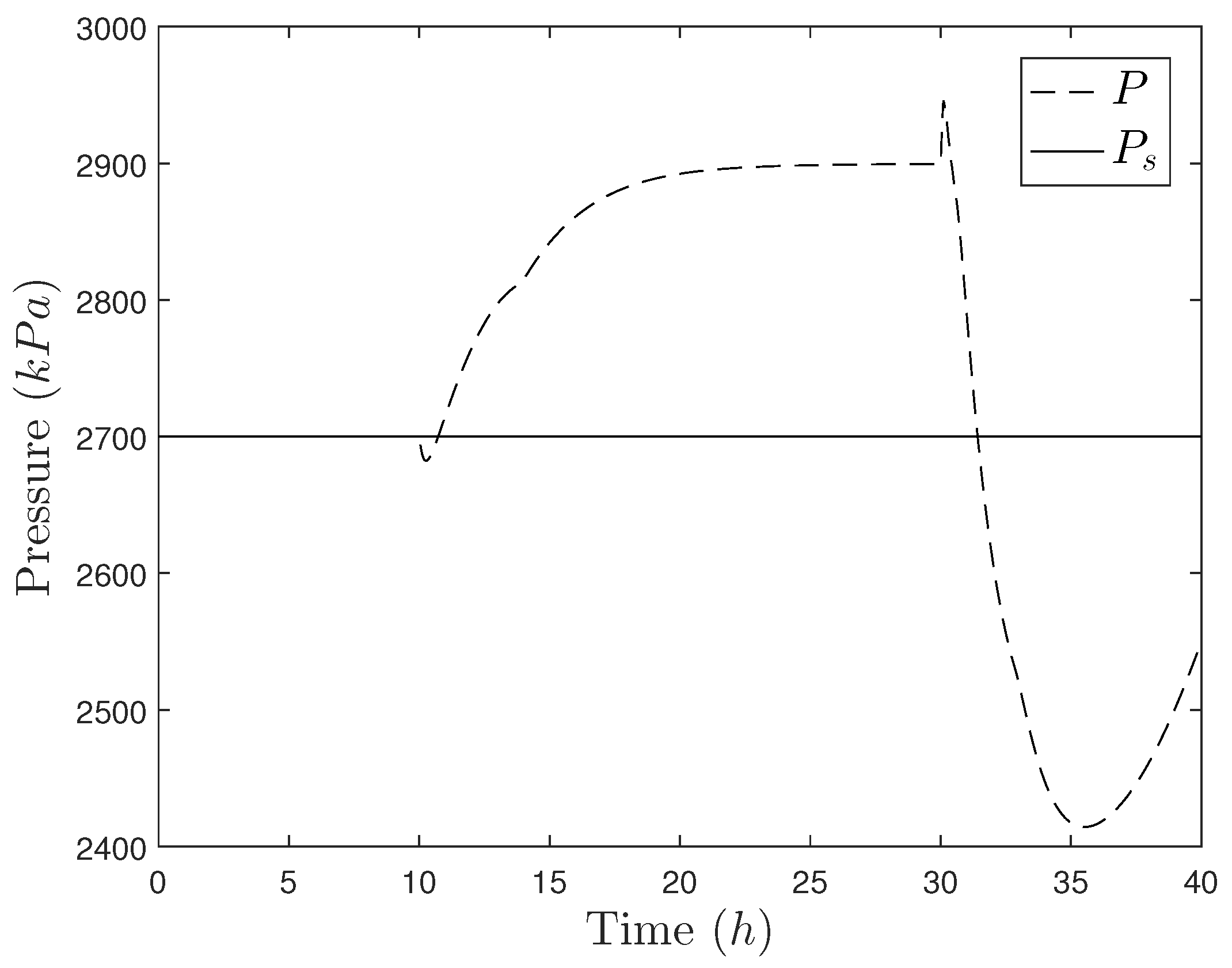
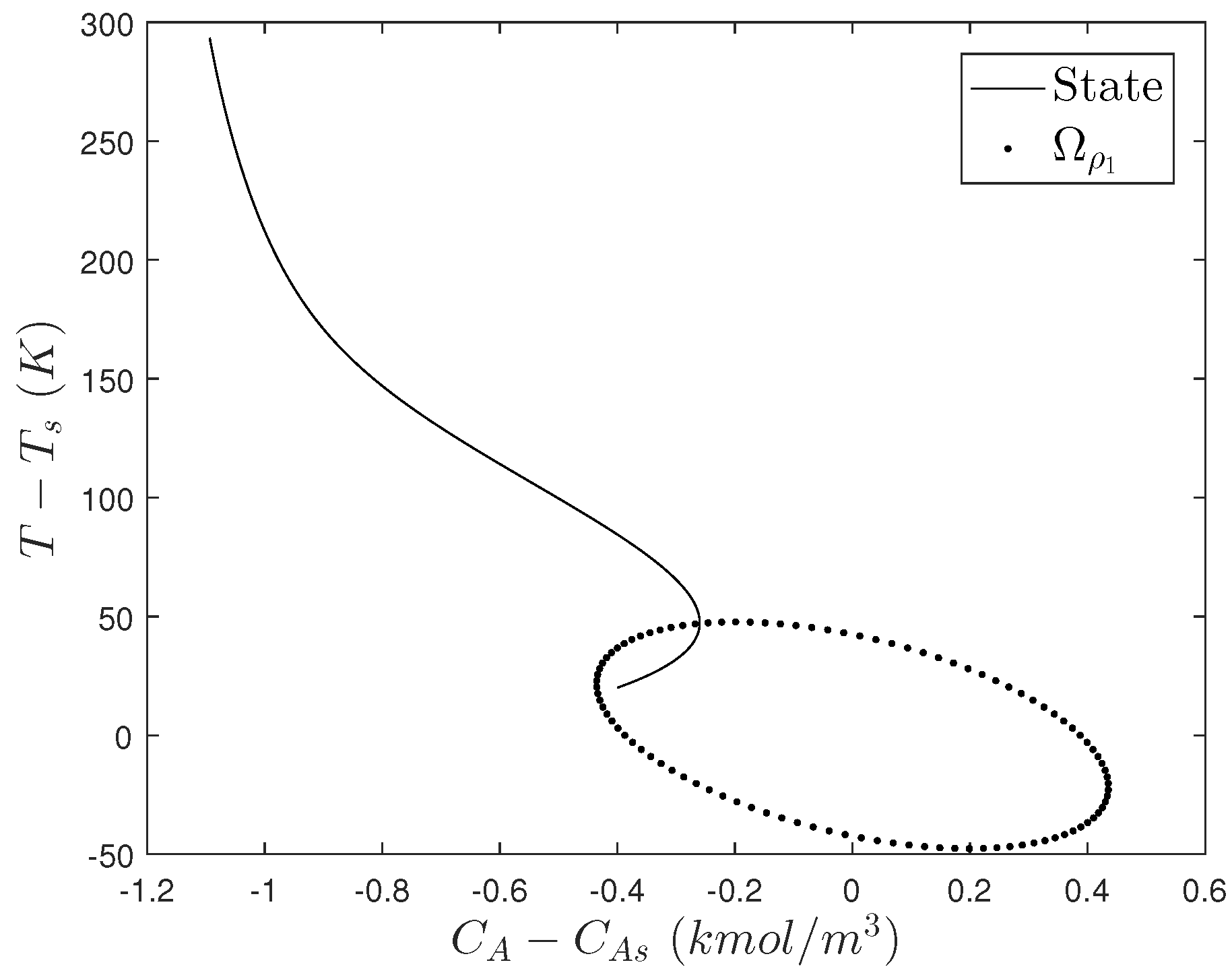
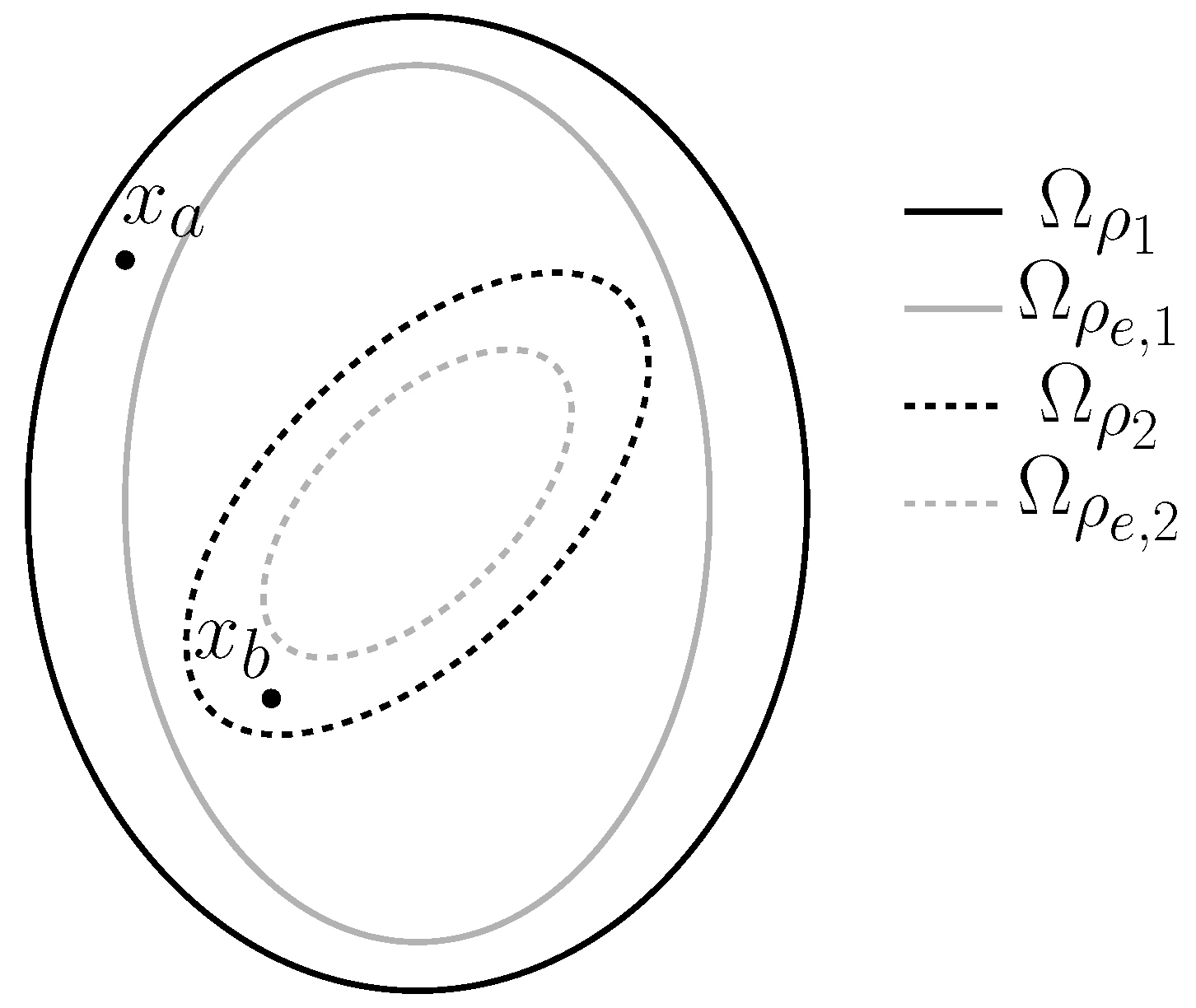
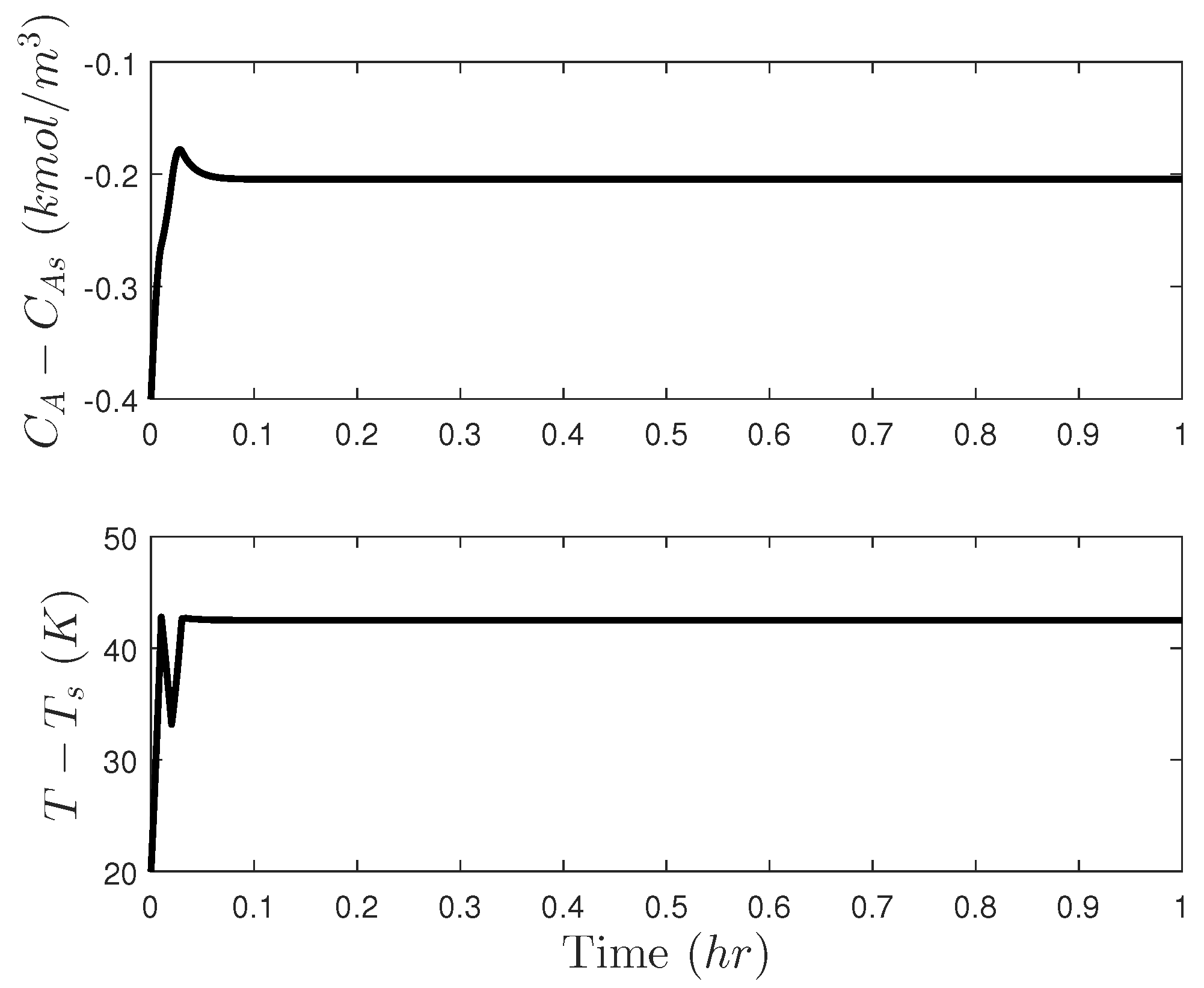
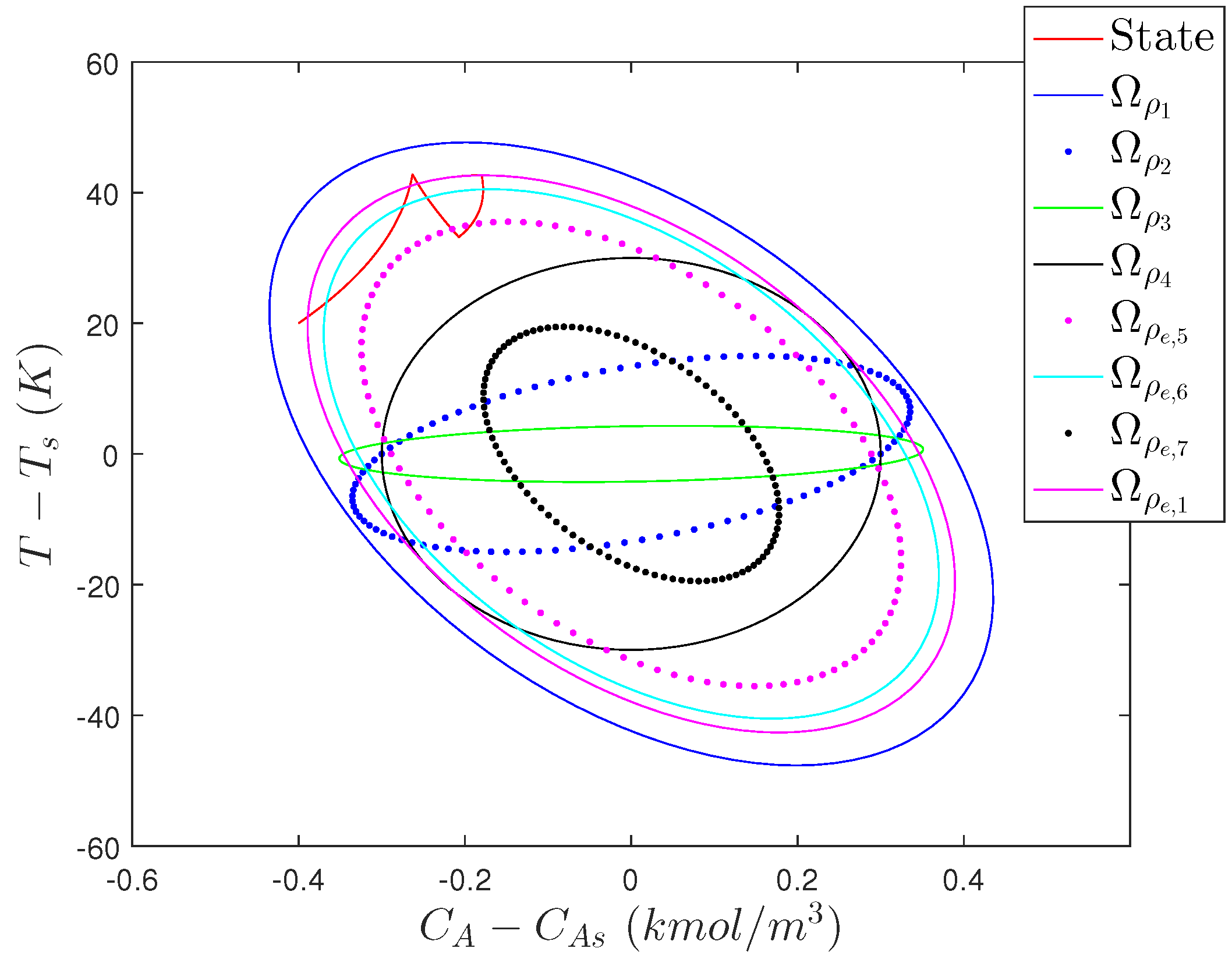
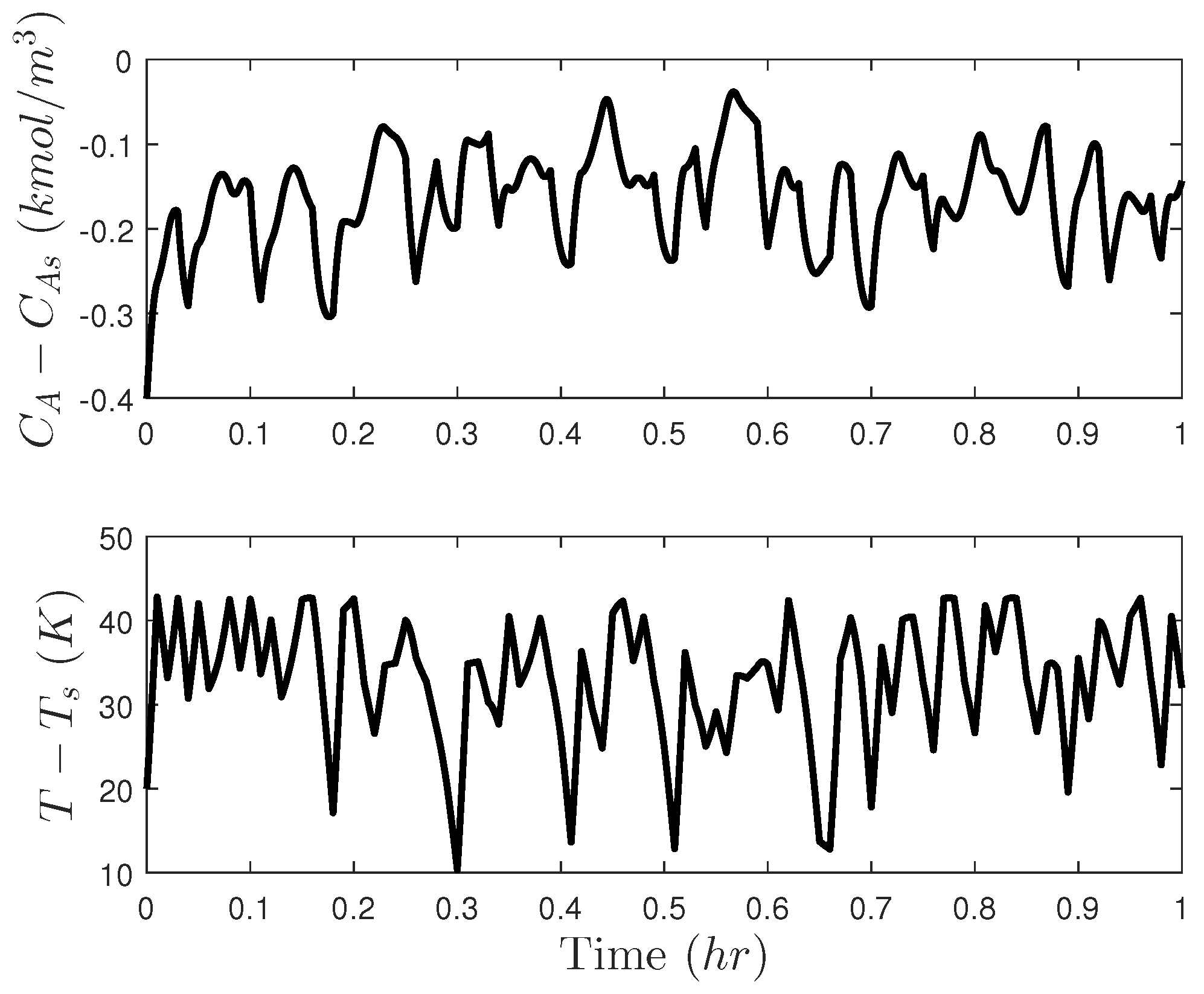
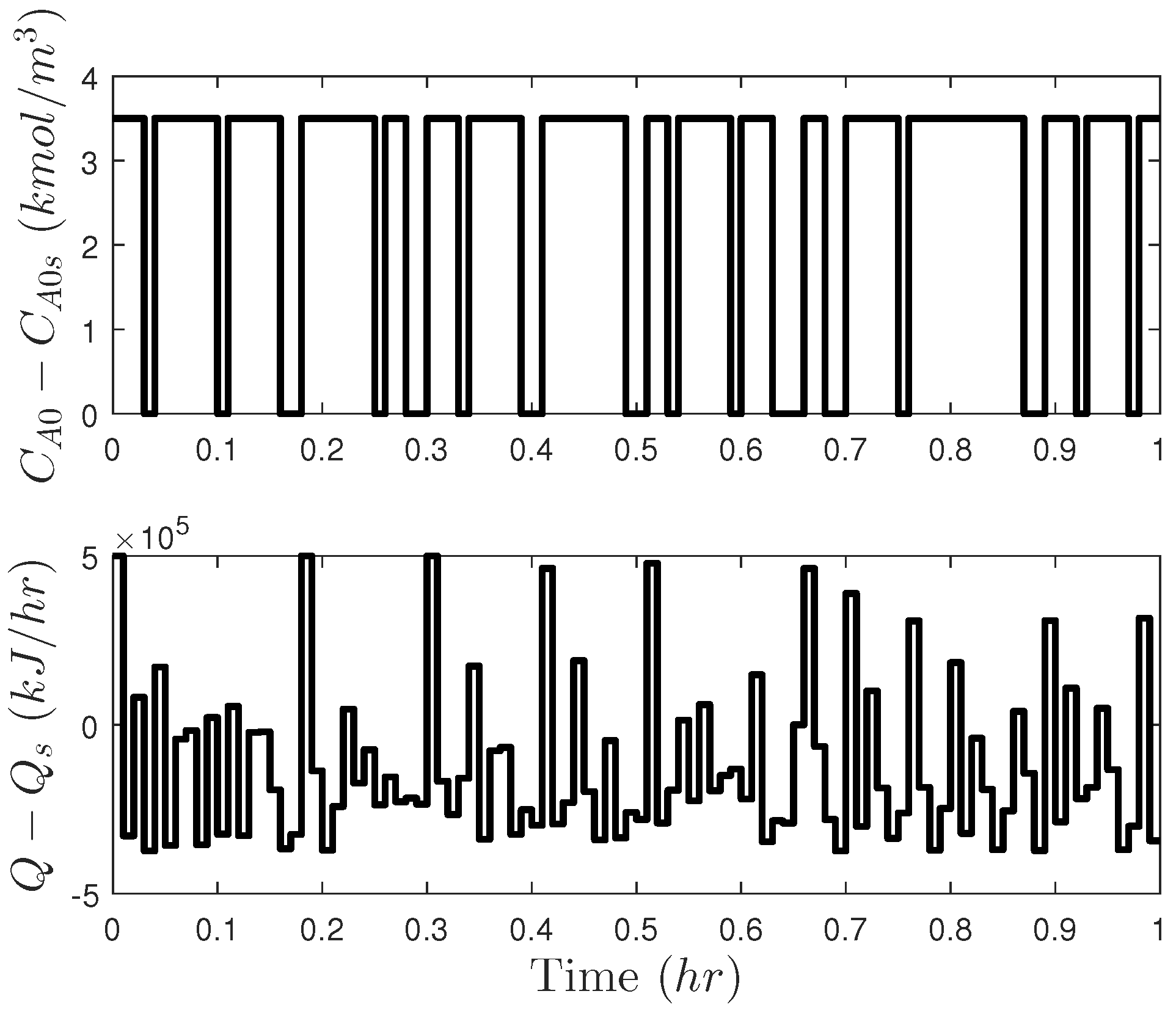
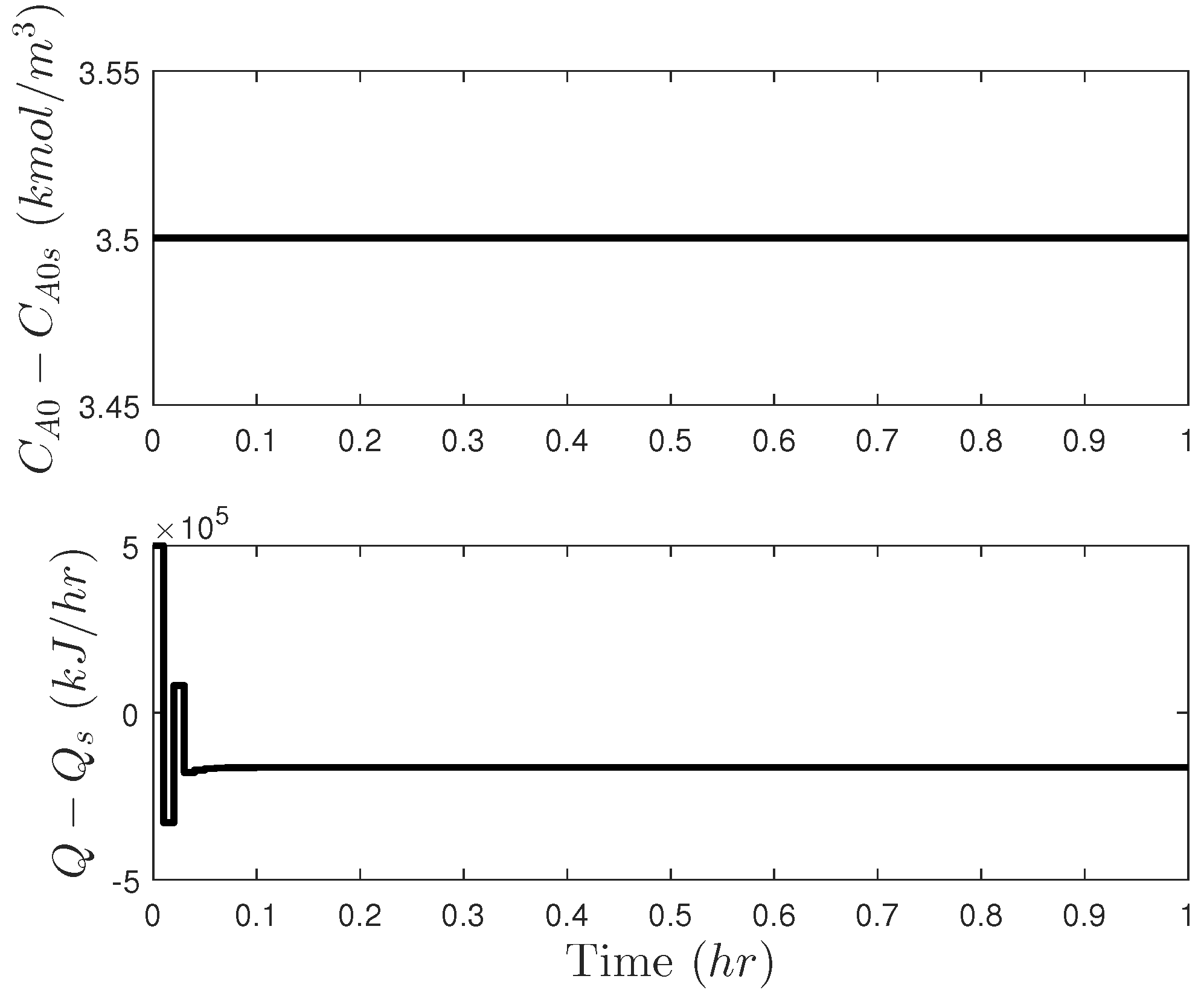
| Parameter | Value | Unit |
|---|---|---|
| 44.49999958429348 | kmol | |
| 13.53296996509594 | kmol | |
| 36.64788062995841 | kmol | |
| 110.0 | kmol | |
| 60.95327313484253 | % | |
| 25.02232231706676 | % | |
| 39.25777017606444 | % | |
| 47.03024823457651 | % | |
| 60.95327313484253 | % | |
| 25.02232231706676 | % | |
| 39.25777017606444 | % | |
| 44.17670682730923 | % | |
| 201.43 | kmol/h | |
| 5.62 | kmol/h | |
| 7.05 | kmol/h | |
| 100 | kmol/h | |
| 2700 | kPa | |
| 0.47 | - | |
| 0.1429 | - | |
| 0.3871 | - | |
| 0.1 | % h/kmol | |
| 1 | h | |
| 2 | % | |
| 3 | h | |
| –0.25 | %/kPa | |
| 1.5 | h | |
| 0.7 | kmol/kPa·h | |
| 3 | h |
| Parameter | Value | Unit |
|---|---|---|
| V | 1 | m |
| 300 | K | |
| kJ/kg·K | ||
| m/h·kmol | ||
| F | 5 | m/h |
| 1000 | kg/m | |
| E | kJ/kmol | |
| kJ/kmol·K | ||
| kJ/kmol |
| i | |||||
|---|---|---|---|---|---|
| 1 | 1200 | 5 | 0.1 | 180 | 144 |
| 2 | 2000 | –20 | 1 | 180 | 144 |
| 3 | 1500 | –20 | 10 | 180 | 144 |
| 4 | 0.2 | 0 | 2000 | 180 | 144 |
| 5 | 1200 | 5 | 0.1 | 180 | 100 |
| 6 | 1200 | 5 | 0.1 | 180 | 130 |
| 7 | 1200 | 5 | 0.1 | 180 | 30 |
| Seed | Time K (h) |
|---|---|
| 5 | 0.0143 |
| 10 | 0.0148 |
| 15 | 0.0146 |
| 20 | 0.0324 |
| 25 | 0.0146 |
| 30 | 0.0142 |
| 35 | 0.0143 |
| 40 | 0.0147 |
| 45 | 0.0248 |
| 50 | 0.0231 |
| Seed | Time K (h) |
|---|---|
| 5 | 0.0674 |
| 10 | 0.0458 |
| 15 | 0.0555 |
| 20 | 0.0767 |
| 25 | 0.0569 |
| 30 | 0.0418 |
| 35 | 0.0457 |
| 40 | 0.0874 |
| 45 | 0.0580 |
| 50 | 0.0950 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durand, H. A Nonlinear Systems Framework for Cyberattack Prevention for Chemical Process Control Systems †. Mathematics 2018, 6, 169. https://doi.org/10.3390/math6090169
Durand H. A Nonlinear Systems Framework for Cyberattack Prevention for Chemical Process Control Systems †. Mathematics. 2018; 6(9):169. https://doi.org/10.3390/math6090169
Chicago/Turabian StyleDurand, Helen. 2018. "A Nonlinear Systems Framework for Cyberattack Prevention for Chemical Process Control Systems †" Mathematics 6, no. 9: 169. https://doi.org/10.3390/math6090169
APA StyleDurand, H. (2018). A Nonlinear Systems Framework for Cyberattack Prevention for Chemical Process Control Systems †. Mathematics, 6(9), 169. https://doi.org/10.3390/math6090169