Keeping up with the Neighbors: Social Interaction in a Production Economy

Abstract

It is well-documented that individuals care about how others around them are doing. This paper studies a production economy in which consumers provide labor supply to a representative firm to earn income for consumption, and their utility depends on their own leisure time, their own consumption level, as well as their neighbors’ consumption levels. We characterize the unique equilibrium for such an economy, allowing for three different types of effects of the neighborhood size: linear effect, zero effect, and nonlinear effect. Four network structures (empty network, ring network, star network, and core-periphery network) with different production technologies are analyzed. Our work contributes to a better understanding of the general equilibrium effect of social preferences and network structures.

1. Introduction

It has been well-documented that individuals care about how other individuals around them are doing. Beginning with the pioneering work of Veblen (1899) [1], economists have studied preferences with social comparisons among individuals and how such preferences influence individuals' decision making [2,3,4,5,6,7]. More recently, network structures have played an important role in modeling economic behavior with social interactions, serving as a natural tool to study social preferences in scenarios where acquaintances and strangers are treated differently [8,9,10,11,12,13].

In order to study the general equilibrium effect of social preferences with network structure, there are two basic potential frameworks: the pure exchange economy model and the production economy model. Each of them captures a different aspect of real world markets. The pure exchange economy framework emphasizes the relative prices between different consumption goods, while the production economy framework more realistically incorporates firms’ profit maximization using consumers’ labor as an input to production.

Ghiglino and Goyal (2010) study the phenomenon of “keeping up with the neighbors” in a pure exchange economy, where agents consume two goods, one of which involves social comparison [12]. In contrast to Ghiglino and Goyal (2010), we focus on the production economy where agents provide labor supply to a representative firm to earn income for consumption, and their utility depends on their own leisure time, their own consumption level, as well as their neighbor’s consumption level. Note that that we do not model leisure as a consumption involving social comparison. In addition, we assume that in this economy there is only one representative firm on the production side of the market, and that the firm is uniformly owned by all consumers, i.e., every consumer receives an equal share of the profit of the firm.

Alexeev and Chiv (2015), whose work is most related to ours, also consider the status competition in a production economy with network structures [13]. However, their study differs from ours in two aspects: First, they assume a linear production technology while we consider a production technology exhibiting decreasing returns-to-scale; Second, they only consider a linear effect of neighborhood size while we analyze three different types of effects of neighborhood size: linear effect, zero effect (an effect which does not depend specifically on neighborhood size, but this does not mean that there is no network effect present.), and nonlinear effect. 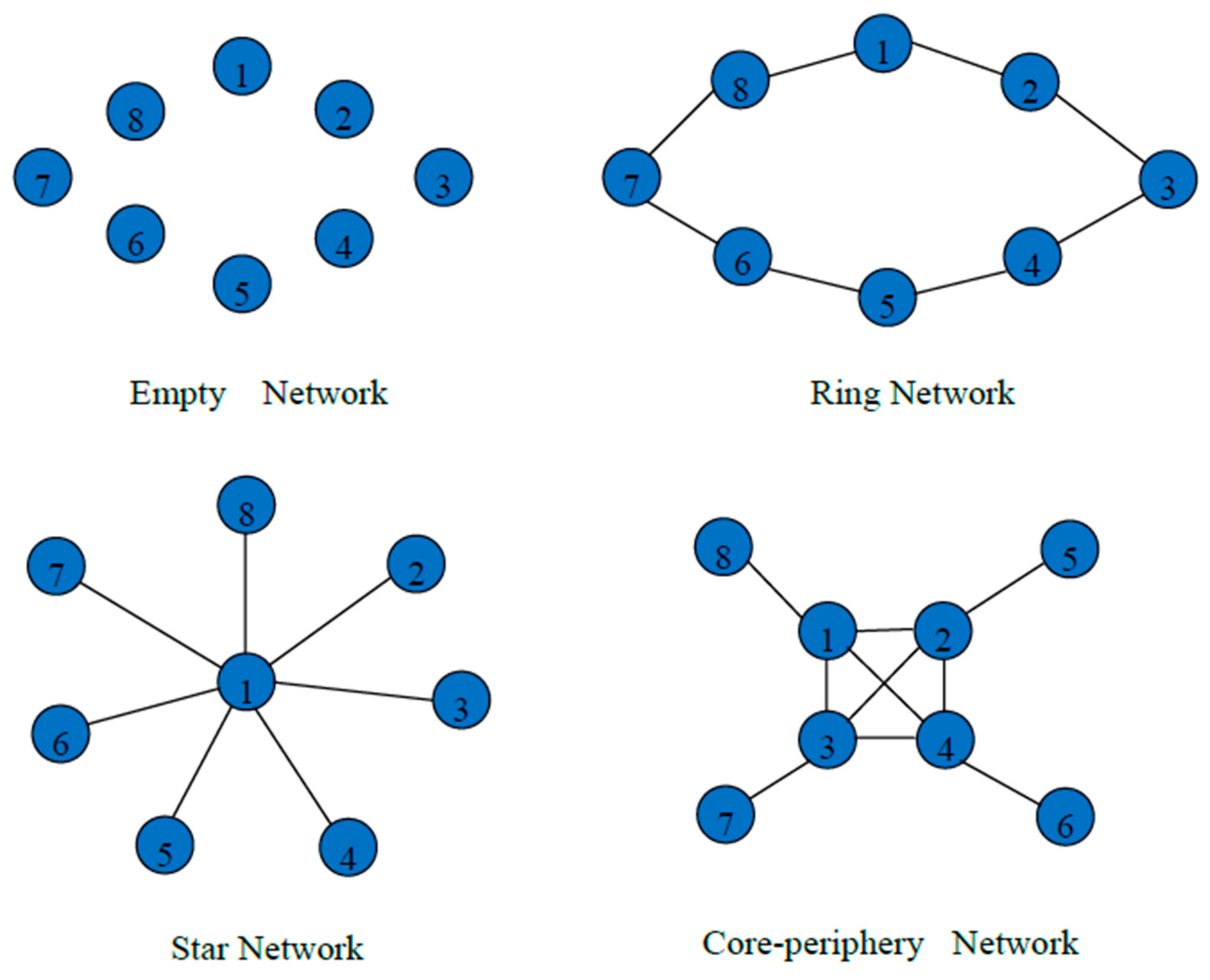In addition, we also provide concrete examples for four network structures with different production technologies: empty network, ring network, star network, and core-periphery network.

The contribution of our work is threefold. First, we extend the general equilibrium model with social network structure to a production economy, and solve for the unique equilibrium under different types of neighborhood size effects. Second, we show by illustration that under each of the four network structures mentioned above, as the production technology improves, the equilibrium wage, the equilibrium consumption and the equilibrium labor supply all increase. Third, we show that when the total number of links in the economy increases, the equilibrium wage decreases while the equilibrium consumption and the equilibrium labor supply increase.

The results highlight one reason that examining network consumption effects in a production economy is important for understanding the overall effects of network-based comparisons of consumers. In the absence of production, consumers care only about their consumption but not meaningfully about their leisure time, since in that case the consumer does not have any chance to be employed in the production process. By accounting for the labor and leisure decision when consumers are also shareholders of firms, a more complete understanding regarding what consumers must do to “keep up with the neighbors” is obtained, as well as an assessment of the economic conditions which make these consumer objectives more easily attainable.

Our paper is related to a recent line of literature that has studied the effects of social status or consumption externalities in economies [2,3,4,14,15,16,17,18,19,20,21,22,23,24]. Bilancini and Boncinelli (2012) consider an economy in which individuals are status-concerned, and the possibility of social redistribution policy is considered. In a status signaling game in which people convey their relative standing by consuming a conspicuous good, they show that when social status is defined cardinally rather than ordinally, progressive redistribution can generate a Pareto improvement; the key reason being that redistribution reduces the competition for being high status [2]. A related study by Hopkins and Kornienko (2010) compares endowment inequality and reward inequality in a societal tournament setting. They show that the effect of inequality on social welfare depends distinctly on the type of inequality, namely that inequality of rewards is harmful to most of society due to the increased effort exerted; by contrast, the middle class may benefit under inequality of endowments [3]. Lian et al. (2018) consider nine different types of preferences with social comparisons and study how these preferences affect consumption, price, and welfare in a general equilibrium model with international trade [4]. These studies model the interaction between consumers or households, but abstract from both the production side of the economy and network structures among consumers, as we consider in this paper.

There is another literature on consumption externalities and economic growth, which is related to our work [5,6]. García-Peñalosa and Turnovsky (2008) examine an economy with heterogeneous consumers and consumption externalities among groups of consumers. They derive the conditions under which the equilibrium with heterogenous consumers replicates the typical model with a representative consumer. One of their main results is that consumption externalities can reduce inequality compared to the benchmark case if the economy is in a growing state [5]. Bilancini and D'Alessandro (2012) analyze an endogenous growth model with externalities in leisure, consumption and production to examine the relationship between growth and welfare. Notably, they provide a condition for an optimal growth path which includes production and consumption downscaling, while providing an increase in welfare [6]. However, similarly to the previously mentioned studies, these studies also do not analyze the network structure with regard to the consumption externalities.

Our paper is also related to a broader literature on social preferences and reference dependence [7,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. Sobel (2005) summarizes the literature on social preference models in economics [7]. Postlewaite (1998) studies the social basis of interdependent preferences [26]. Lien and Zheng (2017) experimentally test reference-dependent preferences in a social comparison domain [35]. Zhang and Zheng (2017) investigate the bubble equilibrium in an economy with reference-dependent agents [39]. In contrast to our work, none of these studies consider a production economy with a network structure.

Last but not least, we relate our work to the literature on network-based origins of social preferences [8,9,10,11,40]. Jackson (2010) describes frameworks for analyzing strategic interactions between players on a network, in which players may have a payoff or belief that depends on the choices that their direct or indirect neighbors made [8]. An example is Golub and Jackson (2010), which models a situation in which agents form their opinions by naively taking the weighted average of their neighbors’ opinions [9]. Calvo-Armengol and Jackson (2010) provide a model of positive and negative peer pressure in a framework where agents care about their neighbors’ actions and can exert costly pressure on them [10]. Immorlica et al. (2017) consider a network model where agents with status seeking preferences play a social status game [11]. The main difference between these studies and ours is that they focus on game theoretical interactions while we use the general equilibrium approach to study social comparisons in a production economy.

The rest of the paper is organized as follows. Section 2 sets up the basic model, solves for the unique equilibrium, and provides examples for different network structures; Section 3 discusses alternative ways to model the effect of neighborhood size; Section 4 concludes.

2. Model

2.1. Setup

We consider a production economy populated with N consumers, indexed $i=1,\cdots ,N$. Let $N(i)$ be the set of neighbors of consumer i and $n_i=\left|N(i)\right|$ be the cardinal number of set $N(i)$, i.e., the number of neighbors for individual i. The pattern of neighborhood is represented by the adjacent matrix G, which is a $N\times N$ matrix. The element $G_{ij}$ equals to 1 if i and j are directly connected, that is, i and j are each other’s neighbors, and takes the value of 0 otherwise. We also set the diagonal elements to be 0. To put it formally, we have:

$$G_{ij}=\{\begin{array}{l}\begin{array}{ccc}1& if& j\in N(i)\end{array}\\ \begin{array}{ccc}0& if& j\notin N(i)\end{array}\end{array}$$

Each consumer is endowed with one unit of time that could be spent for providing labor (denoted by L_i) or leisure (l_i). In this economy, besides leisure, there is only one kind of consumption good x, which is the numeraire good. We assume that a consumer i’s utility depends on her leisure time ($1-L_i$), her own consumption level x_i, and her neighbors’ consumption levels $x_j,j\in N(i)$. To specifically model such a preference with social comparison, we consider the following adjusted Cobb-Douglas utility functional form:

$$u_i(L_i,x_i,x_{-i})={(1-L_i)}^{\sigma }{(x_i+\rho S(n_i)(x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}^{1-\sigma }$$

Note that $\sigma \in (0,1)$ measures the importance of leisure relative to consumption in the utility; $\rho >0$ represents consumers’ incentive to keep up with the neighbors: A consumer’s utility is negatively affected by an increase in consumption by neighbors; $S(n_i)$ captures the effect of the neighborhood size: In the baseline model, we set $S(n_i)=n_i$ to study the linear effect of the neighborhood size, and we later consider alternative assumptions in which $S(n_i)=1$ (no effect of the neighborhood size) or $S(n_i)=\sqrt{n_i}$ (nonlinear effect of the neighborhood size).

On the production side, we assume there exists a representative profit-maximizing firm, evenly owned by all the consumers. This firm hires labor at per unit cost (wage) $w$ to produce the consumption good, with production function $Q=L^{\alpha }$, where $\alpha \in (0,1)$ represents decreasing returns-to-scale technology.

2.2. Analysis

2.2.1. Consumer’s Utility Maximization Problem

A typical consumer i in this economy faces the following optimization problem:

$$\begin{array}{l}{\max }_{\{x_i,L_i\}}{u}_i={(h_i-L_i)}^{\sigma }{(x_i+\rho n_i(x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}^{1-\sigma }\\ s.t.x_i\le w{L}_i+\frac{1}{N}\pi ;\\ 0\le L_i\le 1;x_i\ge 0,\end{array}$$

(1)

where π is the profit of the representative firm.

First note that at optimum the inequality constraints $0\le L_i\le 1;x_i\ge 0$ in the above optimization problem are not binding. Thus, applying the Lagrange multiplier method to the optimization problem, we have the following Lagrange function:

$$\ell (L_i,x_i,\lambda )={(1-L_i)}^{\sigma }{(x_i+\rho n_i(x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}^{1-\sigma }+\lambda (w{L}_i+\frac{\pi }{N}-x_i)$$

(2)

Given that $l_i=1-L_i$, we obtain the following first order conditions (FOCs):

• $-\sigma l_i{}^{\sigma -1}{(x_i+\rho n_i(x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}^{1-\sigma }+\lambda w=0$ (for L_i);
• $l_i{}^{\sigma }(1-\sigma )(1+\rho n_i){(x_i+\rho n_i(x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}^{-\sigma }-\lambda =0$ (for x_i);
• $x_i+w{l}_i-w-\frac{\pi }{N}=0$ (for λ).

From the first two FOCs, we can express the wage $w$ in terms of l_i and x_i:

$$\frac{\sigma (x_i+\rho n_i(x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}{l_i(1-\sigma )(1+\rho n_i)}=w$$

(3)

Combining (3) with the third FOC, we obtain:

$$x_i-\frac{\sigma \rho }{1+\rho n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}=(1-\sigma )(w+\frac{\pi }{N})$$

(4)

(4) can be expressed in matrix form as:

$$X^{*}=(1-\sigma )(w+\frac{\pi }{N})B$$

(5)

where $B={(I-\sigma \rho G^{*})}^{-1}J$, $G_i^{*}=G_i/(1+\rho n_i)$ is the normalized version of G_i, G_i is the i-th row of G, G is the adjacency matrix, and J is a N × 1 column vector with all elements taking value of 1. The notation we adopt for the network structures follow Ghiglino and Goyal (2010) [12] and Alexeev and Chih (2015) [13]. It should be noted that each element B_i of vector B represents the Katz-Bonacich network centrality of consumer i. Let $\overline{B}=\frac{1}{N}{\displaystyle {\sum }_{k=1}^N{B}_k}$, so $\overline{B}$ measures the average centrality of the network structure.

With the above notation set up to characterize the properties of any given network, we can derive the optimal choice of a typical consumer i’s utility maximization problem:

$$x^{*}{}_i=(1-\sigma )(w+\frac{\pi }{N})B_i$$

(6)

$$L^{*}{}_i=(1-\sigma )B_i+((1-\sigma )B_i-1)\frac{\pi }{wN}$$

(7)

2.2.2. Firm’s Profit Maximization Problem

A representative firm in this economy faces the following optimization problem:

$${\max }_L\pi =Q-wL=L^{\alpha }-wL$$

(8)

where Q is the output of production in the economy, L is the input of labor, and $w$ is the wage. From first order condition, we obtain

$$\alpha L^{\alpha -1}-w=0$$

Thus, we can derive the optimal choice of the firm’s profit maximization problem:

$$L^{*}={(\frac{w}{\alpha })}^{\frac{1}{\alpha -1}}$$

(9)

$$Q^{*}={(\frac{w}{\alpha })}^{\frac{\alpha }{\alpha -1}}$$

(10)

$${\pi }^{*}={(\frac{w}{\alpha })}^{\frac{\alpha }{\alpha -1}}(1-\alpha )$$

(11)

2.2.3. Equilibrium

In equilibrium the commodity market clears, requiring:

$$Q^{*}={\displaystyle {\sum }_{i=1}^N{x}_i^{*}}$$

(12)

(In equilibrium the labor market also clears, requiring $L^{*}={\displaystyle {\sum }_{i=1}^N{l}_i^{*}}={\displaystyle {\sum }_{i=1}^N(1-L_i^{*})}$. Note that we only need one market clearing condition to derive the equilibrium).

Combing (12) together with (6), (10) and (11), we have:

$$\begin{array}{ll}{(\frac{w}{\alpha })}^{\frac{\alpha }{\alpha -1}}& ={\displaystyle {\sum }_{i=1}^N(1-\sigma )(w+\frac{\pi }{N})B_i}\\ & =w(1-\sigma )N\overline{B}+(1-\sigma )({(\frac{w}{\alpha })}^{\frac{\alpha }{\alpha -1}}-w{(\frac{w}{\alpha })}^{\frac{1}{\alpha -1}})\overline{B}\\ & =w(1-\sigma )N\overline{B}+(1-\sigma ){(\frac{w}{\alpha })}^{\frac{\alpha }{\alpha -1}}(1-\alpha )\overline{B}\\ & =(1-\sigma )\overline{B}(wN+{(\frac{w}{\alpha })}^{\frac{\alpha }{\alpha -1}}(1-\alpha ))\end{array}$$

(13)

Rearranging (13), we can solve for the equilibrium wage $w$:

$$w^{*}={\alpha }^{\alpha }{\left(\frac{(1-\sigma )N\overline{B}}{(1-(1-\sigma )(1-\alpha )\overline{B})}\right)}^{\alpha -1}$$

(14)

Substituting (14) into (11), we can derive the firm’s equilibrium profit:

$${\pi }^{*}=(1-\alpha ){\left(\frac{\alpha (1-\sigma )N\overline{B}}{(1-(1-\sigma )(1-\alpha )\overline{B})}\right)}^{\alpha }$$

(15)

Similarly, substituting (14) and (15) into (6) and (7) respectively, we can derive the individual consumer’s equilibrium consumption level and labor supply:

$$x_i^{*}=\frac{B_i}{N\overline{B}}{\left(\frac{\alpha (1-\sigma )N\overline{B}}{1-(1-\sigma )(1-\alpha )\overline{B}}\right)}^{\alpha }$$

(16)

$$L_i^{*}=(1-\sigma )B_i+((1-\sigma )B_i-1)\frac{(1-\sigma )(1-\alpha )\overline{B}}{1-(1-\sigma )(1-\alpha )\overline{B}}$$

(17)

Note that since $0\le L_i\le 1$, it must be that for any i,

$$(1-\alpha )\overline{B}\le B_i\le \frac{1}{1-\sigma }$$

(18)

Substituting (14) into (10), we can solve for the equilibrium commodity supply:

$$Q^{*}={\left(\frac{\alpha (1-\sigma )N\overline{B}}{1-(1-\sigma )(1-\alpha )\overline{B}}\right)}^{\alpha }$$

(19)

Substituting (14) into (9), we can also solve for the equilibrium labor demand:

$$L^{*}=\frac{\alpha (1-\sigma )N\overline{B}}{1-(1-\sigma )(1-\alpha )\overline{B}}$$

(20)

We describe the general equilibrium of this production economy in the following proposition.

Proposition 1.

Suppose $S(n_i)=n_i$ and condition (18) holds. In this N-consumer 1-firm production economy, where consumer’s problem is specified by (1) and firm’s problem is specified by (8), the equilibrium $(x_i^{*},L_i^{*};Q^{*},L^{*};w^{*})$ uniquely exists and is determined by (16), (17), (19), (20), and (14).

2.3. Applications

In this subsection, keeping other parameters fixed ($\sigma =\rho =0.5,N=8$), we consider four different network structures (empty, ring, star, core-periphery) by three different production technologies ($\alpha =0.3,0.5,0.7$), and study how the social network effect and the technology effect shape the general equilibrium pattern.

The four network structures are described in Figure 1, where in the empty network every consumer is isolated from others (without any neighbor), in the ring network every consumer is connected to two other consumers, in the star network seven consumers $(2\le i\le 8)$ have one common neighbor (consumer 1), and in the core-periphery network, four consumers $(1\le i\le 4)$ have four neighbors and the other four consumers $(5\le i\le 8)$ have only one neighbor.

For the parameters $\sigma =\rho =0.5,N=8$, we assume these values by following Ghiglino and Goyal (2010) [12]. In addition, since $\sigma$ measures the importance of leisure relative to consumption in the utility, $\sigma =0.5$ represents the case where leisure and consumption have an equal weight in consumer’s utility function. Since $\rho$ captures consumers’ incentive to keep up with the neighbors, $\rho =0.5$ describes the case where such an incentive is moderate. We set $N=8$ so that the network structures we consider can be rich enough without becoming too complex.

For the production technology parameter $\alpha$, we consider three values in the paper: $\alpha =0.3,0.5,0.7$. Since $\alpha$ lies in $(0,1)$, the benchmark case we consider is to set $\alpha$ at the middle point of the $(0,1)$ interval, that is $\alpha =0.5$. Note that in order to have a sensible equilibrium, the parameters must satisfy condition (18), that is $\left(1-\alpha \right)\overline{B}\le B_i\le \frac{1}{1-\sigma }$. Given that $\sigma =0.5$, condition (18) becomes $(1-\alpha )\overline{B}\le B_i\le 2$. Note that for each of the four network structures we consider, $B_i\le 2$ holds for every agent in the network; simple calculations provide the following results: (1) for the empty network, $B_i=1,\forall i$; (2) for the ring network, $B_i=\frac{4}{3},\forall i$; (3) for the star network, $B_i=\left\{\frac{126}{101},\frac{150}{101}\right\},\forall i$; (4) for the core-periphery network, $B_i=\left\{\frac{66}{53},\frac{78}{53}\right\},\forall i$. Thus, we only need to make sure that $\forall i$, $(1-\alpha )\overline{B}\le B_i$ holds for the values of $\alpha$ we choose, which is equivalent to $(1-\alpha )\overline{B}\le {\min }_i{B}_i$. It is easy to see that the lower the value of $\alpha$, the less likely can $(1-\alpha )\overline{B}\le {\min }_i{B}_i$ hold. Therefore, we choose a relatively safe lower bound for the low value of $\alpha$, that is $\alpha =0.3$. By assuming that the upper bound and the lower bound have an equal distance to the benchmark case $\alpha =0.5$, we choose $\alpha =0.7$ as the high value of $\alpha$.

2.3.1. Empty Network

For the empty network, when $\alpha =0.3$, the equilibrium is characterized by profile $\left(0.15,0.23;1.2,1.84;0.2;\alpha =0.3\right)$, where the first entry indicates the homogeneous individual consumption level, the second entry indicates the homogeneous individual labor supply, the third entry is aggregate consumption, the fourth entry is aggregate labor supply, the fifth entry is wage, and the last entry denotes the technology parameter. When $\alpha =0.5$, the equilibrium is characterized by profile $\left(0.20,0.33;1.6,2.64;0.31;\alpha =0.5\right)$. When $\alpha =0.7$, the equilibrium is characterized by profile $\left(0.29,0.41;2.32,3.28;0.49;\alpha =0.7\right)$.

2.3.2. Ring Network

For the ring network, when $\alpha =0.3$, the equilibrium is characterized by profile $\left(0.17,0.37;1.36,2.96;0.14;\alpha =0.3\right)$, where every entry has the same meaning as for the empty network. When $\alpha =0.5$, the equilibrium is characterized by profile $\left(0.25,0.50;2.00,4.00;0.25;\alpha =0.5\right)$. When $\alpha =0.7$, the equilibrium is characterized by profile $\left(0.37,0.58;2.96,4.64;0.44;\alpha =0.7\right)$.

2.3.3. Star Network

For the star network, when $\alpha =0.3$, the equilibrium is characterized by profile $\left(\left(0.20,0.17\right),\left(0.53,0.32\right);1.37,2.77;0.15;\alpha =0.3\right)$, where the first entry indicates heterogeneous individual consumption levels, the second entry indicates heterogeneous individual labor supplies, the third entry is the aggregate consumption, the fourth entry is the aggregate labor supply, the fifth entry is the wage, and the last entry denotes the technology parameter. When $\alpha =0.5$, the equilibrium is characterized by profile $\left(\left(0.28,0.24\right),\left(0.62,0.45\right);1.96,3.77;0.26;\alpha =0.5\right)$. When $\alpha =0.7$, the equilibrium is characterized by profile $\left(\left(0.41,0.35\right),\left(0.68,0.53\right);2.86,4.39;0.45;\alpha =0.7\right)$.

2.3.4. Core-Periphery Network

For the core-periphery network, when $\alpha =0.3$, the equilibrium is characterized by profile $\left(\left(0.19,0.16\right),\left(0.50,0.28\right);1.40,3.12;0.14;\alpha =0.3\right)$, where every entry has the same meaning as for the ring network. (When $\alpha =0.3$, the wage under the ring network is greater than the wage under the core-periphery network, $w_r=0.1390389170>w_c=0.1356416276$). When $\alpha =0.5$, the equilibrium is characterized by profile $\left(\left(0.27,0.23\right),\left(0.60,0.43\right);2.00,4.12;0.25;\alpha =0.5\right)$. When $\alpha =0.7$, the equilibrium is characterized by profile $\left(\left(0.40,0.34\right),\left(0.67,0.53\right);2.96,4.80;0.44;\alpha =0.7\right)$.

We summarize the equilibrium outcomes for the four types of network structures under three different technology environments in

Table 1. Equilibrium outcomes under four types of networks and three technology environments ($S\left(n_i\right)=n_i$).

α	Empty			Ring			Star			Core-Periphery
	0.3	0.5	0.7	0.3	0.5	0.7	0.3	0.5	0.7	0.3	0.5	0.7
High consumption	0.15	0.2	0.29	0.17	0.25	0.37	0.20	0.28	0.41	0.19	0.27	0.40
Low consumption							0.17	0.24	0.35	0.16	0.23	0.34
High labor	0.23	0.33	0.41	0.37	0.50	0.58	0.53	0.62	0.68	0.50	0.60	0.67
Low labor							0.32	0.45	0.53	0.28	0.43	0.53
Wage	0.2	0.31	0.49	0.14	0.25	0.44	0.15	0.26	0.45	0.14	0.25	0.44
Aggregate consumption	1.2	1.6	2.32	1.36	2.00	2.96	1.37	1.96	2.86	1.40	2.00	2.96
Aggregate labor	1.84	2.64	3.28	2.96	4.00	4.64	2.77	3.77	4.39	3.12	4.12	4.80

.

For each network structure, comparing the equilibrium outcomes among three scenarios with different production technologies ($\alpha =0.3,0.5,0.7$), we have the following observation:

Observation 1: Under each of the four network structures, as the production technology improves ($\alpha$ increases), the equilibrium wage increases, the equilibrium individual (and aggregate) consumption increases, and the equilibrium individual (and aggregate) labor supply increases.

The intuition behind Observation 1 is the following. For a better technology, the marginal product of labor will be higher, thus the equilibrium wage for labor will be higher. When the wage becomes higher, consumers tend to consume more (especially due to social comparison) and have less leisure. Since for a typical consumer leisure and labor supply add up to a constant level, less leisure implies greater labor supply.

With each production technology, comparing the equilibrium outcomes among four different network structures (empty, ring, star, core-periphery), we have the following observation:

Observation 2: With each of the three production technologies, as the total number of links in the economy increases, the equilibrium wage decreases, the equilibrium aggregate consumption increases, and the equilibrium aggregate labor supply increases.

The intuition behind Observation 2 is the following. For an economy with more links, due to the social comparison preferences of “keeping up with the neighbors”, a higher level of aggregate consumption will appear in equilibrium. Higher aggregate consumption requires higher output of the production, which in turn determines a lower level of marginal product due to the assumption of non-linear (indeed concave) production function. Since the wage measures the marginal product level, this means the equilibrium wage will be lower. Given a lower wage, in order to have a higher consumption level, consumers have to increase their labor supply.

We can also compare the individual consumer’s behavior within a heterogenous network structure (namely the ring network and the core-periphery network), and have the following observation:

Observation 3: With each of three production technologies, under either the ring network or the core-periphery network, the more neighbors a consumer has, the higher individual consumption she has, and the higher individual labor supply she provides.

The intuition behind Observation 3 is the following. For a given network structure, for those consumers who have more links, the impact of the social comparison preferences of “keeping up with the neighbors” on their utility is larger compared to those consumers who have fewer links. Such a larger impact will lead to a higher individual consumption level for those consumers. Since the wage rate is the same for all consumers, regardless of the number of their neighbors, in order to have a higher consumption level, those with more neighbors must have higher labor supply compared to those with fewer neighbors.

3. Discussion

3.1. No Effect of the Neighborhood Size

Now we consider the case where $S(n_i)=1$. This assumption captures the scenario where consumers do not care about the size of their neighborhood and only the average consumption by neighbors matters. Many scenarios where consumers care about their own income as well as how their own income compares with the average income of people they are familiar with, can be modeled under such an assumption.

A typical consumer i in this economy now faces the following optimization problem:

$$\begin{array}{l}{\max }_{\{x_i,L_i\}}{u}_i={(h_i-L_i)}^{\sigma }{(x_i+\rho (x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}^{1-\sigma }\\ s.t.x_i\le w{L}_i+\frac{1}{N}\pi ;\\ 0\le L_i\le 1;x_i\ge 0.\end{array}$$

(21)

Similar to the analysis in Section 2.2, applying the Lagrange multiplier method to the optimization problem, we have the following Lagrange function:

$$\ell (L_i,x_i,\lambda )={(1-L_i)}^{\sigma }{(x_i+\rho (x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}^{1-\sigma }+\lambda (w{L}_i+\frac{\pi }{N}-x_i)$$

(22)

Solving for the first order conditions, we can obtain the optimal consumption in matrix form:

$$X^{*}=(1-\sigma )(w+\frac{\pi }{N})B^{\prime }$$

(23)

where $B^{\prime }={(I-\sigma \rho {G^{\prime }}^{*})}^{-1}J$ and $G_i^{{}^{\prime }*}=G_i/(1+\rho )n_i$ is the normalized version of $G_i$ (We define $G_i^{{}^{\prime }*}=0$ if $n_i=0$ (and $G_i=0$), where $0$ is the $N\times 1$ column vector with all elements taking value of 0). Note that $G_i^{{}^{\prime }*}$ is different from $G_i^{*}$, since $G_i^{{}^{\prime }*}=G_i/(1+\rho )n_i$ while $G_i^{*}=G_i/(1+\rho n_i)$. Let $\overline{B^{\prime }}=\frac{1}{N}{\displaystyle {\sum }_{k=1}^N{B}_k^{\prime }}$, so $\overline{B^{\prime }}$ measures the average centrality of the network structure when $S(n_i)=1$.

Now we can derive the optimal choice of a typical consumer i’s utility maximization problem when $S(n_i)=1$:

$$x^{*}{}_i=(1-\sigma )(w+\frac{\pi }{N})B_i^{\prime }$$

(24)

$$L^{*}{}_i=(1-\sigma )B_i^{\prime }+((1-\sigma )B_i^{\prime }-1)\frac{\pi }{wN}$$

(25)

Since the firm’s profit maximization problem is independent of the network structure, the analysis remains the same for the case $S(n_i)=1$, compared to the case $S(n_i)=n_i$. Thus, when we use the market clearing condition to pin down the equilibrium, we can simply substitute $B^{\prime }$ for $B$ and $\overline{B^{\prime }}$ for $\overline{B}$ in Equations (14)–(20) (equilibrium characterization when $S(n_i)=n_i$), in order to obtain all the equilibrium outcomes for the case $S(n_i)=1$. Namely,

$$w^{*}={\alpha }^{\alpha }{\left(\frac{\alpha (1-\sigma )N\overline{B^{\prime }}}{(1-(1-\sigma )(1-\alpha )\overline{B^{\prime }})}\right)}^{\alpha -1}$$

(26)

$${\pi }^{*}=(1-\alpha ){\left(\frac{\alpha (1-\sigma )N\overline{B^{\prime }}}{(1-(1-\sigma )(1-\alpha )\overline{B^{\prime }})}\right)}^{\alpha }$$

(27)

$$x_i^{*}=\frac{B_i^{\prime }}{N\overline{B^{\prime }}}{\left(\frac{\alpha (1-\sigma )N\overline{B^{\prime }}}{(1-(1-\sigma )(1-\alpha )\overline{B^{\prime }})}\right)}^{\alpha }$$

(28)

$$L_i^{*}=(1-\sigma )B_i^{\prime }+((1-\sigma )B_i^{\prime }-1)\frac{(1-\sigma )\overline{B^{\prime }}}{1-(1-\sigma )(1-\alpha )\overline{B^{\prime }}}$$

(29)

$$Q^{*}={\left(\frac{\alpha (1-\sigma )N\overline{B^{\prime }}}{(1-(1-\sigma )(1-\alpha )\overline{B^{\prime }})}\right)}^{\alpha }$$

(30)

$$L^{*}=\frac{\alpha (1-\sigma )N\overline{B^{\prime }}}{(1-(1-\sigma )(1-\alpha )\overline{B^{\prime }})}$$

(31)

Note that since $0\le L_i\le 1$, it must be that for any i,

$$(1-\alpha )\overline{B^{\prime }}\le B_i\le \frac{1}{1-\sigma }$$

(32)

We describe the general equilibrium of this production economy when $S(n_i)=1$ in the following proposition.

Proposition 2.

Suppose $S(n_i)=1$ and condition (32) holds. In this N-consumer 1-firm production economy, where consumer’s problem is specified by (21) and firm’s problem is specified by (8), the equilibrium $(x_i^{*},L_i^{*};Q^{*},L^{*};w^{*})$ uniquely exists and is determined by (28), (29), (30), (31), and (26).

3.2. Nonlinear Effect of the Neighborhood Size

Now we consider the case where $S(n_i)=\sqrt{n_i}$. This assumption captures the scenario where the marginal effect of the neighborhood size is positive but decreasing. Those scenarios where the difference between a consumer’s own consumption and the average consumption of his/her friends generates a diminishing marginal utility as the number of his/her friends increases, can be modeled under such an assumption.

A typical consumer i in this economy now faces the following optimization problem:

$$\begin{array}{l}{\max }_{\{x_i,L_i\}}{u}_i={(h_i-L_i)}^{\sigma }{(x_i+\rho \sqrt{n_i}(x_i-\frac{1}{n_i}{\displaystyle \sum _{j\in N(i)}{x}_j}))}^{1-\sigma }\\ s.t.x_i\le w{L}_i+\frac{1}{N}\pi ;\\ 0\le L_i\le 1;x_i\ge 0.\end{array}$$

(33)

Solving for the first order conditions, we can obtain the optimal consumption in matrix form:

$$X^{*}=(1-\sigma )(w+\frac{\pi }{N})B^{″}$$

(34)

where $B^{″}={(I-\sigma \rho {G^{″}}^{*})}^{-1}J$ and $G_i^{{}^{″}*}=G_i/(\sqrt{n_i}+\rho n_i)$ is the normalized version of $G_i$. (We define $G_i^{{}^{\prime }*}=0$ if $n_i=0$ (and $G_i=0$), where $0$ is the $N\times 1$ column vector with all elements taking value of 0.). Note that $G_i^{{}^{″}*}$ is different from $G_i^{*}$ and $G_i^{{}^{\prime }*}$, since $G_i^{{}^{″}*}=G_i/(\sqrt{n_i}+\rho n_i)$ while $G_i^{*}=G_i/(1+\rho n_i)$ and $G_i^{{}^{\prime }*}=G_i/(1+\rho )n_i$. Let $\overline{B^{″}}=\frac{1}{N}{\displaystyle {\sum }_{k=1}^N{B}_k^{″}}$, so $\overline{B^{″}}$ measures the average centrality of the network structure when $S(n_i)=\sqrt{n_i}$.

Similarly to the analysis in Section 3.1, we can simply substitute $B^{″}$ for $B$ and $\overline{B^{″}}$ for $\overline{B}$ in Equations (14)–(20) to obtain all the equilibrium outcomes for the case $S(n_i)=\sqrt{n_i}$. Namely,

$$w^{*}={\alpha }^{\alpha }{\left(\frac{\alpha (1-\sigma )N\overline{B^{″}}}{(1-(1-\sigma )(1-\alpha )\overline{B^{″}})}\right)}^{\alpha -1}$$

(35)

$${\pi }^{*}=(1-\alpha ){\left(\frac{\alpha (1-\sigma )N\overline{B^{″}}}{(1-(1-\sigma )(1-\alpha )\overline{B^{″}})}\right)}^{\alpha }$$

(36)

$$x_i^{*}=\frac{B_i^{″}}{N\overline{B^{″}}}{\left(\frac{\alpha (1-\sigma )N\overline{B^{″}}}{(1-(1-\sigma )(1-\alpha )\overline{B^{″}})}\right)}^{\alpha }$$

(37)

$$L_i^{*}=(1-\sigma )B_i^{″}+((1-\sigma )B_i^{″}-1)\frac{(1-\sigma )\overline{B^{″}}}{1-(1-\sigma )(1-\alpha )\overline{B^{″}}}$$

(38)

$$Q^{*}={\left(\frac{\alpha (1-\sigma )N\overline{B^{″}}}{(1-(1-\sigma )(1-\alpha )\overline{B^{″}})}\right)}^{\alpha }$$

(39)

$$L^{*}=\frac{\alpha (1-\sigma )N\overline{B^{″}}}{(1-(1-\sigma )(1-\alpha )\overline{B^{″}})}$$

(40)

Note that since $0\le L_i\le 1$, it must be that for any i,

$$(1-\alpha )\overline{B^{″}}\le B_i\le \frac{1}{1-\sigma }$$

(41)

We describe the general equilibrium of this production economy when $S(n_i)=\sqrt{n_i}$ in the following proposition.

Proposition 3.

Suppose $S(n_i)=\sqrt{n_i}$ and condition (41) holds. In this N-consumer 1-firm production economy, where consumer’s problem is specified by (33) and firm’s problem is specified by (8), the equilibrium $(x_i^{*},L_i^{*};Q^{*},L^{*};w^{*})$ uniquely exists and is determined by (37), (38), (39), (40), and (35).

4. Conclusions

In this paper, we study a production economy where a representative firm hires labor to produce a consumption good and consumers’ utility depends on their own leisure time, their own consumption level, as well as their neighbor’s consumption level. We characterize the unique equilibrium for such an economy and analyze examples with four network structures and three production technologies. We also consider three different types of effects of the neighborhood size.

Our work contributes to the literature in three perspectives: First, we are among the first to study the social interaction in a production economy with non-linear technology and various types of effects of neighborhood size. It is noted that the last paragraph in Ghiglino and Goyal (2010) [12] comments that: “We have focused on the case of pure exchange. The impact of social comparisons on incentives, and the work leisure trade-off is worth studying… In future work we hope to explore these ideas” [2]. By extending their framework, we are able to provide an answer to the question they raised eight years ago by carefully studying the impact of social comparisons on a production economy. Furthermore, we extend Alexeev and Chih’s (2015) [13] linear production technology to a more general non-linear environment and consider three different types of effects of the neighborhood size: linear effect, zero effect, and nonlinear effect. Such a generalization makes our study on social comparisons more applicable to real-world situations.

Second, we analyze how the equilibrium is affected by the change in production technology under each of the four network structures (empty network, ring network, star network, and core-periphery network). Our result shows that as the production technology improves, the equilibrium wage, the equilibrium consumption and the equilibrium labor supply all increase. We also provide intuitive explanations for this result, which very much reflects how technology advances improve people’s living standard in modern society.

Third, we provide insights on how equilibrium changes when the network structure changes. When the network becomes more complex in terms of having more links, we find that the equilibrium wage drops while both the equilibrium aggregate consumption and the equilibrium labor supply increase. The intuition behind this result is also provided. An implication from this observation is that a society with more socially involved individuals tends to have more consumption, less leisure and lower wages.

To better understand the role that social comparisons play in the production economy, there are several potential directions for future work. In this paper we assume all agents are homogeneous in terms of productivity, while an economy with heterogeneous agents may function differently. We currently only consider the Cobb-Douglas utility function, whereas alternative preferences, for example, CES (constant elasticity of substitution) utility function or Leontief utility function, may lead to new results. Another direction may be to consider the interplay between social interactions and the dynamic interactions between different generations.