Resolving Decompositions for Polynomial Modules

Abstract

We introduce the novel concept of a resolving decomposition of a polynomial module as a combinatorial structure that allows for the effective construction of free resolutions. It provides a unifying framework for recent results of the authors for different types of bases.

1. Introduction

The determination of free resolutions for polynomial modules is a fundamental task in computational commutative algebra and algebraic geometry. Free resolutions are needed for derived functors like Ext and Tor and many important homological invariants like the projective dimension or the Castelnuovo-Mumford regularity are defined via the minimal resolution. Furthermore, already the Betti numbers, which measure the size of the minimal free resolution, give valuable information about the geometry and topology of varieties.

Unfortunately, resolutions are computationally rather expensive. A rough estimate says that a resolution of length ℓ requires to compute ℓ Gröbner bases. In many situations, partial information like the Betti numbers already suffice. However, all classical algorithms for the computation of Betti numbers require to always determine a full resolution. Indeed, one can observe in computer algebra systems like Singular that computing the Betti numbers needs as much computation time as computing a full resolution.

In the recent work [1], we developed a novel approach to this question consisting of a combination of the theory of involutive bases—in the form of Pommaret bases—(see [2] for a general survey on involutive bases) and of algebraic discrete Morse theory (see [3,4]). We also implemented it in the CoCoALib [5]. To the best of our knowledge, this approach is the only one that is able to compute (even individual) Betti numbers without first determining a full resolution. For most ideals, it is therefore much faster than classical methods (see the detailed benchmarks given in [1,6]). Furthermore, the new approach can be easily parallelised and scales much better with the problem size.

Because of these advantages, a generalisation of our approach to other situations is of great interest. Furthermore, it should be noted that Pommaret bases exist only in generic coordinates. As a first step, we extended it therefore to Janet bases [6], as these can be computed more efficiently and always exist. While the proofs follow the same lines, the use of a different involutive division entailed the adaption of many technical points. Furthermore, we are currently considering the use of alternative ideal bases not necessarily coming from an involutive division, but inducing combinatorial decompositions of the ideal with essentially the same properties. The development of a syzygy theory for such bases again proceeds along the same ideas, but various proofs have to be modified in minor ways.

In a different line of work, we recently introduced the concept of a module marked on a quasi-stable submodule which is very useful for the explicit determination of equations for Hilbert and Quot schemes [7,8]. The marking induces a combinatorial decomposition based on Pommaret multiplicative variables, but this time the key issue is that the head terms are not chosen with respect to a term order. Nevertheless, we showed that the most important results on resolutions presented [1] still remain essentially true. Again the proofs follow the same basic ideas, but require smaller technical modifications at some places.

This article represents a revised and expanded version of [9] which was presented at the conference Computer Algebra in Scientific Computing. Its main objective is to unify all our above-mentioned works in a general axiomatic framework. It centers about the novel concept of a resolving decomposition of an ideal. It refines the classical Stanley decompositions by certain additional axioms implying the existence of standard representations and normal forms. We then discuss how a free resolution and Betti numbers can be determined from a resolving decomposition.

The goal of this unification is not the development of any new algorithms. In particular, no algorithm for the construction of resolving decomposition will be presented. Instead, our results should be considered as a “meta-machinery” which augments any concept of a basis that induces a resolving decomposition with an effective syzygy theory. As already mentioned above, we applied this “meta-machinery” already for the special case of Janet or Pommaret bases (including a concrete implementation in the CoCoALib) [1,6]. The case of marked bases is considered in great detail in [7,8] (the latter reference also describes a concrete implementation in CoCoALib for the case of ideals).

The article is structured as follows. The next section provides the definition of a resolving decomposition and shows explicitly that all the cases mentioned above are contained in it. The third section discusses the construction of a syzygy resolution out of a resolving decomposition and some of its properties. In the fourth section, an explicit formula for the differential of this resolution is derived by relating our construction with the work of Sköldberg [10]. Finally, some conclusions are given.

2. Resolving Decompositions

Throughout this article, we will use the following notations. Let $\mathbb{k}$ be a field and $𝒫=\mathbb{k}\left[\mathbf{x}\right]$ the polynomial ring in the variable $\mathbf{x}=(x_0,\dots ,x_n)$. We write $\mathbb{T}$ for the set of terms $x^{\mu }\in 𝒫$. Let ${𝒫}_{\mathbf{d}}^m={⨁}_{i=1}^m𝒫(-d_i){\mathbf{e}}_i^{(0)}$ be a finitely generated free $𝒫$-module with grading $\mathbf{d}=(d_1,\dots ,d_m)$ and free generators ${\mathbf{e}}_1^{(0)},\dots ,{\mathbf{e}}_m^{(0)}$. A module $U\subseteq {𝒫}_{\mathbf{d}}^m$ is called monomial module, if it is of the form ${\oplus }_{k=1}^m{J}^{(k)}{\mathbf{e}}_k^{(0)}$ with each $J^{(k)}$ a monomial ideal in $𝒫$. A module term (with index i) is a term of the form $x^{\mu }{\mathbf{e}}_i^{(0)}$. If $J\subseteq 𝒫$ is a monomial ideal, we denote by $\mathcal{N}(J)\subseteq \mathbb{T}$ the set of terms in $\mathbb{T}$ not belonging to J. In the case of monomial module U, we analogously write $\mathcal{N}(U)={\bigcup }_{k=1}^m\mathcal{N}(J^{(k)}){\mathbf{e}}_k^{(0)}$. The support of an element $\mathbf{f}\in {𝒫}_{\mathbf{d}}^m$ is the set $supp(\mathbf{f})$ of all module terms appearing in $\mathbf{f}$ with a non-zero coefficient, thus $\mathbf{f}={\sum }_{x^{\alpha }{\mathbf{e}}_{i_{\alpha }}^{(0)}\in supp(\mathbf{f})}{c}_{\alpha }{x}^{\alpha }{\mathbf{e}}_{i_{\alpha }}^{(0)}$. If $\mathcal{B}$ is a set of homogeneous elements of degree s in ${𝒫}_{\mathbf{d}}^m$, we write ${\langle \mathcal{B}\rangle }_{\mathbb{k}}$ for the $\mathbb{k}$-vector space generated by $\mathcal{B}$ in ${({𝒫}_{\mathbf{d}}^m)}_s$. For a module $U\subseteq {𝒫}_{\mathbf{d}}^m$, we denote by $pd(U)$ the projective dimension and by $reg(U)$ the (Castelnuovo-Mumford) regularity of U.

Let $\mathcal{B}=\{{\mathbf{h}}_1,\dots ,{\mathbf{h}}_s\}$ be a finite set of homogeneous elements in ${𝒫}_{\mathbf{d}}^m$. We need the following data to define a resolving decomposition of the submodule U defined by $\mathcal{B}$. For every generator ${\mathbf{h}}_i\in \mathcal{B}$, we choose a term $x^{{\mu }_i}{\mathbf{e}}_{k_i}^{(0)}\in supp{\mathbf{h}}_i$ denoted by $hm({\mathbf{h}}_i)$ and call it the head module term of ${\mathbf{h}}_i$. Furthermore, we define the head module terms of $\mathcal{B}$ by $hm(\mathcal{B}):=\left\{hm(\mathbf{h})|\mathbf{h}\in \mathcal{B}\right\}$ and the head module of U by $hm(U)=\langle hm\mathcal{B}\rangle$. Obviously, the monomial module $hm(U)$ depends on the choice of both the generating set $\mathcal{B}$ and the head module terms $hm(\mathcal{B})$. Furthermore, we assign to every head module term $hm(\mathbf{h})$ with $\mathbf{h}\in \mathcal{B}$ a set of multiplicative variables $X_{\mathcal{B}}(\mathbf{h})\subseteq \mathbf{x}$ and denote by $X_{\mathcal{B}}$ the set of all these sets. Finally, we choose a term order ${\prec }_{\mathcal{B}}$ on ${𝒫}^s$ with s the number of generators in $\mathcal{B}$.

Definition 1.

The above introduced quadruple $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ defines a resolving decomposition of a submodule $U\subseteq {𝒫}_{\mathbf{d}}^m$, if the following five properties hold:

(i)

$U=\langle \mathcal{B}\rangle$.

(ii)

Let $\mathbf{h}\in \mathcal{B}$ be an arbitrary generator. Each module term $x^{\mu }{\mathbf{e}}_k^{(0)}\in supp(\mathbf{h})\backslash \{hm(\mathbf{h})\}$ must satisfy $x^{\mu }{\mathbf{e}}_k^{(0)}\notin hm(U)$.

(iii)

The assigned multiplicative variables induce direct sum decompositions of both the head module

$$hm(U)=\underset{\mathbf{h}\in \mathcal{B}}{⨁}\mathbb{k}\left[X_{\mathcal{B}}(\mathbf{h})\right]·hm(\mathbf{h})$$

(1)

and the module itself

$$U=\underset{\mathbf{h}\in \mathcal{B}}{⨁}\mathbb{k}\left[X_{\mathcal{B}}(\mathbf{h})\right]·\mathbf{h}.$$

(2)

(iv)

We have a direct sum decomposition ${({𝒫}_{\mathbf{d}}^m)}_r=U_r\oplus {\langle \mathcal{N}{(hm(U))}_r\rangle }_{\mathbb{k}}$ for all degrees $r\ge 0$.

(v)

Let $\{{\mathbf{e}}_1^{(1)},\dots ,{\mathbf{e}}_s^{(1)}\}$ denote the canonical basis of the free module ${𝒫}^s$. Given an arbitrary term $x^{\delta }\in \mathbb{T}$ and an arbitrary generator ${\mathbf{h}}_{\alpha }\in \mathcal{B}$, we find for every term $x^{ϵ}{\mathbf{e}}_i^{(0)}\in supp(x^{\delta }{\mathbf{h}}_{\alpha })\cap hm(U)$ a unique ${\mathbf{h}}_{\beta }\in hm(\mathcal{B})$ such that $x^{ϵ}{\mathbf{e}}_i^{(0)}=x^{{\delta }^{\prime }}hm({\mathbf{h}}_{\beta })$ with $x^{{\delta }^{\prime }}\in \mathbb{k}\left[X_{\mathcal{B}}({\mathbf{h}}_{\beta })\right]$ by (iii). Then the inequality $x^{\delta }{\mathbf{e}}_{\alpha }^{(1)}{⪰}_{\mathcal{B}}{x}^{{\delta }^{\prime }}{\mathbf{e}}_{\beta }^{(1)}$ holds with respect to the term order ${\prec }_{\mathcal{B}}$.

In the sequel, we will always assume that $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ is a resolving decomposition of the finitely generated module $U=\langle \mathcal{B}\rangle \subseteq {𝒫}_{\mathbf{d}}^m$. In addition to the multiplicative variables, we define for $\mathbf{h}\in \mathcal{B}$ the non-multiplicative variables as ${\overline{X}}_{\mathcal{B}}(\mathbf{h})=\{x_0,\dots ,x_n\}\backslash X_{\mathcal{B}}(\mathbf{h})$.

Remark 1.

Resolving decompositions refine the classical concept of Stanley decompositions [11]. Indeed, the equalities (1) and (2) simply represents Stanley decompositions of the head module of U and of U itself, respectively. This observation makes it straightforward to compute the Hilbert functions of $hm(U)$ and of U, respectively. Since the two Stanley decompositions possess an identical structure, the arising Hilbert functions trivially coincides. This fact represents a built-in term order free version of the well-known Macaulay theorem for Gröbner bases—see e.g., [12]).

Condition (iii) implies the existence of a unique standard representation

$$\mathbf{f}=\sum _{\alpha =1}^s{P}_{\alpha }{\mathbf{h}}_{\alpha }$$

with $P_{\alpha }\in \mathbb{k}\left[X_{\mathcal{B}}({\mathbf{h}}_{\alpha })\right]$ for every $\mathbf{f}\in U$. Note that these representations are indeed unique due to the fact that each coefficient may only depend on the multiplicative variables. Condition (iv) implies the existence of unique normal forms modulo U for all homogeneous elements $\mathbf{f}\in {𝒫}_{\mathbf{d}}^m$. Due to it, we find a unique coefficient $P_{\alpha }\in \mathbb{k}\left[X_{\mathcal{B}}({\mathbf{h}}_{\alpha })\right]$ for each generator ${\mathbf{h}}_{\alpha }\in \mathcal{B}$ such that ${\mathbf{f}}^{\prime }=\mathbf{f}-{\sum }_{\alpha =1}^s{P}_{\alpha }{\mathbf{h}}_{\alpha }\in {\langle \mathcal{N}(hm(U))\rangle }_{\mathbb{k}}$. It also follows trivially from (1) that for every generator in the basis $\mathcal{B}$ a different head module term is chosen.

For the goals of this article, the mere existence of normal forms suffices. Nevertheless, we remark that Condition (v) entails that these normal forms can be effectively determined. The head terms and multiplicative variables inherent to a resolving decomposition allows for the definition of a natural reduction relation. If there exists a term $x^{ϵ}{\mathbf{e}}_i^{(0)}\in supp(\mathbf{f})\cap hm(U)$ for some module element $\mathbf{f}\in {𝒫}_{\mathbf{d}}^m$, then we find a unique head module term $\mathbf{h}\in hm(\mathcal{B})$ such that $x^{ϵ}{\mathbf{e}}_i^{(0)}=x^{\delta }hm(\mathbf{h})$ with $x^{\delta }\in \mathbb{k}\left[X_{\mathcal{B}}(\mathbf{h})\right]$ and consequently a reduction $\mathbf{f}\stackrel{\mathcal{B}}{⟶}\mathbf{f}-c{x}^{\delta }\mathbf{h}$ is possible for a suitably chosen scalar $c\in \mathbb{k}$.

Lemma 1.

For any resolving decomposition $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ the transitive closure $\stackrel{\mathcal{B}}{⟶}{\phantom{\to }}^{\ast }$ of the reduction relation $\stackrel{\mathcal{B}}{⟶}$ is Noetherian and confluent.

Proof. 

It is sufficient to prove that for every term $x^{\gamma }{\mathbf{e}}_k^{(0)}$ in $hm(U)$, there is a unique $g\in {𝒫}_{\mathbf{d}}^m$ such that $x^{\gamma }{\mathbf{e}}_k^{(0)}\stackrel{\mathcal{B}}{⟶}{\phantom{\to }}^{\ast }g$ and $g\in \langle \mathcal{N}(hm(U))\rangle$. Since $x^{\gamma }{\mathbf{e}}_k^{(0)}\in hm(U)$, there exists a unique $x^{\delta }{\mathbf{h}}_{\alpha }\in U$ such that $x^{\delta }hm({\mathbf{h}}_{\alpha })=x^{\gamma }{\mathbf{e}}_k^{(0)}$ and $x^{\delta }\in X_{\mathcal{B}}({\mathbf{h}}_{\alpha })$. Hence, $x^{\gamma }{\mathbf{e}}_k^{(0)}\stackrel{\mathcal{B}}{⟶}{x}^{\gamma }{\mathbf{e}}_k^{(0)}-c{x}^{\delta }{\mathbf{h}}_{\alpha }$ for a suitably chosen coefficient $c\in \mathbb{k}$. Denoting again the canonical basis of ${𝒫}^s$ by $\{{\mathbf{e}}_1^{(1)},\dots ,{\mathbf{e}}_s^{(1)}\}$, we associate the term $x^{\delta }{\mathbf{e}}_{\alpha }^{(1)}$ with this reduction step. If we could proceed infinitely with further reduction steps, then the reduction process would induce a sequence of terms in ${𝒫}^s$ containing an infinite chain which, by Condition (v) of Definition 1, is strictly descending for ${\prec }_{\mathcal{B}}$. However, this is impossible, since ${\prec }_{\mathcal{B}}$ is a well-ordering. Hence $\stackrel{\mathcal{B}}{⟶}{\phantom{\to }}^{\ast }$ is Noetherian. Confluence is immediate by the uniqueness of the element that is used at each reduction step. ☐

The following examples show that involutive and marked bases, respectively, do indeed induce resolving decomposition as claimed in the introduction. In fact, one can say that the definition of resolving decompositions evolved from an abstraction and combination of these two basic examples: the emphasis on Stanley decompositions and unique normal forms represents a key feature of involutive bases and the somewhat convoluted last condition in Definition 1 stems from the theory of marked bases where it allows for the introduction of a Noetherian reduction relation without having head terms selected by a term order. The cited literature implicitly provides many concrete instances of resolving decompositions stemming either from involutive or marked bases. We refrain from repeating them, as this is, at least in the first case, rather standard now.

Example 1.

An involutive basis is a Gröbner basis with additional combinatorial properties (see [2] for a general introduction and a survey of their basic theoretical and algorithmic properties). It is defined with respect to a term order ≺ on the free module ${𝒫}_{\mathbf{d}}^m$ and an involutive division L (see ([2], Definition 2.1)). Given a finite set $\mathcal{B}\subset {𝒫}_{\mathbf{d}}^m$ of terms, an involutive division associates with each term in $\mathcal{B}$ a set of multiplicative variables. $\mathcal{B}$ is an L-involutive basis, if it suffices to multiply each term with terms in each multiplicative variable to obtain the whole module generated by $\mathcal{B}$. The extension to general polynomial modules is straightforward using the term order ≺ and normal form arguments. Note that the existence of Stanley decompositions induced by the multiplicative variables is thus a central part of the definition of involutive bases.

Assume now that L is a continuous division, ≺ an arbitrary term order and $\mathcal{B}\subset {𝒫}_{\mathbf{d}}^m$ a finite, L-involutively autoreduced set ([2], Definition 5.8) which defines a strong L-involutive basis ([2], Definition 5.1) of the polynomial submodule $U\subseteq {𝒫}_{\mathbf{d}}^m$ it generates. We choose the head module $hm(\mathcal{B})=\{lt({\mathbf{h}}_1),\dots ,lt({\mathbf{h}}_s)\}$ via the leading terms for the given term order ≺. The multiplicative variables $X_{\mathcal{B}}$ are of course assigned according to the involutive division L. Finally, we take for the term order ${\prec }_{\mathcal{B}}$ the classical Schreyer order induced by $\mathcal{B}$ and ≺ as it appears in Schreyer’s theorem (see e.g., ([13], Chapt. 5, Thm. 3.3)). Then the quadruple $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ defines a resolving decomposition of U.

The proof that all conditions of Definition 1 are satisfied consists simply of recalling some basic results about involutive bases. Condition (i) is entailed by ([2], Corollary 5.5). Condition (ii) follows from the fact that the set $\mathcal{B}$ is assumed to be involutively autoreduced and Condition (iii) is a consequence of ([2], Lemma 5.12). Furthermore, by ([2], Proposition 5.13), every module element $\mathbf{f}\in {𝒫}_{\mathbf{d}}^m$ has a unique normal form with respect to U. Remark 1 discusses that this property is equivalent to the fourth condition. Finally, Condition (v) is satisfied because of ([14], Lemma 5.5), asserting the existence of an L-ordering for any continuous division.

Example 2.

The key point about marked modules and marked bases, introduced in the first version of [8], is that no term order is used for the selection of the head terms. Given a basis $\mathcal{B}$ of the polynomial module $U\subset {𝒫}_{\mathbf{d}}^m$, one can in principle choose any term in the support of a generator as head term. However, in general such a choice will not lead to a Noetherian reduction relation. Therefore, certain restrictions apply. The chosen head terms must define a quasi-stable module which is equivalent to saying that they form a Pommaret basis of the head module. This fact immediately entails that most polynomial modules do not possess a marked basis. Indeed, the point of marked bases is not that one wants to compute one for a given module $U\subset {𝒫}_{\mathbf{d}}^m$, but that one prescribes a quasi-stable module $\mathcal{V}\subseteq {𝒫}_{\mathbf{d}}^m$ by giving its Pommaret basis and then constructs all possible marked bases where the set of head terms coincides with this Pommaret basis. This construction is a key step for obtaining local equations for Hilbert and Quot schemes modulo coordinate transformations (see [7,8] for more details).

More precisely, let $\mathscr{H}=\{x^{{\mu }_1}{\mathbf{e}}_{k_1}^{(0)},\dots x^{{\mu }_s}{\mathbf{e}}_{k_s}^{(0)}\}$ be a monomial Pommaret basis and $\mathcal{V}\subseteq {𝒫}_{\mathbf{d}}^m$ the quasi-stable module generated by $\mathscr{H}$. A marked basis $\mathcal{B}=\{{\mathbf{h}}_1,\dots ,{\mathbf{h}}_s\}$ then firstly satisfies $hm({\mathbf{h}}_i)=x^{{\mu }_i}{\mathbf{e}}_{k_i}^{(0)}$ and $supp({\mathbf{h}}_i-x^{{\mu }_i}{\mathbf{e}}_{k_i}^{(0)})\subseteq {\langle \mathcal{N}{(\mathcal{V})}_{deg(x^{{\mu }_i}{\mathbf{e}}_{k_i}^{(0)})}\rangle }_{\mathbb{k}}$ for each index $1\le i\le s$. Secondly, we require that the homogeneous component $\mathcal{N}{(\mathcal{V})}_r$ of degree r induces a $\mathbb{k}$-linear basis of the factor module ${({𝒫}_{\mathbf{d}}^m)}_r/{\langle \mathcal{B}\rangle }_r$ for any $r\ge 0$. Note that this fact entails the decompositions ${({𝒫}_{\mathbf{d}}^m)}_r={\langle \mathcal{B}\rangle }_r\oplus {\langle \mathcal{N}{(\mathcal{V})}_r\rangle }_{\mathbb{k}}$ for all r. For a more detailed discussion of marked bases, we refer to ([8], Section 2). For the desired resolving decomposition, we take as multiplicative variables $X_{\mathcal{B}}$ simply the multiplicative variables of the Pommaret basis $\mathscr{H}$. Recall that if $1\le c\le n$ is the minimal index value such that the multi index μ has a non-zero entry at position c (this value is called the class of μ), then the variables $x_1,\dots ,x_c$ are Pommaret multiplicative for $x^{\mu }{\mathbf{e}}_k^{(0)}$. Finally, we choose as module term order ${\prec }_{\mathcal{B}}$ the standard TOP lift of the classical lexicographic order [15].

We claim now again that $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ defines a resolving decomposition of U. Indeed, it follows immediately by construction that the Conditions (i), (ii) and (iv) are satisfied. The first part of Condition (iii) is a consequence of the fact that $\mathscr{H}=hm(\mathcal{B})$ is a Pommaret basis and the second part of the uniqueness of the reduction process ([8], Lemma 5.1) (here it is crucial that in this particular case the reduction process is essentially the Pommaret normal form algorithm, as otherwise no Noetherian reduction relation would arise). Finally, Condition (v) is entailed by ([8], Lemma 3.6).

The main obstacle in checking whether or not a given quadruple $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ defines a resolving decomposition is Condition (v). It can be tackled with the help of a directed graph induced by any decomposition $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ satisfying the first four conditions of Definition 1. Its vertices are given by the elements in $\mathcal{B}$. If $x_j\in {\overline{X}}_{\mathcal{B}}(\mathbf{h})$ for some $\mathbf{h}\in \mathcal{B}$, then, by definition, $\mathcal{B}$ contains a unique generator ${\mathbf{h}}^{\prime }$ such that $x_{j}hm(\mathbf{h})=x^{\mu }hm({\mathbf{h}}^{\prime })$ with $x^{\mu }\in \mathbb{k}\left[X_{\mathcal{B}}({\mathbf{h}}^{\prime })\right]$. In this case we include a directed edge from $\mathbf{h}$ to ${\mathbf{h}}^{\prime }$. We call the thus defined graph the $\mathcal{B}$-graph and show now that acyclicity of it is a necessary condition for a resolving decomposition.

Proposition 1.

The $\mathcal{B}$-graph of a resolving decomposition $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ is always acyclic.

Proof. 

Assume the $\mathcal{B}$-graph was cyclic. Then we can find pairwise distinct generators ${\mathbf{h}}_{k_1},\dots ,{\mathbf{h}}_{k_t}\in \mathcal{B}$ plus a non-multiplicative variable $x_{i_j}\in {\overline{X}}_{\mathcal{B}}(hm({\mathbf{h}}_{k_j}))$ and a multiplicative term $x^{{\mu }_j}\in \mathbb{k}\left[X_{\mathcal{B}}(hm({\mathbf{h}}_{k_j}))\right]$ for each $j\in \{1,\dots ,t\}$ such that

$$\begin{array}{c}{x}_{i_1}hm({\mathbf{h}}_{k_1})=x^{{\mu }_2}hm({\mathbf{h}}_{k_2}),\\ x_{i_2}hm({\mathbf{h}}_{k_2})=x^{{\mu }_3}hm({\mathbf{h}}_{k_3}),\\ ⋮\\ x_{i_t}hm({\mathbf{h}}_{k_t})=x^{{\mu }_1}hm({\mathbf{h}}_{k_1}).\end{array}$$

Multiplying with some variables, we obtain the following chain of equations:

$$\begin{array}{cc}\hfill x_{i_1}\cdots x_{i_t}hm({\mathbf{h}}_{k_1})& =x_{i_2}\cdots x_{i_t}{x}^{{\mu }_2}hm({\mathbf{h}}_{k_2})\hfill \\ \hfill & =x_{i_3}\cdots x_{i_t}{x}^{{\mu }_2}{x}^{{\mu }_3}hm({\mathbf{h}}_{k_3})\hfill \\ \hfill & ⋮\hfill \\ \hfill & =x_{i_t}{x}^{{\mu }_2}\cdots x^{{\mu }_t}hm({\mathbf{h}}_{k_t})\hfill \\ \hfill & =x^{{\mu }_1}\cdots x^{{\mu }_t}hm({\mathbf{h}}_{k_1})\hfill \end{array}$$

which implies that $x_{i_1}\cdots x_{i_t}=x^{{\mu }_1}\cdots x^{{\mu }_t}$. Furthermore, Condition (v) of Definition 1 implies in ${𝒫}^s$ the following chain:

$$x_{i_1}\cdots x_{i_t}{\mathbf{e}}_{k_1}^{(1)}{⪰}_{\mathcal{B}}{x}_{i_2}\cdots x_{i_t}{x}^{{\mu }_2}{\mathbf{e}}_{k_2}^{(1)}{⪰}_{\mathcal{B}}\cdots {⪰}_{\mathcal{B}}{x}^{{\mu }_1}\cdots x^{{\mu }_t}{\mathbf{e}}_{k_1}^{(1)}.$$

Because of $x_{i_1}\cdots x_{i_t}=x^{{\mu }_1}\cdots x^{{\mu }_t}$, we must have throughout equality entailing that $k_1=\cdots =k_t$ which contradicts our assumptions. ☐

The following two results provide a converse of this proposition for the special case of a monomial generating set $\mathcal{B}$ by showing that whenever the $\mathcal{B}$-graph of such a set is acyclic, then there exists a term order satisfying Condition (v).

Lemma 2.

Let $\mathcal{B}$ be a generating set consisting only of module terms. Assume that for the chosen multiplicative variables $X_{\mathcal{B}}$, the $\mathcal{B}$-graph is acyclic. Then it is not possible to find a chain of equalities of the form

$$\begin{array}{cc}\hfill x^{{\nu }_1}{\mathbf{h}}_{k_1}& =x^{{\mu }_2}{\mathbf{h}}_{k_2},\hfill \end{array}$$

(3a)

$$\begin{array}{c}{x}^{{\nu }_2}{\mathbf{h}}_{k_2}=x^{{\mu }_3}{\mathbf{h}}_{k_3},\\ ⋮\end{array}$$

(3b)

$$\begin{array}{cc}\hfill x^{{\nu }_t}{\mathbf{h}}_{k_t}& =x^{{\mu }_1}{\mathbf{h}}_{k_1}\hfill \end{array}$$

(3c)

with multiplicative terms $x^{{\mu }_i}\in \mathbb{k}\left[X_{\mathcal{B}}({\mathbf{h}}_{k_i})\right]$ and arbitrary terms $x^{{\nu }_i}\in \mathbb{T}$. Furthermore, whenever an equality $x^{\nu }hm({\mathbf{h}}_i)=x^{\mu }hm({\mathbf{h}}_j)$ holds with a multiplicative term $x^{\mu }\in \mathbb{k}\left[X_{\mathcal{B}}({\mathbf{h}}_j)\right]$, then the $\mathcal{B}$-graph contains a directed path from ${\mathbf{h}}_i$ to ${\mathbf{h}}_j$.

Proof. 

We show that any chain of the form (3) induces a cycle in the $\mathcal{B}$-graph and thus violates the assumed acyclicity. Without loss of generality, we may assume that $gcd(x^{{\nu }_i},x^{{\mu }_{i+1}})=1$ and $x^{{\nu }_i}\notin \mathbb{k}\left[X_{\mathcal{B}}({\mathbf{h}}_{k_i})\right]$. This implies the existence of a non-multiplicative variable $x_{i_0}\in {\overline{X}}_{\mathcal{B}}({\mathbf{h}}_{k_1})$ dividing $x^{{\nu }_1}$. Set $x^{{\rho }_0}=x^{{\nu }_1}/x_{i_0}$ and let the normal form of $x_{i_0}{\mathbf{h}}_{k_1}$ be $x^{{\tau }_1}{\mathbf{h}}_{l_1}$. Then $x^{{\rho }_0}{x}^{{\tau }_1}{\mathbf{h}}_{l_1}=x^{{\mu }_2}{\mathbf{h}}_{k_2}$. By assumption, there exists a non-multiplicative variable $x_{i_1}\in {\overline{X}}_{\mathcal{B}}({\mathbf{h}}_{l_1})$ dividing $x^{{\rho }_0}{x}^{{\tau }_1}$. Now set $x_{{\rho }_1}=x^{{\rho }_0}{x}^{{\tau }_1}/x_{i_1}$ and repeat the procedure.

Due to the fact that the $\mathcal{B}$-graph is acyclic and that there are only finitely many terms $x^{\rho },x^{\tau }$ and generators ${\mathbf{h}}_l$ such that $x^{\rho }{x}^{\tau }{\mathbf{h}}_l=x^{{\mu }_2}{\mathbf{h}}_{k_2}$, we find after finitely many steps $x_{l_t}$ and ${\mathbf{h}}_{l_t}$ such that $x_{l_t}\in {\overline{X}}_{\mathcal{B}}({\mathbf{h}}_{l_t})$ divides $x^{{\rho }_{t-1}}{x}^{{\tau }_t}$ and such that the normal form of $x_{l_t}{\mathbf{h}}_{l_t}$ is $x^{{\mu }_2}{\mathbf{h}}_{k_2}$. Now we do the same for ${\mathbf{h}}_{k_2},{\mathbf{h}}_{k_3},\dots$ at the end we reach again ${\mathbf{h}}_{k_1}$. Hence, we have constructed a cycle in the $\mathcal{B}$-graph.

The final assertion follows immediately from the construction above. ☐

Lemma 3.

Let $\mathcal{B}=\{{\mathbf{h}}_1,\dots ,{\mathbf{h}}_s\}$ be a generating set consisting only of module terms. Assume that for the chosen multiplicative variables $X_{\mathcal{B}}$ Conditions (i) to (iv) of Definition 1 are satisfied. Furthermore, let the $\mathcal{B}$-graph be acyclic and the elements of $\mathcal{B}$ be numbered in such a way that for any path from ${\mathbf{h}}_i$ to ${\mathbf{h}}_j$ in the $\mathcal{B}$-graph we always have $i<j$. If ${\prec }_{\mathcal{B}}$ is an arbitrary term order on ${𝒫}^s$ such that $x^{\alpha }{\mathbf{e}}_i^{(0)}{\succ }_{\mathcal{B}}{x}^{\beta }{\mathbf{e}}_j^{(0)}$ whenever $i<j$, then $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$ is a resolving decomposition.

Proof. 

We first remark that a numbering of the set $\mathcal{B}$ as assumed in the Lemma always exists for an acyclic graph. Now we only have to check Condition (v) of Definition 1. Take a generator ${\mathbf{h}}_i\in \mathcal{B}$ and an arbitrary term $x^{\delta }\in \mathbb{T}$. Then $x^{\delta }{\mathbf{h}}_i=x^{\alpha }{\mathbf{h}}_j$ for a suitable multiplicative term $x^{\alpha }\in \mathbb{k}\left[X_{\mathcal{B}}({\mathbf{h}}_j)\right]$. By Lemma 2, there exists a path from ${\mathbf{h}}_i$ to ${\mathbf{h}}_j$ in the $\mathcal{B}$-graph and hence $i<j$. However, this implies $x^{\delta }{\mathbf{e}}_i^{(0)}{\succ }_{\mathcal{B}}{x}^{\alpha }{\mathbf{e}}_j^{(0)}$ proving the missing condition in the definition of a resolving decomposition. ☐

The last lemma provides us with a simple check whether a monomial generating set together with the chosen assignment of multiplicative variables can be used for defining a resolving decomposition: we only have to check whether the induced $\mathcal{B}$-graph is acyclic. If this is the case, then we can choose any term order satisfying the property of Lemma 3 to complete the definition of a resolving decomposition. The existence of such a term order is obvious, as every POT lift fulfils this property [16].

Example 3.

Set $𝒫=\mathbb{k}[x_0,x_1,x_2,x_3]$ with the standard grading and $m=1$. Let U be the ideal generated by $x_0{x}_1,x_1^2,x_2{x}_3,x_3^3$ in $𝒫$. A Stanley decomposition of U is then given by the set

$$\begin{array}{cc}\hfill \mathcal{B}=\{& {\mathbf{h}}_1=x_0{x}_1,{\mathbf{h}}_2=x_0{x}_1{x}_2,{\mathbf{h}}_3=x_0^2{x}_1,{\mathbf{h}}_4=x_1^2,{\mathbf{h}}_5=x_1^2{x}_3,\hfill \\ \hfill & {\mathbf{h}}_6=x_0{x}_1{x}_3,{\mathbf{h}}_7=x_1^2{x}_3^2,{\mathbf{h}}_8=x_0{x}_1{x}_3^2,{\mathbf{h}}_9=x_3^3,{\mathbf{h}}_{10}=x_2{x}_3\}\hfill \end{array}$$

with multiplicative variables

$$\begin{array}{cccc}\hfill X_{\mathcal{B}}({\mathbf{h}}_1)& =\varnothing ,\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_2)& =\{x_0,x_2\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_3)& =\{x_0,x_2\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_4)& =\{x_0,x_1,x_2\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_5)& =\{x_1\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_6)& =\{x_0,x_1\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_7)& =\{x_1\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_8)& =\{x_0,x_1\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_9)& =\{x_0,x_1,x_3\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_{10})& =\{x_0,x_1,x_2,x_3\}.\hfill \end{array}$$

The corresponding $\mathcal{B}$-graph is

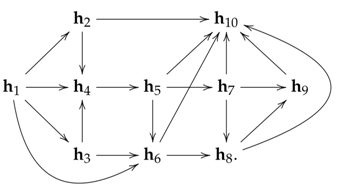and obviously acyclic. Hence we can choose an arbitrary term order ${\prec }_{\mathcal{B}}$ as described in Lemma 3 to complete the definition of a resolving decomposition $(\mathcal{B},hm(\mathcal{B}),X_{\mathcal{B}},{\prec }_{\mathcal{B}})$.

Example 4.

It should be emphasised that not even in the monomial case does every Stanley decomposition induce a resolving decomposition, i.e., we cannot always find a corresponding term order ${\prec }_{\mathcal{B}}$. A simple counterexample can already be given based on the homogeneous maximal ideal U in $𝒫$ for $n=4$ and the standard grading. In ([17], Page 31), it is shown that a Stanley decomposition of U is defined by the set

$$\begin{array}{cc}\hfill \mathcal{B}=\{& {\mathbf{h}}_1=x_0,{\mathbf{h}}_2=x_1,{\mathbf{h}}_3=x_2,{\mathbf{h}}_4=x_3,{\mathbf{h}}_5=x_4,{\mathbf{h}}_6=x_0{x}_1{x}_3,{\mathbf{h}}_7=x_0{x}_2{x}_3,\hfill \\ \hfill & {\mathbf{h}}_8=x_0{x}_2{x}_4,{\mathbf{h}}_9=x_1{x}_2{x}_4,{\mathbf{h}}_{10}=x_1{x}_3{x}_4,{\mathbf{h}}_{11}=x_0{x}_1{x}_2{x}_3{x}_4\}\hfill \end{array}$$

with multiplicative variables

$$\begin{array}{cccc}\hfill X_{\mathcal{B}}({\mathbf{h}}_1)& =\{x_0,x_1,x_2\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_2)& =\{x_1,x_2,x_3\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_3)& =\{x_2,x_3,x_4\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_4)& =\{x_0,x_3,x_4\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_5)& =\{x_0,x_1,x_4\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_6)& =\{x_0,x_1,x_2,x_3\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_7)& =\{x_0,x_2,x_3,x_4\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_8)& =\{x_0,x_1,x_2,x_4\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_9)& =\{x_1,x_2,x_3,x_4\},\hfill & \hfill X_{\mathcal{B}}({\mathbf{h}}_{10})& =\{x_0,x_1,x_3,x_4\}\hfill \\ \hfill X_{\mathcal{B}}({\mathbf{h}}_{11})& =\{x_0,x_1,x_2,x_3,x_4\}.\hfill \end{array}$$

The $\mathcal{B}$-graph corresponding to this basis is

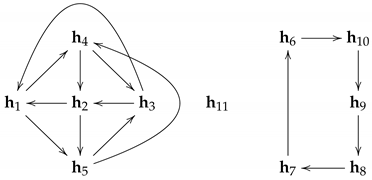and obviously contains several cycles. Therefore, it is not possible to find a term order ${\prec }_{\mathcal{B}}$, which makes this Stanley decomposition into a resolving one.

This phenomenon is typical for Stanley decompositions considered in the context of the Stanley conjecture, i.e., for decompositions where one tries to maximise the Stanley depth which is given by the minimal number of multiplicative variables of a generator (see [17] and references therein for more details on the Stanley conjecture).

3. The Syzygy Resolutions Induced by a Resolving Decomposition

Let now $U=\langle {\mathcal{B}}^{(0)}\rangle$ with ${\mathcal{B}}^{(0)}=\{{\mathbf{h}}_1,\dots ,{\mathbf{h}}_{s_1}\}$ be a finitely generated graded submodule of ${𝒫}_{{\mathbf{d}}_0}^m$, the graded free polynomial module with canonical basis $\{{\mathbf{e}}_1^{(0)},\dots ,{\mathbf{e}}_m^{(0)}\}$ and grading defined by the vector ${\mathbf{d}}_0=(d_1^{(0)},\dots d_m^{(0)})$. We assume that we have somehow obtained a resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ of U. Our first step consists of showing that it induces in a natural way a resolving decomposition $({\mathcal{B}}^{(1)},hm({\mathcal{B}}^{(1)}),X_{{\mathcal{B}}^{(1)}},{\prec }_{{\mathcal{B}}^{(1)}})$ of the first syzygy module $\mathrm{Syz}({\mathcal{B}}^{(0)})\subseteq {𝒫}^{s_1}$. This result represents an extension or refinement of the classical Schreyer theorem providing a Gröbner basis ${\mathcal{G}}^{(1)}$ for the syzygy module $\mathrm{Syz}({\mathcal{G}}^{(0)})$ of a Gröbner basis ${\mathcal{G}}^{(0)}$ (see e.g., ([13], Chapt. 5, Thm. 3.3)).

By the definition of a resolving decomposition, we have for every non-multiplicative variable $x_k$ of each generator ${\mathbf{h}}_{\alpha }\in {\mathcal{B}}^{(0)}$ a unique standard representation $x_k{\mathbf{h}}_{\alpha }={\sum }_{\beta =1}^{s_1}{P}_{\beta }^{(\alpha ;k)}{\mathbf{h}}_{\beta }$ corresponding to the syzygy

$${\mathbf{S}}_{\alpha ;k}=x_k{\mathbf{e}}_{\alpha }^{(1)}-\sum _{\beta =1}^{s_1}{P}_{\beta }^{(\alpha ;k)}{\mathbf{e}}_{\beta }^{(1)}$$

(4)

where $\{{\mathbf{e}}_1^{(1)},\dots ,{\mathbf{e}}_{s_1}^{(1)}\}$ denotes the canonical basis of the graded free polynomial module ${𝒫}_{{\mathbf{d}}_1}^{s_1}$ with grading defined by the degree vector ${\mathbf{d}}_1=(deg({\mathbf{h}}_1),\dots ,deg({\mathbf{h}}_s))$.

Lemma 4.

Let $S={\sum }_{\alpha =1}^{s_1}{S}_{\alpha }{\mathbf{e}}_{\alpha }^{(1)}$ be an arbitrary syzygy of ${\mathcal{B}}^{(0)}$ with coefficients $S_{\alpha }\in 𝒫$. Then we have $S_{\alpha }\in \mathbb{k}\left[X_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })\right]$ for all $1\le \alpha \le s_1$, if and only if $S=0$.

Proof. 

If $S\in \mathrm{Syz}({\mathcal{B}}^{(0)})$, then ${\sum }_{\alpha =1}^{s_1}{S}_{\alpha }{\mathbf{h}}_{\alpha }=0$. By definition of a resolving decomposition, each $\mathbf{f}\in U$ can be uniquely written in the form $\mathbf{f}={\sum }_{\alpha =1}^{s_1}{P}_{\alpha }{\mathbf{h}}_{\alpha }$ with ${\mathbf{h}}_{\alpha }\in {\mathcal{B}}^{(0)}$ and $P_{\alpha }\in \mathbb{k}\left[X_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })\right]$. In particular, this holds for $0\in U$. Thus $0=S_{\alpha }\in \mathbb{k}\left[X_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_l)\right]$ for all $\alpha$ and hence $S=0$. ☐

We denote the non-multiplicative variables of the generator ${\mathbf{h}}_{\alpha }\in {\mathcal{B}}^{(0)}$ by $\{x_{i_1^{\alpha }},\dots ,x_{i_{r_{\alpha }}^{\alpha }}\}$ where we assume that $i_1^{\alpha }<\dots <i_{r_{\alpha }}^{\alpha }$. Then we take as ${\mathcal{B}}^{(1)}$ the set $\left\{{\mathbf{S}}_{\alpha ;i_k^{\alpha }}\mid 1\le \alpha \le s_1,1\le k\le i_{r_{\alpha }}^{\alpha }\right\}$ consisting of all syzygies constructed as above from the products of generators by non-multiplicative variables.

Theorem 1.

For each syzygy $S_{\alpha ;i_k^{\alpha }}\in {\mathcal{B}}^{(1)}$, we choose as head term

$$hm(S_{\alpha ;i_k^{\alpha }})=x_{i_k^{\alpha }}{\mathbf{e}}_{\alpha }^{(1)}$$

and as multiplicative variables

$$X_{{\mathcal{B}}^{(1)}}({\mathbf{S}}_{\alpha ;i_k^{\alpha }})=\{x_0,\dots x_n\}\backslash \{x_{i_1^{\alpha }},\dots ,x_{i_{k-1}^{\alpha }}\}.$$

Furthermore, we take for ${\prec }_{{\mathcal{B}}^{(1)}}$ the Schreyer order associated to ${\mathcal{B}}^{(0)}$ and ${\prec }_{{\mathcal{B}}^{(0)}}$. Then the quadruple $({\mathcal{B}}^{(1)},hm({\mathcal{B}}^{(1)}),X_{{\mathcal{B}}^{(1)}},{\prec }_{{\mathcal{B}}^{(1)}})$ defines a resolving decomposition of the syzygy module $\mathrm{Syz}({\mathcal{B}}^{(0)})$.

Proof. 

We first show that $({\mathcal{B}}^{(1)},hm({\mathcal{B}}^{(1)}),X_{{\mathcal{B}}^{(1)}},{\prec }_{{\mathcal{B}}^{(1)}})$ is a resolving decomposition of $\langle {\mathcal{B}}^{(1)}\rangle$. In a second step, we prove that furthermore $\langle {\mathcal{B}}^{(1)}\rangle =\mathrm{Syz}({\mathcal{B}}^{(0)})$.

The first condition of Definition 1 is trivially satisfied. By construction, it is obvious that

$$hm(\langle {\mathcal{B}}^{(1)}\rangle )=\underset{\alpha =1}{\overset{s_1}{⨁}}\langle {\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })\rangle {\mathbf{e}}_{\alpha }^{(1)}.$$

(5)

It follows from (4) that any non head term $x^{\mu }{\mathbf{e}}_l^{(1)}\in supp({\mathbf{S}}_{\alpha ;k}-x_k{\mathbf{e}}_{\alpha }^{(1)})$ must satisfy $x^{\mu }\in \mathbb{k}\left[X_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_l)\right]$ and hence we find $x^{\mu }{\mathbf{e}}_l^{(1)}\notin hm(\langle {\mathcal{B}}^{(1)}\rangle )$ implying Condition (ii). Furthermore, it is obvious that

$$\langle {\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })\rangle {\mathbf{e}}_{\alpha }^{(1)}=\underset{k=1}{\overset{r_{\alpha }}{⨁}}\mathbb{k}\left[X_{{\mathcal{B}}^{(1)}}({\mathbf{S}}_{\alpha ,i_k^{\alpha }})\right]x_{i_k^{\alpha }}{\mathbf{e}}_{\alpha }^{(1)}.$$

If we combine this equation with (5), then the first part of Condition (iii) follows immediately.

The second part of this condition is a bit harder to prove. We take an arbitrary module element $\mathbf{f}\in \langle {\mathcal{B}}^{(1)}\rangle$ and construct its standard representation using $hm(\langle {\mathcal{B}}^{(1)}\rangle )$. Assume first that the support of $\mathbf{f}$ contains no multiple of a head term, i.e., $supp(\mathbf{f})\cap hm(\langle {\mathcal{B}}^{(1)}\rangle )=\varnothing$. Then all terms $x^{ϵ}{\mathbf{e}}_{\alpha }^{(1)}\in supp(\mathbf{f})$ in the support must satisfy $x^{ϵ}\in X_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })$. Therefore, we get that $\mathbf{f}=0$ due to Lemma 4.

We may thus assume that $supp(\mathbf{f})\cap hm(\langle {\mathcal{B}}^{(1)}\rangle )\ne \varnothing$ and we take the biggest term $x^{\mu }{\mathbf{e}}_{\alpha }^{(1)}$ in this set with respect to the order ${\prec }_{{\mathcal{B}}^{(0)}}$. By the already proven first part of Condition (iii), there must be a syzygy ${\mathbf{S}}_{\alpha ;i}$ such that $x_i\mid x^{\mu }$ and $x^{\mu }/x_i\in \mathbb{k}\left[X_{{\mathcal{B}}^{(1)}}({\mathbf{S}}_{\alpha ;i})\right]$. We reduce $\mathbf{f}$ by this syzygy and obtain the new module element

$${\mathbf{f}}^{\prime }=\mathbf{f}-c\frac{x^{\mu }}{x_i}{\mathbf{S}}_{\alpha ;i}$$

for a suitable constant $c\in \mathbb{k}$ such that the term $x^{\mu }{\mathbf{e}}_{\alpha }^{(1)}$ is no longer in support of ${\mathbf{f}}^{\prime }$. Every term $x^{\lambda }{\mathbf{e}}_{\beta }^{(1)}\in supp({\mathbf{f}}^{\prime })$ that is newly introduced by the subtraction of $c\frac{x^{\mu }}{x_i}{\mathbf{S}}_{\alpha ;i}$ and that also lies in $hm(\langle {\mathcal{B}}^{(1)}\rangle )$ must be strictly less than the removed term $x^{\mu }{\mathbf{e}}_{\alpha }^{(1)}$ by Condition (v) of Definition 1 and by Equation (4) defining the syzygy ${\mathbf{S}}_{\alpha ;i}$.

We repeat this reduction procedure until we eventually obtain a module element ${\mathbf{f}}^{″}$ such that $supp({\mathbf{f}}^{″})\cap hm(\langle {\mathcal{B}}^{(1)}\rangle )=\varnothing$. This will happen after a finite number of steps, since the reduced terms forms a decreasing sequence with respect to the well-order ${\prec }_{{\mathcal{B}}^{(0)}}$. By the same argument as above, this implies that we must have ${\mathbf{f}}^{″}=0$, which concludes the proof of this condition.

The above procedure provides us with an algorithm to compute arbitrary normal forms and hence Condition (iv) follows immediately. For the last condition in Definition 1, we observe that the head term $x_i{\mathbf{e}}_{\alpha }^{(1)}$ is the leading term of the syzygy ${\mathbf{S}}_{\alpha ;i}$ for the module term order ${\prec }_{{\mathcal{B}}^{(0)}}$. Thus the used Schreyer order indeed satisfies Condition (v). ☐

As is the case for the classical Schreyer theorem, this construction can now be iterated to obtain resolving decompositions of the second and higher syzygy modules. This iteration thus leads to a (generally non-minimal) free resolution of the submodule U where the constructed syzygies define the columns of the matrices of the differentials. Note that for actually writing down all these syzygies, we must compute many standard representations of products of generators by non-multiplicative variables. This fact does not change compared to the classical situation (where one considers S-polynomials instead of products by variables). However, since a resolving decomposition contains much more information than a Gröbner basis, it is now possible to make at least precise statements about the shape of the resolution. More precisely, it turns out that, without any further computations, it is now possible to predict solely on the basis of the resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ the head terms of all higher syzygies and thus in particular their numbers corresponding to the ranks of the free modules appearing in the resolution. Furthermore, the length of the resolution can also be easily read off from $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$.

Theorem 2.

Let $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ define a resolving decomposition of the graded submodule $U\subset {𝒫}_{{\mathbf{d}}_0}^m$. Denote by ${\beta }_{0,j}^{(k)}$ the number of generators $\mathbf{h}\in {\mathcal{B}}^{(0)}$ which are of degree j and have k multiplicative variables. Furthermore, we write $d=min\{k\mid \exists j:{\beta }_{0,j}^{(k)}>0\}$ for the minimal number of multiplicative variables of a generator. Then the submodule U possesses a graded free resolution of length $n-d+1$ of the form

$$0\to \underset{j}{⨁}𝒫{(-j)}^{r_{n+1-d,j}}\to \cdots \to \underset{j}{⨁}𝒫{(-j)}^{r_{1,j}}\to \underset{j}{⨁}𝒫{(-j)}^{r_{0,j}}\to U\to 0$$

(6)

where the graded ranks of the appearing free modules are given by

$$r_{i,j}=\sum _{k=1}^{n+1-i}\left(\genfrac{}{}{0pt}{}{n+1-k}{i}\right){\beta }_{0,j-i}^{(k)}.$$

Proof. 

Iterating Theorem 1, we can construct a resolving decomposition $({\mathcal{B}}^{(i)},hm({\mathcal{B}}^{(i)}),X_{{\mathcal{B}}^{(i)}},{\prec }_{{\mathcal{B}}^{(i)}})$ of the ith syzygy module ${\mathrm{Syz}}_i(U)$ for any i. Given an index $1\le l\le m$ and a non-multiplicative variable $x_k\in {\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha (l)})$, we find $|{\overline{X}}_{{\mathcal{B}}^{(1)}}(S_{l;k})|<|{\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha (l)})|$.

If $d_i$ denotes the minimal number of multiplicative variables assigned to a head module term in $hm({\mathcal{B}}^{(i)})$, then it is easy to see that the minimal number of multiplicative variables assigned to a head term in $hm({\mathcal{B}}^{(1)})$ is $d+1$. This fact immediately entails the claimed length of the resolution (6). Furthermore, it follows from our construction of the basic syzygies via products of generators by non-multiplicative variables that $deg({\mathbf{S}}_{k;i})=deg({\mathbf{h}}_k)+1$.

The assertion about the graded ranks of the modules is obtained by a combinatorial calculation. We denote by ${\beta }_{i,j}^{(k)}$ the number of generators in ${\mathcal{B}}^{(i)}$ of degree j with k multiplicative variables. It follows from our construction, that we have

$${\beta }_{i,j}^{(k)}=\sum _{t=1}^{k-1}{\beta }_{i-1,j-1}^{(t)},$$

as each generator in ${\mathcal{B}}^{(i-1)}$ of degree $j-1$ with less than k multiplicative variables contributes one generator in ${\mathcal{B}}^{(i)}$ with k multiplicative variables. We will now show by induction how ${\beta }_{i,j}^{(k)}$ can be expressed in terms of ${\beta }_{0,j}^{(k)}$, namely that

$${\beta }_{i,j}^{(k)}=\sum _{t=1}^{k-i}\left(\genfrac{}{}{0pt}{}{k-t-1}{i-1}\right){\beta }_{0,j-i}^{(t)}.$$

The base case $i=1$ is trivial. For the inductive step, we first note that obviously ${\beta }_{i,j}^{(\ell )}=0$ if $\ell <i+1$. Using this observation and the inductive hypothesis, we get

$${\beta }_{i+1,j}^{(k)}=\sum _{\ell =i+2}^{k-1}{\beta }_{i,j-1}^{(\ell )}=\sum _{\ell =i+2}^{k-1}\sum _{t=1}^{\ell -i}\left(\genfrac{}{}{0pt}{}{\ell -t-1}{i-1}\right){\beta }_{0,j-i}^{(t)}=\sum _{t=1}^{k-i-1}\left[\sum _{\ell =i+t}^{k-1}\left(\genfrac{}{}{0pt}{}{\ell -t-1}{i-1}\right)\right]{\beta }_{0,j-i}^t.$$

A shift of the index in the inner sum by $t+1$ proves our claim via the following identity obtained by summing over one column in the Pascal triangle:

$$\sum _{m=i-1}^{k-t-2}\left(\genfrac{}{}{0pt}{}{m}{i-1}\right)=\left(\genfrac{}{}{0pt}{}{k-t-2}{i}\right).$$

For the ranks of the free modules, we compute

$$r_{i,j}=\sum _{k=1}^{n+1}{\beta }_{i,j}^{(k)}=\sum _{k=1}^{n+1}\sum _{t=1}^{k-i}\left(\genfrac{}{}{0pt}{}{k-t-1}{i-1}\right){\beta }_{0,j-i}^{(t)}=\sum _{k=1}^{n+1-i}\left(\genfrac{}{}{0pt}{}{n+1-k}{i}\right){\beta }_{0,j-i}^{(k)}$$

where we used again the above identity for binomial coefficients for obtaining the last equality. ☐

We now take a closer look at this iterative construction of the resolving decompositions $({\mathcal{B}}^{(j)},hm({\mathcal{B}}^{(j)}),X_{{\mathcal{B}}^{(j)}},{\prec }_{{\mathcal{B}}^{(j)}})$ for the syzygy modules ${\mathrm{Syz}}_j(U)$. To define an element of ${\mathcal{B}}^{(j)}$, we consider for each generator ${\mathbf{h}}_{\alpha }\in {\mathcal{B}}^{(0)}$ all ordered integer sequences $\mathbf{k}=(k_1,\dots ,k_j)$ with $0\le k_1<\dots <k_j\le n$ of length $\left|\mathbf{k}\right|=j$ such that $x_{k_i}\in {\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })$ for all $1\le i\le j$. We denote for any $1\le i\le j$ by ${\mathbf{k}}_i$ the sequence obtained by eliminating $k_i$ from $\mathbf{k}$. Then the generator ${\mathbf{S}}_{\alpha ;\mathbf{k}}$ arises recursively from the standard representation of $x_{k_j}{\mathbf{S}}_{\alpha ;{\mathbf{k}}_j}$ according to the resolving decomposition $({\mathcal{B}}^{(j-1)},hm({\mathcal{B}}^{(j-1)}),X_{{\mathcal{B}}^{(j-1)}},{\prec }_{{\mathcal{B}}^{(j-1)}})$:

$$x_{k_j}{\mathbf{S}}_{\alpha ;{\mathbf{k}}_j}=\sum _{\beta =1}^{s_1}\sum _{\mathbf{l}}{P}_{\beta ;\mathbf{l}}^{(\alpha ;\mathbf{k})}{\mathbf{S}}_{\beta ;\mathbf{l}}.$$

(7)

The second sum is over all ordered integer sequences $\mathbf{l}$ of length $j-1$ such that for each entry ${\ell }_i$ the variable $x_{{\ell }_i}$ is non-multiplicative for the generator ${\mathbf{h}}_{\beta }\in {\mathcal{B}}^{(0)}$. Denoting the free generators of the free module which contains the jth syzygy module by ${\mathbf{e}}_{\alpha ,\mathbf{l}}^{(j)}$, such that $\alpha \in \{1,\dots ,s_1\}$ and $\mathbf{l}$ is an ordered subset of ${\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })$ of length $j-1$ we get the following representation for ${\mathbf{S}}_{\alpha ,\mathbf{k}}$:

$${\mathbf{S}}_{\alpha ;\mathbf{k}}=x_{k_j}{\mathbf{e}}_{\alpha ;{\mathbf{k}}_j}^{(j)}-\sum _{\beta =1}^{s_1}\sum _{\mathbf{l}}{P}_{\beta ;\mathbf{l}}^{(\alpha ;\mathbf{k})}{\mathbf{e}}_{\beta ;\mathbf{l}}^{(j)}.$$

An important consequence of our construction is that it allows us to bound certain homological invariants of the submodule U in terms of data easily read off from the resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$. Note, however, that in contrast to the situation in [14] where the resolution induced by a Pommaret basis was considered, we obtain indeed only bounds, whereas a Pommaret basis gives directly the exact values of the invariants.

Corollary 1.

In the situation of Theorem 2, define

$$d=min\left\{k\mid \exists j:{\beta }_{0,j}^{(k)}>0\right\},q=deg({\mathcal{B}}^{(0)})=max\left\{deg(\mathbf{h})\mid \mathbf{h}\in {\mathcal{B}}^{(0)}\right\}.$$

Then we obtain the following bounds for the projective dimension, the Castelnuovo-Mumford regularity and the depth, respectively, of the submodule U:

$$pd(U)\le n+1-d,reg(U)\le q,depth(U)\ge d.$$

Proof. 

The first estimate follows immediately from the resolution (6) induced by the resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ of U. The last estimate is a simple consequence of the first one and the graded form of the Auslander-Buchsbaum formula ([18], Ex. 19.8). By construction, the module ${\mathrm{Syz}}_i({\mathcal{B}}^{(0)})$ is generated by syzygies of degree less than or equal to $q+i$. Hence U is q-regular which implies by definition the second estimate. ☐

Remark 2.

If one takes a closer look at the construction of the resolving decomposition $({\mathcal{B}}^{(1)},hm({\mathcal{B}}^{(1)}),X_{{\mathcal{B}}^{(1)}},{\prec }_{{\mathcal{B}}^{(1)}})$ of $\mathrm{Syz}({\mathcal{B}}^{(0)})$ provided in Theorem 1, then one notices that ${\mathcal{B}}^{(1)}$ is always a Janet basis of $\mathrm{Syz}({\mathcal{B}}^{(0)})$ for the order ${\prec }_{{\mathcal{B}}^{(0)}}$. This follows simply from the fact that the way in which we choose in Theorem 1 the multiplicative variables for $(B^{(1)},hm(B^{(1)}),X_{B^{(1)}},{\prec }_{B^{(1)}})$ is inspired by the definition of the Janet division. Thus, if the resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ stems from a Pommaret or a Janet basis, then all the resolving decompositions $(B^{(i)},hm(B^{(i)}),X_{B^{(i)}},{\prec }_{B^{(i)}})$ are actually also induced by Pommaret or Janet bases for a Schreyer order.

Gerdt [19] introduced a new involutive division called alex, since it is based on the anti degree lexicographic order (a local term order for which terms of higher degree are always smaller than those of lower degree). It is easy to see that a Janet basis which only consists of variables defines also an involutive basis for the alex division. Hence, the same assertions are true for resolving decompositions induced by alex bases.

Such observations already demonstrate some advantages of the introduction of such a general framework, like resolving decomposition. In our previous works on the free resolutions induced by an involutive basis, we always needed the assumption that the used involutive division L is of Schreyer type to ensure that our construction yields at each step again an L-involutive basis for the syzygy module for a suitable Schreyer order. The construction in Theorem 1 always yields a Janet basis for $\mathrm{Syz}({\mathcal{B}}^{(0)})$, as in a resolving decomposition we can choose the head terms and the multiplicative variables as we like. This allows us to extend the results of [14] to involutive bases for arbitrary involutive divisions (not necessarily of Schreyer type), provided the L-graph of the L-involutive basis is acyclic (which is guaranteed for continuous division). Note that, in contrast to the old approach, the here presented construction will not necessarily lead to an L-involutive basis for each syzygy module, but for most applications this fact is irrelevant.

4. Explicitly Determining the Differentials

As in the previous section, let ${𝒫}_{{\mathbf{d}}_0}^m$ be a graded free module with free generators ${\mathbf{e}}_1^{(0)},\dots {\mathbf{e}}_m^{(0)}$ and a grading defined by the vector ${\mathbf{d}}_0=(d_1^{(0)},\dots d_m^{(0)})$. We will always work with a finitely generated graded submodule $U\subset {𝒫}_{{\mathbf{d}}_0}^m$ with a resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ where ${\mathcal{B}}^{(0)}=\{{\mathbf{h}}_1,\dots ,{\mathbf{h}}_{s_1}\}$.

While Theorem 2 provides us with the shape of the induced resolution 6, we cannot obtain explicit expressions for the differentials in the resolution. As discussed above, we only now the head term of each higher syzygy. Our goal in this section is to derive such explicit fomulae. We first describe the complex underlying the resolution (6) in a different manner. For this purpose, we introduce two free $𝒫$-modules, $\mathcal{W}={⨁}_{\alpha =1}^{s_1}𝒫{\mathbf{w}}_{\alpha }$ and $\mathcal{V}={⨁}_{i=0}^n𝒫{\mathbf{v}}_i$, the ranks of which are determined by the size of the resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ and by the number of variables in the polynomial ring $𝒫$, respectively. Then we set ${\mathcal{C}}_i=\mathcal{W}{\otimes }_{𝒫}{\mathsf{\Lambda }}_i\mathcal{V}$ where ${\mathsf{\Lambda }}_{•}$ denotes the exterior product. A $𝒫$-linear basis of ${\mathcal{C}}_i$ is provided by the elements ${\mathbf{w}}_{\alpha }\otimes {\mathbf{v}}_{\mathbf{k}}$ where ${\mathbf{v}}_{\mathbf{k}}={\mathbf{v}}_{k_1}\wedge \cdots \wedge {\mathbf{v}}_{k_i}$ for an ordered sequence $\mathbf{k}=(k_1,\dots ,k_i)$ with $0\le k_1<\cdots <k_i\le n$. Then the free subcomplex ${\mathcal{S}}_{•}\subset {\mathcal{C}}_{•}$ generated by all elements ${\mathbf{w}}_{\alpha }\otimes {\mathbf{v}}_{\mathbf{k}}$ with $\mathbf{k}\subseteq {\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })$ corresponds to (6), if we identify ${\mathbf{e}}_{\alpha ;\mathbf{k}}^{(i+1)}\leftrightarrow {\mathbf{w}}_{\alpha }\otimes {\mathbf{v}}_{\mathbf{k}}$. Let $k_{i+1}\in {\overline{X}}_{{\mathcal{B}}^0}({\mathbf{h}}_{\alpha })\backslash \mathbf{k}$, then the differential comes from (7),

$$d_{\mathcal{S}}({\mathbf{w}}_{\alpha }\otimes {\mathbf{v}}_{\mathbf{k},k_{i+1}})=x_{k_{i+1}}{\mathbf{w}}_{\alpha }\otimes {\mathbf{v}}_{\mathbf{k}}-\sum _{\beta ,\mathbf{l}}{P}_{\beta ;\mathbf{l}}^{(\alpha ;\mathbf{k},k_{i+1})}{\mathbf{w}}_{\beta }\otimes {\mathbf{v}}_{\mathbf{l}},$$

and thus requires the explicit determination of all the higher syzygies (7).

We will now present a method to directly compute the differential without computing higher syzygies. It extends a construction of Sköldberg [10] using algebraic discrete Morse theory [3,4] and generalises our results in [1,6] for the resolution induced by a Pommaret or a Janet basis.

Definition 2.

The graded submodule U possesses head linear syzygies, if it has a finite presentation

$$0⟶ker\eta ⟶\mathcal{W}=\underset{\alpha =1}{\overset{s}{⨁}}𝒫{\mathbf{w}}_{\alpha }\stackrel{\eta }{⟶}U⟶0$$

(8)

such that $ker\eta$ can be generated by a finite set $\mathscr{H}=\{{\mathbf{h}}_1,\dots ,{\mathbf{h}}_t\}$ where one can choose for each generator ${\mathbf{h}}_{\alpha }\in \mathscr{H}$ a head module term $hm({\mathbf{h}}_{\alpha })$ of the form $x_i{\mathbf{w}}_{\alpha }$.

Sköldberg’s construction begins with the following two-sided Koszul complex $(\mathcal{F},d_{\mathcal{F}})$ defining a free resolution of U. Let V be a $\mathbb{k}$-linear space with basis $\{{\mathbf{v}}_0,\dots ,{\mathbf{v}}_n\}$ and introduce the free $𝒫$-module ${\mathcal{F}}_j=𝒫{\otimes }_{\mathbb{k}}{\mathsf{\Lambda }}_{j}V{\otimes }_{\mathbb{k}}U$. Any $\mathbb{k}$-linear basis $\{m_a\mid a\in A\}$ of U induces a $𝒫$-linear basis of ${\mathcal{F}}_j$ consisting of all elements of the form $1\otimes v_{\mathbf{k}}\otimes m_a$ with ordered sequences $\mathbf{k}$ of length j. The differential $d_{\mathcal{F}}$ of the two-sided Koszul complex $\mathcal{F}$ is now defined as

$$d_{\mathcal{F}}(1\otimes {\mathbf{v}}_{\mathbf{k}}\otimes m_a)=\sum _{i=1}^j{(-1)}^{i+1}\left(x_{k_i}\otimes {\mathbf{v}}_{{\mathbf{k}}_i}\otimes m_a-1\otimes {\mathbf{v}}_{{\mathbf{k}}_i}\otimes x_{k_i}{m}_a\right).$$

(9)

Note that the second term on the right hand side is not yet expressed in the chosen $\mathbb{k}$-linear basis of U and that this resolution is generally of infinite size, as the index set A is almost always infinite. For notational simplicity, we will drop in the sequel the tensor sign ⊗ and leading factors 1 when writing elements of ${\mathcal{F}}_{•}$.

Sköldberg uses a specialisation of head linear terms. He requires that for a given term order ≺ the leading module of $ker\eta$ in the presentation (8) must be generated by terms of the form $x_i{\mathbf{w}}_{\alpha }$. In this case, he says that U has initially linear syzygies. Our definition is term order free. Furthermore, Sköldberg considered exclusively the case that the presentation (8) is minimal. However, this represents a severe restriction, as the existence of such presentations cannot be guaranteed. As his construction needs this restriction only to ensure that the final resolution is minimal, we have dropped it.

For a module U with head linear syzygies via a presentation (8), we now construct a finite resolution $(\mathcal{G},d_{\mathcal{G}})$ via a Morse matching. We call the variables

$$crit({\mathbf{w}}_{\alpha })=\{x_j\mid x_j{\mathbf{w}}_{\alpha }\in hm(\mathscr{H})\},$$

where $\mathscr{H}$ is chosen as in Definition 2, critical for the generator ${\mathbf{w}}_{\alpha }$; the remaining non-critical ones are contained in the set $ncrit({\mathbf{w}}_{\alpha })$. Then a $\mathbb{k}$-linear basis of U is given by all elements $x^{\mu }{\mathbf{h}}_{\alpha }$ with ${\mathbf{h}}_{\alpha }=\eta ({\mathbf{w}}_{\alpha })$ and $x^{\mu }\in \mathbb{k}[ncrit({\mathbf{w}}_{\alpha })]$. Following [4], we define ${\mathcal{G}}_j\subseteq {\mathcal{F}}_j$ as the free submodule generated by those vertices ${\mathbf{v}}_{\mathbf{k}}{\mathbf{h}}_{\alpha }$ where the ordered sequences $\mathbf{k}$ are of length j and such that every entry $k_i$ is critical for ${\mathbf{w}}_{\alpha }$. In particular $\mathcal{W}\cong {\mathcal{G}}_0$ with an isomorphism induced by ${\mathbf{w}}_{\alpha }\mapsto {\mathbf{v}}_{\varnothing }{\mathbf{h}}_{\alpha }$.

The description of the differential $d_{\mathcal{G}}$ is based on reduction paths in the associated Morse graph (for a detailed treatment of these notions, see [1,3,4]) and expresses the differential as a triple sum. If we assume that, after expanding the right hand side of (9) in the chosen $\mathbb{k}$-linear basis of U, the differential of the complex ${\mathcal{F}}_{•}$ can be expressed as

$$d_{\mathcal{F}}({\mathbf{v}}_{\mathbf{k}}{\mathbf{h}}_{\alpha })=\sum _{\mathbf{m},\mu ,\gamma }{Q}_{\mathbf{m},\mu ,\gamma }^{\mathbf{k},\alpha }{\mathbf{v}}_{\mathbf{m}}(x^{\mu }{\mathbf{h}}_{\gamma }),$$

then $d_{\mathcal{G}}$ is defined by

$$d_{\mathcal{G}}({\mathbf{v}}_{\mathbf{k}}{\mathbf{h}}_{\alpha })=\sum _{\mathbf{l},\beta }\sum _{\mathbf{m},\mu ,\gamma }\sum _p{\rho }_p\left(Q_{\mathbf{m},\mu ,\gamma }^{\mathbf{k},\alpha }{\mathbf{v}}_{\mathbf{m}}(x^{\mu }{\mathbf{h}}_{\gamma })\right)$$

(10)

where the first sum ranges over all ordered sequences $\mathbf{l}$ which consists entirely of critical indices for ${\mathbf{w}}_{\beta }$. Moreover, the second sum may be restricted to all values such that a polynomial multiple of ${\mathbf{v}}_{\mathbf{m}}(x^{\mu }{\mathbf{h}}_{\gamma })$ effectively appears in $d_{\mathcal{F}}({\mathbf{v}}_{\mathbf{k}}{\mathbf{h}}_{\alpha })$ and the third sum ranges over all reduction paths p going from ${\mathbf{v}}_{\mathbf{m}}(x^{\mu }{\mathbf{h}}_{\gamma })$ to ${\mathbf{v}}_{\mathbf{l}}{\mathbf{h}}_{\beta }$. Finally ${\rho }_p$ is the reduction associated with the reduction path p satisfying

$${\rho }_p\left({\mathbf{v}}_{\mathbf{m}}(x^{\mu }{\mathbf{h}}_{\gamma })\right)=q_p{\mathbf{v}}_{\mathbf{l}}{\mathbf{h}}_{\beta }$$

for some polynomial $q_p\in 𝒫$.

Remark 3.

The explicit formula (10) with its complicated summation ranges obviously looks rather cumbersome and does not appear to be very useful for practical purposes. However, this first impression is misleading. In fact, (10) can be well exploited both theoretically and computationally. As shown by theCoCoALibimplementations described in [1,6], it is for a computer rather straightforward to evaluate (10) for any concrete submodule U. Moreover, the most valuable feature of (10) is that it provides an explicit expression for each entry in the differential which is independent of all other entries of the differential. This observation will be the key for the efficient determination of Betti numbers (even individual ones).

In the sequel, we will show that for a finitely generated graded module U with resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ the resolution constructed by Sköldberg’s method is isomorphic to the resolution which is induced by the resolving decomposition, if we choose the head linear syzygies properly. Firstly, we obtain the following trivial assertion.

Lemma 5.

If the graded submodule $U\subseteq {𝒫}_{{\mathbf{d}}_0}^{s_1}$ possesses a resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$, then it has head linear syzygies. More precisely, we can set $crit({\mathbf{w}}_{\alpha })={\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })$, i.e., the critical variables of the vector ${\mathbf{w}}_{\alpha }$ are simply the non-multiplicative variables of the generator ${\mathbf{h}}_{\alpha }=\eta ({\mathbf{w}}_{\alpha })$.

We will subsequently apply some lemmata from [1]. In this reference, they are formulated only for the special case that the resolution is induced by a Pommaret basis. Nevertheless, if not explicitly stated otherwise, we can still use them in our more general setting, as their proofs remain correct also for arbitrary resolving decompositions. This is due to the fact that the proofs only require the existence of unique standard representations and a separation of the variables into multiplicative and non-multiplicative ones. In some proofs, the notion of the class of a generator in ${\mathcal{B}}^{(0)}$ appears. As already mentioned above, it is used to assign multiplicative variables for the Pommaret division. When working with an arbitrary resolving decomposition, one must simply substitute it by the maximal index of a multiplicative variable of the considered generator.

We could see above that the explicit description of the differential $d_{\mathcal{G}}$ is based on reduction paths in the associated Morse graph. We now take a closer look at them and their properties. Any reduction path can be decomposed into so-called elementary ones which are always of length two. One can distinguish three different types of elementary reductions paths ([1], Section 4). Those of type 0 are irrelevant ([1], Lemma 4.5); the other ones have the form

$${\mathbf{v}}_{\mathbf{k}}(x^{\mu }{\mathbf{h}}_{\alpha })⟶{\mathbf{v}}_{\mathbf{k}\cup i}(\frac{x^{\mu }}{x_i}{\mathbf{h}}_{\alpha })⟶{\mathbf{v}}_{\mathbf{l}}(x^{\nu }{\mathbf{h}}_{\beta }).$$

Here $\mathbf{k}\cup i$ denotes the ordered sequence arising when i is inserted into the sequence $\mathbf{k}$; likewise $\mathbf{k}\backslash i$ stands for the sequence obtained by removing an index $i\in \mathbf{k}$. Now we distinguish two further types of elementary reduction paths depending on the form of the associated reduction.

Type 1:

This is the case where $\mathbf{l}=(\mathbf{k}\cup i)\backslash j$, $x^{\nu }=\frac{x^{\mu }}{x_i}$ and $\beta =\alpha$. Note that it is allowed that $i=j$. We define $ϵ(i;\mathbf{k})={(-1)}^{|\{j\in \mathbf{k}\mid j>i\}|}$. Then the corresponding reduction is

$$\rho ({\mathbf{v}}_{\mathbf{k}}{x}^{\mu }{\mathbf{h}}_{\alpha })=ϵ(i;\mathbf{k}\cup i)ϵ(j;\mathbf{k}\cup i)x_j{\mathbf{v}}_{(\mathbf{k}\cup i)\backslash j}\left(\frac{x^{\mu }}{x_i}{\mathbf{h}}_{\alpha }\right).$$

Type 2:

In this case $\mathbf{l}=(\mathbf{k}\cup i)\backslash j$ and the term $x^{\nu }{\mathbf{h}}_{\beta }$ appears in the involutive standard representation of the product $\frac{x^{\mu }{x}_j}{x_i}{\mathbf{h}}_{\alpha }$ with the coefficient ${\lambda }_{j,i,\alpha ,\mu ,\nu ,\beta }\in \mathbb{k}$. By the construction of the Morse matching, we now always find $i\ne j$. The corresponding reduction is

$$\rho ({\mathbf{v}}_{\mathbf{k}}{x}^{\mu }{\mathbf{h}}_{\alpha })=-ϵ(i;\mathbf{k}\cup i)ϵ(j;\mathbf{k}\cup i){\lambda }_{j,i,\alpha ,\mu ,\nu ,\beta }{\mathbf{v}}_{(\mathbf{k}\cup i)\backslash j}(x^{\nu }{\mathbf{h}}_{\beta }).$$

This case distinction comes from the differential (9). Summands appearing in it possess one of the following two possible forms: $x_{k_i}{\mathbf{v}}_{{\mathbf{k}}_i}{m}_a$ or ${\mathbf{v}}_{{\mathbf{k}}_i}(x_{k_i}{m}_a)$. Each of these summands corresponds to a directed edge in the Morse graph ${\mathsf{\Gamma }}_{{\mathcal{F}}_{•}}^A$. Consider now an elementary reduction path

$${\mathbf{v}}_{\mathbf{k}}(x^{\mu }{\mathbf{h}}_{\alpha })⟶{\mathbf{v}}_{\mathbf{k}\cup i}\left(\frac{x^{\mu }}{x_i}{\mathbf{h}}_{\alpha }\right)⟶{\mathbf{v}}_{\mathbf{l}}(x^{\nu }{\mathbf{h}}_{\beta }).$$

If the second edge starts at a summand of the first resp. second form, then the elementary reduction path is of type 1 resp. type 2.

For the proof of the existence of an isomorphism relating the resolution induced by a resolving decomposition to the resolution constructed via the above outlined method of Sköldberg, we recall a well-known result about the uniqueness of free resolutions.

Theorem 3.

([20], Theorem 1.6) Let U be a finitely generated graded $𝒫$-module. If $\mathcal{F}$ is the graded minimal free resolution of U and $\mathcal{G}$ an arbitrary graded free resolution of U, then $\mathcal{G}$ is isomorphic to the direct sum of $\mathcal{F}$ and a trivial complex.

Theorem 4.

Let $U\subset {𝒫}_{\mathbf{d}}^m$ be a graded submodule. The graded free resolution $\mathcal{F}$ induced by a resolving decomposition $({\mathcal{B}}^{(0)},hm({\mathcal{B}}^{(0)}),X_{{\mathcal{B}}^{(0)}},{\prec }_{{\mathcal{B}}^{(0)}})$ of U and the graded free resolution $\mathcal{G}$ obtained by the method of Sköldberg in the case that the head linear syzygies have been chosen in such a way that $crit({\mathbf{h}}_{\alpha })={\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })$ for every generator ${\mathbf{h}}_{\alpha }\in {\mathcal{B}}^{(0)}$ are isomorphic.

Proof. 

It is not difficult to see that bases for the free modules in the resolution $\mathcal{G}$ constructed by Sköldberg’s method consists of those generators ${\mathbf{v}}_{\mathbf{k}}{\mathbf{h}}_{\alpha }$ with $x_k\in {\overline{X}}_{{\mathcal{B}}^{(0)}}({\mathbf{h}}_{\alpha })$ for all indices k contained in $\mathbf{k}$. In the discussion following the proof of Theorem 2, we showed that bases for the modules in the resolution $\mathcal{F}$ coming from the resolving decomposition are induced by the syzygies ${\mathbf{S}}_{\alpha ,\mathbf{k}}$ and are thus of the same cardinality. Hence, the two resolutions considered possess the same shape, meaning that the homogeneous components of the contained free modules satisfy ${dim}_{\mathbb{k}}{({\mathcal{F}}_i)}_j={dim}_{\mathbb{k}}{({\mathcal{G}}_i)}_j$. The made assertion is now a trivial consequence of Theorem 3. ☐

This proof already indicates that the two considered resolutions actually possess very similar differentials. To deepen the comparison of the resolutions a bit more, we now recall a few further simple observations made in [1]. It turns out that in the resolution $\mathcal{G}$ we may always choose as head module terms for the higher syzygies exactly the same terms that appear as head module terms in the resolving decompositions $({\mathcal{B}}^{(i)},hm({\mathcal{B}}^{(i)}),X_{{\mathcal{B}}^{(i)}},{\prec }_{{\mathcal{B}}^{(i)}})$. In the case that we start with a resolving decomposition induced by an involutive bases and then obtain involutive bases for all syzygy modules (recall Remark 2), this entails that Sköldberg’s method also actually constructs involutive bases.

Lemma 6.

([1], Lemma 4.3) Given an index i such that $x_i\in crit({\mathbf{h}}_{\alpha })$, let $x_i{\mathbf{h}}_{\alpha }={\sum }_{\beta =1}^{s_1}{P}_{\beta }^{(\alpha ;i)}{\mathbf{h}}_{\beta }$ be the standard representation. Then we have $d_{\mathcal{G}}({\mathbf{v}}_i{\mathbf{h}}_{\alpha })=x_i{\mathbf{v}}_{\varnothing }{\mathbf{h}}_{\alpha }-{\sum }_{\beta =1}^{s_1}{P}_{\beta }^{(\alpha ;i)}{\mathbf{v}}_{\varnothing }{\mathbf{h}}_{\beta }$.

Our next statement may be interpreted in the following way. Assume that we choose in the Morse graph a vertex ${\mathbf{v}}_i(x^{\mu }{\mathbf{h}}_{\alpha })$ having certain properties and then follow all possible reduction paths starting at it. Then we will never reach a point where it becomes necessary to calculate a standard representation. Assume furthermore that the chosen vertex possesses no critical (i.e., non-multiplicative) variables. Then no such variables will arise while we follow a reduction path. If we want to generalise this statement to higher homological degrees, then we must only replace the index conditions $x_i\in ncrit({\mathbf{h}}_{\alpha })$ and $x_j\in ncrit({\mathbf{h}}_{\beta })$ by the conditions $x_k\in ncrit({\mathbf{h}}_{\alpha })$ and $x_{\ell }\in ncrit({\mathbf{h}}_{\beta })$ for all indices k and ℓ contained in the ordered sequences $\mathbf{k}$ and $\mathbf{l}$, respectively.

Lemma 7.

([1], Lemma 4.4) Assume that $\{x_i\}\cup supp(x^{\mu })\subseteq ncrit({\mathbf{h}}_{\alpha })$. Then for any reduction path $p={\mathbf{v}}_i(x^{\mu }{\mathbf{h}}_{\alpha })\to \dots \to {\mathbf{v}}_j(x^{\nu }{\mathbf{h}}_{\beta })$ we have $x_j\in ncrit({\mathbf{h}}_{\beta })$. In particular, in this situation there is no reduction path $p={\mathbf{v}}_i(x^{\mu }{\mathbf{h}}_{\alpha })\to \dots \to {\mathbf{v}}_k{\mathbf{h}}_{\beta }$ with $x_k\in crit({\mathbf{h}}_{\beta })$.

Our final corollary now asserts that we can indeed choose in the resolution $\mathcal{G}$ head module terms in such a way that there is a one-to-one correspondence to the head module terms in the resolution $\mathcal{F}$. It is a direct consequence of Lemma 7 and provides us with an alternative explicit proof of Theorem 4.

Corollary 2.

Let $\mathbf{k}=(k_1,\dots ,k_j)$ with $x_{k_i}\in crit{\mathbf{h}}_{\alpha }$ for all i, then

$$x_{k_l}{\mathbf{v}}_{\mathbf{k}\backslash k_l}{\mathbf{h}}_{\alpha }\in supp(d_{\mathcal{G}}({\mathbf{v}}_{\mathbf{k}}{\mathbf{h}}_{\alpha })).$$

5. Conclusions

In this article, we introduced a framework that provides many different types of bases of graded polynomial submodules with an effective syzygy theory. The key is less the properties of the bases themselves and more the combinatorial decompositions induced by them via the choice of head terms and multiplicative variables. Effectivity is guaranteed through the required term order.

Given any basis that induces a resolving decomposition in the sense of Definition 1, we obtain with Theorem 1 a generalised version of the classical Schreyer theorem and iteration leads to a free resolution. One should, however, note the following crucial difference. The classical Schreyer theorem yields only “in principle” a resolution; without actually performing the computations required for every iteration step, no information about the final resolution can be obtained. By contrast, Theorem 2 describes already the full shape of the final resolution based only on the resolving decomposition of the given submodule. Thus we could give (usually quite sharp) bounds for important homological invariants in Corollary 1. In fact, the numbers $r_{i,j}$ given in Theorem 2 can also be interpreted as upper bounds for the Betti numbers.

In [1], we showed that with the help of Pommaret bases Sköldberg’s method for the construction of an explicit resolution can be made fully effective and then yields essentially the same resolution, as the one induced by the Pommaret basis. In Section 4, we extended these results to arbitrary resolving decompositions and thus provided an approach for the explicit computation of free resolutions based on such a decomposition.

In [1,6], we presented a method to effectively compute graded Betti numbers via the induced free resolutions of Janet and Pommaret bases and the method of Sköldberg. It is well-known that one needs only the constant part of an arbitrary free resolution to determine the Betti numbers via linear algebra over the field $\mathbb{k}$. We showed that the method of Sköldberg allows us to compute directly only this constant part instead of the whole resolution which drastically improves the complexity of such a computation. With this approach, it is even possible to determine a single Betti number without computing the complete constant part of the free resolution. The reason for this is that Sköldberg’s formula allows us to compute any entry of a differential in the free resolution independently of the rest of the free resolution. Furthermore, the theorem about the induced free resolution gives us a formula to compute the ranks of any homogeneous component appearing in the resolution. These methods are also applicable for an arbitrary resolving decomposition due to the fact that we proved Theorem 2 and the form of the differential (10).