Computing Eccentricity Based Topological Indices of Octagonal Grid
O
n
m
Abstract
:1. Introduction
2. Methods
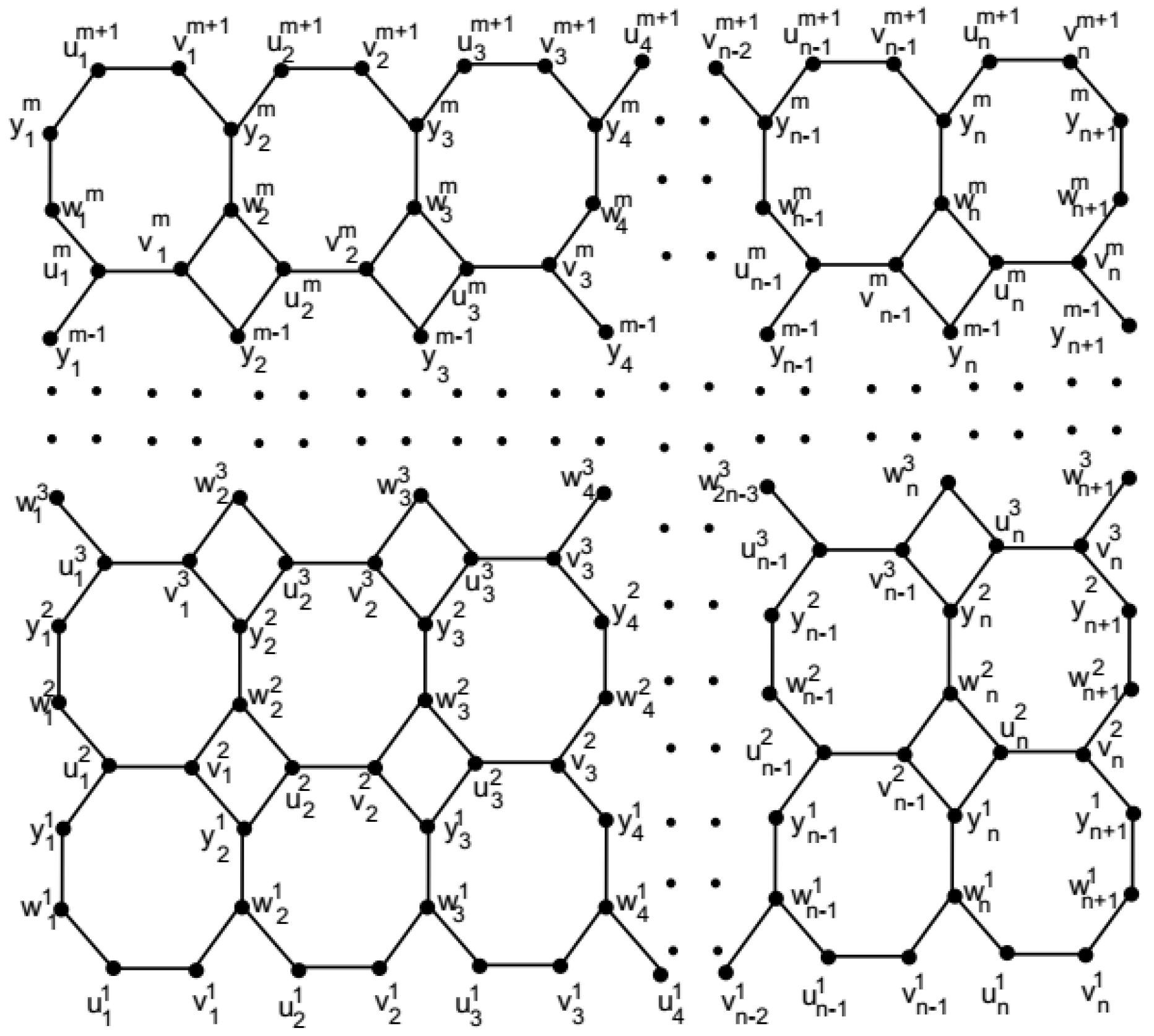
3. The Octagonal Grid
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wiener, H. Correlation of heat of isomerization and difierence in heat of vaporization of isomers among paran hydrocaibons. J. Am. Chem. Soc. 1947, 69, 2636–2638. [Google Scholar] [CrossRef]
- Wiener, H. Influence of interatomic forces on para–n properties. J. Chem. Phys. 1947, 15, 766–767. [Google Scholar] [CrossRef]
- Wiener, H. Vapour-pressure-temperature relations among the branched para–n hydrocarbons. J. Chem. Phys. 1948, 15, 425–430. [Google Scholar] [CrossRef]
- Hosoya, H. Topological index. Newly proposed quautity characterizing the topological nature of structure of isomers of saturated hydrocarbons. Bull. Chem. Soc. Jpn. 1971, 44, 2332–2337. [Google Scholar] [CrossRef]
- Hosoya, H. Topological index as strong sorting device for coding chemical structure. J. Chem. Doc. 1972, 12, 181–183. [Google Scholar] [CrossRef]
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar]
- Došlić, T.; Saheli, M. Eccentric connectivity index of composite graphs. Util. Math. 2014, 95, 3–22. [Google Scholar]
- Gupta, S.; Singh, M.; Madan, A.K. Connective eccentricity index: A novel topological descriptor for predicting biological activity. J. Mol. Graph. Model. 2000, 18, 18–28. [Google Scholar] [CrossRef]
- Yu, G.; Qu, H.; Tang, L.; Feng, L. On the connective eccentricity index of trees and unicyclic graphs with given diameter. J. Math. Anal. Appl. 2014, 420, 1776–1786. [Google Scholar] [CrossRef]
- Huo, Y.; Liu, J.B.; Baig, A.Q.; Sajjad, W.; Farahani, M.R. Connective Eccentric Index of Nanotube. J. Comput. Theor. Nanosci. 2017, 14, 1832–1836. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Gharibi, W. On Zagreb Indices, Zagreb Polynomials of Mesh Derived Networks. J. Comput. Theor. Nanosci. 2016, 13, 8683–8688. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Imran, M.; Ahmad, A. On Zagreb indices, Zagreb polynomials of some nanostar dendrimers. Appl. Math. Comput. 2016, 280, 132–139. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K. Molecular Descriptors of Nanotube, Oxide, Silicate, and Triangulene networks. J. Chem. 2017, 2017, 1–10. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K.; Naeem, M.; Rehman, N.A. Topological Characterization of Carbon Graphite and Crystal Cubic Carbon Structures. Molecules 2017, 22, 1496. [Google Scholar] [CrossRef] [PubMed]
- Idrees, N.; Naeem, M.N.; Hussain, F.; Sadiq, A.; Siddiqui, M.K. Molecular Descriptors of Benzenoid System. Quim. Nova 2017, 40, 143–145. [Google Scholar] [CrossRef]
- Zhou, B.; Du, Z. On eccentric connectivity index. MATCH Commun. Math. Comput. Chem. 2010, 63, 181–198. [Google Scholar]
- Ghorbani, M.; Hosseinzadeh, M.A. A New Version of Zagreb Indices. Filomat 2012, 26, 93–100. [Google Scholar] [CrossRef]
- Alaeiyan, M.; Mojarad, R.; Asadpour, J. A new method for computing eccentric connectivity polynomial of an infinite family of linear polycene parallelogram benzenod. Optoelectron. Adv. Mater.-Rapid Commun. 2011, 5, 761–763. [Google Scholar]
- Diudea, M.V. Nanostructures: Novel Architecture; Nova Science Publishers: New York, NY, USA, 2005; pp. 203–242. [Google Scholar]
- Stefu, M.; Diudea, M.V. Wiener index of C4C8 nanotubes. MATCH Commun. Math. Comput. Chem. 2004, 50, 133–143. [Google Scholar]
- Siddiqui, M.K.; Naeem, M.; Rahman, N.A.; Imran, M. Computing topological indices of certain networks. J. Optoelctron. Adv. Mater. 2016, 18, 884–892. [Google Scholar]
- Siddiqui, M.K.; Miller, M.; Ryan, J. Total edge irregularity strength of octagonal grid graph. Util. Math. 2017, 103, 277–287. [Google Scholar]
| Representative | Degree | Eccentricity | Range | Frequency |
|---|---|---|---|---|
| 2 | , | |||
| 2 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| Representative | Degree | Eccentricity | Range | Frequency |
|---|---|---|---|---|
| 2 | , | |||
| 2 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
| 3 | , | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Siddiqui, M.K.; Naeem, M.; Baig, A.Q.
Computing Eccentricity Based Topological Indices of Octagonal Grid
Zhang X, Siddiqui MK, Naeem M, Baig AQ.
Computing Eccentricity Based Topological Indices of Octagonal Grid
Zhang, Xiujun, Muhammad Kamran Siddiqui, Muhammad Naeem, and Abdul Qudair Baig.
2018. "Computing Eccentricity Based Topological Indices of Octagonal Grid
Zhang, X., Siddiqui, M. K., Naeem, M., & Baig, A. Q.
(2018). Computing Eccentricity Based Topological Indices of Octagonal Grid





