Accounting Games: Using Matrix Algebra in Creating the Accounting Models

Abstract

The aim of this paper is to show the mathematical basis for a precise treatment of double-entry bookkeeping, which was first developed in the nineteenth century by Sir William Rowan Hamilton. This is done by using basic notions of matrix algebra founded on the idea of ordered pairs. We also reveal how complex numbers and rationals (fractions) developed in mainstream accounting science and became a leading platform for the ongoing processes within Industry 4.0. The paper concludes with examples of how accounting operations can be represented by matrix equations with the result of generating a final report. The author presents a mathematical model of accounting which is independent of specific existential forms, but which is capable of undertaking the form of any of them and thus which has the potential of being understood and accepted by specialists globally.

1. Introduction

The research published by Ellerman [1] highlighted the significance of mathematics in double-entry bookkeeping and noted the absence of relevant literature devoted to “the theoretical basis of a mathematical technique applied in business for over five centuries” [1]. This started a research postulate that mathematics plays a significant role in the development of accounting theory and practice. Ellerman’s study also described the suggestion by S. W. Hamilton [2] that a mathematical basis approach be used for a precise treatment of double-entry bookkeeping. Later, the research of Sangster and Scataglinibelghitar [3] addresses the evidence for the mathematical origins of accounting. An earlier review of the literature on matrix accounting was provided by Leech [4]. The publications Leech described demonstrated how accounting matrices transformed typical approaches to accounting practice. Most named publications described the convenience of using mathematics in accounting practice.

Later, Stoner and Vysotskaya [5] described the practice of teaching accounting via a form of matrix mathematics at Southern Federal University, Russia. This method provided useful insights for accounting educators on an alternative way of explaining and understanding the basics of accounting.

Appreciation of the mathematical origins and in particular the use of transaction matrices in accounting, along with technological development, has facilitated the shift towards the new economical era—Industry 4.0. New approaches to doing business require the intensive development of accounting methods for use by enterprises. In the background of these processes, the value of accounting as a tool for business communication has been enhanced. In addition, the mathematical approach to accounting suggests using typical codification that helps with information security issues.

This article starts with a comprehensive literature review of matrix accounting research, which is followed by sections describing approaches to matrix modeling and a game-based example. The paper concludes with an evaluation of the usefulness of the suggested approach.

2. Literature Review

The following are considered among the highlights of publications on the mathematical approach to double-entry bookkeeping: Luca Pacioli’s description of double-entry bookkeeping [6]; Sir William Hamilton’s presentation of the ordered-pairs treatment of complex numbers; and Arthur Cayley’s pamphlet on the mathematical origins of accounting [7]. The matrix algebra approach to accounting starts with the matrix framework for accounting introduced by Augustus De Morgan in 1846. This approach was later developed, along with the development of the PC, in relevant software which allowed accounting practice to become faster and more reliable.

Over several decades, the authors have been making attempts to apply different mathematical approaches to accounting modeling (see, for example, [2,8,9,10,11,12,13,14,15,16,17,18,19]). Most of these papers are devoted to applying matrix algebra to accounting and linking accounting practice with the matrix algebra approach.

A situational-matrix approach served as an alternative language for accounting during the process of its technological transition [16,20,21,22,23,24,25,26,27].

In his papers [20,21,22], Kolvakh especially examines the group of accounting matrix models, calling them “situational-matrix accounting”. This approach appears to be able to combine the situational (or event-driven) nature of accounting with the means of matrix algebra, and consequently serves as a prototype of a mathematical model of accounting.

Research conducted by Vysotskaya [23,27] eliminates the need for modern developments in IT and technology in accounting practice, which should be transformed accordingly, and suggests using this approach in planning practice, e.g., in tax planning.

Finally, Stoner and Vysotskaya [5] examined the relevance of the mathematical approach to accounting to teaching practice, suggesting that alternative mathematical methods of presenting transactions and reports would be useful in providing students with an understanding of accounting basics. Later research by Vysotskaya, Kolvakh and Stoner [28] treated the mathematical accounting game used in teaching a basic accounting course in Russia. This game is useful for teaching students how to understand the basics of recording business transactions through an explanation using mathematics-based algorithmic methods. This kind of competence is important and was outlined by Smirnova, Sokolov and Emmanuel [29], Sangster [3], Vysotskaya, Kolvakh and Stoner [28].

There is certain recognition of accounting teaching based on game theory, since the American Institute of Chartered Professional Accountants supports teachers in their activities in engaging, entertaining and educating high school students by launching different successful classroom teaching methods.

The increasing influence of information technology (IT) on accounting started a debate on the importance of the use of modeling in accounting. In their report [30], the leadership program of the Institute of Chartered Accountants in England and Wales’ Financial Reporting Faculty argued on the assumption that one way of relating the theory of the firm and accounting measurement is via firms’ business models. Along with stating the potential importance of the business model in non-financial reporting, the report sheds light on the potential importance of business models in both financial and non-financial reporting and defines this as a topic of emerging interest.

3. Matrix Accounting Modeling Using Blocks of Matrices

The methods of accounting modeling (from recording transactions to financial reporting) basically repeat the steps implemented in practice by using certain numerical examples. However, the variety of accounting techniques complicates the conceptualization of the accounting system. The main assumption here relates to the evidence that one of the effective tools for creating accounting models can be mathematical modeling, in particular the one which uses the basic notions and operations of matrix algebra.

By using matrix algebra, we found it possible to:

• Record transactions and present the Ledger on their basis in the form of equivalent matrices.
• Transform the initial data into Trial Balances corresponding to their equivalents in the system of matrix algebra transactions.
• Relate the opening and closing account balances by means of the basic accounting equation in matrix form.
• Determine the formulae to receive the trial Balance.
• Determine a matrix model as a system of equivalents of the data presented by corresponding Trial Balances.

The foundations of the system considered below are the well-known categories of accounting such as correspondence of accounts and accounting entry. In this paper they are not defined in conventional terms, but are represented as mathematical concepts and operations of matrix algebra (Vysotskaya and Aleshin, 2013). We provide these definitions below.

Definition 1.

The correspondence matrix is a square matrix E(X,Y) with the dimensions m x m, where the point of intersection of the debit of account X and the credit of account Y is equal to 1, with other matrix elements equal to zero. Thus, the matrix-correspondence is indicated as E(X,Y), and its non-zero elements are always equal to 1 (E(X,Y) = 1).

Definition 2.

The entry matrix represents its connection with the sum of transaction by a correspondence matrix, as follows:

M (X,Y) = S_x,y · E(X,Y).

(1)

The represented definitions of the correspondence matrix and entry matrix are here axioms which provide the foundations of further conceptual theory of matrix accounting. Here we use them as a basis for mathematical constructions with the elements of matrix algebra. Further, we obtain formulae to receive the Ledger Matrix (LM), as follows:

$$\mathbf{L}\mathbf{M}={\displaystyle \sum _{i=1}^n{S}_i}\cdot E(X_i,Y_i)\begin{array}{c}\\ \end{array}$$

(2)

where i is the number of the entry in the journal, S_i is the sum of transactions corresponding to entry i, and E(X_i,Y_i) is a correspondence matrix referring to the entry i.

The formula of the Matrix of Debit Turnovers (MDT) is obtained from the Ledger Matrix (LM), as follows:

$$MDT={\displaystyle \sum _{X=c_1}^{c_m}}{\displaystyle \sum _{Y=c_1}^{c_m}{S}_{X,Y_{}}}\cdot E(X,Y_{})\begin{array}{c}\\ \end{array}$$

(3)

Here $S_{X,Y}={\displaystyle \sum _{i_{XY}=1}^{n_{X,Y}}{S}_{i_{XY}}}$ is the total sum of the transaction referred to the given correspondence of accounts X,Y. In this case, ${\displaystyle \sum _{X=c_1}^{c_m}}{\displaystyle \sum _{Y=c_1}^{c_m}{n}_{XY}}=n$, where n represents the total number of the entries in the Ledger (the total of $n_{XY}$ of similar X,Y). The correspondence of accounts is equal to the total number of entries n in the Ledger.

The formula for the Matrix of Credit Turnovers (MCT) is a transposed matrix MDT, as follows:

$$MCT=MD{T}^{\text{'}}= {\displaystyle \sum }_{Y=C_1}^{C_m}·{\displaystyle \sum }_{X=C_1}^{C_m}{S}_{X,Y}·E\left(Y,X\right)$$

(4)

Here X,Y = c₁, c₂, …, c_m are accounting symbols used to represent the matrix model of an accounting system, where $S_{X,Y}={\displaystyle \sum _{i_{XY}=1}^{n_{X,Y}}{S}_{i_{XY}}}$ is the total sum of the transaction referred to the accounts X,Y. In this case, ${\displaystyle \sum _{X=c_1}^{c_m}}{\displaystyle \sum _{Y=c_1}^{c_m}{n}_{XY}}=n$, where n is the total number of entries in the Ledger.

Here, an example for the Trial Balance in the form of “assets-liabilities-capital” grouping (ALC blocks) is represented as a Matrix of Trial Balance (MTB) and is structured as a block of matrices that consists of nine types of the blocks of matrices, as follows:

• AA—the matrix of “assets-assets” transactions;
• AL—the matrix of “assets-liabilities” transactions;
• LA—the matrix of “liabilities- assets” transactions;
• LL—the matrix of “liabilities-liabilities” transactions;
• CA—the matrix of “capital-assets” transactions;
• CC—the matrix of “capital-capital” transactions.

The basic equation of the Trial Balance (MTB) using the ALC-grouping is represented as follows. (Here the “0” subscript sign means the beginning of the period t − 1 = 0, the “1” sign means the end of the period t = 1.):

$$\begin{array}{c}\mathrm{MTB}=\left(\begin{array}{ccc}\Delta A{A}_0& \Delta A{L}_0& \Delta A{C}_0\\ \Delta L{A}_0& \Delta L{L}_0& \Delta L{C}_0\\ \Delta C{A}_0& \Delta C{L}_0& \Delta C{C}_0\end{array}\right)+\left(\begin{array}{ccc}AA& AL& AC\\ LA& LL& LC\\ CA& CL& LL\end{array}\right)-\left(\begin{array}{ccc}A{A}^{\prime }& L{A}^{\prime }& C{A}^{\prime }\\ A{L}^{\prime }& L{L}^{\prime }& C{L}^{\prime }\\ A{C}^{\prime }& L{C}^{\prime }& C{C}^{\prime }\end{array}\right)=\\ \left(\begin{array}{ccc}\Delta A{A}_1& \Delta A{L}_1& \Delta A{C}_1\\ \Delta L{A}_1& \Delta L{L}_1& \Delta L{C}_1\\ \Delta C{A}_1& \Delta C{L}_1& \Delta C{C}_1\end{array}\right)\end{array}$$

(5)

By multiplying MTB on the corresponding block vector e, the equation of the General Ledger appears:

$$\left(\begin{array}{c}\Delta a_0\\ \Delta l_0\\ \Delta c_0\end{array}\right)+\left(\begin{array}{ccc}AA& AL& AC\\ LA& LL& LC\\ CA& CL& LL\end{array}\right)*\left(\begin{array}{c}{e}_A\\ e_L\\ e_C\end{array}\right)-\left(\begin{array}{ccc}A{A}^{\prime }& L{A}^{\prime }& C{A}^{\prime }\\ A{L}^{\prime }& L{L}^{\prime }& C{L}^{\prime }\\ A{C}^{\prime }& L{C}^{\prime }& C{C}^{\prime }\end{array}\right)*\left(\begin{array}{c}{e}_A\\ e_L\\ e_C\end{array}\right)=\left(\begin{array}{c}\Delta a_1\\ \Delta l_1\\ \Delta c_1\end{array}\right)$$

(6)

Further, we provide the Trial Balance equation, as follows:

$$\left(\begin{array}{c}\Delta a_0\\ \Delta l_0\\ \Delta c_0\end{array}\right)+\left(\begin{array}{ccc}aa+& al+& ac\\ la+& ll+& lc\\ ca+& cl+& cc\end{array}\right)-\left(\begin{array}{ccc}a{a}^{\text{'}}& a{l}^{\text{'}}& a{c}^{\text{'}}\\ l{a}^{\text{'}}& l{l}^{\text{'}}& l{c}^{\text{'}}\\ c{a}^{\text{'}}& c{l}^{\text{'}}& c{c}^{\text{'}}\end{array}\right)=\left(\begin{array}{c}\Delta a_1\\ \Delta l_1\\ \Delta c_1\end{array}\right)$$

(7)

From Equation (7) we can take the Trial Balance matrix with a certain structural change, as follows:

$$\left(\begin{array}{c}aa\\ ll\\ cc\end{array}\right)-\left(\begin{array}{c}a{a}^{\text{'}}\\ l{l}^{\text{'}}\\ c{c}^{\text{'}}\end{array}\right)=\left(\begin{array}{c}\Delta a_{aa}\\ \Delta l_{ll}\\ \Delta c_{cc}\end{array}\right)$$

(8)

Thus, with modification, Equation (9) is derived, which is connected with the closing liabilities, assets and capital accounts:

$$\left(\begin{array}{c}al\\ la\\ cl\end{array}\right)-\left(\begin{array}{c}a{l}^{\text{'}}\\ l{a}^{\text{'}}\\ c{l}^{\text{'}}\end{array}\right)=\left(\begin{array}{c}\Delta a_{al}\\ \Delta l_{la}\\ \Delta c_{cl}\end{array}\right)$$

(9)

The obtained modification (10), derived from the Equation (9) represents the the capital flow, assets and liabilities accounts at the end of the period:

$$\left(\begin{array}{c}ac\\ lc\\ ca\end{array}\right)-\left(\begin{array}{c}a{c}^{\text{'}}\\ l{c}^{\text{'}}\\ c{a}^{\text{'}}\end{array}\right)=\left(\begin{array}{c}\Delta a_{ac}\\ \Delta l_{lc}\\ \Delta c_{ca}\end{array}\right)$$

(10)

These blocks are built on the nine possible types of transactions. By providing Equations (8)–(10), we represent the formulae for the quantitative evaluation of the dynamics of the Trial Balance.

The structure of the transposed matrix is formed in accordance with the rules of block matrices transposition:

$$MCT=MD{T}^{\text{'}}=\left(\begin{array}{ccc}AA& AL& AC\\ LA& LL& LC\\ CA& CL& LL\end{array}\right)=\begin{array}{ccc}A{A}^{\prime }& L{A}^{\prime }& C{A}^{\prime }\\ A{L}^{\prime }& L{L}^{\prime }& C{L}^{\prime }\\ A{C}^{\prime }& L{C}^{\prime }& C{C}^{\prime }\end{array}$$

(11)

The transposed matrix (MCT) contains the data from the transactions with inverted correspondences of the accounts used.

4. Accounting Game by Means of Matrix Modeling

This part of the paper provides a case statement and its solution for the accounting game played during accounting classes at Southern Federal University, Russia and was described in 2016 by Vysotskaya, Kolvakh and Stoner in their accounting education research paper. This game is based on the matrix accounting modeling system described earlier in the current paper.

The game starts by assuming that there are three players: I, II, and III. We also assume that they play a game. The reward will be in the form of money (players can also lose money as a result of play). This game is played between pairs, and can be played in different combinations, e.g., between players I and II, I and III, II and III, etc.

The players start their game by owing money to each other. In order to register the occurring liabilities, one person serves as an accountant and makes notes of transactions in chronological order.

Thus, occurring liabilities are registered with the description in the following suggested form (which resembles a diary):

• January, 5—player I wins $20 from the player II.
• Player III wins $8 from player II on the same date.
• January, 8—player II wins $63 from player I, etc.

With the help of

Table 1. The journal of operations (Ledger) of players I, II, III (January).

#	Date	Liabilities to Receive	Liabilities to Pay	Total ($)
1	5.01	I	II	20
2	5.01	III	I	8
3	8.01	II	I	6
4	16.01	I	III	14
5	18.01	II	III	16
6	25.01	III	II	12
7	29.01	I	II	18
8	31.01	III	I	6
Total				100

, we provide evidence that it is more convenient to register these events by means of a chronological register—The Ledger (Table 1).

This Ledger represents a chronological accounting register, since it contains information about transactions structured in a chronological order. However, we cannot uniquely identify the date of each event, since several events can take place on the same day. Therefore, the identification of the events is supported by the consecutive number or record number.

The labels used in the Ledger’ notional accounts to indicate the players and their roles, e.g., I—to receive, II—to pay, is called the accounts correspondence in accounting. The transaction by itself will have the following interpretation (

Table 2. The transaction interpretation.

Liabilities		Sum (c.u.)
To Receive	To Pay
I	II	20

).

5. The Solution

After doing the calculations of the liabilities totals (“to receive—to pay”) according to the equation presented above, S(X,Y) = Sx,y, where X means “to receive” and Y means “to pay”, the liabilities value is found on the left.

In our case, we assume that the sum of the liabilities of the players I and II will be represented as follows: “I—to receive, II—to pay”. This is equal to the following equation, with the sum of the transaction (S): S(I,II) = S1(I,II + S7 (I,II) = $20 + $18 = $38

Accordingly, S(III,I) = S2(III,I) + S8(III,I) = $8 + $8= $14; S(II,I) = S3(II,I) = $6. This can be continued according to the registered transactions in the Ledger.

After such manipulations, we can record the results as a Ledger, which will represent the total liabilities for the players I, II and III (

Table 3. The Ledger of the total liabilities for players I, II, III (January).

#	Liabilities to Receive	Liabilities to Pay	Total ($)
1	I	II	38
2	III	I	14
3	II	I	6
4	I	III	14
5	II	III	16
6	III	II	12
Total			100

).

We deem such a Ledger a systematic accounting register book because it considers systematization of the data obtained throughout the playing period.

The Ledger can contain different numbers of entries.

In this game, the quantity of the entries in the Ledger is limited to the number of possible pairs of players, namely, to six: I and II, I and III, II and I, II and III, III and I, and III and II.

In the Ledger we have enough data to solve the case for the players I, II, and III through the closing statements, which can be represented in two ways:

1. Gross settlement. This method is often used in bank settlements between clients. In this case, the transactions between the players I and II will appear as: player I receives $38 from player II, player II receives $6 from player I. The total amount needed in order to close accounts and mutual settlements between all players will be equal to the total amount in the Ledger ($100).

2. Netting debts. Using the formula ∆S (X,Y) = S (X,Y) − S (Y,X),

where X,Y can be any of players I, II, III, we calculate the difference.

Based on our case, this is as follows:

∆S (I,II) = S (I,II) – S (II,I) = 38 − 6 = +32 $,
∆S (I, II) = S (I,II) – S (II,I) = 38 − 6 = +32 > 0,
∆S (II,I) = S (II,I) – S (I,II) = 6 − 38 = −32 < 0

(12)

Here “+” means “to receive”, “−”, “to pay”.

These calculations can be rewritten in a systematized form based on the data from the Ledger and represented in the form of a chess balance. Such a chess balance we call a matrix of debit turnovers (MDT). Thus, the chess balance resembles the liability matrix (to receive) and can be represented as follows (

Table 4. The Matrix of Debit Turnovers MDT in a matrix form.

Type of Matrix	To Receive	To Pay			Total to Receive
		I	II	III
MDT=	I	0	38	14	52
	II	6	0	16	22
	III	14	12	0	26
	Total to pay	20	50	30	100

):

By transposing this matrix (to receive), we can obtain a matrix of liabilities (to pay) and matrix of credit turnovers (MCT) (

Table 5. The Matrix of Credit Turnovers MCT in a matrix form.

Type of Matrix	To Receive	To Pay			Total to Receive
		I	II	III
MCT=	I	0	6	14	20
	II	38	0	12	50
	III	14	16	0	30
	Total to pay	52	22	26	100

).

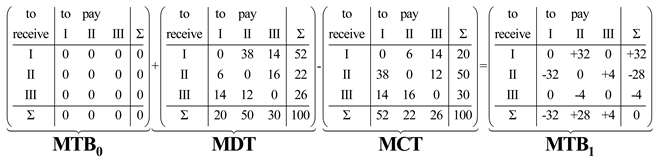
We can then subtract the above matrix (MCT) from a “liabilities to receive” matrix, or Matrix of Debit Turnovers (MDT) in order to obtain a Trial Balance Matrix (MTB) as follows:

MDT − MCT = MTB

(13)

As the result of Equation (13), the MTB can be represented in matrix form as follows (

Table 6. The Matrix of a Trial Balance MTB in matrix form.

Type of Matrix	To Receive	To Pay			Total to Receive
		I	II	III
MTB=	I	0	+32	0	+32
	II	−32	0	+4	−28
	III	0	−4	0	−4
	Total to pay	−32	+28	+4	0

):

Generally, the basic accounting equation in matrix form is as follows:

$$MT{B}_0+MDT-MCT=MT{B}_1$$

(14)

Here $MT{B}_0$ is a matrix of balances for the beginning of the period, and MDT is a matrix of debit turnovers. MCT is a transposition of MDT ($MD{T}^{\text{'}}$), or a matrix of credit turnovers.$MT{B}_{1 }$ is a Trial Balance matrix for the end of the period.

Our game assumes that there were no liabilities of the players at the beginning of this game. Thus, all the elements of the beginning matrix ($MT{B}_0$) are equal to zero. Finally, the basic accounting equation based on our case is as follows:

(15)

6. Conclusions

The equations presented above are the equivalents of the trial balance obtained by using T-accounts. This means that it is possible to use an alternative approach, which differs from T-accounts, and vice versa.

However, the difference of the approaches lies in the manner of the solution of the case. Moreover, the T-accounts method is used primarily for teaching purposes, since a variety of accounting forms are used in practice.

Nevertheless, the matrix model of accounting technology can be considered as an example of solving the case of mutual calculations.

On this basis, we have developed and introduced in 2000 a course based on new principals that is constantly being revised and developed with the participation of the other course staff.

Finally, this paper presents a framework for a further series of articles on how mathematics affects accounting theory and practice in the era of developing blockchain and distributed ledger development. Considering the possibilities of the situational-matrix modeling method used in accounting and Industry 4.0, the increasing impact of digitalization on business processes raised in this paper povides the foundations for building a comprehensive platform for monitoring transactions, along with identifying abnormal or non-efficient ones.