Kinematics in the Information Age
Abstract
1. Introduction
2. Materials and Methods
2.1. Theory of Dynamics
2.1.1. Kinetics
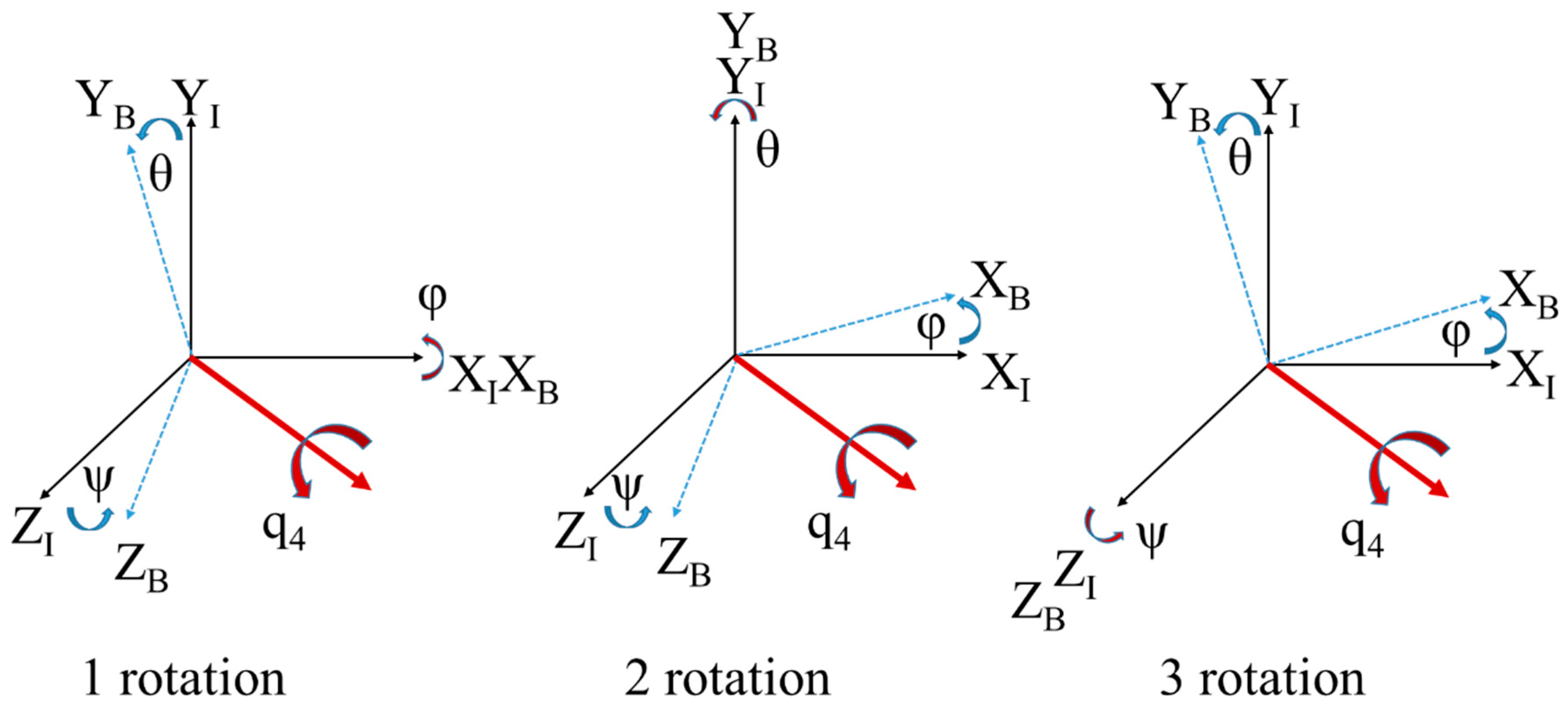
2.1.2. Kinematics, Phoronomics, or “The Laws of Going”
2.1.3. The Orbital Frame
2.1.4. Disturbances
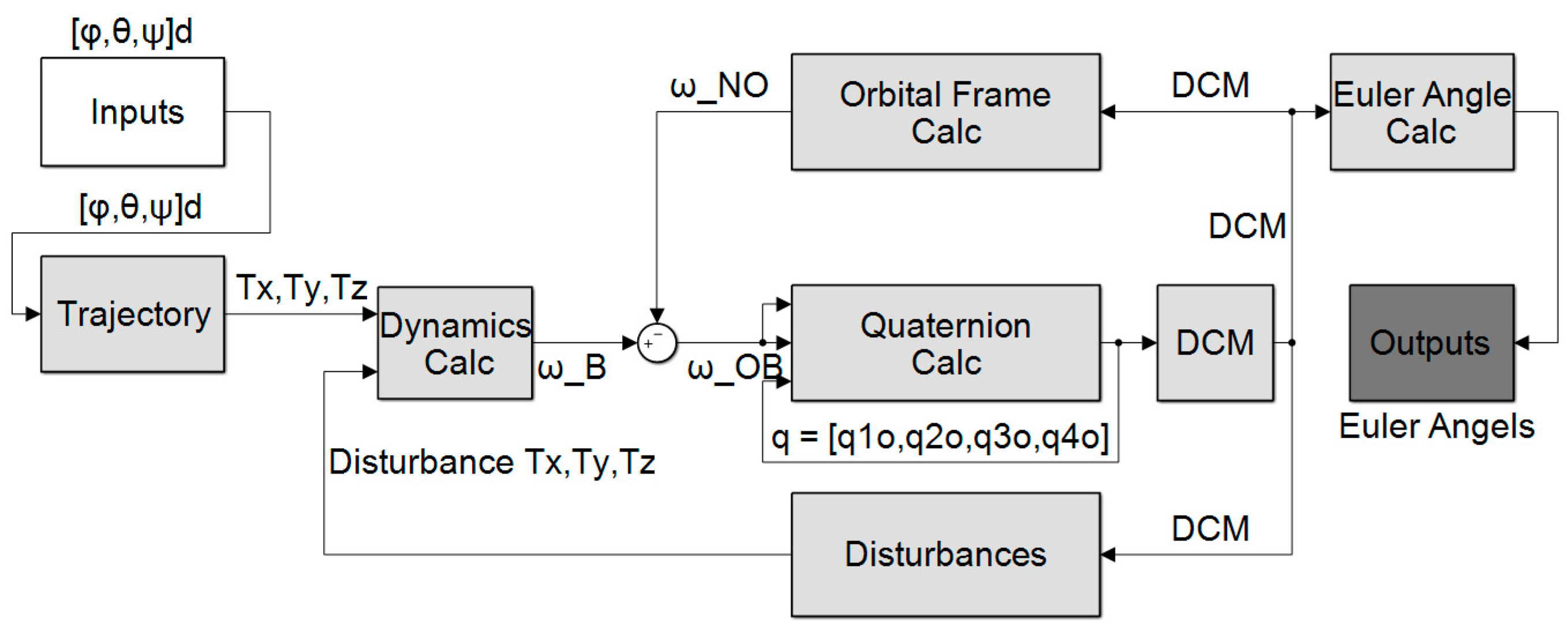
2.2. Experimental Setup
3. Experimental Results and Analysis
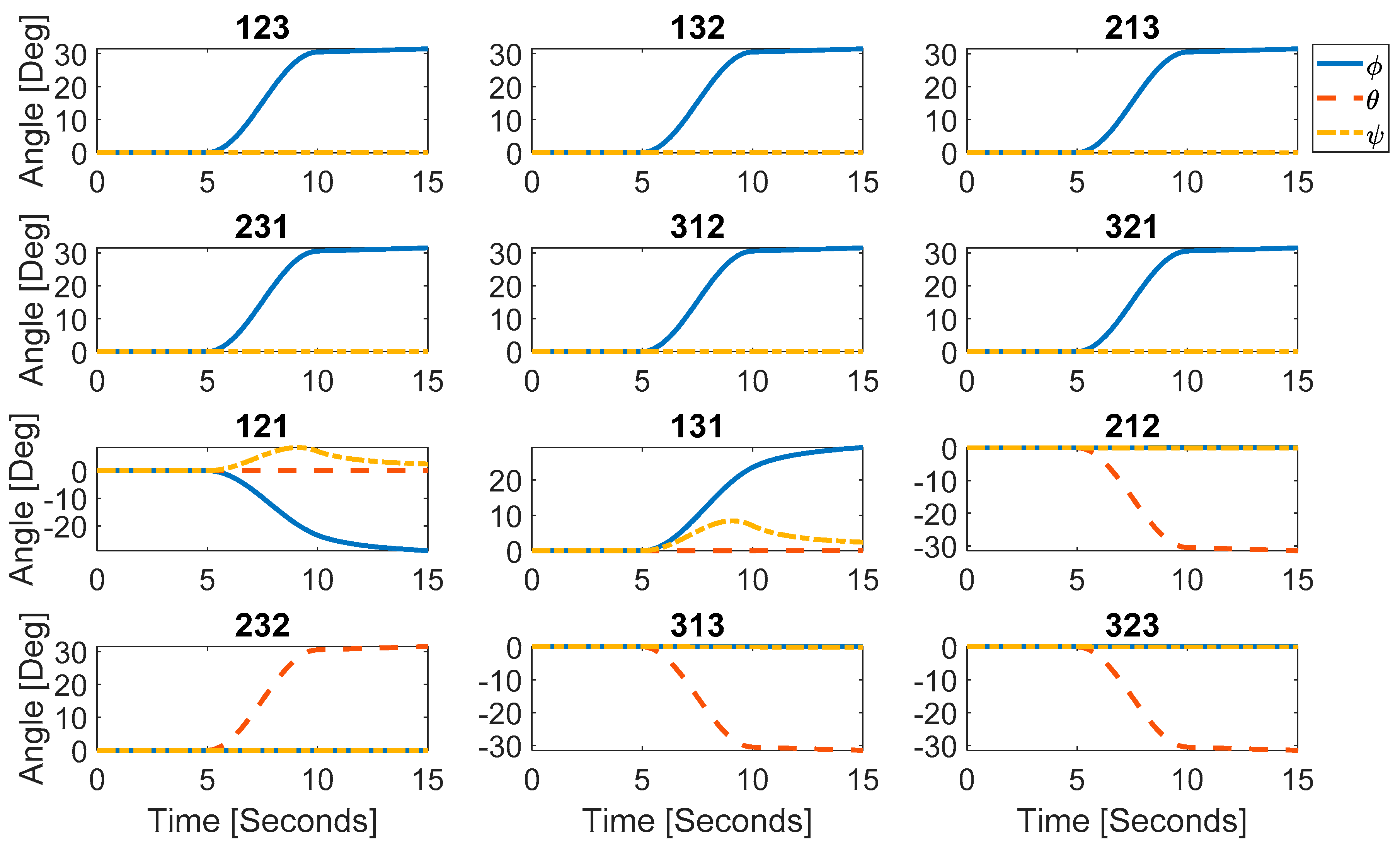
3.1. Euler Angle Calculations and Post-Processing
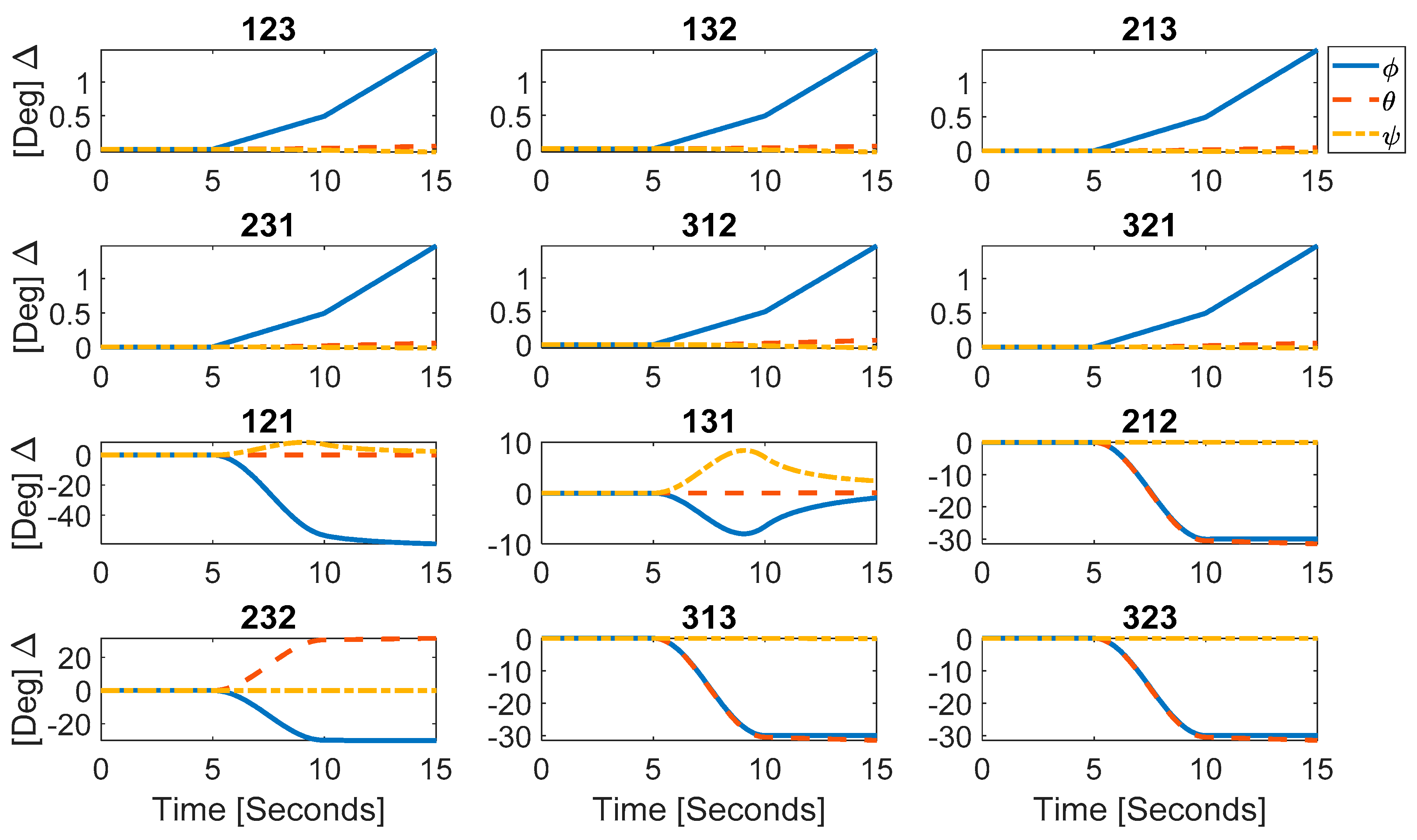
3.2. Euler Angle to Body Angle Accuracy
3.3. Step Size Versus Accuracy
3.4. DCM to Euler Angle Timing
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Euler, L. (Euler) Formulae Generales pro Translatione Quacunque Corporum Rigidorum (General Formulas for the Translation of Arbitrary Rigid Bodies), Presented to the St. Petersburg Academy on 9 October 1775. and First Published in Novi Commentarii Academiae Scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478) and Was Reprinted in Theoria motus corporum rigidorum, ed. nova, 1790, pp. 449–460 (E478a) and Later in His Collected Works Opera Omnia, Series 2, Volume 9, pp. 84–98. Available online: https://math.dartmouth.edu/~euler/docs/originals/E478.pdf (accessed on 22 August 2018).
- Thompson, W.; Tait, P.G. Elements of Natural Philosophy; Cambridge University Press: Cambridge, UK, 1872. [Google Scholar]
- Reuleaux, F.; Kennedy Alex, B.W. The Kinematics of Machinery: Outlines of a Theory of Machines; Macmillan: London, UK, 1876; Available online: https://archive.org/details/kinematicsofmach00reuluoft (accessed on 22 August 2018).
- Wright, T.W. Elements of Mechanics Including Kinematics, Kinetics and Statics; D. Van Nostrand Company: New York, NY, USA; Harvard University: Cambridge, MA, USA, 1896. [Google Scholar]
- Merz, J.T. A History of European Thought in the Nineteenth Century; Blackwood: London, UK, 1903; p. 5. [Google Scholar]
- Whittaker, E.T. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies; Cambridge University Press: Cambridge, UK, 1904. [Google Scholar]
- Whittaker, E.T. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies; Cambridge University Press: Cambridge, UK, 1917. [Google Scholar]
- Whittaker, E.T. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- Whittaker, E.T. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies; Cambridge University Press: Cambridge, UK, 1937. [Google Scholar]
- Church, I.P. Mechanics of Engineering; Wiley: New York, NY, USA, 1908; p. 111. [Google Scholar]
- Wright, T.W. Elements of Mechanics Including Kinematics, Kinetics, and Statics, with Applications; Nostrand: New York, NY, USA, 1909. [Google Scholar]
- Study, E. ; Delphenich, D.H., Translator; Foundations and goals of analytical kinematics. Sitzber. d. Berl. Math. Ges. 1913, 13, 36–60. Available online: http://neo-classical-physics.info/uploads/3/4/3/6/34363841/study-analytical_kinematics.pdf (accessed on 14 April 2017).
- Gray, A. A Treatise on Gyrostatics and Rotational Motion; MacMillan: London, UK, 1918; ISBN 978-1-4212-5592-7. (Published 2007). [Google Scholar]
- Rose, M.E. Elementary Theory of Angular Momentum; John Wiley & Sons: New York, NY, USA, 1957; ISBN 978-0-486-68480-2. (Published 1995). [Google Scholar]
- Kane, T.R. Analytical Elements of Mechanics Volume 1; Academic Press: New York, NY, USA; London, UK, 1959. [Google Scholar]
- Kane, T.R. Analytical Elements of Mechanics Volume 2 Dynamics; Academic Press: New York, NY, USA; London, UK, 1961. [Google Scholar]
- Thompson, W. Space Dynamics; Wiley and Sons: New York, NY, USA, 1961. [Google Scholar]
- Greenwood, D. Principles of Dynamics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1965; ISBN 9780137089741. (Reprinted in 1988 as 2nd ed.). [Google Scholar]
- Fang, A.C.; Zimmerman, B.G. Digital Simulation of Rotational Kinematics; NASA Technical Report NASA TN D-5302; NASA: Washington, DC, USA, October 1969. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19690029793.pdf (accessed on 22 August 2018).
- Henderson, D.M. Euler Angles, Quaternions, and Transformation Matrices—Working Relationships; As NASA Technical Report NASA-TM-74839; July 1977. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770024290.pdf (accessed on 22 August 2018).
- Henderson, D.M. Euler Angles, Quaternions, and Transformation Matrices for Space Shuttle Analysis; Houston Astronautics Division as NASA Design Note 1.4-8-020; 9 June 1977. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770019231.pdf (accessed on 22 August 2018).
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1981. [Google Scholar]
- Kane, T.; David, L. Dynamics: Theory and Application; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Huges, P. Spacecraft Attitude Dynamics; Wiley and Sons: New York, NY, USA, 1986. [Google Scholar]
- Wiesel, W. Spaceflight Dynamics, 2nd ed.; Irwin McGraw-Hill: Boston, MA, USA, 1989, 1997. [Google Scholar]
- Wie, B. Space Vehicle Dynamics and Control; AIAA: Reston, VA, USA, 1998. [Google Scholar]
- Slabaugh, G.G. Computing Euler Angles from a Rotation Matrix. January 1999, Volume 6, pp. 39–63. Available online: http://www.close-range.com/docs/Computing_Euler_angles_from_a_rotation_matrix.pdf (accessed on 22 August 2018).
- Vallado, D. Fundamentals of Astrodynamics and Applications, 2nd ed.; Microcosm Press: El Segundo, CA, USA, 2001. [Google Scholar]
- Roithmayr, C.M.; Hodges, D.H. Dynamics: Theory and Application of Kane’s Method; Cambridge University Press: New York, NY, USA, 2016. [Google Scholar]
- Sands, T.; Mihalik, R. Outcomes of the 2010 and 2015 nonproliferation treaty review conferences. World J. Soc. Sci. Hum. 2016, 2, 46–51. Available online: http://pubs.sciepub.com/wjssh/2/2/4/index.html (accessed on 22 August 2018). [CrossRef]
- Sands, T. Strategies for combating Islamic state. Soc. Sci. 2016, 5, 39. Available online: www.mdpi.com/2076-0760/5/3/39/pdf (accessed on 22 August 2018). [CrossRef]
- Mihalik, R.; Camacho, H.; Sands, T. Continuum of learning: Combining education, training and experiences. Education 2017, 8, 9–13. [Google Scholar] [CrossRef]
- Sands, T.; Camacho, H.; Mihalik, R. Education in nuclear deterrence and assurance. J. Def. Manag. 2017, 7, 166. [Google Scholar] [CrossRef]
- Sands, T.; Mihalik, R. Theoretical Context of the Nuclear Posture Review. J. Soc. Sci. 2018, 14, 124–128. [Google Scholar] [CrossRef]
- Sands, T. Satellite electronic attack of enemy air defenses. Proc. IEEE CDC 2009, 434–438. [Google Scholar] [CrossRef]
- Sands, T. Space mission analysis and design for electromagnetic suppression of radar. Int. J. Electromagn. Appl. 2018, 8, 1–25. [Google Scholar] [CrossRef]
- Sands, T.; Lu, D.; Chu, J.; Cheng, B. Developments in Angular Momentum Exchange. Int. J. Aerosp. Sci. 2018, 6, 1–7. [Google Scholar] [CrossRef]
- Sands, T.A.; Kim, J.J.; Agrawal, B. 2H Singularity free momentum generation with non-redundant control moment gyroscopes. Proc. IEEE CDC 2006, 1551–1556. [Google Scholar] [CrossRef]
- Sands, T. Fine Pointing of Military Spacecraft. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2007. [Google Scholar]
- Kim, J.J.; Sands, T.; Agrawal, B.N. Acquisition, tracking, and pointing technology development for bifocal relay mirror spacecraft. Proc. SPIE 2007, 6569. [Google Scholar] [CrossRef]
- Sands, T.A.; Kim, J.J.; Agrawal, B. Control moment gyroscope singularity reduction via decoupled control. Proc. IEEE SEC 2009, 1551–1556. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.J.; Agrawal, B.N. Nonredundant single-gimbaled control moment gyroscopes. J. Guid. Control Dyn. 2012, 35, 578–587. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.; Agrawal, B. Experiments in Control of Rotational Mechanics. Int. J. Autom. Control Intell. Syst. 2016, 2, 9–22. [Google Scholar]
- Agrawal, B.N.; Kim, J.J.; Sands, T.A. Method and Apparatus for Singularity Avoidance for Control Moment Gyroscope (CMG) Systems without Using Null Motion. U.S. Patent 9567112 B1, 14 February 2017. Available online: https://calhoun.nps.edu/handle/10945/51921 (accessed on 22 August 2018).
- Sands, T.; Kim, J.J.; Agrawal, B. Singularity Penetration with Unit Delay (SPUD). Mathematics 2018, 6, 23. Available online: https://www.mdpi.com/2227-7390/6/2/23/pdf (accessed on 22 August 2018). [CrossRef]
- Sands, T.; Lorenz, R. Physics-Based Automated Control of Spacecraft. In Proceedings of the AIAA Space 2009 Conference and Exposition, Pasadena, CA, USA, 14–17 September 2009. [Google Scholar]
- Sands, T. Physics-based control methods. In Advances in Spacecraft Systems and Orbit Determination; InTech: London, UK, 2012; Available online: https://www.intechopen.com/books/advances-in-spacecraft-systems-and-orbit-determination/physics-based-control-methods (accessed on 22 August 2018).
- Sands, T. Improved Magnetic Levitation via Online Disturbance Decoupling. Phys. J. 2015, 1, 272–280. [Google Scholar]
- Nakatani, S. Simulation of spacecraft damage tolerance and adaptive controls. Proc. IEEE Aerosp. 2014, 1–16. [Google Scholar] [CrossRef]
- Nakatani, S. Autonomous damage recovery in space. Int. J. Autom. Control Intell. Syst. 2016, 2, 22–36. [Google Scholar]
- Nakatani, S. Battle-damage tolerant automatic controls. Electr. Electron. Eng. 2018, 8, 10–23. [Google Scholar] [CrossRef]
- Heidlauf, P.; Cooper, M. Nonlinear Lyapunov Control Improved by an Extended Least Squares Adaptive Feed forward Controller and Enhanced Luenberger Observer. In Proceedings of the International Conference and Exhibition on Mechanical & Aerospace Engineering, Las Vegas, NV, USA, 2–4 October 2017. [Google Scholar]
- Cooper, M.; Heidlauf, P.; Sands, T. Controlling Chaos—Forced van der Pol Equation. Mathematics 2017, 5, 70. Available online: https://www.mdpi.com/2227-7390/5/4/70/pdf (accessed on 22 August 2018). [CrossRef]
- Sands, T. Phase Lag Elimination at all Frequencies for Full State Estimation of Spacecraft Attitude. Phys. J. 2017, 3, 1–12. [Google Scholar]
- Sands, T. Nonlinear-adaptive mathematical system identification. Computation 2017, 5, 47–59. Available online: https://www.mdpi.com/2079-3197/5/4/47/pdf (accessed on 22 August 2018). [CrossRef]
- Sands, T.; Kenny, T. Experimental piezoelectric system identification. J. Mech. Eng. Autom. 2017, 7, 179–195. [Google Scholar] [CrossRef]
- Sands, T. Space systems identification algorithms. J. Space Explor. 2017, 6, 138–149. [Google Scholar]
- Sands, T. Experimental Sensor Characterization. J. Space Explor. 2018, 7, 140. [Google Scholar]
- Sands, T.; Armani, C. Analysis, correlation, and estimation for control of material properties. J. Mech. Eng. Autom. 2018, 8, 7–31. Available online: http://www.sapub.org/global/showpaperpdf.aspx?doi=10.5923/j.jmea.20180801.02 (accessed on 22 August 2018). [CrossRef]
- Sands, T. Satellite Electronic Attack of Enemy Air Defenses. In Proceedings of the IEEE SEC, Atlanta, GA, USA, 5–8 March 2009; pp. 434–438. [Google Scholar]
- Remarks by President Trump at a Meeting with the National Space Council and Signing of Space Policy Directive-3. Available online: https://www.whitehouse.gov/briefings-statements/remarks-president-trump-meeting-national-space-council-signing-space-policy-directive-3/ (accessed on 20 June 2018).
- Sands, T.; Bollino, K.; Kaminer, I.; Healey, A. Autonomous Minimum Safe Distance Maintenance from Submersed Obstacles in Ocean Currents. J. Mar. Sci. Eng. 2018, 6, 98. Available online: https://www.mdpi.com/2077-1312/6/3/98/pdf (accessed on 22 August 2018). [CrossRef]
- Kuipers, J.B. Quaternions and Rotation Sequences. In Proceedings of the International Conference on Geometry, Integrability, and Quantization, Varna, Bulgaria, 1–10 September 1999; Coral Press: Sofia, Bulgaria, 2000. [Google Scholar]

| Mean | Standard Deviation | |||||
|---|---|---|---|---|---|---|
| DCM | ϕ | θ | ψ | ϕ | θ | ψ |
| 123 | 0.413 | 0.011 | 0.011 | 0.462 | 0.015 | 0.014 |
| 132 | 0.413 | 0.010 | 0.013 | 0.462 | 0.013 | 0.016 |
| 213 | 0.413 | 0.011 | 0.005 | 0.462 | 0.015 | 0.006 |
| 231 | 0.413 | 0.014 | 0.005 | 0.462 | 0.018 | 0.005 |
| 312 | 0.413 | 0.016 | 0.013 | 0.462 | 0.021 | 0.016 |
| 321 | 0.413 | 0.014 | 0.005 | 0.462 | 0.018 | 0.005 |
| 121 | 27.544 | 0.015 | 2.869 | 25.804 | 0.019 | 2.823 |
| 131 | 2.456 | 0.015 | 2.869 | 2.680 | 0.019 | 2.823 |
| 212 | 14.977 | 15.413 | 0.010 | 13.726 | 14.150 | 0.010 |
| 232 | 15.010 | 15.413 | 0.010 | 13.757 | 14.150 | 0.010 |
| 313 | 14.980 | 15.413 | 0.028 | 13.728 | 14.150 | 0.034 |
| 323 | 14.977 | 15.413 | 0.010 | 13.725 | 14.150 | 0.010 |
| Simulation Execution Time [S] | |||
|---|---|---|---|
| DCM | 0.1 Step size | 0.001 Step size | 0.0001 Step size |
| 123 | 8.408 | 11.836 | 28.433 |
| 132 | 1.533 | 6.789 | 22.187 |
| 213 | 1.419 | 6.978 | 22.102 |
| 231 | 1.188 | 4.436 | 23.259 |
| 312 | 1.549 | 4.302 | 20.971 |
| 321 | 1.018 | 3.475 | 21.420 |
| 121 | 0.952 | 3.715 | 20.505 |
| 131 | 1.190 | 4.082 | 23.331 |
| 212 | 1.015 | 3.860 | 21.005 |
| 232 | 0.931 | 3.710 | 21.410 |
| 313 | 0.939 | 3.789 | 20.908 |
| 323 | 1.091 | 3.955 | 22.044 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smeresky, B.; Rizzo, A.; Sands, T. Kinematics in the Information Age. Mathematics 2018, 6, 148. https://doi.org/10.3390/math6090148
Smeresky B, Rizzo A, Sands T. Kinematics in the Information Age. Mathematics. 2018; 6(9):148. https://doi.org/10.3390/math6090148
Chicago/Turabian StyleSmeresky, Brendon, Alexa Rizzo, and Timothy Sands. 2018. "Kinematics in the Information Age" Mathematics 6, no. 9: 148. https://doi.org/10.3390/math6090148
APA StyleSmeresky, B., Rizzo, A., & Sands, T. (2018). Kinematics in the Information Age. Mathematics, 6(9), 148. https://doi.org/10.3390/math6090148






