Abstract
In this paper, we are concerned with the asymptotic stability of the nontrivial endemic equilibrium of an age-structured susceptible-infective-recovered (SIR) epidemic model. For a special form of the disease transmission function, we perform the reduction of the model into a four-dimensional system of ordinary differential equations (ODEs). We show that the unique endemic equilibrium of the reduced system exists if the basic reproduction number for the original system is greater than unity. Furthermore, we perform the stability analysis of the endemic equilibrium and obtain a fourth-order characteristic equation. By using the Routh–Hurwitz criterion, we numerically show that the endemic equilibrium is asymptotically stable in some epidemiologically relevant parameter settings.
Keywords:
SIR epidemic model; age structure; endemic equilibrium; stability; basic reproduction number MSC:
34D20; 37N25; 92D30
1. Introduction
The mathematical modeling of epidemics in human populations has been studied for a long time [1]. In 1760, Bernoulli used a mathematical model of differential equations to discuss the benefit of smallpox inoculation [2]. In 1911, Ross claimed that malaria could be eradicated by reducing the number of mosquitoes, and constructed a mathematical model of differential equations to theoretically support his claim [3]. In 1927, Kermack and McKendrick constructed the first susceptible-infective-recovered (SIR) epidemic model, in which the total population is divided into three classes called susceptible, infective, and recovered [4]. Since their work, the theory of various epidemic models such as a susceptible-infective-susceptible (SIS) epidemic model [5], a susceptible-exposed-infective-recovered (SEIR)epidemic model [6], and a susceptible-infective-recovered-susceptible (SIRS) epidemic model [7] with various structures such as the age structure [8,9], the space structure [10], and the network structure [11] has been developed from both mathematical and epidemiological points of view.
Epidemiologically, the basic reproduction number for an infectious disease is defined by the expected number of secondary cases produced by a typical infective individual in a completely susceptible population ([9], Chapter 5). Mathematically, is defined by the spectral radius of a linear operator called the next-generation operator [12], and it determines the complete global dynamics of each equilibrium for some basic epidemic models: if , then the trivial disease-free equilibrium is globally asymptotically stable, whereas if , then the nontrivial endemic equilibrium is globally asymptotically stable [13]. However, for some epidemic models, the endemic equilibrium can be stable even if due to the backward bifurcation [14], and it can be unstable even if , which leads to a periodic solution due to the Hopf bifurcation [15].
In [16], some conjectures on the threshold property of for an age-structured SIR epidemic model were proposed, and they were proved in [17]: if , then the disease-free equilibrium is globally asymptotically stable and no endemic equilibrium exists, whereas if , then the endemic equilibrium uniquely exists and it is locally asymptotically stable under some additional conditions. However, in general, it is known that the endemic equilibrium cannot always be unique and stable for . Several authors have studied some special cases where the endemic equilibrium is unstable, and periodic solutions occur through the Hopf bifurcation for [18,19,20,21]. From the viewpoint of application, it is important to investigate when the endemic equilibrium of an age-structured SIR epidemic model is stable and when it is not, as the age distribution of infective individuals in such a model should be stable if one tries to estimate the basic reproduction number for an endemic disease by using statistical data that exhibit an almost unchanged age distribution of infective individuals. The purpose of this study is to obtain a new condition under which the endemic equilibrium of an age-structured SIR epidemic model is (locally) asymptotically stable.
Age-structured SIR epidemic models as stated above are systems of partial differential equations (PDEs), and hence the stability analysis of them often requires a relatively difficult method such as the spectral theory of positive operators ([17], §5). In this paper, we make some assumptions on the parameters of an age-structured SIR epidemic model, under which we can perform the reduction of the model into a four-dimensional system of ordinary differential equations (ODEs). We can then apply the standard method of characteristic equations for the stability analysis of the endemic equilibrium.
This paper is organized as follows. In Section 2, we formulate an age-structured SIR epidemic model, and perform the reduction of it into a four-dimensional system of ODEs. In Section 3, we prove that the reduced system has a unique endemic equilibrium if the basic reproduction number for the original system is greater than unity. Moreover, we investigate the asymptotic stability of the endemic equilibrium, and obtain a fourth-order characteristic equation. As its coefficients have quite complex forms, we only prove their positivity, and numerically show by using the Routh–Hurwitz criterion that the endemic equilibrium is asymptotically stable in some epidemiologically relevant parameter settings in Section 4. In the parameter settings, the essential supremum of the demographic mortality rate is determined based on a dataset for Japan in 2015, and the recovery rate and the basic reproduction number are varied for the cases of an influenza-like disease ( and ), a chlamydia-like sexually transmitted disease ( and ), and a wider range of realistic values of them ( and ). Finally, Section 5 is devoted to the discussion.
2. Reduction of an Age-Structured SIR Epidemic Model into ODEs
We first formulate an age-structured SIR epidemic model. Let , , and denote the susceptible, infective, and recovered populations of age at time , respectively. Let denote the birth rate, let denote the age-specific mortality rate such that , and let denote the recovery rate. As in [18], we focus on the case where the disease transmission function is only dependent on the age of infective individuals: . In this case, the age-structured SIR epidemic model is formulated as follows:
where denotes the initial age distributions of each population. It is easy to see that (1) has the demographic steady state , . Let
We then can normalize (1) as follows.
As shown in [18], for a specific form of such that is sufficiently concentrated in one particular age class, the endemic equilibrium of (2) can be destabilized even if it uniquely exists. Thus, our interest in this paper is when it is stable. In this paper, we assume that has the following form:
Note that is satisfied under this assumption. In this case, the equations of s and i in (2) can be rewritten as follows.
Note that we can omit the equation of r, as it does not affect the dynamics of (4). As in [17], without loss of generality, we can assume that and for all and .
As seen in [17,18], the stability analysis of age-structured PDE systems such as (4) requires complex calculation. In this paper, we perform the reduction of (4) into a four-dimensional system of ODEs. Let
Note that these variables have no specific epidemiological implications except , which implies the force of infection at time . By differentiating , we have
Similarly, we have
and
Hence, combining (5)–(8), we obtain the following new four-dimensional system of ODEs:
Note that since . In what follows, we perform the stability analysis of system (9).
3. Existence, Uniqueness, and Stability of the Endemic Equilibrium
Following the theory in [12], the basic reproduction number for the original (normalized) system (4) can be calculated as follows.
We now prove that system (9) has the unique endemic equilibrium if . Let denote the endemic equilibrium of system (9). The following equations are satisfied:
We prove the following theorem.
Theorem 1.
Let be defined by (10). If , then system (9) has the unique endemic equilibrium .
Proof.
By rearranging the first three equations in (11), we have
By substituting the equations of and into the last equation in (11), we have
Dividing both sides of this equation by and rearranging the equation, we have
Let be a function defined by the right-hand side of this equation. Since is monotonically decreasing to 0 as and
there exists the unique positive root of Equation (13). Substituting it into the three equations in (12), we obtain the unique endemic equilibrium . This completes the proof. ☐
To investigate the asymptotic stability of the endemic equilibrium , we consider the following Jacobian matrix around :
From (12), we have
Using (14), we derive the characteristic polynomial for as follows:
where denotes the identity matrix and
To apply the Routh–Hurwitz criterion, we prove the following proposition.
Proposition 1.
Let and () be defined by (10) and (16), respectively. If , then for all .
Proof.
By Theorem 1, the unique endemic equilibrium exists. From (12) and (13), we have
We then have
This completes the proof. ☐
By Proposition 1, it follows from the Routh–Hurwitz criterion [15] (Proof of Theorem 3.1) that the endemic equilibrium is asymptotically stable if and only if
However, it seems that quite a long calculation is needed to show (17) analytically. Instead, in the next section, we show (17) numerically in some epidemiologically relevant parameter settings.
4. Numerical Results
Let the unit time be 1 year. By the definition in (3), k should satisfy inequality . For the sake of simplicity, we regard (years old) as the maximum age of individuals. In a dataset available in [22], the mortality rate is at most (at ) for males in Japan, 2015. Hence, we fix . By (10), we can determine for chosen and as follows:
We first consider an influenza-like disease which has an infectious period of about 1 week (see [23]). Therefore, let so that the average infectious period is year week. Following the estimation result in [24], we vary the value of from 2 to 3. In Figure 1a, we can confirm that criterion defined in (17) is always positive, and hence, the endemic equilibrium is asymptotically stable. In fact, in Figure 1b, the force of infection converges to the positive equilibrium value as time evolves for .
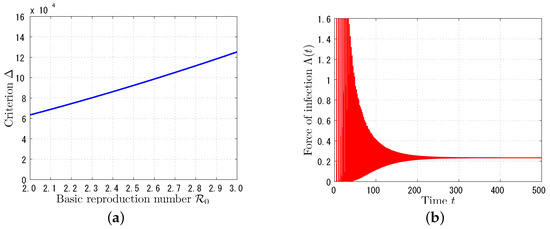
Figure 1.
Numerical confirmation of condition (17) and asymptotic stability of the endemic equilibrium for the case of an influenza-like disease: (a) Variation of defined in (17) for ; (b) Time variation of for .
We next consider a chlamydia-like sexually transmitted disease which has an infectious period of about 1 year (see [25]). Therefore, so that the average infectious period is year. Based on the estimation result in [25], we vary the value of from 1 to . In Figure 2a, we can confirm that criterion is always positive, and hence the endemic equilibrium is asymptotically stable. In fact, in Figure 2b, the force of infection converges to the positive equilibrium value as time evolves for .
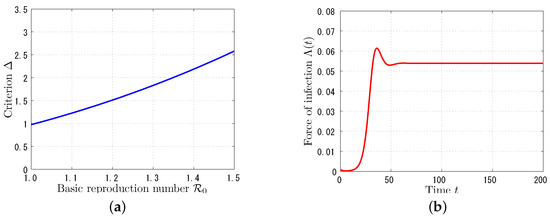
Figure 2.
Numerical confirmation of condition (17) and asymptotic stability of the endemic equilibrium for the case of a chlamydia-like sexually transmitted disease: (a) Variation of defined in (17) for ; (b) Time variation of for .
Finally, we vary the values of from to 365 (i.e., the average infectious period is varied from year = 1 day to 50 years) and from 1 to 50. In Figure 3, we can confirm that criterion is always positive in this parameter region. Hence, we can conclude that the endemic equilibrium is asymptotically stable for epidemiologically relevant values of and .
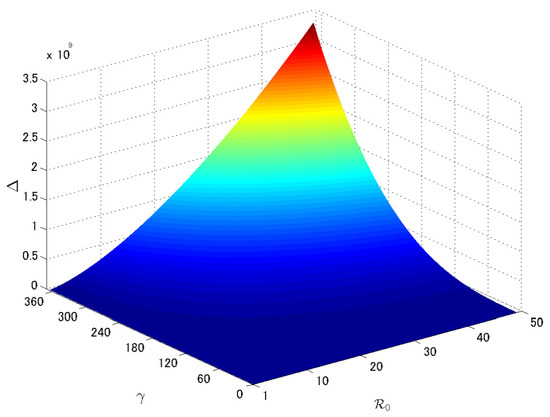
Figure 3.
Numerical confirmation of condition (17) for realistic values of recovery rate and the basic reproduction number .
5. Discussion
In this paper, we formulated an age-structured SIR epidemic model and performed its reduction into a four-dimensional system of ODEs under an additional assumption on the disease transmission function . We proved that if the basic reproduction number is greater than 1, then the system has the unique endemic equilibrium (Theorem 1). Moreover, we obtained a fourth-order characteristic equation, and proved that all of its coefficients are positive (Proposition 1). By the Routh–Hurwitz criterion, the endemic equilibrium is asymptotically stable if and only if . As it seems difficult to show analytically, we showed it numerically in Section 4 for some epidemiologically relevant parameters. We showed that holds for parameters for an influenza-like disease ( and ) and a chlamydia-like disease ( and ). Furthermore, we showed that holds for a wider region of epidemiologically relevant parameters and .
The results in this paper contribute to enlarge the stability region of the endemic equilibrium for to the set where we can perform our reduction method of the PDEs system into the ODEs system. Epidemiologically, our results imply that can be stable for with some realistic parameters, and have broadened the possibilities of application of an age-structured SIR epidemic model for the estimation of based on the real data of endemic diseases.
In this study, we restricted our attention to the case where the disease transmission function is only dependent on the age a of infective individuals. Of course, the case where it depends on the ages of both susceptible and infective individuals is more general and epidemiologically realistic. Nevertheless, the stability of the endemic equilibrium of age-structured SIR epidemic models has not been clarified well enough even for the former case. In fact, the global asymptotic stability of the endemic equilibrium of such models does not generally hold even if the basic reproduction number is greater than unity, as a special case where becomes unstable for was obtained in [18]. As an important future work, we will seek other forms of for which we can apply a similar reduction method to ODEs as in this study.
Funding
This research was funded by Grant-in-Aid for Young Scientists (B) of Japan Society for the Promotion of Science (grant number 15K17585).
Conflicts of Interest
The author declares no conflict of interest.
References
- Bacaër, N. A Short History of Mathematical Population Dynamics; Springer-Verlag: London, UK, 2011. [Google Scholar]
- Bernoulli, D. Réflexions sur les avantages de l’inoculation. Mercue de France 1760, 173–190. [Google Scholar]
- Ross, R. The Prevention of Malaria, 2nd ed.; John Murray: London, UK, 1911. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics—I. Proc. R. Soc. 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Busenberg, S.N.; Iannelli, M.; Thieme, H.R. Global behavior of an age-structured epidemic model. SIAM J. Math. Anal. 1991, 22, 1065–1080. [Google Scholar] [CrossRef]
- Röst, G.; Wu, J. SEIR epidemiological model with varying infectivity and infinite delay. Math. Biosci. Eng. 2008, 5, 389–402. [Google Scholar] [PubMed]
- Enatsu, Y.; Nakata, Y.; Muroya, Y. Global stability of SIRS epidemic models with a class of nonlinear incidence rates and distributed delays. Acta Math. Sci. 2012, 32, 851–865. [Google Scholar] [CrossRef]
- Iannelli, M. Mathematical Theory of Age-Structured Population Dynamics; Giardini Editori e Stampatori: Pisa, France, 1995. [Google Scholar]
- Inaba, H. Age-Structured Population Dynamics in Demography and Epidemiology; Springer: Singapore, 2017. [Google Scholar]
- Ruan, S. Spatial-temporal dynamics in nonlocal epidemiological models. In Mathematics for Life Science and Medicine; Takeuchi, Y., Iwasa, Y., Sato, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 97–122. [Google Scholar]
- Frasca, M.; Buscarino, A.; Rizzo, A.; Fortuna, L.; Boccaletti, S. Dynamical network model of infective mobile agents. Phys. Rev. E 2006, 74, 036110. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.A.J.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Hethcote, H.W. Qualitative analyses of communicable disease models. Math. Biosci. 1976, 28, 335–356. [Google Scholar] [CrossRef]
- Gumel, A.B. Causes of backward bifurcations in some epidemiological models. J. Math. Anal. Appl. 2012, 395, 355–365. [Google Scholar] [CrossRef]
- Greenhalgh, D. Hopf bifurcation in epidemic models with a latent period and nonpermanent immunity. Math. Comput. Model. 1997, 25, 85–107. [Google Scholar] [CrossRef]
- Greenhalgh, D. Threshold and stability results for an epidemic model with an age-structured meeting rate. IMA J. Math. Med. Biol. 1988, 5, 81–100. [Google Scholar] [CrossRef]
- Inaba, H. Threshold and stability results for an age-structured epidemic model. J. Math. Biol. 1990, 28, 411–434. [Google Scholar] [CrossRef] [PubMed]
- Thieme, H. Stability change of the endemic equilibrium in age-structured models for the spread of S-I-R type infectious diseases. In Differential Equations Models in Biology, Epidemiology and Ecology; Busenberg, S., Martelli, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; Volume 92, pp. 139–158. [Google Scholar]
- Andreasen, V. Instability in an SIR-model with age-dependent susceptibility. In Mathematical Population Dynamics: Analysis of Heterogeneity; Arino, O., Axelrod, D., Kimmel, M., Langlais, M., Eds.; Wuerz Publishing: Winnipeg, MB, Canada, 1995; pp. 3–14. [Google Scholar]
- Cha, Y.; Iannelli, M.; Milner, F.A. Stability change of an epidemic model. Dyn. Syst. Appl. 2000, 9, 361–376. [Google Scholar]
- Franceschetti, A.; Pugliese, A.; Breda, D. Multiple endemic states in age-structured SIR epidemic models. Math. Biosci. Eng. 2012, 9, 577–599. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Health, Labour and Welfare, the 22nd Life Tables. Available online: https://www.mhlw.go.jp/english/database /db-hw/lifetb22nd/index.html (accessed on 12 July 2018).
- Centers for Disease Control and Prevention, Clinical Signs and Symptoms of Influenza. Available online: https://www. cdc.gov/flu/professionals/acip/clinical.htm (accessed on 13 July 2018).
- Mills, C.E.; Robins, J.M.; Lipsitch, M. Transmissibility of 1918 pandemic influenza. Nature 2004, 432, 904–906. [Google Scholar] [CrossRef] [PubMed]
- Heijne, J.C.M.; Herzog, S.A.; Althaus, C.L.; Low, N.; Kretzschmar, M. Case and partnership reproduction numbers for a curable sexually transmitted infection. J. Theor. Biol. 2013, 331, 38–47. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).