L-Fuzzy Sets and Isomorphic Lattices: Are All the “New” Results Really New? †
Abstract
1. Introduction
2. Preliminaries
2.1. Truth Values and Bounded Lattices
2.2. Isomorphic Lattices: Some General Consequences
- (i)
- If is a function then the composite function has the same order theoretical properties as f.
- (ii)
- If is a binary operation on and if we define by , then the function is a binary operation on with the same order theoretical properties as F.
- (iii)
- If is an n-ary operation on then, as a straightforward generalization, the composite function given byis an n-ary operation on with the same order theoretical properties as .
- (i)
- Let be an order reversing involution (or double negation) on , i.e., implies , and . Then the function is an order reversing involution on , and the complemented lattice is isomorphic to .
- (ii)
- Let be a residuated lattice, i.e., is a (not necessarily commutative) monoid with neutral element , and for the residua we have that for all the assertion is equivalent to both and . Thenis an isomorphic residuated lattice.
- (iii)
- Let be a triangular norm on , i.e., is an associative, commutative order homomorphism with neutral element . Then the function is a triangular norm on .
- (iv)
- Let be a triangular conorm on , i.e., is an associative, commutative order homomorphism with neutral element . Then the function is a triangular conorm on .
- (v)
- Let be a uninorm on , i.e., is an associative, commutative order homomorphism with neutral element such that . Then the function is a uninorm on with neutral element .
- (vi)
- Let be a nullnorm on , i.e., is an associative, commutative order homomorphism such that there is an with such that for all we have , and for all we have . Then the function is a nullnorm on .
- (vii)
- Let be an n-ary aggregation function on , i.e., is an order homomorphism which satisfies and . Then the function is an n-ary aggregation function on .
3. Some Generalizations of Truth Values and Fuzzy Sets
3.1. The Classical Cases: Crisp and Fuzzy Sets
3.2. Generalizations: The Two-Dimensional Case
- (i)
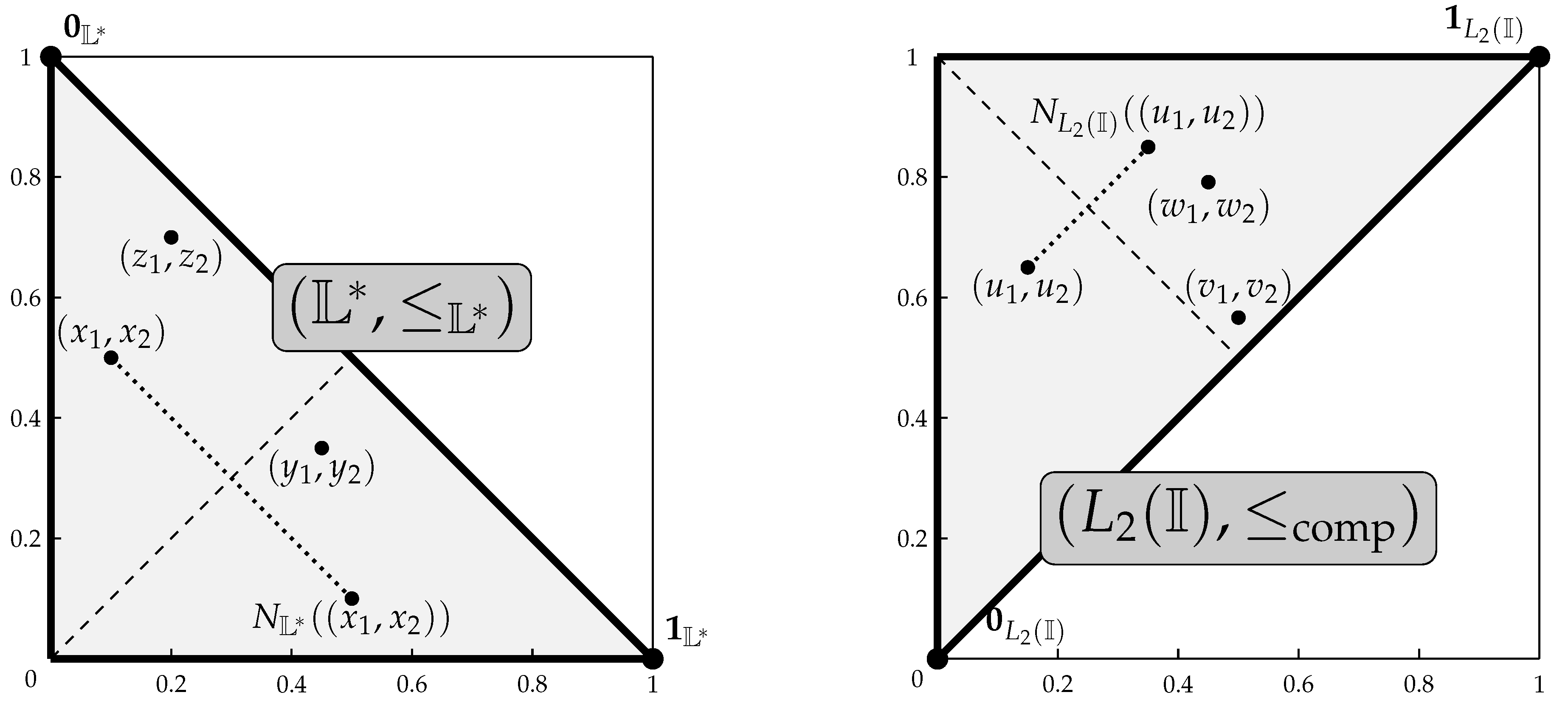
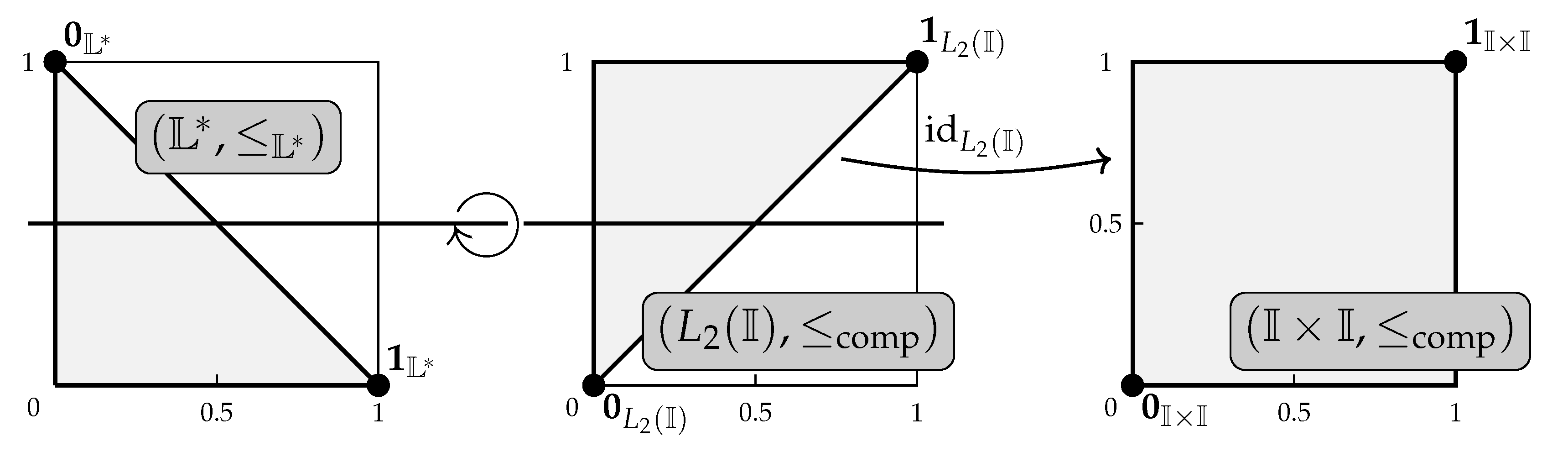
- to the lattice of all closed subintervals of the unit interval , given bywith bottom and top elements and , respectively; a canonical example of an isomorphism between and is provided by the function defined by ;
- (ii)
- to the lattice of all points in the intersection of the unit square and the unit disk with center , i.e.,a canonical example of a lattice isomorphism from to is provided by the function defined by .
- (i)
- The product lattices , , , and are isomorphic to each other.
- (ii)
- The lattices of all -fuzzy subsets of X, of all “intuitionistic” fuzzy subsets of X, of all interval-valued fuzzy subsets of X, of all “Pythagorean” fuzzy subsets of X, and of all -fuzzy subsets of X are isomorphic to each other.
3.3. Generalizations to Higher Dimensions
- (i)
- The lattice is isomorphic to the lattice with top element and bottom element , where the order is given by
- (ii)
- The lattice is isomorphic to the lattice with top element and bottom element , where the order is given by
4. Discussion: Isomorphisms and Questionable Notations
4.1. Isomorphic Lattices: More Consequences
- (i)
- if and are two binary aggregation functions then the function F is a binary aggregation function on ;
- (ii)
- if and are two triangular norms then the function F is a triangular norm on ;
- (iii)
- if and are two triangular conorms then the function F is a triangular conorm on ;
- (iv)
- if and are two uninorms then the function F is a uninorm on ;
- (v)
- if and are two nullnorms then the function F is a nullnorm on .
4.2. The Case of “Intuitionistic” Fuzzy Sets
[...] the logical law of the excluded middle is not valid, similarly to the case in intuitionistic mathematics. Herein emerges the name of that set. [...]
- the mere fact that the law of the excluded middle is violated in the case of -fuzzy sets does not justify to call them “intuitionistic” (also the fuzzy sets in the sense of [1] do not satisfy the law of the excluded middle, in general); moreover (see [53,170,174,175]), the use of an order reversing involution for -fuzzy sets contradicts intuitionistic logic [176]:[...] the connectives of IFS theory violate properties of intuitionistic logic by validating the double negation (involution) axiom [...], which is not valid in intuitionistic logic. (Recall that axioms of intuitionistic logic extended by the axiom of double negation imply classical logic, and thus imply excluded middle [...]
- intuitionistic logic has a close relationship to constructivism:[...] the philosophical ideas behind intuitionism in general, and intuitionistic mathematics and intuitionistic logic in particular have a strong tendency toward constructivist points of view. There are no relationship between these ideas and the basic intuitive ideas of IFS theory [...]
... the term “intuitionistic” in these contexts is historically inappropriate given the standard mathematical usage of “intuitionistic”; and , at every level of existence—powerset level, topological fibre level, categorical level—interval-valued sets, [...], and “intuitionistic” fuzzy sets [...] are redundant...
4.3. The Case of “Pythagorean” Fuzzy Sets
5. Concluding Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Goguen, J.A. L-fuzzy sets. J. Math. Anal. Appl. 1967, 18, 145–174. [Google Scholar] [CrossRef]
- Zadeh, L.A. Quantitative fuzzy semantics. Inf. Sci. 1971, 3, 159–176. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its applications to approximate reasoning. Part I. Inform. Sci. 1975, 8, 199–251. [Google Scholar] [CrossRef]
- Bustince, H.; Barrenechea, E.; Pagola, M.; Fernandez, J.; Xu, Z.; Bedregal, B.; Montero, J.; Hagras, H.; Herrera, F.; De Baets, B. A historical account of types of fuzzy sets and their relationships. IEEE Trans. Fuzzy Syst. 2016, 24, 179–194. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. In VII ITKR’s Session, Sofia, June 1983; Sgurev, V., Ed.; Central Science and Technology Library, Bulgarian Academy of Sciences: Sofia, Bulgaria, 1984. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Deng, J.L. Grey information space. J. Grey Syst. 1989, 1, 103–117. [Google Scholar]
- Gau, W.-L.; Buehrer, D.J. Vague sets. IEEE Trans. Syst. Man Cybern. 1993, 23, 610–614. [Google Scholar] [CrossRef]
- Bedregal, B.; Beliakov, G.; Bustince, H.; Calvo, T.; Mesiar, R.; Paternain, D. A class of fuzzy multisets with a fixed number of memberships. Inf. Sci. 2012, 189, 1–17. [Google Scholar] [CrossRef]
- Jahn, K.-U. Intervall-wertige Mengen. Math. Nachr. 1975, 68, 115–132. [Google Scholar] [CrossRef]
- Sambuc, R. Fonctions φ-Floues: Application à L’aide au Diagnostic en Pathologie Thyroidienne. Ph.D. Thesis, Université Aix-Marseille II, Faculté de Médecine, Marseille, France, 1975. (In French). [Google Scholar]
- Grattan-Guinness, I. Fuzzy membership mapped onto intervals and many-valued quantities. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 1976, 22, 149–160. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets—A new concept for computational intelligence problems. In Proceedings of the Third World Congress on Information and Communication Technologies (WICT 2013), Hanoi, Vietnam, 15–18 December 2013; pp. 1–6. [Google Scholar]
- Cantor, G. Beiträge zur Begründung der transfiniten Mengenlehre. Art. I. Math. Ann. 1895, 46, 481–512. (In German) [Google Scholar] [CrossRef]
- Hausdorff, F. Grundzüge der Mengenlehre; Veit und Comp.: Leipzig, Germany, 1914. (In German) [Google Scholar]
- Boole, G. The Mathematical Analysis of Logic, Being an Essay Towards a Calculus of Deductive Reasoning; Macmillan, Barclay, & Macmillan: Cambridge, UK, 1847. [Google Scholar]
- Boole, G. An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities; Walton: London, UK, 1854. [Google Scholar]
- Menger, K. Probabilistic theories of relations. Proc. Natl. Acad. Sci. USA 1951, 37, 178–180. [Google Scholar] [CrossRef] [PubMed]
- Menger, K. Probabilistic geometry. Proc. Natl. Acad. Sci. USA 1951, 37, 226–229. [Google Scholar] [CrossRef] [PubMed]
- Menger, K. Ensembles flous et fonctions aléatoires. C. R. Acad. Sci. Paris Sér. A 1951, 232, 2001–2003. (In French) [Google Scholar]
- Klaua, D. Über einen Ansatz zur mehrwertigen Mengenlehre. Monatsb. Deutsch. Akad. Wiss. 1965, 7, 859–867. (In German) [Google Scholar]
- Klaua, D. Einbettung der klassischen Mengenlehre in die mehrwertige. Monatsb. Deutsch. Akad. Wiss. 1967, 9, 258–272. (In German) [Google Scholar]
- De Luca, A.; Termini, S. Entropy of L-fuzzy sets. Inf. Control 1974, 24, 55–73. [Google Scholar] [CrossRef]
- Negoita, C.V.; Ralescu, D.A. Applications of Fuzzy Sets to Systems Analysis; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Negoita, C.V.; Ralescu, D.A. L-fuzzy sets and L-flou sets. Elektronische Informationsverarbeitung und Kybernetik 1976, 12, 599–605. [Google Scholar]
- Höhle, U. Representation theorems for L-fuzzy quantities. Fuzzy Sets Syst. 1981, 5, 83–107. [Google Scholar] [CrossRef]
- Sarkar, M. On L-fuzzy topological spaces. J. Math. Anal. Appl. 1981, 84, 431–442. [Google Scholar] [CrossRef]
- Höhle, U. Probabilistic topologies induced by L-fuzzy uniformities. Manuscr. Math. 1982, 38, 289–323. [Google Scholar] [CrossRef]
- Rodabaugh, S.E. Connectivity and the L-fuzzy unit interval. Rocky Mt. J. Math. 1982, 12, 113–121. [Google Scholar] [CrossRef]
- Rodabaugh, S.E. Fuzzy addition in the L-fuzzy real line. Fuzzy Sets Syst. 1982, 8, 39–51. [Google Scholar] [CrossRef]
- Cerruti, U. Completion of L-fuzzy relations. J. Math. Anal. Appl. 1983, 94, 312–327. [Google Scholar] [CrossRef]
- Sugeno, M.; Sasaki, M. L-fuzzy category. Fuzzy Sets Syst. 1983, 11, 43–64. [Google Scholar] [CrossRef]
- Klein, A.J. Generalizing the L-fuzzy unit interval. Fuzzy Sets Syst. 1984, 12, 271–279. [Google Scholar] [CrossRef]
- Kubiak, T. L-fuzzy normal spaces and Tietze Extension Theorem. J. Math. Anal. Appl. 1987, 125, 141–153. [Google Scholar] [CrossRef]
- Flüshöh, W.; Höhle, U. L-fuzzy contiguity relations and L-fuzzy closure operators in the case of completely distributive, complete lattices L. Math. Nachr. 1990, 145, 119–134. [Google Scholar] [CrossRef]
- Kudri, S.R.T. Compactness in L-fuzzy topological spaces. Fuzzy Sets Syst. 1994, 67, 329–336. [Google Scholar] [CrossRef]
- Kudri, S.R.T.; Warner, M.W. L-fuzzy local compactness. Fuzzy Sets Syst. 1994, 67, 337–345. [Google Scholar] [CrossRef]
- Kubiak, T. On L-Tychonoff spaces. Fuzzy Sets Syst. 1995, 73, 25–53. [Google Scholar] [CrossRef]
- Ovchinnikov, S. On the image of an L-fuzzy group. Fuzzy Sets Syst. 1998, 94, 129–131. [Google Scholar] [CrossRef]
- Kubiak, T.; Zhang, D. On the L-fuzzy Brouwer fixed point theorem. Fuzzy Sets Syst. 1999, 105, 287–292. [Google Scholar] [CrossRef]
- Jäger, G. A category of L-fuzzy convergence spaces. Quaest. Math. 2001, 24, 501–517. [Google Scholar] [CrossRef]
- Birkhoff, G. Lattice Theory; American Mathematical Society: Providence, RI, USA, 1973. [Google Scholar]
- Grabisch, M.; Marichal, J.-L.; Mesiar, R.; Pap, E. Aggregation Functions; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Grabisch, M.; Marichal, J.-L.; Mesiar, R.; Pap, E. Aggregation functions: Means. Inf. Sci. 2011, 181, 1–22. [Google Scholar] [CrossRef]
- Pavelka, J. On fuzzy logic. II. Enriched residuated lattices and semantics of propositional calculi. Z. Math. Log. Grundl. Math. 1979, 25, 119–134. [Google Scholar] [CrossRef]
- Höhle, U. Commutative, residuated l-monoids. In Non-Classical Logics and Their Applications to Fuzzy Subsets. A Handbook of the Mathematical Foundations of Fuzzy Set Theory; Höhle, U., Klement, E.P., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995; Chapter IV; pp. 53–106. [Google Scholar]
- Hájek, P. Basic fuzzy logic and BL-algebras. Soft Comput. 1998, 2, 124–128. [Google Scholar] [CrossRef]
- Hájek, P. Metamathematics of Fuzzy Logic; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Turunen, E. BL-algebras of basic fuzzy logic. Mathw. Soft Comput. 1999, 6, 49–61. [Google Scholar]
- Esteva, F.; Godo, L.; Hájek, P.; Navara, M. Residuated fuzzy logics with an involutive negation. Arch. Math. Log. 2000, 39, 103–124. [Google Scholar] [CrossRef]
- Jenei, S. New family of triangular norms via contrapositive symmetrization of residuated implications. Fuzzy Sets Syst. 2000, 110, 157–174. [Google Scholar] [CrossRef]
- Jenei, S.; Kerre, E.E. Convergence of residuated operators and connective stability of non-classical logics. Fuzzy Sets Syst. 2000, 114, 411–415. [Google Scholar] [CrossRef]
- Esteva, F.; Godo, L. Monoidal t-norm based logic: Towards a logic for left-continuous t-norms. Fuzzy Sets Syst. 2001, 124, 271–288. [Google Scholar] [CrossRef]
- Hájek, P. Observations on the monoidal t-norm logic. Fuzzy Sets Syst. 2002, 132, 107–112. [Google Scholar] [CrossRef]
- Esteva, F.; Godo, L.; Montagna, F. Axiomatization of any residuated fuzzy logic defined by a continuous t-norm. In Proceedings of the Congress of the International Fuzzy Systems Association (IFSA), Istanbul, Turkey, 30 June–2 July 2003; pp. 172–179. [Google Scholar]
- Mesiar, R.; Mesiarová, A. Residual implications and left-continuous t-norms which are ordinal sums of semigroups. Fuzzy Sets Syst. 2004, 143, 47–57. [Google Scholar] [CrossRef]
- Montagna, F. On the predicate logics of continuous t-norm BL-algebras. Arch. Math. Log. 2005, 44, 97–114. [Google Scholar] [CrossRef]
- Van Gasse, B.; Cornelis, C.; Deschrijver, G.; Kerre, E.E. A characterization of interval-valued residuated lattices. Int. J. Approx. Reason. 2008, 49, 478–487. [Google Scholar] [CrossRef]
- Van Gasse, B.; Cornelis, C.; Deschrijver, G.; Kerre, E.E. Triangle algebras: A formal logic approach to interval-valued residuated lattices. Fuzzy Sets Syst. 2008, 159, 1042–1060. [Google Scholar] [CrossRef]
- De Baets, B.; Mesiar, R. Triangular norms on product lattices. Fuzzy Sets Syst. 1999, 104, 61–75. [Google Scholar] [CrossRef]
- Saminger-Platz, S.; Klement, E.P.; Mesiar, R. On extensions of triangular norms on bounded lattices. Indag. Math. 2008, 19, 135–150. [Google Scholar] [CrossRef]
- Menger, K. Statistical metrics. Proc. Natl. Acad. Sci. USA 1942, 8, 535–537. [Google Scholar] [CrossRef]
- Schweizer, B.; Sklar, A. Espaces métriques aléatoires. C. R. Acad. Sci. Paris Sér. A 1958, 247, 2092–2094. (In French) [Google Scholar]
- Schweizer, B.; Sklar, A. Statistical metric spaces. Pac. J. Math. 1960, 10, 313–334. [Google Scholar] [CrossRef]
- Schweizer, B.; Sklar, A. Probabilistic Metric Spaces; North-Holland: New York, NY, USA, 1983. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular Norms; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms. Position paper I: Basic analytical and algebraic properties. Fuzzy Sets Syst. 2004, 143, 5–26. [Google Scholar] [CrossRef]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms. Position paper II: General constructions and parameterized families. Fuzzy Sets Syst. 2004, 145, 411–438. [Google Scholar] [CrossRef]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms. Position paper III: Continuous t-norms. Fuzzy Sets Syst. 2004, 145, 439–454. [Google Scholar] [CrossRef]
- Alsina, C.; Frank, M.J.; Schweizer, B. Associative Functions: Triangular Norms and Copulas; World Scientific: Singapore, 2006. [Google Scholar]
- Yager, R.R.; Rybalov, A. Uninorm aggregation operators. Fuzzy Sets Syst. 1996, 80, 111–120. [Google Scholar] [CrossRef]
- Calvo, T.; De Baets, B.; Fodor, J. The functional equations of Frank and Alsina for uninorms and nullnorms. Fuzzy Sets Syst. 2001, 120, 385–394. [Google Scholar] [CrossRef]
- Calvo, T.; Mayor, G.; Mesiar, R. (Eds.) Aggregation Operators. New Trends and Applications; Physica-Verlag: Heidelberg, Germany, 2002. [Google Scholar]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide for Practitioners; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Grabisch, M.; Marichal, J.-L.; Mesiar, R.; Pap, E. Aggregation functions: Construction methods, conjunctive, disjunctive and mixed classes. Inf. Sci. 2011, 181, 23–43. [Google Scholar] [CrossRef]
- Negoita, C.V.; Ralescu, D.A. Representation theorems for fuzzy concepts. Kybernetes 1975, 4, 169–174. [Google Scholar] [CrossRef]
- Shortliffe, E.H.; Buchanan, B.G. A model of inexact reasoning in medicine. Math. Biosci. 1975, 23, 351–379. [Google Scholar] [CrossRef]
- Shortliffe, E.H. Computer Based Medical Consultation—‘MYCIN’; Elsevier: New York, NY, USA, 1976. [Google Scholar]
- Jackson, P. Introduction to Expert Systems; Addison-Wesley: Wokingham, UK, 1986. [Google Scholar]
- Hájek, P.; Havránek, T.; Jiroušek, R. Uncertain Information Processing in Expert Systems; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Atanassov, K.T. Intuitionistic Fuzzy Sets; Physica-Verlag: Heidelberg, Germany, 1999. [Google Scholar]
- Deschrijver, G.; Kerre, E.E. On the relationship between some extensions of fuzzy set theory. Fuzzy Sets Syst. 2003, 133, 227–235. [Google Scholar] [CrossRef]
- Wang, G.-J.; He, Y.-Y. Intuitionistic fuzzy sets and L-fuzzy sets. Fuzzy Sets Syst. 2000, 110, 271–274. [Google Scholar] [CrossRef]
- De Miguel, L.; Bustince, H.; Fernandez, J.; Induráin, E.; Kolesárová, A.; Mesiar, R. Construction of admissible linear orders for interval-valued Atanassov intuitionistic fuzzy sets with an application to decision making. Inf. Fusion 2016, 27, 189–197. [Google Scholar] [CrossRef]
- Dick, S.; Yager, R.R.; Yazdanbakhsh, O. On Pythagorean and complex fuzzy set operations. IEEE Trans. Fuzzy Syst. 2016, 24, 1009–1021. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multi-criteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Harding, J.; Walker, C.; Walker, E. The variety generated by the truth value algebra of type-2 fuzzy sets. Fuzzy Sets Syst. 2010, 161, 735–749. [Google Scholar] [CrossRef]
- Walker, C.; Walker, E. The algebra of fuzzy truth values. Fuzzy Sets Syst. 2005, 149, 309–347. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis; American Research Press: Rehoboth, NM, USA, 1998. [Google Scholar]
- Smarandache, F. A unifying field in logics: Neutrosophic logic. Multiple-Valued Log. 2002, 8, 385–482. [Google Scholar]
- Smarandache, F. Definition of neutrosophic logic—A generalization of the intuitionistic fuzzy logic. In Proceedings of the 3rd Conference of the European Society for Fuzzy Logic and Technology, Zittau, Germany, 10–12 September 2003; pp. 141–146. [Google Scholar]
- Smarandache, F. Neutrosophic set—A generalization of the intuitionistic fuzzy set. In Proceedings of the 2006 IEEE International Conference on Granular Computing, Atlanta, GA, USA, 12–12 May 2006; pp. 38–42. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. In Multispace & Multistructure. Neutrosophic Transdisciplinarity (100 Collected Papers of Sciences); Smarandache, F., Ed.; North-European Scientific Publishers: Hanko, Finland, 2010; Volume IV, pp. 410–413. [Google Scholar]
- Bedregal, B.; Mezzomo, I.; Reiser, R.H.S. n-Dimensional Fuzzy Negations. 2017. Available online: arXiv.org/pdf/1707.08617v1 (accessed on 26 July 2017).
- Bedregal, B.; Beliakov, G.; Bustince, H.; Calvo, T.; Fernández, J.; Mesiar, R. A characterization theorem for t-representable n-dimensional triangular norms. In Eurofuse 2011. Workshop on Fuzzy Methods for Knowledge-Based Systems; Melo-Pinto, P., Couto, P., Serôdio, C., Fodor, J., De Baets, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 103–112. [Google Scholar]
- Cuong, B.C.; Kreinovich, V.; Ngan, R.T. A classification of representable t-norm operators for picture fuzzy sets. In Proceedings of the Eighth International Conference on Knowledge and Systems Engineering (KSE 2016), Hanoi, Vietnam, 6–8 October 2016; pp. 19–24. [Google Scholar]
- Cuong, B.C.; Ngan, R.T.; Ngoc, L.C. Some algebraic properties of picture fuzzy t-norms and picture fuzzy t-conorms on standard neutrosophic sets. arXiv, 2017; arXiv:1701.0144. [Google Scholar]
- Son, L.H.; Viet, P.V.; Hai, P.V. Picture inference system: A new fuzzy inference system on picture fuzzy set. Appl. Intell. 2017, 46, 652–669. [Google Scholar] [CrossRef]
- Bo, C.; Zhang, X. New operations of picture fuzzy relations and fuzzy comprehensive evaluation. Symmetry 2017, 9, 268. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, X.; Tu, H.; Tao, S. Some geometric aggregation operators based on picture fuzzy sets and their application in multiple attribute decision making. Ital. J. Pure Appl. Math. 2017, 37, 477–492. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Stupňanová, A. Picture fuzzy sets and 3-fuzzy sets. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 476–482. [Google Scholar]
- Cuong, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409–420. [Google Scholar]
- Cuong, B.C.; Hai, P.V. Some fuzzy logic operators for picture fuzzy sets. In Proceedings of the Seventh International Conference on Knowledge and Systems Engineering (KSE 2015), Ho Chi Minh City, Vietnam, 8–10 October 2015; pp. 132–137. [Google Scholar]
- Cuong, B.C.; Ngan, R.T.; Hai, B.D. An involutive picture fuzzy negation on picture fuzzy sets and some De Morgan triples. In Proceedings of the Seventh International Conference on Knowledge and Systems Engineering (KSE 2015), Ho Chi Minh City, Vietnam, 8–10 October 2015; pp. 126–131. [Google Scholar]
- Thong, P.H.; Son, L.H. Picture fuzzy clustering: A new computational intelligence method. Soft Comput. 2016, 20, 3549–3562. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. Classes of intuitionistic fuzzy t-norms satisfying the residuation principle. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2003, 11, 691–709. [Google Scholar] [CrossRef]
- Deschrijver, G. The Archimedean property for t-norms in interval-valued fuzzy set theory. Fuzzy Sets Syst. 2006, 157, 2311–2327. [Google Scholar] [CrossRef]
- Deschrijver, G. Arithmetic operators in interval-valued fuzzy set theory. Inf. Sci. 2007, 177, 2906–2924. [Google Scholar] [CrossRef]
- Deschrijver, G. A representation of t-norms in interval-valued L-fuzzy set theory. Fuzzy Sets Syst. 2008, 159, 1597–1618. [Google Scholar] [CrossRef]
- Deschrijver, G. Characterizations of (weakly) Archimedean t-norms in interval-valued fuzzy set theory. Fuzzy Sets Syst. 2009, 160, 778–801. [Google Scholar] [CrossRef]
- Deschrijver, G.; Cornelis, C. Representability in interval-valued fuzzy set theory. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2007, 15, 345–361. [Google Scholar] [CrossRef]
- Deschrijver, G.; Cornelis, C.; Kerre, E.E. On the representation of intuitionistic fuzzy t-norms and t-conorms. IEEE Trans. Fuzzy Syst. 2004, 12, 45–61. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. On the composition of intuitionistic fuzzy relations. Fuzzy Sets Syst. 2003, 136, 333–361. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. Uninorms in L*-fuzzy set theory. Fuzzy Sets Syst. 2004, 148, 243–262. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. Implicators based on binary aggregation operators in interval-valued fuzzy set theory. Fuzzy Sets Syst. 2005, 153, 229–248. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. Triangular norms and related operators in L*-fuzzy set theory. In Logical, Algebraic, Analytic, and Probabilistic Aspects of Triangular Norms; Klement, E.P., Mesiar, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Chapter 8; pp. 231–259. [Google Scholar]
- Abbas, S.E. Intuitionistic supra fuzzy topological spaces. Chaos Solitons Fractals 2004, 21, 1205–1214. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Elements of intuitionistic fuzzy logic. Part I. Fuzzy Sets Syst. 1998, 95, 39–52. [Google Scholar] [CrossRef]
- Atanassov, K.T. More on intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 33, 37–45. [Google Scholar] [CrossRef]
- Atanassov, K.T. Remarks on the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1992, 51, 117–118. [Google Scholar] [CrossRef]
- Atanassov, K.T. New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Atanassov, K.T. Operators over interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 64, 159–174. [Google Scholar] [CrossRef]
- Atanassov, K.T. Remarks on the intuitionistic fuzzy sets—III. Fuzzy Sets Syst. 1995, 75, 401–402. [Google Scholar] [CrossRef]
- Atanassov, K.T. An equality between intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 257–258. [Google Scholar] [CrossRef]
- Atanassov, K.T. Remark on the intuitionistic fuzzy logics. Fuzzy Sets Syst. 1998, 95, 127–129. [Google Scholar] [CrossRef]
- Atanassov, K.T. Two theorems for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 110, 267–269. [Google Scholar] [CrossRef]
- Atanassova, L.C. Remark on the cardinality of the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1995, 75, 399–400. [Google Scholar] [CrossRef]
- Ban, A.I.; Gal, S.G. Decomposable measures and information measures for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 123, 103–117. [Google Scholar] [CrossRef]
- Burillo, P.; Bustince, H. Construction theorems for intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 84, 271–281. [Google Scholar] [CrossRef]
- Burillo, P.; Bustince, H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Syst. 1996, 78, 305–316. [Google Scholar] [CrossRef]
- Bustince, H. Construction of intuitionistic fuzzy relations with predetermined properties. Fuzzy Sets Syst. 2000, 109, 379–403. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Structures on intuitionistic fuzzy relations. Fuzzy Sets Syst. 1996, 78, 293–300. [Google Scholar] [CrossRef]
- Çoker, D. An introduction to intuitionistic fuzzy topological spaces. Fuzzy Sets Syst. 1997, 88, 81–89. [Google Scholar] [CrossRef]
- Çoker, D.; Demirci, M. An introduction to intuitionistic fuzzy topological spaces in šostak’s sense. Busefal 1996, 67, 67–76. [Google Scholar]
- De, S.K.; Biswas, R.; Roy, A.R. Some operations on intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 477–484. [Google Scholar] [CrossRef]
- De, S.K.; Biswas, R.; Roy, A.R. An application of intuitionistic fuzzy sets in medical diagnosis. Fuzzy Sets Syst. 2001, 117, 209–213. [Google Scholar] [CrossRef]
- Demirci, M. Axiomatic theory of intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 110, 253–266. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, E.P. The category of intuitionistic fuzzy topological spaces. Bull. Korean Math. Soc. 2000, 37, 63–76. [Google Scholar]
- Mondal, T.K.; Samanta, S.K. On intuitionistic gradation of openness. Fuzzy Sets Syst. 2002, 131, 323–336. [Google Scholar] [CrossRef]
- Samanta, S.K.; Mondal, T.K. Intuitionistic gradation of openness: Intuitionistic fuzzy topology. Busefal 1997, 73, 8–17. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Brouwer, L.E.J. Intuitionism and formalism. Bull. Am. Math. Soc. 1913, 20, 81–96. [Google Scholar] [CrossRef]
- Brouwer, L.E.J. Intuitionistische verzamelingsleer. Amst. Ak. Versl. 1921, 29, 797–802. (In Dutch) [Google Scholar]
- Brouwer, L.E.J. Intuitionistische splitsing van mathematische grondbegrippen. Amst. Ak. Versl. 1923, 32, 877–880. (In Dutch) [Google Scholar]
- Brouwer, L.E.J. Über die Bedeutung des Satzes vom ausgeschlossenen Dritten in der Mathematik, insbesondere in der Funktionentheorie. J. Reine Angew. Math. 1925, 154, 1–7. (In German) [Google Scholar]
- Brouwer, L.E.J. Zur Begründung der intuitionistischen Mathematik. I. Math. Ann. 1925, 93, 244–257. (In German) [Google Scholar] [CrossRef]
- Brouwer, L.E.J. Zur Begründung der intuitionistischen Mathematik. II. Math. Ann. 1926, 95, 453–472. (In German) [Google Scholar] [CrossRef]
- Brouwer, L.E.J. Zur Begründung der intuitionistischen Mathematik. III. Math. Ann. 1927, 96, 451–488. (In German) [Google Scholar] [CrossRef]
- Brouwer, L.E.J. Intuitionistische Betrachtungen über den Formalismus. Sitz. Preuß. Akad. Wiss. Phys. Math. Kl. 1928, 48–52. [Google Scholar]
- Brouwer, L.E.J. On the significance of the principle of excluded middle in mathematics, especially in function theory. With two Addenda and corrigenda. In From Frege to Gödel. A Source Book in Mathematical Logic, 1879–1931; van Heijenoort, J., Ed.; Harvard University Press: Cambridge, MA, USA, 1967; pp. 334–345. [Google Scholar]
- Van Heijenoort, J. From Frege to Gödel. A Source Book in Mathematical Logic, 1879–1931; Harvard University Press: Cambridge, MA, USA, 1967. [Google Scholar]
- Hilbert, D. Die Grundlagen der Mathematik. Vortrag, gehalten auf Einladung des Mathematischen Seminars im Juli 1927 in Hamburg. Abh. Math. Semin. Univ. Hamb. 1928, 6, 65–85. (In German) [Google Scholar] [CrossRef]
- Hilbert, D.; Bernays, P. Grundlagen der Mathematik. I; Springer: Berlin/Heidelberg, Germany, 1934. (In German) [Google Scholar]
- Hilbert, D. The foundations of mathematics. In From Frege to Gödel. A Source Book in Mathematical Logic, 1879–1931; van Heijenoort, J., Ed.; Harvard University Press: Cambridge, MA, USA, 1967; pp. 464–480. [Google Scholar]
- Kolmogorov, A.N. On the principle of excluded middle. In From Frege to Gödel. A Source Book in Mathematical Logic, 1879–1931; van Heijenoort, J., Ed.; Harvard University Press: Cambridge, MA, USA, 1967; pp. 414–437. [Google Scholar]
- Takeuti, G.; Titani, S. Intuitionistic fuzzy logic and intuitionistic fuzzy set theory. J. Symb. Log. 1984, 49, 851–866. [Google Scholar] [CrossRef]
- Takeuti, G.; Titani, S. Globalization of intuitionistic set theory. Ann. Pure Appl. Log. 1987, 33, 195–211. [Google Scholar] [CrossRef]
- Baaz, M.; Fermüller, C.G. Intuitionistic counterparts of finitely-valued logics. In Proceedings of the 26th International Symposium on Multiple-Valued Logic, Santiago de Compostela, Spain, 19–31 January 1996; pp. 136–141. [Google Scholar]
- Ciabattoni, A. A proof-theoretical investigation of global intuitionistic (fuzzy) logic. Arch. Math. Log. 2005, 44, 435–457. [Google Scholar] [CrossRef]
- Gottwald, S. Universes of fuzzy sets and axiomatizations of fuzzy set theory. I. Model-based and axiomatic approaches. Stud. Log. 2006, 82, 211–244. [Google Scholar] [CrossRef]
- Gottwald, S. Universes of fuzzy sets and axiomatizations of fuzzy set theory. II. Category theoretic approaches. Stud. Log. 2006, 84, 23–50. [Google Scholar] [CrossRef]
- Hájek, P.; Cintula, P. On theories and models in fuzzy predicate logics. J. Symb. Log. 2006, 71, 863–880. [Google Scholar] [CrossRef]
- Dubois, D.; Gottwald, S.; Hajek, P.; Kacprzyk, J.; Prade, H. Terminological difficulties in fuzzy set theory—The case of “Intuitionistic Fuzzy Sets”. Fuzzy Sets Syst. 2005, 156, 485–491. [Google Scholar] [CrossRef]
- Cattaneo, G.; Ciucci, D. Generalized negations and intuitionistic fuzzy sets—A criticism to a widely used terminology. In Proceedings of the 3rd Conference of the European Society for Fuzzy Logic and Technology, Zittau, Germany, 10–12 September 2003; pp. 147–152. [Google Scholar]
- Grzegorzewski, P.; Mrówka, E. Some notes on (Atanassov’s) intuitionistic fuzzy sets. Fuzzy Sets Syst. 2005, 156, 492–495. [Google Scholar] [CrossRef]
- Gutiérrez García, J.; Rodabaugh, S.E. Order-theoretic, topological, categorical redundancies of interval-valued sets, grey sets, vague sets, interval-valued “intuitionistic” sets, “intuitionistic” fuzzy sets and topologies. Fuzzy Sets Syst. 2005, 156, 445–484. [Google Scholar] [CrossRef]
- Atanassov, K. Answer to D. Dubois, S. Gottwald, P. Hajek, J. Kacprzyk and H. Prade’s paper “Terminological difficulties in fuzzy set theory—The case of “Intuitionistic Fuzzy Sets””. Fuzzy Sets Syst. 2005, 156, 496–499. [Google Scholar] [CrossRef]
- Butnariu, D.; Klement, E.P.; Mesiar, R.; Navara, M. Sufficient triangular norms in many-valued logics with standard negation. Arch. Math. Log. 2005, 44, 829–849. [Google Scholar] [CrossRef]
- Cintula, P.; Klement, E.P.; Mesiar, R.; Navara, M. Residuated logics based on strict triangular norms with an involutive negation. Math. Log. Quart. 2006, 52, 269–282. [Google Scholar] [CrossRef]
- Kleene, S.C. Introduction to Metamathematics; North-Holland: Amsterdam, The Netherlands, 1952. [Google Scholar]
- Xia, M.; Xu, Z.; Zhu, B. Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm. Knowl.-Based Syst. 2012, 31, 78–88. [Google Scholar] [CrossRef]
- Rahman, K.; Abdullah, S.; Ahmed, R.; Ullah, M. Pythagorean fuzzy Einstein weighted geometric aggregation operator and their application to multiple attribute group decision making. J. Intell. Fuzzy Syst. 2017, 33, 635–647. [Google Scholar] [CrossRef]
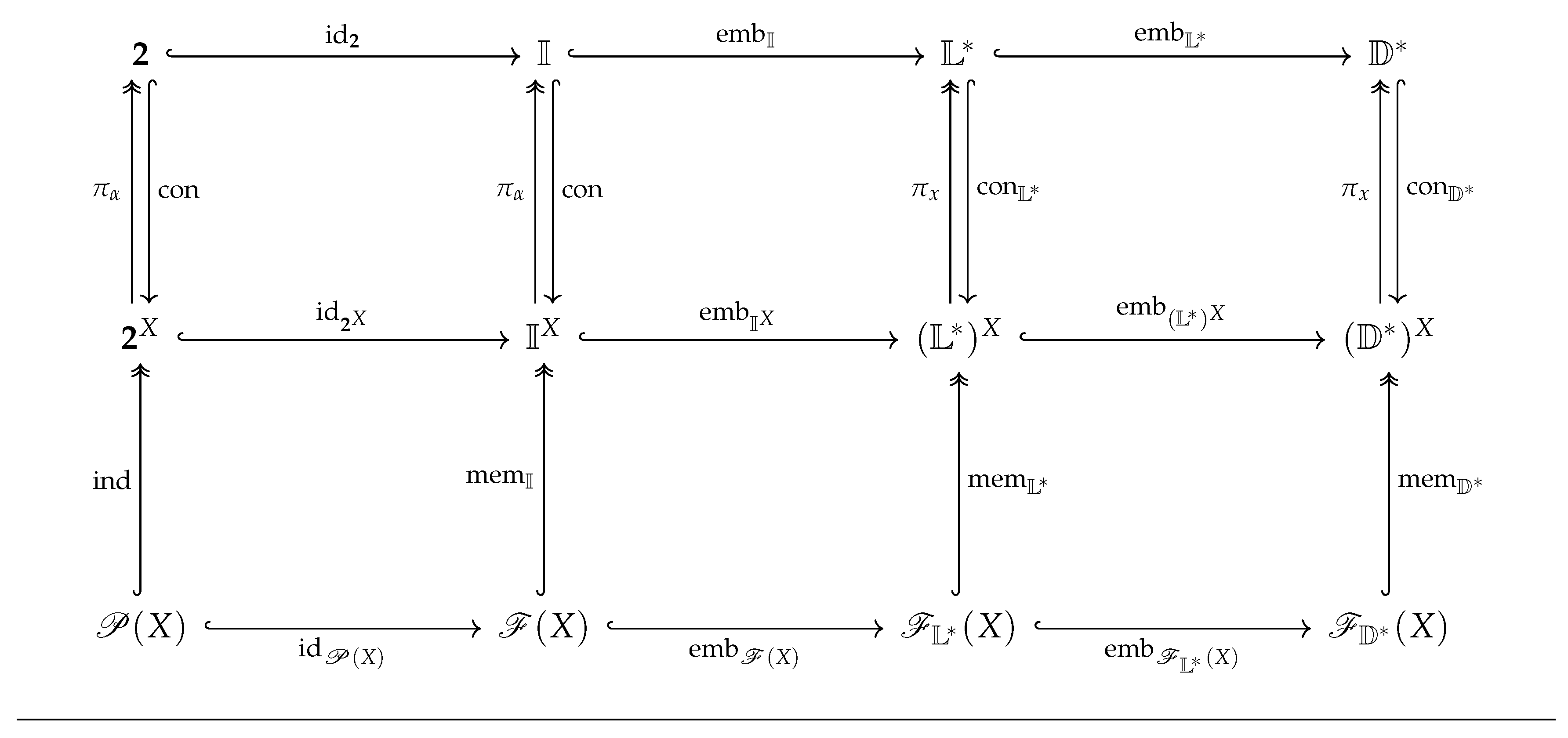
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klement, E.P.; Mesiar, R.
L-Fuzzy Sets and Isomorphic Lattices: Are All the “New” Results Really New?
Klement EP, Mesiar R.
L-Fuzzy Sets and Isomorphic Lattices: Are All the “New” Results Really New?
Klement, Erich Peter, and Radko Mesiar.
2018. "L-Fuzzy Sets and Isomorphic Lattices: Are All the “New” Results Really New?
Klement, E. P., & Mesiar, R.
(2018). L-Fuzzy Sets and Isomorphic Lattices: Are All the “New” Results Really New?





