1. Introduction
The spread of infectious diseases is a major concern for human populations. Disease control by any therapy measure lies on the understanding of the disease itself. Epidemic modeling is an interdisciplinary subject that can be addressed from deterministic applied mathematical models and stochastic processes theory [
1,
2] to quantitative social and biological science and empirical analysis of data [
3]. Epidemic models are also used to describe spreading processes connected with technology, business, marketing or sociology, where the interest is related to dissemination of news, rumors or ideas among different groups [
4,
5,
6,
7,
8]. Mathematical models provide an essential tool for understanding and forecasting the spread of infectious diseases and also to suggest control policies.
There is a large variety of models for describing the spread of an infective process [
1,
2]. An essential distinction is done between deterministic and stochastic models. Deterministic models constitute a vast majority of the existing literature and are formulated in terms of ordinary differential equations (ODE); consequently they predict the same dynamic for an infective process given the same initial conditions. However this is not what it is expected to happen in real world diseases, outbreaks do not involve the same people becoming infected at the same time and uncertainty should be included when modeling diseases. The stochastic models [
2], analogous to those defined by ODE, take into account the random nature of the events and, hence, they are mainly used to measure probabilities of major outbreaks, disease extinction and, in general, to make statistical analysis of some relevant epidemic descriptors.
In any case, both deterministic and stochastic frameworks are important but stochastic models seems to be more appropriate to describe the evolution of an infective process evolving in a small community, rather than their deterministic counterparts (e.g., [
2,
9]). In deterministic models, persistence or extinction of the epidemic process is determined by the basic reproduction number,
(see for instance [
10,
11]). Usually, stochastic models inherited the basic reproduction number from their deterministic counterparts however, in stochastic epidemic where Markov chains model disease spread (see [
12,
13]), two alternative random variables (namely, the exact reproduction number and the population transmission number) provide a real measurement of the spread of the disease at the initial time or at any time during the epidemic process.
Most of the research works, both deterministic and stochastic, deal with continuous-time models. However, one of the earliest works is the model studied by Reed and Frost in 1928, who formulate an SIR model using a discrete-time Markov chain (DTMC) [
1]. In recent years, literature shows an increasing interest in using discrete-time models. Emmert and Allen, in [
14], consider a discrete-time model to investigate the spread of a disease within a structured host population. Allen and van den Driessche [
15] applied the next generation approach for calculating the basic reproduction number to several models related to hantavirus and chytridiomycosis wildlife diseases. In [
16], authors introduce probabilities to formulate death, recovery and incidence rates of epidemic diseases on discrete-time SI and SIS epidemic models with vital dynamics. Bistability of discrete-time SI and SIS epidemic models with vertical transmission is the subject matter of [
17]. An SIS model with a temporary vaccination program is studied in [
18]. D’Onofrio et al. [
19] analyze a discrete-time SIR model where vaccination coverage depends on the risk of infection. In [
20,
21], the Reed–Frost model is generalized by Markovian models of SIR and SEIR types, where transition probabilities depend on the total number of diseased, the number of daily encounters and the probability of transmission per contact. Under demographic population dynamics, van den Driessche and Yakubu [
22] use the next generation method to compute
and to investigate disease extinction and persistence. An approximation of the deterministic multiple infectious model by a Branching process is employed in [
23] to extract information about disease extinction. Accuracy of discrete-time approaches for studying continuous time contagion dynamics is the topic developed in [
24], who show potential limitations of this approach depending on the time-step considered.
In this paper we deal with a stochastic SIS epidemic model, that describes diseases such as tuberculosis, meningitis or some sexually transmitted diseases, in which infected individuals do not present an exposed period and are recovered with no immunity. Hence, individuals have reoccurring infections. The host population is divided into two groups: susceptible (S) or infected (I). We assume that disease transmission depends on the number of infective individuals and also on a contact rate, ; in addition individual recoveries depend on the recovery rate . For any event (in our model, either contact or recovery), the event rate or intensity provides the mean number of events per unit time. Hence, in case of recoveries denotes the mean infectious time. To control the epidemic spread, the population is observed at a fixed time interval.
The aim of this paper is to analyze, for a discrete-time SIS model, the number of inspections that find an active epidemic. We remark that this quantity is the discrete-time analogous of the extinction time that describes the length of the epidemic process.
The extinction time has been the subject of interest of many papers. Many of them focus on the determination of the moments and a few also on whole distribution. In that sense, assuming a finite birth-death process, Norden [
25] first obtained an explicit expression for the mean time to extinction and established that the extinction time, when the initial distribution equals the quasi-stationary distribution, follows a simple exponential distribution. Allen and Burgin [
26], for SIS and SIR models in discrete-time, investigated numerically the expected duration. Stone et al. [
27], for an SIS model with external infection, determine also expressions for higher order moments. Artalejo et al. [
28], for general birth-death and SIR models, develop algorithmic schemes to analyze Laplace transforms and moments of the extinction time and other continuous measures.
We model the evolution of the epidemics in terms of an absorbing DTMC providing the amount of infective individuals at each stage or inspection point, that introduces in the model individual variations coming from chance circumstances. As the extinction of the epidemic process is certain, we will investigate both the distribution and expected values of the number of inspections taking place prior the epidemic end, conditioned to the initial number of infected.
The rest of the paper is organized as follows. In
Section 2, we introduce the discrete-time SIS model and the DTMC describing the evolution of the epidemic. In
Section 3, we present recursive results and develop algorithmic schemes for the distribution of the random variable representing the number of inspections that find an active epidemic process. For any number of initial infected individuals, the expected number of inspections will be explicitly determined. Finally, numerical results regarding the effect of the model parameters are displayed in
Section 4. That also includes an application to evaluate cost and benefit per outbreak in such epidemics.
2. Model Description
Let us consider a closed population of N individuals that is affected by a communicable disease transmitted by direct contact. In addition, it is assumed that there are no births or deaths during disease outbreaks, therefore population size remains constant. Individuals in the population are classified as susceptible, S, or infective, I, according to their health state regarding the disease. Transitions from susceptible to infective depend on the contact rate between individuals and also on the quantity of infective present in the population. Once recovered, individuals become again susceptible to the disease. Consequently, individuals can be infected several times during an epidemic process but the epidemic stops as soon as there are no infective individuals to transmit the contagious disease.
In a discrete-time study, time is discretized into time steps
and transitions from states occur during this time interval with certain probabilities. In chain-Binomial models [
1,
3] the time step corresponds to the length of the incubation period, contact process depend on the Binomial distribution and during a fixed time interval zero, one or even more infections may happen. In [
16] time step is one and probabilities depend on effective transmission through the time. In [
23] a branching process describes transitions and survival probabilities during any stage.
In our model, the population is observed periodically at time points
, with
, where interval’s length
is chosen as to guarantee that between consecutive inspections at most one change—either an infection or a recovery—occurs. The underlying mathematical model is the discrete-time SIS model described, for instance, in [
26] assuming zero births or deaths per individual in the time interval
.
Due to the constant population hypothesis, the evolution of the disease can be represented by a one-dimensional Markov chain, where is a random variable giving the number of infective individuals in the population at the th inspection. State space is finite and contains a single absorbing state, the state zero.
Non-negative transition probabilities depend on the time interval and have the following form, for
:
where
represents the contact rate and
represents the recovery rate.
We need to fix an interval length,
, providing that probabilities in (
1) are well defined and therefore that the chosen time step guarantees that at most one change occurs between successive inspections. In particular, for any choice on the model parameters it is required that,
Which, after some algebra, provides a bound for time step. Hence, in what follows
will be chosen small enough as to satisfy
Notice that the bound given in (
2) can be written in terms of the basic reproduction number,
, as in [
26].
As
is a reducible aperiodic DTMC, with a single absorbing state, the standard theory of Markov chains (see for instance [
29]) gives that
where
is the Kronecker’s delta, defined as one for
and 0, otherwise.
The limiting behavior result (
3) states that in the long term, for any choice on model parameters, there will be no infective individuals in the population. Hence, the end of any outbreak of the disease occurs almost surely, but it may take a long number of inspections until the disease disappears from the population; as it was observed in [
27,
28] for continuous-time models. Thus, a theoretical study of this random variable is well supported.
3. Analysis of the Number of Inspections
We consider the random variable T that counts the number of inspections of the population that find an active epidemic process; i.e., T is the number of steps that it takes, to the DTMC , to reach the state zero. Thus, T can be seen as a first-passage time and we define it as
In this section we describe its probabilistic behavior in terms of distribution functions and expected values. Theoretical discussion is based on the conditional first-passage times , for , defined as the number of inspections that take place during an outbreak, given that at present population contains infected. Notice that, even for a finite population, is a discrete random variable with countable infinite mass points.
Next we introduced some notation for point and cumulative probabilities, and expected values regarding random variables
, for
.
We want to point out some trivial facts. Notice that
(
4) is trivially true due to the definition of
as a first-passage time. On the other hand, condition (5) follows from the fact that, starting with
infective individuals and as at each inspection we observe at most one event, we need at least
i inspections in order to observe that all initial infected have been recovered. Because point probabilities,
, can be determined from cumulative probabilities,
, with the help of the well-known relationship
we present results in order to deal with the cumulative ones.
Next theorem provides a recursive scheme for determining cumulative probabilities associated to an initial number of infective individuals.
Theorem 1. For any initial number of infective individuals, with the set of cumulative probabilities satisfies the following recursive conditions, for Proof. The proof is an application of a first-step analysis by conditioning on the first transition out of the current state. ☐
Remark 1. Notice that , for , because states are a non-decomposable set of states. Consequently, is a non-defective random variable and , for
Remark 2. The use of the iterative Equation (6) produces a sequence of increasing probabilities converging to one but, for computational purposes, a stopping criteria should be provided in order to avoid longer computation runs. For each number of inspections,
, Equation (
6) is solved recursively, with the help of the boundary conditions (
4) and the trivial result (5). Numerical results appearing in the following section have been obtained with the help of a recursive algorithm, that stops as soon as a certain percentile value of the distribution is accumulated. For each initial number of infective individuals,
, cumulative probabilities are computed up to the q-th percentile, using the following pseudo-code.
Remark 3. For any appropriate time interval satisfying (2), point and cumulative probabilities are determined numerically from Algorithm 1. Moreover, for inspections they present the following explicit forms: Explicit values displayed in Remark 3 indicate that distribution of the random variable depends on rates and not only through its ratio. Consequently, models sharing the same basic reproductive number, , present different probabilistic characteristics.
| Algorithm 1: |
The sequence of cumulative probabilities conditioned to the current number of infective individuals, , for , are determined as follows:
Step 0: Set and Step 1: Set and , for Step 2: Set and Step 2a: Set and Step 2b: If compute using Equation ( 6). Step 2c: If and then Stop. Step 2d: If go to step 2a. Step 3: Go to step 2.
|
Expected values , for , provide the long-run average value of inspections prior to the epidemic end, given that the outbreak started with i infected. Typically, expected values can be computed from mass distribution functions but, in our case, the use of the recursive procedure given in Algorithm 1 produces a lower approximation of the true value. Instead of that, next theorem provides a closed form expression for , given any initial number of infective individuals.
Theorem 2. Expected values , present the following form:where , for . Proof. The proof is based on a first-step argument. By conditioning on the state visited by the underlying Markov chain after first transition, we get the following set of equations that involve expected values
, for
initial infective.
But
and
, when
. Substituting in (
9) yields
that is in accordance with results appearing in [
26] (see Section 2.2.5).
Using the normalization condition
, we get that conditioned moments satisfy the following tridiagonal system:
that can be solved explicitly. Note that Equation (
10) can be rewritten as
Now we use a method of finite difference equations. First, we introduce differences
defined as follows
and then substitute (
14) in Equations (
11)–(13). The tridiagonal system is reduced to a bidiagonal one
Moreover, Equation (16) provides a closed expression for
and remainder differences can be expressed in terms of (
17) by noticing that
Using backward substitution and the expressions for transition probabilities (
1), we get that
where
and
On the other hand, from definition (
14) and by noticing that
, we can write
Finally, using (
19) repeatedly in combination with (
20) gives the explicit expressions (
7)–(8). ☐
Remark 4. Notice that, from (7) and (8), expected values depend on contact and recovery rates not only through its ratio . Hence, SIS models sharing the basic reproduction number can present different long run average values for the number of inspections prior to the end of the infective process. 4. Numerical Results
The objective of this section is to reveal the main insights of the mathematical characteristic that is the subject matter of this paper. In the previous section we have derived theoretical and algorithmic results regarding the probabilistic behavior of the random variables
, for
. Probability distribution, conditioned on the initial number of infected, is obtained as the solution of a system of linear equations. But unfortunately, we have not reached a well-known, or even a closed form, distribution for
and, in addition, the model relies on a group of parameters that varies over a fairly broad range. Hence, we are going to examine and quantify the effect of changing one or more of the parameter’s value in the possible outcomes of the number of inspections. In more details, numerical results come from the application of Theorem 1 and Algorithm 1, when we focus on probabilities of different outcomes, and from the explicit Equations (
7)–(8) when the interest are expected values
.
Our aim is two-fold: to investigate the influence of the model parameters in the probabilistic behavior of these random variables and show a possible application in evaluating benefits associated to the quantity of inspections conducted over an outbreak of a discrete-time SIS epidemic model.
4.1. Influence of Model Parameters
First we assume that we are able to detect the epidemics as soon as first infection appears, that is . The objective is to characterize the random variable that counts, from the very beginning of the epidemic, the total number of periodic inspections taking place prior to the epidemics end. We choose a contact rate and a recovery rate
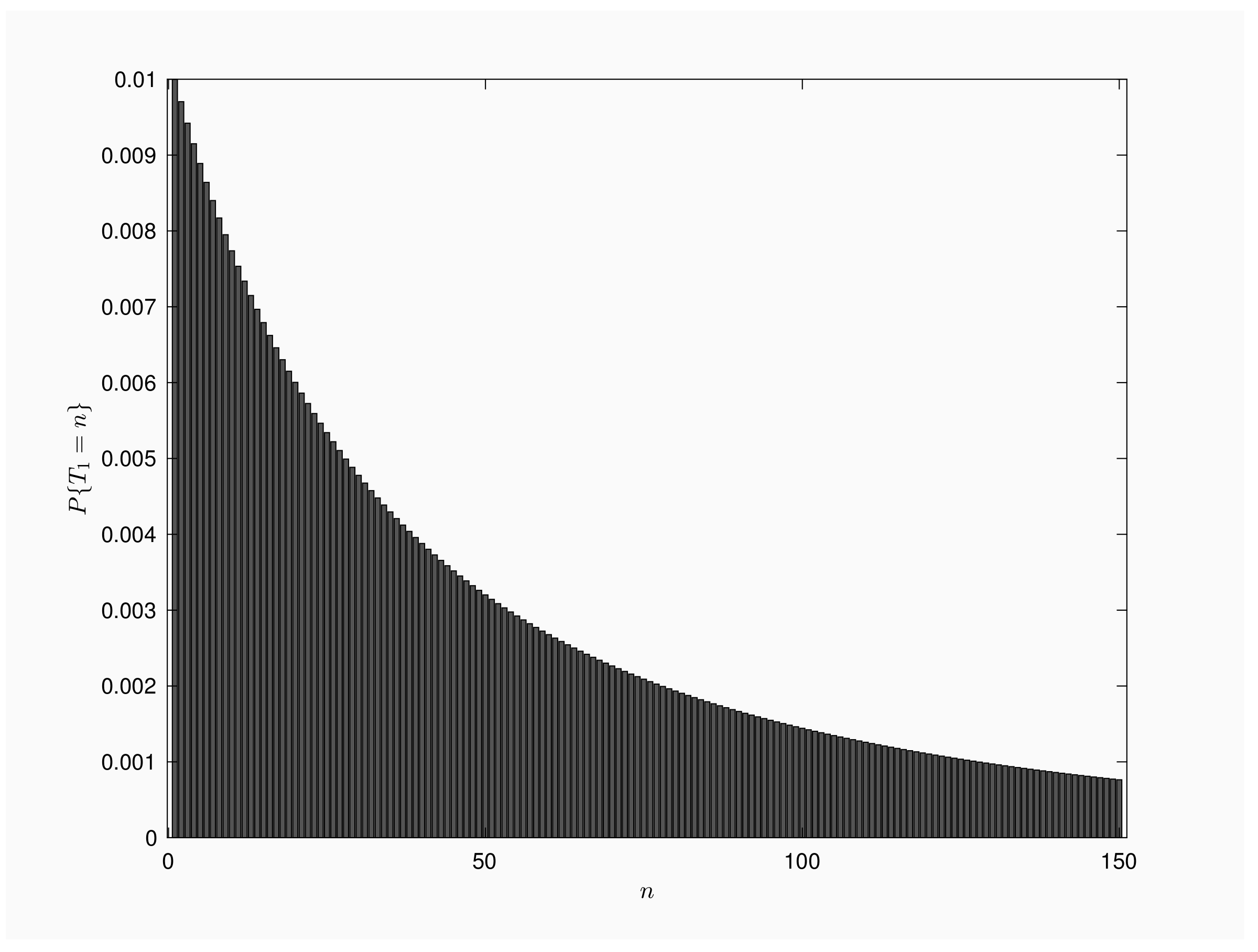
Figure 1 is a bar chart of
for
. We consider a population of
individuals and time interval between inspections is
time units. Mass function presents a decreasing shape, with a single mode for
. From numerical results, we get that 1% of the outbreaks end by the time of the first inspection, but also 1% of the outbreaks will last more than 30,000 inspections.
Table 1 displays several cumulative probabilities up to 150 inspections and the expected value
, for a population of
and 75 individuals. We keep rates
,
and time interval length as
For each population, only 1% of the outbreaks are inspected once before extinction. For a fixed number of inspections, cumulative probabilities are smaller when population size is larger. During outbreaks, large populations are inspected more times, in average, than smaller ones. Even for a small population of 5 individuals, we observe that the 48% of the outbreaks are still in progress at the 150-th inspection and an average of around 295 inspections take place while the epidemic is active.
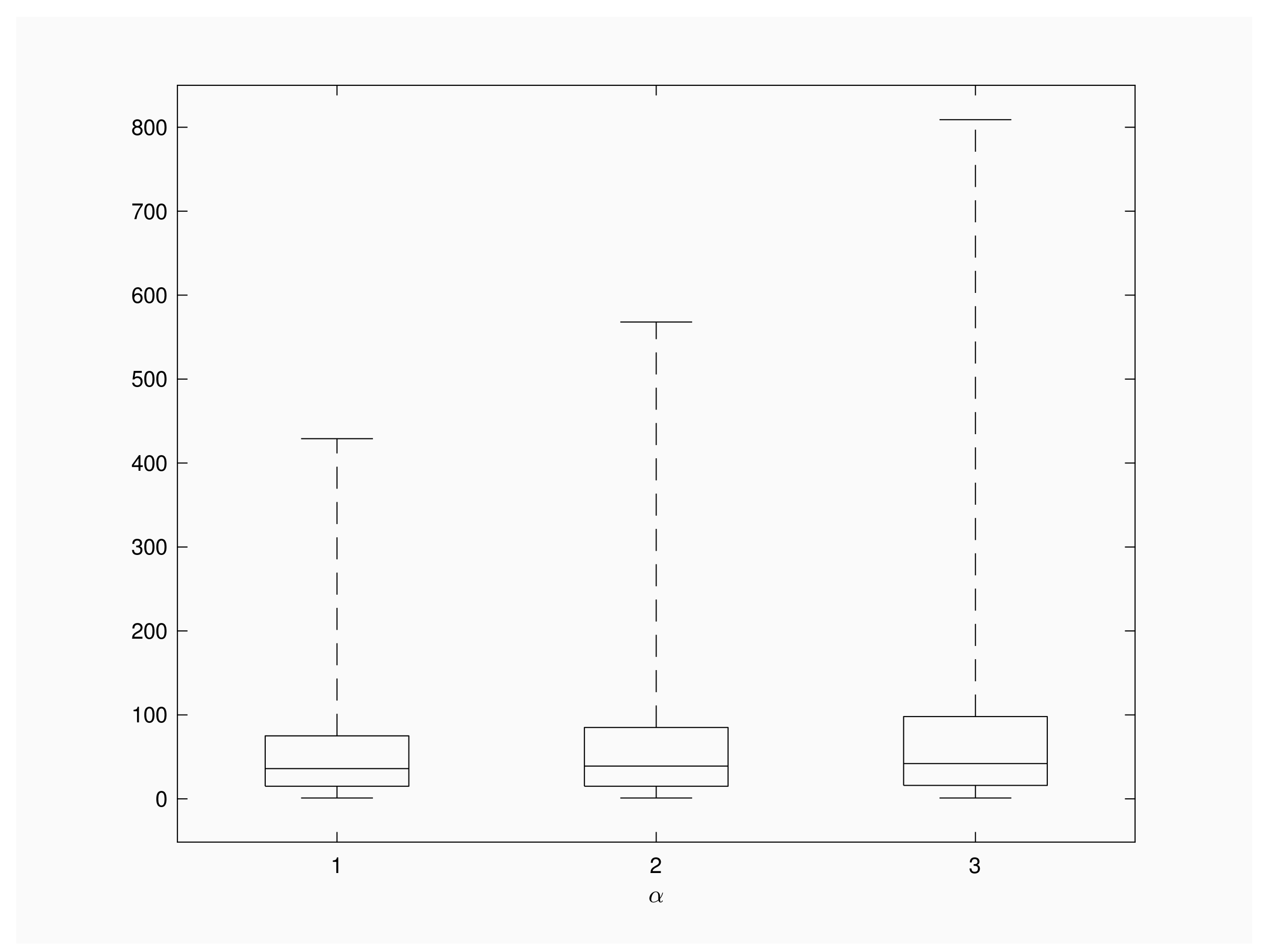
Next, we describe the distribution of using a Box-Whiskers plot diagram. The objective is to compare the patterns of the number of inspections when we vary the contact rate. The box encloses the middle central part of the distribution, lower and upper edges of the box correspond to the lower and the upper quartile, respectively, and the line drawn across the box shows the median of the distribution. Finally, whiskers below start at 1 and whiskers above the boxes reach up to the 99% of the distribution.
Figure 2 shows the distribution of
for
and
. We consider a recovery rate
a population of
individuals and a time interval of
units length between successive inspections. The distribution of the random variable is skewed to the right and longer right tails are observed for larger contact rates. Additional numerical results for
show a similar shape for box plot diagrams, with 99th quantile under 200 inspections. This fact is according to the intuition, because large recovery rates give more chance to recoveries than to new infections and, consequently, outbreaks will involve lesser infective individuals and present shorter extinction times in comparison with
Figure 2’s scenario.
In
Table 2, we display the expected number of inspections for outbreaks starting from a single infective case, we consider several values for contact and recovery rates. Population contains 20 individuals and time interval between inspections is
, for every pair of rates. As was stated on Remark 4, results show that expected values are not a function of the basic reproductive number
. The expected number of inspections prior the end of the infective outbreak increases as a function of contact rate
and decreases as a function of recovery rate. That remark is according to the intuition too, because the epidemic length enlarges when contacts between individuals occur more often and/or when individuals need longer times to be recovered.
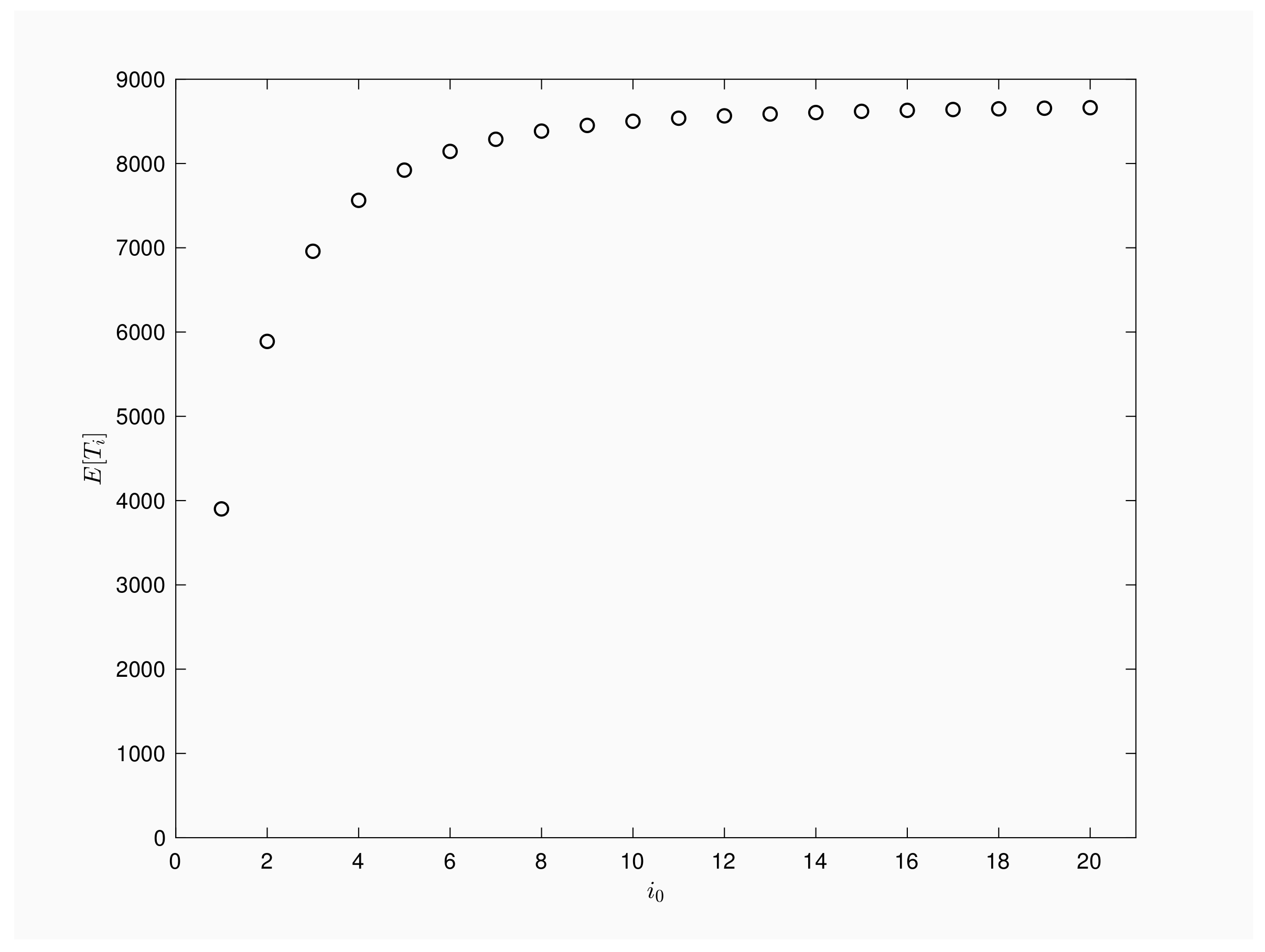
Next we focus on outbreaks that are first observed when the epidemic process involves
i, not necessarily one, infected. Our aim is to describe the expected values
when varying the initial number of infective individuals. Notice that Equation (
20) guarantees that
, for
. Thus, the expected number of inspections taking place prior to the epidemics end is a non-decreasing function regarding the amount of initial infective.
Figure 3 provides a numerical illustration for a population of
, contact rate
, recovery rate
and time interval between periodic inspections
Pictured graph agrees with theoretical results, it quantifies the growth of the number of inspections when infective rises and it shows the importance of an early detection of such a epidemic process. More specifically, outbreaks detected at the first infection will be active, in mean terms, about 4000 inspections while if the outbreak is first checked when two infected are present in the population then, the expected inspections will rise up to 6000 times or up to 8000 inspections when first checking shows five infected.
Additional numerical results, not included here, report that when we choose intervals between inspections with decreasing length
, the mass distribution function of any
, for
, provides an aproximation to the density function of the extinction time of an epidemic process starting with
i infected [
28], that is the continuous counterpart of the number of periodic inspections taking place while the epidemic process is active.
In the following section we present a possible use of the probabilistic behavior of
4.2. Application to Evaluate Outbreak Benefits
Let us assume that every inspection has a travel or approaching cost and, whenever there is a change in the population regarding the immediate previous inspection, we get a profit in terms of information that depends on the type of event. Let and represent recovery and infection detection’s gain, respectively.
Associated to every outbreak, the random variable
provides the total number of inspections conducted during an outbreak that starts from
infective individuals. On the other hand, for outbreaks starting with
infective individuals, Artalejo et al. introduced in [
30] the random variables
and
defined as the number of recoveries and infections per outbreak, respectively. By noticing that the number of recoveries in an outbreak agrees with the total number of infections in the same outbreak, we get
With the help of the above random variables and its relationship (
21), we can determine outbreak’s benefit, for instance, just by defining a benefit function conditioned to the initial number of infective, as follows
The expected benefit per outbreak will depend on the mean values of and , but also on the choice of travel cost and information profits.
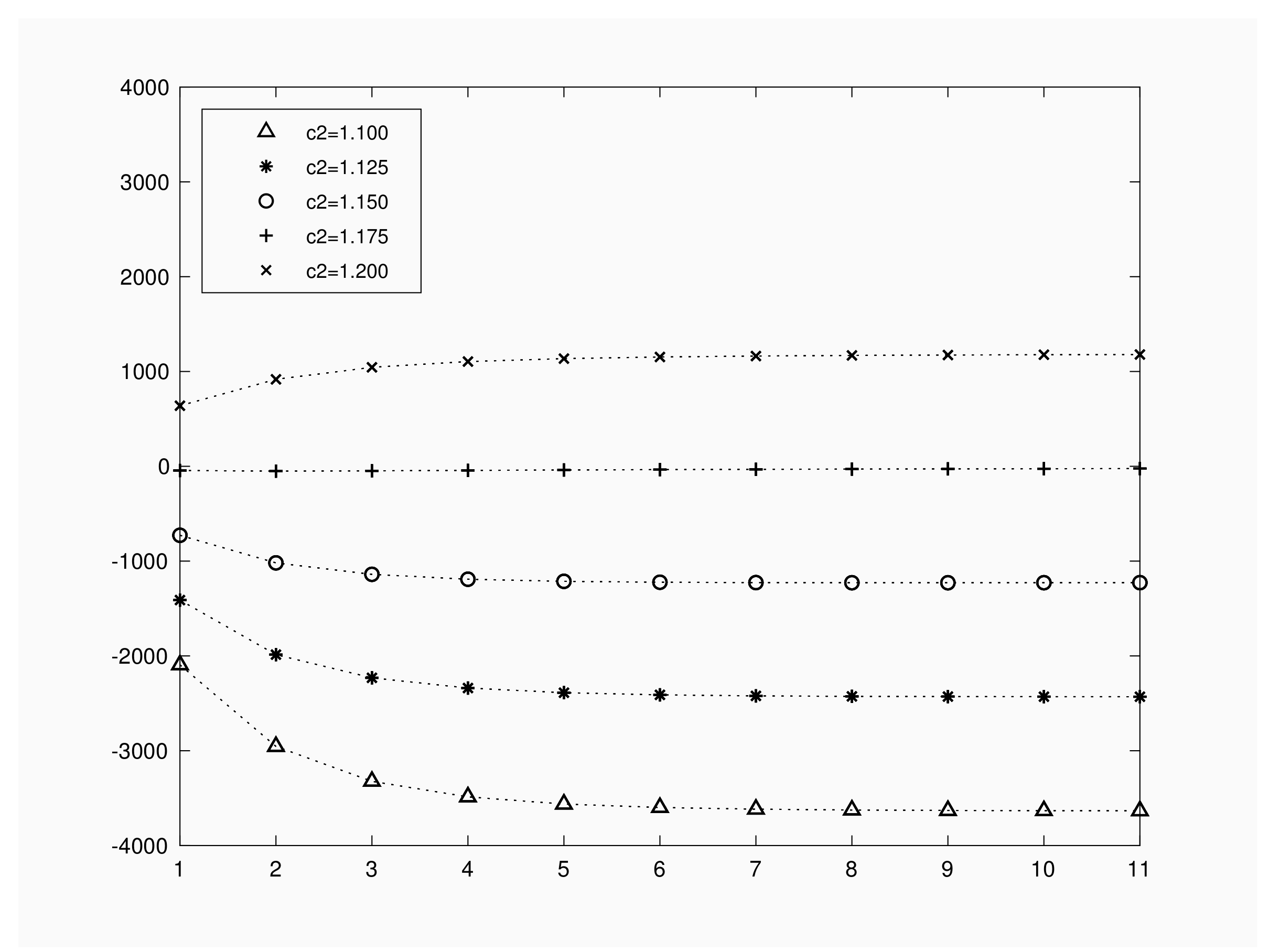
Figure 4 represents expected benefit when the initial number of infective varies in
, for a population of
, with contact rate
, recovery rate of
and a time interval of
units. We fixed a unitary travel cost per the inspection; i.e.
, and gain values per recovery or infection have been chosen as
. Several graphs are drawn by fixing
. We notice first that, for a fixed number of infective and in order to obtain a positive benefit, recovery gain
must satisfy
. Hence, the trivial restriction
does not guarantee a positive expected benefit per outbreak. In any case, the expected benefit is a linear increasing function of the gain value
.
As we can see in
Figure 4, depending on the choice for
, expected benefit functions present different shape as a function of the initial number of infective individuals. Numerical results show that, for
, expected benefit decreases as the initial infected increases. For
we obtain a minimum expected benefit at
infective. When we set
the minimum corresponds to the value
but we obtain expected values close to 0. For
, expected benefit remains almost constant for
. These facts illustrate that a deep knowledge on
or
will help in decision making process regarding travel cost and gain values.
5. Discussion and Conclusions
Literature in mathematical modelization of epidemics includes both continuous and discrete-time models. Continuous-time models are more accurate but more difficult to implement than discrete-time ones. On the other hand, discrete-time models fit better with real information; data related to real-world epidemic processes are often given by unit time, so it is natural to preserve dynamic features by modeling a dynamical system from observations at discrete times which are adapted to time step.
This paper focuses on the discrete-time SIS model, where transition probabilities for event occurring during time-steps are described in terms of an absorbing DTMC. The population is observed at periodic time points assuming that at most one event takes in a time-step. The discrete-time stochastic epidemic SIS models are formulated as DTMC which may be considered approximations to the continuous-time Markov jump processes. The size of the time step must be controlled to assure that the model gives genuine probability distributions.
Our purpose is to study the extinction time counterpart in discrete-time, that is the random variable that counts the total number of inspections that find an active epidemic process.
Subject to the initial number of infective individuals, mass probability function of the number of inspections, , is numerically determined through a recursive scheme; complementing the probabilistic knowledge of this variable provided by its expected value, that comes directly from an explicit expression.
A really interesting extension of this work arises when considering equidistant time inspections relaxing the requirement about the maximum number of events observed during inspections. This problem, that appears to be analytically intractable, is the aim of the paper [
31], where authors tackle this difficulty via the total area between the sample paths of the numbers of infective individuals in the continuous-time process and its discrete-time counterpart.