On the Bounds for a Two-Dimensional Birth-Death Process with Catastrophes
Abstract
1. Introduction
2. Bounds in Norm
3. Bounds in Weighted Norms
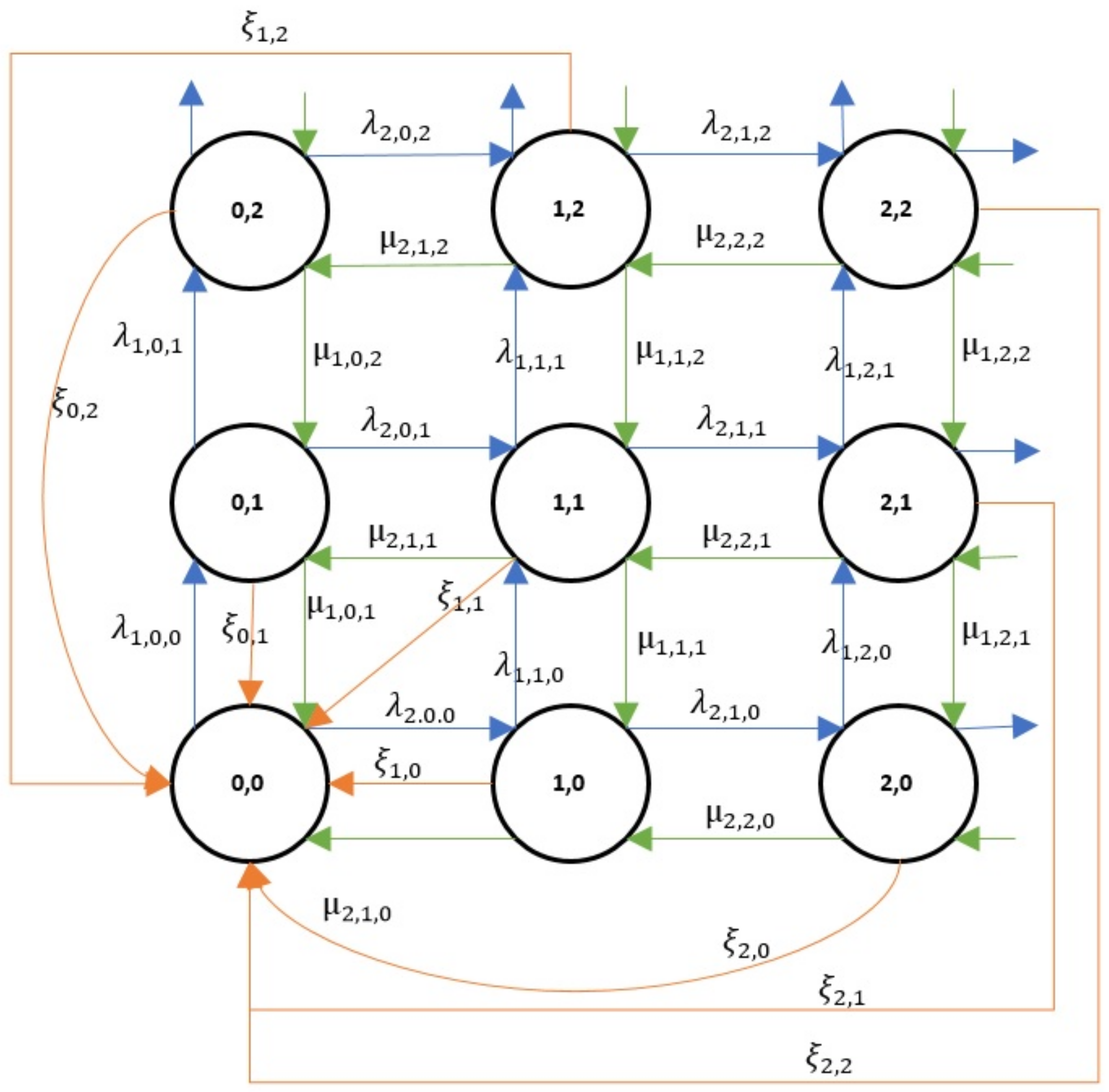
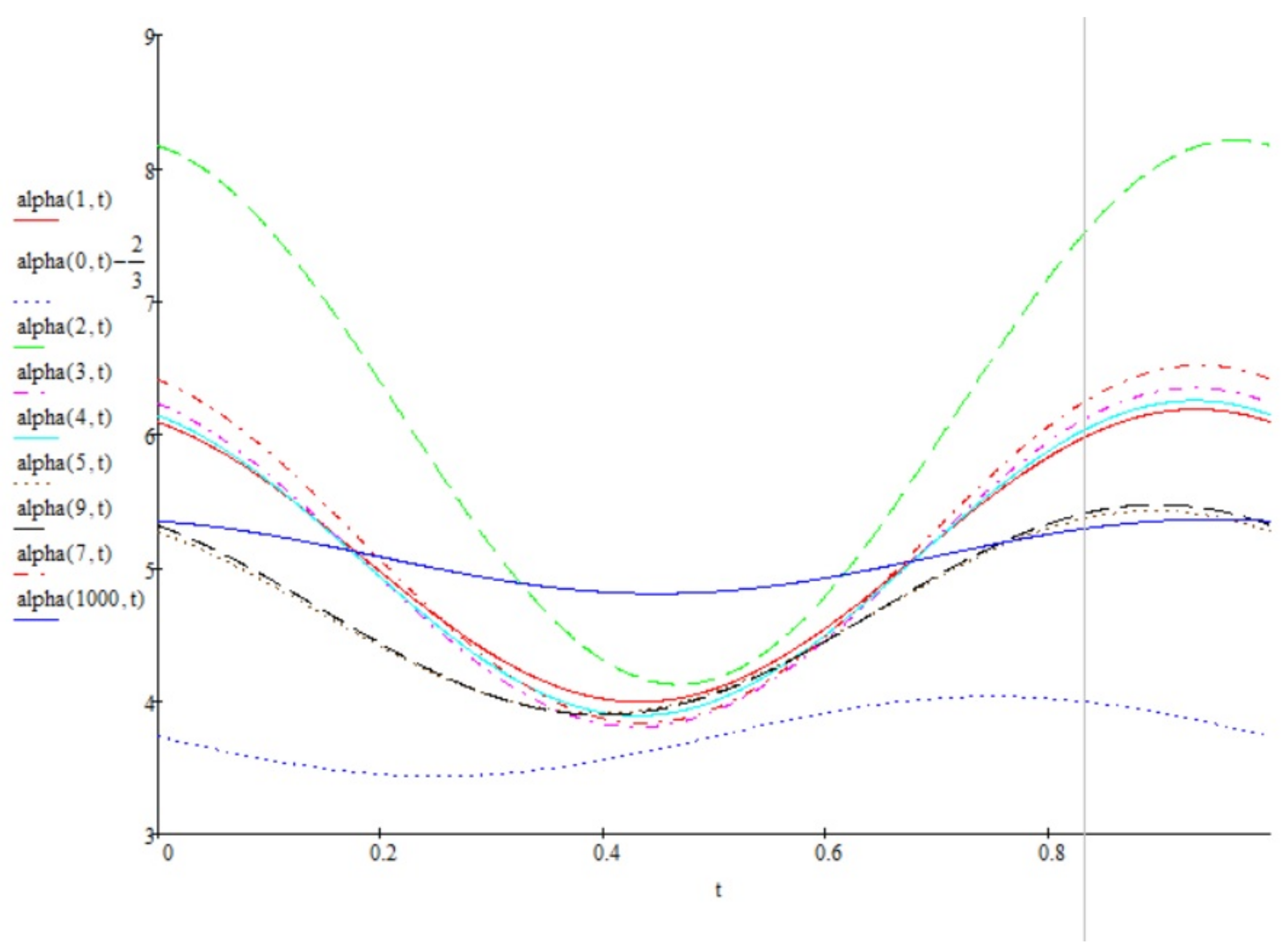
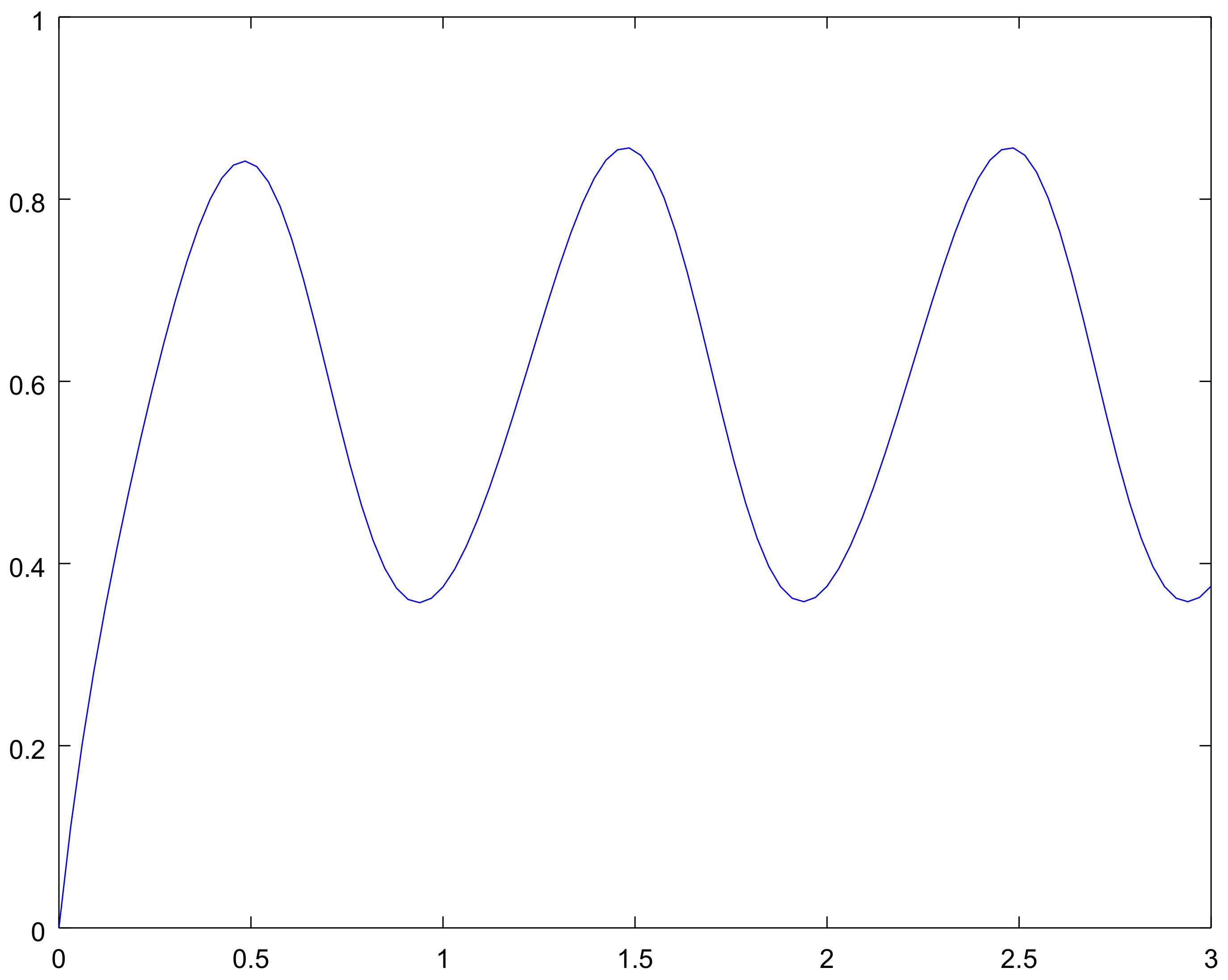
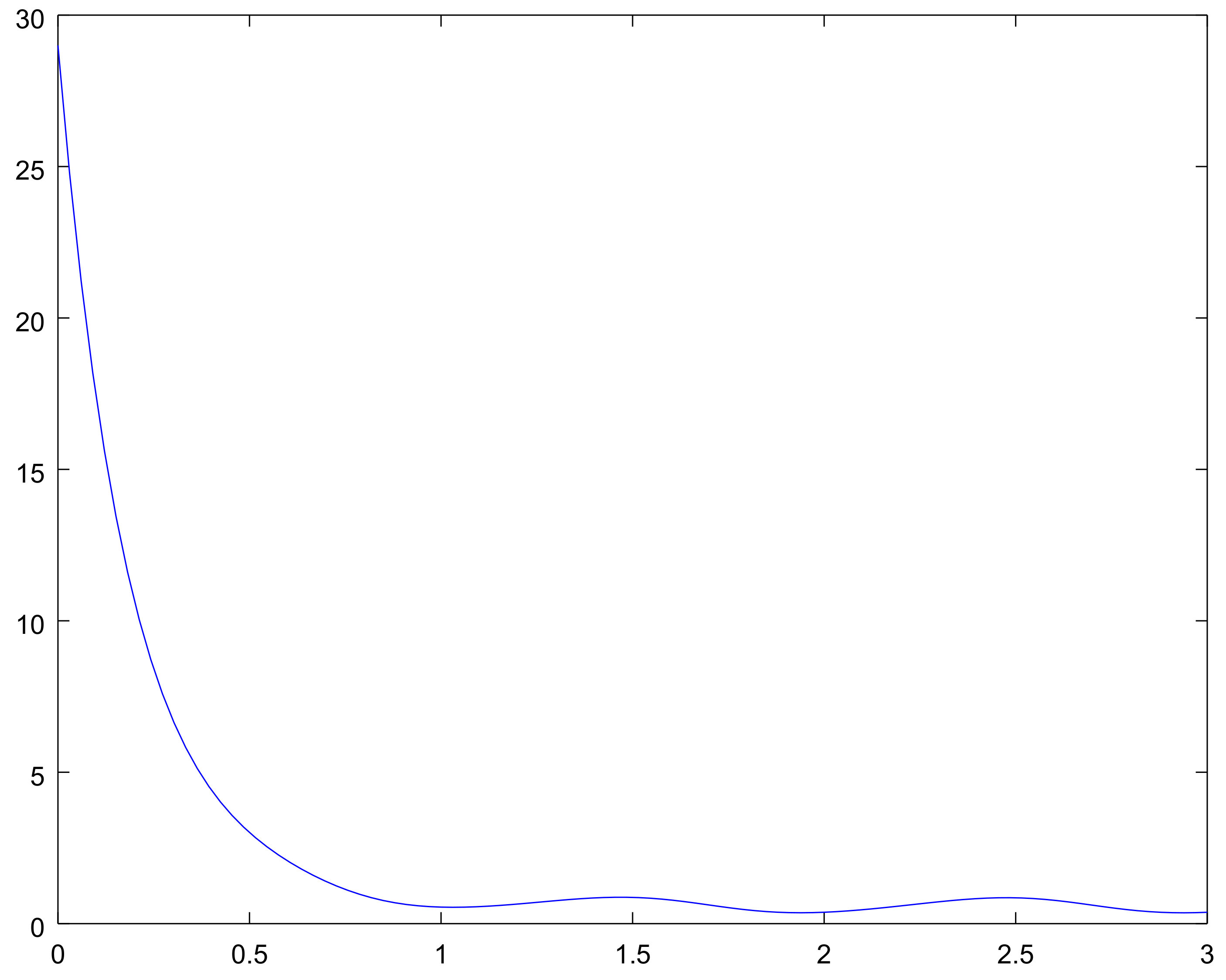
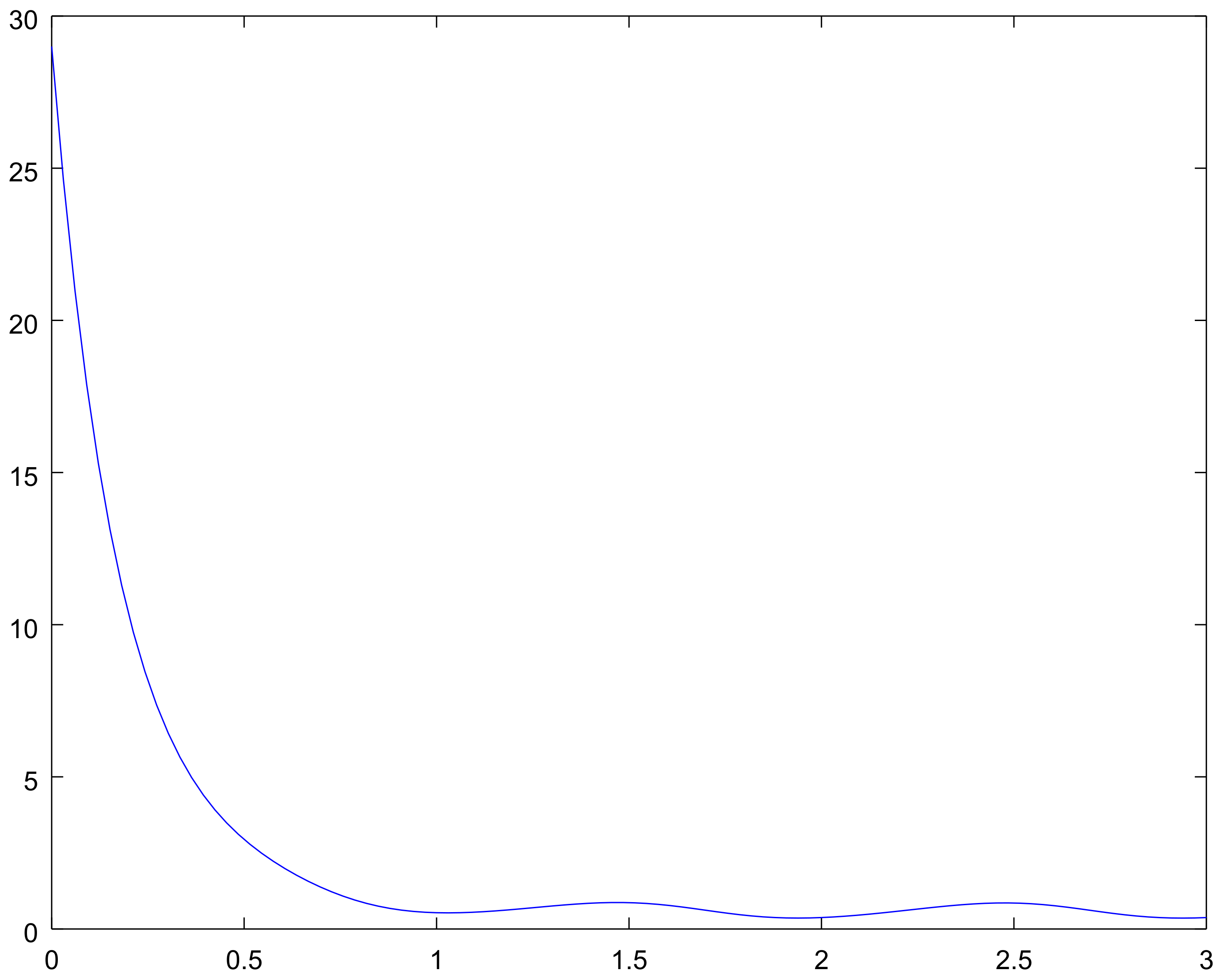
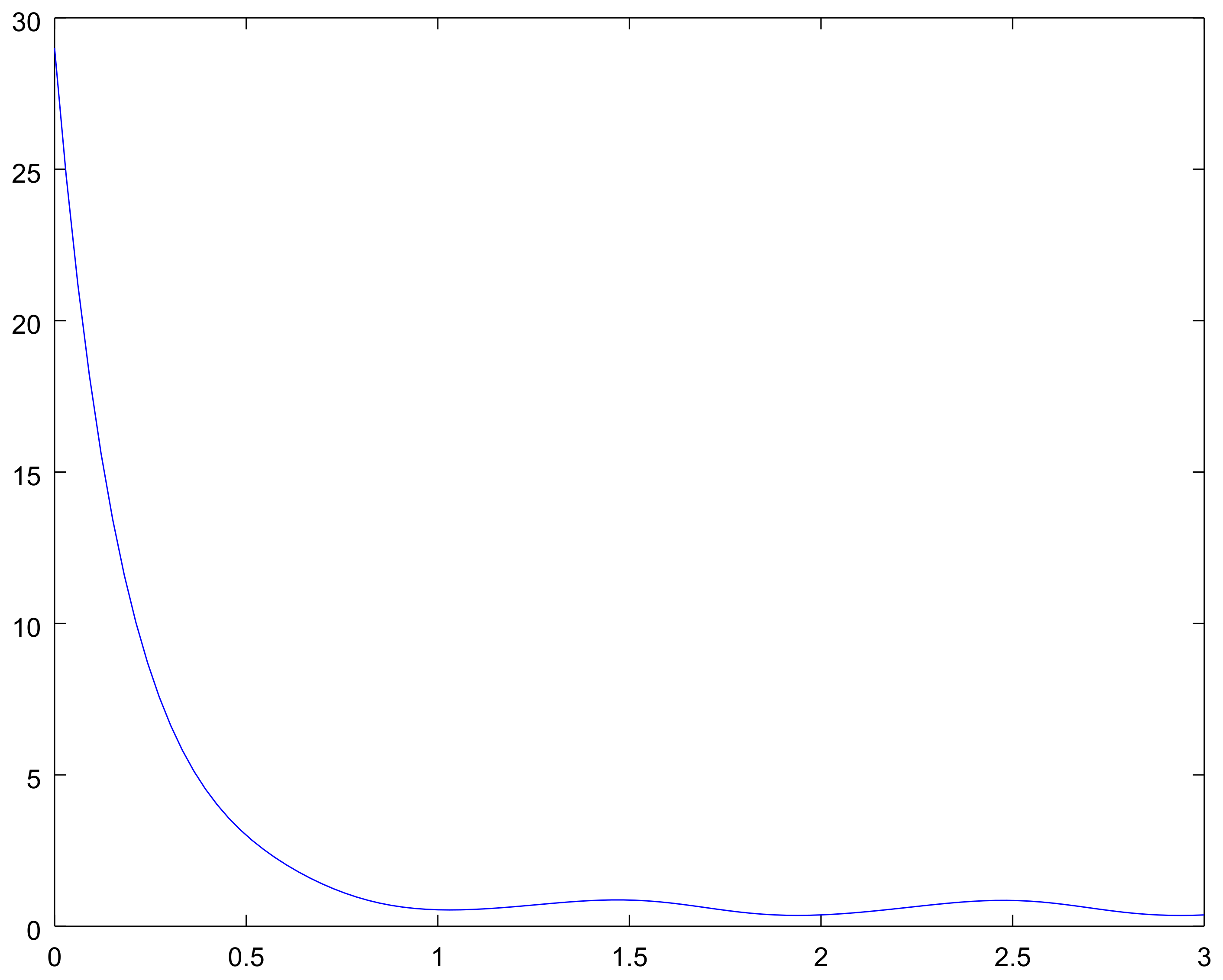
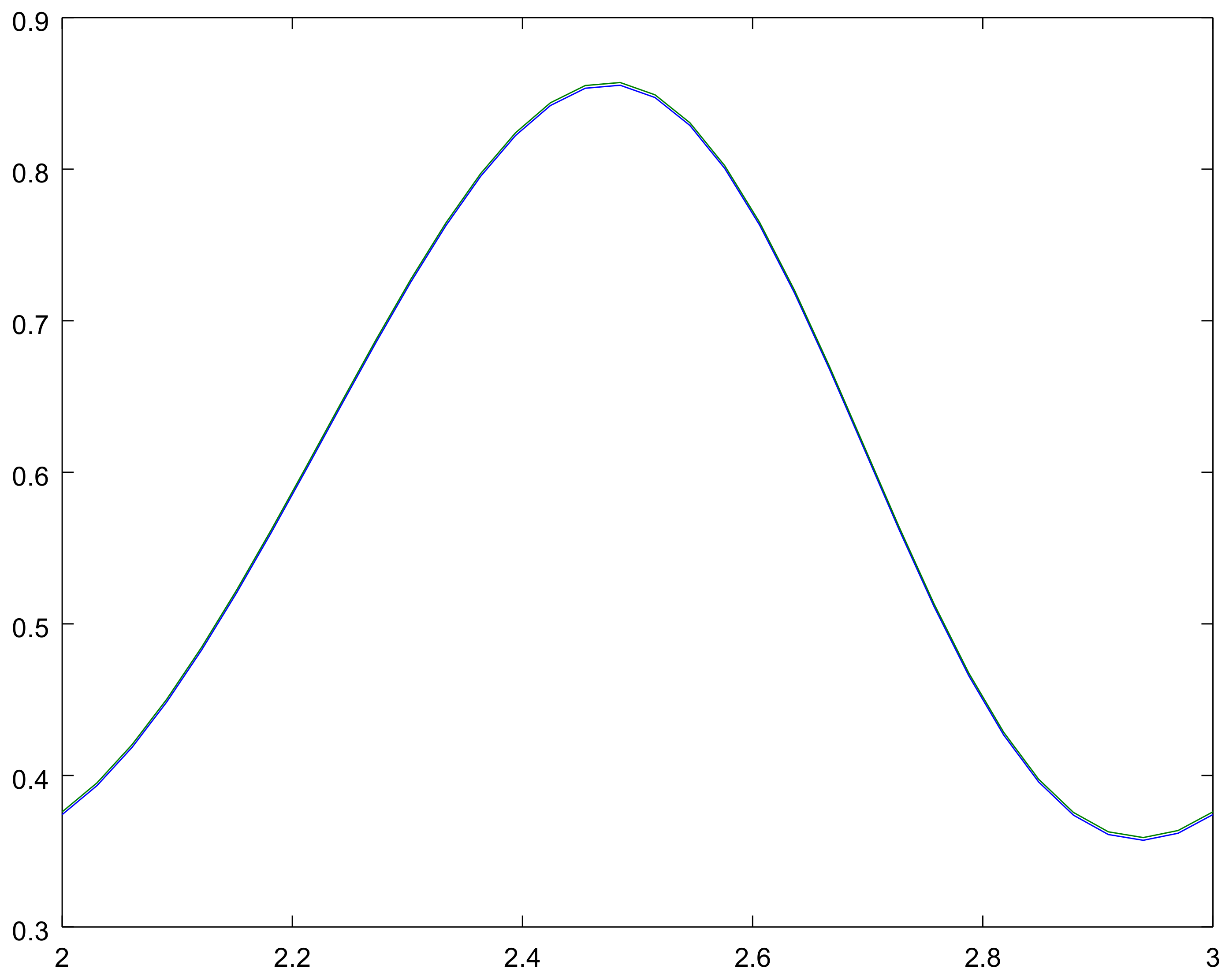
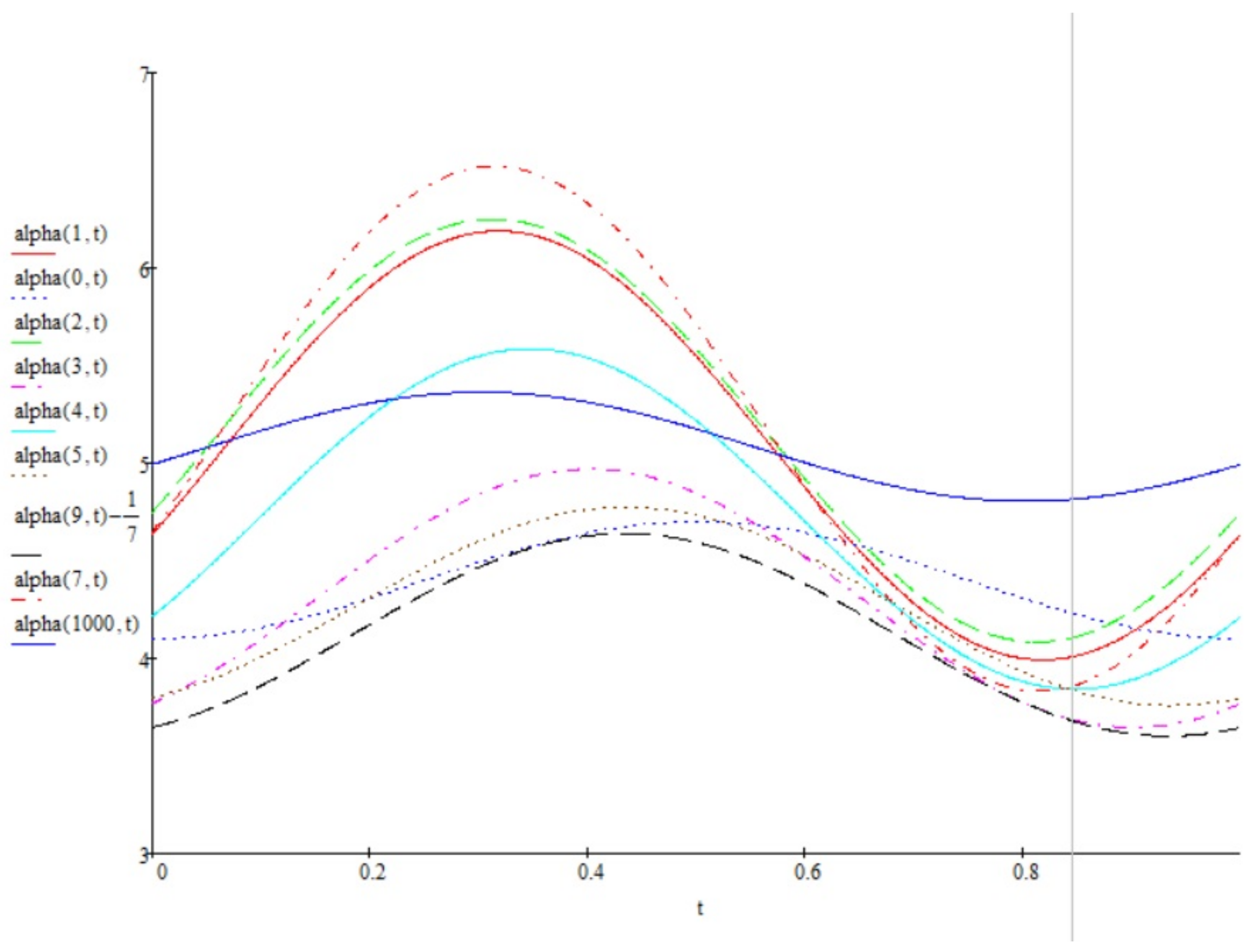
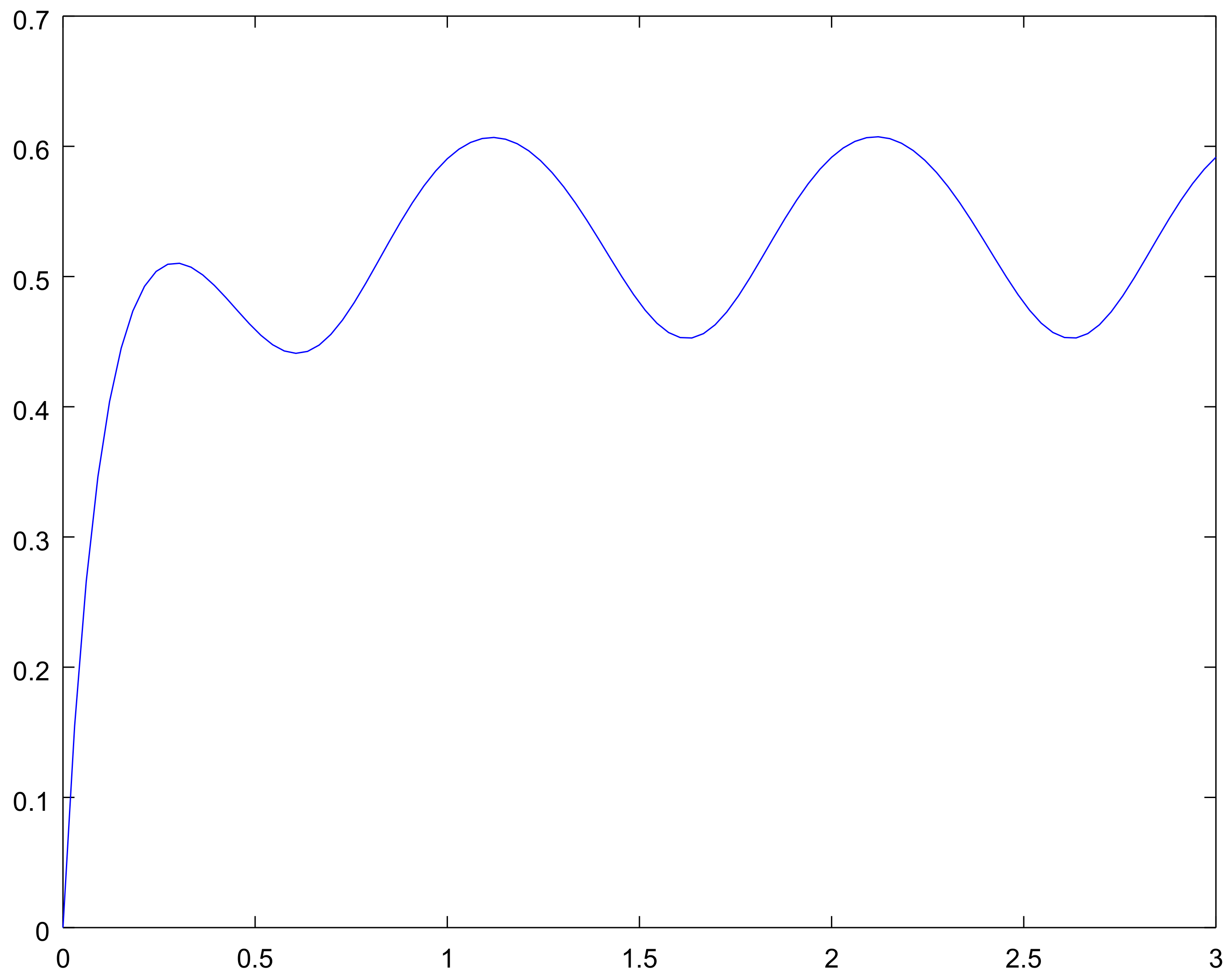
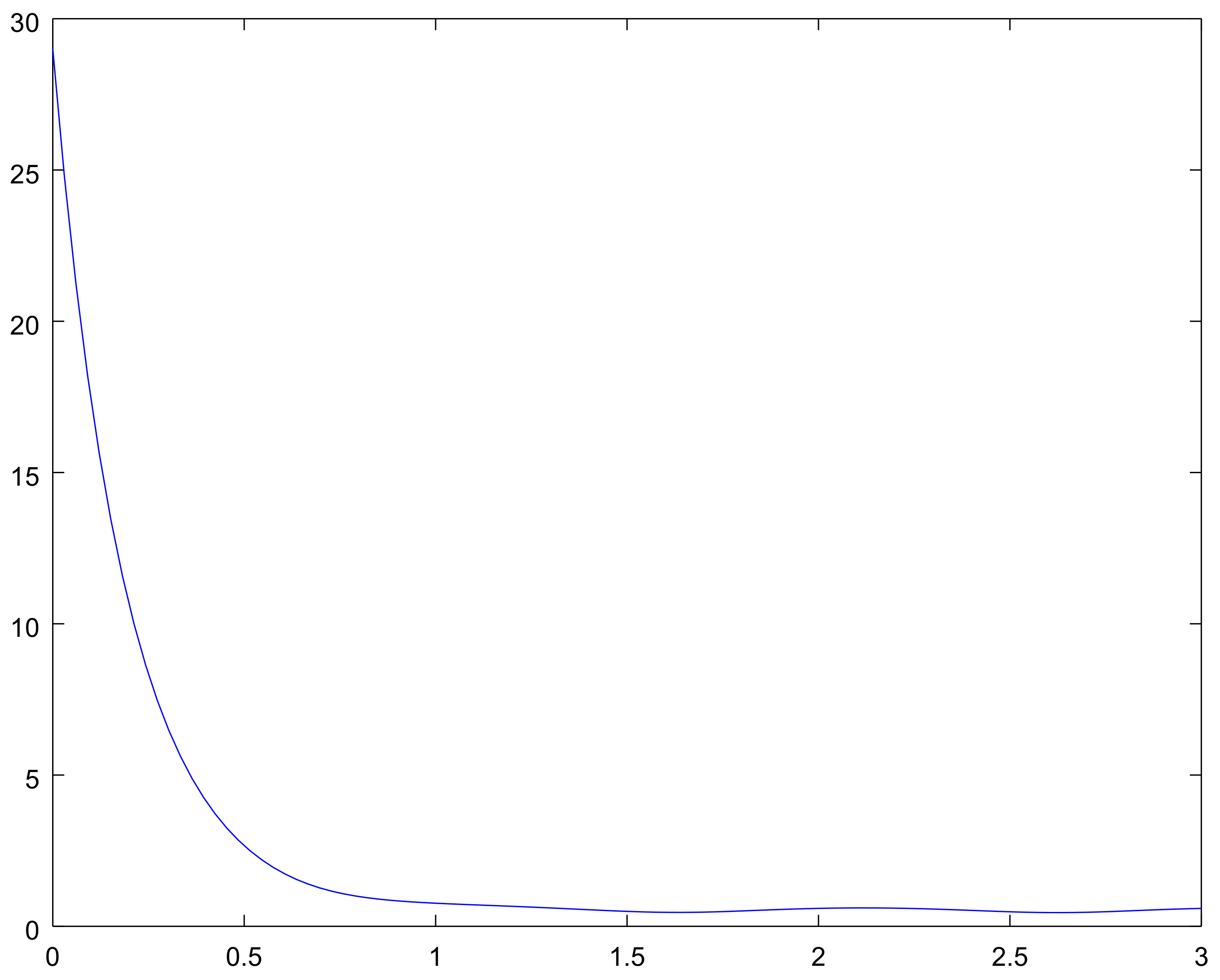
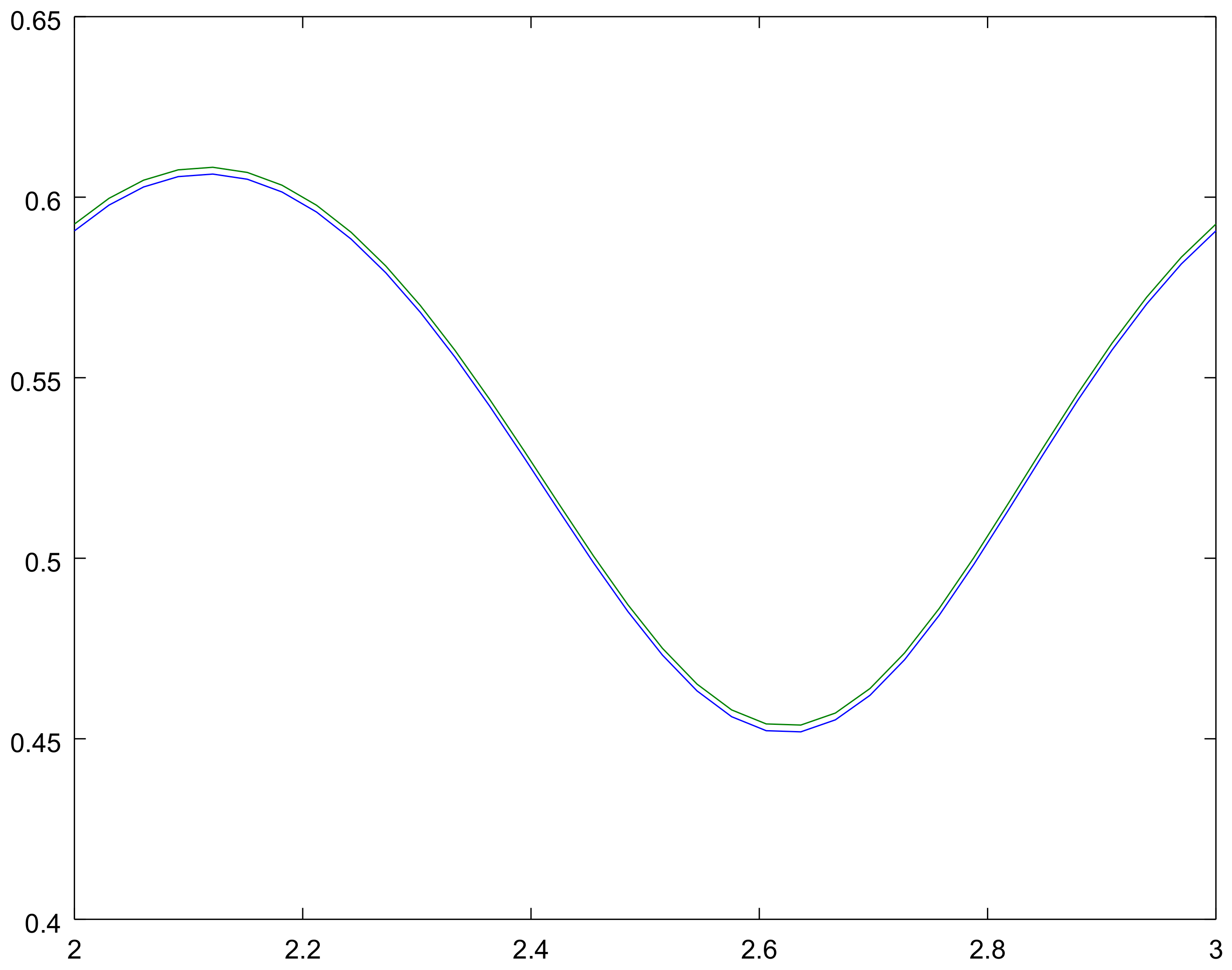
4. Examples
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Di Crescenzo, A.; Giorno, V.; Nobile, A.G.; Ricciardi, L.M. On the M/M/1 queue with catastrophes and its continuous approximation. Queueing Syst. 2003, 43, 329–347. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Giorno, V.; Nobile, A.G.; Ricciardi, L.M. A note on birth-death processes with catastrophes. Stat. Probab. Lett. 2008, 78, 2248–2257. [Google Scholar] [CrossRef][Green Version]
- Di Crescenzo, A.; Giorno, V.; Kumar, B.K.; Nobile, A.G. A double-ended queue with catastrophes and repairs, and a jump-diffusion approximation. Methodol. Comput. Appl. Probab. 2012, 14, 937–954. [Google Scholar] [CrossRef]
- Dharmaraja, S.; Di Crescenzo, A.; Giorno, V.; Nobile, A.G. A continuous-time Ehrenfest model with catastrophes and its jump-diffusion approximation. J. Stat. Phys. 2015, 161, 326–345. [Google Scholar] [CrossRef]
- Dudin, A.; Nishimura, S. A BMAP/SM/1 queueing system with Markovian arrival input of disasters. J. Appl. Probab. 1999, 36, 868–881. [Google Scholar] [CrossRef]
- Dudin, A.; Karolik, A. BMAP/SM/1 queue with Markovian input of disasters and non-instantaneous recovery. Perform. Eval. 2001, 45, 19–32. [Google Scholar] [CrossRef]
- Dudin, A.; Semenova, O. A stable algorithm for stationary distribution calculation for a BMAP/SM/1 queueing system with Markovian arrival input of disasters. J. Appl. Probab. 2004, 41, 547–556. [Google Scholar] [CrossRef]
- Do, T.V.; Papp, D.; Chakka, R.; Sztrik, J.; Wang, J. M/M/1 retrial queue with working vacations and negative customer arrivals. Int. J. Adv. Intell. Paradig. 2014, 6, 52–65. [Google Scholar] [CrossRef]
- Chen, A.Y.; Renshaw, E. The M/M/1 queue with mass exodus and mass arrives when empty. J. Appl. Prob. 1997, 34, 192–207. [Google Scholar] [CrossRef]
- Chen, A.Y.; Renshaw, E. Markov bulk-arriving queues with state-dependent control at idle time. Adv. Appl. Prob. 2004, 36, 499–524. [Google Scholar] [CrossRef]
- Chen, A.Y.; Pollett, P.; Li, J.P.; Zhang, H.J. Markovian bulk-arrival and bulk-service queues with state-dependent control. Queueing Syst. 2010, 64, 267–304. [Google Scholar] [CrossRef]
- Li, J.; Chen, A. The Decay Parameter and Invariant Measures for Markovian Bulk-Arrival Queues with Control at Idle Time. Methodol. Comput. Appl. Probab. 2013, 15, 467–484. [Google Scholar]
- Zhang, L.; Li, J. The M/M/c queue with mass exodus and mass arrivals when empty. J. Appl. Probab. 2015, 52, 990–1002. [Google Scholar] [CrossRef]
- Zeifman, A.; Korotysheva, A.; Satin, Y.; Shorgin, S. On stability for nonstationary queueing systemswith catastrophes. Inform. Appl. 2010, 4, 9–15. [Google Scholar]
- Zeifman, A.; Korotysheva, A.; Panfilova, T.; Shorgin, S. Stability bounds for some queueing systems with catastrophes. Inform. Appl. 2011, 5, 27–33. [Google Scholar]
- Zeifman, A.; Korotysheva, A. Perturbation Bounds for Mt/Mt/N Queue with Catastrophes. Stoch. Model. 2012, 28, 49–62. [Google Scholar] [CrossRef]
- Zeifman, A.; Satin, Y.; Panfilova, T. Limiting characteristics for finite birth-death-catastrophe processes. Mater. Biosci. 2013, 245, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Zeifman, A.; Satin, Y.; Korotysheva, A.; Korolev, V.; Shorgin, S.; Razumchik, R. Ergodicity and perturbation bounds for inhomogeneous birth and death processes with additional transitions from and to origin. Int. J. Appl. Math. Comput. Sci. 2015, 25, 787–802. [Google Scholar] [CrossRef]
- Zeifman, A.; Satin, Y.; Korotysheva, A.; Korolev, V.; Bening, V. On a class of Markovian queuing systems described by inhomogeneous birth-and-death processes with additional transitions. Dokl. Math. 2016, 94, 502–505. [Google Scholar] [CrossRef]
- Zeifman, A.; Korotysheva, A.; Satin, Y.; Kiseleva, K.; Korolev, V.; Shorgin, S. Ergodicity and uniform in time truncation bounds for inhomogeneous birth and death processes with additional transitions from and to origin. Stoch. Model. 2017, 33, 598–616. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.; Spina, S. On some time non-homogeneous queueing systems with catastrophes. Appl. Math. 2014, 245, 220–234. [Google Scholar] [CrossRef]
- Zeifman, A.; Korotysheva, A.; Satin, Y.; Kiseleva, K.; Korolev, V.; Shorgin, S. Bounds for Markovian Queues with Possible Catastrophes. In Proceedings of the 31th European Conference on Modeling and Simulation, Budapest, Hungary, 23–26 May 2017; pp. 628–634. [Google Scholar]
- Daleckii, J.L.; Krein, M.G. Stability of solutions of differential equations in Banach space (No. 43). Am. Math. Soc. 2002, 53, 34–36. [Google Scholar]
- Zeifman, A.; Satin, Y.; Chegodaev, A. On nonstationary queueing systems with catastrophes. Inform. Appl. 2009, 3, 47–54. [Google Scholar]
- Mitrophanov, A.Y. Stability and exponential convergence of continuous-time Markov chains. J. Appl. Prob. 2003, 40, 970–979. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinitcina, A.; Satin, Y.; Zeifman, A.; Shilova, G.; Sipin, A.; Kiseleva, K.; Panfilova, T.; Kryukova, A.; Gudkova, I.; Fokicheva, E. On the Bounds for a Two-Dimensional Birth-Death Process with Catastrophes. Mathematics 2018, 6, 80. https://doi.org/10.3390/math6050080
Sinitcina A, Satin Y, Zeifman A, Shilova G, Sipin A, Kiseleva K, Panfilova T, Kryukova A, Gudkova I, Fokicheva E. On the Bounds for a Two-Dimensional Birth-Death Process with Catastrophes. Mathematics. 2018; 6(5):80. https://doi.org/10.3390/math6050080
Chicago/Turabian StyleSinitcina, Anna, Yacov Satin, Alexander Zeifman, Galina Shilova, Alexander Sipin, Ksenia Kiseleva, Tatyana Panfilova, Anastasia Kryukova, Irina Gudkova, and Elena Fokicheva. 2018. "On the Bounds for a Two-Dimensional Birth-Death Process with Catastrophes" Mathematics 6, no. 5: 80. https://doi.org/10.3390/math6050080
APA StyleSinitcina, A., Satin, Y., Zeifman, A., Shilova, G., Sipin, A., Kiseleva, K., Panfilova, T., Kryukova, A., Gudkova, I., & Fokicheva, E. (2018). On the Bounds for a Two-Dimensional Birth-Death Process with Catastrophes. Mathematics, 6(5), 80. https://doi.org/10.3390/math6050080





