The “Lévy or Diffusion” Controversy: How Important Is the Movement Pattern in the Context of Trapping?
Abstract
1. Introduction
2. BM vs. LW: Equivalence I
2.1. Brownian Motion
2.2. Condition of Equivalence
3. Time-Dependent Diffusion
Equivalence of Trap Counts: Brownian Motion vs. Diffusion in a Semi-Bounded Space
4. BM vs. LW: Equivalence II
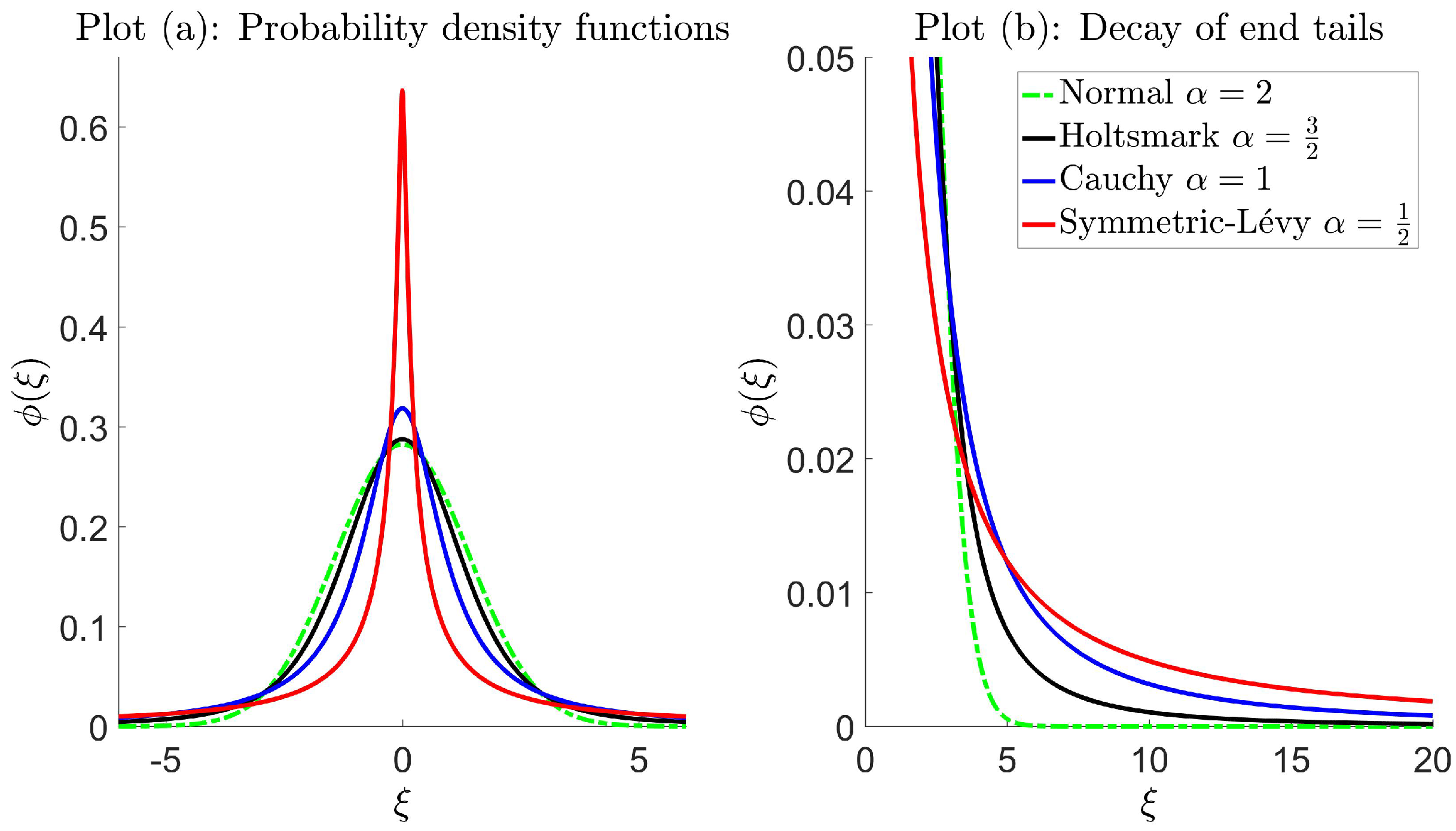
4.1. Stable Laws
4.2. Equivalence of Trap Counts: Cauchy Walk vs. Diffusion
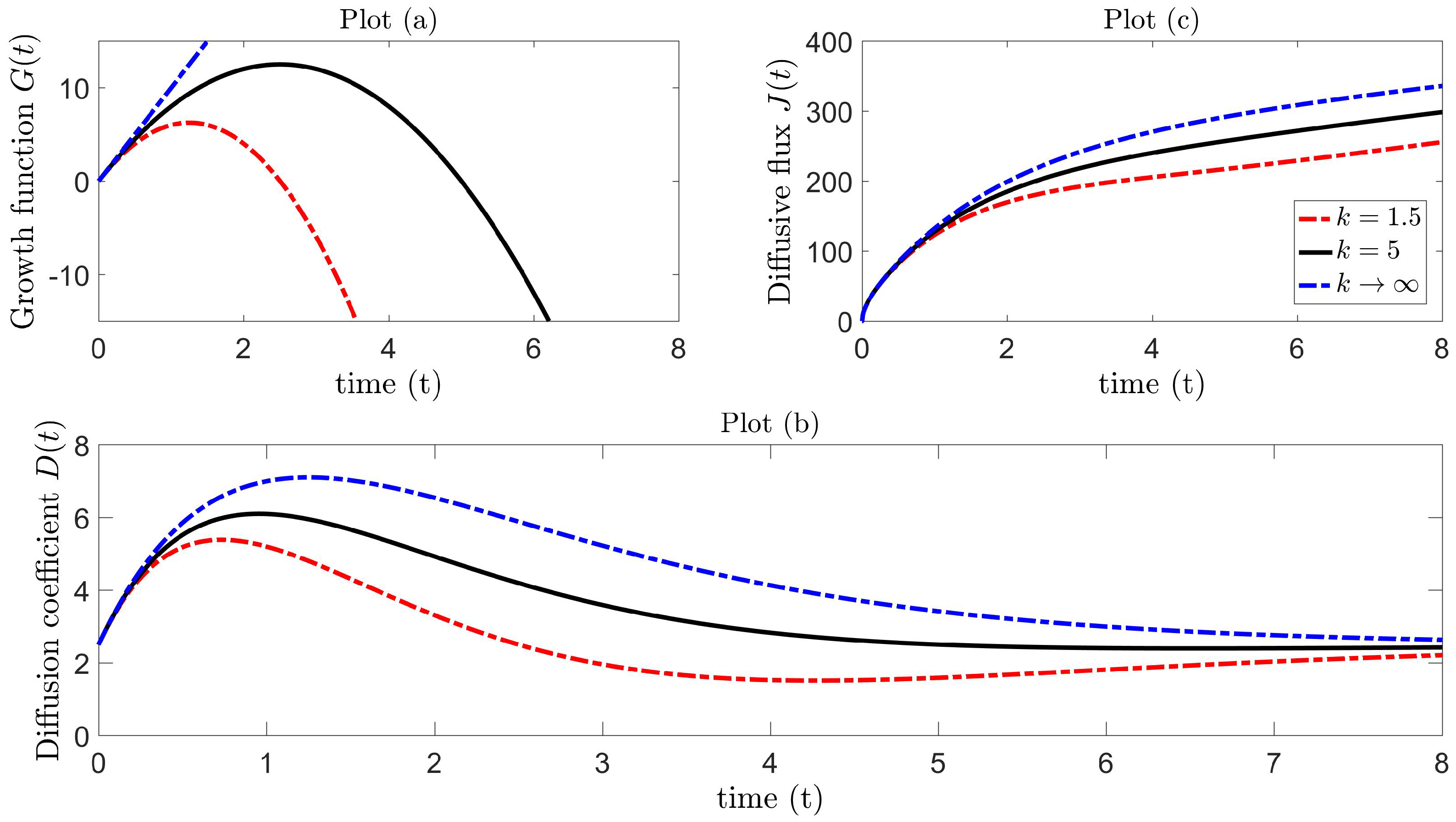
4.3. Proposed Diffusion Coefficient
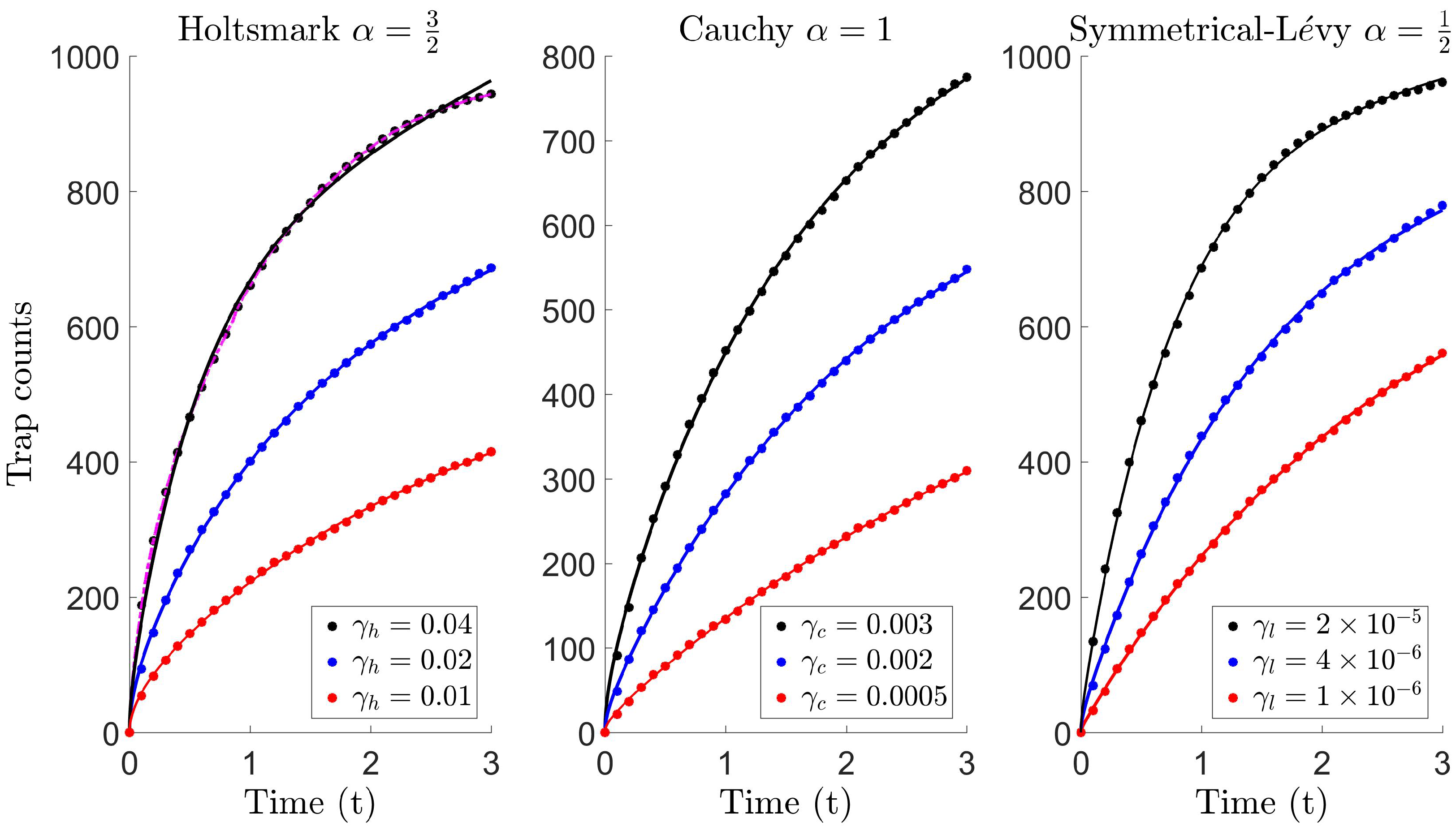
4.4. Reproducing Lévy Trap Counts Using Diffusion
5. Discussion
6. Concluding Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Mean Field Numerical Solution
Appendix B. Trap Count Recordings
| Time | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 54 | 93.8 | 188 | 21.6 | 48.6 | 91 | 32.6 | 69.4 | 134.2 |
| 0.2 | 83.2 | 147.2 | 283.4 | 36.4 | 86.4 | 147.8 | 60.6 | 123.4 | 241.6 |
| 0.3 | 106.6 | 195.6 | 355.2 | 53.2 | 120.2 | 206.2 | 94 | 173 | 324.8 |
| 0.4 | 127.6 | 235.6 | 413.8 | 68.4 | 145 | 252.6 | 123.2 | 222.2 | 399.4 |
| 0.5 | 146.2 | 270.6 | 466 | 78.4 | 171 | 291.2 | 147.4 | 263.6 | 460.8 |
| 0.6 | 163.2 | 299.6 | 510.4 | 91.6 | 194.4 | 328.4 | 171.6 | 305 | 513 |
| 0.7 | 180.6 | 326.2 | 551.8 | 103.8 | 218.6 | 364.4 | 196 | 340.4 | 560. |
| 0.8 | 195.6 | 351.6 | 588.8 | 116.6 | 240.2 | 394.8 | 219.6 | 376.4 | 603. |
| 0.9 | 209.8 | 376.8 | 629.6 | 126 | 262.6 | 425.4 | 238.4 | 409.6 | 645.8 |
| 1.0 | 225.6 | 400.8 | 661 | 133.8 | 282.2 | 451.6 | 258 | 438.2 | 686.4 |
| 1.1 | 238.2 | 421.8 | 689.6 | 143.2 | 302.6 | 476 | 279 | 466.2 | 717.4 |
| 1.2 | 251.4 | 442.4 | 715.2 | 155.4 | 321.6 | 498.4 | 298.6 | 491.6 | 746.4 |
| 1.3 | 260.8 | 460.4 | 740.6 | 166.4 | 335.8 | 521.2 | 321.4 | 513 | 773.2 |
| 1.4 | 271 | 482 | 760.4 | 175.2 | 355 | 545 | 341.4 | 536.2 | 797 |
| 1.5 | 282.6 | 499 | 783 | 184.2 | 372.6 | 563.8 | 358.6 | 555.2 | 820.2 |
| 1.6 | 290.6 | 516.2 | 804 | 194.2 | 384.6 | 584 | 374.8 | 575.8 | 839 |
| 1.7 | 301 | 531.4 | 821.2 | 204.8 | 398 | 600.8 | 390.2 | 596 | 856.8 |
| 1.8 | 311 | 546.4 | 836.4 | 214.2 | 413 | 617.4 | 407.8 | 612.2 | 871.2 |
| 1.9 | 323 | 562.8 | 851.6 | 222.6 | 427 | 633.8 | 422.8 | 632 | 883 |
| 2.0 | 333.2 | 574 | 864 | 231.8 | 439.6 | 652.6 | 435 | 648.6 | 894.8 |
| 2.1 | 342.6 | 586.2 | 877.2 | 333.2 | 574 | 864 | 446.6 | 668.4 | 904.6 |
| 2.2 | 350.4 | 599 | 888.8 | 241.8 | 452.2 | 669 | 462 | 681 | 912.4 |
| 2.3 | 359.2 | 609.2 | 898.8 | 246.4 | 465.2 | 683.8 | 474.2 | 694.2 | 919.4 |
| 2.4 | 369.4 | 620.2 | 907.6 | 254.2 | 476.6 | 695.2 | 488.6 | 704 | 928.2 |
| 2.5 | 376.2 | 631 | 914.8 | 263 | 488.2 | 708.2 | 502.6 | 716.4 | 934.6 |
| 2.6 | 386.2 | 645.8 | 921.8 | 271.6 | 499.2 | 721.2 | 515 | 730.4 | 941.6 |
| 2.7 | 394.4 | 655.4 | 928.4 | 280 | 509 | 735.2 | 525.6 | 747.4 | 946.2 |
| 2.8 | 399.4 | 666.8 | 934.4 | 288 | 518.2 | 745.8 | 538 | 756.4 | 950.2 |
| 2.9 | 407.6 | 678.2 | 938.8 | 294.2 | 527.2 | 757 | 550 | 768.2 | 956.2 |
| 3.0 | 415 | 686.8 | 943.8 | 301.2 | 536.8 | 766.8 | 560.8 | 779.2 | 961.2 |
References
- Burn, A. Integrated Pest Management; Academic Press: New York, NY, USA, 1987. [Google Scholar]
- Kogan, M. Integrated pest management: Historical perspectives and contemporary developments. Annu. Rev. Entomol. 1998, 43, 243–270. [Google Scholar] [CrossRef] [PubMed]
- Millennium Ecosystem Assessment (MEA). Ecosystems and Human Well-Being: Biodiversity Synthesis of the Millennium Ecosystem Assessment; Millennium Ecosystem Assessment World Resources Institute: Washington, DC, USA, 2005. [Google Scholar]
- Cardinale, B.; Duffy, J.; Gonzalez, A.; Hooper, D.; Perrings, C.; Venail, P.; Narwani, A.; Mace, G.; Tilman, D.; Wardle, D.; et al. Biodiversity loss and its impact on humanity. Nature 2012, 486, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, D.; van Bodegom, P.; Tukker, A. Evaluation and selection of functional diversity metrics with recommendations for their use in life cycle assessments. Int. J. Life Cycle Assess. 2018. [Google Scholar] [CrossRef]
- Pimentel, D.; Greiner, A. Environmental and socio-economic costs of pesticide use. In Techniques for Reducing Pesticide Use: Economic and Environmental Benefits; Pimentel, D., Ed.; John Wiley and Sons: New York, NY, USA, 1997. [Google Scholar]
- Alavanja, M.; Ross, M.; Bonner, M. Increased cancer burden among pesticide applicators and others due to pesticide exposure. CA Cancer J. Clin. 2013, 62, 120–142. [Google Scholar] [CrossRef] [PubMed]
- Bourguet, D.; Guillemaud, T. Sustainable Agriculture Reviews; The Hidden and External Costs of Pesticide Use; Springer: Berlin, Germany, 2016; Volume 19, pp. 35–120. [Google Scholar]
- Pimentel, D. Amounts of pesticides reaching target pests: Environmental impacts and ethics. J. Agric. Environ. Ethics 1995, 8, 17–29. [Google Scholar] [CrossRef]
- Alyokhin, A.; Baker, M.; Mota-Sanchez, D.; Dively, G.; Grafius, E. Colorado potato beetle resistance to insecticides. Am. J. Potato Res. 2008, 85, 395–413. [Google Scholar] [CrossRef]
- Sohrabi, F.; Shishehbor, P.; Saber, M.; Mosaddegh, M. Lethal and sub-lethal effects of imidacloprid and buprofezin on the sweet potato whitefly parasitoid Eretmocerus mundus (Hymenoptera: Aphelinidae). Crop. Prot. 2013, 45, 98–103. [Google Scholar] [CrossRef]
- Petrovskii, S.; Ahmed, D.; Blackshaw, R. Estimating Insect Population Density. Ecol. Complex 2012, 10, 69–82. [Google Scholar] [CrossRef]
- Holland, J.M.; Perry, J.N.; Winder, L. The within-field spatial and temporal distribution of arthropods in winter wheat. Bull. Entomol. Res. 1999, 89, 499–513. [Google Scholar] [CrossRef]
- Ferguson, A.W.; Klukowski, Z.; Walczak, B.; Perry, J.N.; Mugglestone, M.A.; Clark, S.J.; Williams, I. The spatio-temporal distribution of adult Ceutorhynchus assimilis in a crop of winter oilseed rape in relation to the distribution of their larvae and that of the parasitoid Trichomalus perfectus. Entomol. Exp. Appl. 2000, 95, 161–171. [Google Scholar] [CrossRef]
- Alexander, C.J.; Holland, J.M.; Winder, L.; Woolley, C.; Perry, J.N. Performance of sampling strategies in the presence of known spatial patterns. Ann. Appl. Biol. 2005, 146, 361–370. [Google Scholar] [CrossRef]
- Byers, J.A.; Anderbrant, O.; Lofqvist, J. Effective attraction radius: A method for comparing species attractants and determining densities of flying insects. J. Chem. Ecol. 1989, 15, 749–765. [Google Scholar] [CrossRef] [PubMed]
- Raworth, D.A.; Choi, M. Determining numbers of active carabid beetles per unit area from pitfall-trap data. Entomol. Exp. Appl. 2001, 98, 95–108. [Google Scholar] [CrossRef]
- Turchin, P. Quantitative Analysis of Movement: Measuring and Modelling Population Redistribution in Animals and Plants; Sinauer Associates: Sunderland, MA, USA, 1998. [Google Scholar]
- Okubo, A.; Levin, S. Diffusion and Ecological Problems: Modern Perspectives; Springer: New York, NY, USA, 2001. [Google Scholar]
- Lewis, M.; Maini, P.; Petrovskii, S. Dispersal, Individual Movement and Spatial Ecology; Springer: Berlin, Germany, 2013. [Google Scholar]
- Levin, S.; Cohen, D.; Hastings, A. Dispersal strategies in patchy environments. Theor. Popul. Biol. 1984, 26, 165–180. [Google Scholar] [CrossRef]
- Reichenbach, T.; Mobilia, M.; Frey, E. Mobility promotes and jeopardizes biodiversity in rock-paper-scissors games. Nature 2007, 448, 1046–1049. [Google Scholar] [CrossRef] [PubMed]
- Hengeveld, R. Dynamics of Biological Invasions; Chapman and Hall: London, UK, 1989. [Google Scholar]
- Shigesada, N.; Kawasaki, K. Biological Invasions: Theory and Practice; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Petrovskii, S.; Brian, L. Exactly Solvable Models of Biological Invasion; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Petrovskii, S.; Petrovskaya, N.; Bearup, D. Multiscale approach to pest insect monitoring: Random walks, pattern formation, synchronization and networks. Phys. Life Rev. 2014, 11, 467–525. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, D.; Petrovskii, S. Time Dependent Diffusion as a Mean Field Counterpart of Lévy Type Random Walk. Math. Model. Nat. Phenom. 2015, 10, 5–26. [Google Scholar] [CrossRef]
- Bearup, D.; Benefer, C.; Petrovskii, S.; Blackshaw, R. Revisiting Brownian motion as a description of animal movement: A comparison to experimental movement data. Methods Ecol. Evol. 2016, 7, 1525–1537. [Google Scholar] [CrossRef]
- Skellam, J. Random dispersal in theoretical populations. Biometrika 1951, 38, 196–218. [Google Scholar] [CrossRef] [PubMed]
- Kareiva, P.; Shigesada, N. Analyzing insect movement as a correlated random walk. Oecologia 1983, 56, 234–238. [Google Scholar] [CrossRef] [PubMed]
- Kareiva, P. Local movement in herbivorous insecta: Applying a passive diffusion model to mark-recapture field experiments. Oecologia 1983, 57, 322–327. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, A.; Smith, A.; Menzel, R.; Greggers, U.; Reynolds, D.; Riley, J. Displaced honey bees perform optimal scale-free search flights. Ecology 2007, 88, 1955–1961. [Google Scholar] [CrossRef] [PubMed]
- Hapca, S.; Crawford, J.; Young, I. Anomalous diffusion of heterogeneous populations characterized by normal diffusion at the individual level. J. R. Soc. Interface 2009, 6, 111–122. [Google Scholar] [CrossRef] [PubMed]
- Jansen, V.; Mashanova, A.; Petrovskii, S. Model selection and animal movement: “Comment on Lévy walks evolve through interaction between movement and environmental complexity”. Science 2012, 335, 918. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, D. Stochastic and Mean Field Approaches for Trap Count Modelling and Interpretation. Ph.D. Thesis, Leicester University, Leicester, UK, 2015. [Google Scholar]
- Petrovskii, S.; Morozov, A.; Li, B. On a possible origin of the fat-tailed dispersal in population dynamics. Ecol. Complex. 2008, 5, 146–150. [Google Scholar] [CrossRef]
- Mashanova, A.; Olive, T.; Jansen, V. Evidence for intermittency and a truncated power law from highly resolved aphid movement data. J. R. Soc. Interface 2010, 7, 199–208. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Knell, A.; Codling, E. Classifying area-restricted search (ARS) using a partial sum approach. Theor. Ecol. 2012, 5, 325–329. [Google Scholar] [CrossRef]
- Sims, D.; Southall, E.; Humphries, N.; Hays, G.; Bradshaw, C.; Pitchford, J.; James, A.; Ahmed, M.; Brierley, A.; Hindell, M.; et al. Scaling laws of marine predator search behavior. Nature 2008, 451, 1098–1102. [Google Scholar] [CrossRef] [PubMed]
- Viswanathan, G.; Afanasyev, V.; Buldryrev, S.; Havlin, S.; da Luz, M.R.; Stanley, H. The Physics of Foraging; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Edwards, A.; Phillips, R.; Watkins, N.; Freeman, M.; Murphy, E.; Afanasyev, V.; Buldyrev, S.; da Luz, M.G.; Raposo, E.; Stanley, H.; et al. Revisiting Lévy flight search patterns of wandering albatrosses, bumblebees and deer. Nature 2007, 449, 1044–1048. [Google Scholar] [CrossRef] [PubMed]
- Benhamou, S. How many animals really do the Lévy walk? Ecology 2007, 88, 1962–1969. [Google Scholar] [CrossRef] [PubMed]
- Shlesinger, M.; Zaslavsky, G.; Klafter, J. Strange kinetics. Nature 1993, 363, 31–37. [Google Scholar] [CrossRef]
- Zaburdaev, Z.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483. [Google Scholar] [CrossRef]
- Viswanathan, G.; Afanasyev, V.; Buldryrev, S.E.A. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Reynolds, A. Olfactory search behavior in the wandering albatross is predicted to give rise to Lévy flight movement patterns. Anim. Behav. 2012, 83, 1225–1229. [Google Scholar] [CrossRef]
- Bartumeus, F.; Catalan, J. Optimal search behavior and classic foraging theory. J. Phys. A 2009, 132, 569–580. [Google Scholar] [CrossRef]
- Petrovskii, S.; Morozov, A. Dispersal in a Statistically Structured Population. Am. Nat. 2008, 173, 278–289. [Google Scholar] [CrossRef] [PubMed]
- Petrovskii, S.; Mashanova, A.; Jansen, V. Variation in individual walking behavior creates the impression of a Lévy flight. Proc. Natl. Acad. Sci. USA 2011, 108, 8704–8707. [Google Scholar] [CrossRef] [PubMed]
- Auger-Méthé, M.; Derocher, A.; Plank, M.; Codling, E.; Lewis, M. Differentiating the Lévy walk from a composite correlated random walk. Methods Ecol. Evol. 2015, 6, 1179–1189. [Google Scholar] [CrossRef]
- De Jager, M.; Weissing, F.; Herman, P.; Nolet, B.; vande Koppel, J. Response to Comment on “Lévy walks evolve through interaction between movement and environmental complexity”. Science 2012, 335, 918. [Google Scholar] [CrossRef]
- Codling, E. Pest insect movement and dispersal as an example of applied movement ecology. Comment on “Multiscale approach to pest insect monitoring: Random walks, pattern formation, synchronization, and networks” by Petrovskii, Petrovskaya and Bearup. Phys. Life Rev. 2014, 11, 533–535. [Google Scholar] [CrossRef] [PubMed]
- Petrovskii, S.; Petrovskaya, N.; Bearup, D. Multiscale ecology of agroecosystems is an emerging research field that can provide a stronger theoretical background for the integrated pest management. Reply to comments on “Multiscale approach to pest insect monitoring: Random walks, pattern formation, synchronization, and networks”. Phys. Life Rev. 2014, 11, 536–539. [Google Scholar] [PubMed]
- Grimm, V.; Railsback, S. Individual Based Modelling and Ecology; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Petrovskii, S.; Petrovskaya, N. Computational ecology as an emerging science. Interface Focus 2012, 2, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Bearup, D.; Petrovskaya, N.; Petrovskii, S. Some analytical and numerical approaches to understanding trap counts resulting from pest insect immigration. Math. Biosci. 2015, 263, 143–160. [Google Scholar] [CrossRef] [PubMed]
- Pyke, G. Understanding movements of organisms: It’s time to abandon the Lévy foraging hypothesis. Methods Ecol. Evol. 2015, 6, 1–16. [Google Scholar] [CrossRef]
- Weiss, G. Aspects and Applications of the Random Walk; North Holland Press: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Codling, E.; Plank, M.; Benhamou, S. Random walk models in biology. J. R. Soc. Interface 2008, 5, 813–834. [Google Scholar] [CrossRef] [PubMed]
- Bearup, D.; Petrovskii, S. On time scale invariance of random walks in confined space. J. Theor. Biol. 2015, 367, 230–245. [Google Scholar] [CrossRef] [PubMed]
- Viswanathan, G.; Buldyrev, S.; Havlin, S. Optimizing the success of random searches. Nature 1999, 401, 911–914. [Google Scholar] [CrossRef] [PubMed]
- Knighton, J.; Dapkey, T.; Cruz, J. Random walk modeling of adult Leuctra ferruginea (stonefly) dispersal. Ecol. Inf. 2014, 19, 1–9. [Google Scholar] [CrossRef]
- Nathan, R.; Getz, W.; Revilla, E.; Holyoak, M.; Kadmon, R.; Saltz, D.; Smouse, P. A movement ecology paradigm for unifying organismal movement research. Proc. Natl. Acad. Sci. USA 2008, 105, 19052–19059. [Google Scholar] [CrossRef] [PubMed]
- Benhamou, S. Of scales and stationarity in animal movements. Ecol. Lett. 2014, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Murray, J. Mathematical Biology: I. An Introduction, 3rd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 17, 549–560. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences, 2nd ed.; Springer: Berlin, Germay, 2004. [Google Scholar]
- Balescu, R. Equilibrium and Non-Equilibrium Statistical Mechanics; John Wiley: New York, NY, USA, 1975. [Google Scholar]
- Kölzsch, A.; Alzate, A.; Bartumeus, F.; de Jager, M.; Weerman, E.; Hengeveld, G.; Naguib, M.; Nolet, B.; van de Koppel, J. Experimental evidence for inherent Lévy search behavior in foraging animals. Proc. R. Soc. B 2015, 282. [Google Scholar] [CrossRef] [PubMed]
- Nolan, J. Stable Distributions—Models for Heavy Tailed Data; Birkhauser: Boston, MA, USA, 2015; In Progress: Chapter 1; Available online: academic2.american.edu/~jpnolan (accessed on 1 December 2017).
- Chambers, J.; Mallows, C.; Stuck, B. A method for simulating stable random variables. JASA 1976, 71, 340–344. [Google Scholar] [CrossRef]
- Weron, R. On the Chambers-Mallows-Stuck method for simulating skewed stable random variables. Stat. Probabil. Lett. 1996, 28, 165–171, See also Weron, R. Correction to: On the Chambers-Mallows-Stuck Method for Simulating Skewed Stable Random Variables, Research Report HSC/96/1, Wroc Law University of Technology, 1996. Available online: http://www.im.pwr.wroc.pl/~hugo/Publications.html (accessed on 1 December 2017). [CrossRef]
- Zolotarev, V. One-Dimensional Stable Distributions; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Samorodnitsky, G.; Taqqu, M. Stable Non-Gaussian Random Processes; Chapman and Hall: Boca Raton, FL, USA, 1994. [Google Scholar]
- Holmes, E.E. Are diffusion models too simple? A comparison with telegraph models of invasion. Am. Nat. 1993, 142, 779–795. [Google Scholar] [CrossRef] [PubMed]
- Brose, U. Body-mass constraints on foraging behavior determine population and food-web dynamics. Funct. Ecol. 2010, 24, 28–34. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I. Anomalous diffusion spreads its wings. Phys. World 2005, 18, 29–32. [Google Scholar] [CrossRef]
- Malchow, H.; Petrovskii, S.; Venturino, E. Spatiotemporal Patterns in Ecology and Epidemiology: Theory, Models, and Simulations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Rosenzweig, M.; MacArthur, R. Graphical representation and stability conditions of predator-prey interaction. Am. Nat. 1963, 97, 209–223. [Google Scholar] [CrossRef]
- Choules, J.; Petrovskii, S. Which Random Walk is Faster? Methods to Compare Different Step Length Distributions in Individual Animal Movement. Math. Model. Nat. Phenom. 2017, 12, 22–45. [Google Scholar] [CrossRef]
- Ott, A.; Bouchaud, J.; Langevin, D.; Urbach, W. Anomalous diffusion in ‘‘living polymers’’: A genuine Lévy flight? Phys. Rev. Lett. 1990, 65, 2201–2204. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Wang, B.; Granick, S. Memoryless self-reinforcing directionality in endosomal active transport within living cells. Nat. Mater. 2015, 14, 589–593. [Google Scholar] [CrossRef] [PubMed]
- Ariel, G.; Rabani, A.; Benisty, S.; Partridge, J.; Harshey, R.; Be’er, A. Swarming bacteria migrate by Lévy Walk. Nat. Commun. 2015, 6, 8396. [Google Scholar] [CrossRef] [PubMed]
- Vallaeys, V.; Tyson, R.; Lane, W.; Deleersnijder, E.; Hanert, E. A Lévy-flight diffusion model to predict transgenic pollen dispersal. J. R. Soc. Interface 2017, 14. [Google Scholar] [CrossRef] [PubMed]
- Harold, H. Energetics of Desert Invertebrates; Springer: Berlin, Germany, 1996. [Google Scholar]
- El Baidouri, F.; Venditti, C.; Humphries, S. Independent evolution of shape and motility allows evolutionary flexibility in Firmicutes bacteria. Nat. Ecol. Evol. 2016, 9, 0009. [Google Scholar] [CrossRef] [PubMed]
- Halsey, L. Terrestrial movement energetics: Current knowledge and its application to the optimising animal. J. Exp. Biol. 2016, 219, 1424–1431. [Google Scholar] [CrossRef] [PubMed]
- Kramer, D.; McLaughlin, R. The Behavioral Ecology of Intermittent Locomotion. Am. Zool. 2015, 41, 137–153. [Google Scholar] [CrossRef]
- Jervis, M. Insects as Natural Enemies: A Practical Perspective; Springer: Berlin, Germany, 2005; p. 281. [Google Scholar]
- Tyson, R. Pest control: A modeling approach. Comment on “Multiscale approach to pest insect monitoring: Random walks, pattern formation, synchronization, and networks” by S. Petrovskii, N. Petrovskaya, D. Bearup. Phys. Life Rev. 2014, 11, 526–528. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, A. Extending Lévy search theory from one to higher dimensions: Lévy walking favours the blind. Proc. Math. Phys. Eng. Sci. 2015, 471. [Google Scholar] [CrossRef] [PubMed]
- Brennan, K.; Majer, J.; Reygaert, N. Determination of an Optimal Pitfall Trap Size for Sampling Spiders in a Western Australian Jarrah Forest. J. Insect Conserv. 1999, 3, 297–307. [Google Scholar] [CrossRef]
- Elkinton, J.; Lance, D.; Boettner, G.; Khrimian, A.; Leva, N. Evaluation of pheromone-baited traps for winter moth and Bruce spanworm (Lepidoptera: Geometridae). J. Econ. Entomol. 2011, 104, 494–500. [Google Scholar] [CrossRef] [PubMed]
- Tuf, I.; Chmelík, V.; Dobroruka, I.; Hábová, L.; Hudcová, P.; Ŝipoŝ, J.; Staŝiov, S. Hay-bait traps are a useful tool for sampling of soil dwelling millipedes and centipedes. Zookeys 2015, 510, 197–207. [Google Scholar] [CrossRef] [PubMed]
- Yamanaka, T.; Tatsuki, S.; Shimada, M. An individual-based model for sex-pheromone-oriented flight patterns of male moths in a local area. Ecol. Model. 2003, 161, 35–51. [Google Scholar] [CrossRef]
- Morton, K.; Mayers, D. Numerical Solution of Partial Differential Equations: An Introduction; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Holmes, M. Introduction to Numerical Methods in Differential Equations; Springer: Berlin, Germany, 2006. [Google Scholar]
- Strauss, W. Partial Differential Equations: An Introduction; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
| 1 | The randomness of animal movement is obviously an idealization, which, however, is well justified under certain conditions, e.g., see [18] for a detailed discussion of this issue. |
| 2 | This is the inverse of the error function defined by |
| 3 | This specific type of random walk is of significant interest in foraging theory since an inverse square power-law distribution of flight lengths provides an optimal strategy to detect target sites provided that the sites are sparse and can be revisited [61]. Furthermore, see Section 2.2. |
| 4 | See Ahmed and Petrovskii [27] for a detailed description of the model previously proposed. |

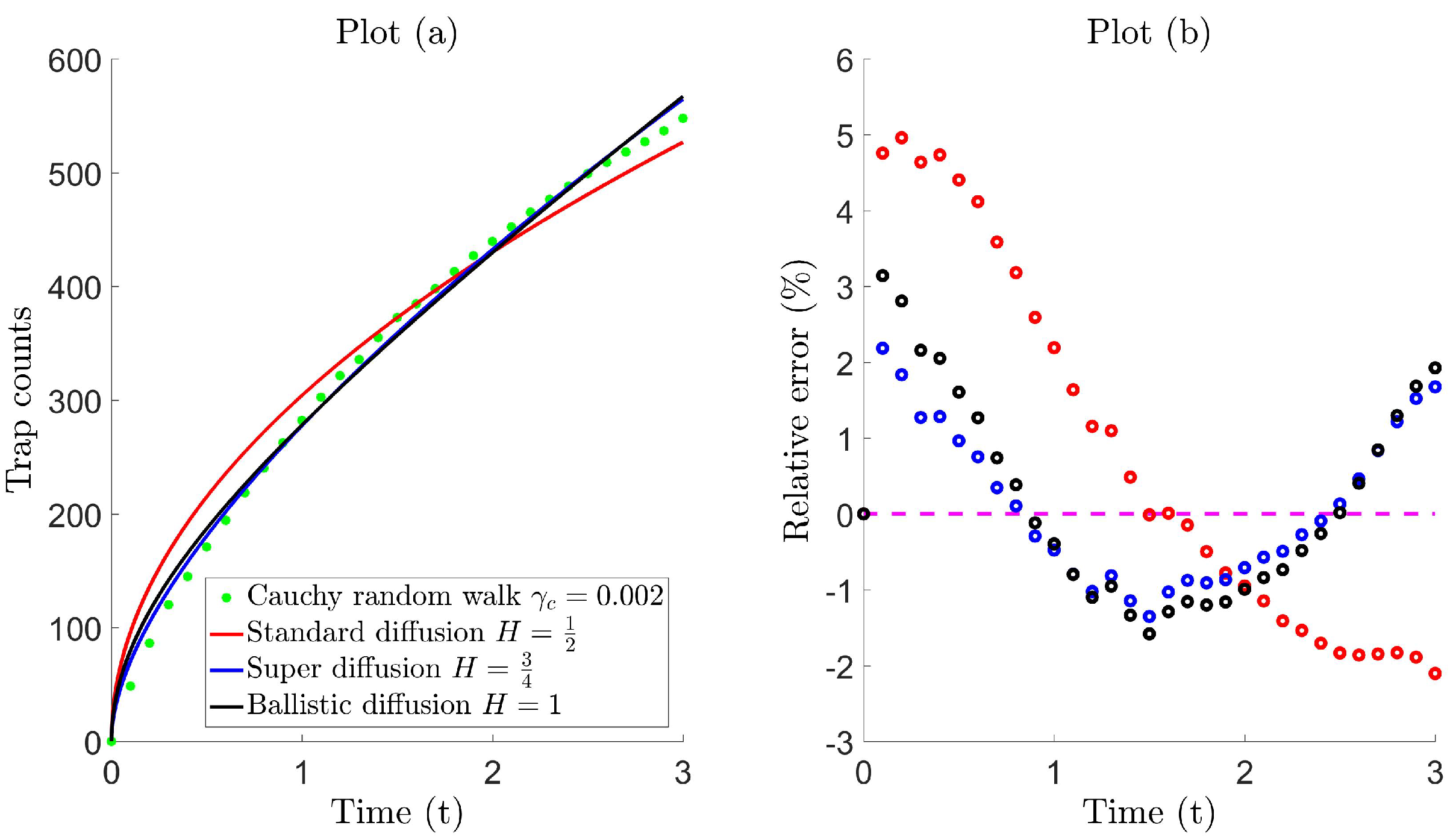
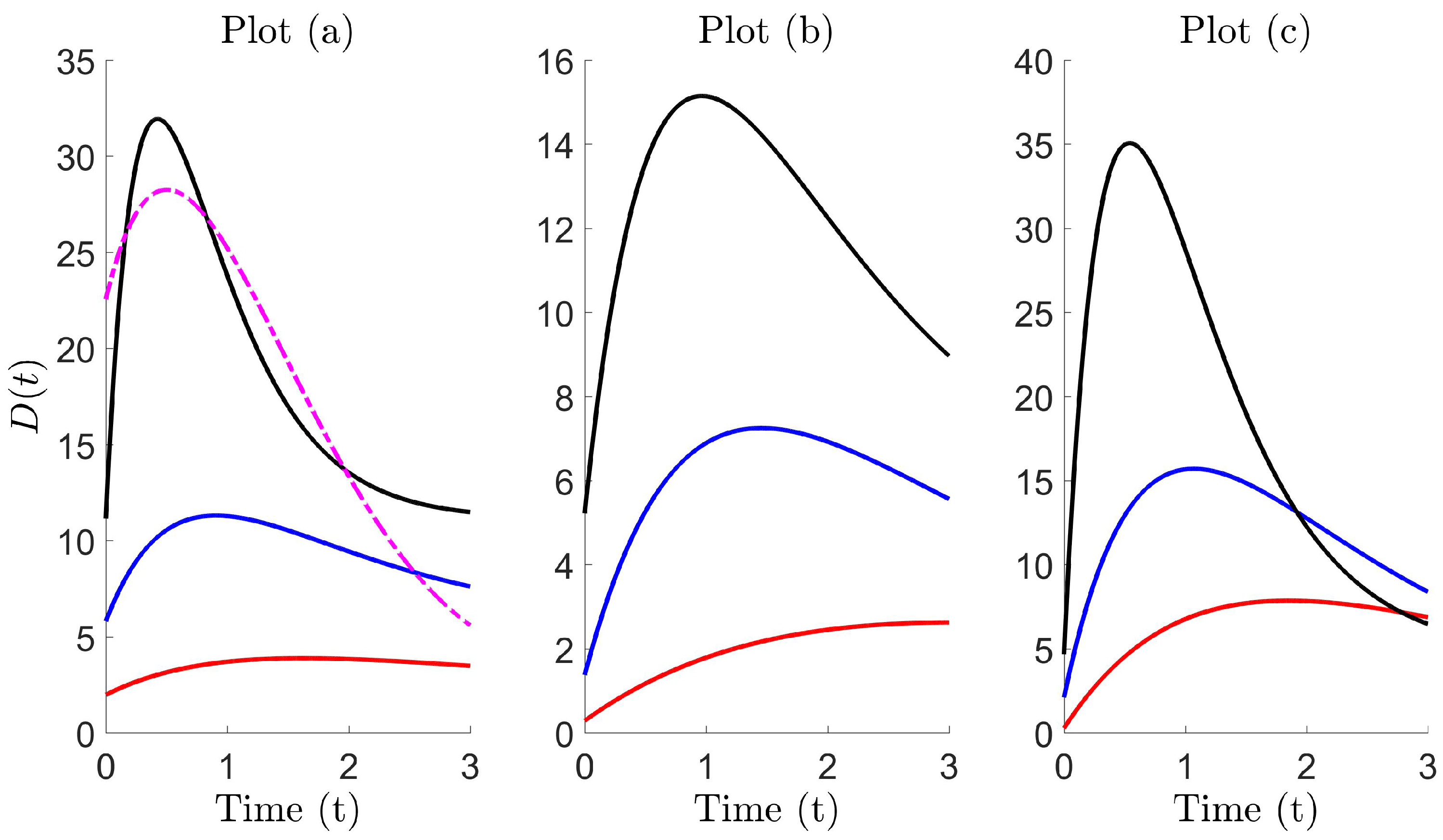
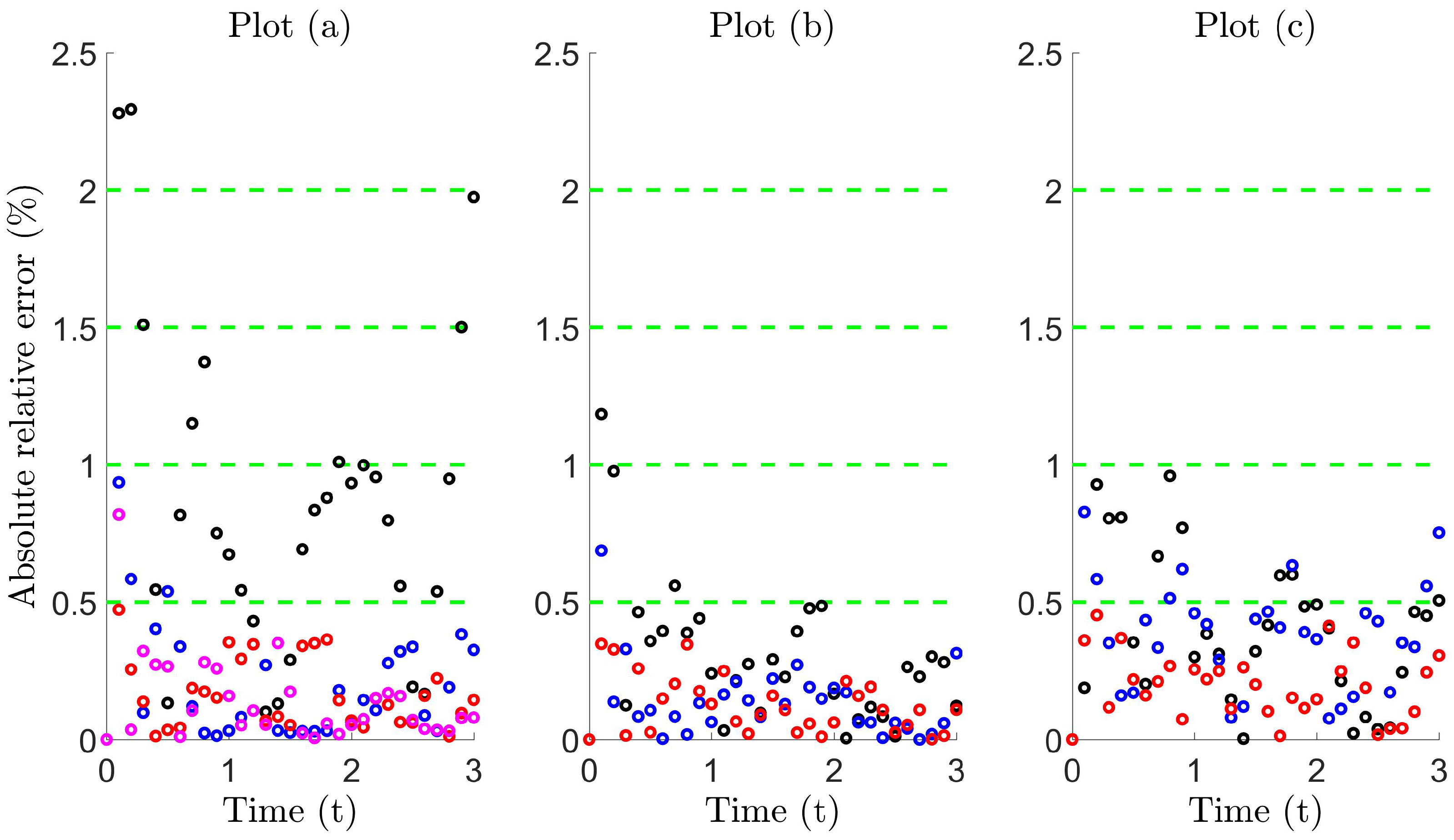
| Standard Diffusion | Super Diffusion | Ballistic Diffusion | |
|---|---|---|---|
| Brownian trap counts | 0.306 | 0.157 | 0.167 |
| Standard Diffusion | Super Diffusion | Ballistic Diffusion | |
|---|---|---|---|
| Brownian trap counts | 0.306 | 0.157 | 0.167 |
| Cauchy trap counts | 2.035 | 0.849 | 1.120 |
| k | |||||||
|---|---|---|---|---|---|---|---|
| 0.01 | 1.974 | 3.186 | 0.615 | 1286.032 | 1.9745 | 3.1834 | 0.6158 |
| 0.02 | 5.798 | 16.488 | 1.102 | 2846.675 | 5.7984 | 16.4881 | 1.1025 |
| 0.04 | 22.552 | 26.262 | 0.631 | 1.235 | 11.1403 | 133.0602 | 2.3539 |
| 0.0005 | 0.286 | 2.083 | 0.327 | 2598.906 | 0.2861 | 2.0828 | 0.3276 |
| 0.002 | 1.374 | 10.971 | 0.687 | 1918.029 | 1.3743 | 10.9709 | 0.6874 |
| 0.003 | 5.218 | 27.968 | 1.036 | 2589.831 | 5.2184 | 27.9676 | 1.0365 |
| 0.271 | 11.137 | 0.541 | 2608.857 | 0.2715 | 11.1369 | 0.5405 | |
| 2.099 | 34.539 | 0.935 | 2613.735 | 2.0992 | 34.5388 | 0.9345 | |
| 4.671 | 152.605 | 1.847 | 5202.465 | 4.6706 | 152.6045 | 1.8471 |
| Diffusion | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Standard | 2.035 | ||||||||
| Super | 0.849 | ||||||||
| Ballistic | 1.120 | ||||||||
| Model 1 (46) | 0.139 | ||||||||
| Model 2 (47) | 0.162 | 0.198 | 0.839 | 0.123 | 0.135 | 0.299 | 0.194 | 0.370 | 0.394 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, D.A.; Petrovskii, S.V.; Tilles, P.F.C. The “Lévy or Diffusion” Controversy: How Important Is the Movement Pattern in the Context of Trapping? Mathematics 2018, 6, 77. https://doi.org/10.3390/math6050077
Ahmed DA, Petrovskii SV, Tilles PFC. The “Lévy or Diffusion” Controversy: How Important Is the Movement Pattern in the Context of Trapping? Mathematics. 2018; 6(5):77. https://doi.org/10.3390/math6050077
Chicago/Turabian StyleAhmed, Danish A., Sergei V. Petrovskii, and Paulo F. C. Tilles. 2018. "The “Lévy or Diffusion” Controversy: How Important Is the Movement Pattern in the Context of Trapping?" Mathematics 6, no. 5: 77. https://doi.org/10.3390/math6050077
APA StyleAhmed, D. A., Petrovskii, S. V., & Tilles, P. F. C. (2018). The “Lévy or Diffusion” Controversy: How Important Is the Movement Pattern in the Context of Trapping? Mathematics, 6(5), 77. https://doi.org/10.3390/math6050077




