Theoretical Study of the One Self-Regulating Gene in the Modified Wagner Model
Abstract
:1. Introduction
2. Studying the Sigmoid Function
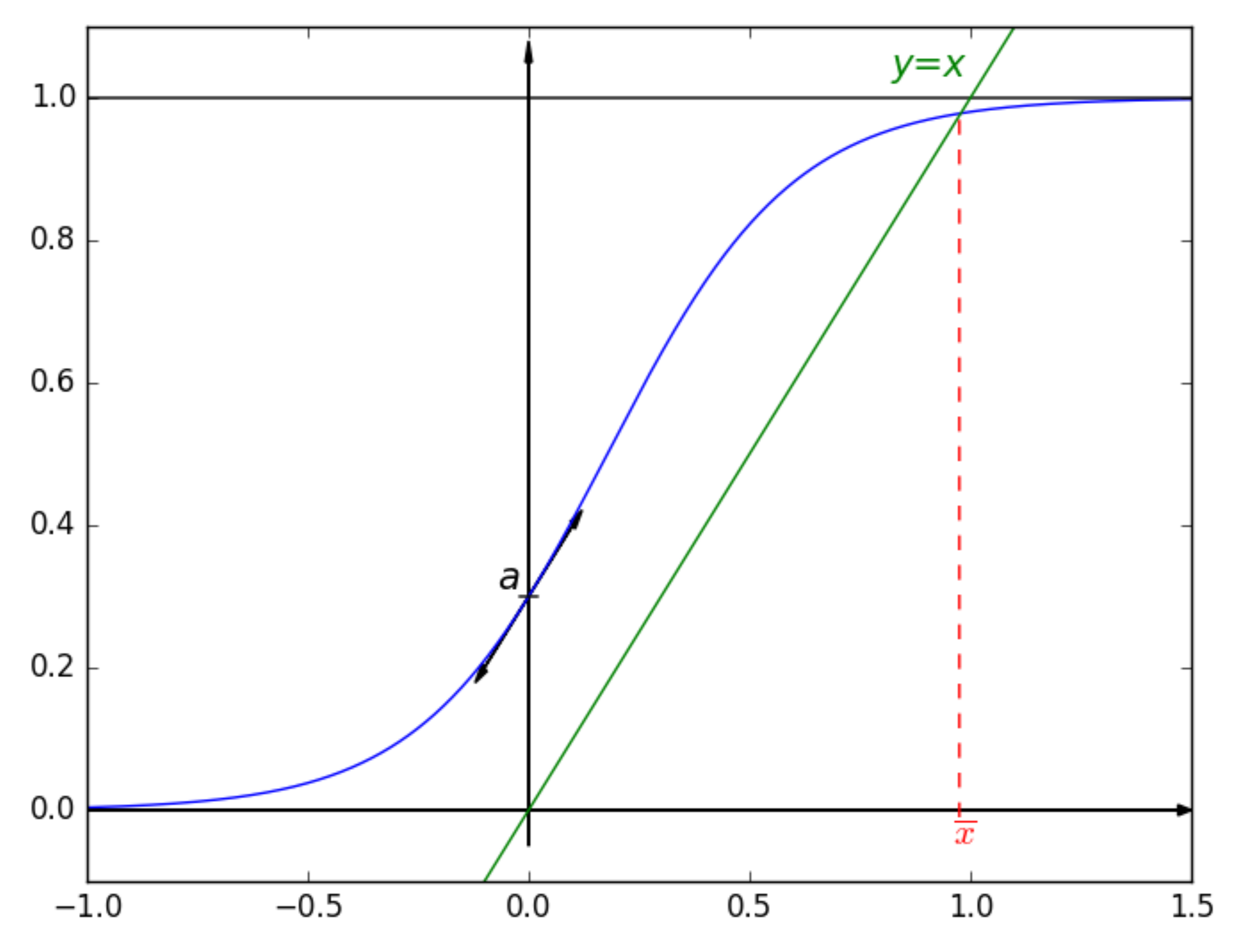
2.1. Introducing the Considered Sigmoid
- a continuous increasing function,
- the limit of as x approaches negative infinity is 0,
- the limit of as x approaches infinity is 1,
- and ,
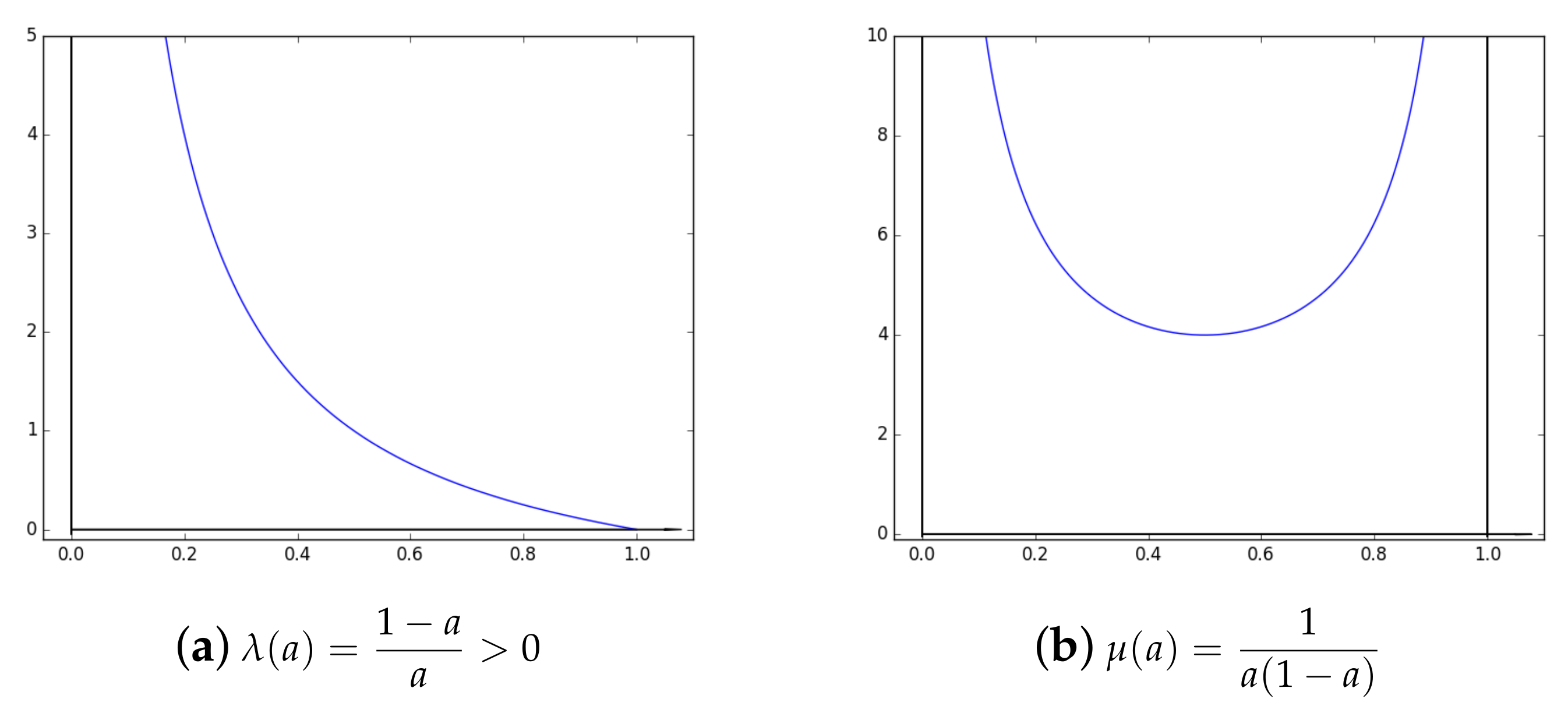
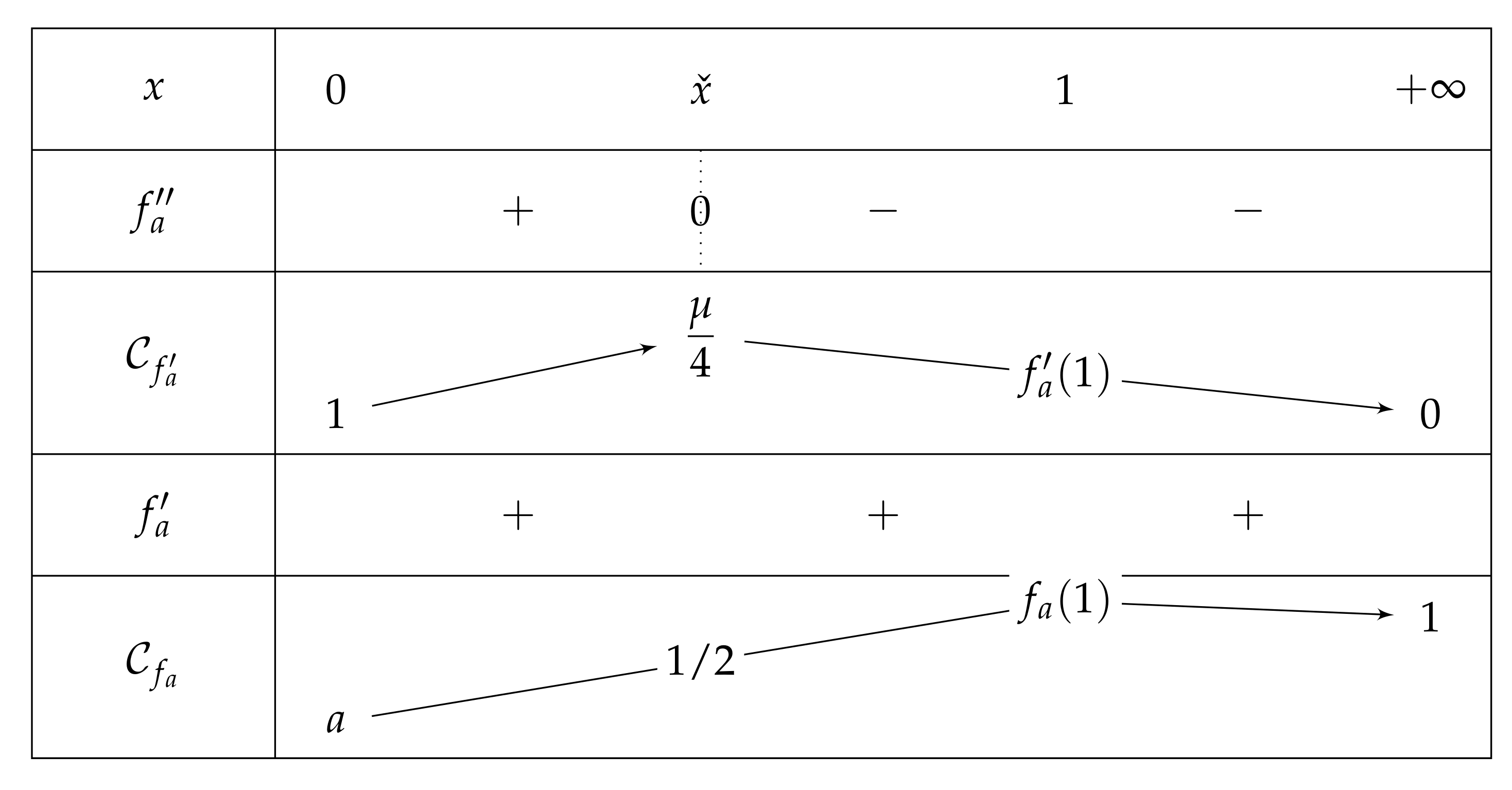
2.2. About and Parameters
2.3. Fixed Point of
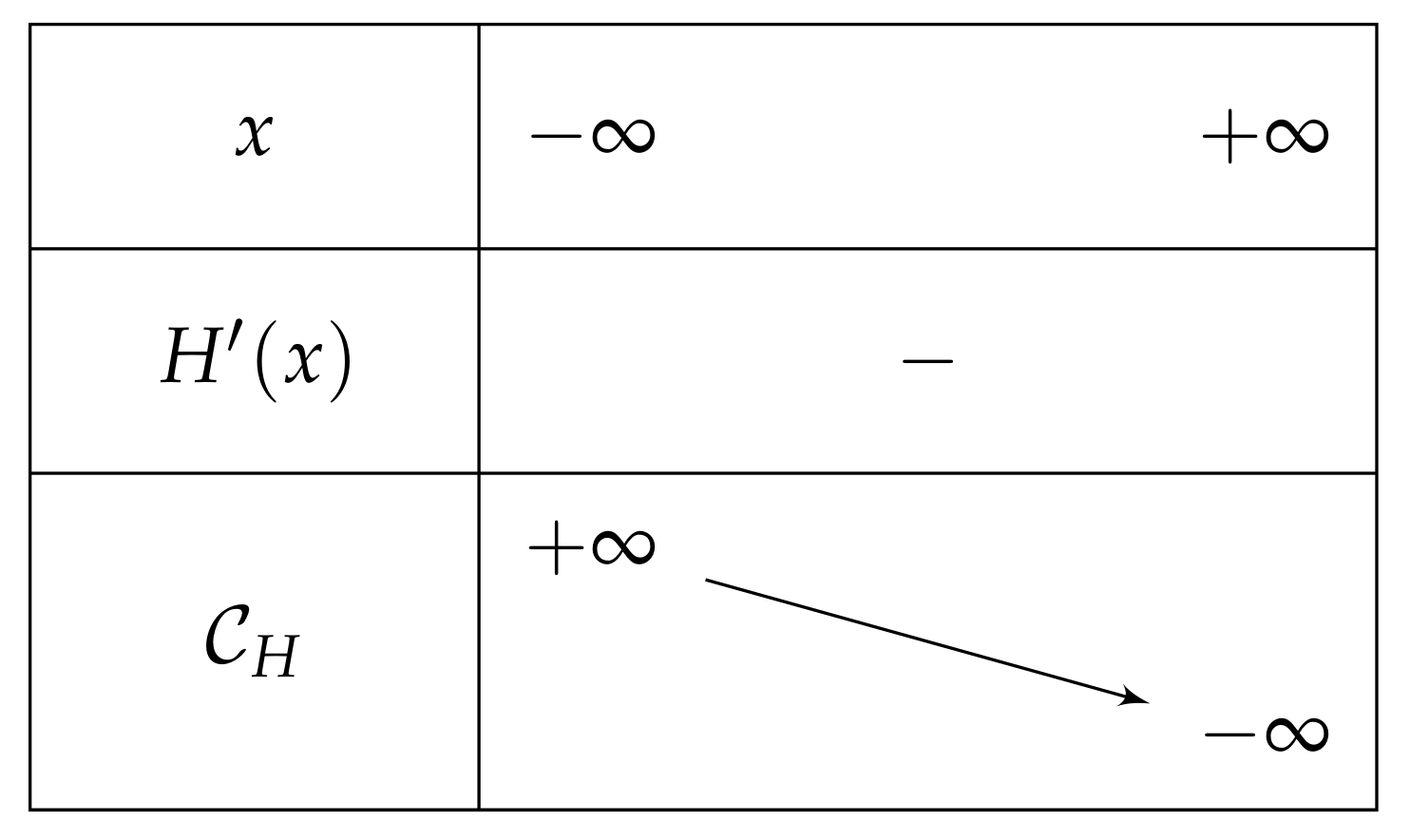
- If , then on , and we have and , which leads to the variations depicted in Figure 5.Consequently, if , then has one unique solution, i.e., has one unique fixed point.
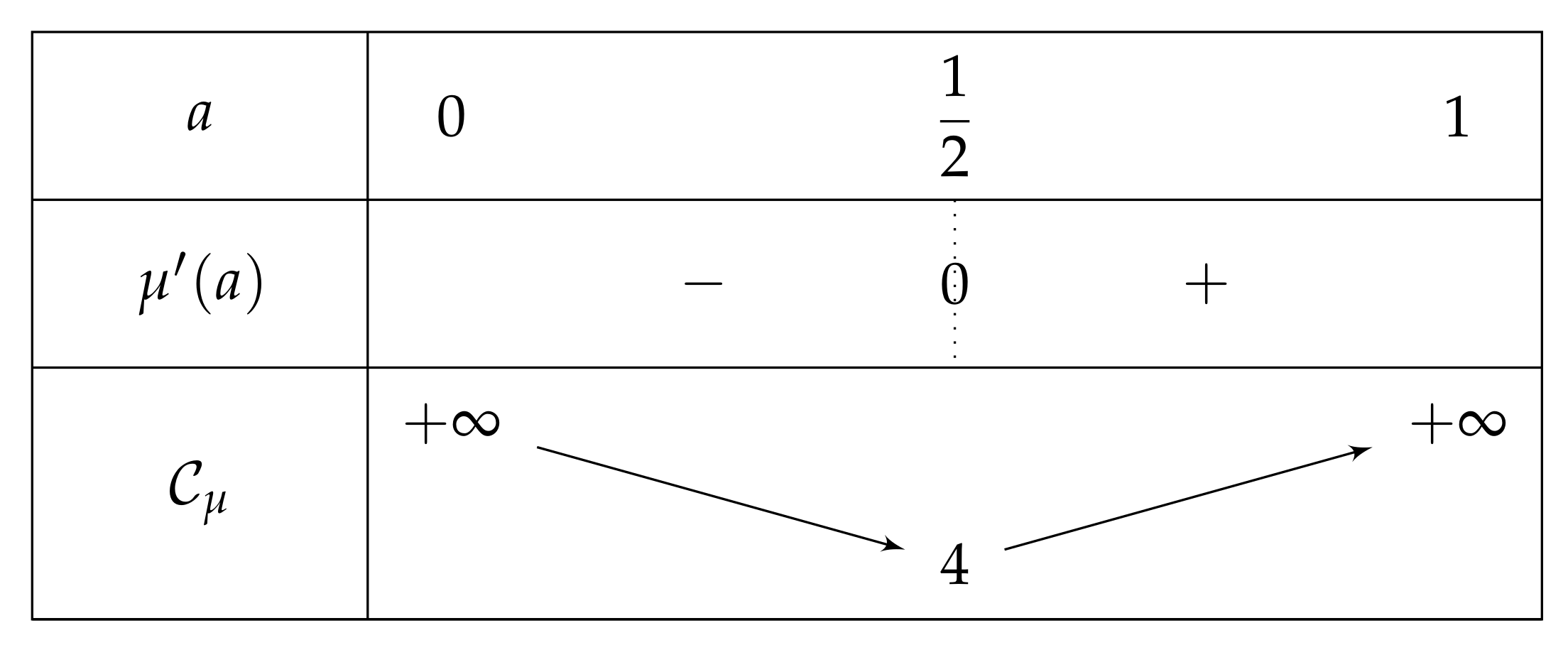
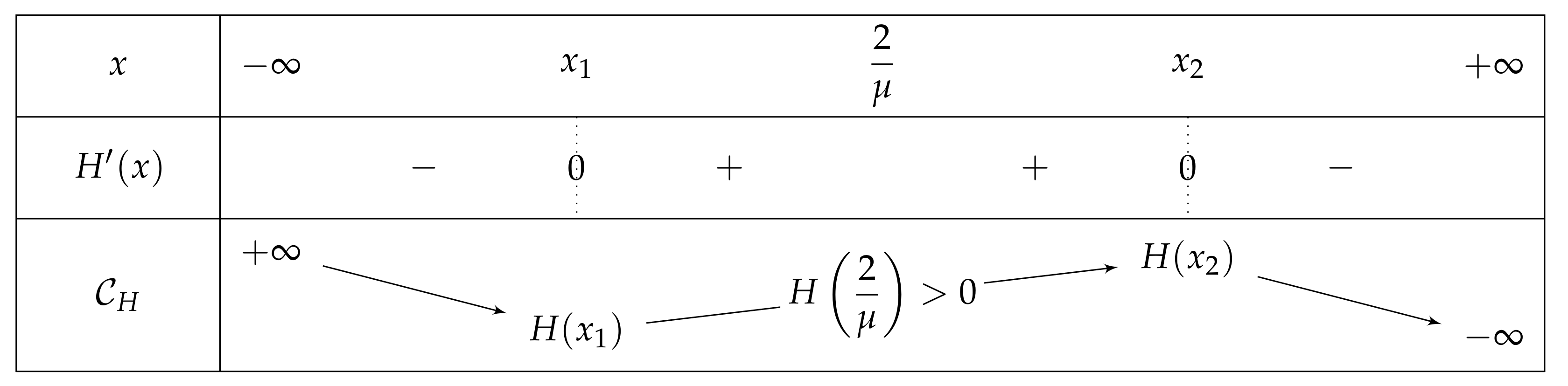
- If , then there exist two real numbers and such that the variation table of Figure 6 is satisfied for H.
- -
- . As , we deduce that . Additionally, and , then . As a conclusion, .As , H is increasing on , H decreases on , and the limit of H of x as x approaches equals , we can deduce that has an unique solution on , on a point . In particular, has one unique fixed point in this interval.
- -
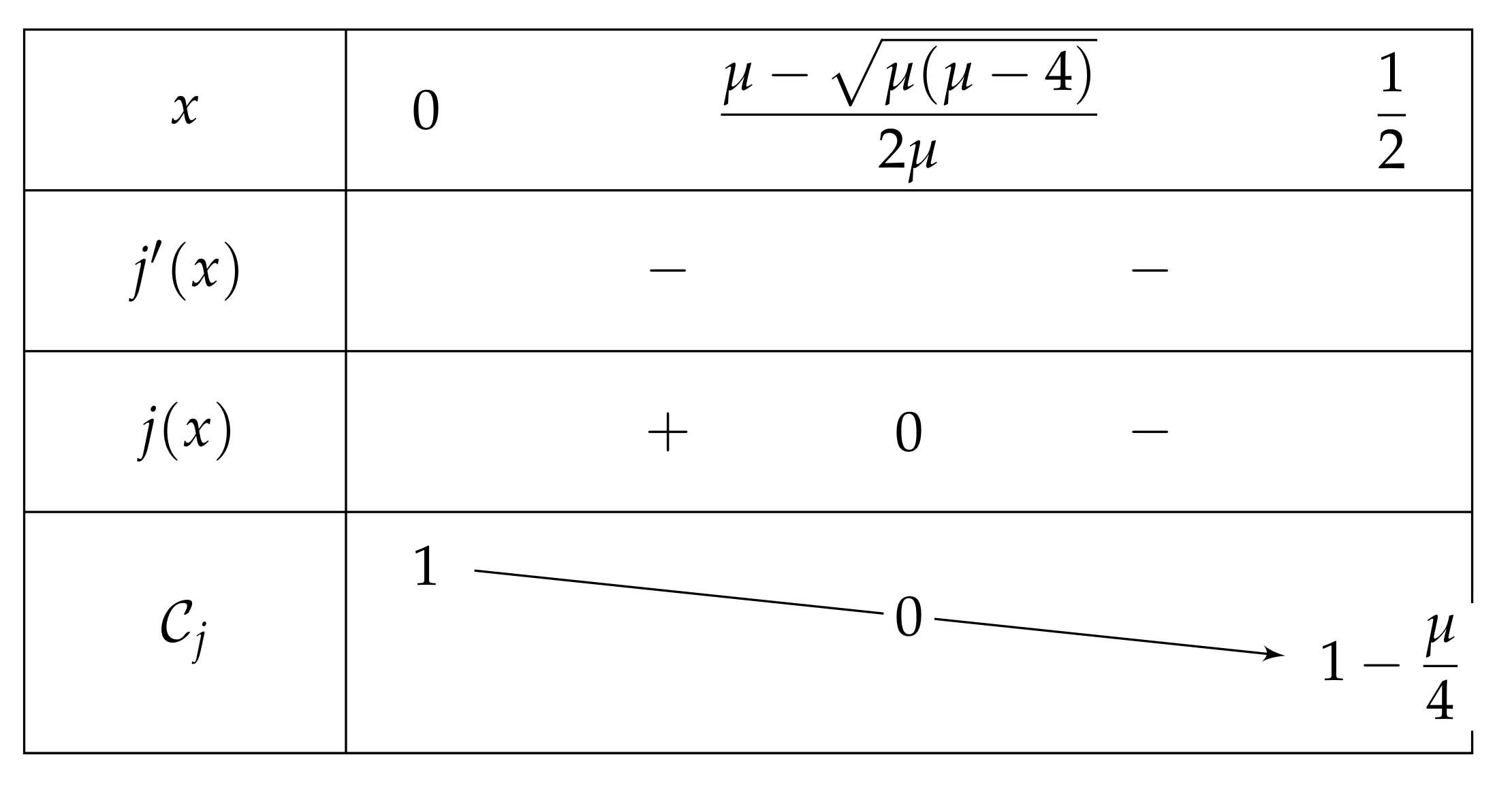
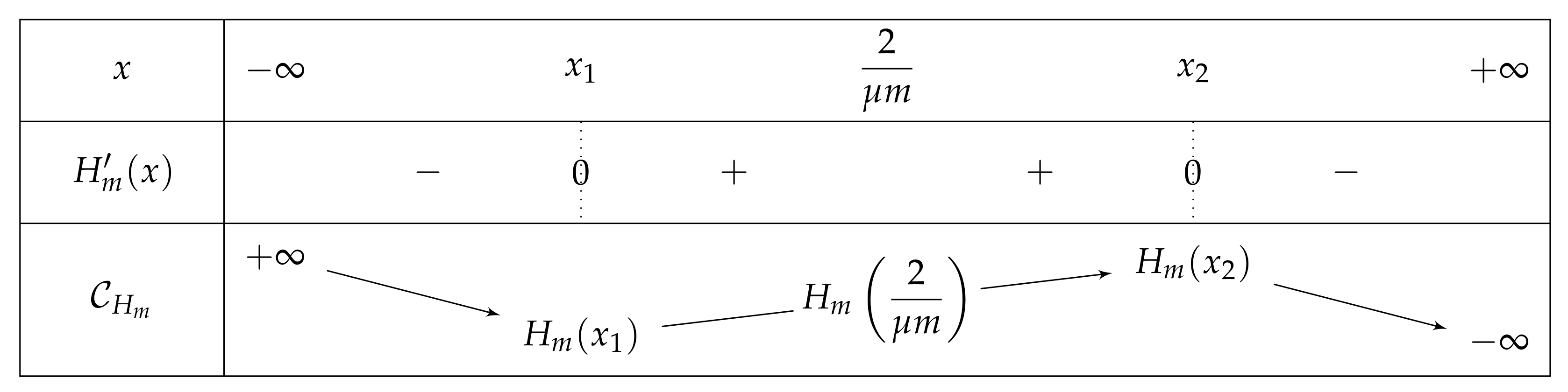
- We show that , and so has no fixed point on ., then . So:Furthermore, , and is increasing on (as on this interval). As , we can deduce that . Consequently, . Let . Since , thus is negative if and only if . We now investigate the sign of j.As , it is sufficient to study j on the interval ., so j is strictly decreasing on I. The discriminant of the quadratic equation being , the latter has two solutions , which are equal when (i.e., when ). Note that only may belong to I, and that the latter is equal to = = . We successively havewhich is positive for each and less than . Thus and we have the variations depicted in Figure 7.If belongs to , then is positive and is negative.Let us show that . As , we then have , and so . Finally, . As stated at the beginning of the proof, since is a root of H, is a fixed point for and thanks to (7)., and so , as j is decreasing with . To put it in a nutshell, .
☐
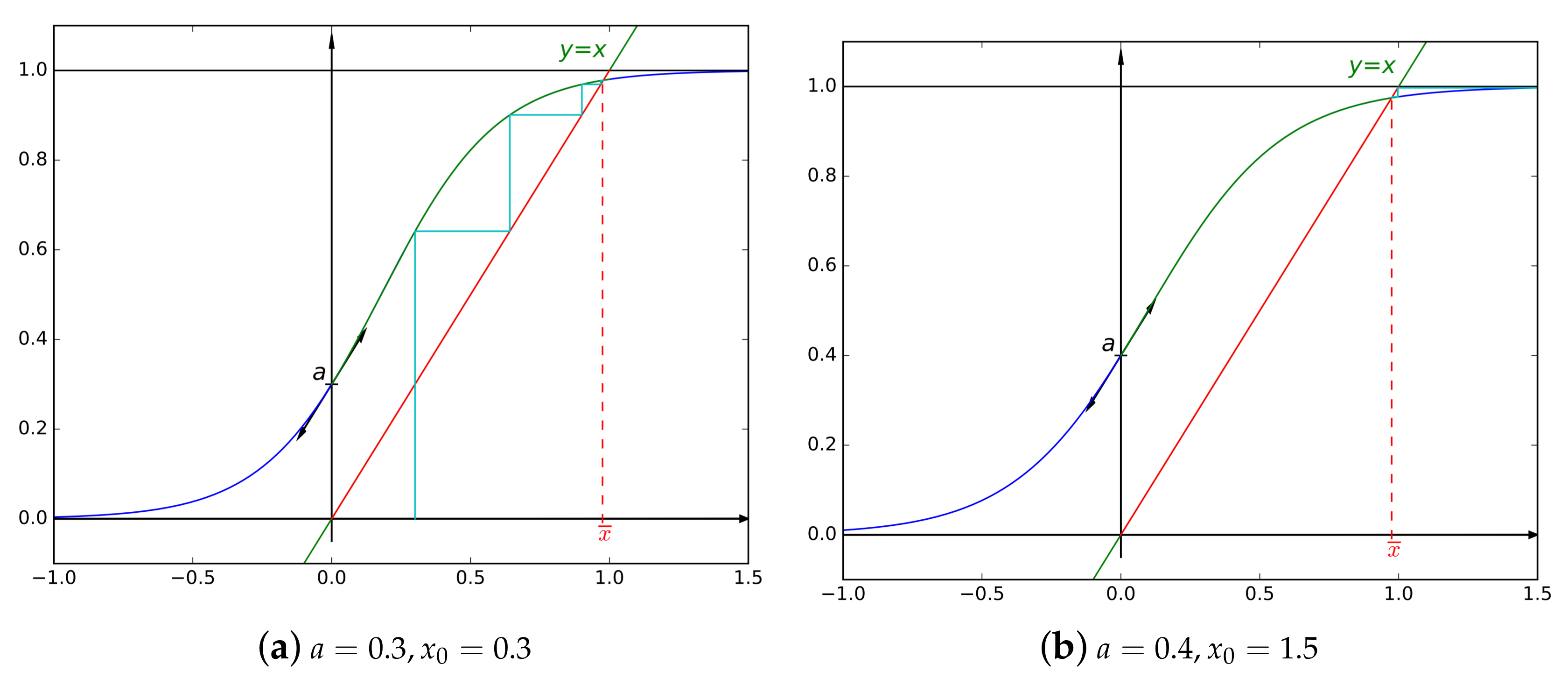
- The unique fixed-point can be found as follows: start with an arbitrary element in and define a sequence by , then .
- For , as , we can deduce that is Lipschitz continuous, with a Lipschitz constant equal to a. As a well-known consequence, the convergence of the aforementioned sequence is at least geometric, with a common ratio of a. For the same conclusion holds but for a constant .
3. The 1-Dimensional Situation ()
3.1. The Discrete Dynamical System under Consideration
3.2. A Fundamental Case:
- exists and is unique,
- is such that ,
- the convergence speed is geometric, of ratio equal to a ().
3.3. General 1-D Case:
3.3.1. Fixed Points of When
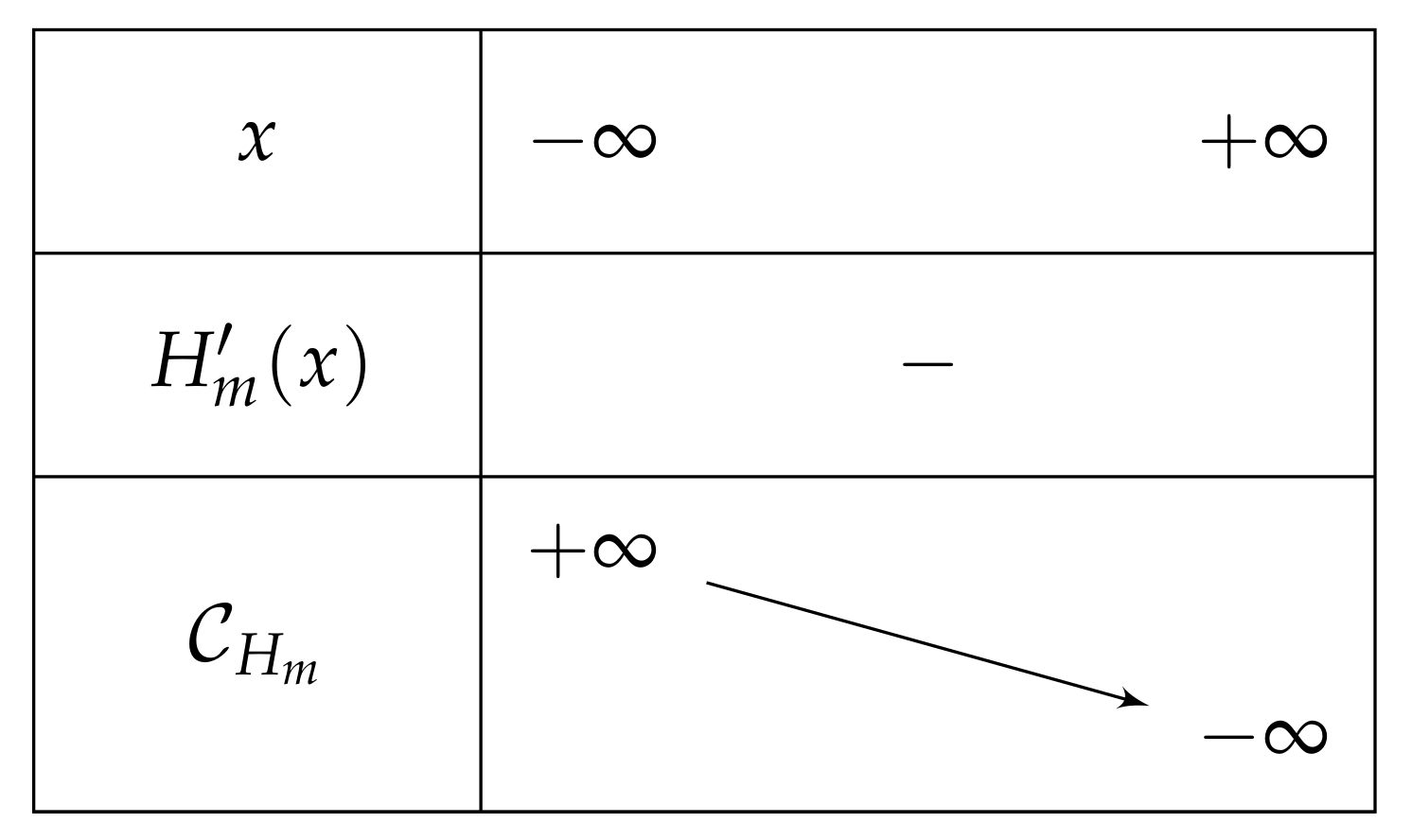
- If , then is negative and then over , and after the computation of the limits of as x approaches , we can deduce the table of variations depicted in Figure 12 (and which is independent of m).Consequently, if , then has one unique solution, i.e., has one unique fixed point.
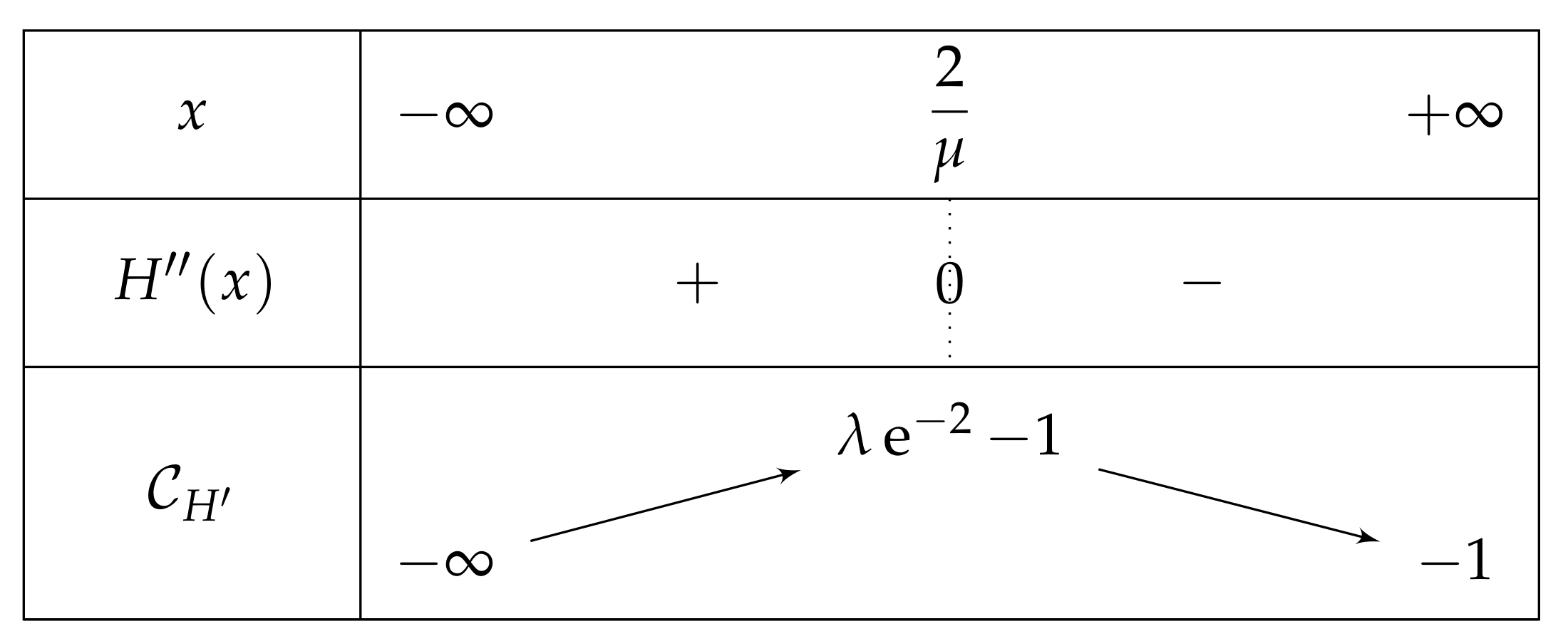
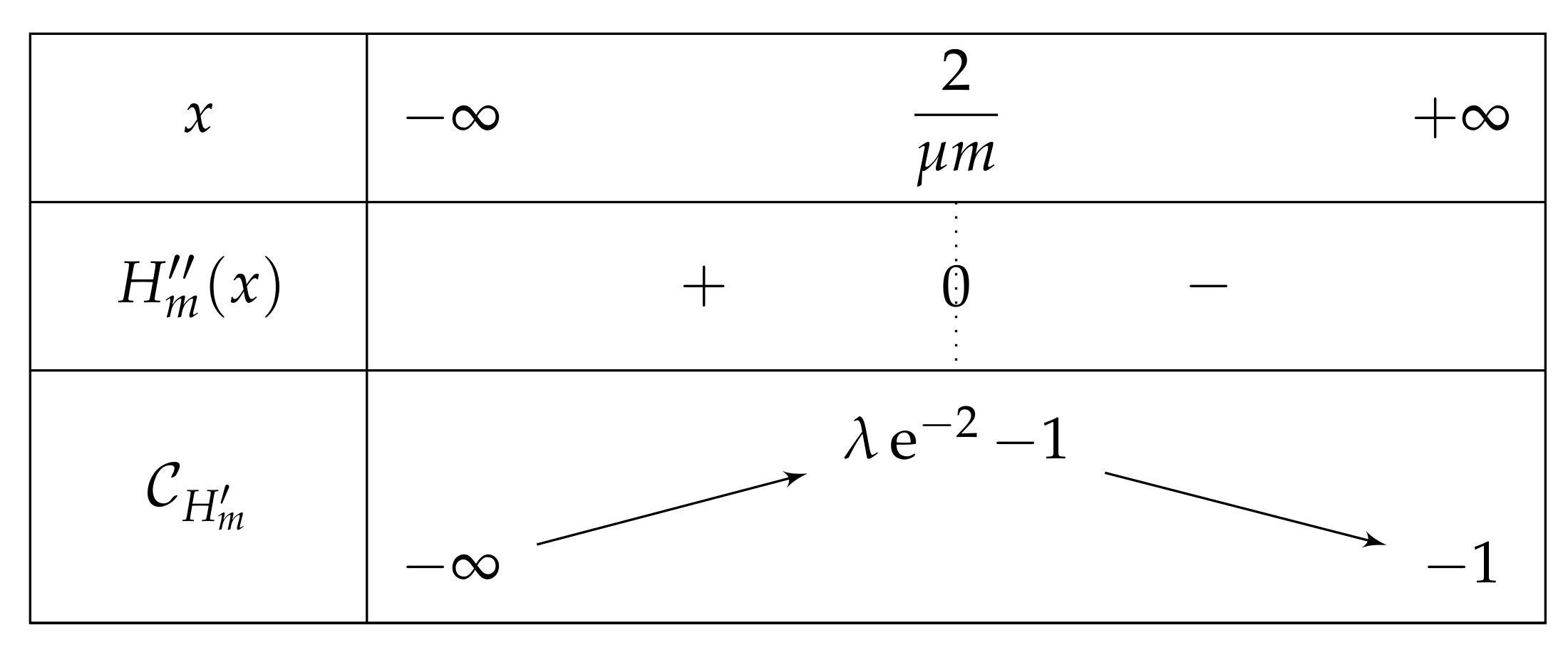
- If , then we obtain a curve similar to the fundamental case for , see Figure 13.As previously, we remark that , so .As a consequence,Again as previously, , is increasing over , and , so . Consequently, since , then , and has the opposite sign of where .Let us study the quadratic polynomial on . Its discriminant is equal to , and it has the sign table described in Figure 14.
- -
- If , then . As , we can conclude that . So . For the same reasons, is negative and has thus only one root, which belongs to . Thus has only one fixed point in this interval.
- -
- If , thenwhich is of the sign of . But . So, for , is strictly negative and similarly. Again, has only one fixed point in the interval .
- -
- If , then . So is positive outside its two roots and negative otherwise. . The largest one is outside . Let us first focus on . Since then and thus . From , one can thus deduce that . Thus, is in and . In other words,
- ∗
- If is large (i.e., is close to 0), is close to . The left root of H, would be s.t. and . In such a case and there is only one fixed point in .
- ∗
- If is close to 4, is close to . The left root of H, would be s.t. and . In such a case and there is one fixed point in , one in and one in .
- ∗
- if , and so . There is one fixed point in and one in .
3.3.2. Fixed Points of When
4. Conclusions and Future Work
Author Contributions
Conflicts of Interest
References
- Bahi, J.M.; Guyeux, C.; Perasso, A. Chaos in DNA evolution. Int. J. Biomath. (IJB) 2016, 9, 1650076. [Google Scholar] [CrossRef]
- Guyeux, C.; Nicod, J.M.; Philippe, L.; Bahi, J.M. The study of unfoldable self-avoiding walks. Application to protein structure prediction software. JBCB J. Bioinform. Comput. Biol. 2015, 13, 1550009. [Google Scholar] [CrossRef] [PubMed]
- Pai, A.A.; Pritchard, J.K.; Gilad, Y. The genetic and mechanistic basis for variation in gene regulation. PLoS Genet. 2015, 11, e1004857. [Google Scholar] [CrossRef] [PubMed]
- Bornholdt, S. Modeling genetic networks and their evolution: A complex dynamical systems perspective. Biol. Chem. 2001, 382, 1289–1299. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Oltvai, Z.N. Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Polynikis, A.; Hogan, S.; di Bernardo, M. Comparing different ODE modelling approaches for gene regulatory networks. J. Theor. Biol. 2009, 261, 511–530. [Google Scholar] [CrossRef] [PubMed]
- Perc, M. Stochastic resonance on paced genetic regulatory small-world networks: Effects of asymmetric potentials. Eur. Phys. J. B 2009, 69, 147–153. [Google Scholar] [CrossRef]
- Gosak, M.; Markovič, R.; Dolenšek, J.; Rupnik, M.S.; Marhl, M.; Stožer, A.; Perc, M. Network science of biological systems at different scales: A review. Phys. Life Rev. 2018, 24, 118–135. [Google Scholar] [CrossRef] [PubMed]
- Wagner, A. Does evolutionary plasticity evolve? Evolution 1996, 50, 1008–1023. [Google Scholar] [CrossRef] [PubMed]
- Fierst, J.L.; Phillips, P.C. Modeling the evolution of complex genetic systems: The gene network family tree. J. Exp. Zool. Part B Mol. Dev. Evol. 2015, 324, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Wagner, A. Evolution of gene networks by gene duplications: A mathematical model and its implications on genome organization. Proc. Natl. Acad. Sci. USA 1994, 91, 4387–4391. [Google Scholar] [CrossRef] [PubMed]
- Masel, J. Genetic assimilation can occur in the absence of selection for the assimilating phenotype, suggesting a role for the canalization heuristic. J. Evolut. Biol. 2004, 17, 1106–1110. [Google Scholar] [CrossRef] [PubMed]
- Pinho, R.; Borenstein, E.; Feldman, M.W. Most networks in Wagner’s model are cycling. PLoS ONE 2012, 7, e34285. [Google Scholar] [CrossRef] [PubMed]
- Siegal, M.L.; Bergman, A. Waddington’s canalization revisited: Developmental stability and evolution. Proc. Natl. Acad. Sci. USA 2002, 99, 10528–10532. [Google Scholar] [CrossRef] [PubMed]
- Carneiro, M.O.; Taubes, C.H.; Hartl, D.L. Model transcriptional networks with continuously varying expression levels. BMC Evolut. Biol. 2011, 11, 363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rünneburger, E.; Le Rouzic, A. Why and how genetic canalization evolves in gene regulatory networks. BMC Evolut. Biol. 2016, 16, 239. [Google Scholar] [CrossRef] [PubMed]
- Huerta-Sanchez, E.; Durrett, R. Wagner’s canalization model. Theor. Popul. Biol. 2007, 71, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Le Cunff, Y.; Pakdaman, K. Phenotype–genotype relation in Wagner’s canalization model. J. Theor. Biol. 2012, 314, 69–83. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guyeux, C.; Couchot, J.-F.; Le Rouzic, A.; Bahi, J.M.; Marangio, L. Theoretical Study of the One Self-Regulating Gene in the Modified Wagner Model. Mathematics 2018, 6, 58. https://doi.org/10.3390/math6040058
Guyeux C, Couchot J-F, Le Rouzic A, Bahi JM, Marangio L. Theoretical Study of the One Self-Regulating Gene in the Modified Wagner Model. Mathematics. 2018; 6(4):58. https://doi.org/10.3390/math6040058
Chicago/Turabian StyleGuyeux, Christophe, Jean-François Couchot, Arnaud Le Rouzic, Jacques M. Bahi, and Luigi Marangio. 2018. "Theoretical Study of the One Self-Regulating Gene in the Modified Wagner Model" Mathematics 6, no. 4: 58. https://doi.org/10.3390/math6040058
APA StyleGuyeux, C., Couchot, J.-F., Le Rouzic, A., Bahi, J. M., & Marangio, L. (2018). Theoretical Study of the One Self-Regulating Gene in the Modified Wagner Model. Mathematics, 6(4), 58. https://doi.org/10.3390/math6040058






