Gray Codes Generation Algorithm and Theoretical Evaluation of Random Walks in N-Cubes
Abstract
:1. Introduction
2. Gray Codes Generation Algorithms
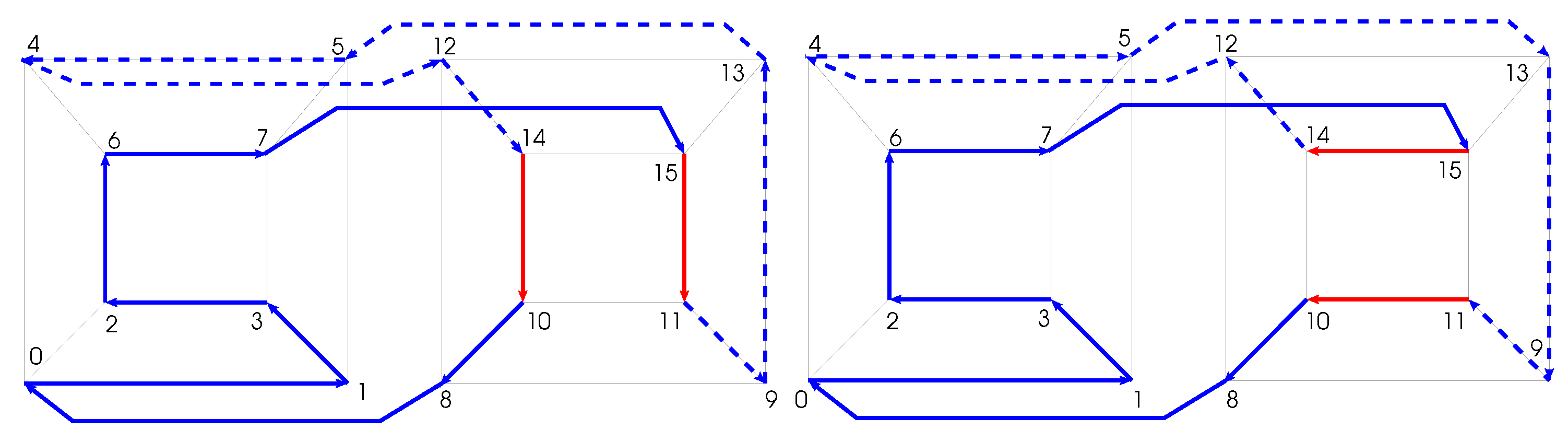
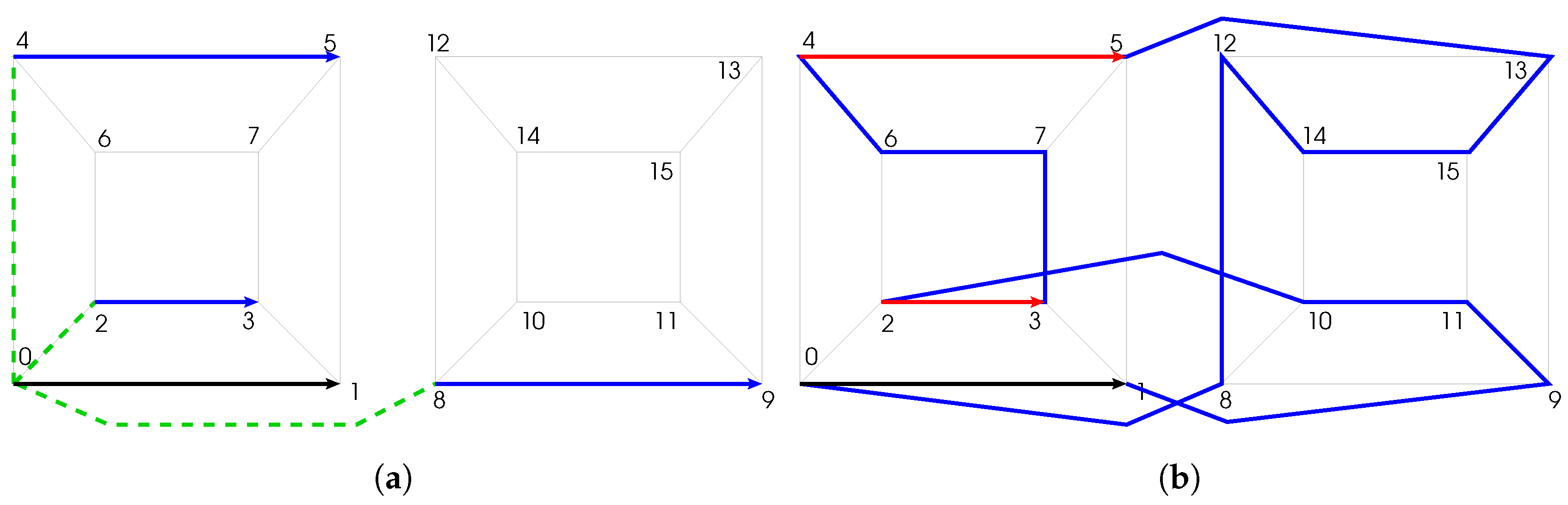
2.1. Inverting Algorithm
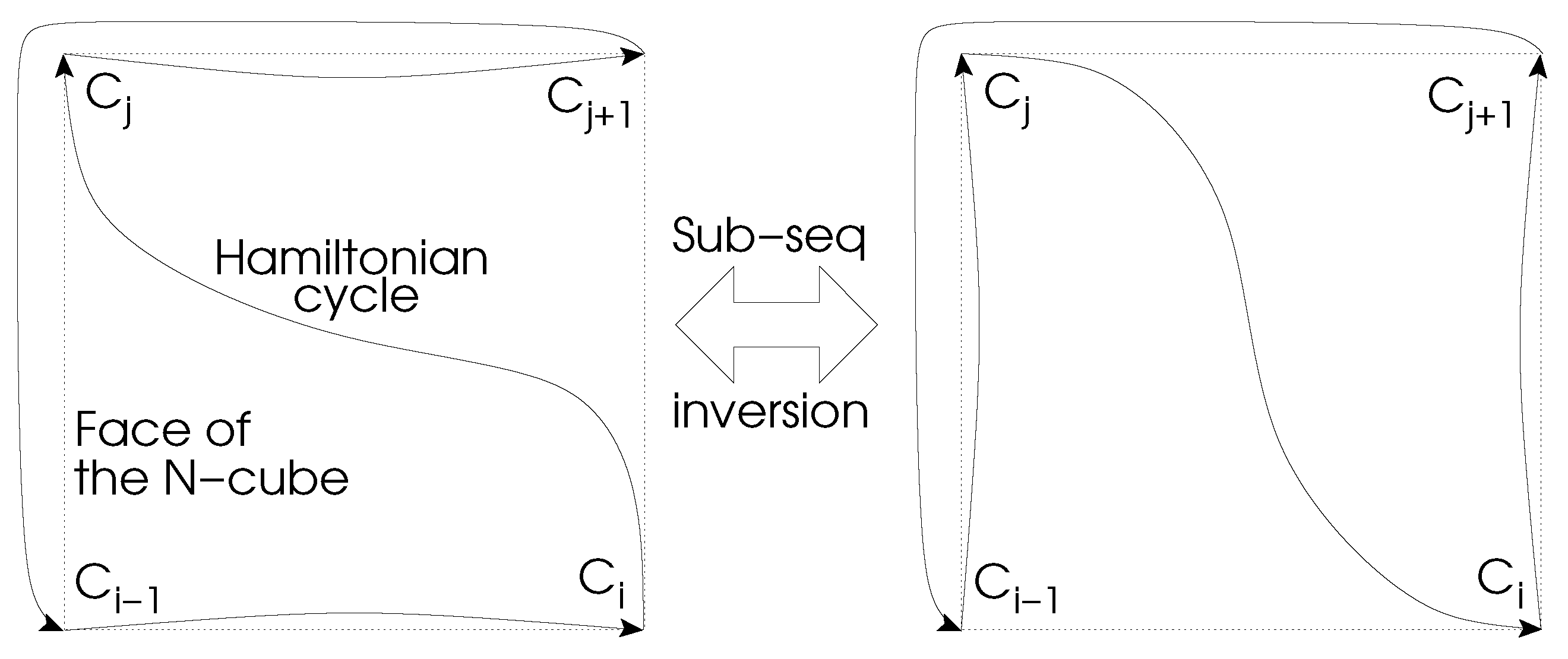
2.2. GC Transformation Principle
- the four vertices must be on the same face of the -cube, i.e., the differences between the four vertices are contained in only two dimensions of the -cube
- and must be diagonally opposed inside the face and, as a consequence, and are diagonally opposed too (this is equivalent to say that transitions and go in the same direction along their dimension)
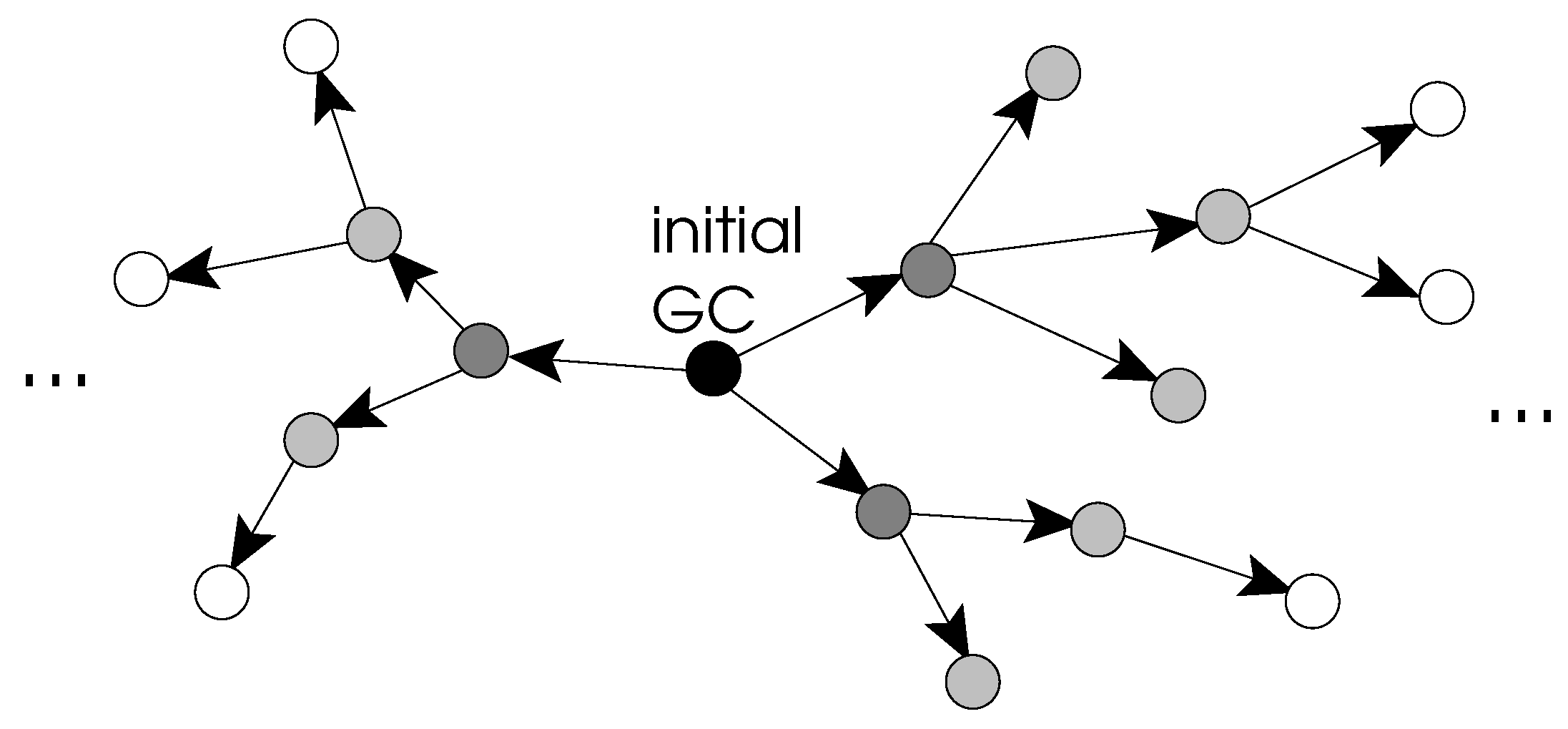
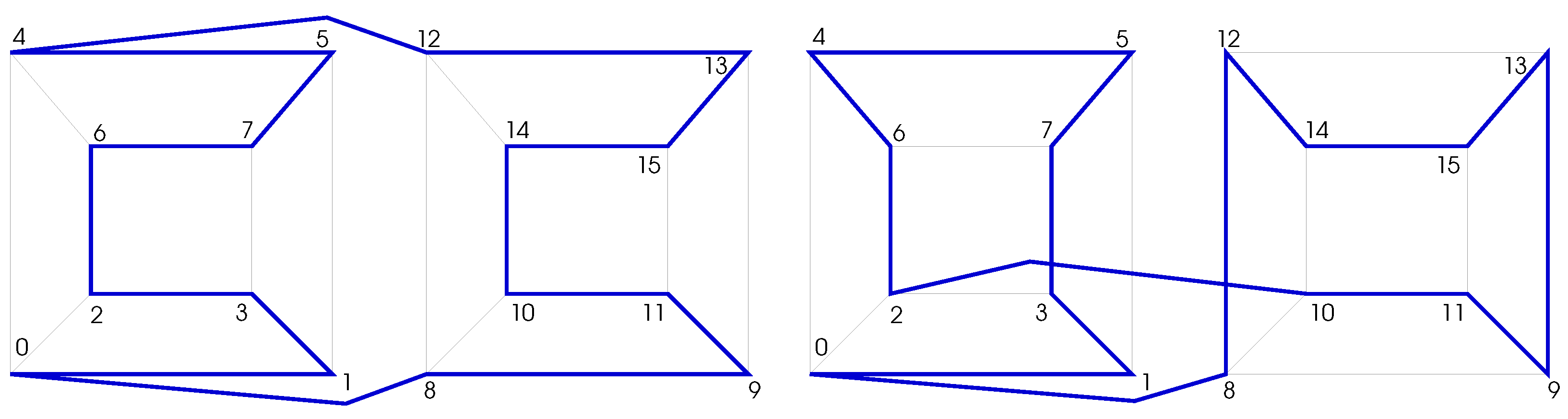
2.3. Generation Algorithm from a Known GC
| Algorithm 1: Function generateFrom(C). |
 |
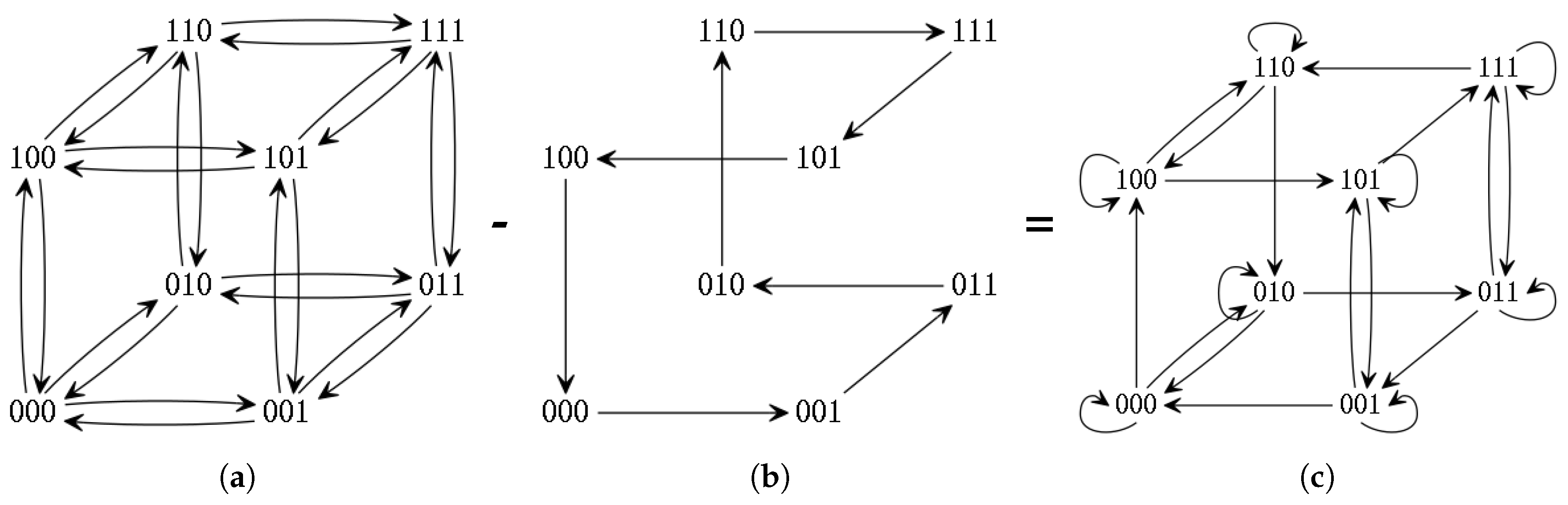
2.4. Transitive Closure Algorithm
| Algorithm 2: Transitive closure generation algorithm. |
 |
3. Using Gray Codes in Chaotic PRNGs
| Algorithm 3: Chaotic PRNG scheme. |
 |
4. Reducing the Mixing Time Upper Bound of Boolean Functions in the N-Cube
4.1. Theoretical Context
- ,
- if and ,
- otherwise.
4.2. A Useful Random Process
- ,
- ,
- ,
- ,
- and ,
- for every ,
4.3. A Coupling for the Markov Chain P
- (1)
- If and , then . Moreover, if then, , otherwise .
- (2)
- If and , then . Moreover, if then, , otherwise .
- (3)
- If and , then . Moreover, if then, , otherwise .
- (4)
- If and , and . If , then . If , then and if , then . Moreover, if then, , otherwise .
- (5)
- If and , and , then . Moreover, if then, , otherwise .
- If , then .
- If , then .
- If , then .
- If , then and .
- If and and . If , then . If and and , then . If or , then with probability and with probability . It follows that, in this case, the probability that is null. The probability that is
- If and and . If , then . If and , then . If , then . The probability that is
- If and . If and , then . If and , then . If , then with probability and with probability . If , then with probability and with probability . It follows that the probability that is , and the probability that is .
- If and . This is a dual case of the previous one with similar calculus, switching and .
- If and , and . If , then . If , then . If , then with probability and with probability . Similarly, If , then with probability and with probability . Consequently, the probability that is . Moreover the probability that is .
- If and , and . If , then . If , then . It follows that the probability that is null and the probability that id
- If . Since f is induced by an Hamiltonian cycle and , we cannot have . If , then . If , . Therefore, the probability that is null and the probability that is .
- If and . If and , then . If , then with probability and with probability . If , then with probability and with probability . Therefore, the probability that is and the probability that .
- If and . It a dual case of the previous one. The probability that is and the probability that .
- If and . If and , then . If (resp. ), then with probability and with probability . Therefore, the probability that is and the probability that .☐
5. Experiments
5.1. Performance of Gray Codes Generation Algorithms
5.2. Statistical Study of the Generation Algorithm
5.3. Discussion over the Mixing Time Distributions in Dimensions 5 and 8
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lovász, L. Random walks on graphs. In Combinatorics, Paul Erdos Is Eighty; János Bolyai Mathematical Society: Budapest, Hungary, 1993; Volume 2, pp. 1–46. [Google Scholar]
- Diaconis, P.; Graham, R.L.; Morrison, J.A. Asymptotic analysis of a random walk on a hypercube with many dimensions. Random Struct. Algorithms 1990, 1, 51–72. [Google Scholar] [CrossRef]
- Lawler, G.F.; Limic, V. Random Walk: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2010; Volume 123. [Google Scholar]
- Scoppola, B. Exact solution for a class of random walk on the hypercube. J. Stat. Phys. 2011, 143, 413–419. [Google Scholar] [CrossRef]
- Levin, D.A.; Peres, Y. Markov Chains and Mixing Times; American Mathematical Soc.: Providence, RI, USA, 2017; Volume 107. [Google Scholar]
- Contassot-Vivier, S.; Couchot, J.F.; Guyeux, C.; Héam, P.C. Random Walk in a N-Cube Without Hamiltonian Cycle to Chaotic Pseudorandom Number Generation: Theoretical and Practical Considerations. Int. J. Bifurcation Chaos 2017, 27, 18. [Google Scholar] [CrossRef]
- Suparta, I.; Zanten, A.V. Totally balanced and exponentially balanced Gray codes. Discrete Anal. Oper. Res. 2004, 11, 81–98. (In Russia) [Google Scholar]
- Contassot-Vivier, S.; Couchot, J.F. Canonical Form of Gray Codes in N-cubes. In Cellular Automata and Discrete Complex Systems, Proceedings of the 23th International Workshop on Cellular Automata and Discrete Complex Systems (AUTOMATA), Milan, Italy, 7–9 June 2017; Part 2: Regular Papers; Dennunzio, A., Formenti, E., Manzoni, L., Porreca, A.E., Eds.; Springer International Publishing: Milan, Italy, 2017; Volume LNCS-10248, pp. 68–80. [Google Scholar]
- Wild, M. Generating all cycles, chordless cycles, and Hamiltonian cycles with the principle of exclusion. J. Discrete Algorithms 2008, 6, 93–102. [Google Scholar] [CrossRef]
- Couchot, J.; Héam, P.; Guyeux, C.; Wang, Q.; Bahi, J.M. Pseudorandom Number Generators with Balanced Gray Codes. In Proceedings of the 11th International Conference on Security and Cryptography SECRYPT, Vienna, Austria, 28–30 August 2014; pp. 469–475. [Google Scholar]
- Bakiri, M.; Couchot, J.; Guyeux, C. CIPRNG: A VLSI Family of Chaotic Iterations Post-Processings for F2-Linear Pseudorandom Number Generation Based on Zynq MPSoC. IEEE Trans. Circuits Syst. 2018, 65, 1628–1641. [Google Scholar] [CrossRef]
- Bahi, J.M.; Couchot, J.F.; Guyeux, C.; Richard, A. On the Link between Strongly Connected Iteration Graphs and Chaotic Boolean Discrete-Time Dynamical Systems. In Fundamentals of Computation Theory; Owe, O., Steffen, M., Telle, J.A., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, Germany, 2011; pp. 126–137. [Google Scholar]
- Guyeux, C.; Couturier, R.; Héam, P.; Bahi, J.M. Efficient and cryptographically secure generation of chaotic pseudorandom numbers on GPU. J. Supercomput. 2015, 71, 3877–3903. [Google Scholar] [CrossRef] [Green Version]
- Bakiri, M.; Couchot, J.; Guyeux, C. FPGA Implementation of F2-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case Study. In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016): SECRYPT, Lisbon, Portugal, 26–28 July 2016; Callegari, C., van Sinderen, M., Sarigiannidis, P.G., Samarati, P., Cabello, E., Lorenz, P., Obaidat, M.S., Eds.; SciTePress: Setúbal, Portugal, 2016; Volume 4, pp. 302–309. [Google Scholar]
- Marsaglia, G. DIEHARD: A Battery of Tests of Randomness. Available online: https://tams.informatik.uni-hamburg.de/paper/2001/SA_Witt_Hartmann/cdrom/Internetseiten/stat.fsu.edu/diehard.html.
- L’Ecuyer, P.; Simard, R. TestU01: A C Library for Empirical Testing of Random Number Generators. ACM Trans. Math. Softw. 2007, 33, 22. [Google Scholar]
- Bakiri, M. Hardware Implementation of Pseudo Random Number Generator Based on Chaotic Iterations. Ph.D Thesis, Université Bourgogne Franch-Comté, Belfort, France, 2018. [Google Scholar]
- L’Ecuyer, P. Handbook of Computational Statistics; Springer-Verlag: Berlin, Germany, 2012; Chapter Random Number Generation; pp. 35–71. [Google Scholar]
- L’Ecuyer, P. History of uniform random number generation. In Proceedings of the WSC 2017-Winter Simulation Conference, Las Vegas, NV, USA, 3–6 December 2017; pp. 202–230. [Google Scholar]
- Robinson, J.P.; Cohn, M. Counting Sequences. IEEE Trans. Comput. 1981, 30, 17–23. [Google Scholar] [CrossRef]
- Bhat, G.S.; Savage, C.D. Balanced Gray Codes. Electr. J. Comb. 1996, 3, 25. [Google Scholar]
- Suparta, I.; Zanten, A.V. A construction of Gray codes inducing complete graphs. Discrete Math. 2008, 308, 4124–4132. [Google Scholar] [CrossRef]
- Bykov, I.S. On locally balanced gray codes. J. Appl. Ind. Math. 2016, 10, 78–85. [Google Scholar] [CrossRef]
- Conder, M.D.E. Explicit definition of the binary reflected Gray codes. Discrete Math. 1999, 195, 245–249. [Google Scholar] [CrossRef]
- Bunder, M.W.; Tognetti, K.P.; Wheeler, G.E. On binary reflected Gray codes and functions. Discrete Math. 2008, 308, 1690–1700. [Google Scholar] [CrossRef]
- Berestycki, N. Mixing Times of Markov Chains: Techniques and Examples. Graduate course at cambridge. University of Cambridge: Cambridge, UK, 2016. Available online: http://www.statslab.cam.ac.uk/ beresty/teach/Mixing/mixing3.pdf.
- Norris, J.R. Markov Chains; Cambridge University Press: Cambridge, UK, 1998; ISBN 9780521633963. [Google Scholar]
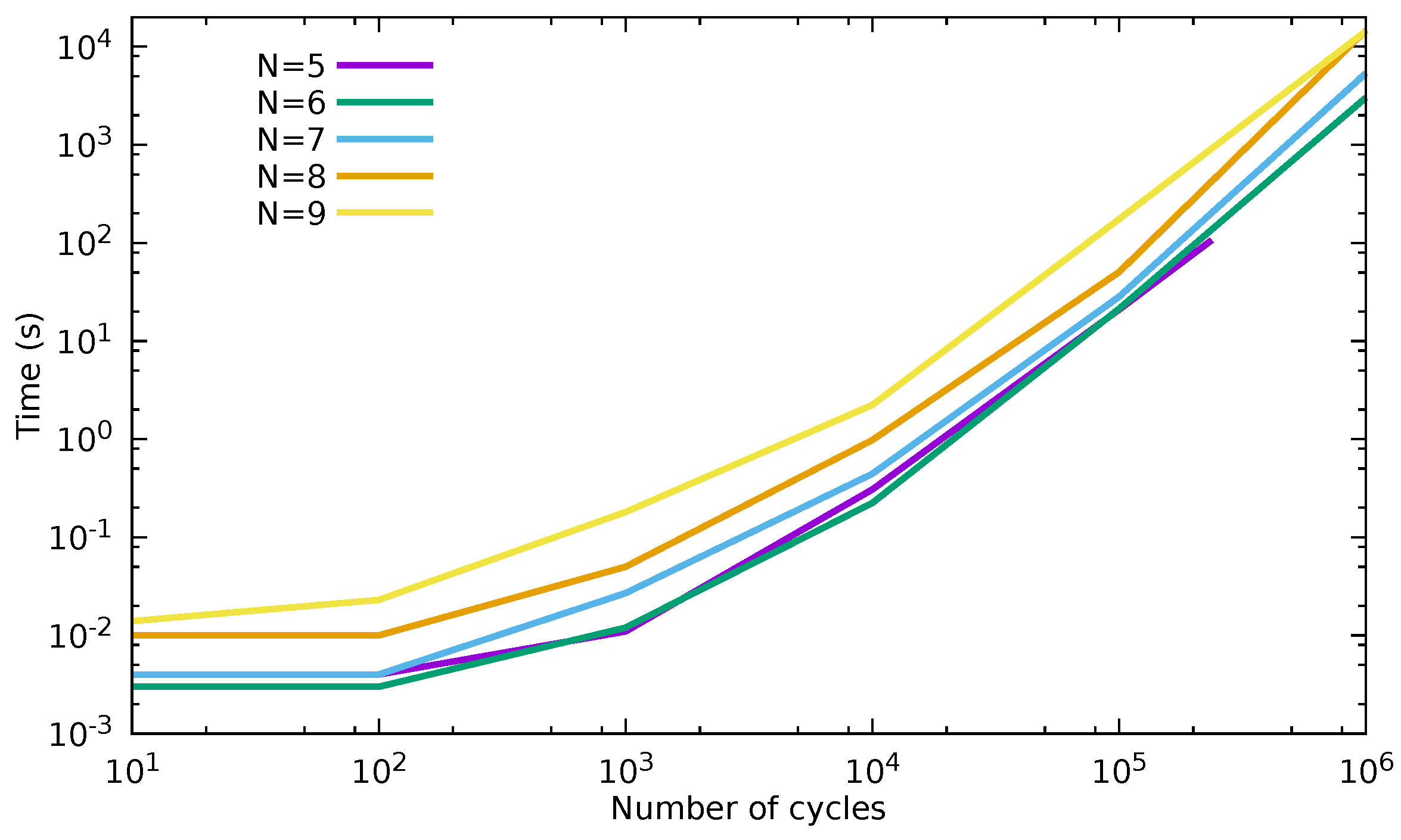
| dim | 5 | 6 | 7 | 8 | 9 | 10 |
| time (s) | 19.61 | 19.93 | 28.17 | 53.60 | 174.43 | 332.29 |
| dim | 2 | 3 | 4 | 5 |
| nb of isolated GCs | 1 | 1 | 3 | 740 |
| total nb of GCs | 1 | 1 | 9 | 237,675 |
| ratio of isolated (%) | 100 | 100 | 33.3 | 0.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contassot-Vivier, S.; Couchot, J.-F.; Héam, P.-C. Gray Codes Generation Algorithm and Theoretical Evaluation of Random Walks in N-Cubes. Mathematics 2018, 6, 98. https://doi.org/10.3390/math6060098
Contassot-Vivier S, Couchot J-F, Héam P-C. Gray Codes Generation Algorithm and Theoretical Evaluation of Random Walks in N-Cubes. Mathematics. 2018; 6(6):98. https://doi.org/10.3390/math6060098
Chicago/Turabian StyleContassot-Vivier, Sylvain, Jean-François Couchot, and Pierre-Cyrille Héam. 2018. "Gray Codes Generation Algorithm and Theoretical Evaluation of Random Walks in N-Cubes" Mathematics 6, no. 6: 98. https://doi.org/10.3390/math6060098
APA StyleContassot-Vivier, S., Couchot, J.-F., & Héam, P.-C. (2018). Gray Codes Generation Algorithm and Theoretical Evaluation of Random Walks in N-Cubes. Mathematics, 6(6), 98. https://doi.org/10.3390/math6060098







