Dynamics of the Almost Periodic Discrete Mackey–Glass Model

Abstract

This paper is concerned with a class of the discrete Mackey–Glass model that describes the process of the production of blood cells. Prior to proceeding to the main results, we prove the boundedness and extinction of its solutions. By means of the contraction mapping principle and under appropriate assumptions, we prove the existence of almost periodic positive solutions. Furthermore and by the implementation of the discrete Lyapunov functional, sufficient conditions are established for the exponential convergence of the almost periodic positive solution. Examples, as well as numerical simulations are illustrated to demonstrate the effectiveness of the theoretical findings of the paper. Our results are new and generalize some previously-reported results in the literature.

1. Introduction and Preliminaries

The nonlinear delay differential equation:

$$x^{\prime }\left(t\right)=-\alpha x\left(t\right)+\frac{\beta }{1+x^n(t-\tau )},$$

(1)

was proposed by Mackey and Glass in [1] as an appropriate model for the dynamics of hematopoiesis, which describes the process of the production of blood cells. Here, x denotes the density of mature cells in blood circulation at time t and $\tau$ is the time delay between the production of immature cells in the bone marrow and their maturation for release in the circulating bloodstream. It is assumed that the cells are lost from the circulation at a rate $\alpha$, and the flux of the cells into the circulation from the stem cell compartment depends on the density of mature cells at the previous time $t-\tau$. The theory of periodic functions, which was established by [2] and developed by [3,4], has direct connection to biological models. Indeed, it has been realized that due to various seasonal effects and certain environmental factors in real-life situations, the study of biological models under periodic or almost periodic perturbations has become obligatory. Many authors have incorporated this idea into their investigations and employed several techniques such as the degree theory, the Lyapunov functional approach, and some fixed point theorems to study the dynamic behavior of this model and its modifications in the last few years [5,6,7,8,9,10,11,12,13,14,15,16]. In [17], Wang and Zhang studied the following Mackey–Glass model:

$$x^{\prime }\left(t\right)=-\alpha \left(t\right)x\left(t\right)+\frac{\beta \left(t\right)x(t-\tau )}{1+x^n(t-\tau )},n>1,$$

(2)

which provides a more realistic description of the process of the production of blood cells. Indeed, the authors employed the fixed point theorem in cones to study the existence, nonexistence, and uniqueness of positive almost periodic solutions. Their approach was based on using a new fixed point theorem without compactness restrictions. In [18], Guo used the Lyapunov functional method and differential inequality techniques to study the exponential stability of pseudo almost periodic solutions of Model (2). Searching the literature and comparing to Model (1), however, one can figure out that the study of Model (2) has gained less attention among researchers.

Recently, it has been realized that difference models are more appropriate than the continuous ones when the size of the population is rarely small or the population has non-overlapping generations. The discrete models can also provide more efficient methods for numerical computations and simulations. Nevertheless, most of models studied in the literature have considered the continuous case of the Mackey–Glass model. To the best of our observation, however, there are no published papers studying the discrete analogue of (2). There are many methods that can be used to derive the discrete equations from the continuous counterparts; see for instance the papers [19,20] for further details. By virtue of these methods, the discrete model of (2) can be viewed as:

$$▵x\left(k\right)=-\alpha \left(k\right)x\left(k\right)+\frac{\beta \left(k\right)x(k-\tau )}{1+x^n(k-\tau )},$$

(3)

where $▵x\left(k\right)=x(k+1)-x\left(k\right)$, $\alpha (·):\mathbb{Z}\to (0,1)$, $\beta (·):\mathbb{Z}\to (0,\infty )$, $\alpha$ and $\beta$ are bounded almost periodic sequences, and $n>1$, $\tau \in {\mathbb{Z}}^{+}$. Due to the biomedical significance, we restrict our attention to positive solutions of (3). The initial condition associated with Model (3) is:

$$x\left(k\right)=\varphi \left(k\right)>0,k\in [-\tau ,0].$$

(4)

The objective of this paper is to investigate the dynamical behavior of solutions of Model (3). Before proceeding to the main result, nevertheless, we present notations, basic definitions, and some preliminary results that are needed in the subsequent sections. For any bounded sequence $\left\{f\right(k\left)\right\}$, we denote:

$$\overline{f}=\underset{k\in \mathbb{Z}}{sup}f\left(k\right)\mathrm{and}\underline{f}=\underset{k\in \mathbb{Z}}{inf}f\left(k\right).$$

In view of Equation (3), we always assume that $n>1$, and the almost periodic sequences satisfy:

$$0<\underline{\alpha }\le \alpha \left(k\right)\le \overline{\alpha }<1\mathrm{and}0<\underline{\beta }\le \beta \left(k\right)\le \overline{\beta }.$$

Let:

$$L_1=\frac{1}{\sqrt[n]{n-1}}/(1+\frac{1}{n-1})\mathrm{and}{L}_2=\frac{{(n-1)}^2}{4n}.$$

Throughout the whole paper, we will make use of the following assumptions:

(C1)

There exist two positive constants $m_1$ and $m_2$ $(m_1>m_2>0)$ such that:

$$m_1\ge \frac{\overline{\beta }{L}_1}{\underline{\alpha }}\mathrm{and}\frac{1}{\sqrt[n]{n-1}}\le m_2\le \frac{\underline{\beta }{m}_1}{\overline{\alpha }(1+m_1^n)}.$$

(C2)

$\frac{\overline{\beta }{L}_2}{\underline{\alpha }}<1$.

Definition 1.

[21] A sequence $x\left(k\right):\mathbb{Z}\to \mathbb{R}$ is called an almost periodic sequence if the ε-translation set $E\{\epsilon ,x\}=\{\delta \in \mathbb{Z}:|x(k+\delta )-x\left(k\right)|<\epsilon ,k\in \mathbb{Z}\}$ is a relatively dense set in $\mathbb{Z}$ for all $\epsilon >0$, that is, for any $\epsilon >0$, there exists a constant $l\left(\epsilon \right)>0$ such that each interval of length $l\left(\epsilon \right)$ contains a number $\delta \in E\{\epsilon ,x\}$ such that $\left|x\right(k+\delta )-x(k\left)\right|<\epsilon$ for all $k\in \mathbb{Z}$. Here, δ is called the ε-translation number of $x\left(k\right)$.

Lemma 1.

[22] Let $f:\mathbb{Z}\to R$ be an almost periodic sequence, then $f\left(k\right)$ is bounded on $\mathbb{Z}$.

Lemma 2.

[22] Let $f,g:\mathbb{Z}\to \mathbb{R}$ be an almost periodic sequence, then $f+g$ and $fg$ are almost periodic.

Lemma 3.

[22] If $f:\mathbb{Z}\to \mathbb{R}$ is an almost periodic sequence and $F(·)$ is defined on the value field of $f\left(k\right)$, then $F\circ f$ is almost periodic.

Lemma 4.

[22] If $f:\mathbb{Z}\to \mathbb{R}$ is an almost periodic sequence, then $F\left(k\right)={\sum }_{i=0}^{k-1}f\left(i\right)$ is almost periodic if and only if F is bounded on $\mathbb{Z}$.

Lemma 5.

Every solution x of the initial value problem (3) and (4) is positive.

Proof. 

It is straightforward to show that the solution x of the initial value problem (3) and (4) can be expressed by:

$$x\left(k\right)=x\left(0\right){\displaystyle \prod _{s=0}^{k-1}}(1-\alpha \left(s\right))+\frac{\beta (k-1)x(k-1-\tau )}{1+x^n(k-1-\tau )}+{\displaystyle \sum _{s=0}^{k-2}}\left(\frac{\beta \left(s\right)x(s-\tau )}{1+x^n(s-\tau )}{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right).$$

Since $x\left(k\right)=\varphi \left(k\right)>0$ for $-\tau \le k\le 0$, we can deduce that $x\left(1\right)>0$, $x\left(2\right)>0$, …, and $x\left(k\right)>0$ for all $k>0,k\in \mathbb{Z}$. ☐

The following two remarks prove monotonicity for certain functions that are needed in our later analysis.

Remark 1.

For the function $f\left(x\right)=\frac{x}{1+x^n}$, $n>1,x\in [0,+\infty )$, f is increasing on $[0,\frac{1}{\sqrt[n]{n-1}}]$ and decreasing on $[\frac{1}{\sqrt[n]{n-1}},\infty )$. Furthermore, f attains its maximum $f_{max}=f\left(\sqrt[n]{n-1}\right)=\sqrt[n]{n-1}/(1+\frac{1}{n-1}):=L_1$.

Remark 2.

For the function $g\left(x\right)=\frac{1-(n-1)x^n}{{(1+x^n)}^2}$, $n>1,x\in [0,+\infty )$, g is increasing on $[\sqrt[n]{\frac{n+1}{n-1}},\infty )$ and decreasing on $[0,\sqrt[n]{\frac{n+1}{n-1}}]$. Furthermore, $g\left(0\right)=1$, $g\left(\frac{1}{\sqrt[n]{n-1}}\right)=0$, $g\left(\sqrt[n]{\frac{n+1}{n-1}}\right)=-\frac{n}{{(1+\frac{n+1}{n-1})}^2}<0$, ${lim}_{x\to \infty }g\left(x\right)=0$, and $\left|g\left(\sqrt[n]{\frac{n+1}{n-1}}\right)\right|=\frac{n}{{(1+\frac{n+1}{n-1})}^2}=\frac{{(n-1)}^2}{4n}$.

The paper is organized as follows: In Section 2, we prove the the boundedness and extinction of solutions of (3). In Section 3, by means of the contraction mapping principle and under suitable conditions, we prove the existence of positive almost periodic solutions. Section 4 is devoted to establishing sufficient conditions for the exponential convergence of the almost periodic positive solution. We provide examples, as well as numerical simulations in Section 5 to demonstrate the theoretical findings of the paper. We conclude our results in Section 6.

2. Boundedness and Extinction of Solutions

Concerning solutions of Model (3), in this section, we prove three results on the boundedness and the fact that $x\left(k\right)\to 0$ as $k\to \infty$.

Theorem 1.

Every solution x of Model (3) is bounded.

Proof. 

Let x be an arbitrary solution of Model (3) with the initial function $x\left(k\right)=\varphi \left(k\right)>0$ for $-\tau \le k\le 0$. By Lemma 5, we know $x\left(k\right)>0$ for all $k>0,k\in {\mathbb{Z}}^{+}$.

Let $M=\frac{\overline{\beta }{L}_1}{\underline{\alpha }}+{max}_{-\tau \le k\le 0,k\in \mathbb{Z}}\varphi \left(k\right)$. Then, we have:

$$x\left(k\right)=\varphi \left(k\right)\le \underset{-\tau \le k\le 0,k\in \mathbb{Z}}{max}\varphi \left(k\right)<\frac{\overline{\beta }{L}_1}{\underline{\alpha }}+\underset{-\tau \le k\le 0,k\in \mathbb{Z}}{max}\varphi \left(k\right)=M,k\in [-\tau ,0].$$

We claim that:

$$x\left(k\right)<M,\mathrm{for}\mathrm{all}k>0,k\in \mathbb{Z}.$$

(5)

Suppose on the contrary that the claim is not true. Then, there exists a $K^{*}\in {\mathbb{Z}}^{+}$ such that $x\left(K^{*}\right)\ge M$ and $x\left(k\right)<M$ for $-\tau \le k<K^{*}$, $k\in \mathbb{Z}$.

It follows from (3) that:

$$x\left(K^{*}\right)-x(K^{*}-1)=-\alpha (K^{*}-1)x(K^{*}-1)+\frac{\beta (K^{*}-1)x(K^{*}-1-\tau )}{1+x^n(K^{*}-1-\tau )}.$$

(6)

By Remark 1, we have $\frac{x(K^{*}-1-\tau )}{1+x^n(K^{*}-1-\tau )}\le L_1$. From (6), we get $x\left(K^{*}\right)-x(K^{*}-1)\le -\underline{\alpha }x(K^{*}-1)+\overline{\beta }{L}_1$. This implies:

$$\begin{array}{ccc}\hfill x\left(K^{*}\right)& \le & (1-\underline{\alpha })x(K^{*}-1)+\overline{\beta }{L}_1<(1-\underline{\alpha })M+\overline{\beta }{L}_1\hfill \\ & =& M-\underline{\alpha }M+\overline{\beta }{L}_1=M-\underline{\alpha }\left(\frac{\overline{\beta }{L}_1}{\underline{\alpha }}+\underset{-\tau \le k\le 0,k\in \mathbb{Z}}{max}\varphi \left(k\right)\right)+\overline{\beta }{L}_1\hfill \\ & =& M-\underline{\alpha }\underset{-\tau \le k\le 0,k\in \mathbb{Z}}{max}\varphi \left(k\right)<M,\hfill \end{array}$$

which contradicts that $x\left(K^{*}\right)\ge M$. Therefore, the claim (5) is true. Thus, $x\left(k\right)<M$ for all $k>0,k\in \mathbb{Z}$. Hence, every solution of Equation (3) is bounded. ☐

Let $S^0=\left\{\varphi \right|m_2<\varphi \left(k\right)<m_1,k\in J\}$, where $J=\{-\tau ,-\tau +1,\dots ,-2,-1,0\}$.

Theorem 2.

Assume that (C1) holds. Then, every solution x of Model (3) with initial function $\varphi \in S^0$ satisfies $m_2<x\left(k\right)<m_1$ for all $k>0$, $k\in {\mathbb{Z}}^{+}$.

Proof. 

For $k\in J$, $x\left(k\right)=\varphi \left(k\right)\in S^0$ and $m_2<\varphi \left(k\right)<m_1$. We proceed inductively and prove that $m_2<x\left(1\right)<m_1$. From Model (3), we have:

$$x\left(1\right)-x\left(0\right)=-\alpha \left(0\right)x\left(0\right)+\frac{\beta \left(0\right)x(-\tau )}{1+x^n(-\tau )}\ge -\overline{\alpha }x\left(0\right)+\underline{\beta }\frac{x(-\tau )}{1+x^n(-\tau )},$$

which yields:

$$x\left(1\right)\ge (1-\overline{\alpha })x\left(0\right)+\underline{\beta }\frac{x(-\tau )}{1+x^n(-\tau )}>(1-\overline{\alpha })m_2+\underline{\beta }\frac{x(-\tau )}{1+x^n(-\tau )}.$$

(7)

By Remark 1 and since $\frac{1}{\sqrt[n]{n-1}}\le m_2<x(-\tau )<m_1,$ we have $f\left(x(-\tau )\right)>f\left(m_1\right)$. That is:

$$\frac{x(-\tau )}{1+x^n(-\tau )}>\frac{m_1}{1+m_1^n}.$$

(8)

By virtue of (C1), (7) and (8), we get:

$$x\left(1\right)>(1-\overline{\alpha })m_2+\underline{\beta }\frac{m_1}{1+m_1^n}\ge m_2.$$

(9)

On the other hand, we get:

$$x\left(1\right)-x\left(0\right)=-\alpha \left(0\right)x\left(0\right)+\frac{\beta \left(0\right)x(-\tau )}{1+x^n(-\tau )}\le -\underline{\alpha }x\left(0\right)+\overline{\beta }\frac{x(-\tau )}{1+x^n(-\tau )}.$$

(10)

By Remark 1, we have:

$$\frac{x(-\tau )}{1+x^n(-\tau )}\le L_1.$$

(11)

By virtue of (C1), (10), and (11), we have:

$$x\left(1\right)\le (1-\underline{\alpha })x\left(0\right)+\overline{\beta }\frac{x(-\tau )}{1+x^n(-\tau )}\le (1-\underline{\alpha })x\left(0\right)+\overline{\beta }{L}_1<(1-\underline{\alpha })m_1+\overline{\beta }{L}_1\le m_1.$$

(12)

Thus, (9) and (12) imply that $m_2<x\left(1\right)<m_1$. Furthermore, we have:

$$x\left(2\right)-x\left(1\right)=-\alpha \left(1\right)x\left(1\right)+\frac{\beta \left(1\right)x(1-\tau )}{1+x^n(1-\tau )}\ge -\overline{\alpha }x\left(1\right)+\underline{\beta }\frac{x(1-\tau )}{1+x^n(1-\tau )},$$

(13)

which leads to:

$$\begin{array}{ccc}\hfill x\left(2\right)& \ge & (1-\overline{\alpha })x\left(1\right)+\underline{\beta }\frac{x(1-\tau )}{1+x^n(1-\tau )}>(1-\overline{\alpha })m_2+\underline{\beta }\frac{x(1-\tau )}{1+x^n(1-\tau )}\hfill \\ & >& (1-\overline{\alpha })m_2+\underline{\beta }\frac{m_1}{1+m_1^n}\ge m_2.\hfill \end{array}$$

(14)

We also have:

$$x\left(2\right)-x\left(1\right)=-\alpha \left(1\right)x\left(1\right)+\frac{\beta \left(1\right)x(1-\tau )}{1+x^n(1-\tau )}\le -\underline{\alpha }x\left(1\right)+\overline{\beta }\frac{x(1-\tau )}{1+x^n(1-\tau )}.$$

Therefore, we get:

$$x\left(2\right)\le (1-\underline{\alpha })x\left(1\right)+\overline{\beta }\frac{x(1-\tau )}{1+x^n(1-\tau )}\le (1-\underline{\alpha })x\left(1\right)+\overline{\beta }{L}_1<(1-\underline{\alpha })m_1+\overline{\beta }{L}_1\le m_1.$$

(15)

By virtue of (14) and (15), we have $m_2<x\left(2\right)<m_1$. Repeating the above steps, we can deduce that $m_2<x\left(k\right)<m_1$ for all $k>0,k\in {\mathbb{Z}}^{+}$. ☐

Theorem 3.

Let $\underline{\alpha }>\overline{\beta }$. Then, every solution x of Model (3) tends to extinction, that is, $x\left(k\right)\to 0$ as $k\to \infty$.

Proof. 

Let x be an arbitrary solution of (3) with initial function $x\left(k\right)=\varphi \left(k\right)>0$ for $-\tau \le k\le 0$. By Lemma 5 and Theorem 1, we know that $0<x\left(k\right)<M$ for all $k>0$, $k\in {\mathbb{Z}}^{+}$ where $M=\frac{\overline{\beta }{L}_1}{\underline{\alpha }}+{max}_{-\tau \le k\le 0,k\in \mathbb{Z}}\varphi \left(k\right)$.

Consider the function $G\left(x\right)=\overline{\beta }{e}^{(\tau +1)x}-\underline{\alpha }{e}^x+e^x-1,x\in [0,1]$. Since $G\left(0\right)=\overline{\beta }-\underline{\alpha }<0$, then there exists a constant $\lambda \in (0,1)$ such that $G\left(\lambda \right)<0$. That is, we get:

$$-\underline{\alpha }{e}^{\lambda }+e^{\lambda }+\overline{\beta }{e}^{\lambda (\tau +1)}<1.$$

(16)

Let $W\left(k\right)=x\left(k\right)e^{\lambda k}$, then we have:

$$\begin{array}{ccc}\hfill W(k+1)-W\left(k\right)& =& x(k+1)e^{\lambda (k+1)}-x\left(k\right)e^{\lambda k}\hfill \\ \hfill & =& \left(x(k+1)-x\left(k\right)\right)e^{\lambda (k+1)}+(e^{\lambda }-1)x\left(k\right)e^{\lambda k}\hfill \\ & =& \left(-\alpha \left(k\right)x\left(k\right)+\frac{\beta \left(k\right)x(k-\tau )}{1+x^n(k-\tau )}\right)e^{\lambda (k+1)}+(e^{\lambda }-1)x\left(k\right)e^{\lambda k}\hfill \\ \hfill & =& \left(-\alpha \left(k\right)e^{\lambda }+e^{\lambda }-1\right)x\left(k\right)e^{\lambda k}+\beta \left(k\right)e^{\lambda }\frac{x(k-\tau )}{1+x^n(k-\tau )}{e}^{\lambda k}.\hfill \end{array}$$

(17)

Let $Q=M+{max}_{-\tau \le k\le 0,k\in \mathbb{Z}}\varphi \left(k\right)$. Then, we get:

$$W\left(k\right)=x\left(k\right)e^{\lambda k}\le x\left(k\right)=\varphi \left(k\right)\le \underset{-\tau \le k\le 0,k\in \mathbb{Z}}{max}\varphi \left(k\right)<M+\underset{-\tau \le k\le 0,k\in \mathbb{Z}}{max}\varphi \left(k\right)=Q,k\in [-\tau ,0].$$

Now, we prove the claim that:

$$W\left(k\right)<Q\mathrm{for}\mathrm{all}k>0,k\in {\mathbb{Z}}^{+}.$$

(18)

Suppose on the contrary that (18) does not hold true. Then, there exists a $\tilde{K}\in {\mathbb{Z}}^{+}$ such that $W\left(\tilde{K}\right)\ge Q$ and $W\left(k\right)<Q$ for $-\tau \le k<\tilde{K},k\in \mathbb{Z}$. It follows from (17) that:

$$\begin{array}{ccc}\hfill W\left(\tilde{K}\right)-W(\tilde{K}-1)& =& \left(-\alpha (\tilde{K}-1)e^{\lambda }+e^{\lambda }-1\right)x(\tilde{K}-1)e^{\lambda (\tilde{K}-1)}\hfill \\ \hfill & +& \beta (\tilde{K}-1)e^{\lambda }\frac{x(\tilde{K}-1-\tau )}{1+x^n(\tilde{K}-1-\tau )}{e}^{\lambda (\tilde{K}-1)}\hfill \\ & =& \left(-\alpha (\tilde{K}-1)e^{\lambda }+e^{\lambda }-1\right)W(\tilde{K}-1)\hfill \\ \hfill & +& \beta (\tilde{K}-1)e^{\lambda }\frac{x(\tilde{K}-1-\tau )}{1+x^n(\tilde{K}-1-\tau )}{e}^{\lambda (\tilde{K}-1)}\hfill \\ \hfill & \le & \left(-\underline{\alpha }{e}^{\lambda }+e^{\lambda }-1\right)W(\tilde{K}-1)+\overline{\beta }{e}^{\lambda }x(\tilde{K}-1-\tau )e^{\lambda (\tilde{K}-1)}.\hfill \end{array}$$

(19)

It follows that:

$$\begin{array}{ccc}\hfill W\left(\tilde{K}\right)& \le & \left(-\underline{\alpha }{e}^{\lambda }+e^{\lambda }\right)W(\tilde{K}-1)+\overline{\beta }{e}^{\lambda }x(\tilde{K}-1-\tau )e^{\lambda (\tilde{K}-1)}\hfill \\ \hfill & =& \left(-\underline{\alpha }{e}^{\lambda }+e^{\lambda }\right)W(\tilde{K}-1)+\overline{\beta }{e}^{\lambda }x(\tilde{K}-1-\tau )e^{\lambda (\tilde{K}-1-\tau )}{e}^{\lambda \tau }\hfill \\ & =& \left(-\underline{\alpha }{e}^{\lambda }+e^{\lambda }\right)W(\tilde{K}-1)+\overline{\beta }{e}^{\lambda }W(\tilde{K}-1-\tau )e^{\lambda \tau }\hfill \\ \hfill & <& \left(-\underline{\alpha }{e}^{\lambda }+e^{\lambda }\right)Q+\overline{\beta }{e}^{\lambda }Q{e}^{\lambda \tau }\hfill \\ \hfill & =& \left(-\underline{\alpha }{e}^{\lambda }+e^{\lambda }+\overline{\beta }{e}^{\lambda (\tau +1)}\right)Q\hfill \end{array}$$

(20)

Hence, (16) and (20) imply that $W\left(\tilde{K}\right)<Q$. This contradicts that $W\left(\tilde{K}\right)\ge Q$. Therefore, the claim (18) is true. Thus, $W\left(k\right)=x\left(k\right)e^{\lambda \tau }$ for all $k>0,k\in {\mathbb{Z}}^{+}$. It follows that $0<x\left(k\right)<Q{e}^{-\lambda k}$ for all $k>0,k\in {\mathbb{Z}}^{+}$, which implies that $x\left(k\right)\to 0$ as $k\to \infty$. ☐

3. Existence of the Almost Periodic Positive Solution

Let $X=\left\{x\right(k):x(k):\mathbb{Z}\to \mathbb{R},x(k)$ is almost periodic function} with the norm $\parallel x\parallel ={sup}_{k\in \mathbb{Z}}\left|x\left(k\right)\right|$. It is clear that X is a Banach space.

It is easy to verify that x is the solution of Model (3) if and only if x is the solution of the equation below:

$$x\left(k\right)=\frac{\beta (k-1)x(k-1-\tau )}{1+x^n(k-1-\tau )}+{\displaystyle \sum _{s=-\infty }^{k-2}}\left(\frac{\beta \left(s\right)x(s-\tau )}{1+x^n(s-\tau )}{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right).$$

We define the operator $A:X\to X$ by:

$$\left(Ax\right)\left(k\right)=\frac{\beta (k-1)x(k-1-\tau )}{1+x^n(k-1-\tau )}+{\displaystyle \sum _{s=-\infty }^{k-2}}\left(\frac{\beta \left(s\right)x(s-\tau )}{1+x^n(s-\tau )}{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right).$$

Obviously, $x\in X$ is the almost periodic solution of Model (3) if and only if x is the fixed point of the operator A.

$$\mathrm{Define}\Omega =\{x:x\in X,m_2\le x\left(k\right)\le m_1,k\in \mathbb{Z}\}$$

Theorem 4.

Assume that (C1) and (C2) hold, then Model (3) has an almost periodic positive solution on Ω.

Proof. 

For all $x\in \Omega$, we have:

$$\begin{array}{ccc}\hfill \left(Ax\right)\left(k\right)& =& \frac{\beta (k-1)x(k-1-\tau )}{1+x^n(k-1-\tau )}+{\displaystyle \sum _{s=-\infty }^{k-2}}\left(\frac{\beta \left(s\right)x(s-\tau )}{1+x^n(s-\tau )}{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right)\hfill \\ & \le & \overline{\beta }\frac{x(k-1-\tau )}{1+x^n(k-1-\tau )}+\overline{\beta }{\displaystyle \sum _{s=-\infty }^{k-2}}\left(\frac{x(s-\tau )}{1+x^n(s-\tau )}{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right).\hfill \end{array}$$

(21)

By virtue of Remark 1, we get $\frac{x(k-1-\tau )}{1+x^n(k-1-\tau )}\le L_1$ and $\frac{x(s-\tau )}{1+x^n(s-\tau )}\le L_1$. It follows from (21) that:

$$\begin{array}{ccc}\hfill \left(Ax\right)\left(k\right)& \le & \overline{\beta }{L}_1+\overline{\beta }{L}_1{\displaystyle \sum _{s=-\infty }^{k-2}}\left({\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right)\le \overline{\beta }{L}_1+\overline{\beta }{L}_1{\displaystyle \sum _{s=-\infty }^{k-2}}\left({\displaystyle \prod _{i=s+1}^{k-1}}(1-\underline{\alpha })\right)\hfill \\ & =& \overline{\beta }{L}_1+\overline{\beta }{L}_1{\displaystyle \sum _{s=-\infty }^{k-2}}{(1-\underline{\alpha })}^{k-1-s}=\overline{\beta }{L}_1+\overline{\beta }{L}_1{\displaystyle \sum _{j=1}^{\infty }}{(1-\underline{\alpha })}^j\hfill \\ & =& \overline{\beta }{L}_1+\overline{\beta }{L}_1\frac{1-\underline{\alpha }}{\underline{\alpha }}=\frac{\overline{\beta }{L}_1}{\underline{\alpha }}\le m_1.\hfill \end{array}$$

On the other hand, we have:

$$\begin{array}{ccc}\hfill \left(Ax\right)\left(k\right)& =& \frac{\beta (k-1)x(k-1-\tau )}{1+x^n(k-1-\tau )}+{\displaystyle \sum _{s=-\infty }^{k-2}}\left(\frac{\beta \left(s\right)x(s-\tau )}{1+x^n(s-\tau )}{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right)\hfill \\ & \ge & \underline{\beta }\frac{x(k-1-\tau )}{1+x^n(k-1-\tau )}+\underline{\beta }{\displaystyle \sum _{s=-\infty }^{k-2}}\left(\frac{x(s-\tau )}{1+x^n(s-\tau )}{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right).\hfill \end{array}$$

(22)

Notice that $\frac{1}{\sqrt[n]{n-1}}\le m_2\le x\left(k\right)\le m_1$ for $k\in \mathbb{Z}$. In view of Remark 1, we have $f\left(x\left(k\right)\right)\ge f\left(m_1\right)$ for $k\in \mathbb{Z}$. That is $\frac{x\left(k\right)}{1+x^n\left(k\right)}\ge \frac{m_1}{1+m_1^n}$ for $k\in \mathbb{Z}$. Therefore, we get:

$$\frac{x(k-1-\tau )}{1+x^n(k-1-\tau )}\ge \frac{m_1}{1+m_1^n}\mathrm{and}\frac{x(s-\tau )}{1+x^n(s-\tau )}\ge \frac{m_1}{1+m_1^n}.$$

By (22), we obtain:

$$\begin{array}{ccc}\hfill \left(Ax\right)\left(k\right)& \ge & \underline{\beta }\frac{m_1}{1+m_1^n}+\underline{\beta }\frac{m_1}{1+m_1^n}{\displaystyle \sum _{s=-\infty }^{k-2}}\left({\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right)\hfill \\ & \ge & \underline{\beta }\frac{m_1}{1+m_1^n}+\underline{\beta }\frac{m_1}{1+m_1^n}{\displaystyle \sum _{s=-\infty }^{k-2}}\left({\displaystyle \prod _{i=s+1}^{k-1}}(1-\overline{\alpha })\right)\hfill \\ & =& \underline{\beta }\frac{m_1}{1+m_1^n}+\underline{\beta }\frac{m_1}{1+m_1^n}{\displaystyle \sum _{s=-\infty }^{k-2}}{(1-\overline{\alpha })}^{k-1-s}\hfill \\ & =& \underline{\beta }\frac{m_1}{1+m_1^n}+\underline{\beta }\frac{m_1}{1+m_1^n}{\displaystyle \sum _{j=1}^{\infty }}{(1-\overline{\alpha })}^j\hfill \\ & =& \underline{\beta }\frac{m_1}{1+m_1^n}+\underline{\beta }\frac{m_1}{1+m_1^n}\frac{1-\overline{\alpha }}{\overline{\alpha }}\hfill \\ & =& \frac{\underline{\beta }{m}_1}{\overline{\alpha }(1+m_1^n)}\ge m_2.\hfill \end{array}$$

Hence, we get $m_2<\left(Ax\right)\left(k\right)<m_1$.

Moreover, since $x\in \Omega$ is almost periodic and by virtue of Lemmas 1–4, as well as the fact that the uniform limit of the almost periodic sequence is almost periodic, we can deduce that A is almost periodic. Therefore, $Ax\in \Omega$, and thus, we have $A\Omega \subset \Omega$.

It remains to prove that A is a contraction mapping on $\Omega$. For all $x,y\in \Omega$, we get:

$$\begin{array}{ccc}\hfill \parallel Ax-Ay\parallel & =& \underset{k\in \mathbb{Z}}{sup}|\left(Ax\right)\left(k\right)-\left(Ay\right)\left(k\right)|\hfill \\ \hfill & =& \underset{k\in \mathbb{Z}}{sup}|\frac{\beta (k-1)x(k-1-\tau )}{1+x^n(k-1-\tau )}-\frac{\beta (k-1)y(k-1-\tau )}{1+y^n(k-1-\tau )}\hfill \\ & +& {\displaystyle \sum _{s=-\infty }^{k-2}}\left(\beta \left(s\right)\left[\frac{x(s-\tau )}{1+x^n(s-\tau )}-\frac{y(s-\tau )}{1+y^n(s-\tau )}\right]{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right)|\hfill \\ \hfill & \le & \underset{k\in \mathbb{Z}}{sup}\left\{\beta (k-1)\right|\frac{x(k-1-\tau )}{1+x^n(k-1-\tau )}-\frac{y(k-1-\tau )}{1+y^n(k-1-\tau )}|\hfill \\ \hfill & +& {\displaystyle \sum _{s=-\infty }^{k-2}}\left(\beta \left(s\right)|\frac{x(s-\tau )}{1+x^n(s-\tau )}-\frac{y(s-\tau )}{1+y^n(s-\tau )}|{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right)\}.\hfill \end{array}$$

(23)

For the function $f\left(x\right)=\frac{1}{1+x^n}$, $n>1$, and by the mean value theorem, we have:

$$|f\left(x\right)-f\left(y\right)|=|f^{\prime }\left(\xi \right)(x-y)|=|\frac{1-(n-1){\xi }^n}{{(1+{\xi }^n)}^2}||x-y|,x,y\in [\frac{1}{\sqrt[n]{n-1}},\infty ),$$

(24)

where $\xi$ lies between x and y. By Remark 2, we have $\left|g\left(x\right)\right|\le L_2$ for all $x\in [\frac{1}{\sqrt[n]{n-1}},\infty )$ where $L_2:=\frac{{(n-1)}^2}{4n}$. Thus, we get $\left|g\left(\xi \right)\right|=\left|\frac{1-(n-1){\xi }^n}{{(1+{\xi }^n)}^2}\right|\le L_2$. Hence, by (24), we obtain the inequality:

$$|f\left(x\right)-f\left(y\right)|\le L_2|x-y|,x,y\in [\frac{1}{\sqrt[n]{n-1}},\infty ),n>1.$$

That is, we have:

$$|\frac{x}{1+x^n}-\frac{y}{1+y^n}|\le L_2|x-y|,x,y\in [\frac{1}{\sqrt[n]{n-1}},\infty ),n>1.$$

(25)

We note that $\frac{1}{\sqrt[n]{n-1}}\le m_2\le x\left(k\right)\le m_1$ and $\frac{1}{\sqrt[n]{n-1}}\le m_2\le y\left(k\right)\le m_1$ for $k\in \mathbb{Z}$. By the inequality (25), therefore, we have:

$$|\frac{x(k-1-\tau )}{1+x^n(k-1-\tau )}-\frac{y(k-1-\tau )}{1+y^n(k-1-\tau )}|\le L_2|x(k-1-\tau )-y(k-1-\tau )|$$

(26)

and:

$$|\frac{x(s-\tau )}{1+x^n(s-\tau )}-\frac{y(s-\tau )}{1+y^n(s-\tau )}|\le L_2|x(s-\tau )-y(s-\tau )|.$$

(27)

Hence, from (23), (26), and (27), we have:

$$\begin{array}{ccc}\hfill \parallel Ax-Ay\parallel & \le & \underset{k\in \mathbb{Z}}{sup}\left\{\beta (k-1)L_2\right|x(k-1-\tau )-y(k-1-\tau )|\hfill \\ & +& {\displaystyle \sum _{s=-\infty }^{k-2}}\left(\beta \left(s\right)L_2|x(s-\tau )-y(s-\tau )|{\displaystyle \prod _{i=s+1}^{k-1}}(1-\alpha \left(i\right))\right)\}\hfill \\ & \le & \underset{k\in \mathbb{Z}}{sup}\left\{\overline{\beta }{L}_2\parallel x-y\parallel +{\displaystyle \sum _{s=-\infty }^{k-2}}\left(\overline{\beta }{L}_2\parallel x-y\parallel {\displaystyle \prod _{i=s+1}^{k-1}}(1-\underline{\alpha })\right)\right\}\hfill \\ & =& \underset{k\in \mathbb{Z}}{sup}\left\{\overline{\beta }{L}_2\parallel x-y\parallel +\overline{\beta }{L}_2\parallel x-y\parallel {\displaystyle \sum _{s=-\infty }^{k-2}}{(1-\underline{\alpha })}^{k-1-s}\right\}\hfill \\ & =& \underset{k\in \mathbb{Z}}{sup}\left\{\overline{\beta }{L}_2\parallel x-y\parallel +\overline{\beta }{L}_2\parallel x-y\parallel {\displaystyle \sum _{j=1}^{\infty }}{(1-\underline{\alpha })}^j\right\}\hfill \\ & =& \underset{k\in \mathbb{Z}}{sup}\left\{\overline{\beta }{L}_2\parallel x-y\parallel +\overline{\beta }{L}_2\parallel x-y\parallel \frac{1-\underline{\alpha }}{\underline{\alpha }}\right\}\hfill \\ & =& \frac{\overline{\beta }{L}_2}{\underline{\alpha }}\parallel x-y\parallel .\hfill \end{array}$$

Since $\frac{\overline{\beta }{L}_2}{\underline{\alpha }}<1$, we have that A is a contraction mapping. Therefore, by the contraction mapping fixed point theorem, the operator A has a unique fixed point $x^{*}$ in $\Omega$. This implies that Model (3) has an almost periodic positive solution $x^{*}$ satisfying $m_2\le x^{*}\left(k\right)\le m_1$. ☐

4. Exponential Convergence

Sufficient conditions for the exponential stability of Model (3) are given by the following theorem. In the proof, we utilize a discrete Lyapunov functional of the form:

$$V\left(k\right)=|x\left(k\right)-x^{*}\left(k\right)|e^{\mu k}.$$

(28)

Definition 2.

Let $x^{*}$ be an almost periodic solution of (3) satisfying $m_2<x^{*}<m_1$. If there exist positive constants H and μ such that:

$$|x\left(k\right)-x^{*}\left(k\right)|\le H{e}^{-\mu k},k\in {\mathbb{Z}}^{+},$$

then we say that $x\left(k\right)$ converges exponentially to $x^{*}\left(k\right)$ as $k\to \infty$.

Theorem 5.

Assume that (C1) and (C2) hold. Then, every solution x of Model (3) with the initial function $\varphi \in S^0$ converges exponentially to $x^{*}$ as $k\to \infty$, where $x^{*}$ is an almost periodic solution of (3) satisfying $m_2<x^{*}<m_1$.

Proof. 

By Theorem 4, we know that Model (3) has an almost periodic positive solution $x^{*}$ satisfying $m_2<x^{*}\left(k\right)<m_1$. Let $x^{*}\left(k\right)=\psi \left(k\right)>0$, $-\tau \le k\le 0$ be the initial function associated with the solution $x^{*}\left(k\right)$ and $x\left(k\right)$ be an arbitrary solution of Model (3) with initial function $\varphi \in S^0$. Then, $m_2<\varphi \left(k\right)<m_1$ and $x\left(k\right)=\varphi \left(k\right)$ for $-\tau \le k\le 0$. By Theorem 2, we know that $m_2<x\left(k\right)<m_1$ for all $k>0,k\in {\mathbb{Z}}^{+}$.

Consider the function $F\left(x\right)=L_2\overline{\beta }{e}^{(\tau +1)x}-\underline{\alpha }{e}^x+e^x-1,x\in [0,1]$. Since $F\left(0\right)=L_2\overline{\beta }-\underline{\alpha }<0$, then there exists a constant $\mu \in (0,1)$ such that $F\left(\mu \right)<0$. That is,

$$-\underline{\alpha }{e}^{\mu }+e^{\mu }+L_2\overline{\beta }{e}^{\mu (\tau +1)}<1$$

(29)

In view of (28), we have:

$$\begin{array}{ccc}\hfill ▵V\left(k\right)& =& V(k+1)-V\left(k\right)=|x(k+1)-x^{*}(k+1)|e^{\mu (k+1)}-|x\left(k\right)-x^{*}\left(k\right)|e^{\mu k}\hfill \\ & =& \left(|x(k+1)-x^{*}(k+1)|-|x\left(k\right)-x^{*}\left(k\right)|\right)e^{\mu (k+1)}+\left(e^{\mu }-1\right)|x\left(k\right)-x^{*}\left(k\right)|e^{\mu k}.\hfill \end{array}$$

Noting that:

$$|x(k+1)-x^{*}(k+1)|-|x\left(k\right)-x^{*}\left(k\right)|=-\alpha \left(k\right)|x\left(k\right)-x^{*}\left(k\right)|+\beta \left(k\right)|\frac{x(k-\tau )}{1+x^n(k-\tau )}-\frac{x^{*}(k-\tau )}{1+{x^{*}}^n(k-\tau )}|,$$

we get:

$$\begin{array}{ccc}\hfill ▵V\left(k\right)& =& V(k+1)-V\left(k\right)\hfill \\ \hfill & \le & \left(-\alpha \left(k\right)|x\left(k\right)-x^{*}\left(k\right)|+\beta \left(k\right)|\frac{x(k-\tau )}{1+x^n(k-\tau )}-\frac{x^{*}(k-\tau )}{1+{x^{*}}^n(k-\tau )}|\right)e^{\mu (k+1)}\hfill \\ & +& \left(e^{\mu }-1\right)|x\left(k\right)-x^{*}\left(k\right)|e^{\mu k}.\hfill \\ \hfill & =& \left(-\alpha \left(k\right)e^{\mu }+e^{\mu }-1\right)|x\left(k\right)-x^{*}\left(k\right)|e^{\mu k}+\beta \left(k\right)e^{\mu }|\frac{x(k-\tau )}{1+x^n(k-\tau )}-\frac{x^{*}(k-\tau )}{1+{x^{*}}^n(k-\tau )}|e^{\mu k}\hfill \\ \hfill & =& \left(-\alpha \left(k\right)e^{\mu }+e^{\mu }-1\right)V\left(k\right)+\beta \left(k\right)e^{\mu }|\frac{x(k-\tau )}{1+x^n(k-\tau )}-\frac{x^{*}(k-\tau )}{1+{x^{*}}^n(k-\tau )}|e^{\mu k}\hfill \end{array}$$

(30)

Let $H:=m_1+{max}_{-\tau \le k\le 0,k\in \mathbb{Z}}|\varphi \left(k\right)-\psi \left(k\right)|$. For all $k\in [-\tau ,0]$, we have:

$$\begin{array}{ccc}\hfill V\left(k\right)& =& |x\left(k\right)-x^{*}\left(k\right)|e^{\mu k}\le |x\left(k\right)-x^{*}\left(k\right)|=|\varphi \left(k\right)-{\psi }^{*}\left(k\right)|\hfill \\ & \le & \underset{-\tau \le k\le 0,k\in \mathbb{Z}}{max}|\varphi \left(k\right)-\psi \left(k\right)|<m_1+\underset{-\tau \le k\le 0,k\in \mathbb{Z}}{max}|\varphi \left(k\right)-\psi \left(k\right)|=H.\hfill \end{array}$$

Now, we prove the following claim:

$$V\left(k\right)<H\mathrm{for}\mathrm{all}k>0,k\in {\mathbb{Z}}^{+}.$$

(31)

Suppose the claim (31) is not true. Then there must exist a $K^{*}\in {\mathbb{Z}}^{*}$ such that $V\left(K^{*}\right)\ge H$ and $V\left(K\right)<H$ for $-\tau \le k<K^{*},k\in \mathbb{Z}$. It follows from (30) that:

$$\begin{array}{ccc}\hfill V\left(K^{*}\right)-V(K^{*}-1)& \le & \left(-\alpha (K^{*}-1)e^{\mu }+e^{\mu }-1\right)V(K^{*}-1)\hfill \\ & +& \beta (K^{*}-1)e^{\mu }|\frac{x(K^{*}-1-\tau )}{1+x^n(K^{*}-1-\tau )}-\frac{x^{*}(K^{*}-1-\tau )}{1+{x^{*}}^n(K^{*}-1-\tau )}|e^{\mu (K^{*}-1)}\hfill \\ \hfill & \le & \left(-\underline{\alpha }{e}^{\mu }+e^{\mu }-1\right)V(K^{*}-1)\hfill \\ \hfill & +& \overline{\beta }{e}^{\mu }|\frac{x(K^{*}-1-\tau )}{1+x^n(K^{*}-1-\tau )}-\frac{x^{*}(K^{*}-1-\tau )}{1+{x^{*}}^n(K^{*}-1-\tau )}|e^{\mu (K^{*}-1)}.\hfill \end{array}$$

(32)

Note that $\frac{1}{\sqrt[n]{n-1}}\le m_2\le x\left(k\right)\le m_1$ and $\frac{1}{\sqrt[n]{n-1}}\le m_2\le x^{*}\left(k\right)\le m_1$ for $k\in \mathbb{Z}$. By the inequality (25), therefore, we have:

$$|\frac{x(K^{*}-1-\tau )}{1+x^n(K^{*}-1-\tau )}-\frac{x^{*}(K^{*}-1-\tau )}{1+{x^{*}}^n(K^{*}-1-\tau )}|\le L_2|x(K^{*}-1-\tau )-x^{*}(K^{*}-1-\tau )|.$$

(33)

Thus, (32) and (33) imply that:

$$\begin{array}{ccc}\hfill V\left(K^{*}\right)-V(K^{*}-1)& \le & \left(-\underline{\alpha }{e}^{\mu }+e^{\mu }-1\right)V(K^{*}-1)+\overline{\beta }{e}^{\mu }{L}_2|x(K^{*}-1-\tau )-x^{*}(K^{*}-1-\tau )|e^{\mu (K^{*}-1)}\hfill \\ \hfill & =& \left(-\underline{\alpha }{e}^{\mu }+e^{\mu }-1\right)V(K^{*}-1)\hfill \\ & +& \overline{\beta }{e}^{\mu }{L}_2|x(K^{*}-1-\tau )-x^{*}(K^{*}-1-\tau )|e^{\mu (K^{*}-1-\tau )}{e}^{\mu \tau }\hfill \\ \hfill & =& \left(-\underline{\alpha }{e}^{\mu }+e^{\mu }-1\right)V(K^{*}-1)+\overline{\beta }{e}^{\mu }{L}_{2}V(K^{*}-1-\tau )e^{\mu \tau }.\hfill \end{array}$$

(34)

From (34), we obtain:

$$\begin{array}{ccc}\hfill V\left(K^{*}\right)& \le & \left(-\underline{\alpha }{e}^{\mu }+e^{\mu }\right)V(K^{*}-1)+\overline{\beta }{e}^{\mu }{L}_{2}V(K^{*}-1-\tau )e^{\mu \tau }\hfill \\ & <& \left(-\underline{\alpha }{e}^{\mu }+e^{\mu }\right)H+\overline{\beta }{e}^{\mu }{L}_{2}H{e}^{\mu \tau }\hfill \\ & =& \left(-\underline{\alpha }{e}^{\mu }+e^{\mu }+\overline{\beta }{L}_2{e}^{\mu (\tau +1)}\right)H<H,\hfill \end{array}$$

which contradicts that $V\left(K^{*}\right)\ge H$. Therefore, the claim (31) is true. Hence, $V\left(k\right)=|x\left(k\right)-x^{*}\left(k\right)|e^{\mu k}<H$ for all $k>0,k\in {\mathbb{Z}}^{+}$. That is, $|x\left(k\right)-x^{*}\left(k\right)|\le H{e}^{-\mu k}$ for all $k>0,k\in {\mathbb{Z}}^{+}$, which implies that $x\left(k\right)$ converges exponentially to $x^{*}\left(k\right)$ as $k\to \infty$. ☐

5. Examples and Numerical Simulations

In this section, we present two numerical examples along with their numerical simulations to demonstrate the effectiveness of our theoretical findings.

Example 1.

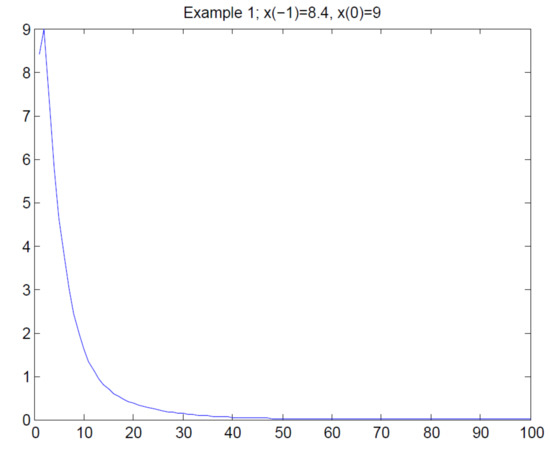
Consider the equation:

$$▵x\left(k\right)=-\left(\frac{1}{5}+\frac{1}{500}sin\sqrt{3}k\right)x\left(k\right)+\frac{\left(\frac{1}{10}+\frac{1}{200}cos\sqrt{5}k\right)x(k-\tau )}{1+x^n(k-\tau )},$$

(35)

where $\alpha \left(k\right)=\frac{1}{5}+\frac{1}{500}sin\sqrt{3}k$, $\beta \left(k\right)=\frac{1}{10}+\frac{1}{200}cos\sqrt{5}k$, $n=2$, $\tau =1$. Since $\underline{\alpha }>\overline{\beta }$, then it follows from Theorem 3 that every solution x of System (35) satisfies $x\left(k\right)\to 0$ as $k\to \infty$. Figure 1 depicts the extinction behavior of the solution of (35).

Figure 1. Extinction pattern for the solution of System (5.1).

Example 2.

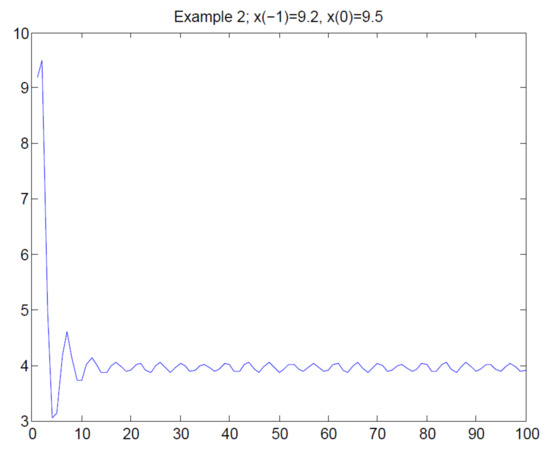
Consider the equation:

$$▵x\left(k\right)=-\left(\frac{3}{5}+\frac{1}{100}sin\sqrt{2}k\right)x\left(k\right)+\frac{\left(10+\frac{1}{20}cos\sqrt{3}k\right)x(k-\tau )}{1+x^n(k-\tau )},$$

(36)

where $\alpha \left(k\right)=\frac{3}{5}+\frac{1}{100}sin\sqrt{2}k$, $\beta \left(k\right)=10+\frac{1}{20}cos\sqrt{3}k$, $n=1.5$, $\tau =1$. It is straightforward to find that $\alpha =0.61$, $\underline{\alpha }=0.59$, $\overline{\beta }=10.05$, $\underline{\beta }=9.95$, $\frac{1}{\sqrt[1.5]{0.5}}\approx 1.59$, $L_1\approx 0.53$, $L_2\approx 0.042$. There exist $m_1=10$, $m_2=2$ such that $m_1>\frac{\overline{\beta }{L}_1}{\underline{\alpha }}\approx 9.028$, $\frac{1}{\sqrt[1.5]{0.5}}<m_2<\frac{\underline{}\beta m_1}{\overline{\alpha }(1+m_1^n)}\approx 5$ where $\frac{\overline{\beta }{L}_2}{\underline{\alpha }}<1$. Therefore, Conditions (C1) and (C2) are satisfied. By Theorem 4 and Theorem 5, we know that for System (36), there exists an almost periodic positive solution $x^{*}$ satisfying $m_2\le x^{*}\left(k\right)\le m_1$. Moreover, every solution x of Equation (36) with initial condition $\varphi \in S^0$ converges exponentially to $x^{*}$ as $k\to \infty$. Figure 2 illustrates the exponential convergence of the solution of System (36) to $x^{*}$.

Figure 2. Exponential convergence pattern of the solution of System (5.2).

6. Conclusions

The study of the Mackey–Glass model, which is referred to in the literature, as the hematopoiesis model has been initiated a long time ago and then developed by systematic study through the contributions of many researchers. The model itself has gained its reputation amongst researchers due to its realistic significance in the description of blood cell production. After the proposal of Model (1) by Mackey and Glass, the authors in [23] investigated the global attractivity of its unique positive equilibrium. The authors in [24], however, considered the following model with variable coefficients:

$$x^{\prime }\left(t\right)=-\alpha \left(t\right)x\left(t\right)+\frac{\beta \left(t\right)}{1+x^n(t-\tau \left(t\right))},t\ge 0$$

(37)

and investigated the oscillation and global attractivity of its solutions, as well as its exponential stability of the positive almost periodic solution. The existence and global exponential convergence of positive almost periodic solutions for the hematopoiesis model with several delays:

$$x^{\prime }\left(t\right)=-\alpha \left(t\right)x\left(t\right)+{\displaystyle \sum _{i=1}^m}\frac{{\beta }_i\left(t\right)}{1+x^n(t-{\tau }_i\left(t\right))}$$

(38)

was investigated in [25]. Later on and by employing a novel argument, the author in [26] established sufficient conditions to ensure the existence, uniqueness, and global exponential stability of positive almost periodic solutions of Model (38). Gopalsamy et al. [27] introduced the more realistic hematopoiesis model (2), which was also under consideration in [28]. On the other hand, the authors in [17,18] conducted an extensive study for the dynamics of almost periodic solutions of Model (2).

The discretization of population models has been the object of research due to their effective applicability when the size of the population has non-overlapping generations. The discrete models are straightforward and can also provide more efficient methods for processes involving numerical computations and simulations. Motivated by the above justifications, the researchers in [29] investigated the model:

$$▵x\left(k\right)=-\alpha \left(k\right)x\left(k\right)+\frac{\beta \left(k\right)}{1+x^n(k-\tau )},$$

(39)

where the permanence, oscillation, and attractivity of solutions have been considered. In [30], the current author established sufficient conditions for the existence and global attractivity of the positive periodic solution of Model (39). To the best of our observation, the discrete analogue of Model (2) has not under consideration in the literature. This paper is devoted to studying the dynamics of the discrete Mackey–Glass model (2). We proved the following:

• the boundedness and extinction of its solutions,
• the existence of almost periodic positive solutions,
• the exponential convergence of the almost periodic positive solution.

To prove our results, we used the contraction mapping principle, as well as the discrete Lyapunov functional to establish sufficient conditions in their less restrictive forms. Examples, as well as numerical simulations were illustrated to demonstrate the effectiveness of the theoretical findings of the paper. Our results are new and generalize some previously-reported results in the literature.