Fractional Modeling for Quantitative Inversion of Soil-Available Phosphorus Content
Abstract
1. Introduction
2. Materials and Methods
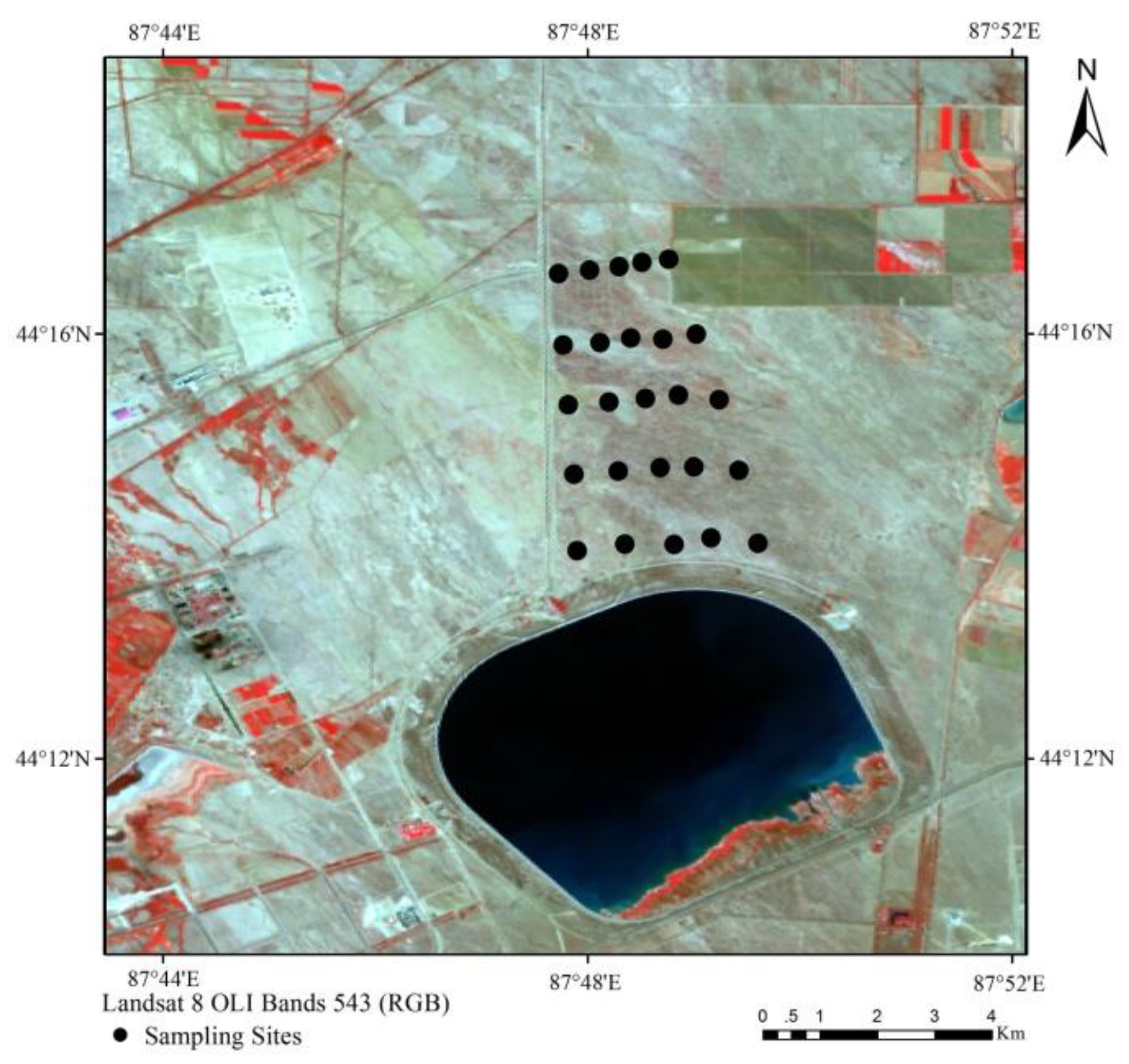
2.1. Research Area
2.2. Sampling Point Layout and Measurement of Available Phosphorus Content
2.3. Field Spectral Data Acquisition
2.4. Fractional Derivative
2.5. Stepwise Multiple Linear Regression
2.6. Model Accuracy Verification Method
3. Results and Discussion
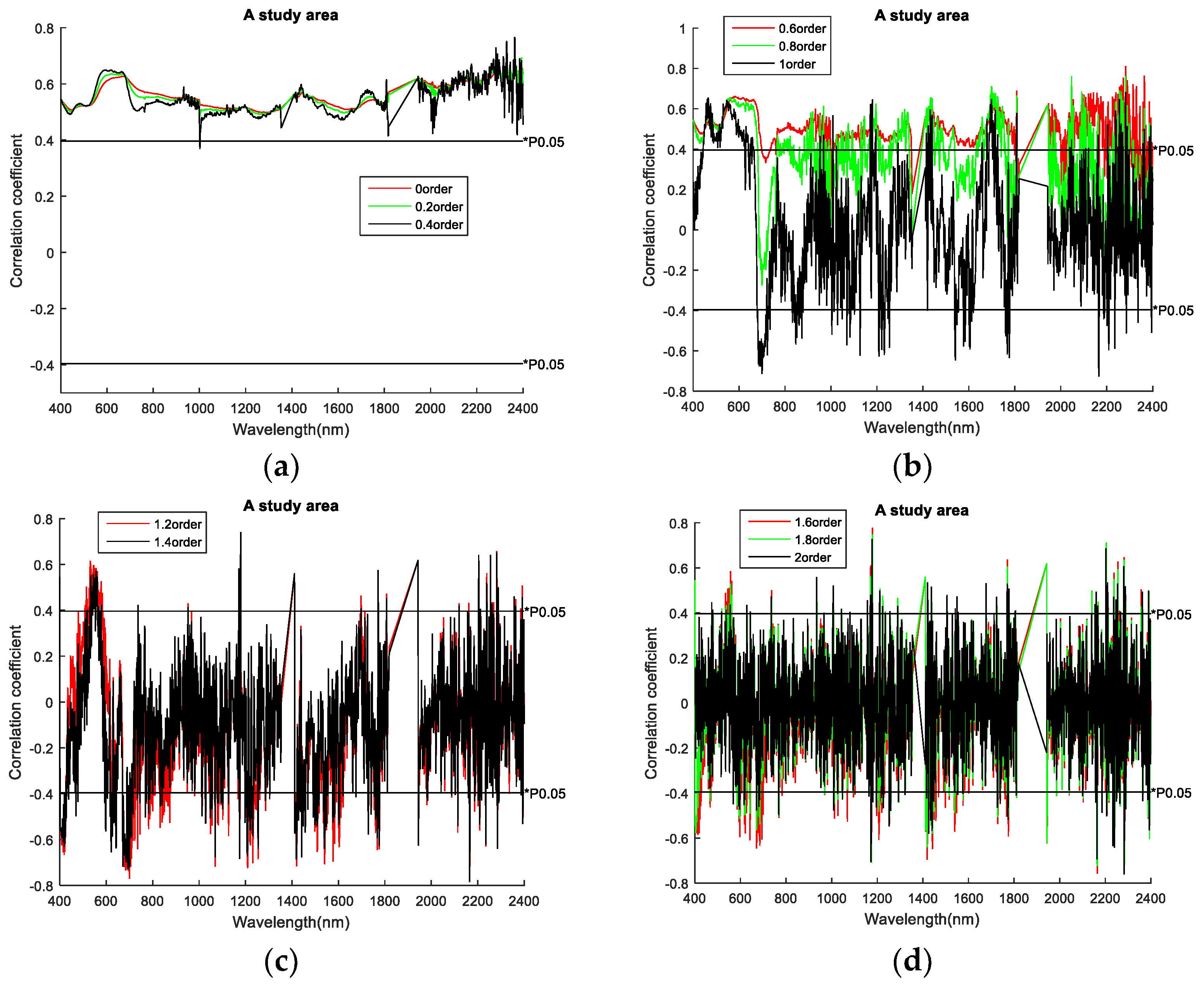
3.1. Correlation Coefficient
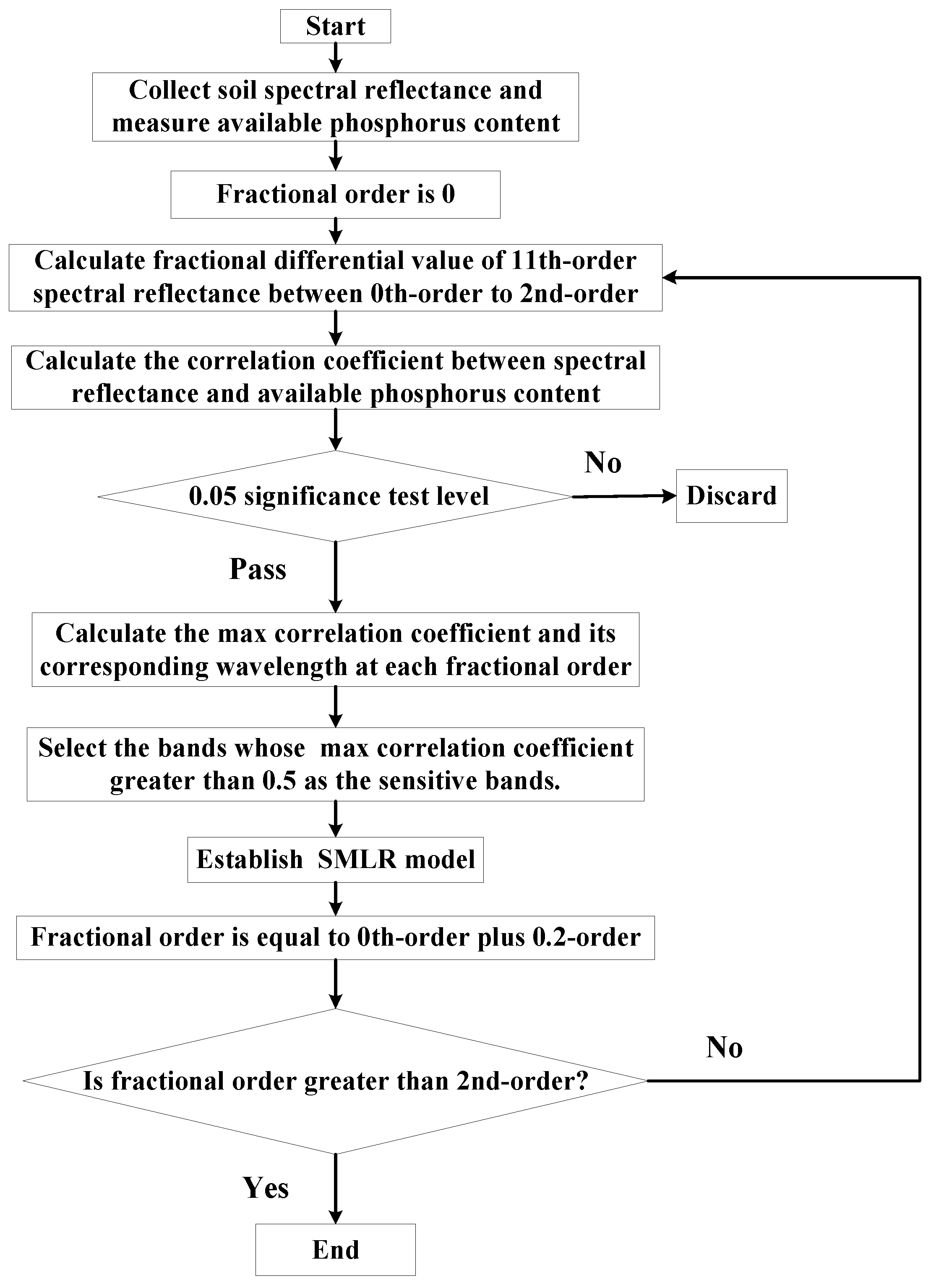
3.2. Modeling Process for Quantitative Analysis Model
- Step 1:
- Calculate the fractional differential value of 11 fractional differentials spectral reflectance between 0th-order and 2nd-order using Equation (4).
- Step 2:
- Calculate the correlation coefficient between spectral reflectance and available phosphorus content and perform a 0.05 significance test.
- Step 3:
- Statistically calculate the absolute value of the maximum correlation coefficient after the 11th-order fractional differential transformation and its corresponding wavelength.
- Step 4:
- Select the bands whose absolute value of maximum correlation coefficient with each fractional order is greater than 0.5 as the sensitive bands.
- Step 5:
- Establish the SMLR model.
- Step 6:
- All fractional spectral data and its corresponding sensitive bands are obtained by traversing 0th-order to 2nd-order at intervals of 0.2 step.
3.3. Model Optimal Wavelength Selection
3.4. Establishment Stepwise Multiple Linear Regression Model
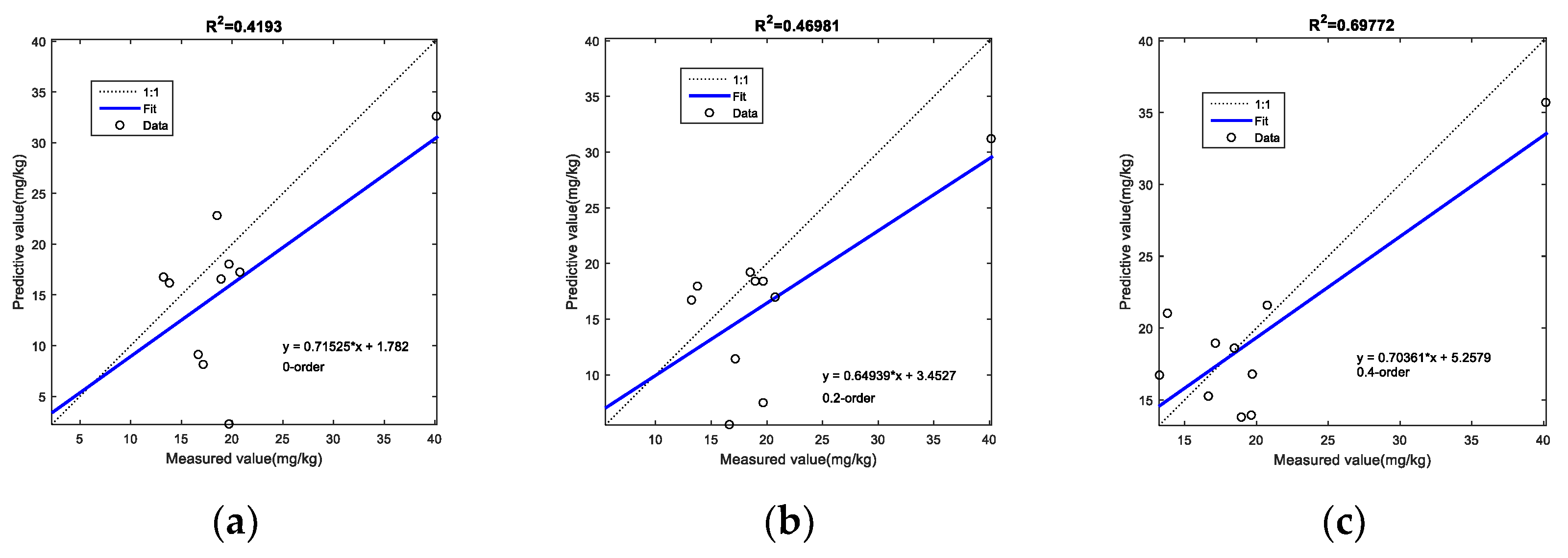
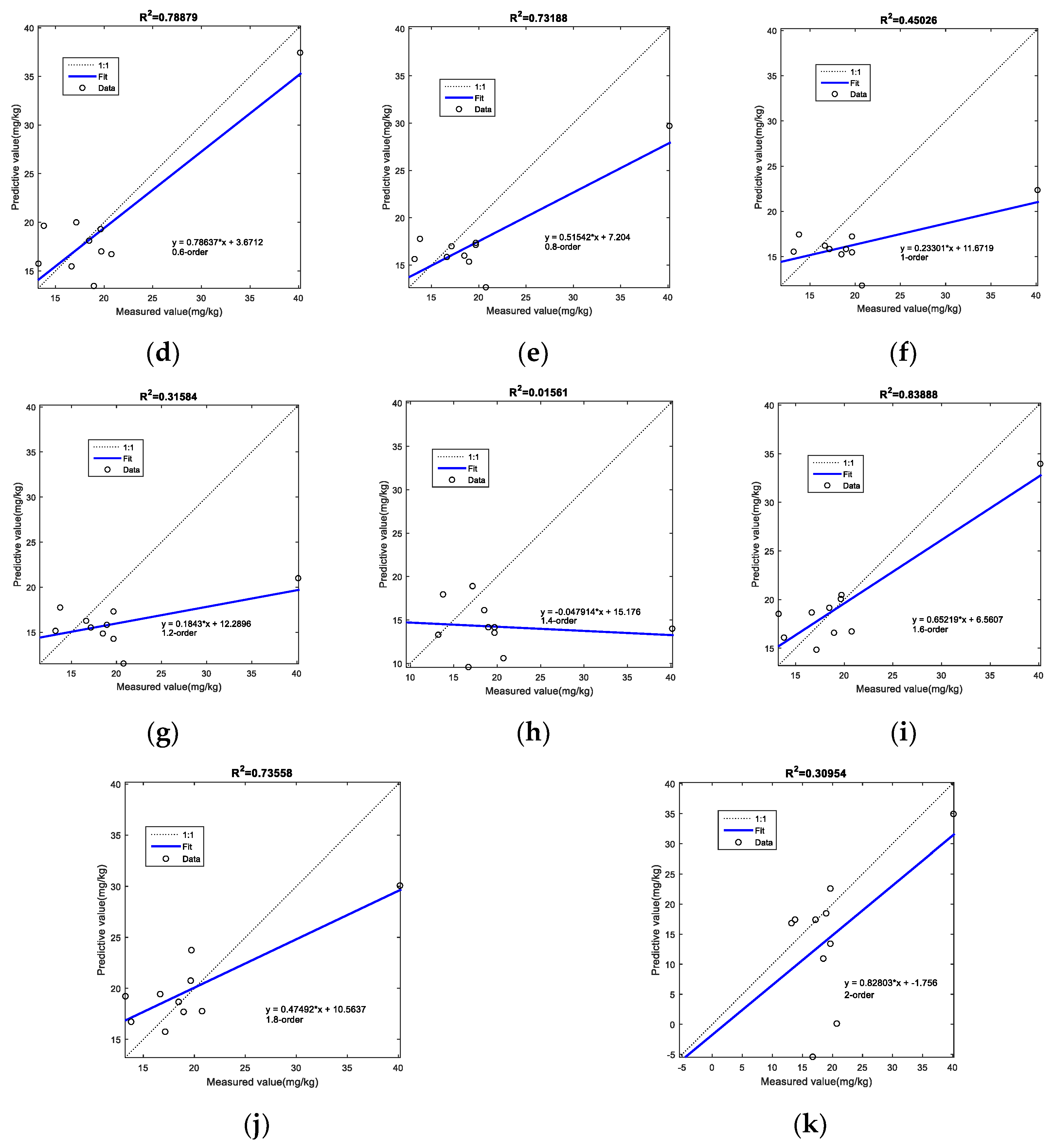
3.5. Predictive Model Accuracy Comparison
3.6. Selection Best Prediction Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shao, Y.; He, Y. Nitrogen, phosphorus, and potassium prediction in soils, using infrared spectroscopy. Soil Res. 2011, 49, 166–172. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; de Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Zhang, W.; Zeng, G.; Chen, X.; Lin, W. Spatial-temporal pattern and source of soil available phosphorus in Minjiang River estuarine wetland. Chin. J. Ecol. 2015, 34, 168–174. [Google Scholar]
- Sarathjith, M.C.; Das, B.S.; Wani, S.P.; Sahrawat, K.L.; Gupta, A. Comparison of Data Mining Approaches for Estimating Soil Nutrient Contents Using Diffuse Reflectance Spectroscopy. Curr. Sci. 2016, 110, 1031. [Google Scholar] [CrossRef]
- Balabin, R.M.; Safieva, R.Z.; Lomakina, E.I. Wavelet neural network (WNN) approach for calibration model building based on gasoline near infrared (NIR) spectra. Chemometr. Intell. Lab. Syst. 2008, 93, 58–62. [Google Scholar] [CrossRef]
- Mouaze, A.M.; Maleki, M.R.; Baerdemaeker, J.D.; Ramon, H. On-line measurement of some selected soil properties using a VIS–NIR sensor. Soil Tillage Res. 2007, 93, 13–27. [Google Scholar] [CrossRef]
- Paz-Kagan, T.; Zaady, E.; Salbach, C.; Schmidt, A.; Lausch, A.; Zacharias, S.; Notesco, G.; Ben-Dor, E.; Karnieli, A. Mapping the Spectral Soil Quality Index (SSQI) Using Airborne Imaging Spectroscopy. Remote Sens. 2015, 7, 15748–15781. [Google Scholar] [CrossRef]
- Bo, S.; Raphaela, V.R.; Abdulmounem, M.; Johanna, W. Visible and near infrared spectroscopy in soil science. Adv. Agron. 2010, 107, 163–215. [Google Scholar]
- Gholizadeh, A.; Boruvka, L.; Saberioon, M.; Němeček, K. Comparing different data preprocessing methods for monitoring soil heavy metals based on soil spectral features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef]
- Rajeev, S.; Madhurama, S.; Yadav, R.K.; Bundela, D.S.; Manjeet, S.; Chattaraj, S.; Singh, S.K. Visible-Near Infrared Reflectance Spectroscopy for Rapid Characterization of Salt-Affected Soil in the Indo-Gangetic Plains of Haryana, India. J. Indian Soc. Remote Sens. 2016, 45, 307–315. [Google Scholar]
- Jia, S.; Yang, X.; Li, G.; Zhang, J. Quantitatively Determination of Available Phosphorus in Soil by Near Infrared Spectroscopy Combining with Recurisive Partial Least Squares. Spectrosc. Spectr. Anal. 2015, 35, 2516–2520. [Google Scholar]
- Kharintsev, S.S.; Salakhov, M.K. Peak Parameters Determination Using Fractional Derivative Spectrometry; Astronomical Observatory of Belgrade: Beograd, Serbia, 2003; pp. 211–214. [Google Scholar]
- Zheng, K.-Y.; Zhang, X.; Tong, P.-J.; Yao, Y.; Du, Y.-P. Pretreating near infrared spectra with fractional order Savitzky–Golay differentiation (FOSGD). Chin. Chem. Lett. 2015, 26, 293–296. [Google Scholar] [CrossRef]
- Zhang, D.; Tashpolat, T.; Ding, J.; Wang, J. Quantitative Estimating Salt Content of Saline Soil Using Laboratory Hyperspectral Data Treated by Fractional Derivative. J. Spectrosc. 2016, 2016. [Google Scholar] [CrossRef]
- Wang, J.; Tashpolat, T.; Zhang, D. Spectral Detection of Chromium Content in Desert Soil Based on Fractional Differential. Trans. Chin. Soc. Agric. Mach. 2017, 152–158. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; Mcgann, A.V. Discretization of Fractional Differential Equations by a Piecewise Constant Approximation. Math. Model. Nat. Phenom. 2016, 12, 23–26. [Google Scholar] [CrossRef]
- Almusalhi, F.; Alsalti, N.; Kerbal, S. Inverse Problems of a Fractional Differential Equation with Bessel Operator. Math. Model. Nat. Phenom. 2017, 12, 105–113. [Google Scholar] [CrossRef]
- Galeone, L.; Garrappa, R. Explicit Methods for Fractional Differential Equations and Their Stability Properties. J. Comput. Appl. Math. 2009, 228, 548–560. [Google Scholar] [CrossRef]
- Latt, Z.Z.; Wittenberg, H. Improving Flood Forecasting in a Developing Country: A Comparative Study of Stepwise Multiple Linear Regression and Artificial Neural Network. Water Resour. Manag. 2014, 28, 2109–2128. [Google Scholar] [CrossRef]
- Zhong, P.; Zhang, P.; Wang, R. Dynamic Learning of SMLR for Feature Selection and Classification of Hyperspectral Data. IEEE Geosci. Remote Sens. Lett. 2008, 5, 280–284. [Google Scholar] [CrossRef]
- Qiao, X.-X.; Wang, C.; Feng, M.-C.; Yang, W.-D.; Ding, G.-W.; Sun, H.; Liang, Z.-Y.; Shi, C.C. Hyperspectral estimation of soil organic matter based on different spectral preprocessing techniques. Spectrosc. Lett. 2017, 50, 156–163. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Arnon, K.; Chen, J.; Han, W. Hyperspectal estimation of desert soil organic matter content based on gray correlation-ridge regressing model. Trans. Chin. Soc. Agric. Eng. 2018, 34, 124–131. [Google Scholar]
- Zhang, Q.; Zhang, H.; Zhang, H.; Wang, X.; Liu, W. Hybrid inversion model of heavy metals with hyperspectral reflectance in cultivated soils of main grain producing areas. Trans. Chin. Soc. Agric. Mach. 2017, 48, 148–155. [Google Scholar]
| Fractional Order | Correlation Coefficient | Band |
|---|---|---|
| 0.0 | 0.67076 | 2393 |
| 0.2 | 0.70252 | 2365 |
| 0.4 | 0.76698 | 2364 |
| 0.6 | 0.81085 | 2283 |
| 0.8 | 0.76230 | 2047 |
| 1.0 | 0.72828 | 2165 |
| 1.2 | 0.78561 | 2165 |
| 1.4 | 0.78276 | 2165 |
| 1.6 | 0.77828 | 1179 |
| 1.8 | 0.74803 | 1179 |
| 2.0 | 0.76187 | 2283 |
| Fractional Order | RMSE | Regression Equation | |
|---|---|---|---|
| 0.0 | 0.424 | 5.138126 | Y = −7.877 + 73.319 × R2393 |
| 0.2 | 0.487 | 4.849662 | Y = 11.929 + 713.184 × R2365 − 646.632 × R2165 |
| 0.4 | 0.761 | 3.309459 | Y = 12.091 + 1852.579 × R2364 − 1605.108 × R1179 |
| 0.6 | 0.750 | 3.382826 | Y = 17.181 − 7257.243 × R2283 − 13134.640 × R2047 − 57458.127 × R1179 |
| 0.8 | 0.744 | 3.427327 | Y = −3.514 + 9907.544 × R2047 − 4796.115 × R2165 |
| 1.0 | 0.591 | 4.3324598 | Y = 12.962 − 11610.572 × R2165 |
| 1.2 | 0.718 | 3.595593 | Y = 13.174 − 11574.405 × R2165 |
| 1.4 | 0.809 | 2.961901 | Y = 19.099 − 7691.730 × R2165 + 80915.009 × R1179 |
| 1.6 | 0.865 | 2.491789 | Y = 16.654 − 8411.379 × R2165 + 75168.550 × R1179 − 1140.389 × R2365 |
| 1.8 | 0.824 | 2.865772 | Y = 17.240 − 7227.992 × R2283 − 13268.074 × R2047 − 63874.358 × R1179 + 1008.311 × R2365 |
| 2.0 | 0.644 | 4.040979 | Y = 19.020 − 8316.207 × R2283 |
| Fractional Order | RMSE | RPD | |
|---|---|---|---|
| 0.0 | 0.4193 | 7.462748 | 1.120282 |
| 0.2 | 0.4698 | 6.570987 | 1.091302 |
| 0.4 | 0.6977 | 3.997434 | 1.594921 |
| 0.6 | 0.7888 | 3.348878 | 2.001142 |
| 0.8 | 0.7318 | 4.791680 | 0.951661 |
| 1.0 | 0.4503 | 6.810229 | 0.385937 |
| 1.2 | 0.3158 | 7.303034 | 0.339882 |
| 1.4 | 0.0156 | 9.784626 | 0.296595 |
| 1.6 | 0.8389 | 3.250759 | 1.657943 |
| 1.8 | 0.7356 | 4.291305 | 1.476663 |
| 2.0 | 0.3095 | 10.349263 | 1.088459 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Xiong, H.; Tian, A. Fractional Modeling for Quantitative Inversion of Soil-Available Phosphorus Content. Mathematics 2018, 6, 330. https://doi.org/10.3390/math6120330
Fu C, Xiong H, Tian A. Fractional Modeling for Quantitative Inversion of Soil-Available Phosphorus Content. Mathematics. 2018; 6(12):330. https://doi.org/10.3390/math6120330
Chicago/Turabian StyleFu, Chengbiao, Heigang Xiong, and Anhong Tian. 2018. "Fractional Modeling for Quantitative Inversion of Soil-Available Phosphorus Content" Mathematics 6, no. 12: 330. https://doi.org/10.3390/math6120330
APA StyleFu, C., Xiong, H., & Tian, A. (2018). Fractional Modeling for Quantitative Inversion of Soil-Available Phosphorus Content. Mathematics, 6(12), 330. https://doi.org/10.3390/math6120330





