Kempe-Locking Configurations

Abstract

The 4-color theorem was proved by showing that a minimum counterexample cannot exist. Birkhoff demonstrated that a minimum counterexample must be internally 6-connected. We show that a minimum counterexample must also satisfy a coloring property that we call Kempe-locking. The novel idea explored in this article is that the connectivity and coloring properties are incompatible. We describe a methodology for analyzing whether an arbitrary planar triangulation is Kempe-locked. We provide a heuristic argument that a fundamental Kempe-locking configuration must be of low order and then perform a systematic search through isomorphism classes for such configurations. All Kempe-locked triangulations that we discovered have two features in common: (1) they are Kempe-locked with respect to only a single edge, say $xy$, and (2) they have a Birkhoff diamond with endpoints x and y as a subgraph. On the strength of our investigations, we formulate a plausible conjecture that the Birkhoff diamond is the only fundamental Kempe-locking configuration. If true, this would establish that the connectivity and coloring properties of a minimum counterexample are indeed incompatible. It would also imply the appealing conclusion that the Birkhoff diamond configuration alone is responsible for the 4-colorability of planar triangulations.

1. Terminology

We use the standard terminology of graph theory: the basic terms vertex, edge, face, simple graph, planar graph, subgraph, induced subgraph, path, cycle, connectivity, adjacent vertices, order, vertex degree, and minimum degree are all assumed to be known (refer to the introductory text by Chartrand and Zhang [1]). This article is primarily about the coloring of planar graphs. We restrict our consideration to coloring the vertices of simple, connected, planar graphs, and, as is usual, to proper colorings of such graphs, colorings in which no two adjacent vertices have the same color. The 4-color theorem states that it takes no more than four distinct colors to color any simple planar graph properly (see [2]). In studying the 4-color problem, we need consider only planar graphs that are triangulations, graphs in which all faces are delineated by three edges. That is because any planar graph that is not a triangulation can be turned into a triangulation by inserting edges until all faces are triangular. After properly coloring the triangulation, the inserted edges can be deleted, leaving the original graph with a proper coloring. If all faces of a planar graph except one are triangular, the graph is referred to as a near-triangulation. Near-triangulations in which the only non-triangular face is four-sided are particularly important in this article; such a near-triangulation can be derived by deleting any edge in a triangulation. As is customary, we use the term configuration for a near-triangulation whose non-triangular face is the infinite face.

2. Introduction

This article is not about finding an alternative proof of the 4-color theorem; instead, it is an exploratory paper aimed at gaining a deeper understanding of why the 4-color theorem is true, what it is about a planar graph that guarantees that it can be 4-colored. We set about this task by focusing on the properties of a minimum counterexample. The two we single out for thorough examination relate to connectivity and coloring. These are the subjects of Section 3 and Section 4. A new approach to understanding why planar graphs are 4-colorable is to investigate whether the connectivity and coloring properties of a minimum counterexample are compatible. We shall see that this approach bears fruit. Our analysis suggests strongly that the two properties are not compatible. An important contribution this article makes to the literature on planar graph coloring is the notion of Kempe-locking, defined in Section 4. If an edge $xy$ is deleted from a planar triangulation T, a near-triangulation $G_{xy}$ results. Consider any 4-coloring of $G_{xy}$ in which vertices x and y have the same color. If T is Kempe-locked with respect to $xy$, then any sequence of interchanges of colors on Kempe chains leaves x and y still sharing the same color. Thus, Kempe interchanges applied to $G_{xy}$ with x and y colored the same cannot result in a 4-coloring of $G_{xy}$ in which the deleted edge $xy$ can be replaced in order to achieve a 4-coloring of T. In Section 4, we prove that a minimum counterexample to the 4-color theorem must be Kempe-locked with respect to every one of its edges. Each edge in a minimum counterexample must have this coloring property.

In Section 5, we present examples of Kempe-locked triangulations. In Section 6, we present a methodology to determine if a triangulation is Kempe-locked and define two key terms, Kempe-locking configuration and fundamental Kempe-locking configuration. We then look back briefly to Section 5 to identify the pertinent Kempe-locking configurations for the various examples. In Section 7, we report the results of an extensive search through all isomorphism classes of planar triangulations of low order. Several Kempe-locked triangulations were discovered, each Kempe-locked with respect to only a single edge. Call that edge $xy$. We find that each such triangulation has a Birkhoff diamond subgraph with endpoints x and y. Our search confirms that the Birkhoff diamond is a fundamental Kempe-locking configuration and strongly suggests that it is the only fundamental Kempe-locking configuration. Section 8 presents an even more fundamental graph—a triangulation of order 9 that gives rise to the Birkhoff diamond. It is constituted as a single vertex within a pentagon within a triangle.

Section 9 concludes the article. It emphasizes the likely singular role of the Birkhoff diamond in the matter of establishing the incompatibility of the connectivity and coloring properties of a minimum counterexample and thus in the matter of the 4-colorability of planar triangulations. It also describes future directions for this research, not the least of which is finding collaborators with substantially greater computing power to extend the search for Kempe-locked triangulations.

Although our primary concern is the theoretical question of 4-colorability of planar graphs, it should be noted that graph coloring finds application more generally to many real-world problems, including the scheduling of sports events, determining examination timetables, and arranging seating plans. Graph coloring also underpins the creation of Sudoku puzzles. While new techniques, such as those discussed in this article, will likely find their way into problems involving complex networks, it is not our intent to explore such applications here.

3. Connectivity Property

A graph G is connected if there is a path joining every pair of vertices. It is said to be k-connected if it has more than k vertices and remains connected whenever fewer than k vertices are deleted. Therefore, for example, if a graph has 4-cycle with vertices both inside and outside the cycle, then deleting the vertices of the 4-cycle (and all their edges) disconnects the graph into the subgraph that lies outside the 4-cycle and the subgraph that lies inside the 4-cycle. Such a graph might be 4-connected but it cannot be 5-connected. A separating k-cycle is a k-cycle in a graph such that there are one or more vertices in the graph both inside and outside the cycle. Thus, a graph with a separating k-cycle can be at most k-connected. A 5-connected triangulation is minimum degree 5 and has no separating 3-cycles or 4-cycles. However, in a 5-connected triangulation, any separating 5-cycle is permitted. Suppose, instead, we consider triangulations for which no separating 5-cycle has two or more vertices both inside and outside the cycle. Then, each separating 5-cycle will have a single vertex either inside or outside the cycle. In other words, each 5-cycle will “enclose” a vertex of degree 5. If that is the case, then the triangulation is said to be internally 6-connected. Internally 6-connected triangulations form a proper subset of 5-connected triangulations.

Property 1.

(Connectivity) A planar triangulation is said to be internally 6-connected if it is minimum degree 5 and has no cycle of length 5 or less for which there are two or more vertices both inside and outside the cycle.

Every existing proof of the 4-color theorem has been based on showing that a minimum counterexample cannot exist. If a counterexample does exist, then there must be one or more smallest counterexamples, where by “smallest” we mean the counterexample(s) having the lowest order (fewest vertices). In a landmark paper in 1913, Birkhoff [3] showed that a minimum counterexample to the 4-color theorem must be internally 6-connected. (That was not a term of his choosing; it arrived on the graph theory scene much later.) In that paper, Birkhoff also introduced the important notion of reducibility. Suppose that an arbitrary planar triangulation T contains a configuration C as a subgraph and let $G=T-C$ denote the near-triangulation formed by removing C from T. The configuration C is said to be reducible if, whenever G is 4-colorable, T is also 4-colorable. Thus, a planar triangulation that is a minimum counterexample to the 4-color theorem cannot contain a reducible configuration.

The Appel–Haken team [4,5] and the Robertson–Sanders–Seymour–Thomas team [6] each proved the 4-color theorem by constructing an unavoidable set of reducible configurations (1482 such configurations for [4,5] and 633 for [6]). The term unavoidable means that every internally 6-connected triangulation contains at least one of the configurations from the set as a subgraph—the set cannot be avoided. Then, because each configuration in the set is reducible, no internally 6-connected triangulation can be a minimum counterexample.

4. Coloring Property

We follow the standard practice of indicating the color of a vertex by using one of the integers 1, 2, 3, 4, …. If the first k integers are used to color the vertices of a graph, we say that the graph is k-colored. It is important to understand what we mean by a distinct coloring of G. Another way to think of a k-coloring of G is that the set of all vertices in G has been partitioned into k independent sets, each set assigned a distinct color from 1 to k. An independent set of vertices is one in which no two vertices are adjacent. What matters is the partition (what vertices belong to what independent set); it does not matter how we assign colors to the various independent sets. Thus, a mere permutation of colors does not lead to a distinctly different coloring of G.

A useful tool in graph coloring is the Kempe chain, named after the British mathematician whose attempt at proving the 4-color theorem failed [7]. In a given coloring of a graph G, a Kempe chain is a maximal, connected, induced subgraph of G whose vertices use only two colors, let us say colors i and j. An i-j Kempe chain is “maximal” in that every vertex adjacent to, but not in, the chain uses a color other than i or j. In the six-panel figure that accompanies the first example presented in Section 5, there is a single 1–2 Kempe chain in each of the four uppermost graphs and two distinct 1–2 Kempe chains in each of the two lowermost graphs. It is customary to consider a vertex colored i not adjacent to any vertex colored j a short i-j chain and likewise a vertex colored j not adjacent to any vertex colored i.

Kempe chains are particularly useful in “navigating” among the various distinct 4-colorings of a graph G because interchanging colors on a chain—that is, interchanging the color labels i and j for all vertices constituting an i-j chain—leaves G properly colored. Interchanging colors on an i-j Kempe chain does not lead to a distinctly different coloring of G if there is only one i-j chain. However, for example, if there are three distinct i-j chains, then interchanging colors on any one or on any pair of those chains does lead to a distinctly different coloring of G. A straightforward description of using Kempe chains to color and recolor graphs can be found in [8].

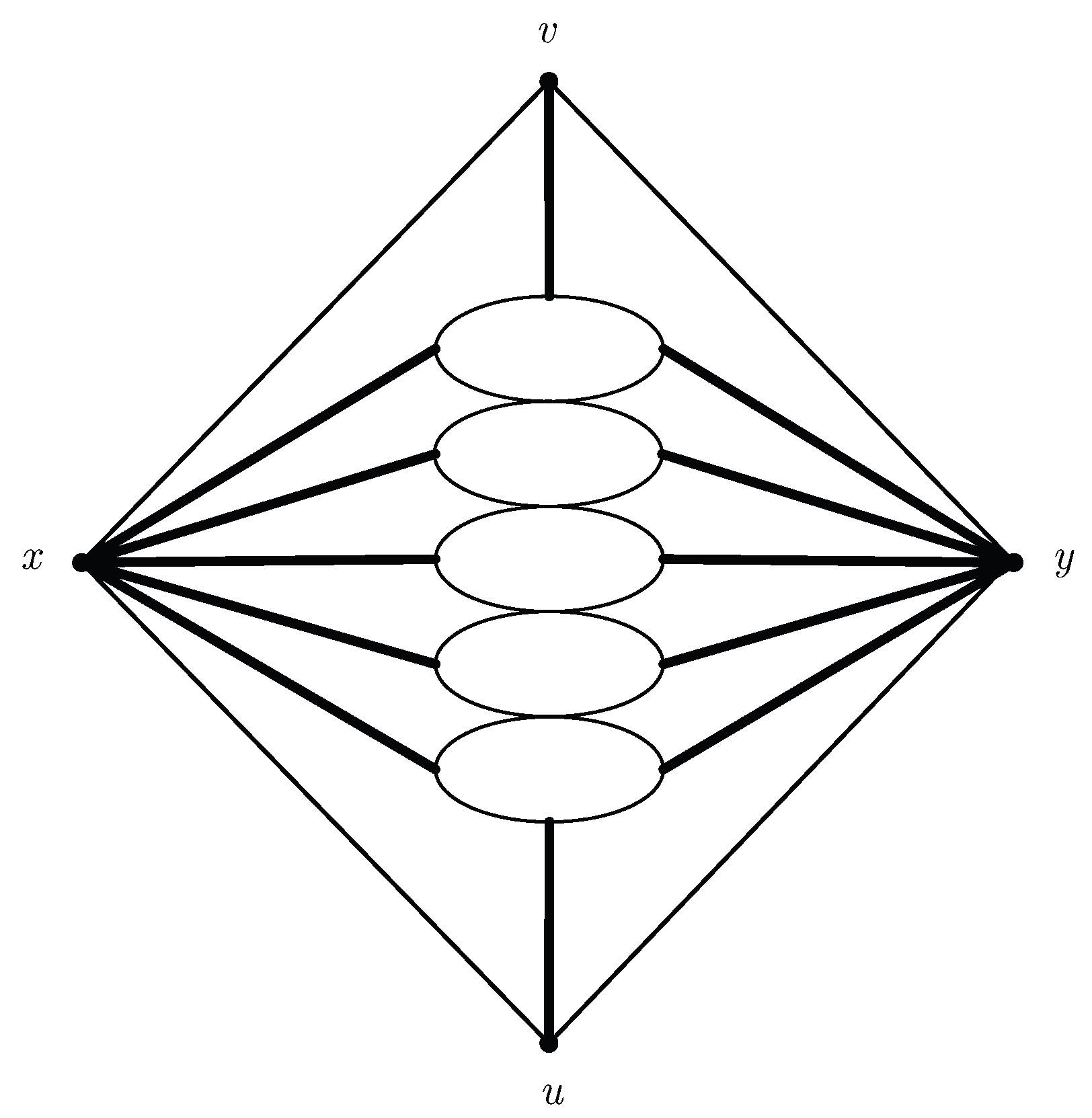
The idea that underpins our different approach to the question of 4-colorability derives from a graph-coloring problem that is the subject of another article [9], a coloring problem posed for planar graphs that are near-triangulations in which the single non-triangular face is quadrilateral. Although we do not pursue that coloring problem per se in this article, we do focus on near-triangulations with a 4-face and find it useful to establish a few conventions regarding the drawing and vertex labeling of such graphs. In this article, we always draw them with the 4-face as the infinite (exterior) region oriented as shown in Figure 1 and we always label the boundary cycle of the 4-face $uxvy$ with u the bottom vertex, x the left-hand vertex, v the top vertex, and y the right-hand vertex. Then x and y constitute one pair of opposite vertices and u and v the other pair. We use the notation $G_{xy}$ to refer to the near-triangulation that results when the edge $xy$ is deleted from a planar triangulation T. Such a near-triangulation can always be drawn as depicted in Figure 1.

Property 2.

(Coloring) A planar triangulation T is Kempe-locked with respect to the edge $xy$ if, in every 4-coloring of $G_{xy}$ in which the colors of x and y are the same, there are precisely three distinct Kempe chains that include both x and y.

Kempe-locking is a property associated with an edge in a triangulation. A triangulation can be Kempe-locked with respect to one particular edge and not with respect to any of its other edges. If T is Kempe-locked with respect to the edge $xy$, then given a 4-coloring of $G_{xy}$ in which x and y are both colored 1, there must be 1–2, 1–3, and 1–4 Kempe chains including both x and y. Interchanging colors on any of those chains leaves x and y sharing the same color. Moreover, for any such 4-coloring, because T is Kempe-locked, interchanging colors on any Kempe chain that does not include x and y must lead to a 4-coloring in which there are 1–2, 1–3, and 1–4 Kempe chains that include both x and y. Thus, if interchanging colors on Kempe chains is the only method of recoloring available, $G_{xy}$ is “locked into” a state in which x and y have the same color.

The notion of Kempe-locking should not be confused with the matter of entangled Kempe chains, the condition that afflicted Kempe’s attempted proof of the 4-color theorem (see [2]). If an i-j Kempe chain and a j-k Kempe chain, $i\ne k$, intersect at one or more vertices colored j, then the two chains are said to be entangled. By this definition, there are entangled Kempe chains in every 4-coloring of every triangulation. (Consider any vertex v colored j in a triangulation on at least four vertices; v is adjacent to at least three other vertices that form a cycle enclosing v. Because that cycle must involve at least two colors different from j, say i and k, there will be i-j and j-k Kempe chains entangled at v.) In contrast, Kempe-locking turns out to be rare—it is a coloring property that characterizes not merely a pair of Kempe chains, but an entire triangulation. It refers to a coloring condition shared by all members of a particular set of 4-colorings of the near-triangulation derived by deleting a specified edge from its parent triangulation.

To demonstrate that a minimum counterexample has Property 2, we first need to describe the notion of an edge contraction, also known as vertex identification. Adjacent vertices x and y are said to be identified, or equivalently, the edge $xy$ is said to be contracted, if x and y are coalesced into a single vertex w, with all edges formerly incident to x and y now incident to w. The act of contracting $xy$ makes a smaller graph; it decreases the order of the graph by one.

Theorem 1.

A minimum counterexample to the 4-color theorem is Kempe-locked with respect to every one of its edges.

Proof. 

Let T be a minimum counterexample to the 4-color theorem. Contract an arbitrary edge $xy$ by coalescing x and y into w. This edge contraction yields a new triangulation $T^{\prime }$ with one fewer vertex than T. Because T is assumed to be a minimum counterexample, $T^{\prime }$ can be 4-colored. Then, when w is split apart into the original x and y, but without replacing the edge $xy$, we obtain a near-triangulation $G_{xy}$ in which the colors of x and y are the same.

Now suppose that T is not Kempe-locked with respect to the edge $xy$. Then there must be a 4-coloring of $G_{xy}$ in which x and y are colored the same and in which there is a Kempe chain that includes x but does not include y. Interchanging colors on such a chain results in a 4-colored $G_{xy}$ with the color of x not the same as the color of y. In this 4-coloring, the edge $xy$ can be inserted to yield a 4-coloring for T, in contradiction to the assumption that T is a minimum counterexample. □

In contrast to the situation of a minimum counterexample, no 4-colorable planar triangulation can be Kempe-locked with respect to every one of its edges. The proof of that result can be found in Appendix A.

The key point of this article is that Property 1 and Property 2—connectivity and coloring—are likely incompatible. If that could be proved, then the 4-color theorem would be proved because a minimum counterexample, unable to exhibit both properties, could not exist. We capture this idea in the form of a plausible conjecture, one likely to be true but beyond difficult to prove.

Conjecture 1.

No planar triangulation that is Kempe-locked with respect to an edge is internally 6-connected.

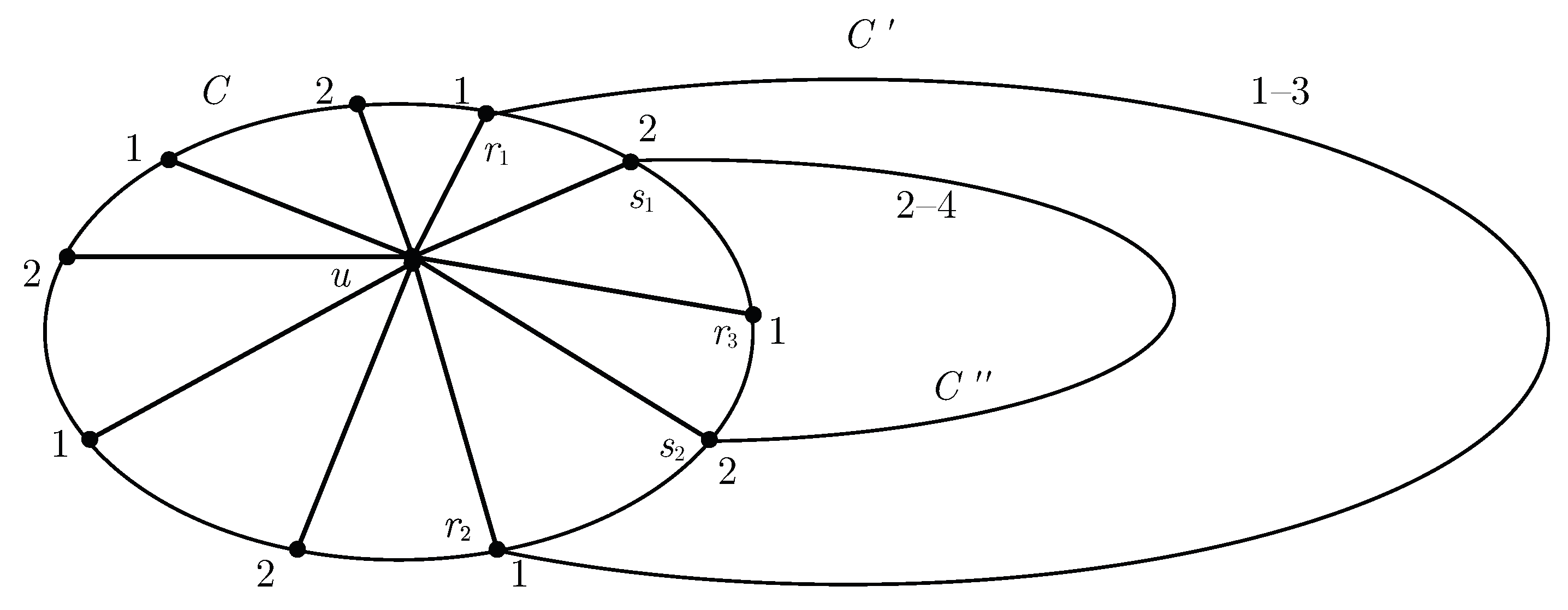
To investigate Conjecture 1, we set about trying to find planar triangulations that are Kempe-locked with respect to some edge. Obviously, we need to consider only internally 6-connected triangulations; however, to find as many Kempe-locked triangulations as possible so that we can learn what structural properties they might have in common, we cast a wider net by searching for any that are at least 4-connected. Because we are studying the properties of a minimum counterexample to the 4-color theorem, we can omit 3-connected triangulations from consideration by virtue of the following argument. Any 3-connected planar triangulation T on more than four vertices must have a separating triangle. Assume that T is a minimum counterexample. Then, the vertex sets of both (1) the induced proper subgraph of T consisting of the separating triangle and everything outside it and (2) the induced proper subgraph of T consisting of the separating triangle and everything inside it can be 4-colored in such a way that the separating triangle is colored identically in each subgraph (through a permutation of colors, as necessary). Thus, T can be 4-colored, a contradiction.

5. Examples of Kempe-Locked Triangulations

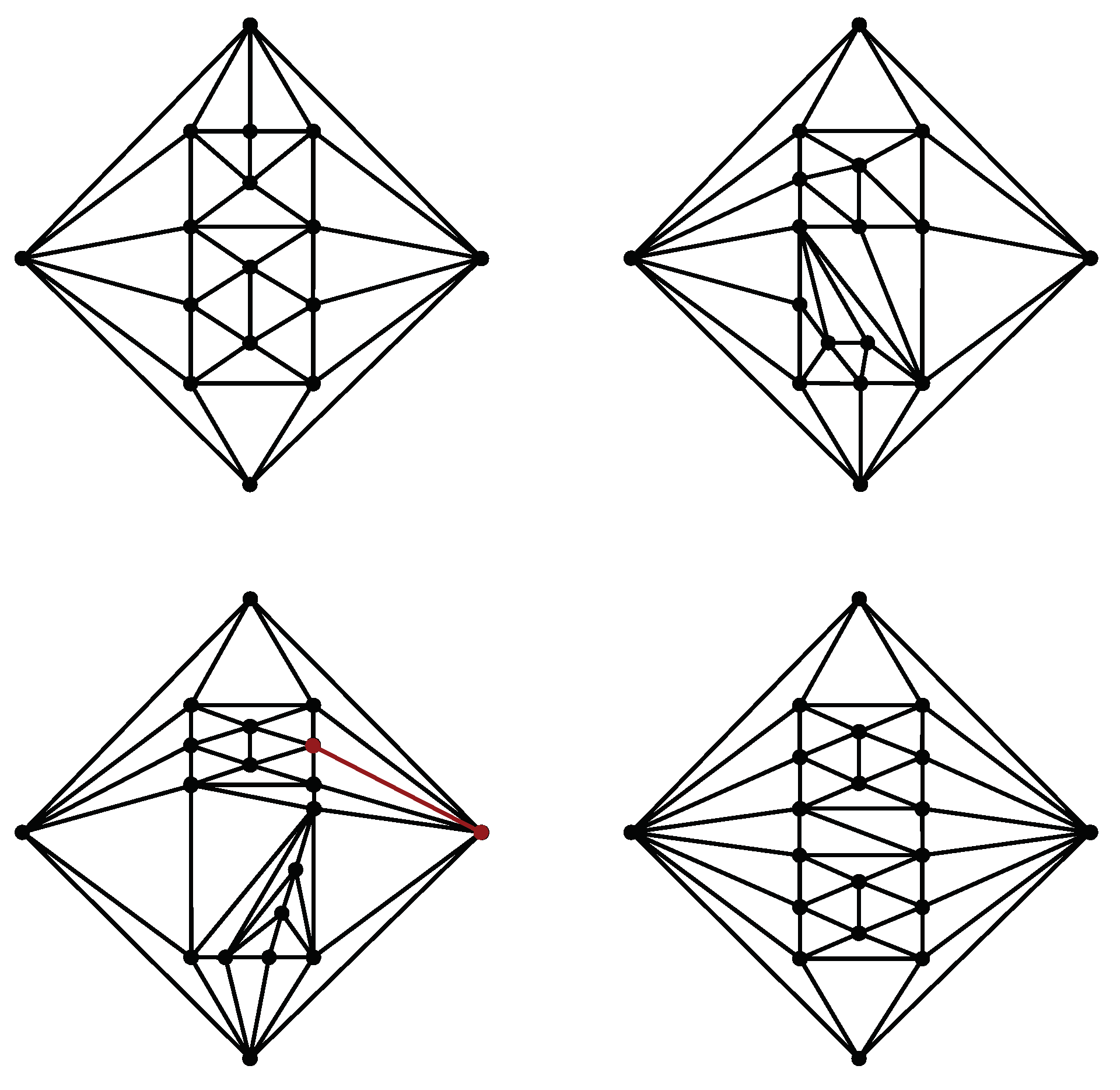
Figure 2 shows the six distinct 4-colorings of a particular near-triangulation $G_{xy}$ of order 12. These are the only 4-colorings in which x and y (the leftmost and rightmost vertices on the exterior 4-face) are colored the same. This can be seen by noting, without loss of generality, that x and y can be colored 1 and v (the topmost vertex on the exterior 4-face) colored 2. Then, the other two vertices adjacent to v must be colored 3 and 4. Without loss of generality, the vertex adjacent to both x and v can be colored 3 and the vertex adjacent to both y and v can be colored 4. There are seven vertices remaining to be colored. Noting the color possibilities for each remaining vertex and then successively trying each, one quickly discovers that there are only six distinct 4-colorings of $G_{xy}$. As can be seen from Figure 2, in each of the 4-colorings there are 1–2, 1–3, and 1–4 Kempe chains that include both x and y. Thus, the triangulation T formed by joining x and y is Kempe-locked with respect to the edge $xy$. T does not contradict Conjecture 1 because the bottommost and topmost vertices on the 4-face (u and v, respectively) have degree 4. Indeed, T is 4-connected.

We note that the near-triangulation shown in Figure 2 becomes the icosahedron when u and v, instead of x and y, are joined. In that situation, we refer to the near-triangulation as $G_{uv}$ because it is the edge $uv$ that is deleted from the icosahedron to form the near-triangulation. In neither of the bottom two 4-colorings of $G_{uv}$ in Figure 2, in which u and v and both colored 2, are there 2–3 or 2–4 Kempe chains that include both u and v. Because $(u,v)$ can be taken to represent any pair of adjacent vertices in the highly symmetric and regular icosahedron, we conclude that the icosahedron is not Kempe-locked with respect to any of its edges.

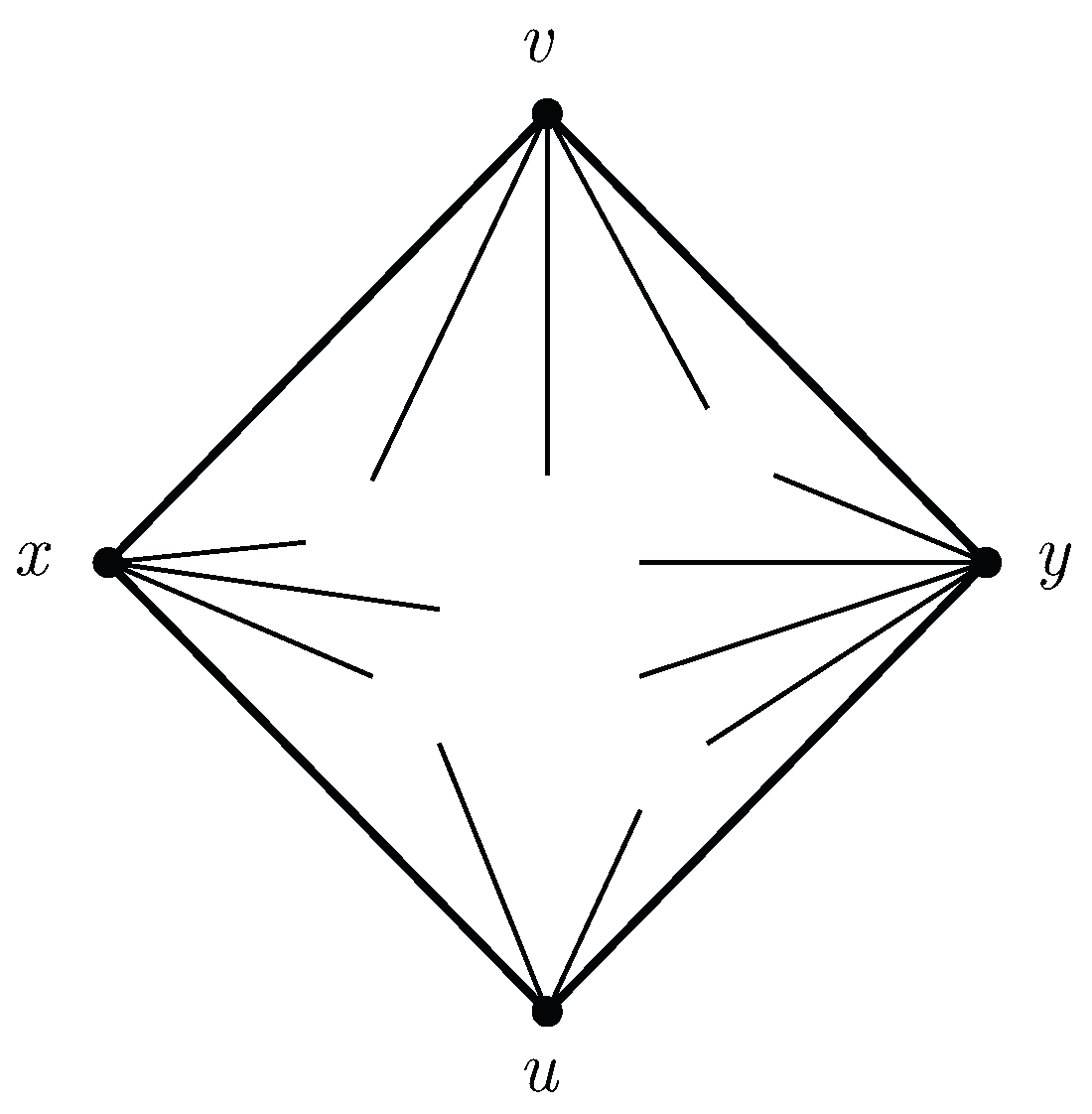
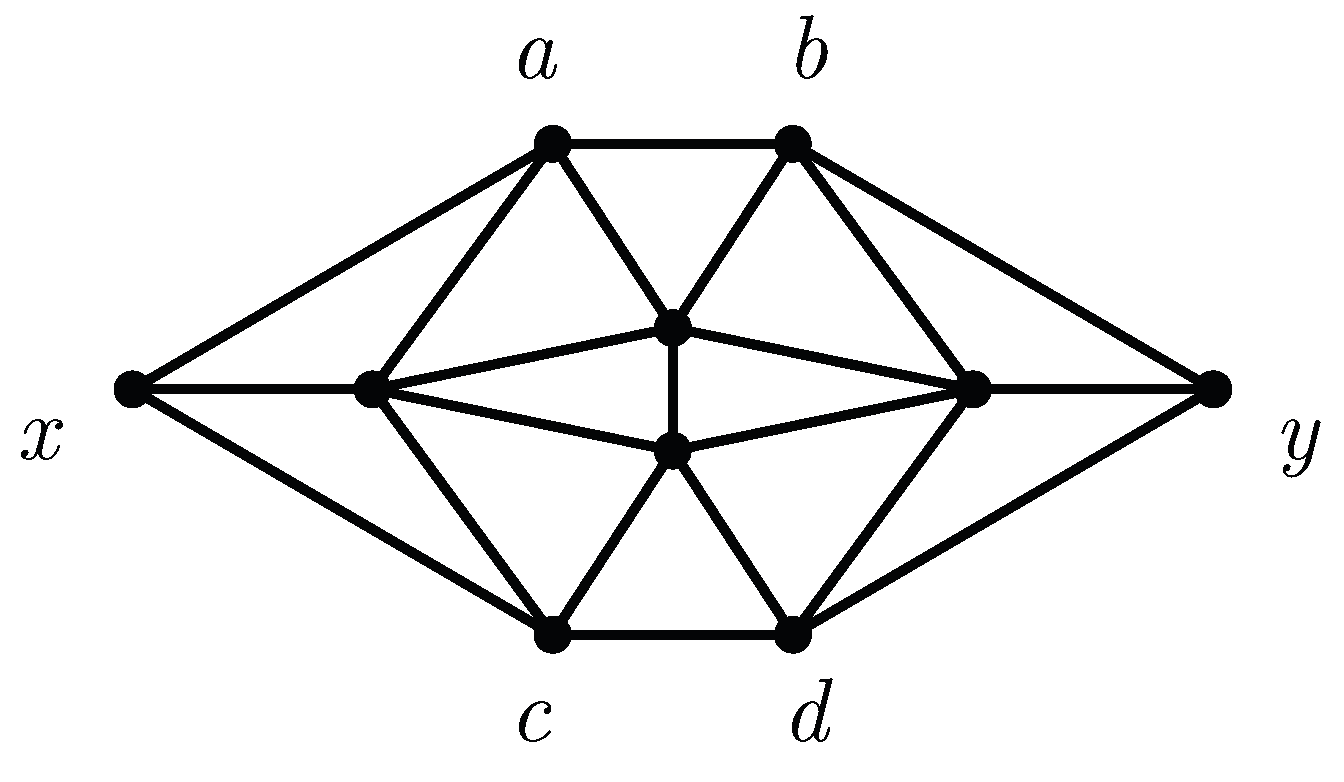
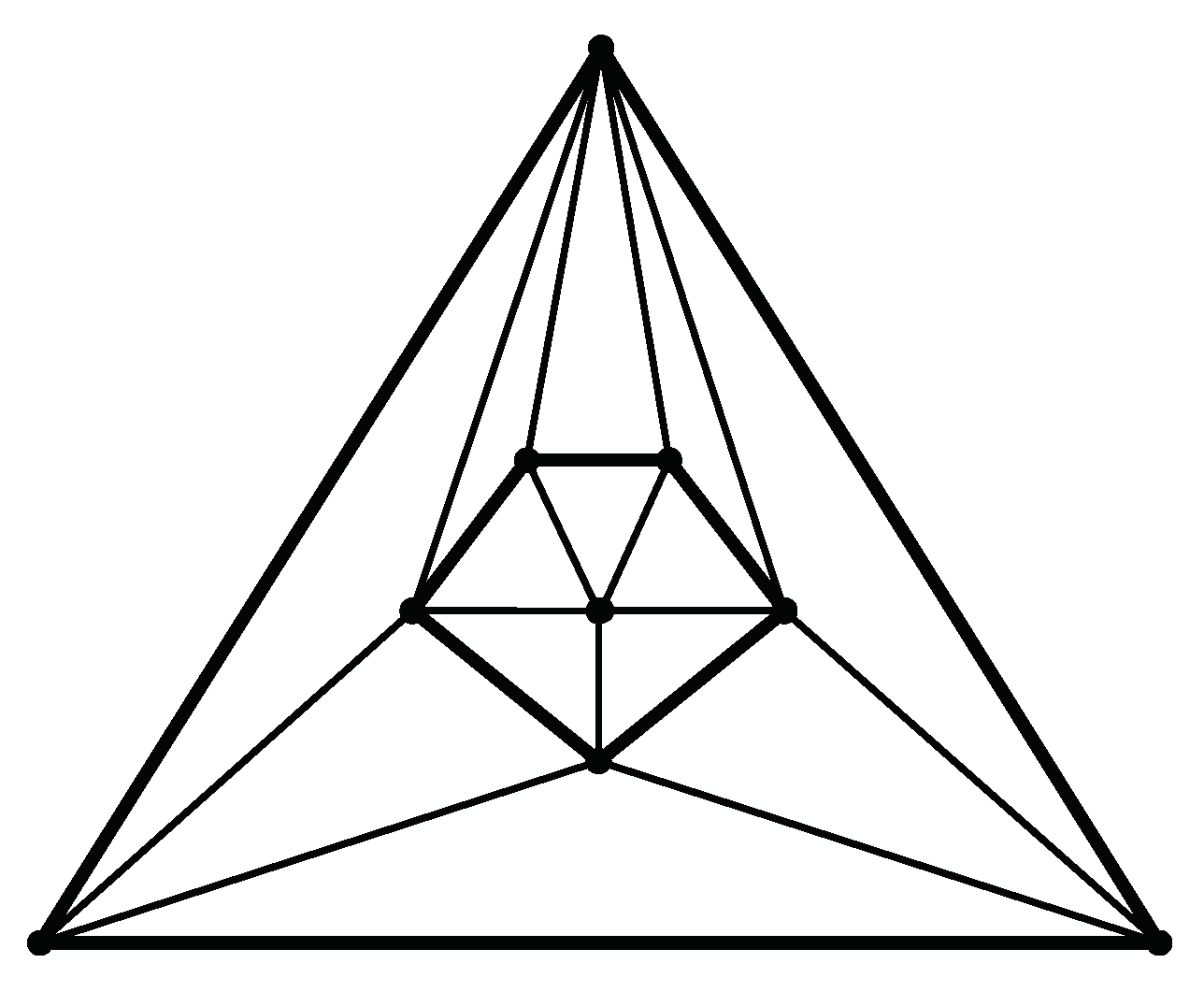
Figure 3 shows a particular induced subgraph of order 10 of the near-triangulation of order 12 in Figure 2. That subgraph, a configuration, is known as the Birkhoff diamond, named for the mathematician who first highlighted its importance in the 4-color problem [3]: it was the very first configuration to be proved reducible; its presence in a triangulation guarantees that the triangulation cannot be a minimum counterexample. Ironically, we will see that the Birkhoff diamond makes its appearance in our analysis in an opposite way—namely, that it likely must be present for a triangulation to be Kempe-locked with respect to an edge and thus possibly a candidate to be a minimum counterexample. Our systematic search among 4-connected and 5-connected triangulations, which we shall describe in Section 7, uncovered a number of Kempe-locked triangulations. All share a common feature: one or more Birkhoff diamond subgraphs with endpoints x and y.

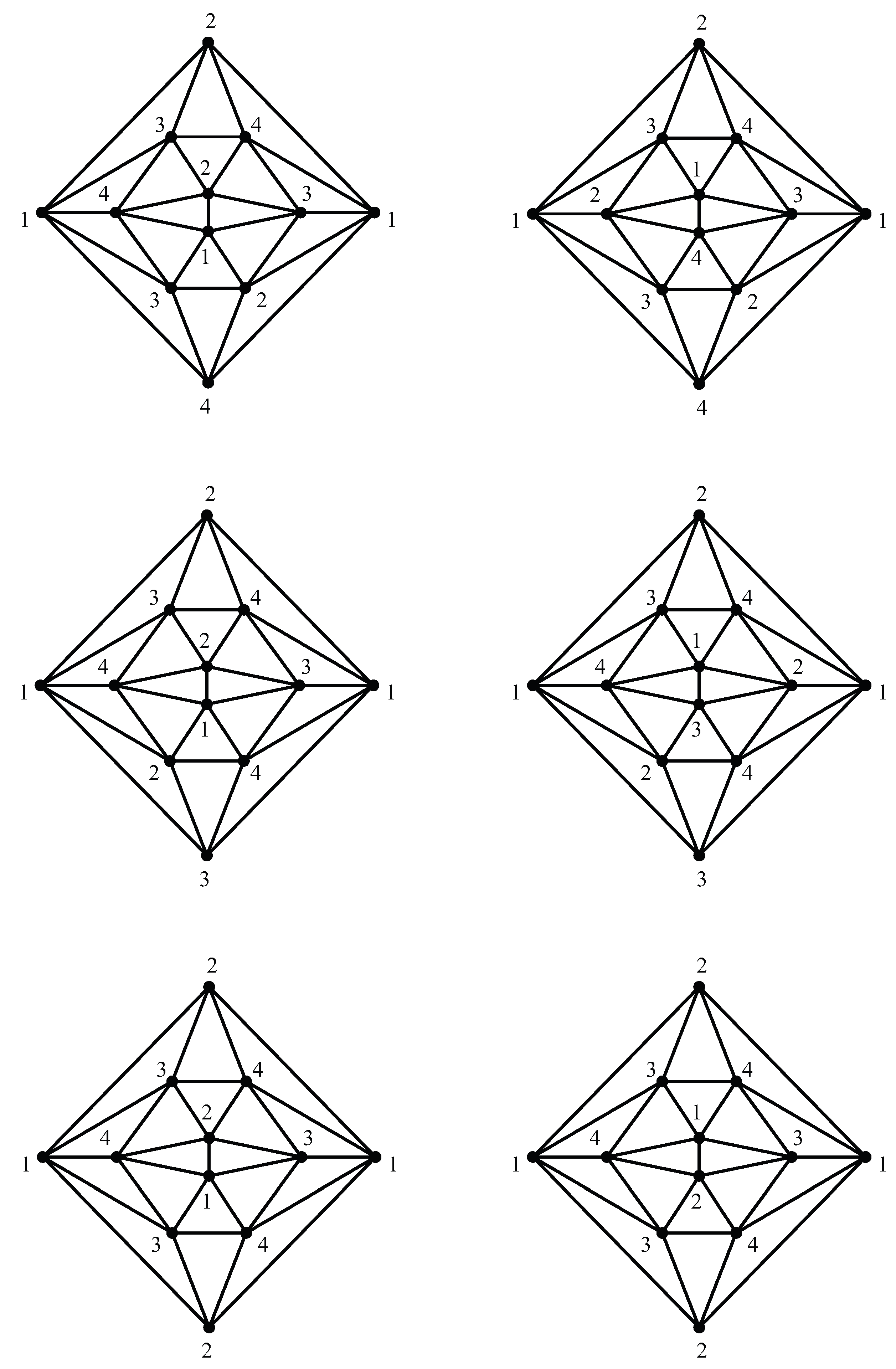
Four additional examples of Kempe-locked triangulations (once x and y are joined) are illustrated in Figure 4. It is not obvious by inspection that any of these triangulations is Kempe-locked. Using a computer program to determine all possible 4-colorings of each triangulation quickly establishes the Kempe-locking. Note that each of the four triangulations features a Birkhoff diamond subgraph with endpoints x and y. The graph in the lower right panel suggests that by including an arbitrary number of Birkhoff diamonds with endpoints x and y in an appropriate way in a triangulation that is Kempe-locked with respect to $xy$, we can obtain an infinite number of Kempe-locked triangulations. This surmise becomes evidently correct by applying the type of analysis discussed in Section 6 to a vertical stack of Birkhoff diamonds with appropriate intervening configurations. However, we should note that not all triangulations containing one or more Birkhoff diamonds with endpoints x and y are Kempe-locked—we shall have more to say on this point in the following Section 6.

6. Kempe-Locking Configurations

As is our established convention, we let $G_{xy}$ be the near-triangulation obtained by deleting the edge $xy$ in a triangulation T. Figure 5 depicts the general structure of such a $G_{xy}$. Every thick solid line represents one or more edges. Any oval, together with the thick solid lines that join it to endpoints x and y, represents a configuration, which, because all the configurations we are interested in include both x and y, we shall refer to as an $xy$-configuration. Figure 5 shows five such $xy$-configurations but there can be any (non-negative) number of them. The bottom boundary of each $xy$-configuration in the vertical stack always coincides with the top boundary of the next lower $xy$-configuration, if there is one. Because $xy$-configurations can be combined into a single larger $xy$-configuration or deconstructed into smaller $xy$-configurations, any given $G_{xy}$ can be represented in multiple ways as a vertical stack of $xy$-configurations. However, for a given purpose, there is often a choice that renders the desired analysis more straightforward. For example, because we have now observed the importance of the Birkhoff diamond, the near-triangulation shown in Figure 2 is best displayed in the form of Figure 5 with a single $xy$-configuration, a Birkhoff diamond: v is joined to that configuration by two edges, and likewise for u, and that configuration includes three edges emanating from each of x and y. The near-triangulation in the lower right of Figure 4 can be put into the general form of Figure 5 most usefully with three $xy$-configurations, two Birkhoff diamonds with an $xy$-configuration between them. The middle configuration has order 6—endpoint vertices x and y and four others, two on the top boundary, one adjacent to x, and one adjacent to y, and the same for the two on the bottom boundary, one adjacent to x and one adjacent to y.

This manner of representing $G_{xy}$ allows us to think somewhat differently about what it takes for T to be Kempe-locked with respect to the edge $xy$. The definition states that in every 4-coloring of $G_{xy}$ in which the colors of x and y are the same there must be three Kempe chains that include x and y. Without loss of generality, let the common color of x and y be 1 and the color of v be 2. Then the three required chains are colored 1–2, 1–3, and 1–4. We are interested in finding an equivalent condition that might be of greater utility in understanding what is necessary to create a Kempe-locked triangulation. We proceed by considering two cases:

• If the color of u is 2, then there cannot be either a 2–3 path or a 2–4 path between v and u because the first would have to intersect the 1–4 Kempe chain that includes both x and y and the second would have to intersect the 1–3 Kempe chain that includes both x and y, neither of which is possible.
• If the color of u is not 2, we can choose it to be 3 without loss of generality. There cannot be a 2–3 path between v and u because it cannot intersect the 1–4 Kempe chain that includes both x and y. Obviously there cannot be a 2–4 path between v and u when v is colored 2 and u is colored 3.

We have just shown that the existence of three Kempe chains including both x and y implies the non-existence of any 2-color paths between v and u using colors different from the common color of x and y. The converse is proved in [9], thus establishing the truth of the following Theorem 2.

Theorem 2.

Let T be a planar triangulation and $G_{xy}$ the near-triangulation derived from it by deleting the edge $xy$. Let $uxvy$ be the 4-cycle delineating the 4-face of $G_{xy}$. Then T is Kempe-locked with respect to the edge $xy$ if and only if, in every 4-coloring of $G_{xy}$ in which the colors of x and y are the same, there is no 2-color path between v and u that uses colors different from the common color of x and y.

Consider Figure 5 with x and y both colored 1 and v colored 2. If a 2–3 path between v and u were to exist, it would have to pass through every $xy$-configuration in the vertical stack on its way from v to u. Thus, there would have to exist a 4-coloring for each $xy$-configuration that transmits the 2–3 path from the configuration’s top boundary to its bottom boundary and such 4-colorings for the various $xy$-configurations would have to match along their coincident boundaries. Each $xy$-configuration would have to be able to take the 2–3 path presented to it as input at its top boundary and carry it through to the bottom boundary, that output then passed along as input to the next $xy$-configuration. Thus, there might exist certain $xy$-configurations for which this “passing along” cannot be assured or which make it impossible to “complete” the path at vertex u and achieve a proper coloring of $G_{xy}$. Such a configuration potentially enables a Kempe-locked triangulation. The Birkhoff diamond is one of these special configurations.

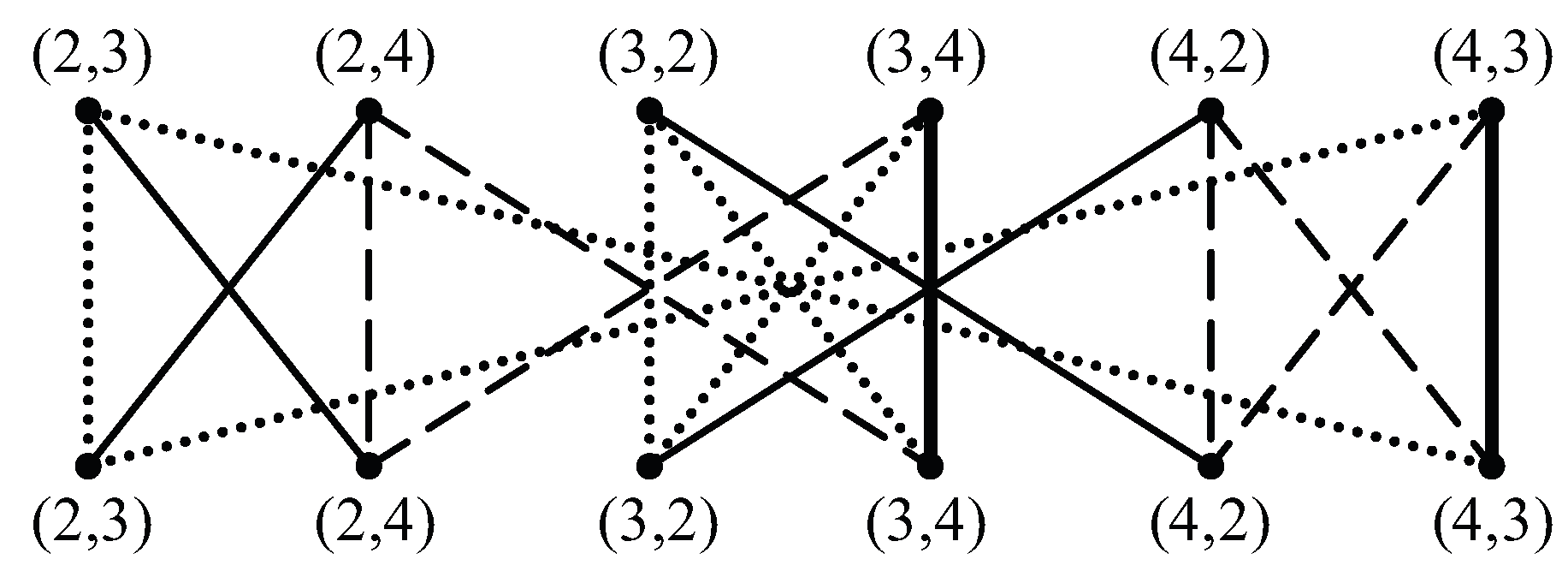
To understand how the Birkhoff diamond can prevent a 2-color path between v and u, we analyze all possible colorings of Figure 3 when x and y are both colored 1. Because the vertices a, b, c, and d are all adjacent to either x or y, they must take their colors from {2,3,4}. There are six possible pairings of colors for either $(a,b)$ or $(c,d)$: (2,3), (2,4), (3,2), (3,4), (4,2), and (4,3). The various proper colorings of the Birkhoff diamond subject to this constraint are not provided here—they are easily determined. Instead, we summarize the results in terms of the possible transitions from the colors of the $(a,b)$ pair along the top boundary of the Birkhoff diamond to the colors of the $(c,d)$ pair along the bottom boundary. We can represent the permitted transitions between $(a,b)$ and $(c,d)$ as a bipartite graph, a graph in which each vertex is assigned to one of two independent sets and the only edges in the graph thus occur between a vertex in one set and a vertex in the other. Figure 6 shows such a graph for the Birkhoff diamond with both x and y constrained to have color 1. The possibilities for $(a,b)$ appear as the top set of six vertices and the possibilities for $(c,d)$ appear as the bottom set of six vertices. An edge exists between a vertex in the top set and a vertex in the bottom set if and only if there exists a proper 4-coloring of the Birkhoff diamond for that pairing of top and bottom vertices. We have depicted the various edges in Figure 6 as thin or thick solid lines or as dotted or dashed lines. A thin solid line indicates the presence of both a 2–3 path and a 2–4 path between $(a,b)$ and $(c,d)$, a thick solid line indicates the absence of both a 2–3 path and a 2–4 path, a dotted line the presence of a 2–3 path only, and a dashed line the presence of a 2–4 path only.

We can use Figure 6 to provide a straightforward demonstration that the triangulation giving rise to the near-triangulation depicted in Figure 2 is Kempe-locked with respect to the edge $xy$. With x and y both colored 1 and v colored 2, the only possibilities for $(a,b)$ are (3,4) and (4,3). Consider the case (3,4). From Figure 6, we see that the only possibilities for $(c,d)$ are (2,4), (3,2), and (3,4). (This conclusion is confirmed by inspection of Figure 2.) There is only a 2–4 path between (3,4) and (2,4) and it cannot be completed because u must then take color 3 for a proper coloring. There is only a 2–3 path between (3,4) and (3,2) and it cannot be completed because u must then take color 4 for a proper coloring. Finally, there is neither a 2–3 nor a 2–4 path between (3,4) and (3,4). Thus, for the near-triangulation $G_{xy}$ in Figure 2, neither a 2–3 nor a 2–4 path between v and u can exist if $(a,b)$ is (3,4). Interchanging colors 3 and 4 throughout $G_{xy}$ leads to the same conclusion when $(a,b)$ is (4,3). The bipartite graph in Figure 6 explains the Birkhoff diamond’s ability to enable a Kempe-locked triangulation. With only minor modifications, this methodology can be used to show that each near-triangulation in Figure 4 derives from a Kempe-locked triangulation.

Appealing to the bipartite methodology may seem like overkill. Why not just use Figure 2 to prove that there is no 2–3 or 2–4 path between v and u? For such an uncomplicated situation, the bipartite analysis is indeed unnecessary, but it becomes highly useful in more complicated situations in which it is not feasible, either manually or with the aid of a computer, to list all possible distinct 4-colorings in which x and y are both colored 1. In such situations, representing a near-triangulation $G_{xy}$ as a stack of $xy$-configurations and then analyzing each configuration in the stack separately permits us to determine more easily whether a 2–3 or 2–4 path can be transmitted from v to u. Moreover, Figure 5, combined with the bipartite analysis, sheds light on how an $xy$-configuration can prevent the transmission or completion of a 2-color path, whereas simply analyzing a long list of all distinct colorings of a candidate near-triangulation does not.

In Section 5, we stated that not all triangulations that include a Birkhoff diamond subgraph with endpoints x and y are Kempe-locked. The bipartite methodology can be used to understand why this statement is true. From Figure 6, we see that all coloring states of the top edge $(a,b)$ other than (3,4) and (4,3) can transmit both 2–3 and 2-4 paths through the diamond to its bottom edge $(c,d)$. Thus, many near-triangulations $G_{xy}$ having a Birkhoff diamond subgraph with endpoints x and y will not be Kempe-locked. The mere presence of a Birkhoff diamond is not sufficient—if there is any chance for the triangulation T of which the Birkhoff diamond is a subgraph to be Kempe-locked, the Birkhoff diamond has to appear in just the right way relative to the other $xy$-configurations in the vertical stack. As an example of this, take the graph in the lower right panel of Figure 4 and eliminate the middle $xy$-configuration entirely; squeeze the two Birkhoff diamonds together so that the bottom boundary of the upper diamond coincides with the top boundary of the lower diamond, then apply Figure 6 twice to verify that the triangulation with x and y joined is not Kempe-locked with respect to $xy$.

The foregoing discussion motivates the following definitions of Kempe-locking configurations and fundamental Kempe-locking configurations, those particular $xy$-configurations that enable a triangulation T to be Kempe-locked with respect to an edge $xy$.

Definition 1.

Let T be a planar triangulation that is at least 4-connected and $G_{xy}$ the near-triangulation derived from it by deleting the edge $xy$. Let $uxvy$ be the 4-cycle delineating the 4-face of $G_{xy}$. If T is Kempe-locked with respect to the edge $xy$, then the $xy$-configuration $K_{xy}$ induced by all vertices of $G_{xy}$ other than u and v is the Kempe-locking configuration for T.

Definition 2.

Let $K_{xy}$ be the Kempe-locking configuration for a planar triangulation T (that is at least 4-connected) with an edge $xy$. Then $K_{xy}$ is said to be a fundamental Kempe-locking configuration if it contains no proper subgraph $K_{xy}^{\prime }$ that is the Kempe-locking configuration for some planar triangulation $T^{\prime }$ (that is at least 4-connected) with an edge $xy$.

On the basis of these definitions, we see readily that none of the Kempe-locking configurations for the graphs in Figure 4 is fundamental, since, in each case, the Kempe-locking configuration is obtained by deleting vertices v and u and their incident edges. We note that each such Kempe-locking configuration has a Birkhoff diamond with endpoints x and y as a proper subgraph and the Birkhoff diamond is the Kempe-locking configuration for the triangulation obtained by joining x and y in the near-triangulation shown in Figure 2. We will see in Section 7 that the Birkhoff diamond is actually a fundamental Kempe-locking configuration.

7. The Search for Fundamental Kempe-Locking Configurations

The approach we adopted in searching for fundamental Kempe-locking configurations is analogous to that of experimental physicists in their search for a new elementary particle with specified properties. Physicists confine their explorations to collision events involving total energy in an interval sufficient to bring the sought-after particle into being. Similarly, we explored planar triangulations of orders in which fundamental Kempe-locking configurations would be expected to be found. The best chance to discover those configurations would seem to occur when there is a small number of distinct 4-colorings of a near-triangulation $G_{xy}$ with x and y the same color, thus admitting the possibility that every one of those few colorings will feature three Kempe chains that include both x and y. Equivalently (by means of Theorem 2), we note that in a $G_{xy}$ of large order with x and y colored the same there are sufficiently many possibilities for 2-color paths from v to u using colors different from the common color of x and y to render it a virtual certainty that at least one such 2-color path will form part of a proper coloring of $G_{xy}$. Quite simply, the combinatorial possibilities for coloring a high-order planar triangulation militate against the existence of a high-order fundamental Kempe-locking configuration.

To assure that we did not miss any low-order triangulations, we generated the full set of 8044 isomorphism classes for 4-connected triangulations of orders 6–15 and the full set of 9733 isomorphism classes for 5-connected triangulations of orders 12–24 (see [10,11]). Because Kempe-locking is associated with an edge of a triangulation, we tested every edge separately in a triangulation from each of the isomorphism classes. Referring to the edge being tested as $xy$, we deleted the edge and then determined whether there are any 4-colorings with x and y colored the same but with fewer than three Kempe chains that include both x and y. It turns out to be rare for this not to be the case. The only Kempe-locked triangulations we encountered were 4-connected; there were none at all among 5-connected triangulations (and hence none at all among internally 6-connected triangulations). There are no Kempe-locked triangulations of order less than 12 and a single 4-connected Kempe-locked triangulation of order 12, the one illustrated in Figure 2 with the leftmost and rightmost vertices on the 4-face joined. Thus, the Birkhoff diamond is a fundamental Kempe-locking configuration. There are no Kempe-locked triangulations of order 13, and one 4-connected Kempe-locked triangulation for each of orders 14 and 15, each of those featuring a Birkhoff diamond with endpoints x and y and each Kempe-locked with respect to only a single edge.

In an expanded search for fundamental Kempe-locking configurations, we examined 4-connected triangulations of orders 16–20. Because the number of isomorphism classes grows rapidly with increasing order (from 30,926 at order 16 to 24,649,284 at order 20—refer to [11]) and because the number of edges in a triangulation increases with increasing order (a planar triangulation of order n has $3n-6$ edges—see [1]), we soon ran into computation-time limitations imposed by our laptop computer. After deciding to limit aggregate computer execution time to several weeks instead of several months, we proceeded in the expanded search by examining all 30,926 isomorphism classes of order 16 and all 158,428 isomorphism classes of order 17, but only 100,000 randomly generated non-isomorphic triangulations for each order from 18 through 20.

For orders 16 and 17, we discovered 8 and 14 non-isomorphic triangulations, respectively, that are Kempe-locked, all with respect to a single edge, call it $xy$ in each case. Each of those 4-connected Kempe-locked triangulations features a Birkhoff diamond with x and y as endpoints. Figure 4 shows the $G_{xy}$ derived from two such Kempe-locked triangulations. In the random samples of 100,000 triangulations each for orders 18–20, we discovered additional non-isomorphic Kempe-locked triangulations: 10 of order 18, 8 of order 19, and 5 of order 20, all locked with respect to a single edge $xy$ and all featuring a Birkhoff diamond configuration with x and y as endpoints. Figure 4 also shows near-triangulations $G_{xy}$ arising from Kempe-locked triangulations of orders 19 and 20. It is an open question whether there are any triangulations that are at least 4-connected and Kempe-locked with respect to more than a single edge.

Let us take stock of the results of our search for fundamental Kempe-locking configurations. We found no 5-connected (and hence no internally 6-connected) Kempe-locked triangulations of orders 12–24. The only fundamental Kempe-locking configuration we found is the Birkhoff diamond of order 10. We have shown that there are no fundamental Kempe-locking configurations of orders 9 or lower or between 11 and 15, inclusive, and a sample of 100,000 non-isomorphic 4-connected triangulations each for orders 18–20 turned up no fundamental Kempe-locking configurations of orders 16–18. We conclude that the “experimental” case is strong that the Birkhoff diamond is the only fundamental Kempe-locking configuration.

Conjecture 2.

The Birkhoff diamond is the sole fundamental Kempe-locking configuration.

Conjecture 2 implies Conjecture 1. To see this, refer to the vertex labeling for the Birkhoff diamond given in Figure 3. We observe that a triangulation T that is Kempe-locked with respect to an edge $xy$ by means of a Birkhoff diamond subgraph with endpoints x and y is at most 4-connected because both $xaby$ and $xcdy$ are separating 4-cycles. Hence, all triangulations we discovered that exhibit Property 2 (Kempe-locking) are 4-connected and cannot satisfy Property 1 (internal 6-connectivity). Moreover, our computer search through low-order isomorphism classes of 5-connected triangulations found no Kempe-locked triangulations. Hence, every triangulation that satisfied Property 1 (internally 6-connected triangulations are a subset of all 5-connected triangulations—refer to the discussion in the first paragraph of Section 3) did not satisfy Property 2. To sum up, the “experimental” results presented and discussed in this article (strongly) suggest that Property 1 and Property 2 are incompatible.

Furthermore, if Conjecture 2 is true, then a minimum counterexample simply cannot be constructed because the vertices x and y serving as endpoints for any edge $xy$ that is Kempe-locked must have degree at least 6. Because the signature feature of a Birkhoff diamond is its four central vertices of degree 5, none of the five edges involving pairs of those four central vertices can be Kempe-locked and, by Theorem 1, a counterexample cannot exist. Conjecture 2 alone has sufficient power to imply 4-colorability of planar graphs.

8. An Even More Fundamental Graph

Based on the arguments and analysis presented in this article, it is highly likely that the Birkhoff diamond serves an essential role in creating a Kempe-locked triangulation. Thus, it is illuminating to consider an even more fundamental graph from which the Birkhoff diamond naturally arises. Key to the notion of Kempe-locking with respect to a deleted edge $xy$ is that the vertices x and y have the same color and that they cannot be made to differ in color through any sequence of Kempe exchanges. Consequently, we need to analyze all possible 4-colorings of Figure 3 in which x and y have the same color. That set consists of the six distinct 4-colorings shown in Figure 2 as restricted to the Birkhoff diamond subgraph. In turn, we note that that particular set of six distinct 4-colorings is identical to the set of all possible 4-colorings of the triangulation of order 9 formed by coalescing x and y into a single vertex of degree 6. That triangulation can be drawn as depicted in Figure 7—a triangle enclosing a pentagon enclosing a single vertex. It is quite satisfying to think that such an elegant graph might lie at the heart of why a minimum counterexample to the 4-color theorem does not exist, at the heart of why all planar triangulations must be 4-colorable.

9. Conclusions and Future Directions

We have introduced the key notion of Kempe-locking and have used it to establish the coloring property that a minimum counterexample to the 4-color theorem must satisfy with respect to each of its edges. After an exhaustive search through low-order isomorphism classes of 4-connected and 5-connected triangulations, we found no 5-connected triangulations that are Kempe-locked. The only Kempe-locked triangulations we found are Kempe-locked with respect to only a single edge, far from what is necessary for a minimum counterexample. Moreover, each discovered Kempe-locked triangulation, Kempe-locked with respect to an edge $xy$, features a Birkhoff diamond with endpoints x and y. The mere presence of a Birkhoff diamond subgraph renders the triangulation at most 4-connected. These results strongly suggest that the connectivity and coloring properties of a minimum counterexample are incompatible. They also point to the likely singular role that the Birkhoff diamond and its progenitor, the single-vertex-within-a-pentagon-within-a-triangle graph, play in the matter of the 4-colorability of planar graphs.

What future directions does this work indicate? First, since the matter of graph coloring has applications to various problems in graph theory, the notion of Kempe-locking may find practical application beyond its theoretical use in this article. Second, with respect to further experimental studies, it would be helpful if researchers with substantially more powerful computing resources than a laptop computer could complete the search for Kempe-locked configurations among the isomorphism classes for 4-connected triangulations of orders 18, 19, and 20, and perhaps for even higher orders. Such extensions of the study reported here would either solidify support for or refute Conjecture 2. Because Conjecture 2 implies Conjecture 1 and lends itself to an appealing explanation for why a planar graph must be 4-colorable, it is the conjecture on which to focus. Even better than further experimental studies would be a direct proof of Conjecture 2, but that may well be a more difficult task than was proving the 4-color theorem.