Recurrent Neural Network-Based Model Predictive Control for Continuous Pharmaceutical Manufacturing
Abstract
1. Introduction
2. Plant Model and Control Scenarios
2.1. Plant Model
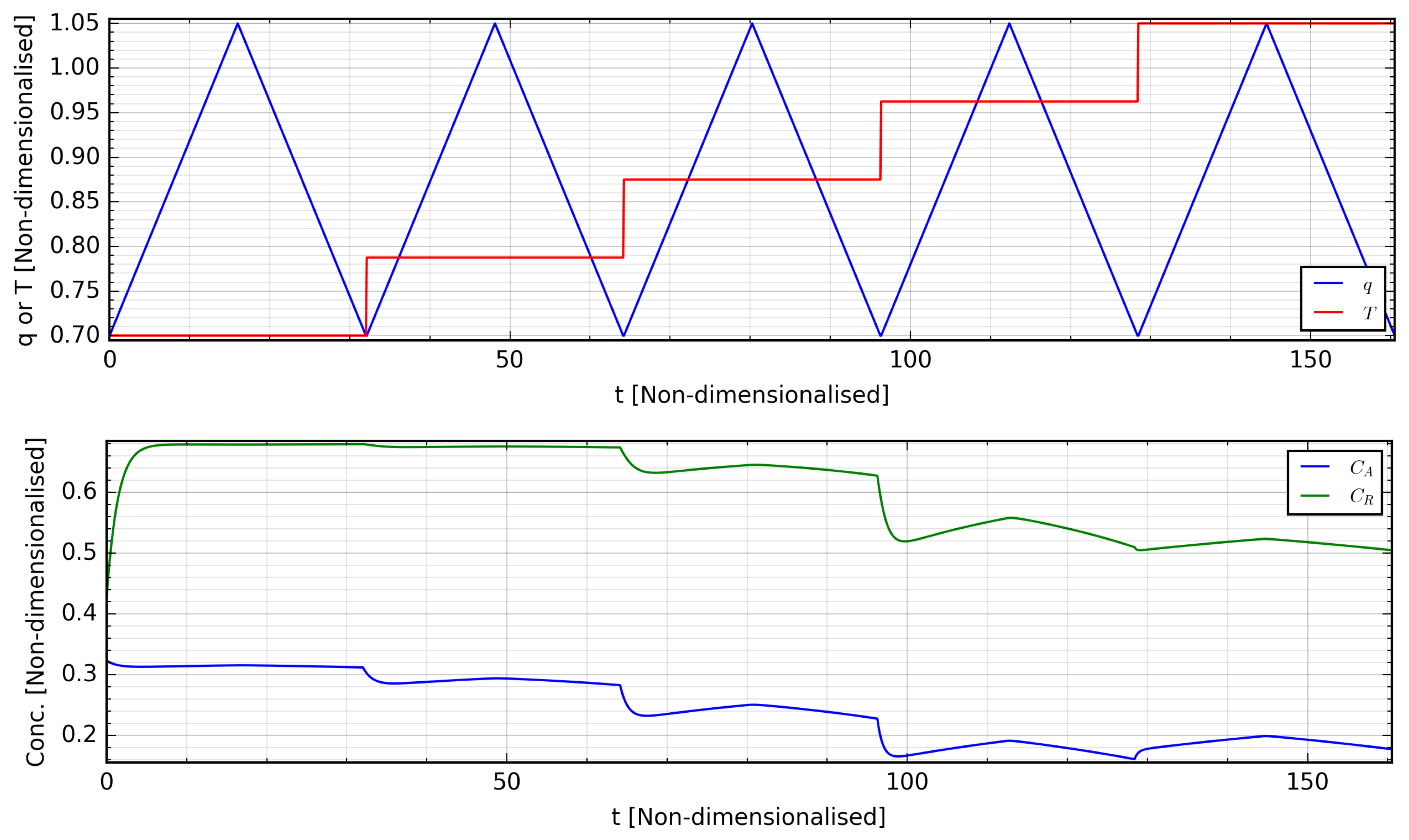
2.2. Closed-Loop Control Scenarios
3. Methodology
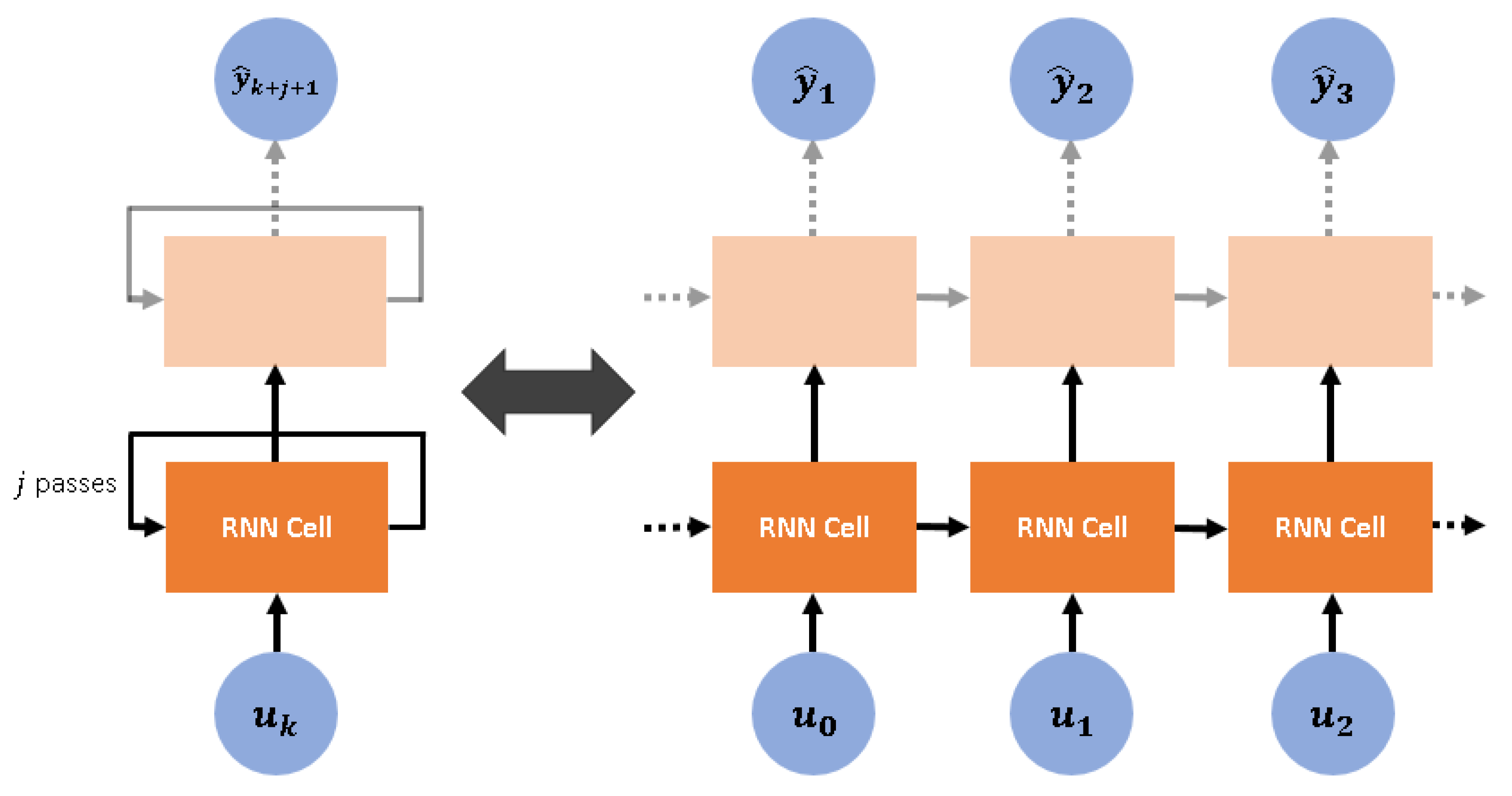
3.1. Non-Linear Time-Series System Identification via Recurrent Neural Networks
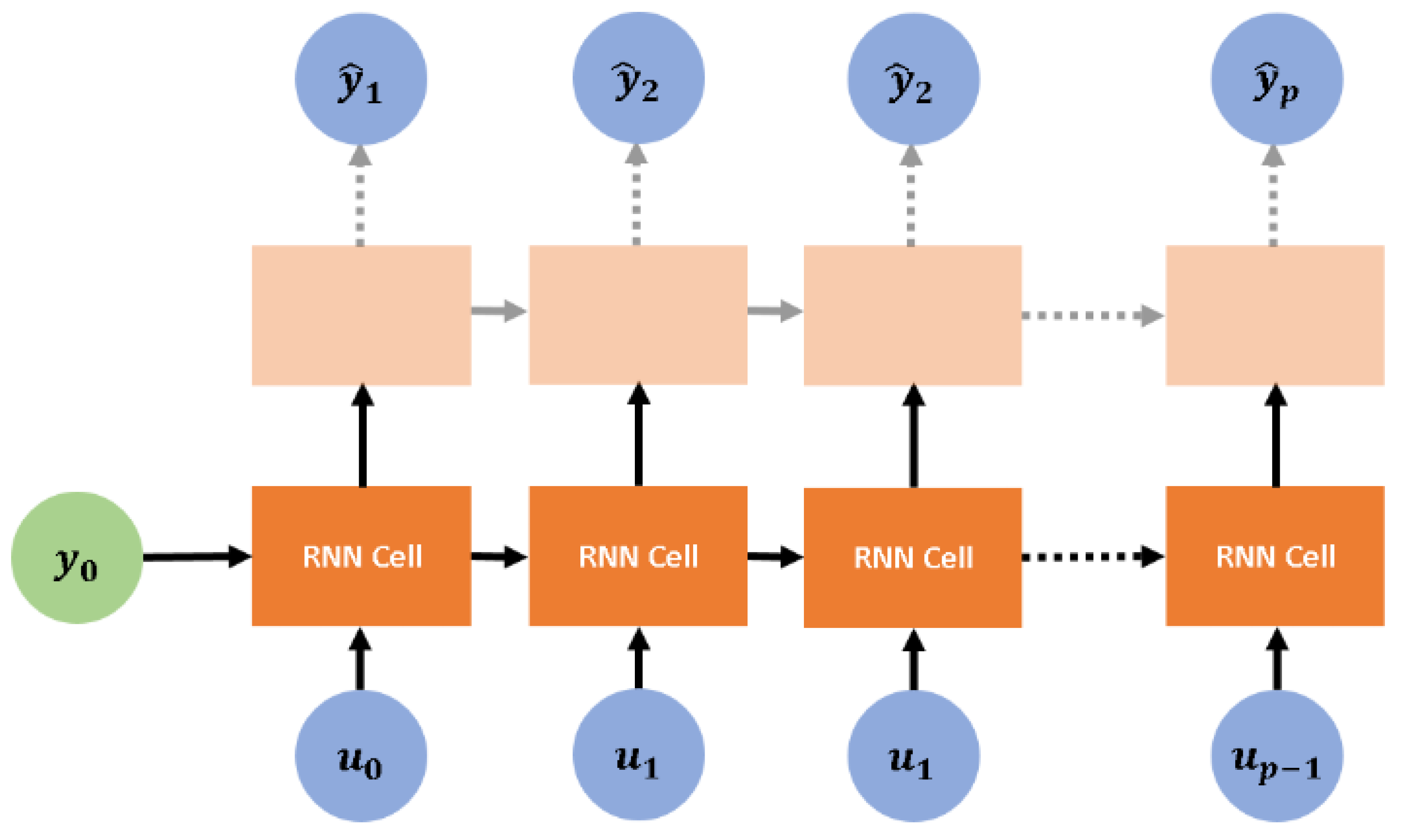
3.2. Control Problem Formulation
4. Results and Discussion
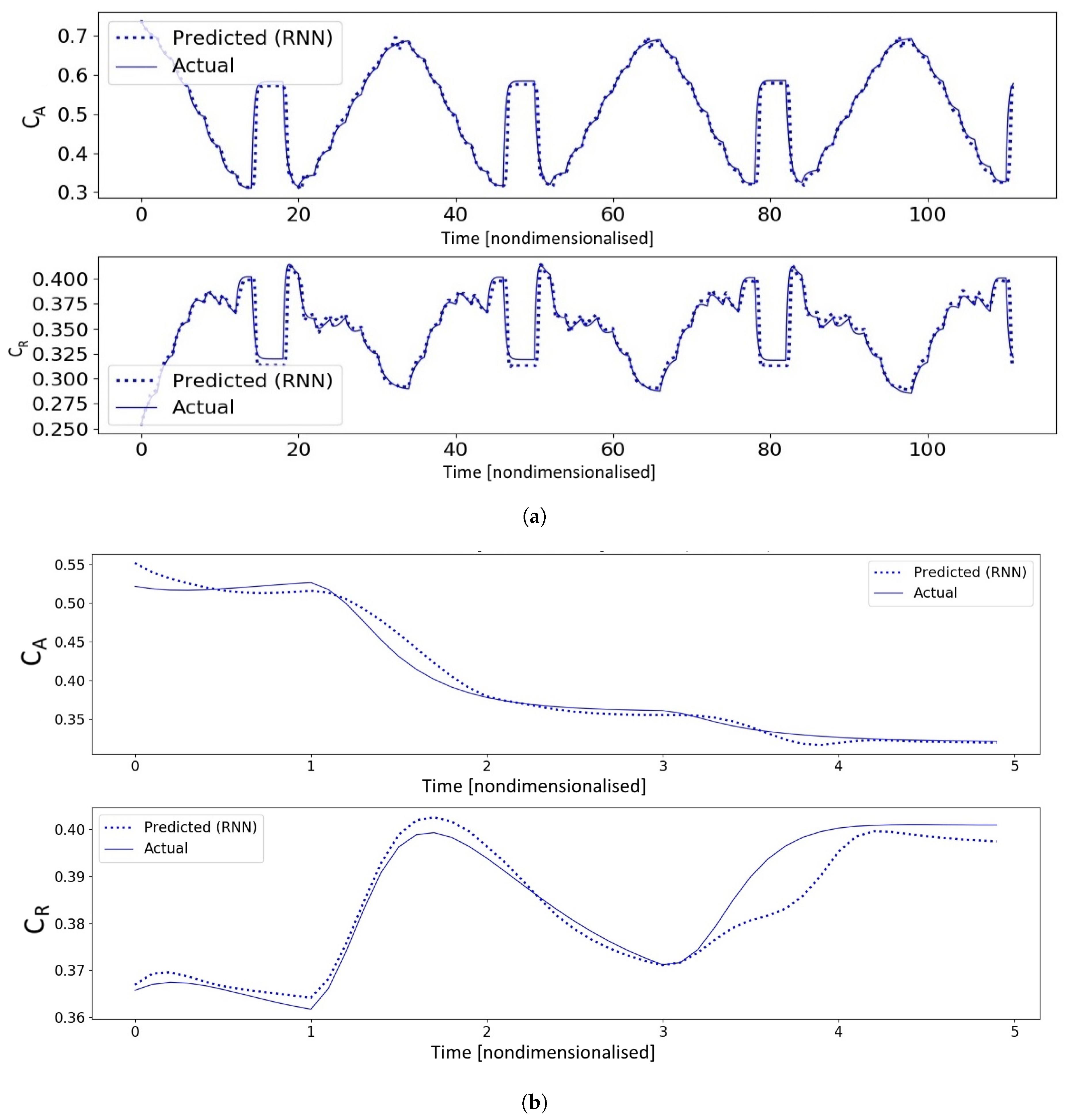
4.1. System Identification
4.2. RNN-MPC Closed-Loop Control Performance
5. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Adam | Adaptive Moment Estimation |
| ANN | Artificial Neural Network |
| API | Active Pharmaceutical Ingredient |
| BPTT | Back-Propagation Through Time |
| CPP | Critical Process Parameter |
| CQA | Critical Quality Attribute |
| CSTR | Continuous-Stirred Tank Reactor |
| FBU | Feeding Blending Unit |
| LSTM | Long Short-Term Memory |
| MPC | Model Predictive Control |
| MV | Manipulated Vector |
| NLP | Non-Linear Programming |
| NMPC | Non-Linear MPC |
| PID | Proportional-Integral-Derivative (Control) |
| QbD | Quality by Design |
| QDMC | Quadratic Dynamic Matrix Control |
| RMSE | Root-Mean-Square Error |
| RNN | Recurrent Neural Network |
| RNN-MPC | RNN-based MPC |
| SLSQP | Sequential Least Squares Quadratic Programming |
Appendix A. Kinetic Parameters for Plant Model
Appendix B. Long Short-Term Memory Cells
References
- Lakerveld, R.; Benyahia, B.; Heider, P.L.; Zhang, H.; Wolfe, A.; Testa, C.J.; Ogden, S.; Hersey, D.R.; Mascia, S.; Evans, J.M.; et al. The application of an automated control strategy for an integrated continuous pharmaceutical pilot plant. Org. Process Res. Dev. 2015, 19, 1088–1100. [Google Scholar] [CrossRef]
- Schaber, S.D.; Gerogiorgis, D.I.; Ramachandran, R.; Evans, J.M.B.; Barton, P.I.; Trout, B.L. Economic analysis of integrated continuous and batch pharmaceutical manufacturing: A case study. Ind. Eng. Chem. Res. 2011, 50, 10083–10092. [Google Scholar] [CrossRef]
- Glasnov, T. Continuous-Flow Chemistry in the Research Laboratory: Modern Organic Chemistry in Dedicated Reactors at the Dawn of the 21st Century; Springer International Publishing: Basel, Switzerland, 2016; p. 119. [Google Scholar]
- Gutmann, B.; Cantillo, D.; Kappe, C.O. Continuous-flow technology—A tool for the safe manufacturing of active pharmaceutical ingredients. Angew. Chem. Int. Ed. 2015, 54, 6688–6728. [Google Scholar] [CrossRef] [PubMed]
- Poechlauer, P.; Colberg, J.; Fisher, E.; Jansen, M.; Johnson, M.D.; Koenig, S.G.; Lawler, M.; Laporte, T.; Manley, J.; Martin, B.; et al. Pharmaceutical roundtable study demonstrates the value of continuous manufacturing in the design of greener processes. Org. Process Res. Dev. 2013, 17, 1472–1478. [Google Scholar] [CrossRef]
- Benyahia, B.; Lakerveld, R.; Barton, P.I. A plant-wide dynamic model of a continuous pharmaceutical process. Ind. Eng. Chem. Res. 2012, 51, 15393–15412. [Google Scholar] [CrossRef]
- Susanne, F.; Martin, B.; Aubry, M.; Sedelmeier, J.; Lima, F.; Sevinc, S.; Piccioni, L.; Haber, J.; Schenkel, B.; Venturoni, F. Match-making reactors to chemistry: A continuous manufacturing-enabled sequence to a key benzoxazole pharmaceutical intermediate. Org. Process Res. Dev. 2017, 21, 1779–1793. [Google Scholar] [CrossRef]
- Mascia, S.; Heider, P.L.; Zhang, H.; Lakerveld, R.; Benyahia, B.; Barton, P.I.; Braatz, R.D.; Cooney, C.L.; Evans, J.M.B.; Jamison, T.F.; et al. End-to-end continuous manufacturing of pharmaceuticals: Integrated synthesis, purification, and final dosage formation. Angew. Chem. Int. Ed. 2013, 52, 12359–12363. [Google Scholar] [CrossRef] [PubMed]
- Brueggemeier, S.B.; Reiff, E.A.; Lyngberg, O.K.; Hobson, L.A.; Tabora, J.E. Modeling-based approach towards quality by design for the ibipinabant API step modeling-based approach towards quality by design for the ibipinabant API step. Org. Process Res. Dev. 2012, 16, 567–576. [Google Scholar] [CrossRef]
- Mesbah, A.; Paulson, J.A.; Lakerveld, R.; Braatz, R.D. Model predictive control of an integrated continuous pharmaceutical manufacturing pilot plant. Org. Process Res. Dev. 2017, 21, 844–854. [Google Scholar] [CrossRef]
- Rasoulian, S.; Ricardez-Sandoval, L.A. Stochastic nonlinear model predictive control applied to a thin film deposition process under uncertainty. Chem. Eng. Sci. 2016, 140, 90–103. [Google Scholar] [CrossRef]
- Rasoulian, S.; Ricardez-Sandoval, L.A. A robust nonlinear model predictive controller for a multiscale thin film deposition process. Chem. Eng. Sci. 2015, 136, 38–49. [Google Scholar] [CrossRef]
- Hussain, M.A. Review of the applications of neural networks in chemical process control simulation and online implementation. Artif. Intell. Eng. 1999, 13, 55–68. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, W.; Hou, Z.G.; Yu, J.; Tan, M. Neural-network-based nonlinear model predictive control for piezoelectric actuators. IEEE Trans. Ind. Electron. 2015, 62, 7717–7727. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, J. A batch-to-batch iterative optimal control strategy based on recurrent neural network models. J. Process Control 2005, 15, 11–21. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, J.; Morris, J. Modeling and optimal control of a batch polymerization reactor using a hybrid stacked recurrent neural network model. Ind. Eng. Chem. Res. 2001, 40, 4525–4535. [Google Scholar] [CrossRef]
- Mujtaba, I.; Hussain, M. Applications of Neural Networks and Other Learning Technologies in Process Engineering; Imperial College Press: London, UK, 2001. [Google Scholar]
- Nagy, Z.K. Model based control of a yeast fermentation bioreactor using optimally designed artificial neural networks. Chem. Eng. J. 2007, 127, 95–109. [Google Scholar] [CrossRef]
- Alanqar, A.; Durand, H.; Christofides, P.D. On identification of well-conditioned nonlinear systems: Application to economic model predictive control of nonlinear processes. AIChE J. 2015, 61, 3353–3373. [Google Scholar] [CrossRef]
- Wang, X.; El-Farra, N.H.; Palazoglu, A. Proactive Reconfiguration of Heat-Exchanger Supernetworks. Ind. Eng. Chem. Res. 2015, 54, 9178–9190. [Google Scholar] [CrossRef]
- Byeon, W.; Breuel, T.M.; Raue, F.; Liwicki, M. Scene labeling with LSTM recurrent neural networks. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3547–3555. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gülçehre, Ç.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv, 2014; arXiv:1406.1078. [Google Scholar]
- Lee, J.H.; Shin, J.; Realff, M.J. Machine learning: Overview of the recent progresses and implications for the process systems engineering field. Comput. Chem. Eng. 2018, 114, 111–121. [Google Scholar] [CrossRef]
- Rehrl, J.; Kruisz, J.; Sacher, S.; Khinast, J.; Horn, M. Optimized continuous pharmaceutical manufacturing via model-predictive control. Int. J. Pharm. 2016, 510, 100–115. [Google Scholar] [CrossRef] [PubMed]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill: Madison, WI, USA, 2009. [Google Scholar]
- Tatjewski, P. Advanced Control of Industrial Processes, Structures and Algorithms; Springer: London, UK, 2007. [Google Scholar]
- Garcia, C.E.; Morshedi, A. Quadratic programming solution of dynamic matrix control (QDMC). Chem. Eng. Commun. 1986, 46, 73–87. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, J. Model predictive control of unknown nonlinear dynamical systems based on recurrent neural networks. IEEE Trans. Ind. Electron. 2012, 59, 3089–3101. [Google Scholar] [CrossRef]
- Seyab, R.A. Differential recurrent neural network based predictive control. Comput. Chem. Eng. 2008, 32, 1533–1545. [Google Scholar] [CrossRef]
- Koppel, L.B. Input multiplicities in nonlinear, multivariable control systems. AIChE J. 1982, 28, 935–945. [Google Scholar] [CrossRef]
- Seki, H.; Ooyama, S.; Ogawa, M. Nonlinear model predictive control using successive linearization—Application to chemical reactors. Trans. Soc. Instrum. Control Eng. 2004, E-3, 66–72. [Google Scholar]
- Bequette, B.W. Non-linear model predictive control : A personal retrospective. Can. J. Chem. Eng. 2007, 85, 408–415. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Pascanu, R.; Gulcehre, C.; Cho, K.; Bengio, Y. How to construct deep recurrent neural networks. arXiv, 2013; arXiv:1312.6026. [Google Scholar]
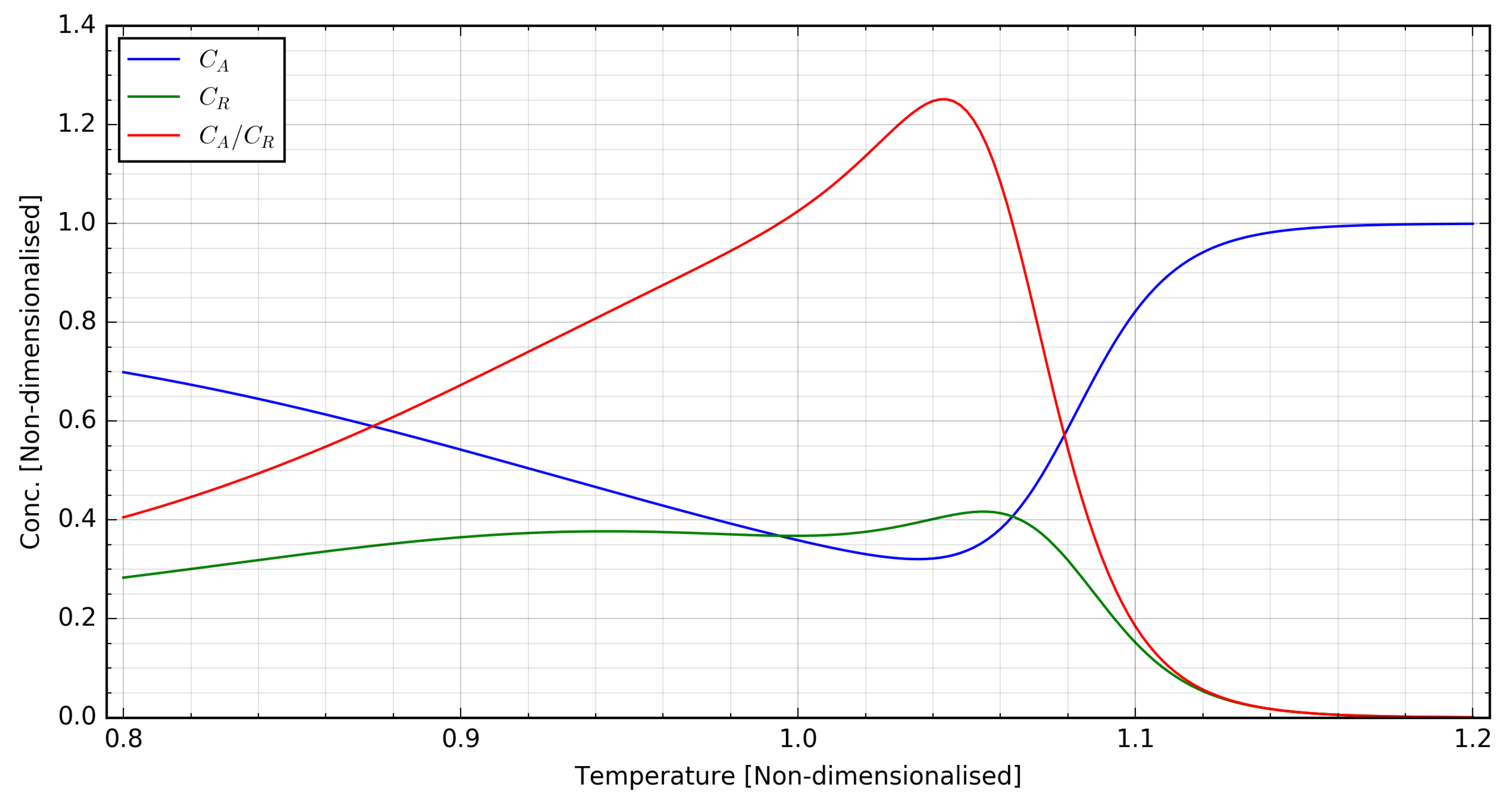
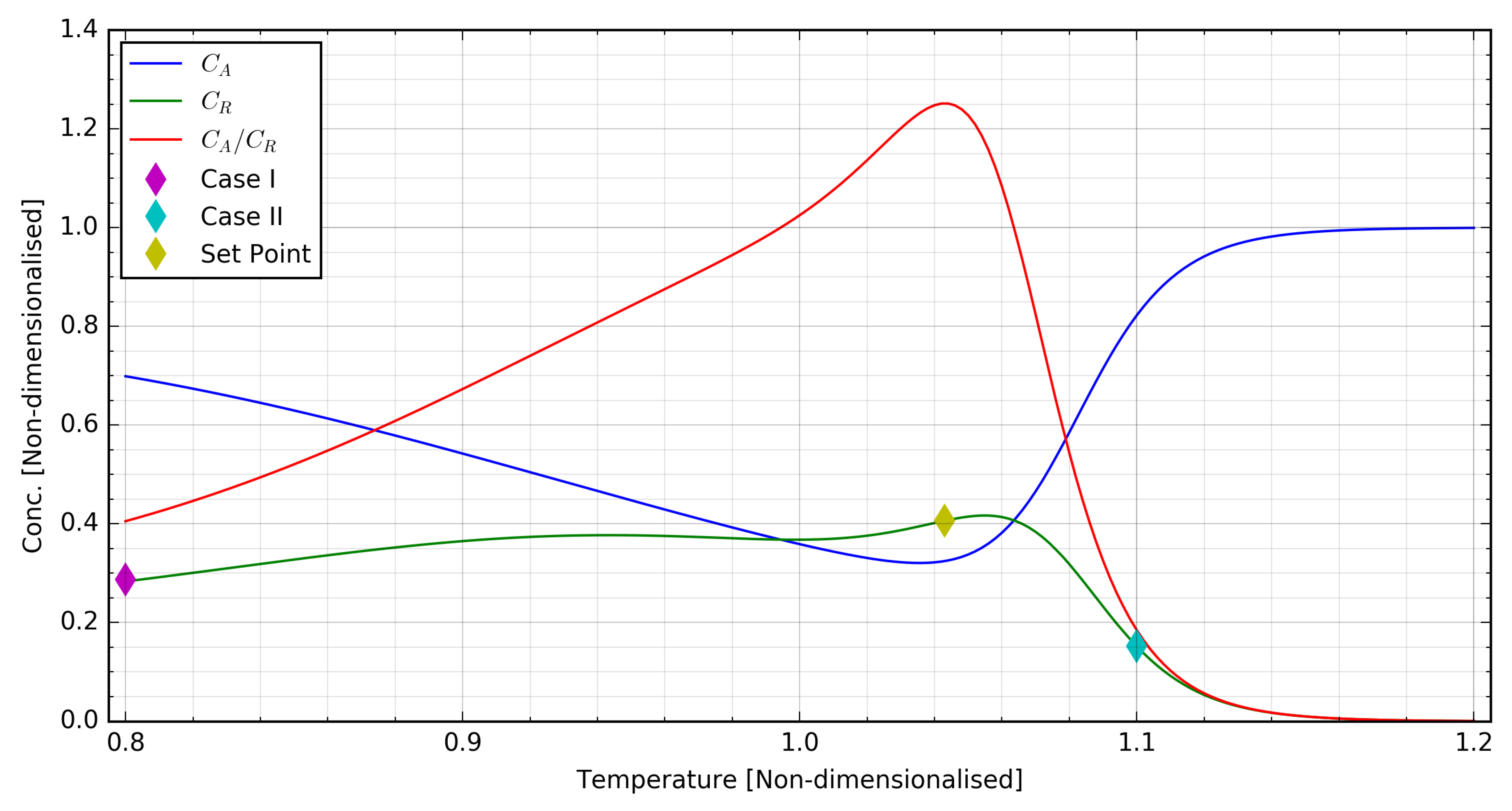
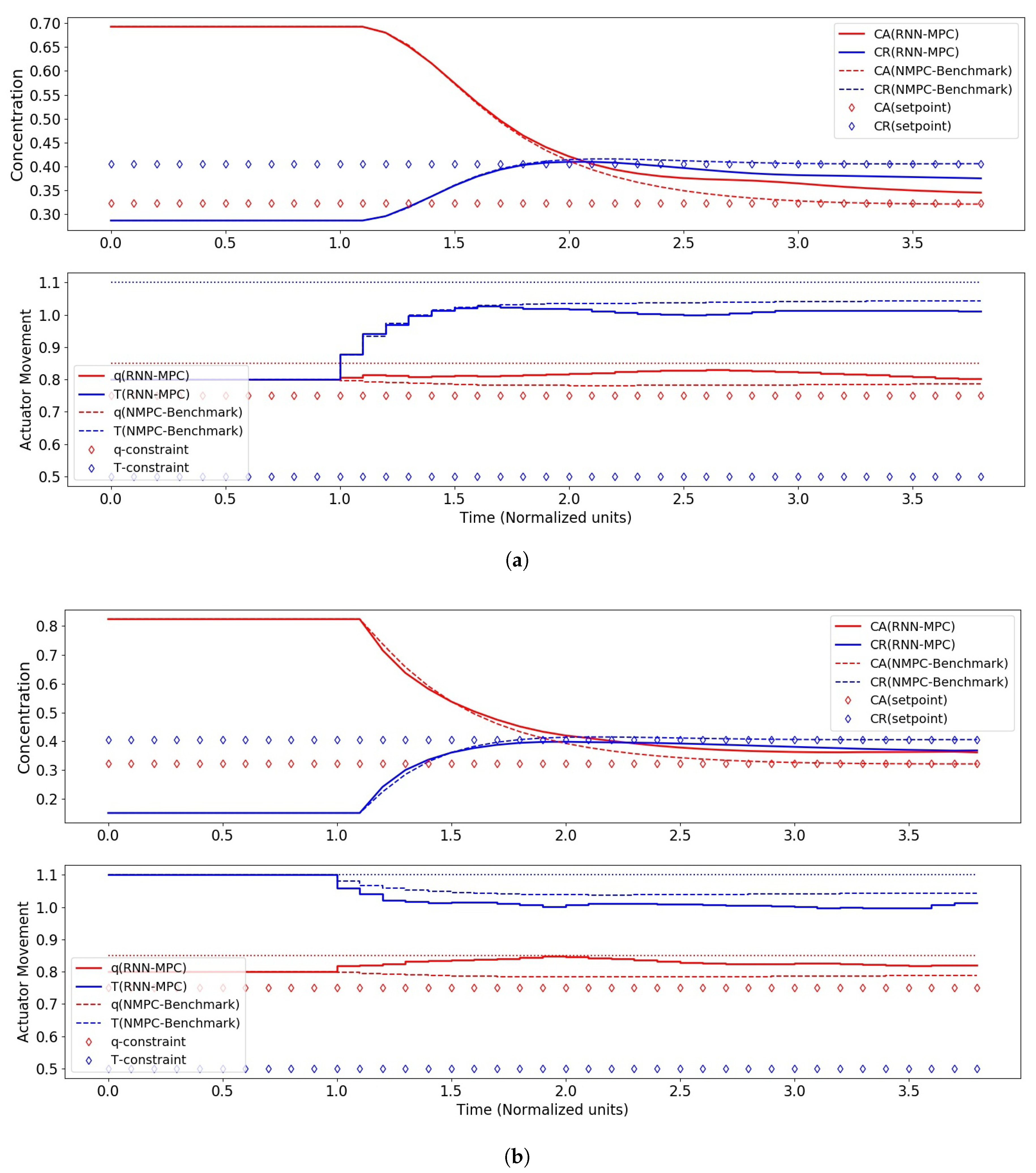
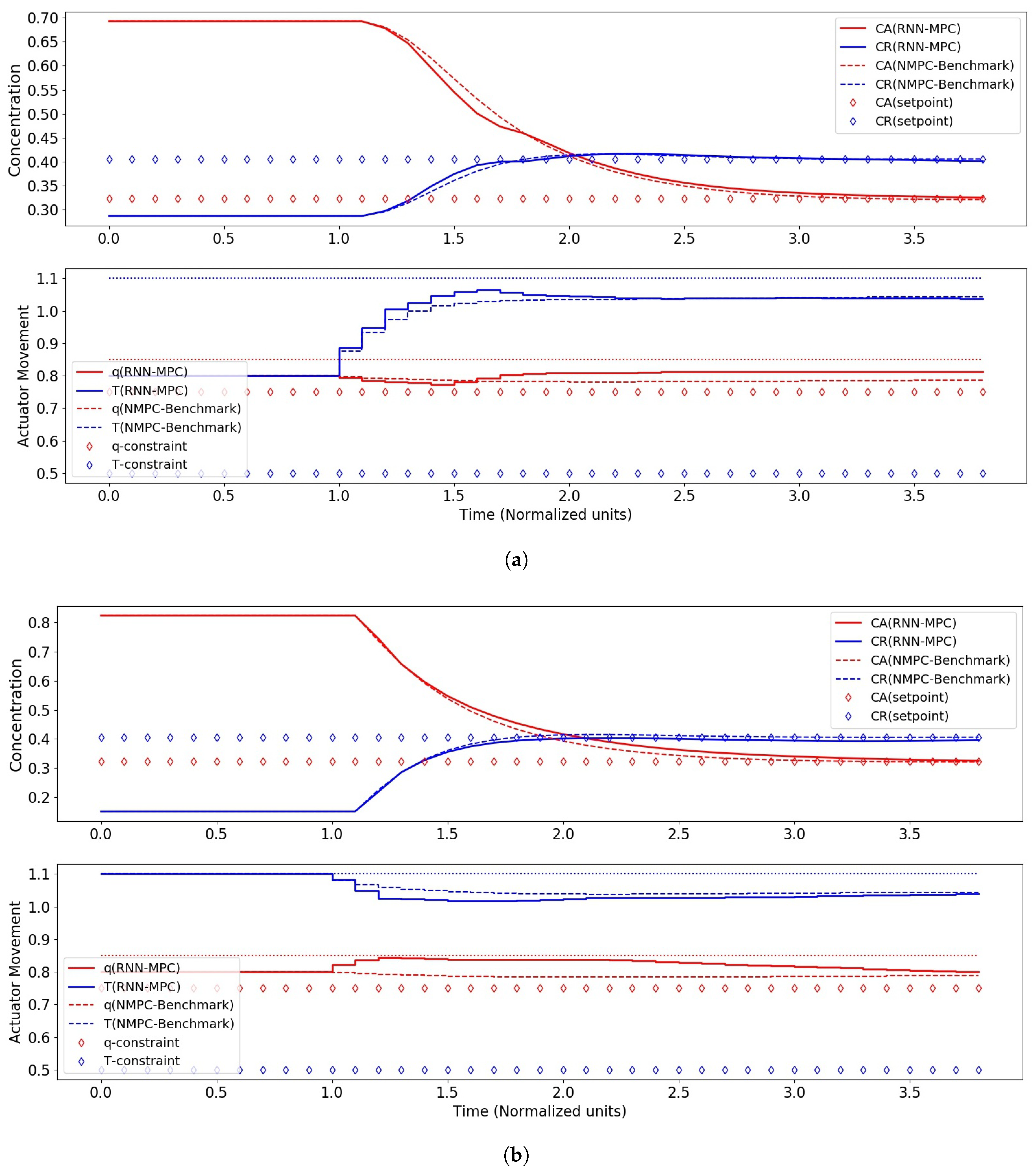
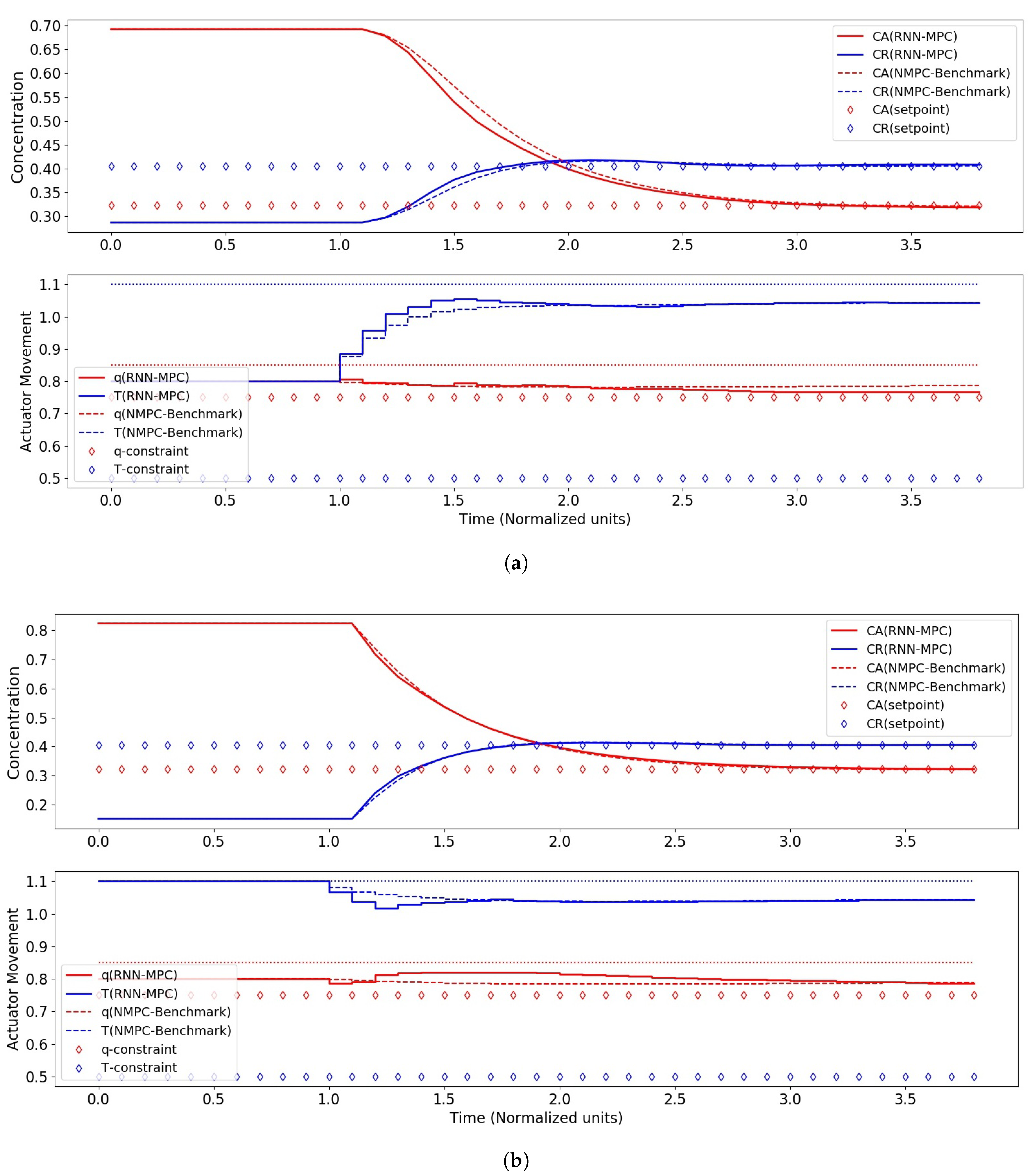
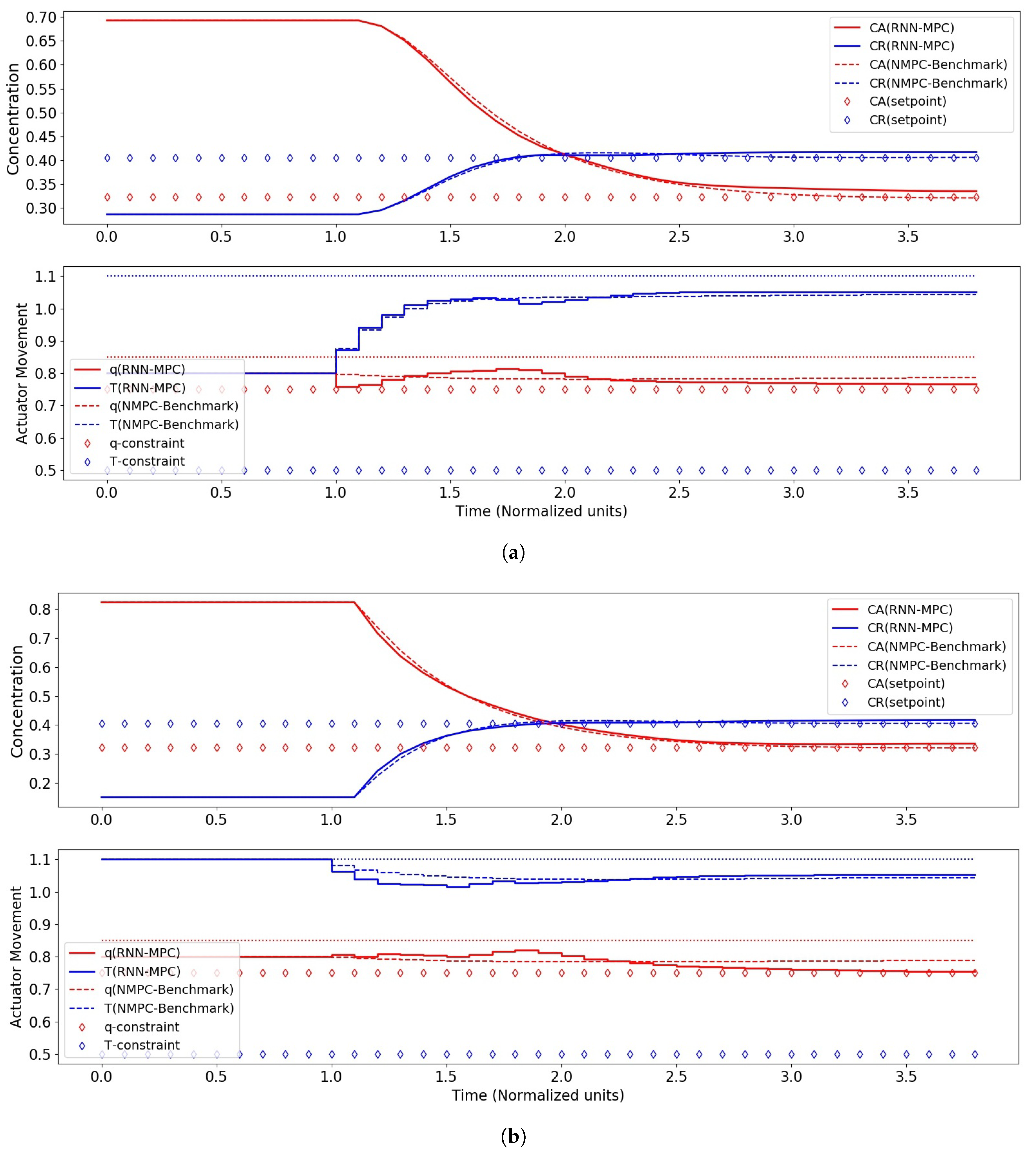
| Control Scenario | q | T | ||
|---|---|---|---|---|
| I: Start-up | 0.692 | 0.287 | 0.800 | 0.800 |
| II: Upset-recovery | 0.822 | 0.152 | 0.800 | 1.100 |
| Set-point (maximum ) | 0.324 | 0.406 | 0.800 | 1.043 |
| No. Layers / No. Nodes | 250 | 500 | 1000 |
|---|---|---|---|
| 1 | 0.0299 | 0.0268 | 0.0206 |
| 2 | 0.0238 | 0.0118 | 0.0083 |
| 3 | 0.0262 | 0.0119 | 0.0125 |
| No. Layers | No. Nodes | RMSE |
|---|---|---|
| 2 | 1000 | 0.0083 |
| 2 | 2000 | 0.0177 |
| No. Nodes | Average Performance Index, | Comments |
| 250 | 93.7 | Steady-state Offset |
| 500 | 95.8 | Steady-state Offset |
| 1000 | 100.0 | Desired Performance |
| 2000 | 98.6 | Steady-state Offset |
| NMPC | RNN-MPC | |
|---|---|---|
| Time required | 1.55 ms | 1.17 ms |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wong, W.C.; Chee, E.; Li, J.; Wang, X. Recurrent Neural Network-Based Model Predictive Control for Continuous Pharmaceutical Manufacturing. Mathematics 2018, 6, 242. https://doi.org/10.3390/math6110242
Wong WC, Chee E, Li J, Wang X. Recurrent Neural Network-Based Model Predictive Control for Continuous Pharmaceutical Manufacturing. Mathematics. 2018; 6(11):242. https://doi.org/10.3390/math6110242
Chicago/Turabian StyleWong, Wee Chin, Ewan Chee, Jiali Li, and Xiaonan Wang. 2018. "Recurrent Neural Network-Based Model Predictive Control for Continuous Pharmaceutical Manufacturing" Mathematics 6, no. 11: 242. https://doi.org/10.3390/math6110242
APA StyleWong, W. C., Chee, E., Li, J., & Wang, X. (2018). Recurrent Neural Network-Based Model Predictive Control for Continuous Pharmaceutical Manufacturing. Mathematics, 6(11), 242. https://doi.org/10.3390/math6110242






