Energy-Efficient Scheduling for a Job Shop Using an Improved Whale Optimization Algorithm
Abstract
1. Introduction
2. Problem Description
- (1)
- Any job can not be processed on more than one machine simultaneously.
- (2)
- Each machine can only process one operation at a time.
- (3)
- Preemption is not allowed once a job starts to be processed on a machine.
- (4)
- Setup time is not considered in this paper.
- (5)
- The speed of a machine can not be changed during the processing of an operation.
- (6)
- Each machine can not be turned off completely until all jobs assigned to it are finished. During the idle periods, each machine will be on a stand-by mode with energy consumption cost per unit time .
3. Overview of the Original WOA
3.1. Exploitation Phase
- (1)
- Shrinking encircling mechanism
- (2)
- Spiral updating mechanism
3.2. Exploration Phase
3.3. Pseudo Code of WOA
4. Implement of the Proposed IWOA
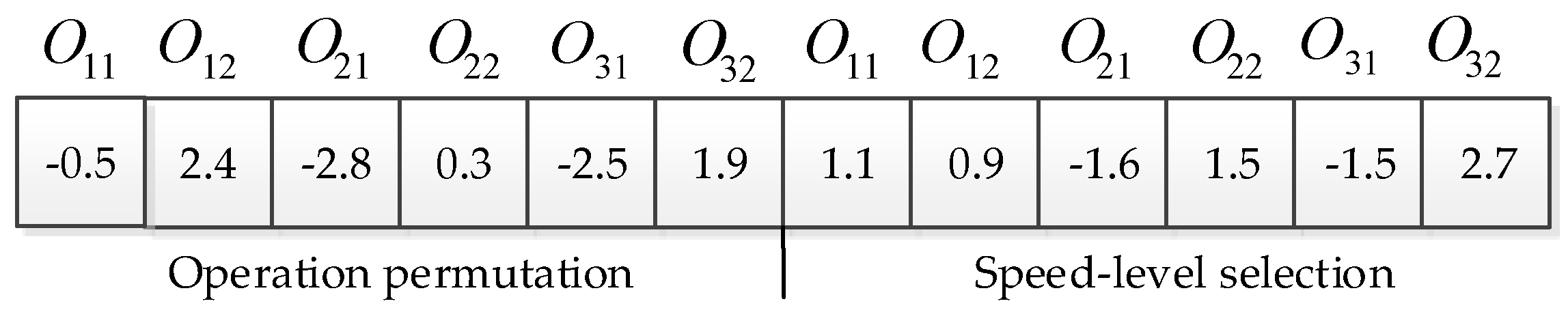
4.1. Scheduling Solution Representation
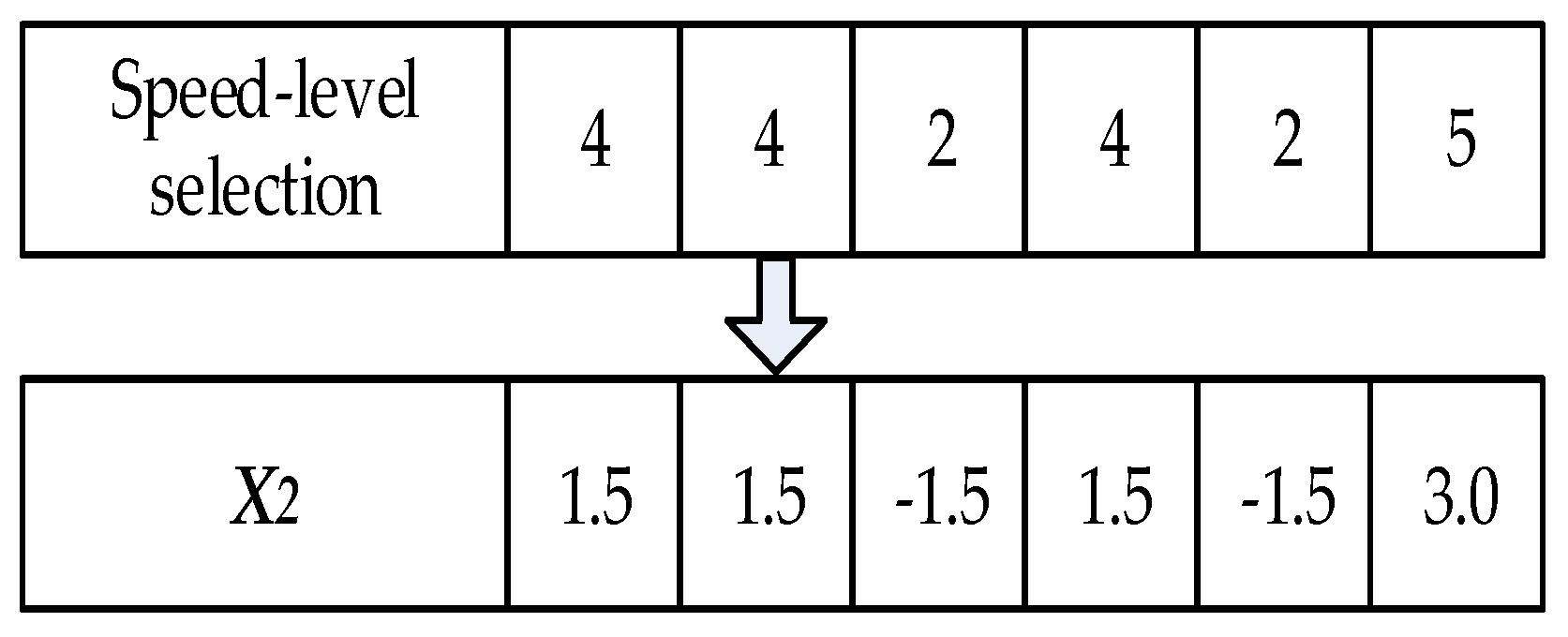
4.2. Individual Position Vector
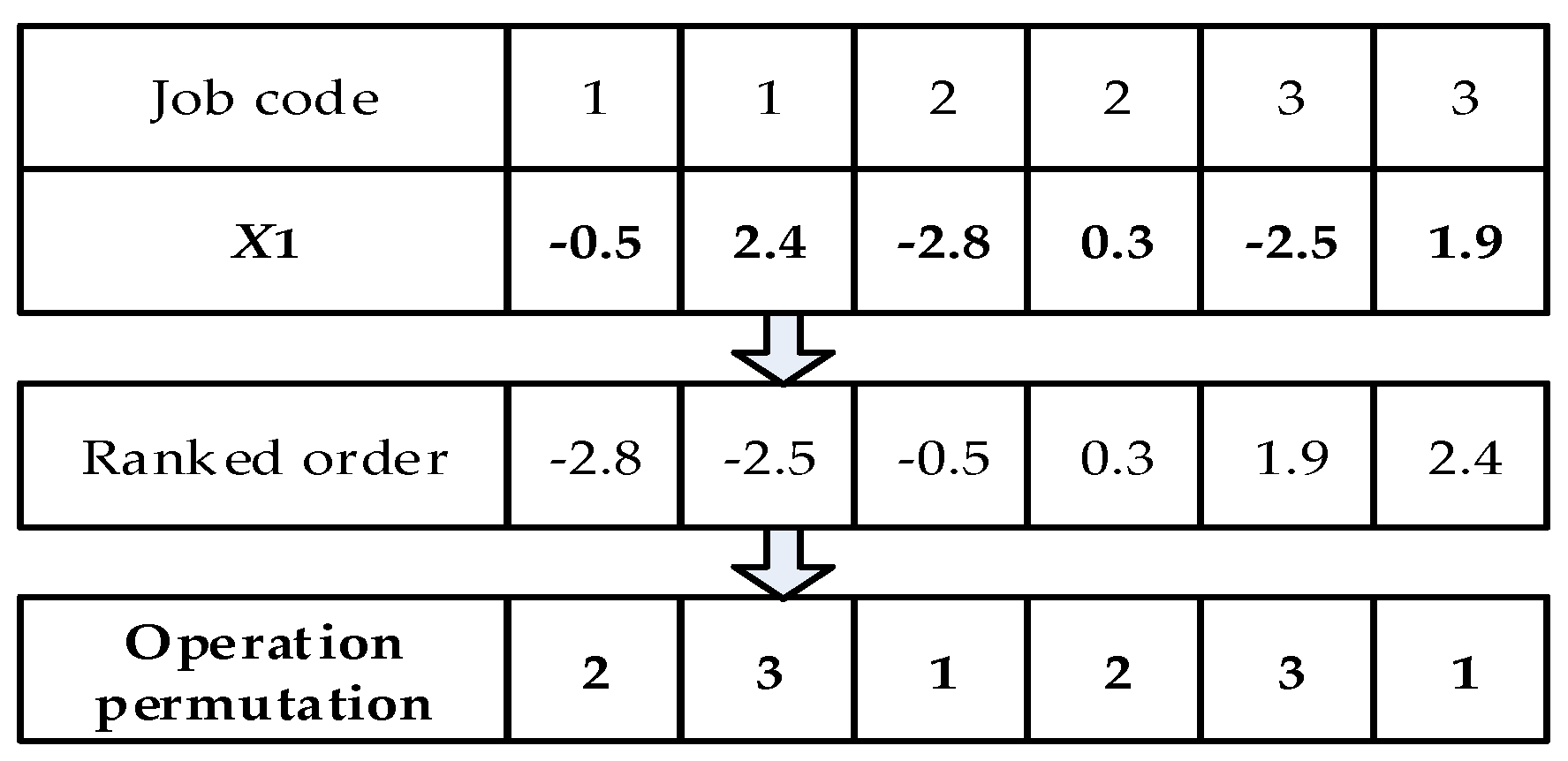
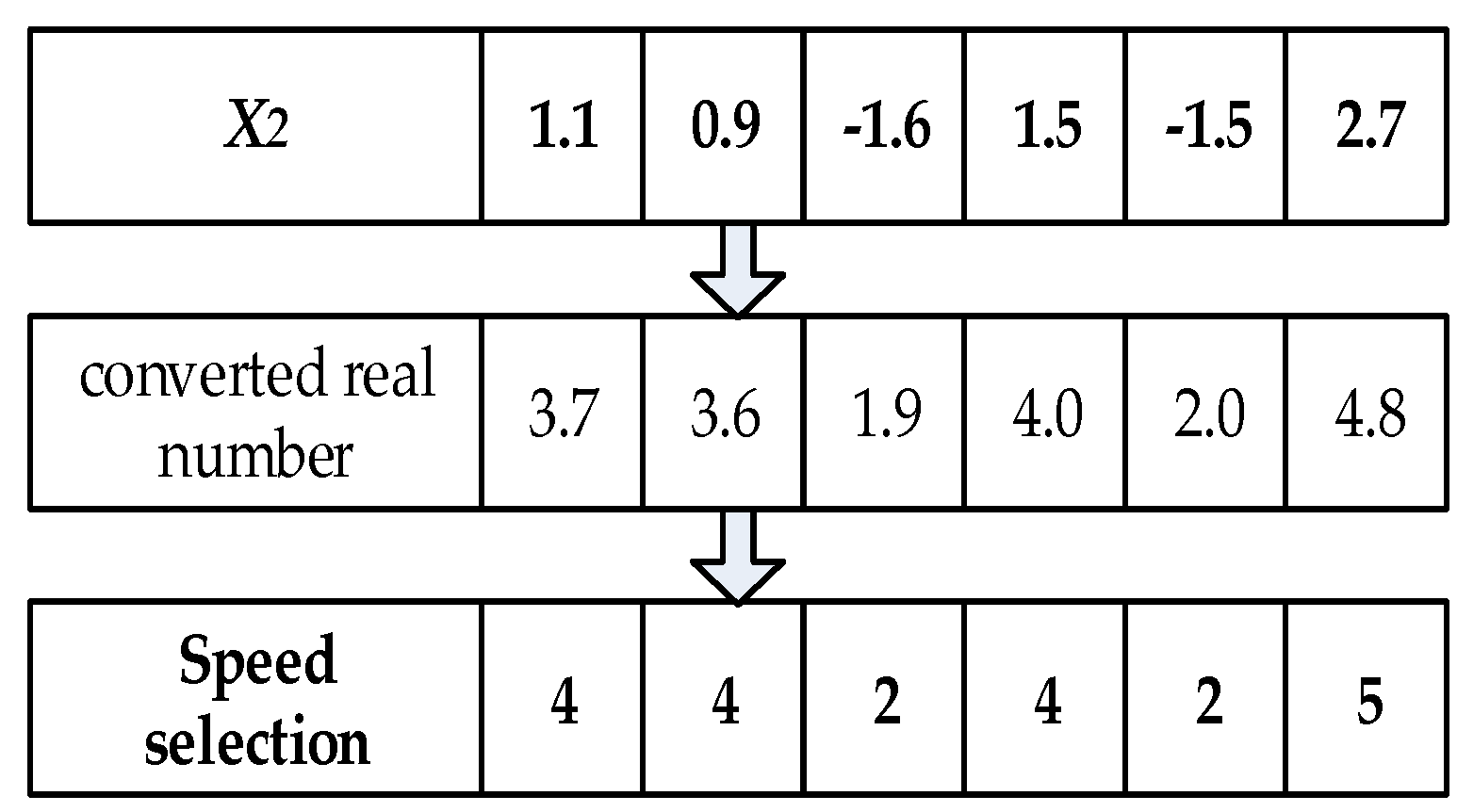
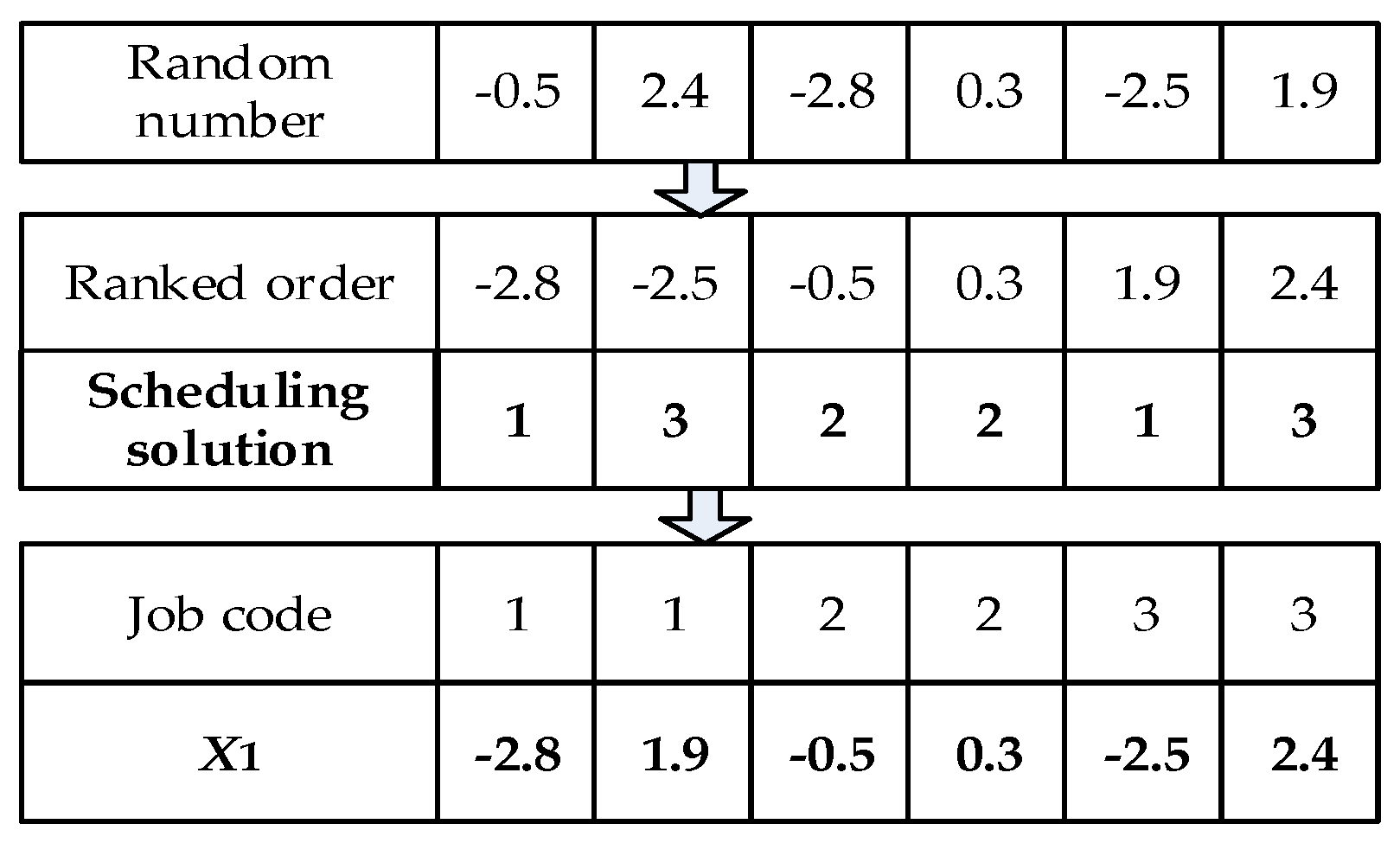
4.3. Conversion between Individual Position Vector and Scheduling Solution
4.3.1. Conversion from Individual Position Vector to Scheduling Solution
4.3.2. Conversion from Scheduling Solution to Individual Position Vector
4.4. Initial Scheduling Generation
- MWR: give the highest priority to the job with the most amount of remaining work.
- MOR: give the highest priority to the job with the most number of remaining operations.
- SPT: give the highest priority to the job with the shortest processing time.
- LPT: give the highest priority to the job with the longest processing time.
- RR: select jobs for the permutation at random.
4.5. Nonlinear Convergence Factor
4.6. Mutation Operation
4.7. Pseudo Code of IWOA
5. Computational Results
5.1. Experimental Settings
5.2. Effectiveness of the Improvement Strategies
5.3. Effectiveness of the Proposed IWOA
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Duflou, J.R.; Sutherland, J.W.; Dornfeld, D.; Herrmann, C.; Jeswiet, J.; Kara, S.; Hauschild, M.; Kellens, K. Towards energy and resource efficient manufacturing: A processes and systems approach. CIRP Ann.-Manuf. Technol. 2012, 61, 587–609. [Google Scholar] [CrossRef]
- Fang, K.; Uhan, N.; Zhao, F.; Sutherland, J.W. A New Shop Scheduling Approach in Support of Sustainable Manufacturing; Glocalized solutions for sustainability in manufacturing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 305–310. [Google Scholar]
- Liu, Y.; Dong, H.; Lohse, N.; Petrovic, S.; Gindy, V. An investigation into minimising total energy consumption and total weighted tardiness in job shops. J. Clean. Prod. 2014, 65, 87–96. [Google Scholar] [CrossRef]
- Mouzon, G.; Yildirim, M.B.; Twomey, J. Operational methods for minimization of energy consumption of manufacturing equipment. Int. J. Prod. Res. 2007, 45, 4247–4271. [Google Scholar] [CrossRef]
- Mouzon, G.; Yildirim, M.B. A framework to minimise total energy consumption and total tardiness on a single machine. Int. J. Sustain. Eng. 2008, 1, 105–116. [Google Scholar] [CrossRef]
- Yildirim, M.B.; Mouzon, G. Single-machine sustainable production planning to minimize total energy consumption and total completion time using a multiple objective genetic algorithm. IEEE. Trans. Eng. Manag. 2012, 59, 585–597. [Google Scholar] [CrossRef]
- Shrouf, F.; Ordieres-Meré, J.; García-Sánchez, A.; Ortega-Mier, M. Optimizing the production scheduling of a single machine to minimize total energy consumption costs. J. Clean. Prod. 2014, 67, 197–207. [Google Scholar] [CrossRef]
- Che, A.; Zeng, Y.; Lyu, K. An efficient greedy insertion heuristic for energy-conscious single machine scheduling problem under time-of-use electricity tariffs. J. Clean. Prod. 2016, 129, 565–577. [Google Scholar] [CrossRef]
- Li, J.Q.; Sang, H.Y.; Han, Y.Y.; Wang, C.G.; Gao, K.Z. Efficient multi-objective optimization algorithm for hybrid flow shop scheduling problems with setup energy consumptions. J. Clean. Prod. 2018, 181, 584–598. [Google Scholar] [CrossRef]
- Liu, G.S.; Zhang, B.X.; Yang, H.D.; Chen, X.; Huang, G.Q. A branch-and-bound algorithm for minimizing the energy consumption in the PFS problem. Math. Probl. Eng. 2013, 2013, 546810. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A.; Li, W.D. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm. Robot. Comput.-Int. Manuf. 2013, 29, 418–429. [Google Scholar] [CrossRef]
- Ding, J.Y.; Song, S.; Wu, C. Carbon-efficient scheduling of flow shops by multi-objective optimization. Eur. J. Oper. Res. 2016, 248, 758–771. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Aktas, E.; Besikci, U. Green scheduling of a two-machine flowshop: Trade-off between makespan and energy consumption. Eur. J. Oper. Res. 2016, 248, 772–788. [Google Scholar] [CrossRef]
- Luo, H.; Du, B.; Huang, G.Q.; Chen, H.; Li, X. Hybrid flow shop scheduling considering machine electricity consumption cost. Int. J. Prod. Econ. 2013, 146, 423–439. [Google Scholar] [CrossRef]
- Salido, M.A.; Escamilla, J.; Giret, A.; Barber, F. A genetic algorithm for energy-efficiency in job-shop scheduling. Int. J. Adv. Manuf. Technol. 2016, 85, 1303–1314. [Google Scholar] [CrossRef]
- Zhang, R.; Chiong, R. Solving the energy-efficient job shop scheduling problem: A multi-objective genetic algorithm with enhanced local search for minimizing the total weighted tardiness and total energy consumption. J. Clean. Prod. 2016, 112, 3361–3375. [Google Scholar] [CrossRef]
- Tang, D.; Dai, M. Energy-efficient approach to minimizing the energy consumption in an extended job-shop scheduling problem. Chin. J. Mech. Eng. 2015, 28, 1048–1055. [Google Scholar] [CrossRef]
- Escamilla, J.; Salido, M.A.; Giret, A.; Barber, F. A metaheuristic technique for energy-efficiency in job-shop scheduling. Knowl. Eng. Rev. 2016, 31, 475–485. [Google Scholar] [CrossRef]
- Yin, L.; Li, X.; Gao, L.; Lu, C.; Zhang, Z. Energy-efficient job shop scheduling problem with variable spindle speed using a novel multi-objective algorithm. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Wang, G.G.; Tan, Y. Improving metaheuristic algorithms with information feedback models. IEEE. Trans. Cybern. 2017. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. Stud krill herd algorithm. Neurocomputing 2014, 128, 363–370. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.; Gandomi, A.H.; Hao, G.S.; Wang, H. Chaotic krill herd algorithm. Inform. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Wang, H.; Duan, H.; Liu, L.; Li, J. Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Comput. Appl. 2014, 24, 853–871. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.G.; Dong, J.; Wang, L. Opposition-based learning monarch butterfly optimization with Gaussian perturbation for large-scale 0-1 knapsack problem. Comput. Electr. Eng. 2018, 67, 454–468. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Sehiemy, R.A.; Wang, G.G. A novel parallel hurricane optimization algorithm for secure emission/economic load dispatch solution. Appl. Soft. Comput. 2018, 63, 206–222. [Google Scholar] [CrossRef]
- Jiang, T.H.; Zhang, C. Application of Grey Wolf Optimization for solving combinatorial problems: Job shop and flexible job shop scheduling cases. IEEE. Access. 2018, 6, 26231–26240. [Google Scholar] [CrossRef]
- Jiang, T.H.; Deng, G.L. Optimizing the low-carbon flexible job shop scheduling problem considering energy consumption. IEEE. Access. 2018, 6, 46346–46355. [Google Scholar] [CrossRef]
- Han, Y.Y.; Gong, D.W.; Jin, Y.C.; Pan, Q.K. Evolutionary Multi-objective Blocking Lot-streaming Flow Shop Scheduling with Machine Breakdowns. IEEE. Trans. Cybern. 2018. [Google Scholar] [CrossRef]
- Han, Y.Y.; Liang, J.; Pan, Q.K.; Li, J.Q. Effective hybrid discrete artificial bee colony algorithms for the total flow time minimization in the blocking flow shop problem. Int. J. Adv. Manuf. Technol. 2013, 67, 397–414. [Google Scholar] [CrossRef]
- Han, Y.Y.; Pan, Q.K.; Li, J.Q.; Sang, H.Y. An improved artificial bee colony algorithm for the blocking flow shop scheduling problem. Int. J. Adv. Manuf. Technol. 2012, 60, 1149–1159. [Google Scholar] [CrossRef]
- Li, J.Q.; Duan, P.Y.; Sang, H.Y.; Wang, S.; Liu, Z.M.; Duan, P. An efficient optimization algorithm for resource-constrained steelmaking scheduling problems. IEEE. Access. 2018, 6, 33883–33894. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Ling, Y.; Zhou, Y.; Luo, Q. Lévy flight trajectory-based whale optimization algorithm for global optimization. IEEE. Access. 2017, 5, 6168–6186. [Google Scholar] [CrossRef]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft. Comput. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- El Aziz, M.A.; Ewees, A.A.; Hassanien, A.E. Multi-objective whale optimization algorithm for content-based image retrieval. Multimed. Tools Appl. 2018, 77, 26135–26172. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Sangaiah, A.K. A modified nature inspired meta-heuristic whale optimization algorithm for solving 0–1 knapsack problem. Int. J. Mach. Learn. Cybern. 2017, 1–20. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; El-Shahat, D.; Mirjalili, S. A hybrid whale optimization algorithm based on local search strategy for the permutation flow shop scheduling problem. Future Gener. Comput. Syst. 2018, 85, 129–145. [Google Scholar] [CrossRef]
- Jiang, T.H. Flexible job shop scheduling problem with hybrid grey wolf optimization algorithm. Control Decis. 2018, 33, 503–508. (In Chinese) [Google Scholar]
- Yuan, Y.; Xu, H. Flexible job shop scheduling using hybrid differential evolution algorithms. Comput. Ind. Eng. 2013, 65, 246–260. [Google Scholar] [CrossRef]
- Fisher, H.; Thompson, G.L. Probabilistic learning combinations of local job-shop scheduling rules. Ind. Sched. 1963, 3, 225–251. [Google Scholar]
- Lawrence, S. Resource Constrained Project Scheduling: An Experimental Investigation of Heuristic Scheduling Techniques; Graduate School of Industrial Administration (GSIA), Carnegie Mellon University: Pittsburgh, PA, USA, 1984. [Google Scholar]
- Baykasoglu, A.; Hamzadayi, A.; Kose, S.Y. Testing the performance of teaching-learning based optimization (TLBO) algorithm on combinatorial problems: Flow shop and job shop scheduling cases. Inform. Sci. 2014, 276, 204–218. [Google Scholar] [CrossRef]



| Instance | IWOA-R | IWOA-L | IWOA-NMO | IWOA | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Avg | SD | Time | Best | Avg | SD | Time | Best | Avg | SD | Time | Best | Avg | SD | Time | |
| FT06 | 1364.4 | 1381.5 | 13.1 | 27.0 | 1374.4 | 1384.3 | 6.7 | 27.0 | 1383.3 | 1389.8 | 6.9 | 15.9 | 1370.4 | 1382.8 | 6.2 | 26.9 |
| FT10 | 31,756.9 | 32,689.8 | 652.5 | 108.2 | 31,809.4 | 32,564.2 | 569.2 | 109.6 | 31,720.1 | 32,394.9 | 322.9 | 64.0 | 31,619.3 | 32,726.4 | 649.4 | 107.8 |
| FT20 | 35,225.1 | 35,925.9 | 337.0 | 111.5 | 35,138.0 | 35,888.1 | 425.9 | 113.7 | 35,005.8 | 35,525.3 | 370.1 | 66.2 | 34,544.2 | 35,155.7 | 376.8 | 111.4 |
| LA01 | 18,053.5 | 18,278.0 | 164.1 | 40.8 | 18,031.3 | 18,281.8 | 157.6 | 39.2 | 18,033.6 | 18,408.3 | 243.7 | 23.6 | 18,096.0 | 18,204.8 | 88.8 | 39.0 |
| LA02 | 17,663.3 | 17,893.5 | 131.0 | 38.5 | 17,699.8 | 17,935.7 | 160.5 | 38.7 | 17,911.5 | 18,253.6 | 218.7 | 23.3 | 17,661.0 | 17,967.5 | 157.8 | 38.2 |
| LA03 | 15,679.5 | 15,877.2 | 142.5 | 38.5 | 15,765.6 | 15,989.5 | 189.1 | 38.8 | 15,873.5 | 16,153.8 | 183.0 | 23.2 | 15,679.6 | 15,913.4 | 219.2 | 38.7 |
| LA04 | 16,114.6 | 16,327.7 | 119.2 | 38.0 | 16,223.0 | 16,384.8 | 107.1 | 40.0 | 16,129.9 | 16,467.2 | 215.8 | 23.5 | 16,039.7 | 16,209.3 | 136.1 | 38.0 |
| LA05 | 14,506.1 | 14,667.6 | 96.0 | 38.6 | 14,447.2 | 14,657.9 | 133.4 | 39.7 | 14,613.5 | 14,813.4 | 138.4 | 23.6 | 14,442.6 | 14,608.0 | 97.8 | 38.2 |
| LA06 | 25,145.6 | 25,529.1 | 206.2 | 68.7 | 25,248.1 | 25,654.4 | 204.1 | 69.4 | 25,464.8 | 25,758.7 | 196.6 | 40.8 | 25,198.4 | 25,501.0 | 134.8 | 68.2 |
| LA07 | 24,510.7 | 24,770.1 | 183.8 | 67.0 | 24,534.1 | 24,868.4 | 227.2 | 67.1 | 24,513.2 | 24,867.2 | 238.4 | 39.9 | 24,172.9 | 24,619.2 | 203.1 | 66.3 |
| LA08 | 24,511.2 | 24,765.4 | 213.7 | 73.6 | 24,717.8 | 24,889.7 | 132.6 | 73.9 | 24,700.3 | 24,922.0 | 140.0 | 39.5 | 24,422.8 | 24,775.7 | 202.1 | 67.6 |
| LA09 | 27,349.1 | 27,538.6 | 136.5 | 72.3 | 27,401.1 | 27,692.2 | 122.0 | 74.0 | 27,610.5 | 27,798.6 | 149.9 | 44.0 | 27,329.5 | 27,608.6 | 122.5 | 73.5 |
| LA10 | 24,959.0 | 25,349.7 | 216.4 | 73.6 | 25,210.1 | 25,455.5 | 164.4 | 73.5 | 25,206.4 | 25,405.9 | 164.9 | 43.9 | 25,081.3 | 25,315.5 | 178.9 | 73.2 |
| LA11 | 34,287.2 | 34,668.2 | 213.6 | 112.6 | 34,406.6 | 34,697.8 | 220.4 | 113.9 | 34,227.4 | 34,706.6 | 233.3 | 64.6 | 34,221.7 | 34,659.8 | 258.5 | 110.1 |
| LA12 | 29,927.1 | 30,282.2 | 178.2 | 110.8 | 30,213.3 | 30,432.0 | 163.0 | 111.9 | 30,088.7 | 30,287.8 | 159.4 | 64.3 | 29,905.6 | 30,221.5 | 173.9 | 111.6 |
| LA13 | 32,974.4 | 33,316.7 | 232.8 | 110.4 | 33,379.4 | 33,617.1 | 143.1 | 117.0 | 33,192.5 | 33,401.8 | 124.9 | 67.5 | 33,198.1 | 33,490.7 | 216.0 | 110.2 |
| LA14 | 33,991.7 | 34,116.7 | 114.7 | 113.3 | 34,084.4 | 34,478.8 | 187.5 | 114.7 | 33,979.4 | 34,398.0 | 249.7 | 67.2 | 33,794.5 | 34,214.3 | 242.8 | 114.0 |
| LA15 | 35,817.5 | 36,102.2 | 159.3 | 113.9 | 36,017.9 | 36,327.0 | 209.0 | 115.1 | 35,979.6 | 36,315.0 | 258.1 | 66.2 | 35,802.4 | 36,199.8 | 203.0 | 113.1 |
| LA16 | 31,572.7 | 32,171.2 | 549.2 | 109.1 | 31,746.8 | 32,480.8 | 453.5 | 111.4 | 32,215.1 | 32,856.2 | 313.0 | 64.5 | 31,516.7 | 32,118.2 | 397.7 | 108.9 |
| LA17 | 27,734.0 | 28,259.8 | 249.5 | 110.7 | 28,258.8 | 28,710.7 | 265.3 | 111.4 | 28,103.6 | 28,570.6 | 277.9 | 64.4 | 27,606.6 | 28,166.0 | 377.8 | 110.1 |
| LA18 | 30,631.3 | 31,300.5 | 291.1 | 106.2 | 31,147.3 | 31,530.1 | 188.4 | 108.3 | 31,192.0 | 31,465.4 | 243.4 | 63.0 | 30,826.6 | 31,480.9 | 525.1 | 107.5 |
| LA19 | 30,938.3 | 31,432.7 | 270.4 | 108.1 | 30,951.9 | 31,608.5 | 343.4 | 109.3 | 30,626.6 | 31,684.9 | 491.6 | 63.3 | 31,167.9 | 31,653.8 | 352.9 | 108.5 |
| LA20 | 32,959.8 | 33,481.9 | 379.0 | 108.3 | 33,121.5 | 33,816.8 | 501.0 | 108.0 | 33,213.6 | 33,863.7 | 365.5 | 61.6 | 32,675.2 | 33,359.4 | 384.3 | 104.1 |
| LA21 | 46,010.4 | 46,775.4 | 473.7 | 199.4 | 46,475.3 | 47,252.7 | 665.3 | 196.7 | 45,814.5 | 46,567.8 | 707.6 | 115.4 | 46,139.7 | 46,595.8 | 256.6 | 190.7 |
| LA22 | 41,008.2 | 42,285.9 | 721.5 | 191.3 | 41,528.4 | 42,418.6 | 430.6 | 197.2 | 40,960.6 | 42,078.4 | 640.5 | 116.3 | 41,378.6 | 42,185.1 | 556.5 | 193.9 |
| LA23 | 44,957.1 | 45,687.4 | 619.0 | 191.6 | 45,303.6 | 46,203.4 | 602.4 | 203.2 | 45,527.4 | 46,142.1 | 722.9 | 116.1 | 44,848.3 | 45,655.5 | 626.4 | 195.5 |
| LA24 | 42,921.1 | 44,018.8 | 442.6 | 191.0 | 43,142.3 | 44,258.3 | 614.3 | 185.4 | 42,587.5 | 43,819.4 | 775.2 | 108.0 | 41,747.3 | 43,487.9 | 869.3 | 191.3 |
| LA25 | 42,397.1 | 42,925.9 | 332.0 | 184.0 | 42,805.1 | 43,693.6 | 470.3 | 186.2 | 42,602.1 | 43,175.7 | 310.0 | 106.4 | 43,328.0 | 43,686.9 | 364.9 | 185.7 |
| LA26 | 59,010.9 | 59,783.1 | 426.7 | 289.8 | 60,087.4 | 60,912.2 | 569.9 | 299.8 | 58,381.8 | 59,645.3 | 745.5 | 171.7 | 58,956.5 | 60,361.9 | 792.4 | 292.0 |
| LA27 | 60,258.6 | 62,040.3 | 1017.7 | 288.8 | 60,815.2 | 62,214.4 | 871.5 | 286.9 | 60,106.7 | 61,706.2 | 867.3 | 166.3 | 60,345.2 | 61,834.3 | 701.7 | 287.3 |
| LA28 | 59,776.6 | 60,419.2 | 606.8 | 268.6 | 59,157.5 | 61,859.0 | 1448.4 | 292.5 | 59,131.6 | 60,600.6 | 777.6 | 162.5 | 59,361.1 | 60,933.3 | 580.5 | 282.0 |
| LA29 | 57,139.0 | 58,076.0 | 596.4 | 278.2 | 56,908.8 | 58,345.2 | 1148.2 | 290.1 | 56,927.2 | 58,145.1 | 705.9 | 169.8 | 56,971.4 | 58,028.9 | 934.3 | 289.8 |
| LA30 | 60,689.9 | 61,396.5 | 696.2 | 279.7 | 61,680.8 | 62,924.5 | 1226.9 | 280.1 | 60,856.4 | 62,305.2 | 1064.5 | 156.9 | 60,849.4 | 61,970.9 | 753.8 | 280.0 |
| LA31 | 85,498.9 | 87,045.9 | 1149.1 | 532.6 | 85,708.0 | 87,871.1 | 1597.1 | 587.8 | 85,180.3 | 86,549.2 | 1422.7 | 320.8 | 85,121.3 | 86,301.1 | 551.2 | 588.0 |
| LA32 | 90,282.2 | 93,019.1 | 1049.8 | 572.0 | 92,704.6 | 94,834.7 | 1647.9 | 572.5 | 89,949.9 | 92,833.3 | 1937.3 | 321.6 | 91,552.0 | 92,848.3 | 1208.2 | 570.5 |
| LA33 | 83,128.1 | 84,780.9 | 1376.6 | 592.1 | 85,535.2 | 86,504.5 | 712.2 | 563.3 | 83,408.3 | 84,776.2 | 1063.2 | 314.6 | 83,406.5 | 84,898.0 | 667.4 | 557.6 |
| LA34 | 85,278.7 | 87,079.6 | 1172.8 | 596.9 | 86,813.6 | 88,850.1 | 1395.4 | 590.0 | 84,950.7 | 86,471.5 | 1615.4 | 334.5 | 85,921.4 | 87,369.6 | 1379.5 | 578.7 |
| LA35 | 86,418.3 | 88,466.7 | 1606.2 | 578.2 | 88,908.5 | 90,462.3 | 1168.2 | 582.1 | 87,212.1 | 87,976.7 | 590.0 | 327.6 | 87,327.1 | 89,208.7 | 1336.9 | 563.3 |
| Instancce | GA1 | GA2 | TLBO | IWOA | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Avg | SD | Time | Best | Avg | SD | Time | Best | Avg | SD | Time | Best | Avg | SD | Time | |
| FT06 | 1528.0 | 1540.6 | 10.0 | 6.2 | 1550.6 | 1582.9 | 20.0 | 7.3 | 1639.3 | 1658.4 | 13.5 | 81.9 | 1370.4 | 1382.8 | 6.2 | 26.9 |
| FT10 | 37,145.2 | 38,322.0 | 819.8 | 22.8 | 38,638.7 | 39,772.5 | 620.2 | 30.1 | 38,719.6 | 39,618.0 | 423.7 | 370.4 | 31,619.3 | 32,726.4 | 649.4 | 107.8 |
| FT20 | 41,573.8 | 42,212.4 | 496.4 | 25.7 | 42,777.3 | 43,877.3 | 514.1 | 32.7 | 41,716.3 | 42,161.3 | 245.1 | 772.6 | 34,544.2 | 35,155.7 | 376.8 | 111.4 |
| LA01 | 20,929.0 | 21,239.9 | 166.4 | 9.9 | 21,845.8 | 22,302.7 | 279.7 | 11.6 | 22,766.9 | 23,052.0 | 181.5 | 163.8 | 18,096.0 | 18,204.8 | 88.8 | 39.0 |
| LA02 | 20,321.9 | 20,801.4 | 219.9 | 9.8 | 21,223.0 | 21,626.4 | 330.1 | 11.3 | 21,480.3 | 21,875.7 | 200.7 | 164.8 | 17,661.0 | 17,967.5 | 157.8 | 38.2 |
| LA03 | 18,436.8 | 18,895.8 | 299.5 | 9.9 | 19,269.9 | 19,624.5 | 227.7 | 11.5 | 19,640.7 | 20,034.8 | 158.8 | 163.2 | 15,679.6 | 15,913.4 | 219.2 | 38.7 |
| LA04 | 18,390.9 | 19,037.8 | 277.2 | 9.9 | 19,085.3 | 19,620.1 | 216.7 | 11.5 | 19,983.2 | 20,447.2 | 265.1 | 163.1 | 16,039.7 | 16,209.3 | 136.1 | 38.0 |
| LA05 | 16,501.3 | 16,829.2 | 185.7 | 9.8 | 17,424.2 | 17,732.9 | 228.1 | 11.6 | 18,111.9 | 18,372.4 | 121.5 | 163.4 | 14,442.6 | 14,608.0 | 97.8 | 38.2 |
| LA06 | 29,645.5 | 29,832.5 | 156.9 | 16.7 | 30,332.6 | 31,156.2 | 428.6 | 21.1 | 30,925.3 | 31,757.5 | 351.9 | 390.8 | 25,198.4 | 25,501.0 | 134.8 | 68.2 |
| LA07 | 28,288.9 | 28,821.7 | 306.8 | 16.7 | 29,614.2 | 30,278.9 | 422.5 | 21.2 | 30,293.6 | 30,494.5 | 156.5 | 409.5 | 24,172.9 | 24,619.2 | 203.1 | 66.3 |
| LA08 | 28,418.7 | 28,959.5 | 288.3 | 17.0 | 29,442.4 | 30,591.2 | 463.1 | 21.3 | 30,574.5 | 30,829.1 | 168.8 | 416.2 | 24,422.8 | 24,775.7 | 202.1 | 67.6 |
| LA09 | 31,487.4 | 32,028.0 | 300.4 | 16.9 | 32,652.8 | 33,383.0 | 476.8 | 21.3 | 33,563.3 | 34,137.6 | 391.2 | 412.3 | 27,329.5 | 27,608.6 | 122.5 | 73.5 |
| LA10 | 29,021.5 | 29,703.9 | 356.9 | 16.8 | 30,753.2 | 31,272.7 | 276.3 | 21.2 | 32,018.4 | 32,311.7 | 201.3 | 416.1 | 25,081.3 | 25,315.5 | 178.9 | 73.2 |
| LA11 | 39,735.1 | 40,732.2 | 563.2 | 25.6 | 40,691.1 | 42,380.5 | 694.1 | 29.9 | 42,098.2 | 42,568.8 | 250.3 | 831.8 | 342,21.7 | 34,659.8 | 258.5 | 110.1 |
| LA12 | 34,360.3 | 35,109.6 | 567.1 | 25.2 | 36,116.2 | 36,705.9 | 364.6 | 30.2 | 36,685.3 | 37,024.0 | 210.6 | 767.1 | 29,905.6 | 30,221.5 | 173.9 | 111.6 |
| LA13 | 37,641.6 | 38,759.5 | 902.9 | 25.5 | 40,046.0 | 41,036.5 | 377.0 | 30.8 | 40,866.4 | 41,199.9 | 168.7 | 775.3 | 33,198.1 | 33,490.7 | 216.0 | 110.2 |
| LA14 | 40,079.5 | 40,657.0 | 407.2 | 25.5 | 42,035.5 | 42,668.4 | 307.0 | 30.3 | 42,644.1 | 43,063.7 | 235.5 | 804.6 | 33,794.5 | 34,214.3 | 242.8 | 114.0 |
| LA15 | 42,138.3 | 42,630.5 | 355.8 | 25.6 | 44,265.0 | 44,865.7 | 406.6 | 30.6 | 43,729.4 | 44,087.5 | 250.3 | 800.1 | 35,802.4 | 36,199.8 | 203.0 | 113.1 |
| LA16 | 37,245.6 | 38,160.1 | 775.0 | 23.2 | 39,352.3 | 40,191.7 | 505.5 | 28.0 | 39,637.1 | 40,341.5 | 366.2 | 406.5 | 31,516.7 | 32,118.2 | 397.7 | 108.9 |
| LA17 | 32,693.6 | 33,180.5 | 450.0 | 23.0 | 34,319.1 | 35,011.7 | 475.3 | 27.9 | 34,707.3 | 35,280.3 | 375.9 | 400.3 | 27,606.6 | 28,166.0 | 377.8 | 110.1 |
| LA18 | 35,469.3 | 36,751.3 | 648.4 | 23.2 | 37,326.8 | 38,536.1 | 611.9 | 27.9 | 38,204.9 | 39,038.9 | 368.0 | 392.1 | 30,826.6 | 31,480.9 | 525.1 | 107.5 |
| LA19 | 36,099.4 | 37,003.0 | 649.9 | 23.1 | 38,359.7 | 39,177.2 | 405.7 | 27.7 | 38,186.7 | 38,962.7 | 391.6 | 404.3 | 31,167.9 | 31,653.8 | 352.9 | 108.5 |
| LA20 | 38,179.1 | 39,348.4 | 546.1 | 22.8 | 40,626.2 | 41,834.9 | 596.4 | 28.1 | 41,519.6 | 41,982.8 | 278.8 | 400.4 | 32,675.2 | 33,359.4 | 384.3 | 104.1 |
| LA21 | 54,607.7 | 55,786.4 | 641.3 | 40.5 | 57,276.3 | 58,907.5 | 656.6 | 52.5 | 56,961.4 | 57,707.3 | 389.4 | 949.1 | 46,139.7 | 46,595.8 | 256.6 | 190.7 |
| LA22 | 49,559.5 | 51,284.0 | 755.0 | 40.6 | 51,457.2 | 53,373.3 | 924.2 | 50.9 | 52,280.6 | 52,541.4 | 183.0 | 893.2 | 41,378.6 | 42,185.1 | 556.5 | 193.9 |
| LA23 | 53,917.7 | 54,612.9 | 561.0 | 40.6 | 56,499.0 | 57,683.4 | 682.8 | 52.0 | 56,709.3 | 57,164.8 | 259.8 | 955.8 | 44,848.3 | 45,655.5 | 626.4 | 195.5 |
| LA24 | 51,056.0 | 52,393.9 | 826.4 | 40.7 | 54,503.0 | 55,457.0 | 716.7 | 53.2 | 53,032.8 | 54,086.9 | 559.4 | 936.2 | 41,747.3 | 43,487.9 | 869.3 | 191.3 |
| LA25 | 51,583.8 | 52,236.1 | 389.8 | 40.5 | 54,128.9 | 51,823.4 | 496.6 | 51.8 | 52,744.1 | 53,644.7 | 485.7 | 940.4 | 43,328.0 | 43,686.9 | 364.9 | 185.7 |
| LA26 | 70,951.3 | 72,097.3 | 895.9 | 60.7 | 75,180.8 | 75,817.0 | 547.6 | 80.9 | 73,634.3 | 73,967.6 | 288.3 | 1807.0 | 58,956.5 | 60,361.9 | 792.4 | 292.0 |
| LA27 | 72,413.8 | 74,974.8 | 1004.8 | 61.3 | 76,673.0 | 78,085.6 | 807.9 | 86.4 | 75,245.7 | 75,683.7 | 322.5 | 1845.4 | 60,345.2 | 61,834.3 | 701.7 | 287.3 |
| LA28 | 71,365.7 | 72,774.3 | 782.7 | 61.3 | 74,918.6 | 76,472.9 | 834.1 | 85.3 | 73,722.1 | 74,669.0 | 608.7 | 1780.7 | 59,361.1 | 60,933.3 | 580.5 | 282.0 |
| LA29 | 67,354.4 | 69,077.6 | 1235.2 | 60.9 | 70,744.8 | 72,150.4 | 1041.7 | 84.8 | 69,980.3 | 70,706.9 | 482.7 | 1777.3 | 56,971.4 | 58,028.9 | 934.3 | 289.8 |
| LA30 | 72,707.5 | 73,966.6 | 589.3 | 59.8 | 76,737.0 | 77,547.9 | 659.0 | 85.1 | 74,160.6 | 75,329.5 | 711.6 | 1792.8 | 60,849.4 | 61,970.9 | 753.8 | 280.0 |
| LA31 | 99,556.7 | 104,319.6 | 2041.1 | 113.8 | 106,691.4 | 108,275.1 | 979.2 | 168.9 | 103,707.5 | 104,566.3 | 703.8 | 4807.2 | 85,121.3 | 86,301.1 | 551.2 | 588.0 |
| LA32 | 110,241.3 | 112,299.6 | 1208.0 | 113.8 | 115,254.6 | 117,103.4 | 859.6 | 165.9 | 113,250.8 | 113,450.3 | 220.1 | 4958.3 | 91,552.0 | 92,848.3 | 1208.2 | 570.5 |
| LA33 | 100,960.7 | 102,467.9 | 1171.0 | 111.3 | 104,826.8 | 106,660.0 | 957.1 | 172.8 | 102,476.4 | 103,051.6 | 428.6 | 5273.3 | 83,406.5 | 84,898.0 | 667.4 | 557.6 |
| LA34 | 102,234.6 | 104,521.0 | 1902.4 | 111.2 | 106,811.5 | 108,573.6 | 734.5 | 172.7 | 105,440.0 | 105,768.8 | 275.5 | 5064.8 | 85,921.4 | 87,369.6 | 1379.5 | 578.7 |
| LA35 | 104,497.8 | 105,599.2 | 1097.5 | 112.0 | 107,670.7 | 110,468.2 | 1210.6 | 190.6 | 106,133.5 | 106,803.1 | 720.4 | 4814.7 | 87,327.1 | 89,208.7 | 1336.9 | 563.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, T.; Zhang, C.; Zhu, H.; Gu, J.; Deng, G. Energy-Efficient Scheduling for a Job Shop Using an Improved Whale Optimization Algorithm. Mathematics 2018, 6, 220. https://doi.org/10.3390/math6110220
Jiang T, Zhang C, Zhu H, Gu J, Deng G. Energy-Efficient Scheduling for a Job Shop Using an Improved Whale Optimization Algorithm. Mathematics. 2018; 6(11):220. https://doi.org/10.3390/math6110220
Chicago/Turabian StyleJiang, Tianhua, Chao Zhang, Huiqi Zhu, Jiuchun Gu, and Guanlong Deng. 2018. "Energy-Efficient Scheduling for a Job Shop Using an Improved Whale Optimization Algorithm" Mathematics 6, no. 11: 220. https://doi.org/10.3390/math6110220
APA StyleJiang, T., Zhang, C., Zhu, H., Gu, J., & Deng, G. (2018). Energy-Efficient Scheduling for a Job Shop Using an Improved Whale Optimization Algorithm. Mathematics, 6(11), 220. https://doi.org/10.3390/math6110220






