Some Reverse Degree-Based Topological Indices and Polynomials of Dendrimers
Abstract
:1. Introduction
2. Preliminaries
3. Main Results
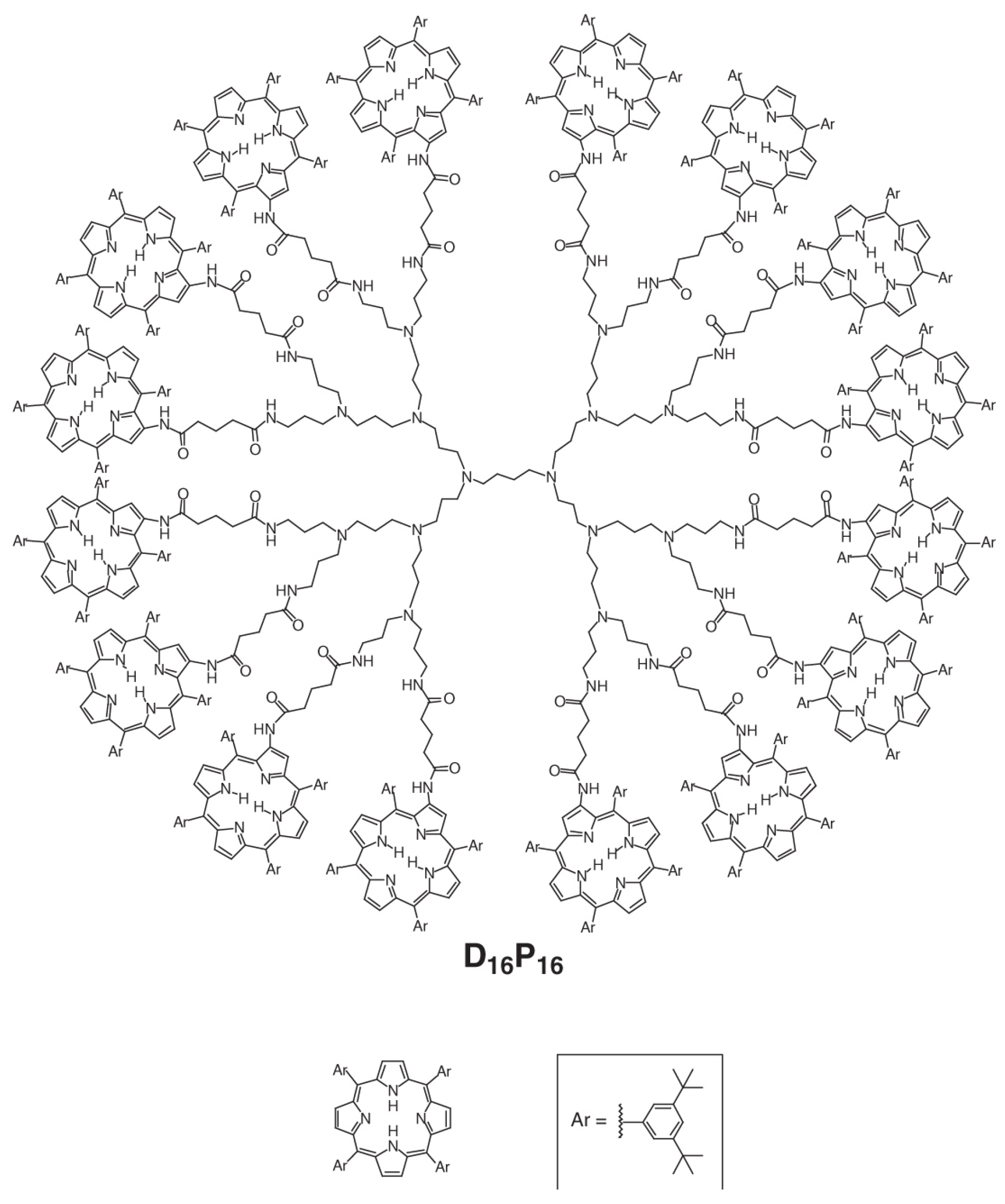
3.1. Prophyrin Dendrimer
- 1.
- 2.
- (i)
- Now, using the definition of reverse first Zagreb index, we have
- (ii)
- Using the definition of reverse second Zagreb index, we have
- 1.
- 2.
- (i)
- Using the information given in Theorem 1 and definition of reverse first Zagreb polynomial, we have
- (ii)
- Using the information given in Theorem 1 and definition of reverse second Zagreb polynomial, we have
- 1.
- 2.
- (i)
- Using the information given in Theorem 1 and definition of reverse first hyper-Zagreb index, we have
- (ii)
- Using the information given in Theorem 1 and definition of reverse second hyper-Zagreb index, we have
- 1.
- 2.
- (i)
- Using the information given in Theorem 1 and definition of reverse first hyper-Zagreb polynomial, we have
- (ii)
- Using the information given in Theorem 1 and definition of reverse second hyper-Zagreb polynomial, we have
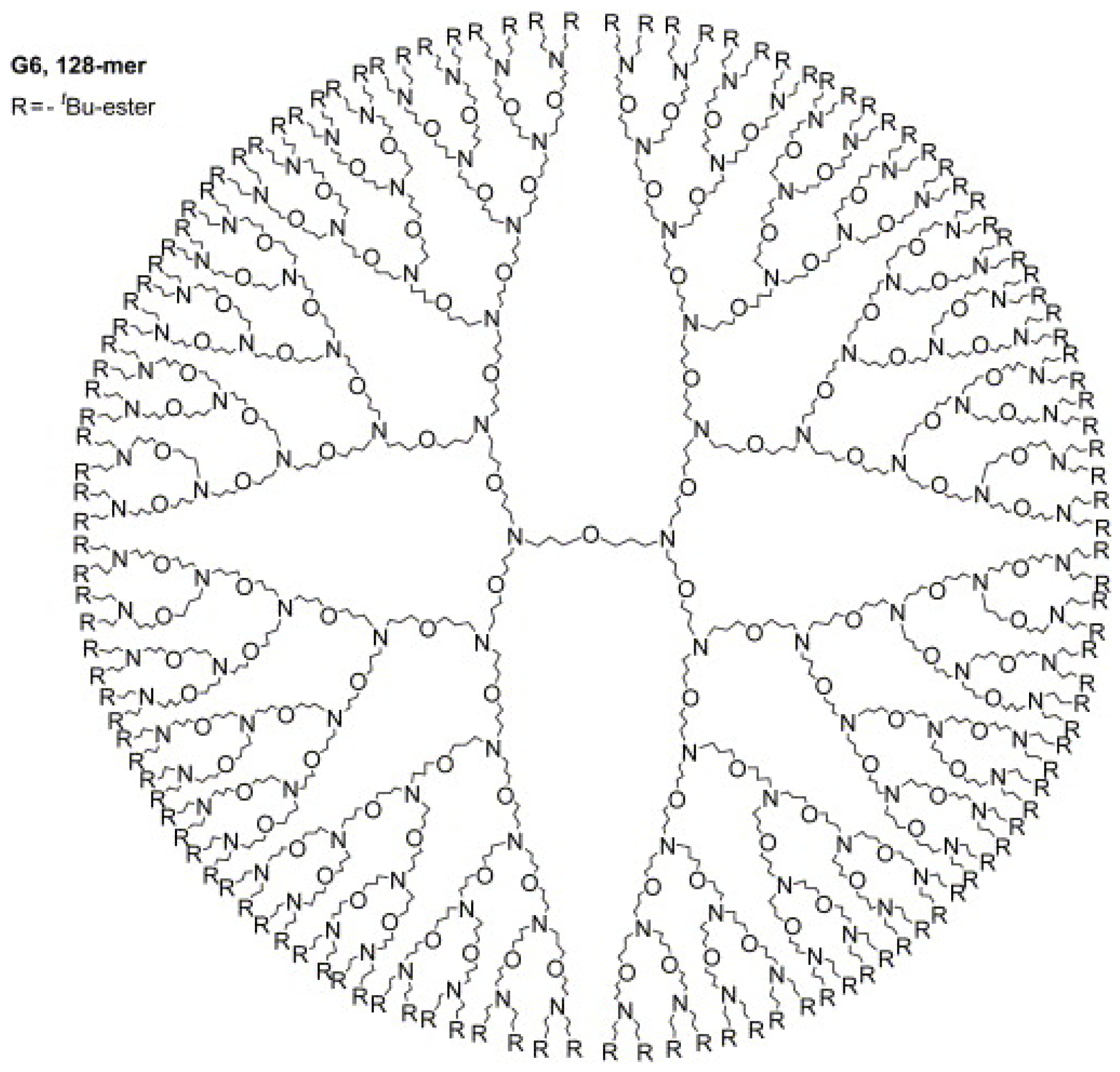
3.2. Propyl Ether Imine Dendrimer
- 1.
- 2.
- (i)
- Now, from the definition of reverse first Zagreb index, we have
- (ii)
- From the definition of reverse second Zagreb index, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 5 and by the definition of reverse first Zagreb polynomial, we have
- (ii)
- From the information given in Theorem 5 and by the definition of reverse second Zagreb polynomial, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 5 and by the definition of reverse first hyper-Zagreb index, we have
- (ii)
- From the information given in Theorem 5 and by the definition of reverse second hyper-Zagreb index, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 5 and by the definition of reverse first hyper-Zagreb polynomial, we have
- (ii)
- From the information given in Theorem 5 and by the definition of reverse second hyper-Zagreb polynomial, we have
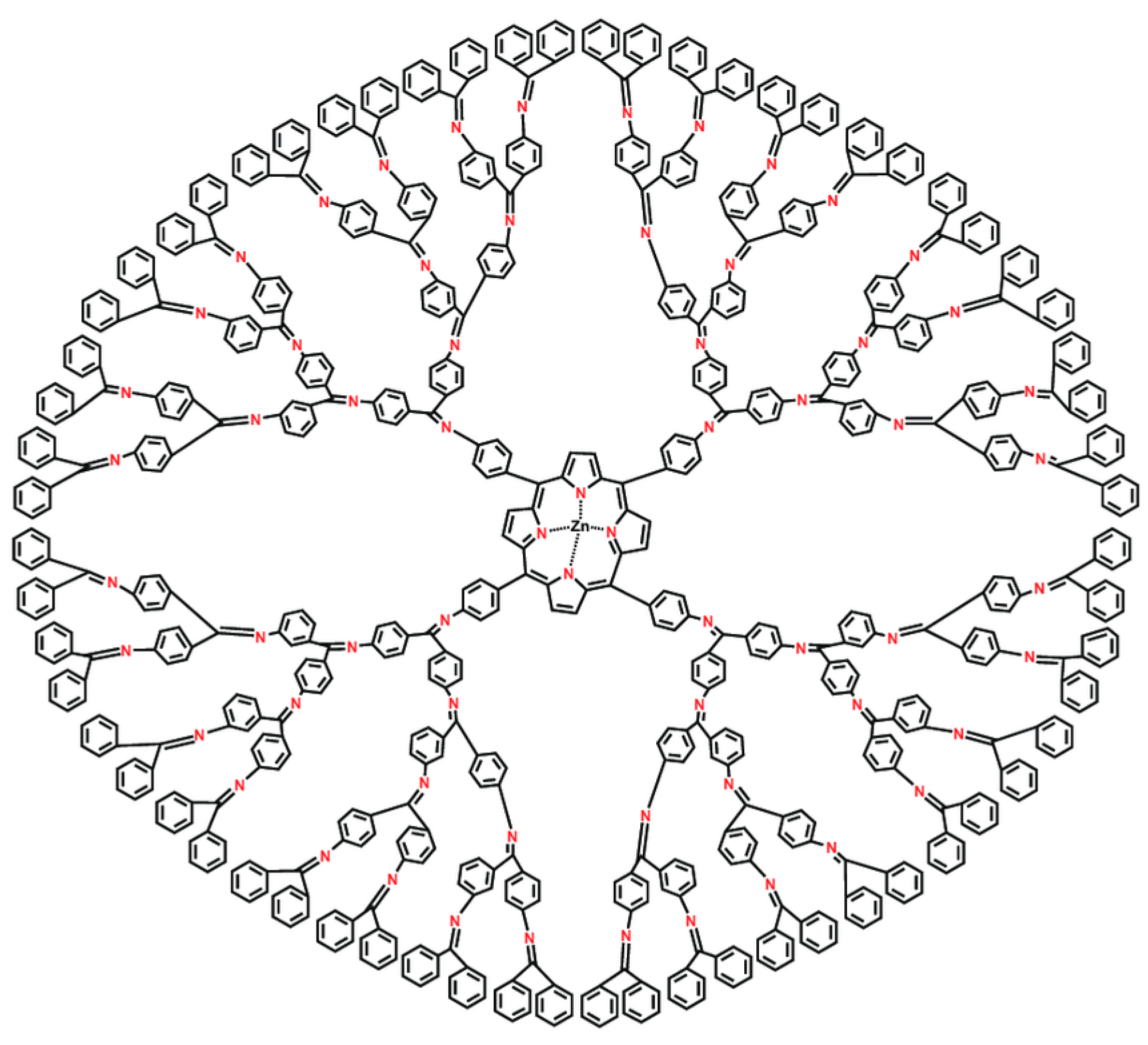
3.3. Zinc Prophyrin Dendrimer
- 1.
- 2.
- (i)
- Now, from the definition of reverse first Zagreb index, we have
- (ii)
- From the definition of reverse second Zagreb index, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 9 and by the definition of reverse first Zagreb polynomial, we have
- (ii)
- From the information given in Theorem 9 and by the definition of reverse second Zagreb polynomial, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 9 and by the definition of reverse first hyper-Zagreb index, we have
- (ii)
- From the information given in Theorem 9 and by the definition of reverse first hyper-Zagreb index, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 9 and by the definition of reverse first hyper-Zagreb polynomial, we have
- (ii)
- From the information given in Theorem 9 and by the definition of reverse second hyper-Zagreb polynomial, we have
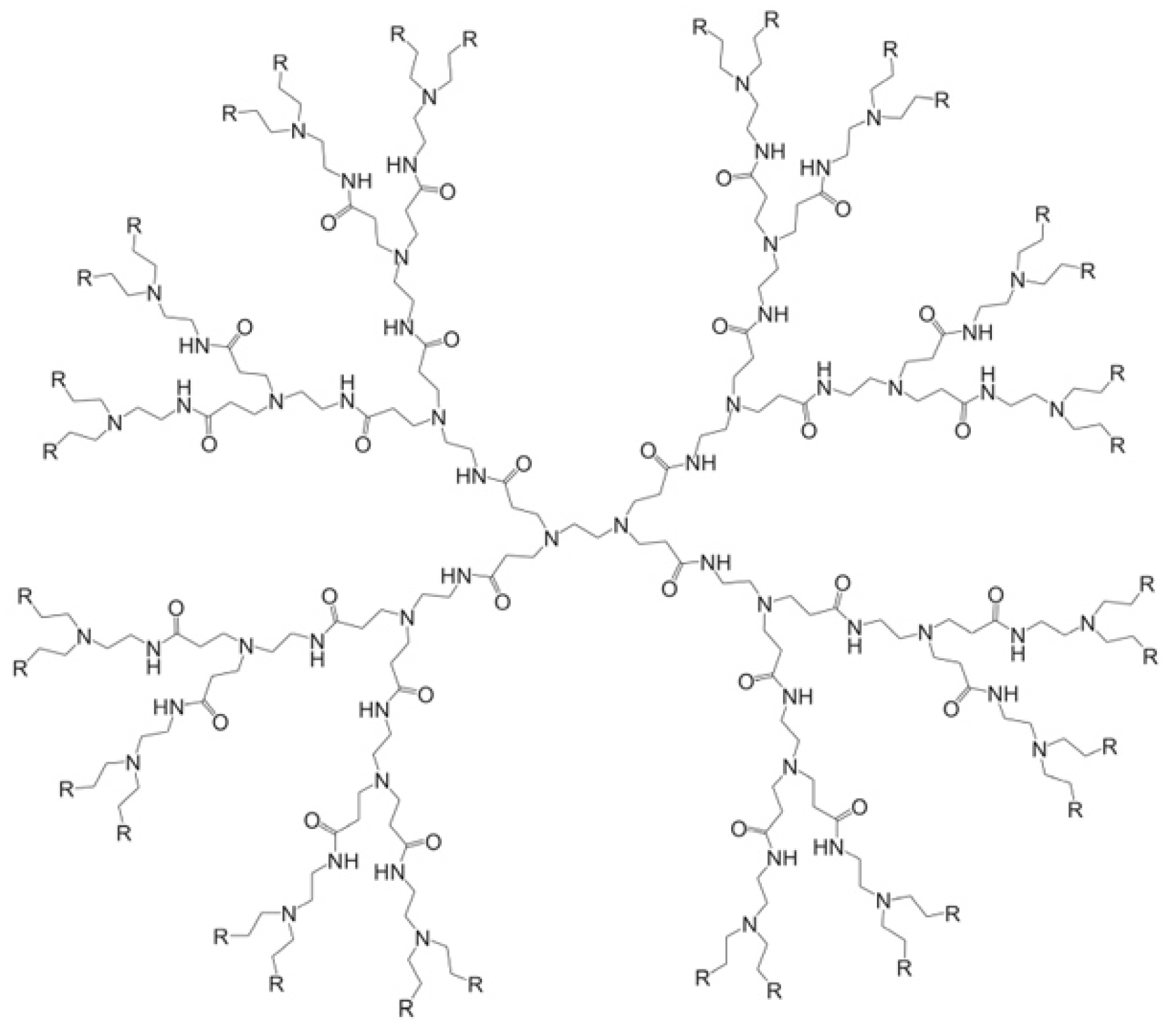
3.4. Poly(EThylene Amide Amine) Dendrimer
- 1.
- 2.
- (i)
- Now, from the definition of reverse first Zagreb index, we have
- (ii)
- From the definition of reverse Zagreb index, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 13 and by the definition of reverse first Zagreb polynomial, we have
- (ii)
- From the information given in Theorem 13 and by the definition of reverse second Zagreb polynomial, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 13 and by the definition of reverse first hyper-Zagreb index, we have
- (ii)
- From the information given in Theorem 13 and by the definition of reverse second hyper-Zagreb index, we have
- 1.
- 2.
- (i)
- From the information given in Theorem 13 and by the definition of reverse first hyper-Zagreb polynomial, we have
- (ii)
- From the information given in Theorem 13 and by the definition of reverse second hyper-Zagreb polynomial, we have
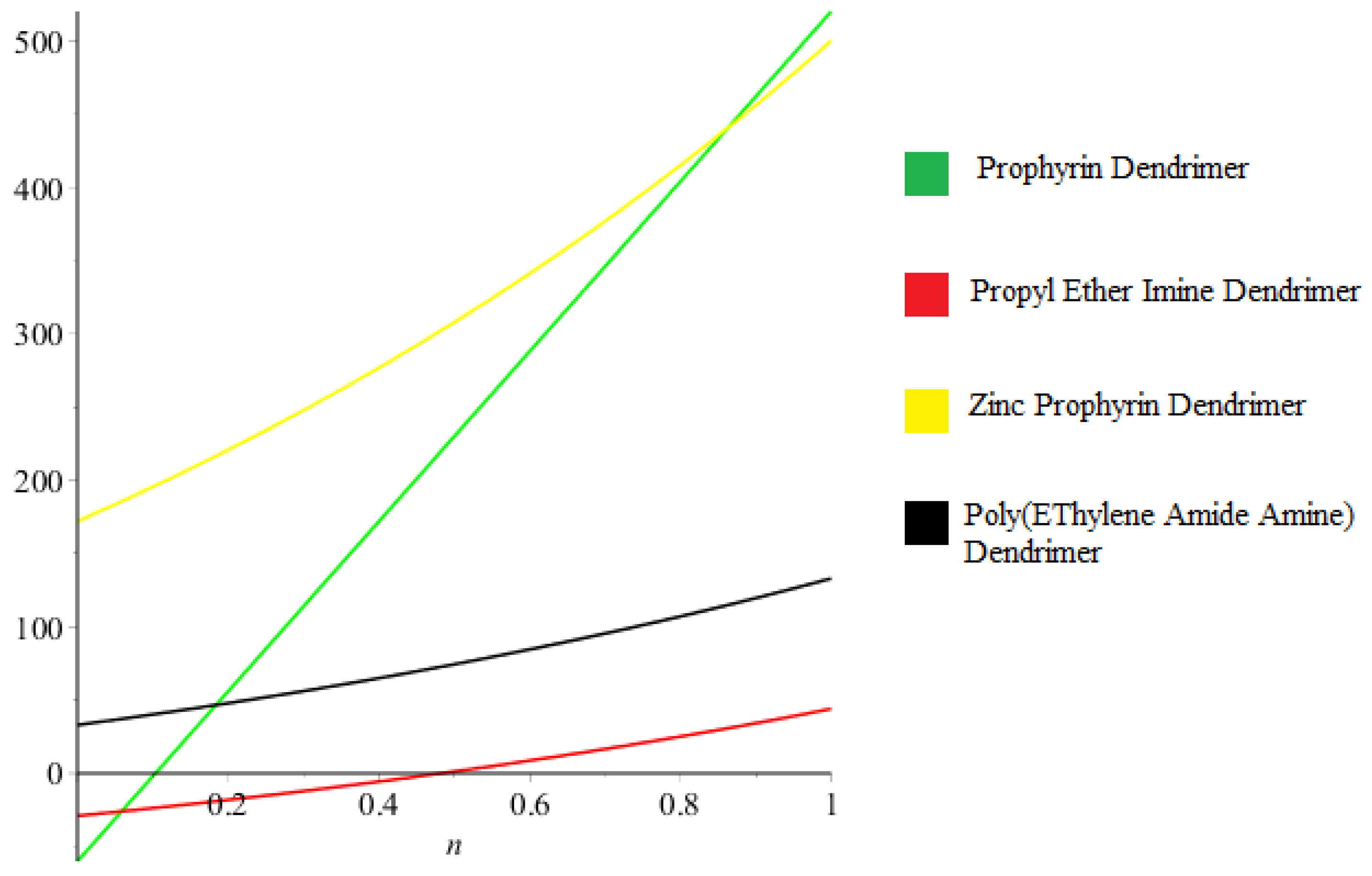
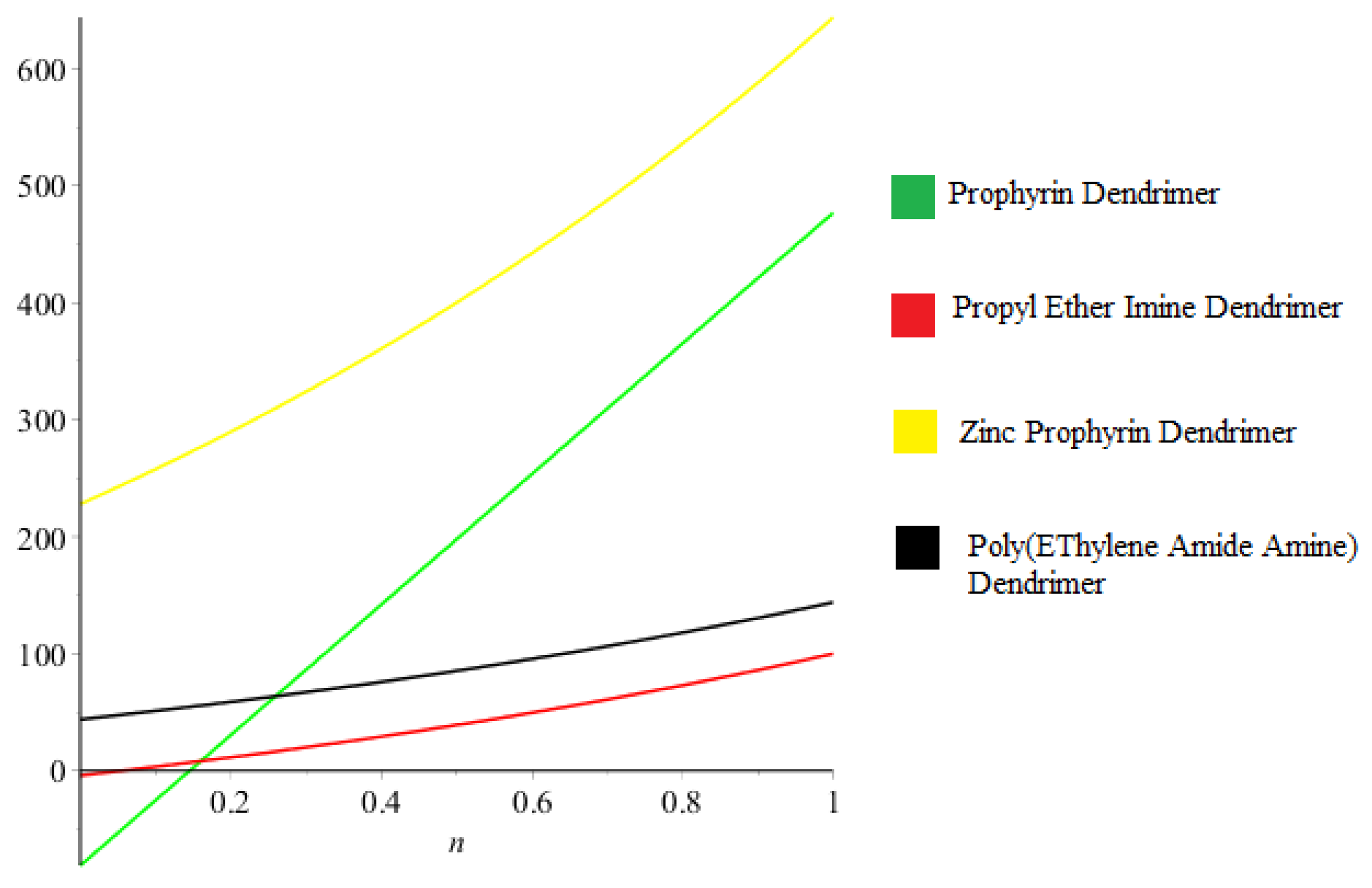
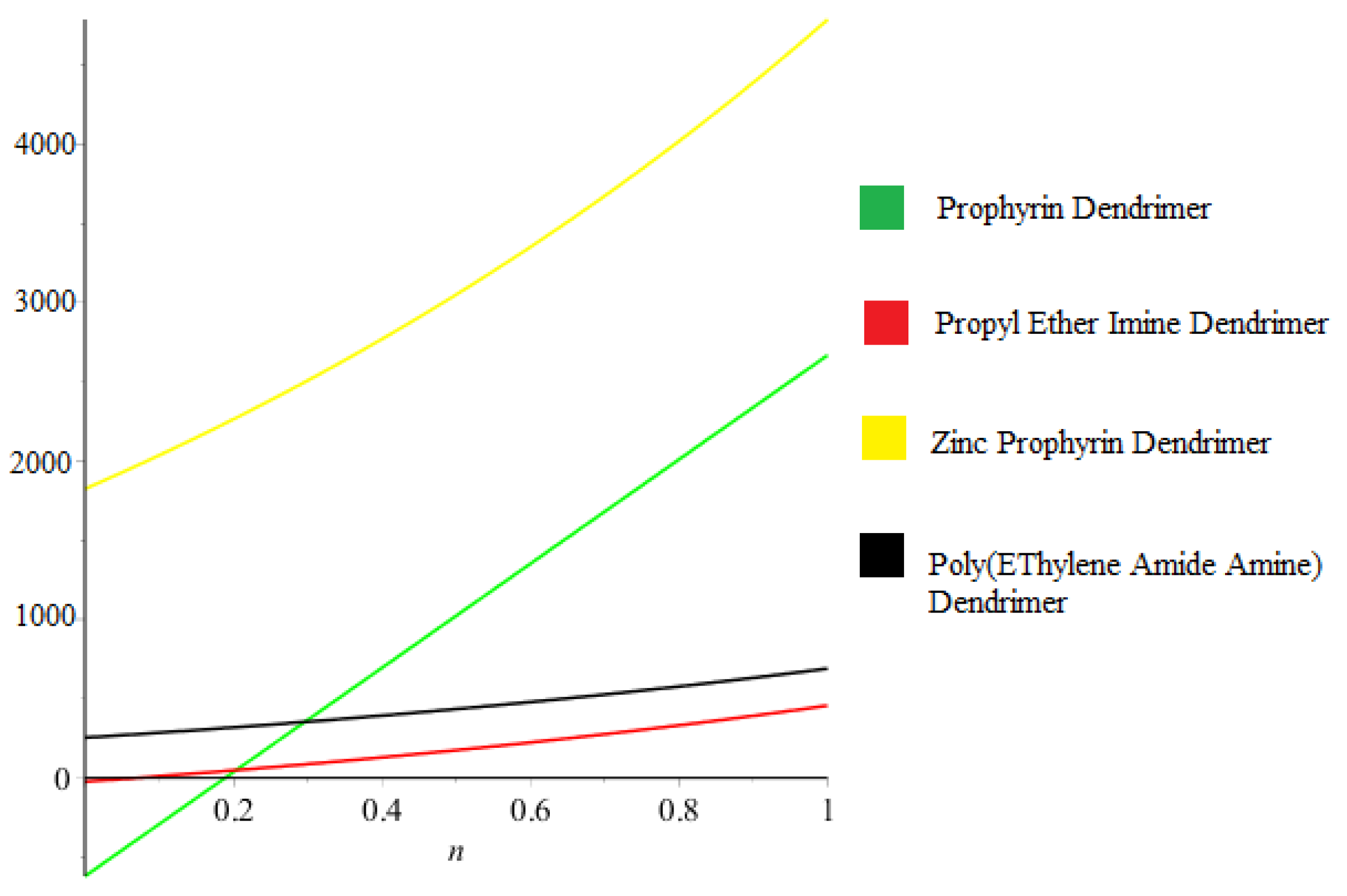
4. Graphical Comparison and Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Astruc, D.; Boisselier, E.; Ornelas, C. Dendrimers designed for functions: From physical, photophysical, and supramolecular properties to applications in sensing, catalysis, molecular electronics, and nanomedicine. Chem. Rev. 2010, 110, 1857–1959. [Google Scholar] [CrossRef] [PubMed]
- Vogtle, F.; Richardt, G.; Werner, N. Dendrimer Chemistry Concepts, Syntheses, Properties, Applications; Wiley: Hoboken, NJ, USA, 2009; ISBN 3-527-32066-0. [Google Scholar]
- Hirsch, B.E.; Lee, S.; Qiao, B.; Chen, C.; McDonald, K.P.; Tait, S.L.; Flood, A.H. Anion-induced dimerization of 5-fold symmetric cyanostars in 3D crystalline solids and 2D self-assembled crystals. Chem. Commun. 2014, 50, 9827–9830. [Google Scholar] [CrossRef] [PubMed]
- Buhleier, E.; Wehner, W.; Vogtle, F. “Cascade”- and “Nonskid-Chain-like” Syntheses of molecular cavity topologies. Synthesis 1978, 9, 155–158. [Google Scholar] [CrossRef]
- Denkewalter, R.G.; Kolc, J.; Lukasavage, W.J. Macromolecular Highly Branched Homogeneous Compound Based on Lysine Units. U.S. Patent 4,289,872, 6 April 1979. [Google Scholar]
- Denkewalter, R.G.; Kolc, J.F.; Lukasavage, W.J. Macromolecular Highly Branched Homogeneous Compound. U.S. Patent 4,410,688, 29 April 1981. [Google Scholar]
- Tomalia, A.D.; Dewald, R.J. Dense Star Polymers Having Core, Core Branches, Terminal Groups. U.S. Patent 4,507,466, 7 January 1983. [Google Scholar]
- Tomalia, D.A.; Baker, H.; Dewald, J.; Hall, M.; Kallos, G.; Martin, S.; Roeck, J.; Ryder, J.; Smith, P. A new class of polymers: Starburst-dendritic macromolecules. Polym. J. 1985, 17, 117–132. [Google Scholar] [CrossRef]
- Donald, A. Treelike molecules branch out. Tomalia synthesized first dendrimer molecule-chemistry-brief article. Sci. News 1996, 149, 17–32. [Google Scholar]
- Graovac, A.; Ghorbani, M.; Hosseinzadeh, M.A. Computing fifth geometric-arithmetic index for nanostar dendrimers. J. Math. NanoSci. 2011, 1, 33–42. [Google Scholar]
- Ashrafi, A.R.; Mirzargar, M. PI, Szeged and Edge Szeged Indices of an Infinite Family of Nanostar Dendrimers; CSIR: New Delhi, India, 2008. [Google Scholar]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S. M-polynomial and related topological indices of nanostar dendrimers. Symmetry 2016, 8, 97. [Google Scholar] [CrossRef]
- Ghorbani, M.; Hosseinzadeh, M.A. Computing ABC4 index of nanostar dendrimers. Optoelectron. Adv. Mater. Rapid Commun. 2010, 4, 1419–1422. [Google Scholar]
- Madanshekaf, A.; Ghaneeei, M. Computing two topological indices of nanostars dendrimer. Optoelectron. Adv. Mater. Rapid Commun. 2010, 4, 2200–2202. [Google Scholar]
- Dorosti, N.; Iranmanesh, A.; Diudea, M.V. Computing the cluj index of dendrimer nanostars. Match 2009, 62, 389–395. [Google Scholar]
- Aslam, A.; Bashir, Y.; Rafiq, M.; Haider, F.; Muhammad, N.; Bibi, N. Three new/old vertex-degree-based topological indices of some dendrimers structure. Electron. J. Biol. 2017, 13, 94–99. [Google Scholar]
- Gao, W.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aamir, M.; Aslam, A. On eccentricity-based topological indices study of a class of porphyrin-cored dendrimers. Biomolecules 2018, 8, 71. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.M.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aslam, A.; Nazeer, W. On eccentricity-based topological indices and polynomials of phosphorus-containing dendrimers. Symmetry 2018, 10, 237. [Google Scholar] [CrossRef]
- Kang, S.M.; Zahid, M.A.; Nazeer, W.; Gao, W. Calculating the degree-based topological indices of dendrimers. Open Chem. 2018, 16, 681–688. [Google Scholar] [CrossRef]
- Kulli, V.R. Reverse Zagreb and reverse hyper-Zagreb indices and their polynomials of rhombus silicate networks. Ann. Pure Appl. Math. 2018, 16, 47–51. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 2. [Google Scholar]
- Hosoya, H. On some counting polynomials in chemistry. Discret. Appl. Math. 1988, 19, 239–257. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Imran, M.; Ahmad, A. On Zagreb indices, Zagreb polynomials of some nanostar dendrimers. Appl. Math. Comput. 2016, 280, 132–139. [Google Scholar] [CrossRef]
- Deutsch, E.; Klavzar, S. M-polynomial and degree-based topological indices. arXiv, 2014; arXiv:1407.1592. [Google Scholar]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry 2016, 8, 149. [Google Scholar] [CrossRef]
- Fath-Tabar, G. Zagreb polynomial and PI indices of some nano structures. Digest J. Nanomater. Biostructures 2009, 4, 189–191. [Google Scholar]
- Iranmanesh, M.; Saheli, M. On the harmonic index and harmonic polynomial of caterpillars with diameter four. Iran. J. Math. Chem. 2015, 6, 41–49. [Google Scholar]
- Devillers, J.; Balaban, A.T. (Eds.) Topological Indices and Related Descriptors in QSAR and QSPAR; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Karelson, M. Molecular Descriptors in QSAR/QSPR; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Karelson, M.; Lobanov, V.S.; Katritzky, A.R. Quantum-chemical descriptors in QSAR/QSPR studies. Chem. Rev. 1996, 96, 1027–1044. [Google Scholar] [CrossRef] [PubMed]
- Bashir, Y.; Aslam, A.; Kamran, M.; Qureshi, M.I.; Jahangir, A.; Rafiq, M.; Muhammad, N. On forgotten topological indices of some dendrimers structure. Molecules 2017, 22, 867. [Google Scholar] [CrossRef] [PubMed]
- Aslam, A.; Guirao, J.L.G.; Ahmad, S.; Gao, W. Topological indices of the line graph of subdivision graph of complete bipartite graphs. Appl. Math. 2017, 11, 1631–1636. [Google Scholar] [CrossRef]
- Aslam, A.; Ahmad, S.; Gao, W. On certain topological indices of boron triangular nanotubes. Z. Naturforsch. A 2017, 72, 711–716. [Google Scholar] [CrossRef]
- Gao, W.; Wang, W.F.; Dimitrov, D.; Wang, Y.Q. Nano properties analysis via fourth multiplicative ABC indicator calculating. Arabian J. Chem. 2018, 11, 793–801. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Randić, M. Characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y. A survey on the Randić index. MATCH Commun. Math. Comput. Chem. 2008, 59, 127–156. [Google Scholar]
- Hu, Y.; Li, X.; Shi, Y.; Xu, T.; Gutman, I. On molecular graphs with smallest and greatest zeroth-order general Randić index. MATCH Commun. Math. Comput. Chem. 2005, 54, 425–434. [Google Scholar]
- Li, X.; Yang, Y. Sharp bounds for the general Randić index. MATCH Commun. Math. Comput. Chem. 2004, 51, 155–166. [Google Scholar]
- Clark, L.H.; Moon, J.W. On the general Randić index for certain families of trees. Ars Comb. 2000, 54, 223–235. [Google Scholar]
- Hu, Y.; Li, X.; Yuan, Y. Trees with minimum general Randić index. MATCH Commun. Math. Comput. Chem. 2004, 52, 119–128. [Google Scholar]
- Gutman, I.; Das, K.C. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Gutman, I. An exceptional property of first Zagreb index. MATCH Commun. Math. Comput. Chem. 2014, 72, 733–740. [Google Scholar]
- Hosamani, S.M.; Basavanagoud, B. New upper bounds for the first Zagreb index. MATCH Commun. Math. Comput. Chem. 2015, 74, 97–101. [Google Scholar]
- Das, K.C.; Gutman, I. Some properties of the second Zagreb index. MATCH Commun. Math. Comput. Chem. 2004, 52, 3. [Google Scholar]
- Zhou, B.; Gutman, I. Further properties of Zagreb indices. MATCH Commun. Math. Comput. Chem. 2005, 54, 233–239. [Google Scholar]
- Gao, W.; Wu, H.L.; Siddiqui, M.K.; Baig, A.Q. Study of biological networks using graph theory. Saudi J. Biol. Sci. 2018, 25, 1212–1219. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Younas, M.; Farooq, A.; Mahboob, A.; Nazeer, W. M-polynomials and degree-based topological indices of crystallographic structure of molecules. Biomolecules. 2018, 8, 107. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B. Zagreb indices. MATCH-Commun. Math. Comput. Chem. 2004, 52, 113–118. [Google Scholar]
- Milicevic, A.; Nikolic, S.; Trinajstic, N. On reformulated Zagreb indices. Mol. Divers. 2004, 8, 393–399. [Google Scholar] [CrossRef] [PubMed]
- Eliasi, M.; Iranmanesh, A.; Gutman, I. Multiplicative versions of first Zagreb index. Match-Commun. Math. Comput. Chem. 2012, 68, 217. [Google Scholar]
- Hao, J. Theorems about Zagreb indices and modified Zagreb indices. MATCH Commun. Math. Comput. Chem. 2011, 65, 659–670. [Google Scholar]
- Kulli, V.R. Multiplicative hyper-zagreb indices and coindices of graphs: computing these indices of some nanostructures. Int. Res. J. Pure Algebra 2016, 6, 7. [Google Scholar]
- Kwun, Y.C.; Virk, A.R.; Nazeer, W.; Kang, S.M. On the multiplicative degree-based topological indices of silicon-carbon Si2C3-I[p,q] and Si2C3-II[p,q]. Symmetry 2018, 10, 320. [Google Scholar] [CrossRef]
- Shirdel, G.H.; Ezapour, H.; Sayadi, A.M. The hyper-Zagreb index of graph operations. Iran. J. Math. Chem. 2013, 4, 213–220. [Google Scholar]
- Soleimani, N.; Bahnamiri, S.B.; Nikmehr, M.J. Study of dendrimers by topological indices. Acta Chem. Iasi 2017, 25, 145–162. [Google Scholar] [CrossRef]
- Omolara, O.A. The mechanisms, kinetics and thermodynamics of the gas-phase pyrolysis of sec-butyl bromide: A computational approach. Int. Res. J. Pure Appl. Chem. 2018, 16, 1–10. [Google Scholar]

| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
|---|---|---|---|---|---|---|---|---|---|
| First Reverse Zagreb Index | 448 | 956 | 1464 | 1972 | 2480 | 2988 | 3496 | 4004 | 4512 |
| Second Reverse Zagreb Index | 497 | 1055 | 1613 | 2171 | 2729 | 3287 | 3845 | 4403 | 4961 |
| First Reverse Hyper-Zagreb Index | 2182 | 4694 | 7206 | 9718 | 12,230 | 14,742 | 17,254 | 19,766 | 22,278 |
| Second Reverse Hyper-Zagreb Index | 2669 | 5959 | 9249 | 12,539 | 15,829 | 19,119 | 22,409 | 25,699 | 28,989 |
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
|---|---|---|---|---|---|---|---|---|---|
| First Reverse Zagreb Index | 44 | 190 | 482 | 1066 | 2234 | 4570 | 9242 | 18,586 | 37,274 |
| Second Reverse Zagreb Index | 100 | 308 | 724 | 1556 | 3220 | 6548 | 13,204 | 26,516 | 53,140 |
| First Reverse Hyper-Zagreb Index | 410 | 1258 | 2954 | 6346 | 13,130 | 26,698 | 53,834 | 108,106 | 216,650 |
| Second Reverse Hyper-Zagreb Index | 456 | 1416 | 3336 | 7176 | 14,856 | 30,216 | 60,936 | 122,376 | 245,256 |
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
|---|---|---|---|---|---|---|---|---|---|
| First Reverse Zagreb Index | 500 | 1156 | 2468 | 5092 | 10,340 | 20,836 | 41,828 | 83,812 | 167,780 |
| Second Reverse Zagreb Index | 644 | 1476 | 3140 | 6468 | 13,124 | 26,436 | 53,060 | 106,308 | 212,804 |
| First Reverse Hyper-Zagreb Index | 2644 | 6052 | 12,868 | 26,500 | 53,764 | 108,292 | 217,348 | 435,460 | 871,684 |
| Second Reverse Hyper-Zagreb Index | 4788 | 10,716 | 22,572 | 46,284 | 93,708 | 188,556 | 378,252 | 757,644 | 1,516,428 |
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
|---|---|---|---|---|---|---|---|---|---|
| First Reverse Zagreb Index | 133 | 333 | 733 | 1533 | 3133 | 6333 | 12,733 | 25,533 | 51,133 |
| Second Reverse Zagreb Index | 144 | 344 | 744 | 1544 | 3144 | 6344 | 12,744 | 25,544 | 51,144 |
| First Reverse Hyper-Zagreb Index | 599 | 1439 | 3119 | 6479 | 13,199 | 26,639 | 53,519 | 107,279 | 214,799 |
| Second Reverse Hyper-Zagreb Index | 690 | 1562 | 3306 | 6794 | 13,770 | 27,722 | 55,626 | 111,434 | 223,050 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Younas, M.; Farooq, A.; Virk, A.U.R.; Nazeer, W. Some Reverse Degree-Based Topological Indices and Polynomials of Dendrimers. Mathematics 2018, 6, 214. https://doi.org/10.3390/math6100214
Gao W, Younas M, Farooq A, Virk AUR, Nazeer W. Some Reverse Degree-Based Topological Indices and Polynomials of Dendrimers. Mathematics. 2018; 6(10):214. https://doi.org/10.3390/math6100214
Chicago/Turabian StyleGao, Wei, Muhammad Younas, Adeel Farooq, Abaid Ur Rehman Virk, and Waqas Nazeer. 2018. "Some Reverse Degree-Based Topological Indices and Polynomials of Dendrimers" Mathematics 6, no. 10: 214. https://doi.org/10.3390/math6100214
APA StyleGao, W., Younas, M., Farooq, A., Virk, A. U. R., & Nazeer, W. (2018). Some Reverse Degree-Based Topological Indices and Polynomials of Dendrimers. Mathematics, 6(10), 214. https://doi.org/10.3390/math6100214





