2.2. Lower Bound for Double Roman Domination Number of
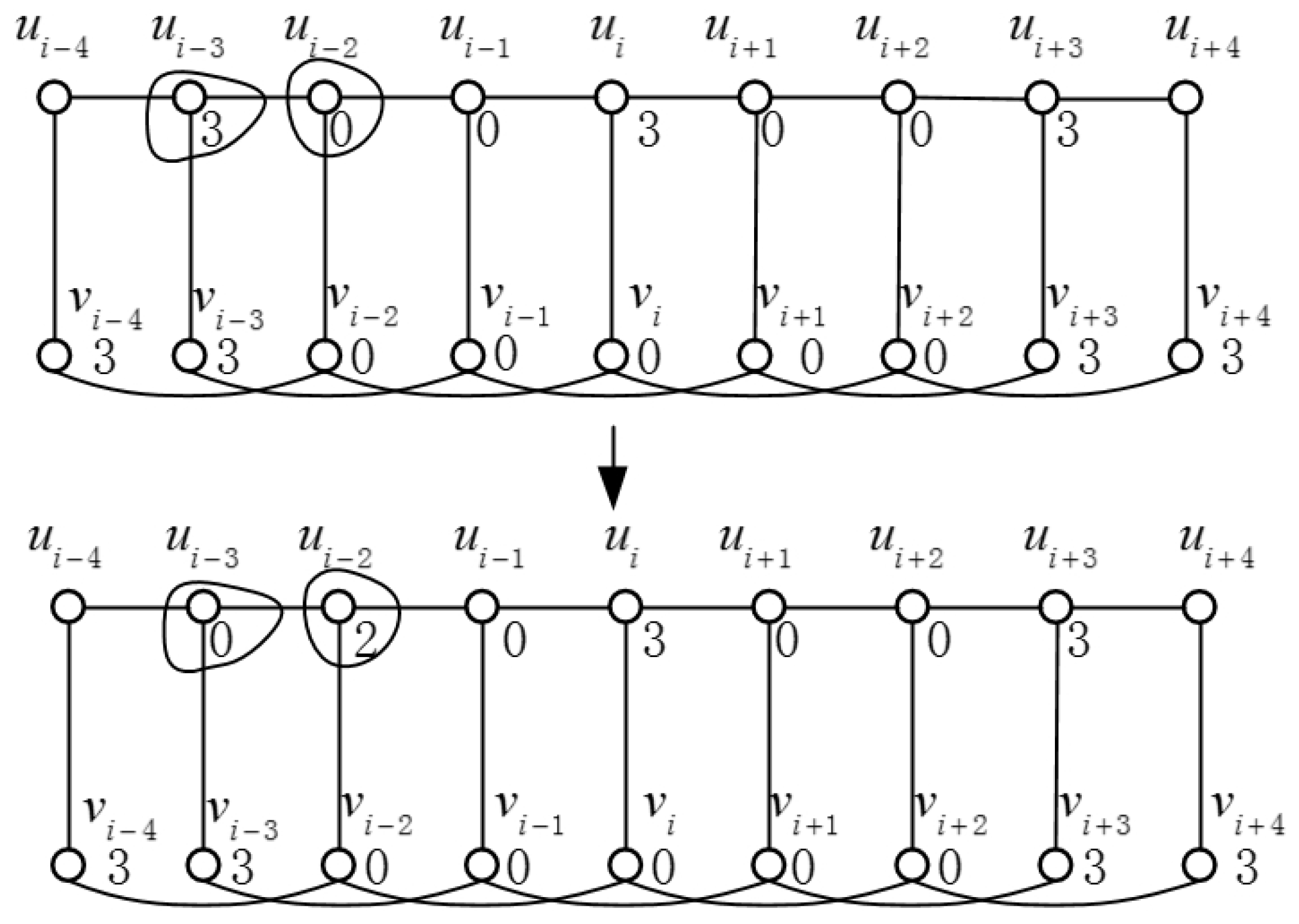
Lemma 2. Let f be a -function of with . Then, .
Proof. Since
and
need to be double Roman dominated by vertices in
, we have
. Now, we will show that
. Otherwise, it is clear that
, and
for any
. Since
and
need to be double Roman dominated, we have
. Now, we can obtain a DRDF
from
f by letting
,
and
for
. Then, we have
, a contradiction (see
Figure 1). Therefore,
. ☐
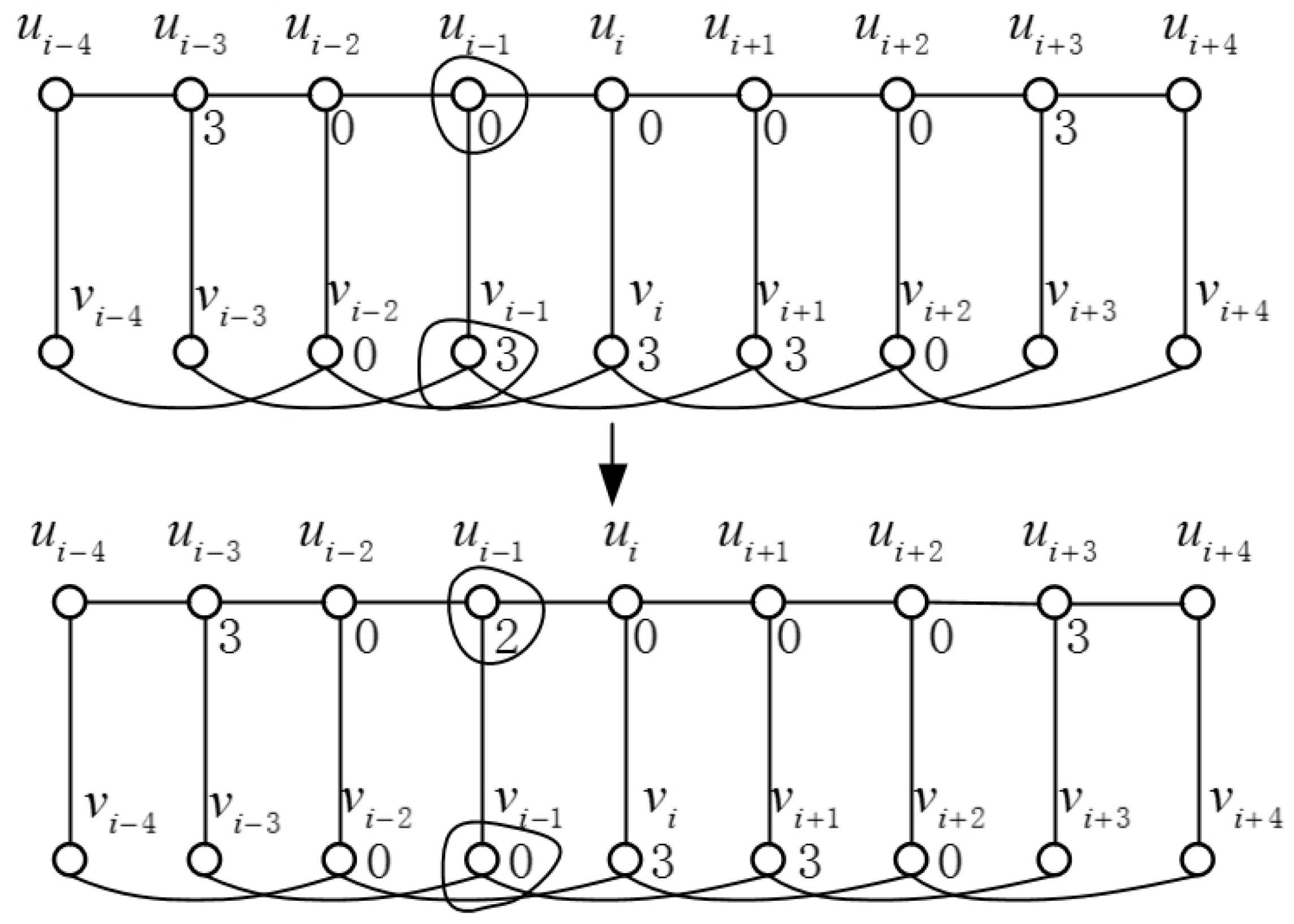
Lemma 3. Let f be a -function of with . Then, for any , it is impossible that and for any .
Proof. Suppose to the contrary that
and
for
. Then, we have
. Now, we can obtain a DRDF
from
f by letting
,
and
for
. Then, we have
, a contradiction (see
Figure 2). ☐
Lemma 4. Let f be a -function of with . Then, for each , there exists a neighbor y of x such that , or equivalently, it is impossible that for any , for any .
Proof. Suppose to the contrary that there is a vertex such that for every neighbor y of x. Now, it is sufficient to consider the following two cases.
Case 1: for some i.
In this case, we have and for . Then, we have , contradicting Lemma 2.
Case 2: for some i.
In this case, since and need to be double Roman dominated, we have and . By Lemma 3, such a case is impossible. ☐
Discharging procedure: Let f be a DRDF of . We set the initial charge of every vertex x be . We use the discharging procedure, leading to a final charge , defined by applying the following rules:
- R1:
Each for which transmits 0.8 charge to each neighbor y with transmits 0.6 charge to each neighbor y with .
- R2:
Each for which transmits 0.4 charge to each neighbor y with .
Proposition 2. If , then .
Proof. Assume f is a -function of . We use the above discharging procedure. Now, it is sufficient to consider the following three cases.
Case 1: By Lemma 4, there exists a vertex z with for some , for any . Therefore, by rule R1, for each , the final charge is at least . For each , then the final charge is at least .
Case 2: By rule R2, for each , the final charge is at least .
Case 3: For each , the final charge is 0.8 by rule R1. For each , the final charge is at least 0.8 by rules R1 and R2.
Hence, . Since is an integer, we have . ☐
By using the above discharging rules, we have the following lemma immediately, and the proof is omitted.
Lemma 5. Let f be a -function of with . If we use the above discharging procedure for f on , then:
- (a)
if there exists a path P of type , or type , or type , or type , or type , or type , or type or a subgraph P of type , then .
- (b)
if there exist a path of type and a path of type , then .
- (c)
if there exists a subgraph H of type , then .
- (d)
if there exist a path P of type , together with a subgraph H of type or type , then .
- (e)
if there exist three paths of type , then .
Lemma 6. Let f be a -function of with weight , then there exists no edge for which .
Proof. We use the above discharging procedure for
f on
, and similar to the proof of Proposition 2, we have:
and so:
By Lemma 5a and Equation (
2), we have that there exists no edge
.
Now, suppose to the contrary that there exists an edge , and it is sufficient to consider the following three cases.
Case 1: .
We have
. Otherwise, there exists a path
P of type
or type
. By Lemma 5a, we have
, contradicting Equation (
2).
Since needs to be double Roman dominated, we have . Otherwise, for some or .
If
for some
, there exists a path
P of type
. By Lemma 5a, we have
, contradicting Equation (
2).
If
, there exists a subgraph
H of type
. By Lemma 5c, we have
, contradicting Equation (
2).
Now, it is sufficient to consider the following two cases.
Case 1.1: , .
To double Roman dominate
, we have
or
. First, we have
and
. Otherwise,
or
is a path
P of type
. By Lemma 5a, we have
, contradicting Equation (
2).
Now, we have that it is impossible
. Otherwise, the set
induces a subgraph
H of type
. By Lemma 5c, we have
, contradicting Equation (
2).
Therefore, we have . Now, it is sufficient to consider the following two cases.
Case 1.1.1: , .
Since
and
need to be double Roman dominated, we have
,
. Then, there exists a path
of type
and a path
of type
. By Lemma 5b, we have
, contradicting Equation (
2).
Case 1.1.2: , .
Since
and
need to be double Roman dominated, we have
. Then, there exist a path
of type
and a path
of type
. By Lemma 5b,
, contradicting Equation (
2).
Case 1.2: , .
Since
needs to be double Roman dominated, we have
. Then, there exist a path
of type
and a path
of type
. By Lemma 5b,
, contradicting Equation (
2).
Case 2: .
We have
. Otherwise, there exists a path
P of type
or type
. By Lemma 5a, we have
, contradicting Equation (
2).
Since
needs to be double Roman dominated, we have
. Otherwise, by Lemma 5a or Lemma 5c, we obtain a contradiction with Equation (
2).
Now, we consider the following two subcases.
Case 2.1: , .
Since
needs to be double Roman dominated, we have
. Then, there exist a path
of type
and a path
of type
. By Lemma 5b,
, contradicting Equation (
2).
Case 2.2: , .
Since
needs to be double Roman dominated, we have
for some
or
. If
for some
, there exist a path
of type
and a path
of type
. By Lemma 5b,
, contradicting Equation (
2).
If
, then by Lemma 5b,c, we have
. Since
needs to be double Roman dominated, we have
. Then, there exist a path
of type
and a path
of type
. By Lemma 5b,
, contradicting Equation (
2).
Case 3: .
We have
. Otherwise, there exists a path
P of type
or type
. By Lemma 5a, we have
, contradicting Equation (
2).
Since needs to be double Roman dominated, we have or .
Case 3.1: , .
By Lemma 5b,c and Equation (
2), we have
. Since
needs to be double Roman dominated, we have
. Considering isomorphism, we without loss of generality assume
and
. Since
needs to be double Roman dominated,
. Then, there exist a path
of type
and a path
of type
. By Lemma 5b,
, contradicting Equation (
2).
Case 3.2: , .
By Lemma 5a and Equation (
2), we have
. Since
needs to be double Roman dominated, we have
. Then, there exist a path
of type
and a path
of type
. By Lemma 5b,
, contradicting Equation (
2).
Therefore, the proof is complete. ☐
Lemma 7. Let f be a -function of with weight , and , then .
Proof. We use the above discharging procedure for
f on
. By Lemma 4, we have
. Now, suppose to the contrary that
. By rules R1 and R2 and Equation (
1), we have:
contradicting Equation (
2). ☐
Lemma 8. If and f is a -function of with for some , then .
Proof. Suppose to the contrary that there exists a -function f with such that for some . By Lemma 6, we have . Let . By Lemma 7, we have . Therefore, we just need to consider the following two cases.
Case 1: .
We may w.l.o.g assume that
,
,
=
or
and
. Since
need to be double Roman dominated, we have
, and thus,
. Since
needs to be double Roman dominated, we have
. Thus,
. Since
need to be double Roman dominated, we have
. Then, there exist three paths
of type
. By Lemma 5e, we have
, contradicting Equation (
2).
Case 2: .
It is sufficient to consider the following cases.
Case 2.1: and .
Since
need to be double Roman dominated, we have
. Then, there exist a path
P of type
, and a subgraph
H of type
or type
. By Lemma 5d, we have
, contradicting Equation (
2).
Case 2.2: , and .
First, we have
. Otherwise, we may without loss of generality assume that
. Since
need to be double Roman dominated, we have
. Then, there exist a path
P of type
, and a path
H of type
. By Lemma 5d, we have
, contradicting Equation (
2).
Then, since need to be double Roman dominated, we have . By Lemma 6, we have . Since need to be double Roman dominated, we have and .
It is impossible that
and
. Otherwise, there exists a path
P of type
or a subgraph
P of type
. By Lemma 5a, we have
, contradicting Equation (
2).
It is impossible
. Otherwise, there exists a path
P of type
. By Lemma 5a, we have
, contradicting Equation (
2).
Then, we may without loss of generality assume that
and
. Then, there exists a path
P of type
. By Lemma 5a, we have
, contradicting Equation (
2). ☐
Lemma 9. If and f is a -function of with for some , then .
Proof. Suppose to the contrary that there exists a -function f with such that for some . By Lemma 6, we have . Let . By Lemma 7, we have , and we just need to consider the following two cases.
Case 1: .
We may without loss of generality assume that , , = or and . Since and need to be double Roman dominated, we have , contradicting Lemma 8.
Case 2: .
Now, it is sufficient to consider the following two cases.
Case 2.1: and .
Since need to be double roman dominated, we have , contradicting Lemma 8.
Case 2.2: , where and .
By Lemma 8, for each , and thus, .
Then, we have . Otherwise, or . By symmetry, we may assume without loss of generality that . Thus, we have . Since need to be double Roman dominated, we have , contradicting Lemma 8.
Now, it is sufficient to consider the following three cases.
Case 2.2.1: .
By Lemma 6, we have .
Since needs to be double Roman dominated and by Lemma 8, we have . Since needs to be double Roman dominated, we have . Thus, there exists an edge , a contradiction with Lemma 6.
Case 2.2.2: .
By Lemma 6, we have .
Since need to be double Roman dominated, we have . Thus, there exists an edge , a contradiction with Lemma 6.
Case 2.2.3: .
By Lemma 6, we have .
Since needs to be double Roman dominated, we have . By Lemma 6, we have . Since needs to be double Roman dominated and by Lemma 8, we have . Since needs to be double Roman dominated, we have . Thus, there exists an edge , a contradiction with Lemma 6. ☐
Lemma 10. Let and (mod 5). If f is a -function of , then .
Proof. Suppose to the contrary that . By Lemmas 8 and 9, we have . Now, we have:
Claim 1. for any with .
Proof. Suppose to the contrary that there exists a vertex with and . We consider the following two cases.
Case 1: for some .
Since , we have . By Lemma 6, we have , and . Since needs to be double Roman dominated, we have . Since needs to be double Roman dominated, we have . Since , contradicting Lemma 6.
Case 2: for some .
Since , we have . By Lemma 6, we have . Since needs to be double Roman dominated, we have . Since needs to be double Roman dominated, we have . Since , contradicting Lemma 6. ☐
We assume without loss of generality that
. By Lemma 6, we have
,
and
. Since
needs to be double Roman dominated, we assume without loss of generality that
. By Claim 1, we have
. Since
, together with Lemma 6, we have
. Since
needs to be double Roman dominated, we have
. Then, by Lemma 6, we have
. Since
needs to be double Roman dominated, we have
. That is to say, we have:
By repeatedly applying Claim 1 and Lemma 6, can be determined for each , and we have . It is straightforward to see that only if (mod 5), a contradiction. ☐