The Double Roman Domination Numbers of Generalized Petersen Graphs P(n, 2)

Abstract

A double Roman dominating function (DRDF) f on a given graph G is a mapping from $V\left(G\right)$ to $\{0,1,2,3\}$ in such a way that a vertex u for which $f\left(u\right)=0$ has at least a neighbor labeled 3 or two neighbors both labeled 2 and a vertex u for which $f\left(u\right)=1$ has at least a neighbor labeled 2 or 3. The weight of a DRDF f is the value $w\left(f\right)={\sum }_{u\in V\left(G\right)}f\left(u\right)$. The minimum weight of a DRDF on a graph G is called the double Roman domination number ${\gamma }_{dR}\left(G\right)$ of G. In this paper, we determine the exact value of the double Roman domination number of the generalized Petersen graphs $P(n,2)$ by using a discharging approach.

1. Introduction

In this paper, only graphs without multiple edges or loops are considered. For two vertices u and v of a graph G, we say $u\sim v$ in G if $uv\in E\left(G\right)$. For positive integer k and $u,v\in V\left(G\right)$, let $d(u,v)$ be the distance between u and v and $N_k\left(v\right)=\left\{u\right|d(u,v)=k\}$. The neighborhood of v in G is defined to be $N_1\left(v\right)$ (or simply $N\left(v\right)$). The closed neighborhood $N\left[v\right]$ of v in G is defined to be $N\left[v\right]=\left\{v\right\}\cup N\left(v\right)$. For a vertex subset $S\subseteq V\left(G\right)$, we denote by $G\left[S\right]$ the subgraph induced by S. For a positive integer n, we denote $\left[n\right]=\{1,2,\cdots ,n\}$. For a set $S=\{x_1,x_2,\cdots ,x_n\}$, if $x_i=x_j$ for some i and j, then S is considered as a multiset. Otherwise, S is an ordinary set.

For positive integer numbers n and k with n at least $2k+1$, the generalized Petersen graph $P(n,k)$ is a graph with its vertex set $\left\{u_i\right|i=1,2,\cdots ,n\}\cup \left\{v_i\right|i=1,2,\cdots ,n\}$ and its edge set the union of $\{u_i{u}_{i+1},u_i{v}_i,v_i{v}_{i+k}\}$ for $1\le i\le n$, where subscripts are reduced modulo n (see [1]).

A subset D of the vertex set of a graph G is a dominating set if every vertex in $V\left(G\right)\backslash D$ has at least one neighbor in D. The domination number, denoted by $\gamma \left(G\right)$, is the minimum number of vertices over all dominating sets of G.

There have been more than 200 papers studying various domination on graphs in the literature [2,3,4,5,6]. Among them, Roman domination and double Roman domination appear to be a new variety of interest [3,7,8,9,10,11,12,13,14,15].

A double Roman dominating function (DRDF) f on a given graph G is a mapping from $V\left(G\right)$ to $\{0,1,2,3\}$ in such a way that a vertex u for which $f\left(u\right)=0$ has at least a neighbor labeled 3 or two neighbors both labeled 2 and a vertex u for which $f\left(u\right)=1$ has at least a neighbor labeled 2 or 3. The weight of a DRDF f is the value $w\left(f\right)={\sum }_{u\in V\left(G\right)}f\left(u\right)$. The minimum weight of a DRDF on a graph G is called the double Roman domination number ${\gamma }_{dR}\left(G\right)$ of G. A DRDF f of G with $w\left(f\right)={\gamma }_{dR}\left(G\right)$ is called a ${\gamma }_{dR}\left(G\right)$-function. Given a DRDF f of G, we denote $E_{\{x_1,x_2\}}^f=\{uv\in E\left(G\right)|\{f\left(u\right),f\left(v\right)\}=\{x_1,x_2\}\}$. A graph G is a double Roman Graph if ${\gamma }_{dR}\left(G\right)=3\gamma \left(G\right)$.

In [7], Beeler et al. obtained the following results:

Proposition 1

([7]). In a double Roman dominating function of weight ${\gamma }_{dR}\left(G\right)$, no vertex needs to be assigned the value one.

By Proposition 1, we now consider the DRDF of a graph G in which there exists no vertex assigned with one in the following.

Given a DRDF f of a graph G, suppose $(V_0^f,V_2^f,V_3^f)$ is the ordered partition of the vertex set of G induced by f in such a way that $V_i^f=\{v:f\left(v\right)=i\}$ for $i=0,2,3$. It can be seen that there is a 1-1 mapping between f and $(V_0^f,V_2^f,V_3^f)$, and we write $f=(V_0^f,V_2^f,V_3^f)$, or simply $(V_0,V_2,V_3)$. Given a DRDF f of $P(n,2)$ and letting $w_i\in \{0,2,3\}$ for $i=1,2,3$ with $w_1\ge w_2\ge w_3$, we write $V_j^{w_1{w}_2{w}_3}=\{x\in V(P(n,2))|f(x)=j,\{w_1,w_2,w_3\}=\{f(x_1),f(x_2),f(x_3)\}\}$, where $N\left(x\right)=\{x_1,x_2,x_3\}$.

Now, we will use $f(·)=q^{+}$ to represent the value scope $f(·)\ge q$ for an integer q. We say a path $t_1{t}_2\cdots t_k$ is a path of type $c_1-c_2-\cdots -c_k$ if $f(t_i)=c_i$ for $i\in \left[k\right]$. Let H be a subgraph induced by five vertices $s_1$, $s_2$, $s_3$, $s_4$, $s_5$ with $s_1\sim s_2,s_2\sim s_3,s_3\sim s_4$, $s_3\sim s_5$ satisfying $f(s_3)=0$ and $f(s_1)=a$, $f(s_2)=b$, $f(s_4)=c$, $f(s_5)=d$ for some $a,b,c,d\in \{0,2,3\}$, then we say H is a subgraph of type $a-b-0_{-d}^{-c}$.

Let W be a subgraph induced by four vertices $s_1$, $s_2$, $s_3$, $s_4$ with $s_1\sim s_2,s_2\sim s_3,s_2\sim s_4$, satisfying $f(s_1)=a$, $f(s_2)=0$, $f(s_3)=b$ and $f(s_4)=c$ for some $a,b,c\in \{0,2,3\}$, then we say W is a subgraph of type $a-0_{-c}^{-b}$.

In the graph $P(n,2)$, we will denote the set of vertices of $\{u_i,v_i\}$ with $L^{\left(i\right)}$. For a given DRDF f of $P(n,2)$, let $w_f(L^{(i)})$ denote the weight of $L^{\left(i\right)}$, that is $w_f(L^{(i)})={\sum }_{u\in V(L^{(i)})}f(u)$. Let ${\mathcal{B}}_i$ = $\{L^{(i-2)}$, $L^{(i-1)}$, $L^{\left(i\right)}$, $L^{(i+1)}$, $L^{(i+2)}\}$, where the subscripts are taken modulo n. We define $w_f({\mathcal{B}}_i)=\sum _{j=-2}^2{w}_f(L^{(i+j)})$, and:

$$f({\mathcal{B}}_i)=f\left(\begin{array}{ccccc}\hfill u_{i-2}& \hfill u_{i-1}& \hfill u_i& \hfill u_{i+1}& \hfill u_{i+2}\\ \hfill v_{i-2}& \hfill v_{i-1}& \hfill v_i& \hfill v_{i+1}& \hfill v_{i+2}\end{array}\right).$$

Motivation: Beeler et al. [7] put forward an open problem about characterizing the double Roman graphs. As an interesting family of graphs, the domination and its variations of generalized Petersen graphs have attracted considerable attention [1,16]. Therefore, it is interesting to characterize the double Roman graphs in generalized Petersen graphs. In this paper, we focus on finding the double Roman graphs in $P(n,2)$.

2. Double Roman Domination Number of $\mathit{P}(\mathit{n},\mathbf{2})$

2.1. Upper Bound for the Double Roman Domination Number of $P(n,2)$

Lemma 1.

If $n\ge 5$, then:

$${\gamma }_{dR}(P(n,2))\le \left\{\begin{array}{cc}\lceil \frac{8n}{5}\rceil ,\hfill & n\equiv 0\left(\mathrm{mod}5\right),\hfill \\ \lceil \frac{8n}{5}\rceil +1,\hfill & n\equiv 1,2,3,4\left(\mathrm{mod}5\right).\hfill \end{array}\right.$$

Proof. 

We consider the following five cases.

Case 1: $n\equiv 0$ (mod 5).

Let:

$$P_5=\left[\begin{array}{ccccc}\hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2& \hfill 2\end{array}\right].$$

Then, by repeating the pattern of $P_5$, we obtain a DRDF of weight $8k$ of $P(5k,2)$, and the upper bound is obtained.

Case 2: $n\equiv 1$ (mod 5).

If $n=6$, let:

$$P_6=\left[\begin{array}{cccccc}\hfill 0& \hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0\\ \hfill 2& \hfill 0& \hfill 0& \hfill 0& \hfill 2& \hfill 3\end{array}\right].$$

Then, the pattern $P_6$ induces a DRDF of weight 11 of $P(6,2)$, and the desired upper bound is obtained.

If $n\ge 11$, let:

$$P_{11}=\left[\begin{array}{ccccccccccc}\hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0& \hfill 2& \hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2& \hfill 2& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 3& \hfill 2\end{array}\right].$$

Then, by repeating the leftmost five columns of the pattern of $P_{11}$, we obtain a DRDF of weight $8k+3$ of $P(5k+1,2)$, and the desired upper bound is obtained.

Case 3: $n\equiv 2$ (mod 5).

If $n=7$, let:

$$P_7=\left[\begin{array}{ccccccc}\hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0& \hfill 3& \hfill 0\\ \hfill 0& \hfill 0& \hfill 2& \hfill 2& \hfill 0& \hfill 0& \hfill 2\end{array}\right].$$

Then, the pattern $P_7$ induces a DRDF of weight 13 of $P(7,2)$, and the desired upper bound is obtained.

If $n\ge 12$, let:

$$P_{12}=\left[\begin{array}{cccccccccccc}\hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0& \hfill 2& \hfill 0& \hfill 3& \hfill 0& \hfill 2& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2& \hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0& \hfill 0& \hfill 2& \hfill 2\end{array}\right].$$

Then, by repeating the leftmost five columns of the pattern of $P_{12}$, we obtain a DRDF of weight $8k+6$ of $P(5k+2,2)$, and the desired upper bound is obtained.

Case 4: $n\equiv 3$ (mod 5).

If $n\ge 8$, let:

$$P_8=\left[\begin{array}{cccccccc}\hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0& \hfill 2& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2& \hfill 2& \hfill 0& \hfill 2& \hfill 2\end{array}\right].$$

Then, by repeating the leftmost five columns of the pattern of $P_8$, we obtain a DRDF of weight $8k+6$ of $P(5k+3,2)$, and the desired upper bound is obtained.

Case 5: $n\equiv 4$ (mod 5).

If $n\ge 9$, let:

$$P_9=\left[\begin{array}{ccccccccc}\hfill 2& \hfill 0& \hfill 2& \hfill 0& \hfill 0& \hfill 3& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2& \hfill 2& \hfill 0& \hfill 0& \hfill 3& \hfill 2\end{array}\right].$$

Then, by repeating the leftmost five columns of the pattern of $P_9$, we obtain a DRDF of weight $8k+8$ of $P(5k+4,2)$, and the desired upper bound is obtained. ☐

2.2. Lower Bound for Double Roman Domination Number of $P(n,2)$

Lemma 2.

Let f be a ${\gamma }_{dR}$-function of $P(n,2)$ with $n\ge 5$. Then, $w_f({\mathcal{B}}_i)\ge 4$.

Proof. 

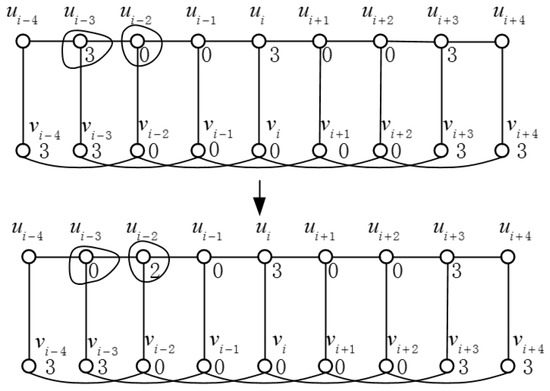
Since $u_i,v_i,u_{i+1}$ and $u_{i-1}$ need to be double Roman dominated by vertices in ${\mathcal{B}}_i$, we have $w_f({\mathcal{B}}_i)\ge 3$. Now, we will show that $w_f({\mathcal{B}}_i)\ne 3$. Otherwise, it is clear that $f(u_i)=3$, and $f\left(x\right)=0$ for any $x\in {\mathcal{B}}_i\backslash \{u_i\}$. Since $v_{i\pm 1}, u_{i\pm 2}$ and $v_{i\pm 2}$ need to be double Roman dominated, we have $f\left(u_{i\pm 3}\right)=f\left(v_{i\pm 3}\right)=f\left(v_{i\pm 4}\right)=3$. Now, we can obtain a DRDF $f^{\prime }$ from f by letting $f^{\prime }\left(u_{i-2}\right)=2$, $f^{\prime }\left(u_{i-3}\right)=0$ and $f^{\prime }\left(v\right)=f\left(v\right)$ for $v\in V(P(n,2))\backslash \{u_{i-2},u_{i-3}\}$. Then, we have $w(f^{\prime })<w\left(f\right)$, a contradiction (see Figure 1). Therefore, $w_f({\mathcal{B}}_i)\ge 4$. ☐

Figure 1. Construct a function $f^{\prime }$ from f used in Lemma 2.

Lemma 3.

Let f be a ${\gamma }_{dR}$-function of $P(n,2)$ with $n\ge 5$. Then, for any $i\in \left[n\right]$, it is impossible that $f(v_{i-1})=f(v_i)=f(v_{i+1})=3$ and $f\left(x\right)=0$ for any $x\in {\mathcal{B}}_i\backslash \{v_{i-1},v_i,v_{i+1}\}$.

Proof. 

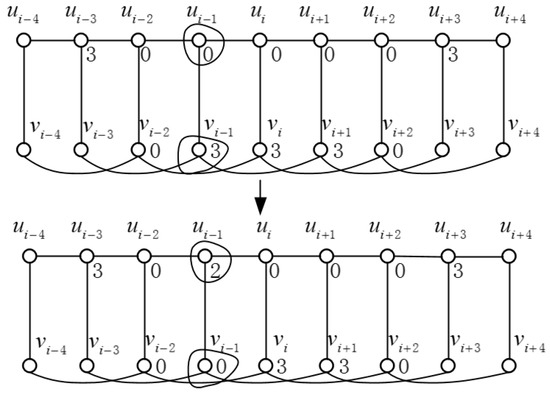
Suppose to the contrary that $f(v_{i-1})=f(v_i)=f(v_{i+1})=3$ and $f\left(x\right)=0$ for $x\in {\mathcal{B}}_i\backslash \{v_{i-1},v_i,v_{i+1}\}$. Then, we have $f(u_{i\pm 3})=3$. Now, we can obtain a DRDF $f^{\prime }$ from f by letting $f^{\prime }(u_{i-1})=2$, $f^{\prime }(v_{i-1})=0$ and $f^{\prime }\left(v\right)=f\left(v\right)$ for $v\in V(P(n,2))\backslash \{v_{i-1},u_{i-1}\}$. Then, we have $w(f^{\prime })<w\left(f\right)$, a contradiction (see Figure 2). ☐

Figure 2. Construct a function $f^{\prime }$ from f in Lemma 3.

Lemma 4.

Let f be a ${\gamma }_{dR}$-function of $P(n,2)$ with $n\ge 5$. Then, for each $x\in V_3^{000}$, there exists a neighbor y of x such that $y\in V_0^{320}\cup V_0^{330}\cup V_0^{322}\cup V_0^{332}\cup V_0^{333}$, or equivalently, it is impossible that for any $x\in V_3^{000}$, $f\left(z\right)=0$ for any $z\in N_2\left(x\right)$.

Proof. 

Suppose to the contrary that there is a vertex $x\in V_3^{000}$ such that $y\in V_0^{300}$ for every neighbor y of x. Now, it is sufficient to consider the following two cases.

Case 1: $x=u_i$ for some i.

In this case, we have $f\left(u_i\right)=3$ and $f\left(x\right)=0$ for $x\in {\mathcal{B}}_i\backslash \{u_i\}$. Then, we have $w_f({\mathcal{B}}_i)=3<4$, contradicting Lemma 2.

Case 2: $x=v_i$ for some i.

In this case, since $u_{i\pm 1}$ and $u_{i\pm 2}$ need to be double Roman dominated, we have $f(v_{i\pm 1})=3$ and $f(u_{i\pm 3})=3$. By Lemma 3, such a case is impossible. ☐

Discharging procedure: Let f be a DRDF of $P(n,2)$. We set the initial charge of every vertex x be $s\left(x\right)=f\left(x\right)$. We use the discharging procedure, leading to a final charge $s^{\prime }$, defined by applying the following rules:

R1:

Each $s\left(x\right)$ for which $s\left(x\right)=3$ transmits 0.8 charge to each neighbor y with $y\in V_0^{300}$ transmits 0.6 charge to each neighbor y with $y\in V_0^{320}\cup V_0^{330}\cup V_0^{322}\cup V_0^{332}\cup V_0^{333}$.

R2:

Each $s\left(x\right)$ for which $s\left(x\right)=2$ transmits 0.4 charge to each neighbor y with $y\in V_0$.

Proposition 2.

If $n\ge 5$, then ${\gamma }_{dR}(P(n,2))\ge \lceil \frac{8n}{5}\rceil$.

Proof. 

Assume f is a ${\gamma }_{dR}$-function of $P(n,2)$. We use the above discharging procedure. Now, it is sufficient to consider the following three cases.

Case 1: By Lemma 4, there exists a vertex z with $f\left(z\right)\ge 2$ for some $z\in N_2\left(x\right)$, for any $x\in V_3^{000}$. Therefore, by rule R1, for each $v\in V_3^{000}$, the final charge $s^{\prime }\left(v\right)$ is at least $3-0.6-0.8-0.8=0.8$. For each $v\in V_3\backslash V_3^{000}$, then the final charge $s^{\prime }\left(v\right)$ is at least $3-0.8-0.8=1.4$.

Case 2: By rule R2, for each $v\in V_2$, the final charge $s^{\prime }\left(v\right)$ is at least $2-0.4-0.4-0.4=0.8$.

Case 3: For each $v\in V_0^{300}$, the final charge $s^{\prime }\left(v\right)$ is 0.8 by rule R1. For each $v\in V_0\backslash V_0^{300}$, the final charge $s^{\prime }\left(v\right)$ is at least 0.8 by rules R1 and R2.

From the above, we have:

$$s^{\prime }\left(v\right)\ge 0.8 \mathrm{for} \mathrm{any} v\in P(n,2).$$

(1)

Hence, $w\left(f\right)=\sum _{v\in V(P(n,2))}s\left(v\right)=\sum _{v\in V(P(n,2))}{s}^{\prime }\left(v\right)\ge 0.8\times 2n=\frac{8n}{5}$. Since $w\left(f\right)$ is an integer, we have $w\left(f\right)\ge \lceil \frac{8n}{5}\rceil$. ☐

By using the above discharging rules, we have the following lemma immediately, and the proof is omitted.

Lemma 5.

Let f be a ${\gamma }_{dR}$-function of $P(n,2)$ with $n\ge 5$. If we use the above discharging procedure for f on $P(n,2)$, then:

(a) 

if there exists a path P of type $2-2-2$, or type $2^{+}-3$, or type $2-2-0-3$, or type $3-0-2^{+}-0-3-0-2^{+}-0-3$, or type $3-0-2^{+}-0-3-0-3$, or type $3-0-3-0-3$, or type $2^{+}-0-3-0-3-0-2^{+}$ or a subgraph P of type $3-0_{-3}^{-3}$, then ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$.

(b) 

if there exist a path $P_1$ of type $2-2$ and a path $P_2$ of type $2^{+}-0-3$, then ${\sum }_{v\in V(P_1)\cup V(P_2)}(s^{\prime }(v)-0.8)\ge 1$.

(c) 

if there exists a subgraph H of type $2-2-0_{-2}^{-2}$, then ${\sum }_{v\in V\left(H\right)}(s^{\prime }(v)-0.8)\ge 1.2$.

(d) 

if there exist a path P of type $3-0-3$, together with a subgraph H of type $2^{+}-0-3-0-2^{+}$ or type $3-0_{-2^{+}}^{-2^{+}}$, then ${\sum }_{v\in V\left(P\right)\cup V\left(H\right)}(s^{\prime }(v)-0.8)\ge 1$.

(e) 

if there exist three paths $P_1,P_2,P_3$ of type $3-0-3$, then ${\sum }_{v\in V\left(P_1\right)\cup V\left(P_2\right)\cup V\left(P_3\right)}(s^{\prime }\left(v\right)-0.8)\ge 1.2$.

Lemma 6.

Let f be a ${\gamma }_{dR}$-function of $P(n,2)$ with weight $\lceil \frac{8n}{5}\rceil$, then there exists no edge $uv\in E(P(n,2))$ for which $uv\in E_{\{2,2\}}^f\cup E_{\{2,3\}}^f\cup E_{\{3,3\}}^f$.

Proof. 

First, we have:

$${\gamma }_{dR}(P(n,2))=w\left(f\right)=\lceil \frac{8n}{5}\rceil \le \frac{8n+4}{5}=\frac{8n}{5}+0.8,$$

and so:

$$w\left(f\right)-\frac{8n}{5}\le 0.8.$$

We use the above discharging procedure for f on $P(n,2)$, and similar to the proof of Proposition 2, we have:

$$w\left(f\right)=\sum _{v\in V\left(P\right(n,2\left)\right)}{s}^{\prime }\left(v\right),$$

and so:

$$\sum _{v\in V(P(n,2))}(s^{\prime }(v)-\frac{4}{5})\le 0.8$$

(2)

By Lemma 5a and Equation (2), we have that there exists no edge $uv\in E_{\{2,3\}}^f\cup E_{\{3,3\}}^f$.

Now, suppose to the contrary that there exists an edge $uv\in E_{\{2,2\}}^f$, and it is sufficient to consider the following three cases.

Case 1: $f(u_i)=f(u_{i+1})=2$.

We have $f(u_{i-1})=f(u_{i+2})=f(v_{i+1})=f(v_i)=0$. Otherwise, there exists a path P of type $2-2-2$ or type $2^{+}-3$. By Lemma 5a, we have ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Since $u_{i+2}$ needs to be double Roman dominated, we have $\{f(u_{i+3}),f(v_{i+2})\}=\{0,2\}$. Otherwise, $f\left(x\right)=3$ for some $x\in \{u_{i+3},v_{i+2}\}$ or $f(u_{i+3})=f(v_{i+2})=2$.

If $f\left(x\right)=3$ for some $x\in \{u_{i+3},v_{i+2}\}$, there exists a path P of type $2-2-0-3$. By Lemma 5a, we have ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

If $f(u_{i+3})=f(v_{i+2})=2$, there exists a subgraph H of type $2-2-0_{-2}^{-2}$. By Lemma 5c, we have ${\sum }_{v\in V\left(H\right)}(s^{\prime }\left(v\right)-0.8)\ge 1.2$, contradicting Equation (2).

Now, it is sufficient to consider the following two cases.

Case 1.1: $f(v_{i+2})=2$, $f(u_{i+3})=0$.

To double Roman dominate $v_{i+1}$, we have $f(v_{i+3})\ge 2$ or $f(v_{i-1})\ge 2$. First, we have $f(v_{i+3})\ne 3$ and $f(v_{i-1})\ne 3$. Otherwise, $u_i{u}_{i+1}{v}_{i+1}{v}_{i+3}$ or $u_i{u}_{i+1}{v}_{i+1}{v}_{i-1}$ is a path P of type $2-2-0-3$. By Lemma 5a, we have ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Now, we have that it is impossible $f(v_{i+3})=f(v_{i-1})=2$. Otherwise, the set $\{u_i,u_{i+1},v_{i+1},v_{i+3},v_{i-1}\}$ induces a subgraph H of type $2-2-0_{-2}^{-2}$. By Lemma 5c, we have ${\sum }_{v\in V\left(H\right)}(s^{\prime }\left(v\right)-0.8)\ge 1.2$, contradicting Equation (2).

Therefore, we have $\{f(v_{i+3}),f(v_{i-1})\}=\{0,2\}$. Now, it is sufficient to consider the following two cases.

Case 1.1.1: $f(v_{i+3})=2$, $f(v_{i-1})=0$.

Since $v_{i-1}$ and $u_{i-1}$ need to be double Roman dominated, we have $f(v_{i-3})=3$, $f(u_{i-2})=2^{+}$. Then, there exists a path $P_1$ of type $2-2$ and a path $P_2$ of type $2^{+}-0-3$. By Lemma 5b, we have ${\sum }_{v\in V(P_1)\cup V(P_2)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Case 1.1.2: $f(v_{i+3})=0$, $f(v_{i-1})=2$.

Since $u_{i+3}$ and $v_{i+3}$ need to be double Roman dominated, we have $f(u_{i+4})=f(v_{i+5})=3$. Then, there exist a path $P_1$ of type $2-2$ and a path $P_2$ of type $3-0-3$. By Lemma 5b, ${\sum }_{v\in V\left(P_1\right)\cup V\left(P_2\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Case 1.2: $f(v_{i+2})=0$, $f(u_{i+3})=2$.

Since $v_{i+2}$ needs to be double Roman dominated, we have $f(v_{i+4})=3$. Then, there exist a path $P_1$ of type $2-2$ and a path $P_2$ of type $2-0-3$. By Lemma 5b, ${\sum }_{v\in V\left(P_1\right)\cup V\left(P_2\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Case 2: $f(v_i)=f(u_i)=2$.

We have $f(u_{i\pm 1})=f(v_{i\pm 2})=0$. Otherwise, there exists a path P of type $2-2-2$ or type $2^{+}-3$. By Lemma 5a, we have ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Since $u_{i+1}$ needs to be double Roman dominated, we have $\{f(u_{i+2}),f(v_{i+1})\}=\{0,2\}$. Otherwise, by Lemma 5a or Lemma 5c, we obtain a contradiction with Equation (2).

Now, we consider the following two subcases.

Case 2.1: $f(v_{i+1})=2$, $f(u_{i+2})=0$.

Since $u_{i+2}$ needs to be double Roman dominated, we have $f(u_{i+3})=3$. Then, there exist a path $P_1$ of type $2-2$ and a path $P_2$ of type $2-0-3$. By Lemma 5b, ${\sum }_{v\in V(P_1)\cup V(P_2)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Case 2.2: $f(v_{i+1})=0$, $f(u_{i+2})=2$.

Since $v_{i+1}$ needs to be double Roman dominated, we have $f\left(x\right)=3$ for some $x\in \{v_{i+3},v_{i-1}\}$ or $f\left(v_{i+3}\right)=f\left(v_{i-1}\right)=2$. If $f\left(x\right)=3$ for some $x\in \{v_{i+3},v_{i-1}\}$, there exist a path $P_1$ of type $2-2$ and a path $P_2$ of type $2-0-3$. By Lemma 5b, ${\sum }_{v\in V\left(P_1\right)\cup V\left(P_2\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

If $f(v_{i+3})=f(v_{i-1})=2$, then by Lemma 5b,c, we have $u_{i-2}=0$. Since $u_{i-2}$ needs to be double Roman dominated, we have $f(u_{i-3})=3$. Then, there exist a path $P_1$ of type $2-2$ and a path $P_2$ of type $2-0-3$. By Lemma 5b, ${\sum }_{v\in V\left(P_1\right)\cup V\left(P_2\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Case 3: $f(v_{i+1})=f(v_{i-1})=2$.

We have $f(u_{i\pm 1})=f(v_{i\pm 3})=0$. Otherwise, there exists a path P of type $2-2-2$ or type $2^{+}-3$. By Lemma 5a, we have ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Since $u_i$ needs to be double Roman dominated, we have $f(u_i)=2$ or $f(v_i)=3$.

Case 3.1: $f\left(u_i\right)=2$, $f(v_i)=0$.

By Lemma 5b,c and Equation (2), we have $f(u_{i\pm 2})=0$. Since $v_i$ needs to be double Roman dominated, we have $\{f(v_{i-2}),f(v_{i+2})\}=\{0,2\}$. Considering isomorphism, we without loss of generality assume $f(v_{i+2})=2$ and $f(v_{i-2})=0$. Since $u_{i-2}$ needs to be double Roman dominated, $f(u_{i-3})=3$. Then, there exist a path $P_1$ of type $2-2$ and a path $P_2$ of type $2-0-3$. By Lemma 5b, ${\sum }_{v\in V(P_1)\cup V(P_2)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Case 3.2: $f\left(u_i\right)=0$, $f\left(v_i\right)=3$.

By Lemma 5a and Equation (2), we have $f(v_{i\pm 2})=0$. Since $u_{i+1}$ needs to be double Roman dominated, we have $f(u_{i+2})=2$. Then, there exist a path $P_1$ of type $2-2$ and a path $P_2$ of type $2-0-3$. By Lemma 5b, ${\sum }_{v\in V\left(P_1\right)\cup V\left(P_2\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Therefore, the proof is complete. ☐

Lemma 7.

Let f be a ${\gamma }_{dR}$-function of $P(n,2)$ with weight $\lceil \frac{8n}{5}\rceil$, $v\in V_3^{000}$ and $S=\{x|x\in N_2\left(v\right),f\left(x\right)\ge 2\}$, then $1\le |S|\le 2$.

Proof. 

We use the above discharging procedure for f on $P(n,2)$. By Lemma 4, we have $|S|\ge 1$. Now, suppose to the contrary that $\left|S\right|\ge 3$. By rules R1 and R2 and Equation (1), we have:

$$\begin{array}{c}\sum _{v\in V(P(n,2))}(s^{\prime }(v)-\frac{4}{5})\ge \sum _{x\in N[v]\cup N_2\left(v\right)}(s^{\prime }\left(x\right)-\frac{4}{5})\ge 1,\end{array}$$

contradicting Equation (2). ☐

Lemma 8.

If $n\ge 5$ and f is a ${\gamma }_{dR}$-function of $P(n,2)$ with $f(u_i)=3$ for some $i\in [n]$, then $w\left(f\right)\ge \lceil \frac{8n}{5}\rceil +1$.

Proof. 

Suppose to the contrary that there exists a ${\gamma }_{dR}$-function f with $w\left(f\right)=\lceil \frac{8n}{5}\rceil$ such that $f\left(u_i\right)=3$ for some $i\in \left[n\right]$. By Lemma 6, we have $f\left(v_i\right)=f(u_{i\pm 1})=0$. Let $S=\{x|x\in N_2\left(v\right),f\left(x\right)\ge 2\}$. By Lemma 7, we have $\left|S\right|\in \{1,2\}$. Therefore, we just need to consider the following two cases.

Case 1: $\left|S\right|=1$.

We may w.l.o.g assume that $\{f\left(u_{i-2}\right)$, $f\left(v_{i-1}\right)$, $f\left(v_{i-2}\right)\}$ = $\{0,0,2\}$ or $\{0,0,3\}$ and $f\left(v_{i+1}\right)=f\left(v_{i+2}\right)=f\left(u_{i+2}\right)=0$. Since $u_{i+2},v_{i+2}$ need to be double Roman dominated, we have $f\left(u_{i+3}\right)=f\left(v_{i+4}\right)=3$, and thus, $f\left(v_{i+3}\right)=0$. Since $v_{i+1}$ needs to be double Roman dominated, we have $f\left(v_{i-1}\right)=3$. Thus, $f\left(u_{i-2}\right)=f\left(v_{i-2}\right)=0$. Since $u_{i-2},v_{i-2}$ need to be double Roman dominated, we have $f\left(u_{i-3}\right)=f\left(v_{i-4}\right)=3$. Then, there exist three paths $P_1,P_2,P_3$ of type $3-0-3$. By Lemma 5e, we have ${\sum }_{v\in V\left(P_1\right)\cup V\left(P_2\right)\cup V\left(P_3\right)}(s^{\prime }\left(v\right)-0.8)\ge 1.2$, contradicting Equation (2).

Case 2: $\left|S\right|=2$.

It is sufficient to consider the following cases.

Case 2.1: $S\subseteq \{v_{i-1},v_{i-2},u_{i-2}\}$ and $f\left(v_{i+1}\right)=f\left(v_{i+2}\right)=f\left(u_{i+2}\right)=0$.

Since $u_{i+2},v_{i+2}$ need to be double Roman dominated, we have $f\left(u_{i+3}\right)=f\left(v_{i+4}\right)=3$. Then, there exist a path P of type $3-0-3$, and a subgraph H of type $2^{+}-0-3-0-2^{+}$ or type $3-0_{-2^{+}}^{-2^{+}}$. By Lemma 5d, we have ${\sum }_{v\in V\left(P\right)\cup V\left(H\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Case 2.2: $S=\{s_1,s_2\}$, $s_1\in \{v_{i-1},v_{i-2},u_{i-2}\}$ and $s_2\in \{v_{i+1},v_{i+2},u_{i+2}\}$.

First, we have $f\left(v_{i\pm 1}\right)=0$. Otherwise, we may without loss of generality assume that $f\left(v_{i+1}\right)\ge 2$. Since $u_{i+2},v_{i+2}$ need to be double Roman dominated, we have $f\left(u_{i+3}\right)=f\left(v_{i+4}\right)=3$. Then, there exist a path P of type $3-0-3$, and a path H of type $2^{+}-0-3-0-2^{+}$. By Lemma 5d, we have ${\sum }_{v\in V\left(P\right)\cup V\left(H\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Then, since $v_{i+1},v_{i-1}$ need to be double Roman dominated, we have $f(v_{i+3})=f(v_{i-3})=3$. By Lemma 6, we have $f(u_{i+3})=f(u_{i-3})=0$. Since $u_{i\pm 2}$ need to be double Roman dominated, we have $(f(u_{i-2}),f(v_{i-2}))\in \{(0,3),(2,0),(3,0)\}$ and $(f\left(u_{i+2}\right),f\left(v_{i+2}\right))\in \{(0,3),(2,0),(3,0)\}$.

It is impossible that $f\left(v_{i+2}\right)+f\left(u_{i+2}\right)=3$ and $f\left(v_{i-2}\right)+f\left(u_{i-2}\right)=3$. Otherwise, there exists a path P of type $3-0-3-0-3$ or a subgraph P of type $3-0_{-3}^{-3}$. By Lemma 5a, we have ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

It is impossible $f\left(u_{i\pm 2}\right)\ge 2$. Otherwise, there exists a path P of type $3-0-2^{+}-0-3-0-2^{+}-0-3$. By Lemma 5a, we have ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2).

Then, we may without loss of generality assume that $f\left(u_{i+2}\right)=2$ and $f\left(v_{i-2}\right)=3$. Then, there exists a path P of type $3-0-2-0-3-0-3$. By Lemma 5a, we have ${\sum }_{v\in V\left(P\right)}(s^{\prime }\left(v\right)-0.8)\ge 1$, contradicting Equation (2). ☐

Lemma 9.

If $n\ge 5$ and f is a ${\gamma }_{dR}$-function of $P(n,2)$ with $f\left(v_i\right)=3$ for some $i\in \left[n\right]$, then $w\left(f\right)\ge \lceil \frac{8n}{5}\rceil +1$.

Proof. 

Suppose to the contrary that there exists a ${\gamma }_{dR}$-function f with $w\left(f\right)=\lceil \frac{8n}{5}\rceil$ such that $f\left(v_i\right)=3$ for some $i\in \left[n\right]$. By Lemma 6, we have $f\left(u_i\right)=f\left(v_{i\pm 2}\right)=0$. Let $S=\{x|x\in N_2\left(v\right),f\left(x\right)\ge 2\}$. By Lemma 7, we have $1\le \left|S\right|\le 2$, and we just need to consider the following two cases.

Case 1: $\left|S\right|=1$.

We may without loss of generality assume that $\{f\left(u_{i-1}\right)$, $f\left(u_{i-2}\right)$, $f\left(v_{i-4}\right)\}$ = $\{0,0,2\}$ or $\{0,0,3\}$ and $f\left(u_{i+1}\right)=f\left(u_{i+2}\right)=f\left(v_{i+4}\right)=0$. Since $u_{i+1}$ and $u_{i+2}$ need to be double Roman dominated, we have $f\left(v_{i+1}\right)=f\left(u_{i+3}\right)=3$, contradicting Lemma 8.

Case 2: $\left|S\right|=2$.

Now, it is sufficient to consider the following two cases.

Case 2.1: $S\subseteq \{u_{i-1},u_{i-2},v_{i-4}\}$ and $f\left(u_{i+1}\right)=f\left(u_{i+2}\right)=f\left(v_{i+4}\right)=0$.

Since $u_{i+1},u_{i+2}$ need to be double roman dominated, we have $f\left(v_{i+1}\right)=f\left(u_{i+3}\right)=3$, contradicting Lemma 8.

Case 2.2: $S=\{s_1,s_2\}$, where $s_1\in \{u_{i-1},u_{i-2},v_{i-4}\}$ and $s_2\in \{u_{i+1},u_{i+2},v_{i+4}\}$.

By Lemma 8, $f\left(u_k\right)\ne 3$ for each $k\in \{1,2,\cdots ,n\}$, and thus, $\{f\left(u_{i+1}\right),$ $f\left(u_{i+2}\right),$ $f\left(u_{i-2}\right),$ $f\left(u_{i-1}\right)\}=\{0,2\}$.

Then, we have $f\left(v_{i+4}\right)=f\left(v_{i-4}\right)=0$. Otherwise, $f(v_{i+4})\ne 0$ or $f(v_{i-4})\ne 0$. By symmetry, we may assume without loss of generality that $f\left(v_{i+4}\right)\ne 0$. Thus, we have $f\left(u_{i+1}\right)=f\left(u_{i+2}\right)=0$. Since $u_{i+1},u_{i+2}$ need to be double Roman dominated, we have $f\left(v_{i+1}\right)=f\left(u_{i+3}\right)=3$, contradicting Lemma 8.

Now, it is sufficient to consider the following three cases.

Case 2.2.1: $f(u_{i+1})=f(u_{i-1})=2$.

By Lemma 6, we have $f(u_{i\pm 2})=f(v_{i\pm 1})=0$.

Since $u_{i+2}$ needs to be double Roman dominated and by Lemma 8, we have $f(u_{i+3})=2$. Since $v_{i+1}$ needs to be double Roman dominated, we have $f(v_{i+3})\ge 2$. Thus, there exists an edge $e\in E_{\{2,2^{+}\}}^f$, a contradiction with Lemma 6.

Case 2.2.2: $f(u_{i+2})=f(u_{i-2})=2$.

By Lemma 6, we have $f\left(u_{i\pm 3}\right)=f\left(u_{i\pm 1}\right)=0$.

Since $u_{i+1},u_{i-1}$ need to be double Roman dominated, we have $f\left(v_{i\pm 1}\right)=2$. Thus, there exists an edge $e\in E_{\{2,2\}}^f$, a contradiction with Lemma 6.

Case 2.2.3: $f\left(u_{i+1}\right)=f\left(u_{i-2}\right)=2$.

By Lemma 6, we have $f\left(u_{i-3}\right)=f\left(v_{i+1}\right)=f\left(u_{i+2}\right)=0$.

Since $u_{i+2}$ needs to be double Roman dominated, we have $f\left(u_{i+3}\right)=2$. By Lemma 6, we have $f\left(v_{i+3}\right)=f\left(u_{i+4}\right)=0$. Since $u_{i+4}$ needs to be double Roman dominated and by Lemma 8, we have $f\left(u_{i+5}\right)=2$. Since $v_{i+3}$ needs to be double Roman dominated, we have $f(v_{i+5})\ge 2$. Thus, there exists an edge $e\in E_{\{2,2^{+}\}}^f$, a contradiction with Lemma 6. ☐

Lemma 10.

Let $n\ge 5$ and $n\not\equiv 0$ (mod 5). If f is a ${\gamma }_{dR}$-function of $P(n,2)$, then $w\left(f\right)\ge \lceil \frac{8n}{5}\rceil +1$.

Proof. 

Suppose to the contrary that $w\left(f\right)=\lceil \frac{8n}{5}\rceil$. By Lemmas 8 and 9, we have $|V_3|=0$. Now, we have:

Claim 1.

$|V_2\cap N\left(v\right)|=2$ for any $v\in V(P(n,2))$ with $f\left(v\right)=0$.

Proof. 

Suppose to the contrary that there exists a vertex $v\in V\left(P\right(n,2\left)\right)$ with $f\left(v\right)=0$ and $|V_2\cap N\left(v\right)|=3$. We consider the following two cases.

Case 1: $v=u_i$ for some $i\in \left[n\right]$.

Since $|V_2\cap N\left(v\right)|=3$, we have $f\left(u_{i-1}\right)=f\left(u_{i+1}\right)=f\left(v_i\right)=2$. By Lemma 6, we have $f\left(u_{i\pm 2}\right)=0$, $f\left(v_{i\pm 1}\right)=0$ and $f\left(v_{i\pm 2}\right)=0$. Since $v_{i+1}$ needs to be double Roman dominated, we have $f\left(v_{i+3}\right)=2$. Since $u_{i+2}$ needs to be double Roman dominated, we have $f\left(u_{i+3}\right)=2$. Since $v_{i+3}{u}_{i+3}\in E_{\{2,2\}}^f$, contradicting Lemma 6.

Case 2: $v=v_i$ for some $i\in \left[n\right]$.

Since $|V_2\cap N\left(v\right)|=3$, we have $f\left(v_{i-2}\right)=f\left(v_{i+2}\right)=f\left(u_i\right)=2$. By Lemma 6, we have $f\left(u_{i\pm 1}\right)=f\left(u_{i\pm 2}\right)=f\left(v_{i\pm 4}\right)=0$. Since $u_{i+1}$ needs to be double Roman dominated, we have $f(v_{i+1})=2$. Since $u_{i-1}$ needs to be double Roman dominated, we have $f(v_{i-1})=2$. Since $v_{i+1}{v}_{i-1}\in E_{\{2,2\}}^f$, contradicting Lemma 6. ☐

We assume without loss of generality that $f\left(u_i\right)=2$. By Lemma 6, we have $f\left(u_{i-1}\right)=0$, $f\left(v_i\right)=0$ and $f\left(u_{i+1}\right)=0$. Since $v_i$ needs to be double Roman dominated, we assume without loss of generality that $f\left(v_{i-2}\right)=2$. By Claim 1, we have $f(v_{i+2})=0$. Since $f(v_{i-2})=2$, together with Lemma 6, we have $f\left(u_{i-2}\right)=0$. Since $u_{i-1}$ needs to be double Roman dominated, we have $f(v_{i-1})=2$. Then, by Lemma 6, we have $f(v_{i+1})=0$. Since $v_{i+2}$ needs to be double Roman dominated, we have $f(u_{i+2})=2$. That is to say, we have:

$$f({\mathcal{B}}_i)=f\left(\begin{array}{ccccc}\hfill u_{i-2}& \hfill u_{i-1}& \hfill u_i& \hfill u_{i+1}& \hfill u_{i+2}\\ \hfill v_{i-2}& \hfill v_{i-1}& \hfill v_i& \hfill v_{i+1}& \hfill v_{i+2}\end{array}\right)=\left(\begin{array}{ccccc}0\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill \\ 2\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right).$$

By repeatedly applying Claim 1 and Lemma 6, $f\left(x\right)$ can be determined for each $x\in {\mathcal{B}}_{i+5}$, and we have $f\left({\mathcal{B}}_i\right)=f({\mathcal{B}}_{i+5})$. It is straightforward to see that $w\left(f\right)=\lceil \frac{8n}{5}\rceil$ only if $n\equiv 0$ (mod 5), a contradiction. ☐

3. Conclusions

By Lemma 1, Proposition 2 and Lemma 10, we have

Theorem 1.

If $n\ge 5$, then:

$${\gamma }_{dR}(P(n,2))=\left\{\begin{array}{cc}\lceil \frac{8n}{5}\rceil ,\hfill & n\equiv 0\left(\mathrm{mod}5\right),\hfill \\ \lceil \frac{8n}{5}\rceil +1,\hfill & n\equiv 1,2,3,4\left(\mathrm{mod}5\right).\hfill \end{array}\right.$$

Remark 1.

Beeler et al. [7] proposed the concept of the double Roman domination. They showed that $2\gamma \left(G\right)\le {\gamma }_{dR}\left(G\right)\le 3\gamma \left(G\right)$. Moreover, they suggested to find double Roman graphs.

In [17], it was proven that:

Theorem 2.

If $n\ge 5$, then $\gamma (P(n,2))=\lceil \frac{3n}{5}\rceil$.

Therefore, we have that $P(n,2)$ is not double Roman for all $n\ge 5$.

In fact, there exist many double Roman graphs among Petersen graph $P(n,k)$. For example, in [12], it was shown that $P(n,1)$ is a double Roman graph for any $n\not\equiv 2$ (mod 4). Therefore, it is interesting to find other Petersen graphs that are double Roman.