1. Introduction
In recent years, there has been a great growth in the use of networks (systems), such as communication networks and computer networks, in human life. The networks are a set of nodes that are connected by a set of links to exchange data through the links, where some particular nodes in the network are called terminals. Usually, a network can be modeled mathematically as a graph
in which
shows the collection of nodes,
shows the set of links and
denotes the set of terminals. Depending on the purpose of designing a network, the states of the network can be defined in terms of the connections between the terminals. In the simplest case, the networks have two states:
up and
down. However, in some applications, the networks may have several states which are known, in reliability engineering, as the multi-state networks. Multi-state networks have extensive applications in various areas of science and technology. From a mathematical point of view, the states of multi-state networks are usually shown by,
in which
shows the complete failure of the network and
shows the perfect functioning of the network. A large number of research works have been published in literature on the reliability and aging properties of multi-state networks and systems under different scenarios. For the recent works on various applications and reliability properties of networks, we refer to [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10].
When a network is operating during its mission, its states may change over the time according to the change of the states of its components. From the reliability viewpoint, the change in the states of the components may occur based on a specific stochastic mechanism. In a recent book, Gertsbakh and Shpungin [
11] have proposed a new reliability model for a two-state network under the condition that components (with two states) fail according to a renewal process. Motivated by this, Zarezadeh and Asadi [
12] and Zarezadeh et al. [
13] studied the reliability of networks under the assumption that the components are subject to failure according to a counting process. Under the special case that the process of the components’ failure is a nonhomogeneous Poisson process (NHPP), they arrived at some mixture representations for the reliability function of the network lifetime and explored its stochastic and aging properties under different conditions.
The aim of the present paper is to assess the network reliability under the condition that the failure of the components appear according to a recently proposed stochastic process called
geometric counting process (GCP). We assume that the nodes of the network are absolutely reliable and, throughout the paper, whenever we say that the components of the network fail, we mean that the links of the network fail. Let
be a counting process where
denotes the number of events in
. A GCP, introduced in [
14], is a subclass of counting process
, which satisfies the following necessary conditions (for the sufficiently small
)
,
.
To be more precise, a GCP is a counting process
, with
such that, for any interval
,
where
is the mean value function (MVF) of the process. It is usually assumed that
is a smooth function in the sense that there exists a function
such that
The function
is called the intensity function of the process. We have to mention here that, as noted by Cha and Finkelstien [
14], the NHPP also lies in the class of counting process satisfying (i)–(iii), with an additional property that the increments of the process are independent. The motivation of using the GCP, in comparison with NHPP, is natural in some practical situations as we mention in the following. The GCP model, like the NHPP model, has a simple form and easy to handle mathematical characteristics. In an NHPP model, the increments of the process are independent, while, in the GCP model, the increments of the process have positive dependence. In practice, there are situations in which there is positive dependence of increments in a process that occurs naturally. For instance, assume that the components of a railway network destroyed by an earthquake that occurs according to a counting process. Then, the probability of the next earthquake is often higher if the previous earthquake has happened recently, compared with the situation that it happened earlier (see [
14]). Furthermore, the NHPP has a limitation that the mean and the variance of the process are equal, i.e.,
while, in GCP, the variance of the process is always greater than the mean, i.e.,
. This property of the GCP makes it cover many situations that can not be described and covered by the NHPP. For more details on recent mathematical developments and applications of the GCP model, see [
14,
15].
The reminder of the paper is arranged as follows. In
Section 2, we first give the well-known concept of
signature of a network. Then, we consider a two-state network that consists of
n components. We assume that the components of the network fail according to a GCP. We obtain some mixture representations for the reliability of the network based on the signatures. Several aging and stochastic properties of the network are explored. Among others, conditions are investigated under which the monotonicity of the intensity function of the process of component failure implies the monotonicity of the network hazard rate. The reliabilities of the lifetimes of the different networks, subjected to the same or different GCPs, are compared based on the stochastic order between the associated signature vectors. We also study the stochastic properties of the residual lifetime of the network where the components fail based on a GCP.
Section 3 is devoted to the reliability assessment of the single-step three-state networks. Recall that a network is said to be single-step if the failure of one component changes the network state at most by one. First, we give the notion of a two-dimensional signature associated with three-state networks. Then, we consider an
n-component network and assume that the network has three states
up,
partial performance and
down. We again assume that the components of the network are subjected to failure on the basis of GCP, which results in the change of network states. Under these conditions, we obtain several stochastic and dependency characteristics of the networks based on the two-dimensional signature. Several examples and plots are also provided throughout the article for illustration purposes.
Before giving the main results of the paper, we give the following definitions that are useful throughout the paper. For more details, see [
16].
Definition 1. Let X and Y be two random variables (RVs) with survival functions and , probability density functions (PDFs) and , hazard rates and , and reversed hazard rates and , respectively:
X is said to be smaller than Y in the usual stochastic order (denoted by ) if for all x.
X is said to be smaller than Y in the hazard rate order (denoted by ) if for all x.
X is said to be smaller than Y in the reversed hazard rate order (denoted by ) if for all x.
X is said to be smaller than Y in the mean residual life order (denoted by ) if for all x.
X is said to be smaller than Y in likelihood ratio order (denoted by ) if is an increasing function of x.
It can be shown that, if , then and . In addition, implies and .
Definition 2. LetXandYbe two random vectors with survival functions and , respectively.
is said to be smaller than in the upper orthant order (denoted by ) if
is said to be smaller than in the usual stochastic order (denoted by ) if for every increasing function for which the expectations exist.
Definition 3. The nonnegative function is called multivariate totally positive of order 2 (MTP) if , for all , where and .
The RVs X and Y are said to be positively quadrant dependent (PQD) if, for every pair of increasing functions and , The RVs X and Y are said to be associated if for every pair of increasing functions and ,
In a special case when , the is known as totally positive of order 2 ( ).
2. Two-State Networks under GCP of Component Failure
In the reliability engineering literature, several approaches have been employed to assess the reliability of networks and systems. Among various ways that are considered to explore the reliability and aging properties of the networks, an approach is based on the notion of
signature (or
D-spectrum). The concept of signature, which depends only on the network design, has proven very useful in the analysis of the networks performance particularly for comparisons between networks with different structures. Consider a network (system) that consists of
n components. The
signature associated with the network is a vector
, in which the
ith element shows the probability that the
ith component failure in the network causes the network failure, under the condition that all permutations of order of components failure are equally likely. In other words, the
ith element
is equal to
,
, where
is the number of permutations in which the
ith component failure changes the network state from up to down. For more details on signatures and their applications in the study of system reliability, see, for example, Refs. [
17,
18,
19,
20] and references therein. In this section, we give a signature-based mixture representation for the reliability of the network under the condition that the components of the network fail according to a GCP
with MVF
. We have from Equation (
1)
Then, the survival function of the
kth arrival time of process,
, is given as
and the PDF of the
kth arrival time
is achieved as
Let
T denote the lifetime of a network with
n components. The components of network are subjected to failure based on a GCP with MVF
. From the reliability modeling proposed by Zarezadeh and Asadi [
12], the reliability of the network lifetime, denoted by
, is represented as
or equivalently as
where
is the survival signature of the network. Then, the PDF of
T is obtained as
where
. In addition, the hazard rate of network lifetime is given as follows:
With
as the hazard rate of the
kth arrival time of the GCP, it can be seen that the hazard rate of network lifetime can be also written as
which is a mixture representation with mixing probability vector
where, for
,
One can easily show that is the probability that the lifetime of system is equal to the kth arrival time of the process given that the network lifetime is greater than t.
Let us look at the following example.
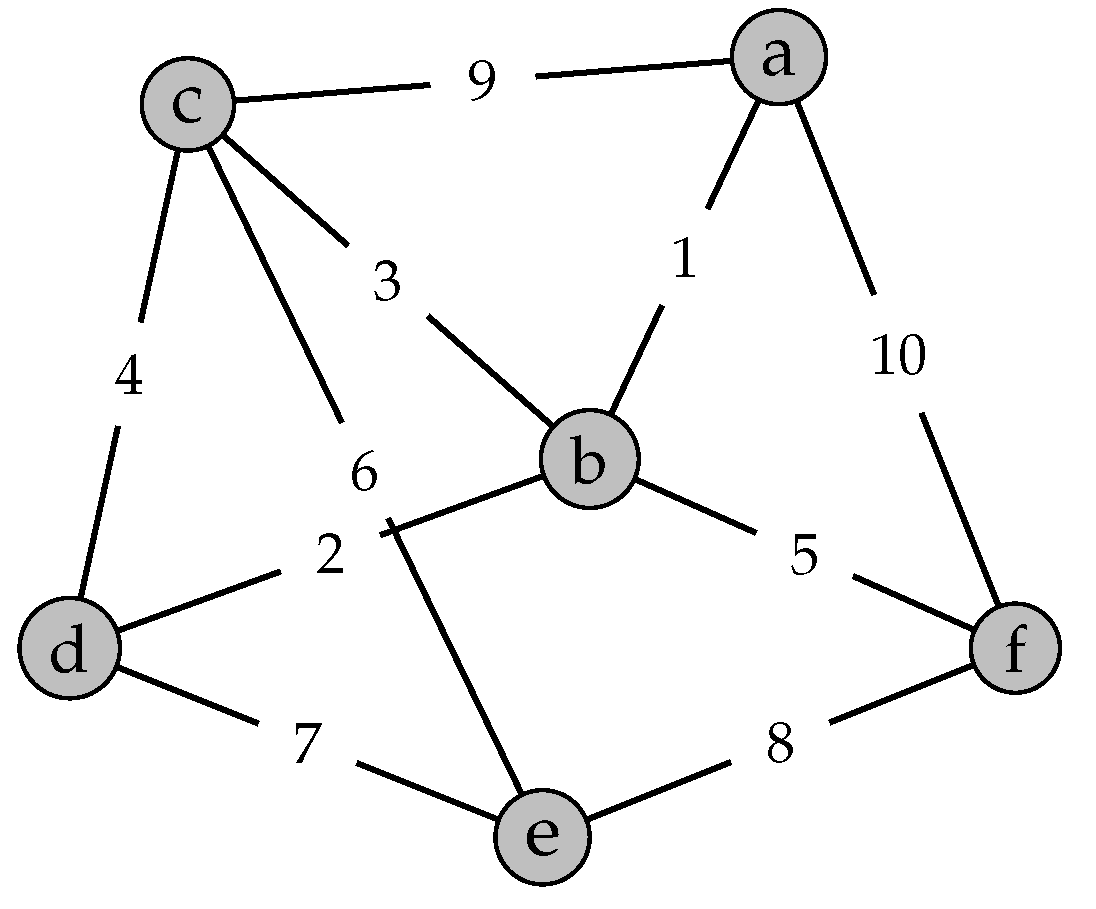
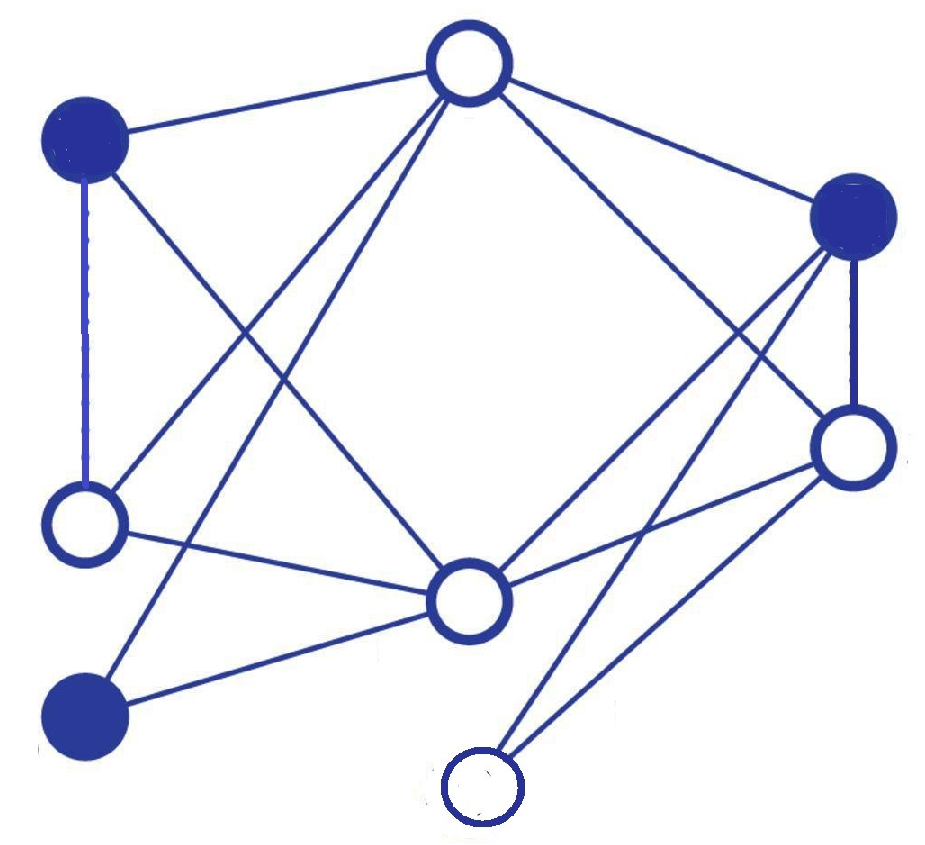
Example 1. Consider a network that consists of six nodes and 10 links with the graph depicted in Figure 1. The network is assumed to work if there is a connection between some of nodes which we consider them as terminals. We consider two different sets of terminals for the network:
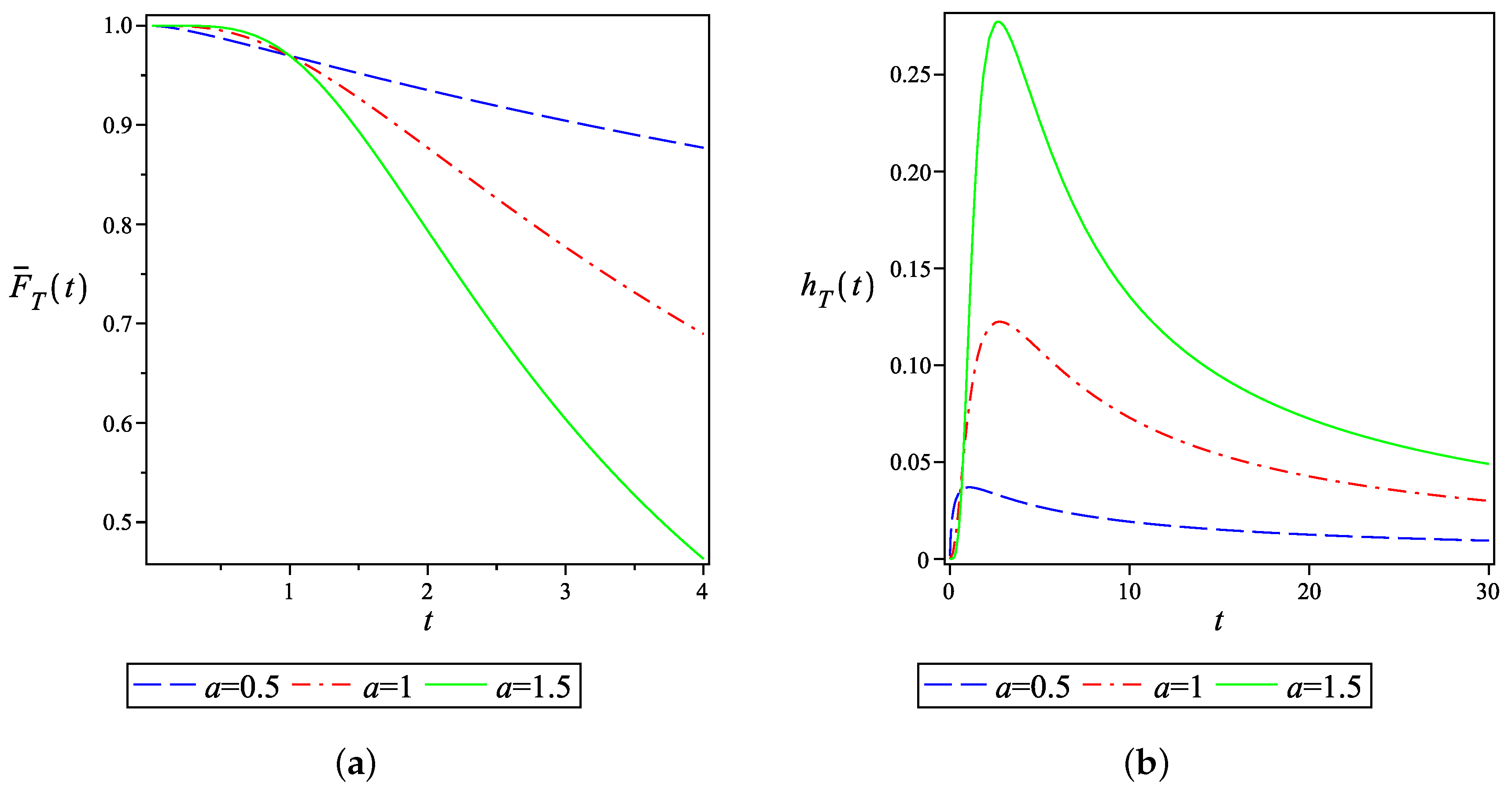
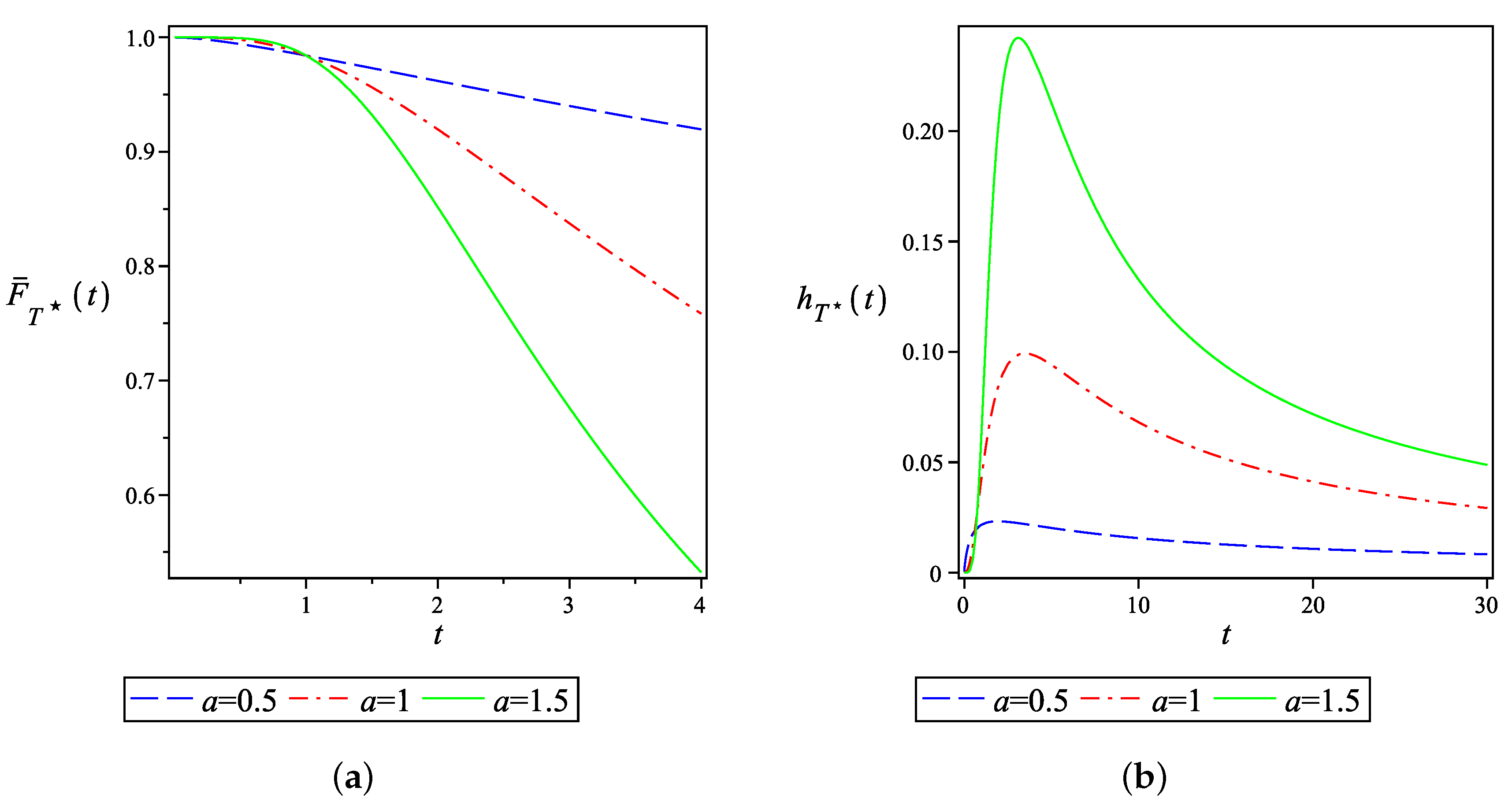
Figure 2a gives the plot of network reliability in the case of all-terminal connectivity, , and when , for different values of a. As seen, the reliability function of network does not order with respect to a for all . Of course, this is true in any network when MVF , . This is so using the fact thatis increasing (decreasing) in a for (), for a general signature vector the reliability of the networkis also increasing (decreasing) in a for (). Figure 2b represents the hazard rate of network when for . Figure 3a,b shows the plots of reliability function and hazard rate of the network lifetime when the terminals set is considered as . It is interesting to compare the network reliability when the failure of components appear according to a GCP and the network reliability when the failure of components occur based on an NHPP. In the sequel, we show that, if the network has a series structure, then the reliability of the network in the GCP model dominates the reliability of the network in an NHPP model. Consider a two-state series network with the property that the first and the last components are considered to be terminals. We assume that the network fails if the linkage between the two terminals are disconnected. This occurs at the time of the first component failure. Let
and
denote the lifetimes of the network when the component failure appears according to NHPP and GCP with the same MVF
, respectively. If
and
denote the arrival times of the first component failure based on NHPP and GCP, respectively, then, from inequality
,
, we can write
Hence, based on the fact that, for a series network
, relation (
2) implies that
.
The following example reveals that the above result, proved for the series network, is not necessarily true for any network.
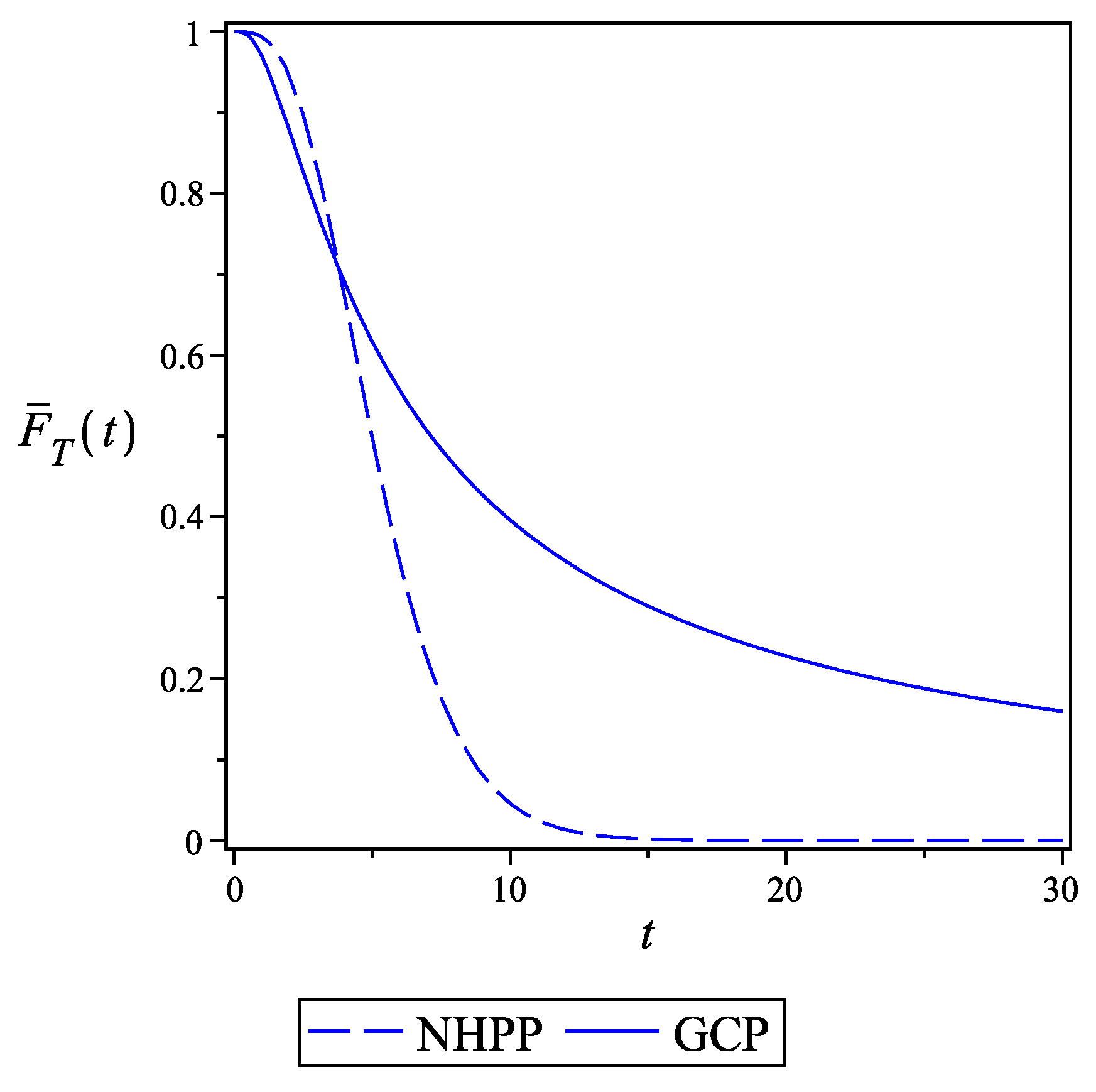
Example 2. Consider the network described in Example 1. Figure 4 shows that the reliability functions of the network for part (a). As the plots show the reliability functions are not ordered in NHPP and GCP models with the same MVFs . The reliability of the network in the NHPP model is higher than the GCP model for the early times of operating of the network. However, when the time goes ahead, the network reliability in NHPP declines rapidly and stays below the reliability of the GCP model. The next theorem explores the monotonicity relation of the intensity function of the process and the hazard rate of the network.
Theorem 1. Let the components of a network fail based on a GCP with increasing intensity function . Then, the hazard rate of network is increasing if and only if is increasing in u where Proof. From (
3) and (
4), the hazard rate of network can be written as
where
is defined in (
8) and
is increasing in
t. If
is increasing, from (
9), it can be easily seen that
is increasing. This completes the ‘if’ part of the theorem. To prove ‘only if’ part of the theorem, let
be increasing and
be decreasing in the interval
. For MVF
,
, and hence
as an increasing function, we conclude that
is decreasing on interval
, which contradicts with the assumption that the hazard rate of network is increasing for all
t. □
Theorem 2. Let T and denote the lifetimes of two networks with signature vectors and , respectively. Suppose that the components of networks fail based on GCPs with MVFs and , respectively. If and for all , then .
Proof. Let
and
denote the
kth arrival times of the two processes,
. Since
, then, from Theorem 1.A.1 of [
16], we can write
. Hence,
In addition, the condition
for all
implies that
,
. Then, we get
Hence, the result follows from (
10) and (
11). □
Theorem 3. For two networks as described in Theorem 2, assume that the failure of components of both networks appear according to the same GCPs:
If , then ,
If , then ,
If , then ,
If , then .
Proof. It can be easily shown that
. Since lr-ordering implies hr-, rh- and st-ordering, parts (i), (ii), (iii), and (iv) are proved, by using (
2), from Theorems 1.A.6, 1.B.14, 1.B.52, and 1.C.17 of [
16], respectively. □
From part (ii) of Theorem 3, since hr-ordering implies mrl-ordering, we conclude that if then . However, the following example shows that the assumption can not be replaced with to have .
Example 3. Consider two networks with signature vectors and . It is easy to see that . However, and hence . Assume that the components of both networks fail based on the same GCPs with MVF . Then, a straightforward calculation gives , which, in turn, implies that .
Residual Lifetime of a Working Network
Let
T denote the lifetime of a network whose components are subjected to failure based on a GCP with MVF
. If the network is up at time
t, then the residual lifetime of the network is presented by the conditional RV
with conditional reliability function given as
where
is the
kth element of vector
as defined in (
6). This shows that the reliability function of the residual lifetime of the network is a mixture of the reliability functions of residual lifetimes of the first
n arrival times of GCP, where the mixing probability vector is
. As we have already mentioned,
is in fact the probability that the
kth component failure causes the failure of the network, given that the lifetime of the network is more than
t; that is,
In what follows, we call the vector as the conditional signature of the network. In the sequel, we give some stochastic properties of the conditional signature of network under the condition that the components of the network fail based on GCP model.
Theorem 4. Consider a network with signature vector . With , and where and , .
Proof. Then, it is easily seen that, for any
i,
and hence
On the other hand, for
,
and consequently the result follows. □
Example 4. For the network in Example 1, with , we have Hence, it is easily seen that . Thus, based on (5) and Theorem 4, we have for any network structure. Theorem 5. Consider a network whose components fail based on two different GCPs with MVFs and , respectively. Denote by and the corresponding conditional signatures of the two networks. Then,
Proof. With
, from (
6), for each MVF
,
can be written as
where
. Then, we have
in which
For
,
is increasing in
u and hence
is TP
in
i and
u. Using this fact and Lemma 2.4 of [
13]:
Since
is increasing in
u, then, for an arbitrary MVF
, we have
Since
is increasing in
u, and
for all
, then
Therefore, the proof of the theorem is complete. □
The following lemma from [
13] is useful to get some stochastic properties of conditional signature expressed in (
6). Before expressing the lemma, we recall that a non-negative function
,
, is said to be upside-down bathtub-shaped if it is increasing on
, is constant on
and is decreasing on
where
.
Lemma 1. Let and be non-negative discrete functions and γ be positive and real-valued. Definewhere , and . Assume that is a non-constant decreasing (increasing) function on . Then, for and ( and ), we have Now, we have the following theorem.
Theorem 6. For a network with signature vector ,
is decreasing in t and is increasing in t where and ;
, , is upside-down bathtub-shaped with a single change-point;
, , is bounded above by ;
The maximum value of , , does not depend on the MVF .
Proof. Assume that
. From (
12), we can write
As seen in (
13),
, for
, is increasing in
x. Since
is increasing in
t, then it can be concluded that
is also increasing in
t, for
. Based on this fact and (
15), we observe that
is a decreasing function of
t and
is an increasing function of
t. This completes the proof of part (a).
From relation (
7), we have
With
,
,
,
,
and
in (
14), define
. Then, we can write
Since is increasing in t, parts (b) and (c) follow from parts (i) and (ii) of Lemma 1.
Part (d) can be proved from the fact that
□
The following theorem compares the performance of two used networks based on their conditional signatures.
Theorem 7. Let and be the conditional signatures of two networks with lifetimes T and , respectively. Suppose that the component failure in both networks appear based on the same GCPs.
If then ;
If then ;
If then ;
If then .
Proof. It can be easily seen that
,
. Then, from Theorem 1.C.6 of [
16], we have, for
and
,
Hence, these residual lifetimes are also hr-, rh- and st-ordered. Since
, from Theorem 1.A.6 of [
16], we have, for all
,
This establishes part (a). The proof of parts (b), (c) and (d) are obtained similarly by using Theorems 1.B.14, 1.B.52, and 1.C.17 of [
16], respectively. □
3. Three-State Networks under GCP of Component Failure
In this section, we study the reliability of the lifetimes of the networks with three states under the condition that the components fail according to a GCP with MVF
. In order to develop the results, we need the notion of two-dimensional signature that has been defined for single-step three-state networks by Gertsbakh and Shpungin [
11]. Throughout this section, we are dealing with a single-step three-state network consisting of
n binary components where we assume that the network has three states:
up (denoted by
),
partial performance (denoted by
) and
down (denoted by
). Suppose that the network starts to operate at time
where it is in state
. Denote by
the time that the network remains in state
and by
the network lifetime i.e., the entrance time into state
. Let
I (
J) be the number of failed components when the network enters into state
(
). Gertsbakh and Shpunging [
11] introduced the notion of two-dimensional signature as
where
represents the number of permutations in which the
ith and the
jth components failure change the network states from
to
and from
to
, respectively. We denote by matrix
the two-dimensional signature with elements defined in (
16). In the following, we first obtain the joint reliability function of
. Under the assumption that all orders of components failure are equally probable, we have
in which the second equality follows from the fact that the event
depends only on the network structure and does not depend on the mechanism of the components failure. In addition, it can be shown, by changing the order of summations, that
where
.
Suppose that the component failures occur at random times
that are corresponding to the first
n arrival times of the GCP
. Using the fact that the event
occurs if and only if
, it can be shown that
Assuming that the MVF of the GCP is
, Di Crescenzo and Pellerey [
15] obtained the PDF of
as
Using (
19), the joint PDF of
and
is achieved as
In the following, we present an example of a three-state network whose components fail according to a GCP with MVF .
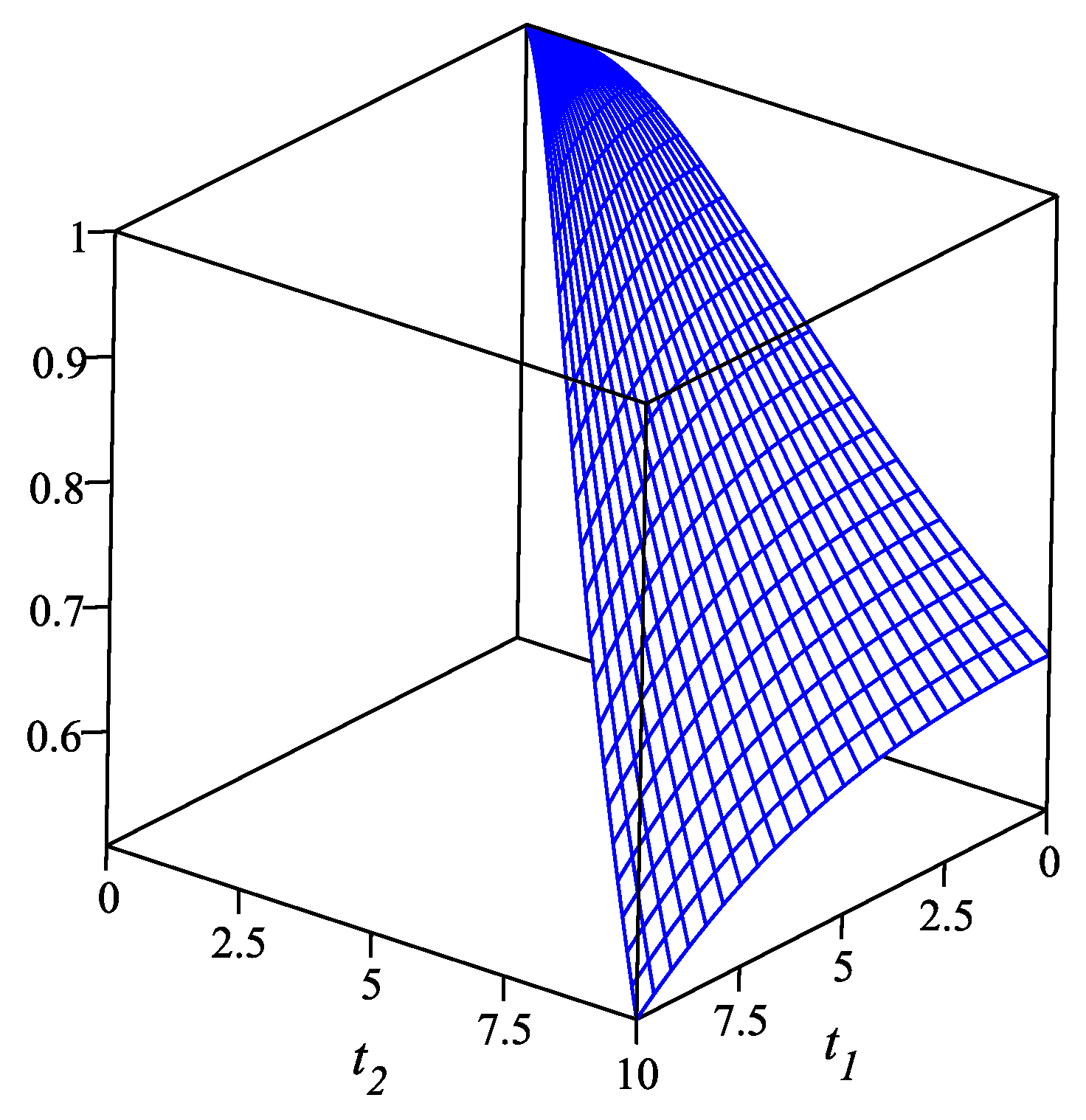
Example 5. Consider a network with a graph as depicted in Figure 5. The network has 14 links and eight nodes in which the dark nodes are considered to be terminals. Suppose that the nodes are absolutely reliable and the links are subjected to failure. Assume that the network is in up state if all terminals are connected, in partial performance state if two terminals are connected and in down state if all terminals are disconnected. Let the network components fail according to a GCP with intensity function and all orders of links failure are equally likely. Figure 6 presents the plot of joint reliability function of the network lifetimes . The elements of the two-dimensional signature are calculated using an algorithm by the authors, which can be provided to the readers upon the request. In the following theorem, we compare the state lifetimes of two three-state networks. In order to do this, we need the following Lemma.
Lemma 2. Assume that and are two GCPs with intensity functions , and , respectively. Let and denote the arrival times corresponding to the two processes, respectively. If then for every .
Proof. Using relation (
19), it can be seen that
is
, which implies that
,...,
are associated,
. In addition, we have
which is increasing in
. Therefore, the required result is concluded from Theorem 6.B.8 of [
16]. □
Theorem 8. Consider two three-state networks that each consist of n components having signature matrices and , respectively. Let the components of ith network fail according to GCP , with intensity function . Let denote the arrival times corresponding to . Suppose that and are the corresponding state lifetimes of the two networks, respectively:
If and , then
If and , then
Proof. From Lemma 2, if , then which implies for all .
Using representation (
17), we have
where the first inequality follows from the assumption that
and the second inequality follows from
for
.
Using the fact that
for all
and the assumption that
, the required result is concluded from Theorem 3.3 of [
21].
□
In the sequel, we investigate the dependency between
and
based on the dependency between RVs
I and
J. In fact, we show that, if
I and
J are PQD (associated), then
and
are also PQD (associated). Before that, let
and
.
Theorem 9. Let be the lifetime of a three-state network in state and be the lifetime of the network. Let the components failure of the network appear according to the GCP with arrival times .
If I and J are PQD, then and are PQD.
If I and J are associated, then and are associated.
Proof. From representation (
20), one can show that
is
, which implies that
and
are associated and PQD.
- (a)
Let
and
be two increasing functions. From representation (
18), we have
where the first inequality follows from the fact that
and
are PQD and the second inequality follows from the assumption that
I and
J are PQD.
- (b)
Proof of part (b) is the same as the proof of part (a) using the fact that, for every two-variate increasing functions
and
,
□
The results of the theorem are interesting in the sense that the PQD (associated) property of I and J, which is non-aging and depends only on the structure of the network, is transferred to the PQD (associated) property of and , which is the aging characteristic of the network.
Example 6. Consider again the network presented in Example 5. It can be seen that, for every , . This implies that I and J are PQD. Hence, if the components fail according to a GCP, then and are PQD.