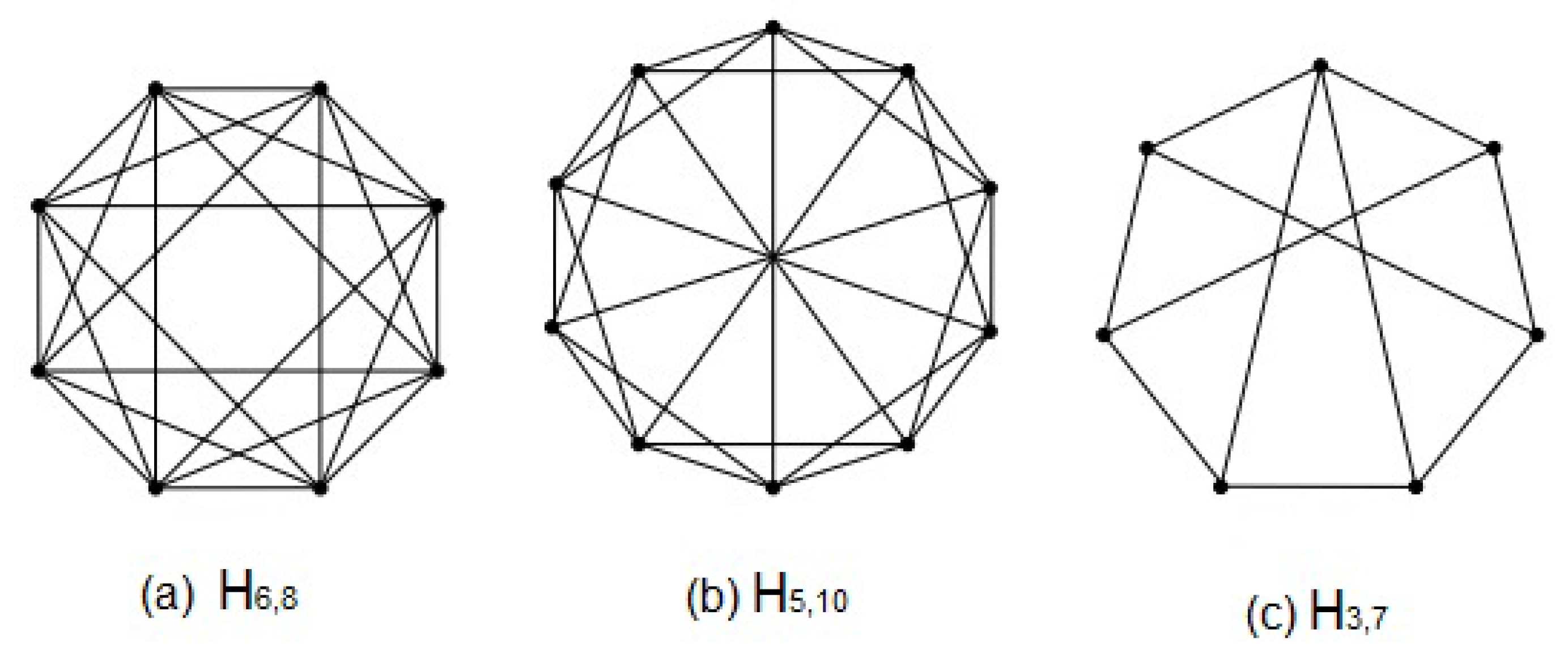
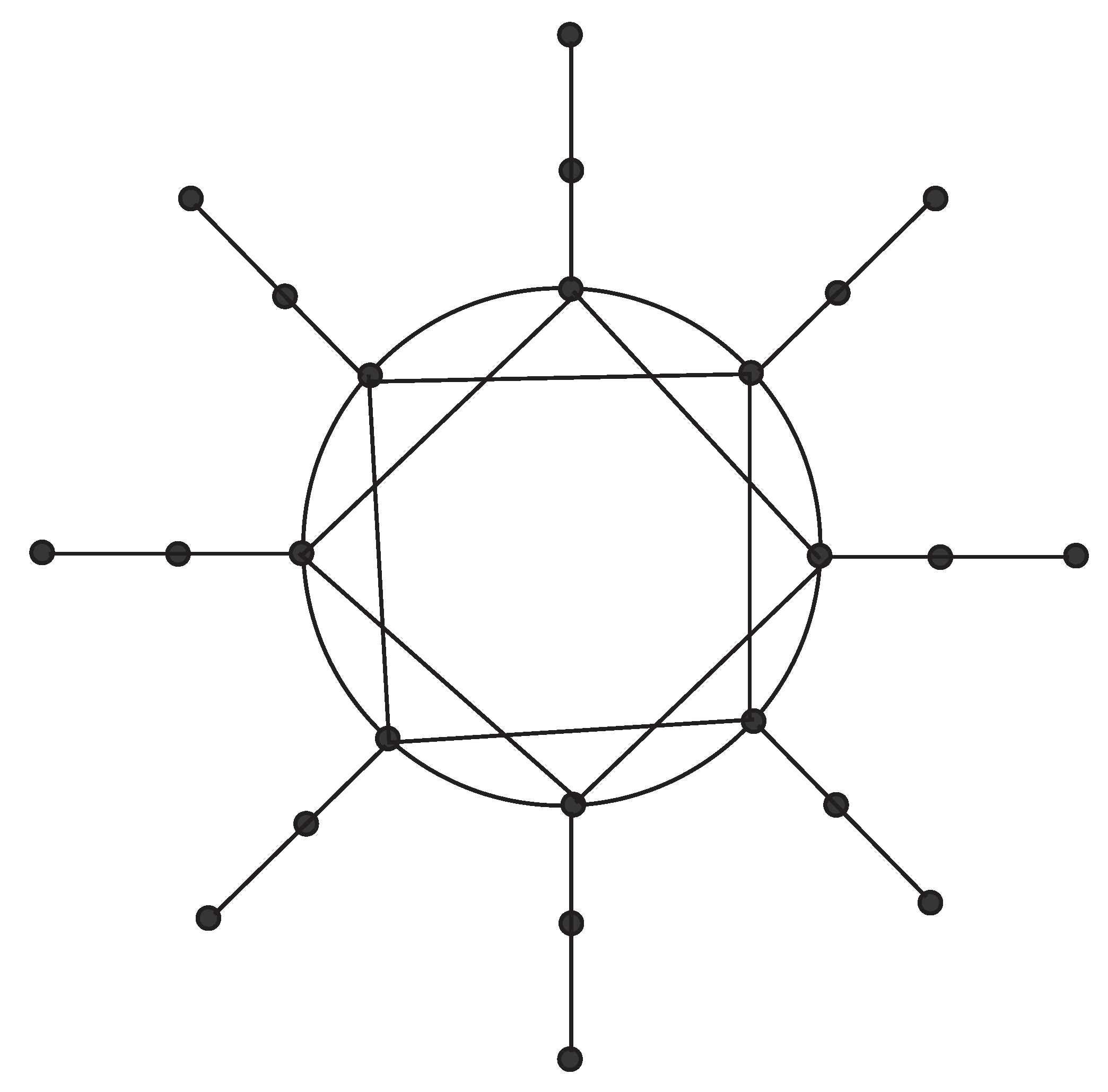
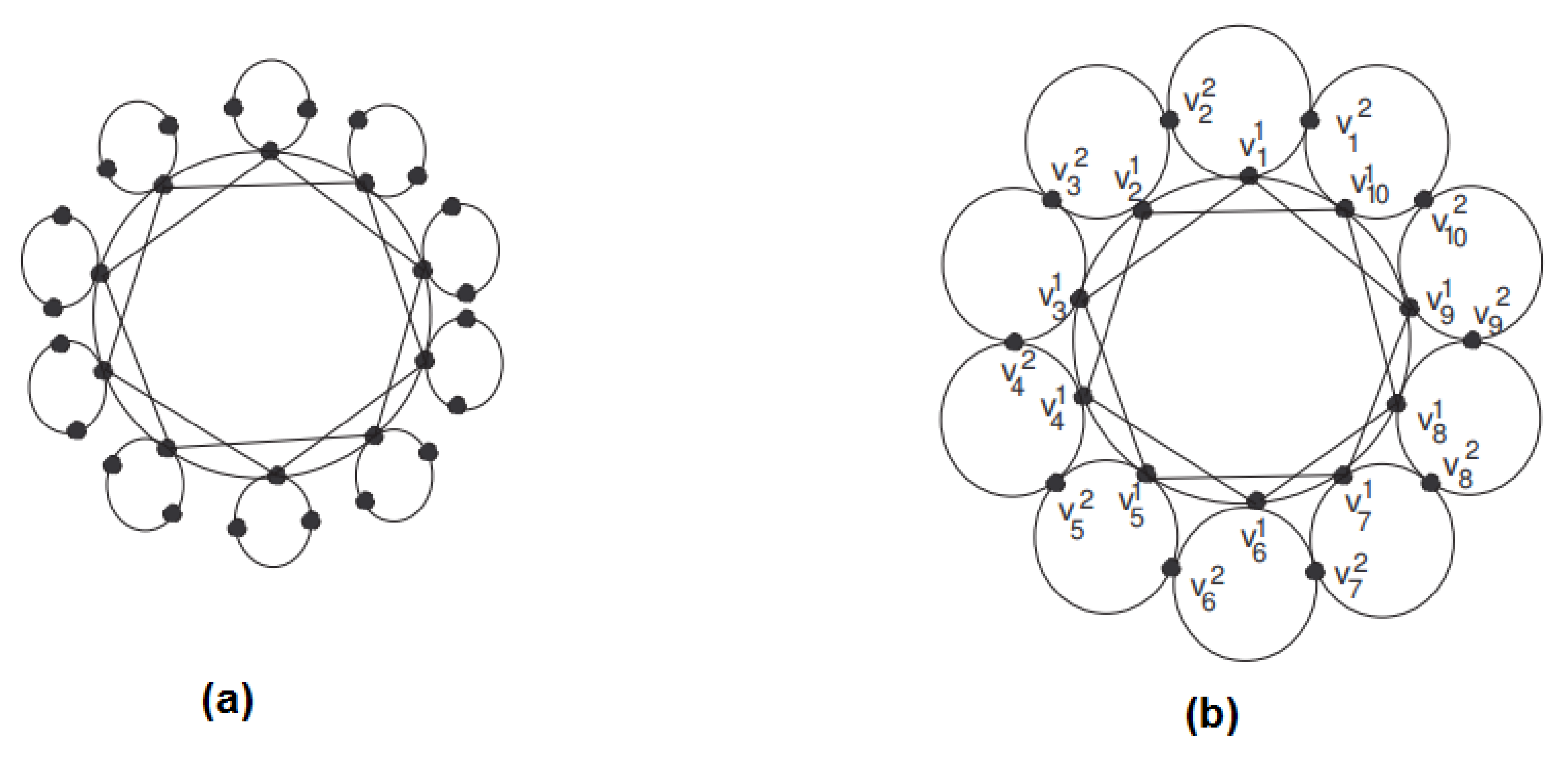
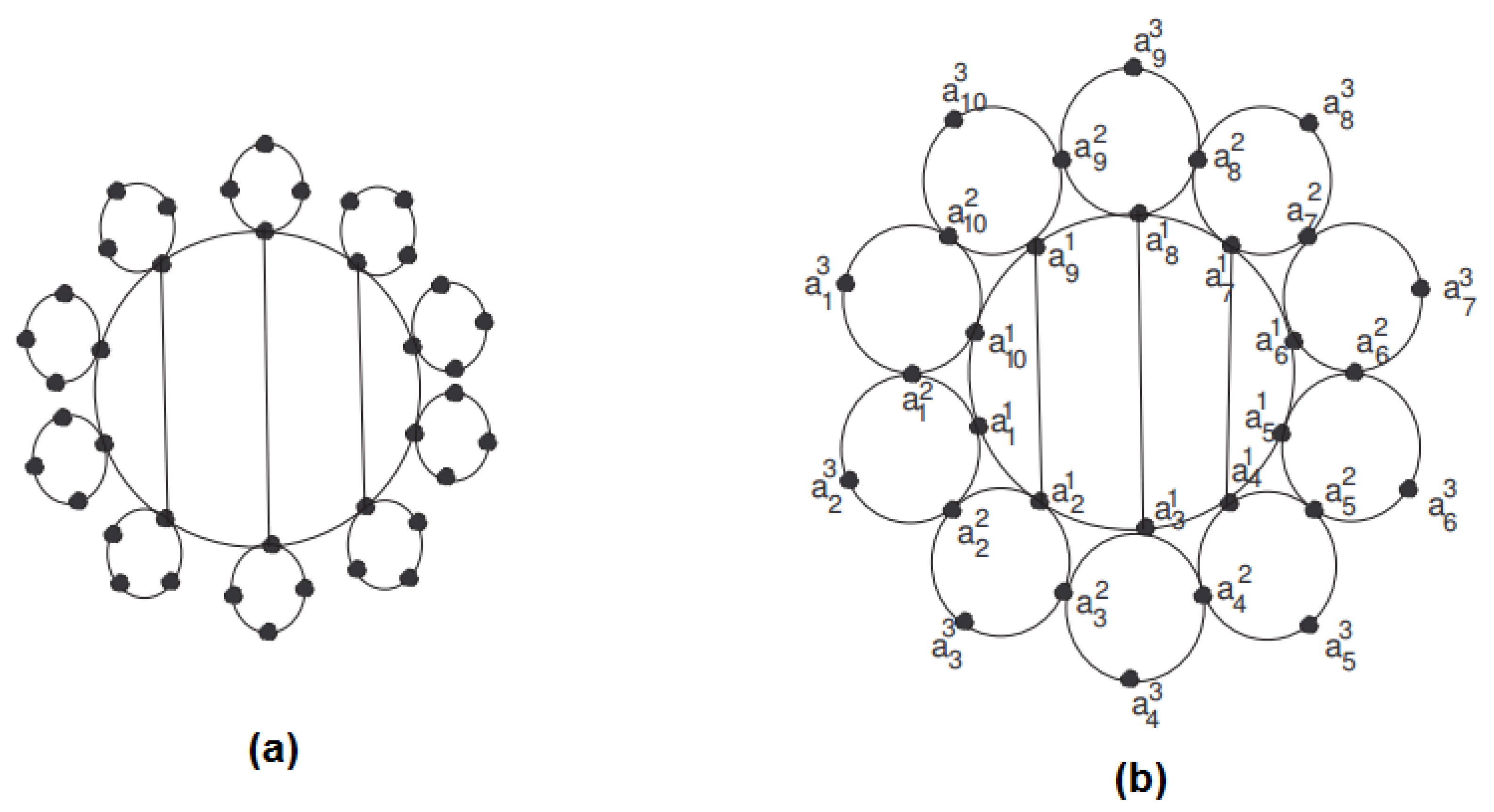
Proof. Case-I when (mod4) i.e., and .
be the resolving set of G then ,
,,,,
,,,,
,,,,
For let be the resolving set of G then
,,,,
,,,,
,,,,
,,,,
,,,,
.
For
let
be the resolving set of
G then
,
,
,
,,,
,,,
,,.
Since distinct vertices have distinct representation, in this case. However, by Theorem 1 no two vertices can resolve G into distinct representation so . Hence
Case-II when (mod4) i.e., .
For let be the resolving set of G then ,
,,,,
,.
For
let
be the resolving set of
G then
,,,
,,,
,,,
,,.
Since distinct vertices have distinct representation, in this case. However, by Theorem 1 no two vertices can resolve G into distinct representation so . Hence
Case-III when (mod4) i.e., .
For let be the resolving set of G then ,
,,,,
,,,,
,.
For let be the resolving set of G then
,,,,
,,,,
,,,,
,,,,
,,.
For
let
be the resolving set of
G then
,
,
,
,,,
,,,
,,
,,,
,,,
,,.
Since distinct vertices have distinct representation, in this case. However, by theorem 1 no two vertices can resolve G into distinct representation so .
Hence
Case-IV when i.e., .
For let be the subset of and ,
,,,,
,,,,
since ⇒ is the resolving set of G.
⇒
For let be the subset of and ,
,,,,
,,,,
,,,,
,,,
.
since ⇒ is the resolving set of G.
⇒
For
let
be the subset of
then
,
,
,,,
,,
,,,
,,,
,. since ⇒ is the resolving set of G.
⇒. This complete the proof. □
Proof. Case-I when i.e., and .
Let
be the resolving set of
G then
For ,,
,.
Since distinct vertices have distinct representation, in this case. Now we prove that when (mod4). Since every vertex that lies on cycle has degree 5, by Theorem 1 we shall take the vertices on pendents uncommon to the cycle when . Without loss of generality we can say
and , represent all possible cases in which and in each case the following contradictions arise.
Take then a contradiction.
Take , then a contradiction.
Take , then a contradiction.
Take , then a contradiction.
hence .
Case-II when i.e., , .
Let
be the resolving set of
G then
For , ,,
,.
Since distinct vertices have distinct representation, in this case. Now we prove that when (mod4). Since every vertex lies that on cycle has degree 5, by theorem 1 we shall take the vertices on pendents uncommon to the cycle when . Without loss of generality we can say
and , represent all possible cases in which and in each case the following contradictions arise. Take then a contradiction.
Take , then a contradiction.
Take , then a contradiction.
Take , then a contradiction.
Take then a contradiction.
hence .
Case-III when i.e., , .
Let
be the resolving set of
G then
For , ,, .
Since distinct vertices have distinct representation, in this case. Now we prove that when (mod4). Since every vertex that lies on cycle has degree 5, by Theorem 1 we shall take the vertices on pendents uncommon to the cycle when . Without loss of generality we can say:
and , represent all possible cases in which and in each case the following contradictions arise. Take then a contradiction.
Take , then a contradiction.
Take , then a contradiction.
Take , then a contradiction.
hence .
Case-IV when i.e., , .
Let
be the resolving set of
G then
For , ,
,,
. Since distinct vertices have distinct representation so in this case. This complete the proof. □