Numerical Solution of Multiterm Fractional Differential Equations Using the Matrix Mittag–Leffler Functions
Abstract
1. Introduction
2. Fractional Differential Equations
- 1.
- 2.
3. Matrix Approach for the Solution of Linear MTFDEs
4. Numerical Solution of FDEs
4.1. Product Integration Rules
4.2. Numerical Tests
4.2.1. Bagley–Torvik Equation
4.2.2. The Basset Problem
4.2.3. Fractional Oscillation Equation
4.2.4. Academic Examples
Acknowledgments
Conflicts of Interest
References
- Gorenflo, R.; Mainardi, F. Fractional calculus: Integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics (Udine, 1996); Carpinteri, A., Mainardi, F., Eds.; Springer: Vienna, Austria, 1997; Volume 378, pp. 223–276. [Google Scholar]
- Mainardi, F. Fractional Calculus: Some Basic Problems in Continuum and Statistical Mechanics. In Fractals and Fractional Calculus in Continuum Mechanics (Udine, 1996); Carpinteri, A., Mainardi, F., Eds.; Springer: Vienna, Austria, 1997; pp. 291–348. [Google Scholar]
- Podlubny, I. Fractional differential equations. In Mathematics in Science and Engineering; Academic Press Inc.: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics; Springer-Verlag: Berlin, Germany, 2010; Volume 2004. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Lubich, C. Runge-Kutta theory for Volterra and Abel integral equations of the second kind. Math. Comput. 1983, 41, 87–102. [Google Scholar] [CrossRef]
- Lubich, C. Fractional linear multistep methods for Abel-Volterra integral equations of the second kind. Math. Comput. 1985, 45, 463–469. [Google Scholar] [CrossRef]
- Lubich, C. Discretized fractional calculus. SIAM J. Math. Anal. 1986, 17, 704–719. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, J.M.; Ford, N.J.; Weilbeer, M. Pitfalls in fast numerical solvers for fractional differential equations. J. Comput. Appl. Math. 2006, 186, 482–503. [Google Scholar] [CrossRef]
- Galeone, L.; Garrappa, R. Explicit methods for fractional differential equations and their stability properties. J. Comput. Appl. Math. 2009, 228, 548–560. [Google Scholar] [CrossRef]
- Garrappa, R. On some explicit Adams multistep methods for fractional differential equations. J. Comput. Appl. Math. 2009, 229, 392–399. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. On accurate product integration rules for linear fractional differential equations. J. Comput. Appl. Math. 2011, 235, 1085–1097. [Google Scholar] [CrossRef]
- Garrappa, R. Trapezoidal methods for fractional differential equations: Theoretical and computational aspects. Math. Comput. Simul. 2015, 110, 96–112. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J. Series on Complexity, Nonlinearity and Chaos. In Fractional Calculus: Models and Numerical Methods; World Scientific Publ: Singapore, 2012. [Google Scholar]
- Luchko, Y.; Gorenflo, R. An operational method for solving fractional differential equations with the Caputo derivatives. Acta Math. Vietnam. 1999, 24, 207–233. [Google Scholar]
- Diethelm, K.; Ford, N.J. Multi-order Fractional Differential Equations and Their Numerical Solution. Appl. Math. Comput. 2004, 154, 621–640. [Google Scholar] [CrossRef]
- Diethelm, K.; Luchko, Y. Numerical solution of linear multi-term initial value problems of fractional order. J. Comput. Anal. Appl. 2004, 6, 243–263. [Google Scholar]
- Luchko, Y. Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation. J. Math. Anal. Appl. 2011, 374, 538–548. [Google Scholar] [CrossRef]
- Garrappa, R. Stability-preserving high-order methods for multiterm fractional differential equations. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2012, 22, 1250073. [Google Scholar] [CrossRef]
- Al-Refai, M.; Luchko, Y. Maximum principle for the multi-term time-fractional diffusion equations with the Riemann-Liouville fractional derivatives. Appl. Math. Comput. 2015, 257, 40–51. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. 2017; submitted. [Google Scholar]
- Esmaeili, S. The numerical solution of the Bagley-Torvik equation by exponential integrators. Sci. Iran. 2017, 2941–2951. [Google Scholar] [CrossRef]
- Torvik, P.; Bagley, R. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. Trans. ASME 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, J. Numerical Solution of the Bagley-Torvik Equation. BIT Numer. Math. 2002, 42, 490–507. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler functions and their applications. J. Appl. Math. 2011, 298628. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S. Mittag-Leffler functions. Theory and Applications; Springer Monographs in Mathematics; Springer: Berlin, Germany, 2014. [Google Scholar]
- Garrappa, R.; Popolizio, M. Evaluation of generalized Mittag–Leffler functions on the real line. Adv. Comput. Math. 2013, 39, 205–225. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical evaluation of two and three parameter Mittag-Leffler functions. SIAM J. Numer. Anal. 2015, 53, 1350–1369. [Google Scholar] [CrossRef]
- Moret, I.; Novati, P. On the Convergence of Krylov Subspace Methods for Matrix Mittag–Leffler Functions. SIAM J. Numer. Anal. 2011, 49, 2144–2164. [Google Scholar] [CrossRef]
- Moret, I. A note on Krylov methods for fractional evolution problems. Numer. Funct. Anal. Optim. 2013, 34, 539–556. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Computing the matrix Mittag-Leffler function with applications to fractional calculus. submitted.
- Cameron, R.F.; McKee, S. Product integration methods for second-kind Abel integral equations. J. Comput. Appl. Math. 1984, 11, 1–10. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The FracPECE subroutine for the numerical solution of differential equations of fractional order; Forschung und wissenschaftliches Rechnen 1998; Heinzel, S., Plesser, T., Eds.; Gessellschaft für wissenschaftliche Datenverarbeitung: Goettingen, Germany, 1999; pp. 57–71. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Garrappa, R.; Messina, E.; Vecchio, A. Effect of perturbation in the numerical solution of fractional differential equations. Discret. Contin. Dyn. Syst. Ser. B 2017. [Google Scholar] [CrossRef]
- Higham, N.J. Functions of matrices; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2008. [Google Scholar]
- Garrappa, R.; Moret, I.; Popolizio, M. Solving the time-fractional Schrödinger equation by Krylov projection methods. J. Comput. Phys. 2015, 293, 115–134. [Google Scholar] [CrossRef]
- Garrappa, R.; Moret, I.; Popolizio, M. On the time-fractional Schrödinger equation: Theoretical analysis and numerical solution by matrix Mittag-Leffler functions. Comput. Math. Appl. 2017, 5, 977–992. [Google Scholar] [CrossRef]
- Mainardi, F.; Pironi, P.; Tampieri, F. A numerical approach to the generalized Basset problem for a sphere accelerating in a viscous fluid. In Proceedings of the 3rd Annual Conference of the Computational Fluid Dynamics Society of Canada, Banff, AB, Canada, 25–27 June 1995; Volume II, pp. 105–112. [Google Scholar]
- Mainardi, F.; Pironi, P.; Tampieri, F. On a generalization of the Basset problem via fractional calculus. In Proceedings of the 15th Canadian Congress of Applied Mechanics, Victoria, BC, Canada, 28 May–2 June 1995; Volume II, pp. 836–837. [Google Scholar]
- Garrappa, R.; Mainardi, F.; Maione, G. Models of dielectric relaxation based on completely monotone functions. Fract. Calc. Appl. Anal. 2016, 19, 1105–1160. [Google Scholar] [CrossRef]
- Edwards, J.T.; Ford, N.J.; Simpson, A.C. The numerical solution of linear multi-term fractional differential equations: Systems of equations. J. Comput. Appl. Math. 2002, 148, 401–418. [Google Scholar] [CrossRef]
- Ford, N.J.; Connolly, J.A. Systems-based decomposition schemes for the approximate solution of multi-term fractional differential equations. J. Comput. Appl. Math. 2009, 229, 382–391. [Google Scholar] [CrossRef]
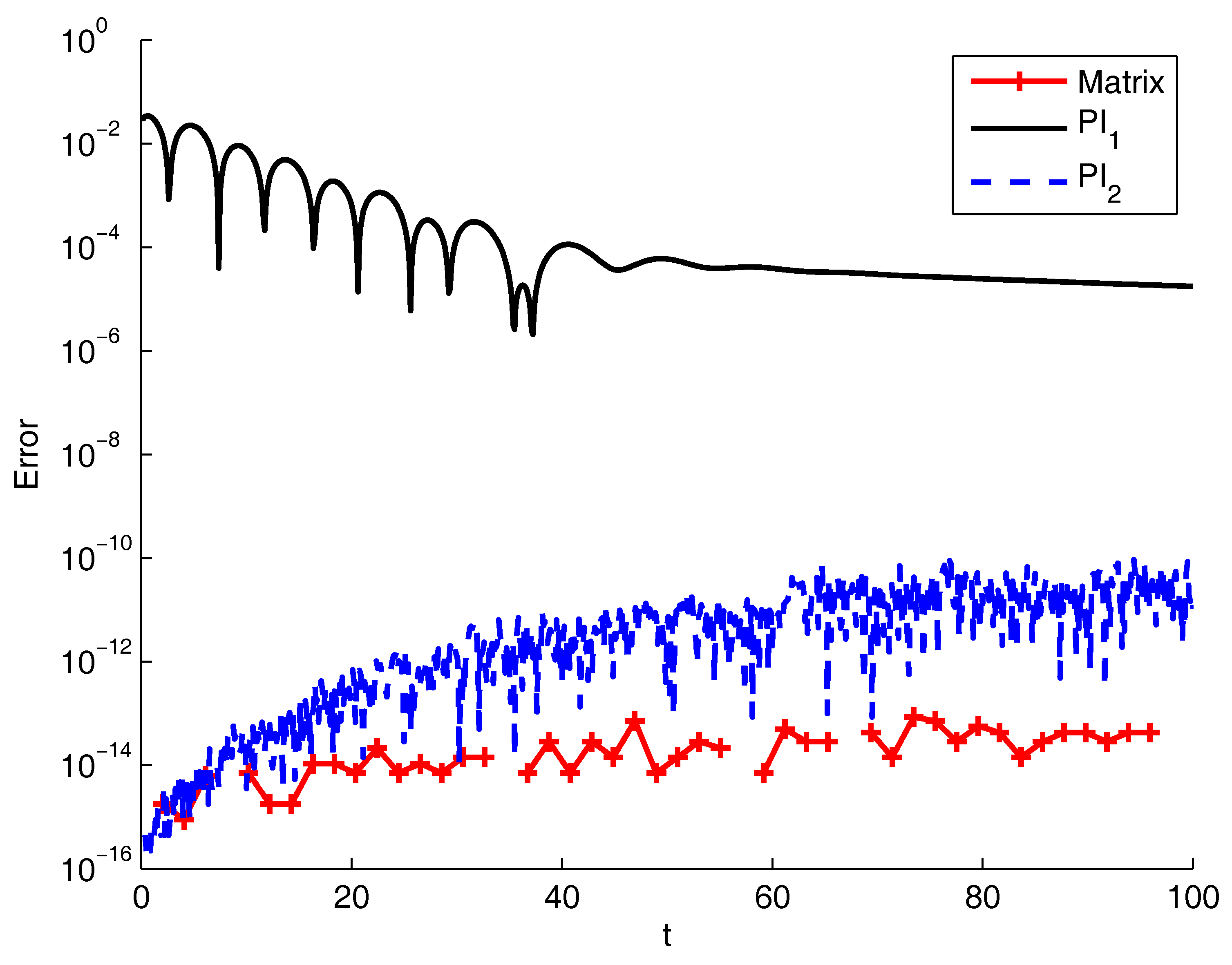
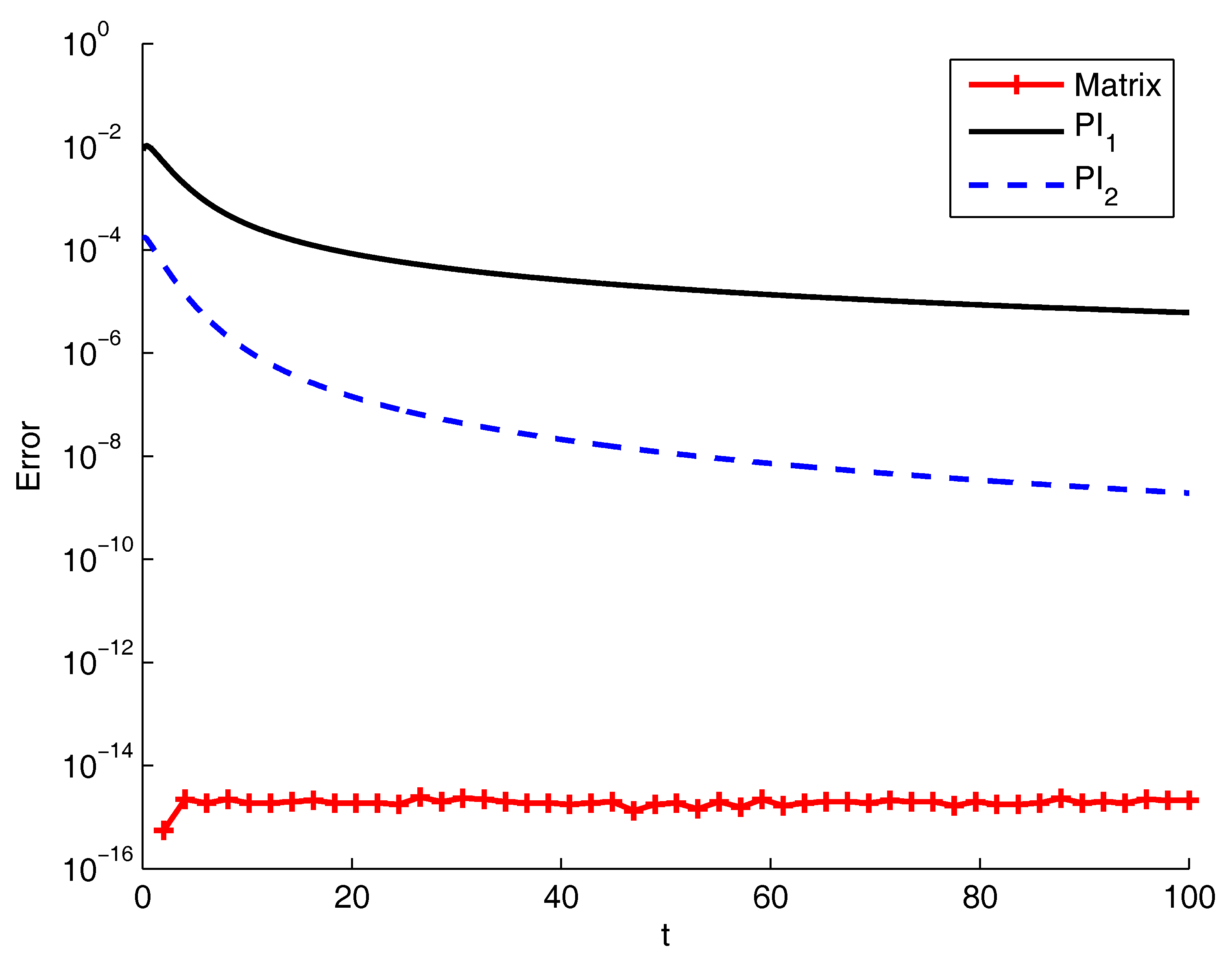
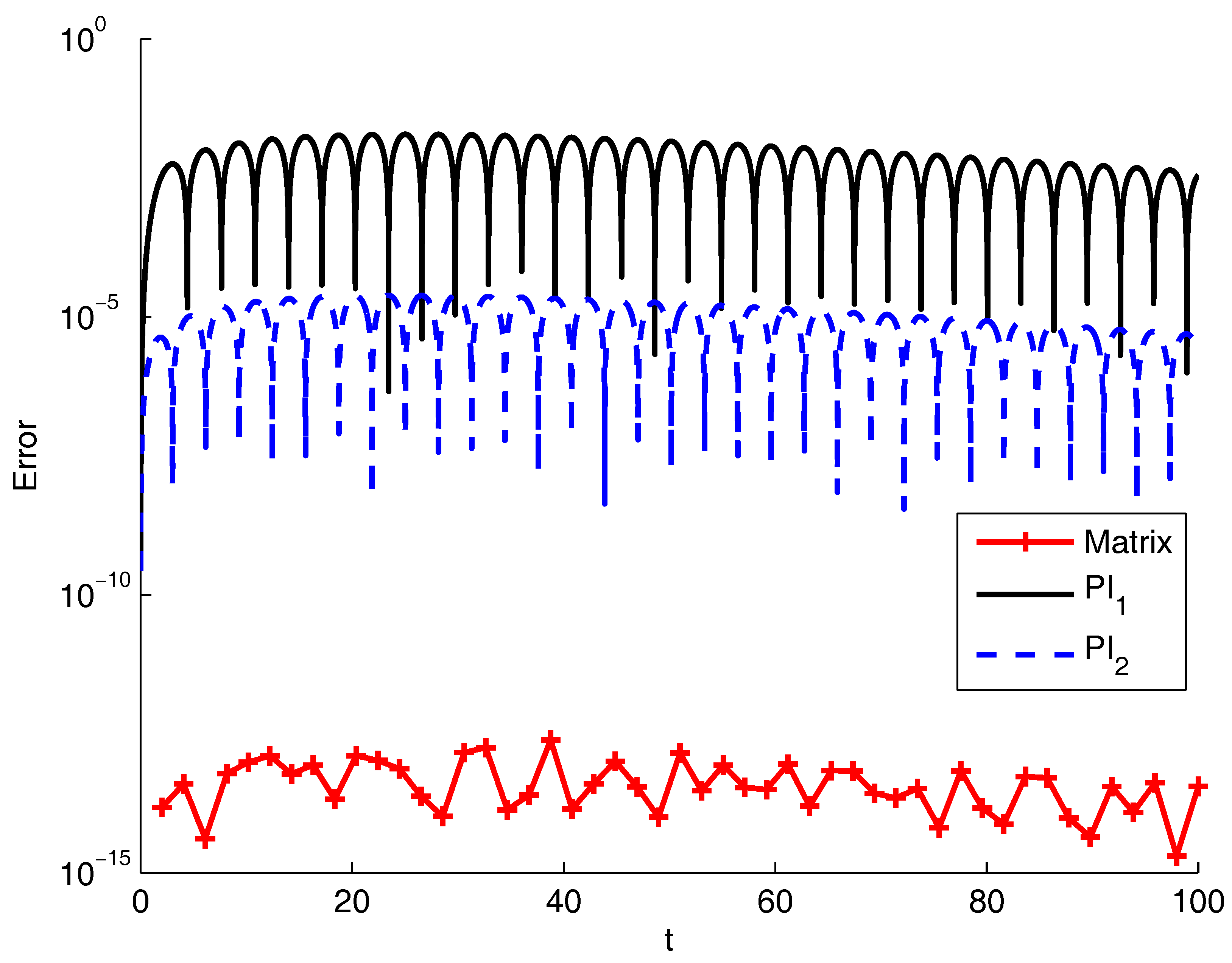
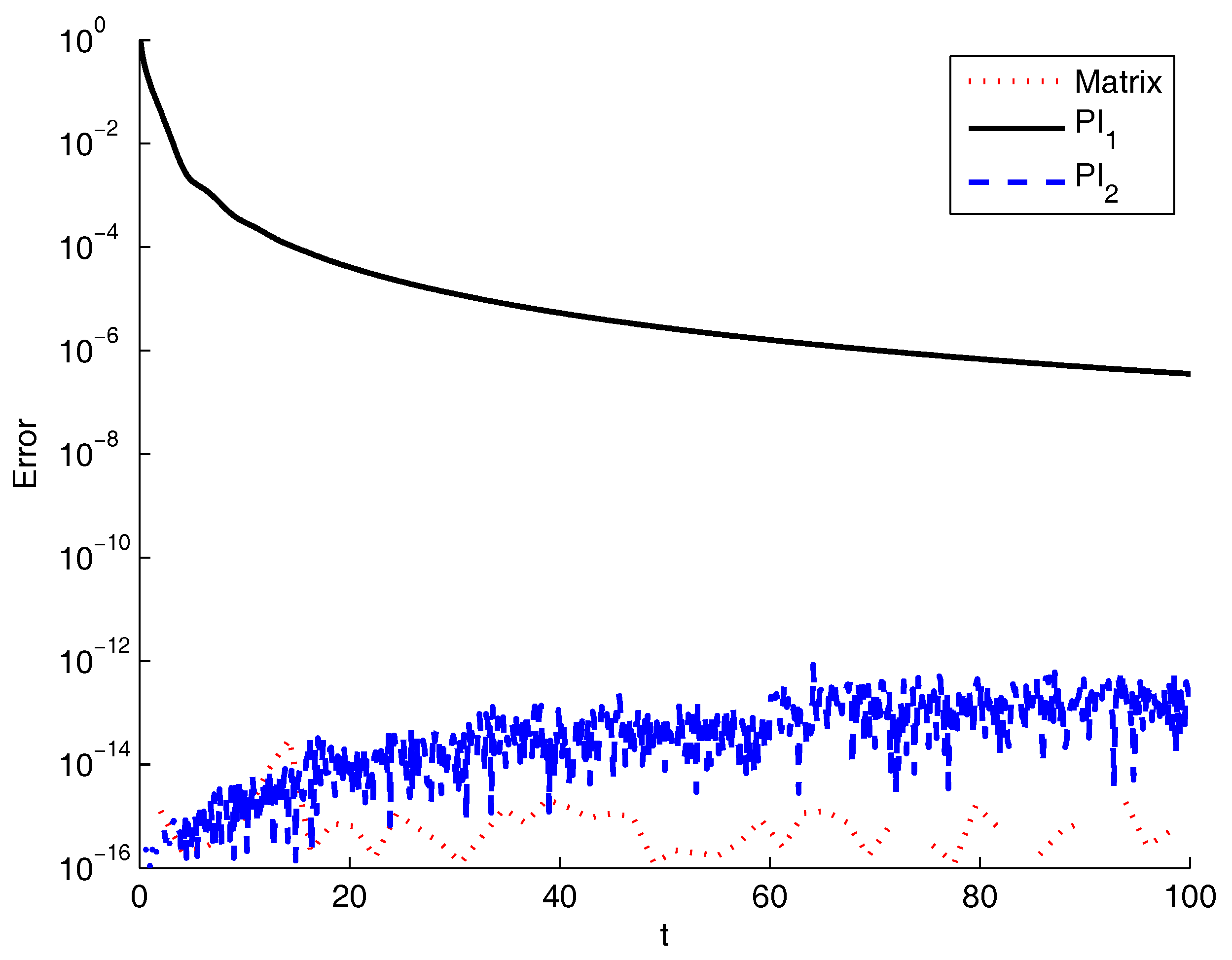
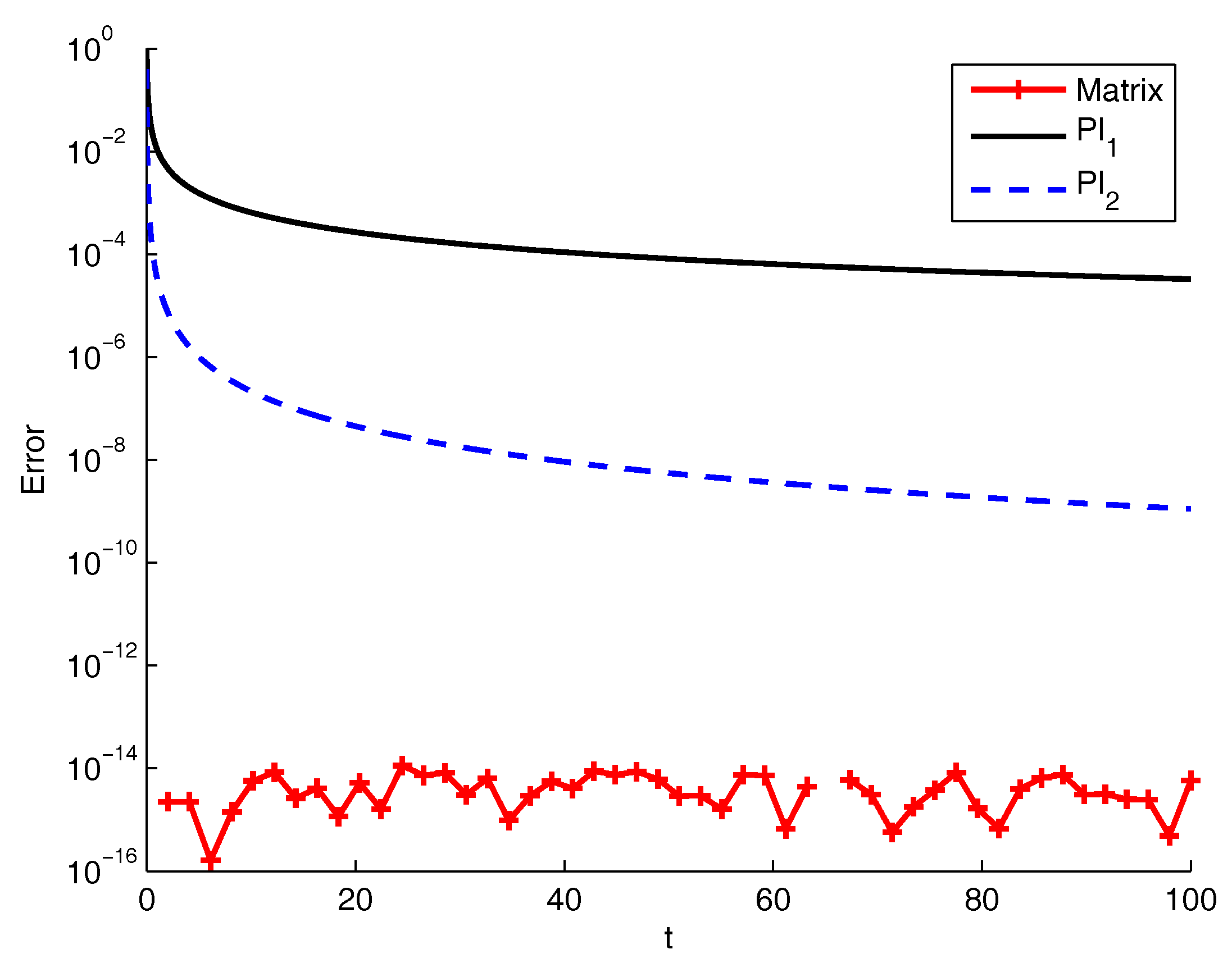
| T | Matrix | PI1 | PI2 |
|---|---|---|---|
| 10 | |||
| 50 | |||
| 100 |
| T | Matrix | PI1 | PI2 |
|---|---|---|---|
| 10 | |||
| 50 | |||
| 100 |
| T | Matrix | PI1 | PI2 |
|---|---|---|---|
| 10 | |||
| 50 | |||
| 100 |
| T | Matrix | PI1 | PI2 |
|---|---|---|---|
| 10 | |||
| 50 | |||
| 100 |
| T | Matrix | PI1 | PI2 |
|---|---|---|---|
| 10 | |||
| 50 | |||
| 100 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popolizio, M. Numerical Solution of Multiterm Fractional Differential Equations Using the Matrix Mittag–Leffler Functions. Mathematics 2018, 6, 7. https://doi.org/10.3390/math6010007
Popolizio M. Numerical Solution of Multiterm Fractional Differential Equations Using the Matrix Mittag–Leffler Functions. Mathematics. 2018; 6(1):7. https://doi.org/10.3390/math6010007
Chicago/Turabian StylePopolizio, Marina. 2018. "Numerical Solution of Multiterm Fractional Differential Equations Using the Matrix Mittag–Leffler Functions" Mathematics 6, no. 1: 7. https://doi.org/10.3390/math6010007
APA StylePopolizio, M. (2018). Numerical Solution of Multiterm Fractional Differential Equations Using the Matrix Mittag–Leffler Functions. Mathematics, 6(1), 7. https://doi.org/10.3390/math6010007





