A Numerical Solution of Fractional Lienard’s Equation by Using the Residual Power Series Method
Abstract
:1. Introduction
2. The Residual Power Series Method for Fractional Lienard’s Equation
3. Convergence Analysis
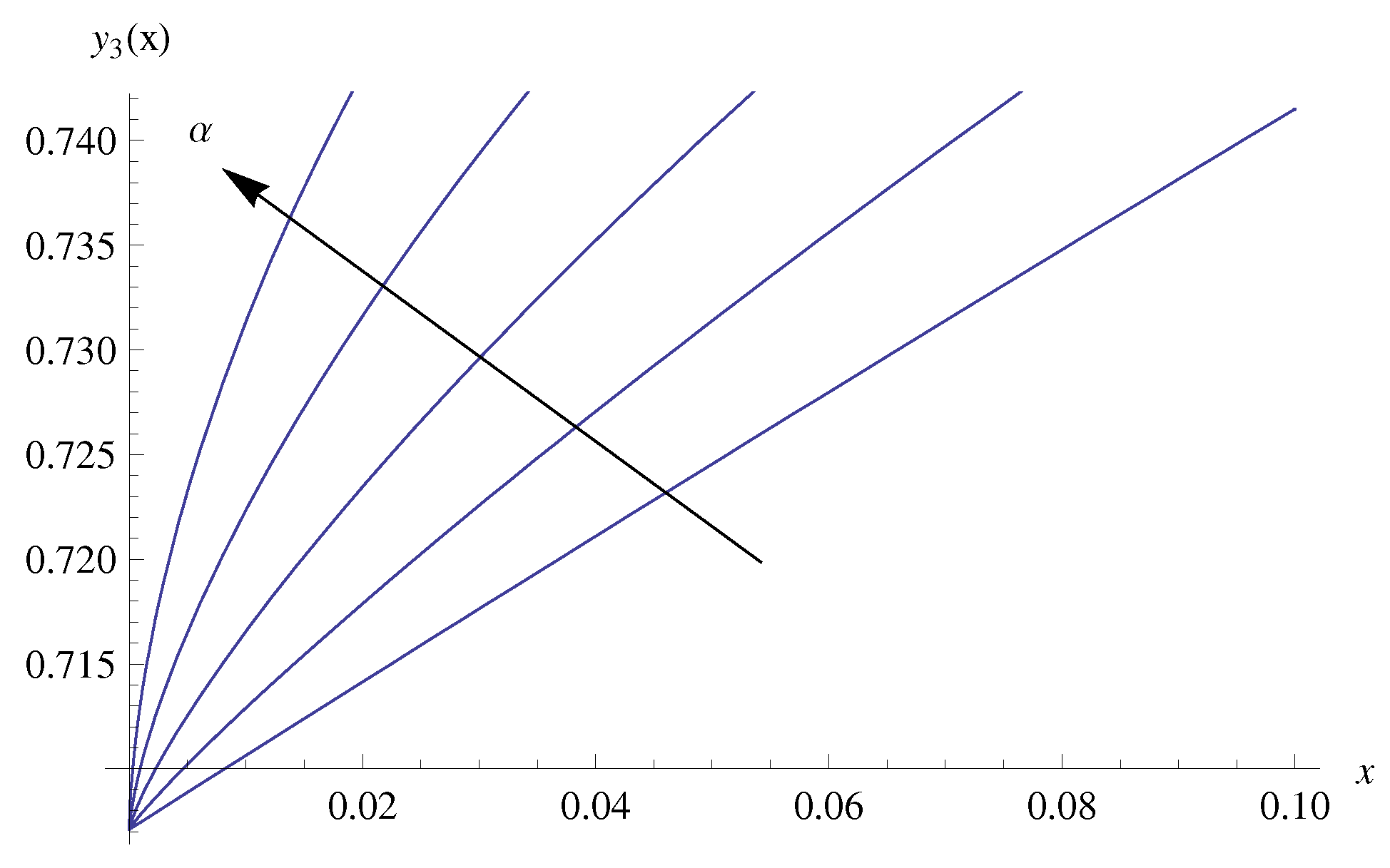
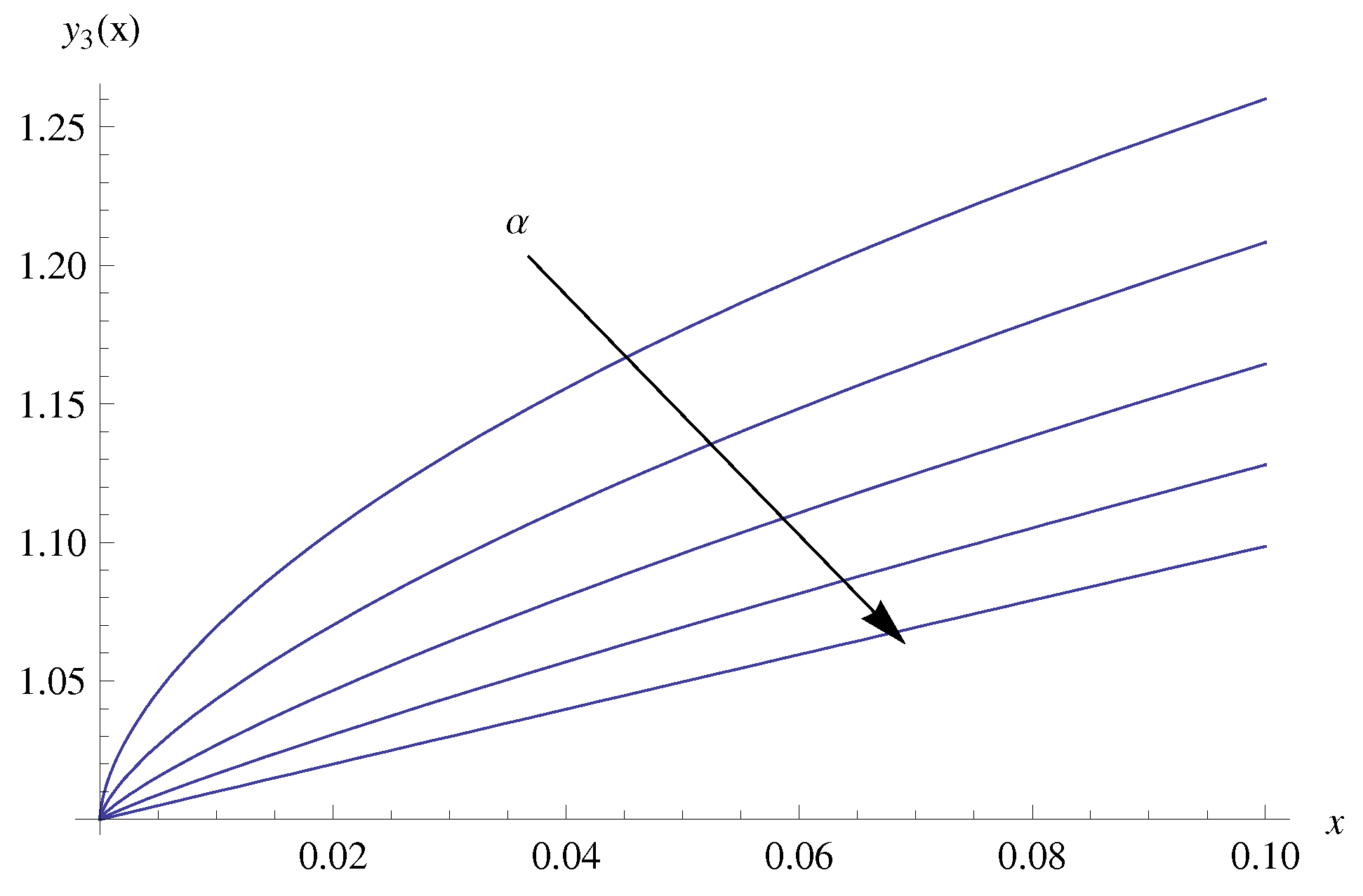
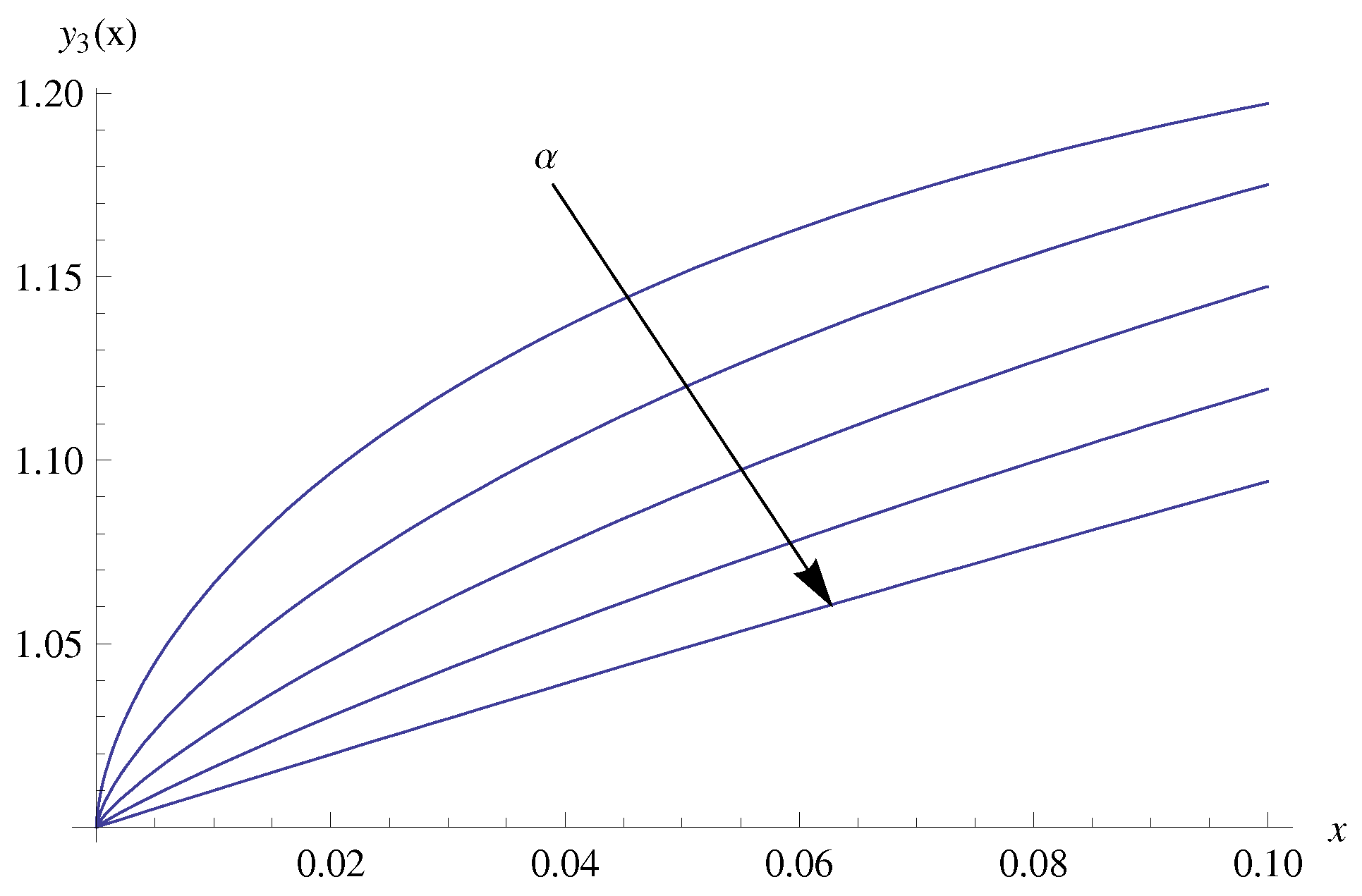
4. Numerical Results
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Guckenheimer, J. Dynamics of the van der Pol equation. IEEE Trans. Circuits Syst. 1980, 27, 983. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Ding, T.; Huang, H.W.; Dong, Z.X. Qualitative Theory of Differential Equations; Science Press: Peking, China, 1985. [Google Scholar]
- Feng, Z. On explicit exact solutions for the Lienard equation and its applications. Phys. Lett. A 2002, 293, 50–56. [Google Scholar] [CrossRef]
- Syam, M.; Attili, B. Numerical solution of singularly perturbed fifth order two point boundary value problem. Appl. Math. Comput. 2005, 170, 1085–1094. [Google Scholar] [CrossRef]
- Attilia, B.; Furati, K.; Syam, M. An efficient implicit Runge–Kutta method for second order systems. Appl. Math. Comput. 2006, 178, 229–238. [Google Scholar] [CrossRef]
- Syam, M.; Siyyam, H. Numerical differentiation of implicitly defined curves. J. Comput. Appl. Math. 1999, 108, 131–144. [Google Scholar] [CrossRef]
- El-Sayed, M.; Syam, M. Electrohydrodynamic instability of a dielectric compressible liquid sheet streaming into an ambient stationary compressible gas. Arch. Appl. Mech. 2007, 77, 613–626. [Google Scholar] [CrossRef]
- Syam, M. The modified Broyden-variational method for solving nonlinear elliptic differential equations. Chaos Solitons Fractals 2007, 32, 392–404. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to Homotopy Analysis Method; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liao, S.J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S.J. An approximate solution technique not depending on small parameters: A special example. Int. J. Non-Linear Mech. 1995, 30, 371–380. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Singh, J. Numerical computation of fractional Black–Scholes equation arising in financial market. Egypt. J. Basic Appl. Sci. 2014, 1, 177–183. [Google Scholar] [CrossRef]
- Kong, D. Explicit exact solutions for the Lienard equation and its applications. Phys. Lett. A 1995, 196, 301–306. [Google Scholar] [CrossRef]
- Matinfar, M.; Hosseinzadeh, H.; Ghanbari, M. A numerical implementation of the variational iteration method for the Lienard equation. World J. Model. Simul. 2008, 4, 205–210. [Google Scholar]
- Matinfar, M.; Mahdavi, M.; Raeisy, Z. Exact and numerical solution of Lienard’s equation by the variational homotopy perturbation method. J. Inf. Comput. Sci. 2011, 6, 73–80. [Google Scholar]
- Rashidi, M.M.; Rostami, B.; Freidoonimehr, N.; Abbasbandy, S. Free convective heat and mass transfer for MHD fluid flow over a permeable vertical stretching sheet in the presence of the radiation and buoyancy effects. Ain Shams Eng. J. 2014, 5, 901–912. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Hassan, H. An analytic solution of micropolar flow in a porous channel with mass injection using homotopy analysis method. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 419–437. [Google Scholar]
- Khuri, S.A. A Laplace decomposition algorithm applied to a class of nonlinear differential equations. J. Appl. Math. 2001, 1, 141–155. [Google Scholar] [CrossRef]
- Khan, M.; Gondal, M.A.; Hussain, I.; Karimi Vanani, S. A new comparative study between homotopy analysis transform method and homotopy perturbation transform method on semi-infinite domain. Math. Comput. Model. 2012, 55, 1143–1150. [Google Scholar] [CrossRef]
- Singh, J.; Swroop, R.; Kumar, D. A computational approach for fractional Convection–Diffusion equation via integral transforms. Ain Shams Eng. J. 2016. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Argyros, I.K. A new analysis for the Keller–Segel model of fractional order. Numer. Algorithms 2016. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Gallo, A. New results on the synthesis of FO-PID controllers. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 997–1007. [Google Scholar] [CrossRef]
- Syam, M. Analytical solution of the Fractional Fredholm integro-differntial equation using the modified residual power series method. Complexity 2017, 2017, 6. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Alquran, M.; Al-Khaled, K.; Sarda, T.; Chattopadhyay, J. Revisited Fisher’s equation in a new outlook: A fractional derivative approach. Phys. A Stat. Mech. Appl. 2015, 438, 81–93. [Google Scholar] [CrossRef]
- Jaradat, H.M.; Al-Shara, S.; Khan, Q.J.A.; Alquran, M.; Al-Khaled, K. Analytical solution of time-fractional Drinfeld-Sokolov-Wilson System using residual power series method. IAENG Int. J. Appl. Math. 2016, 46, 64–70. [Google Scholar]
- Abu Arqub, O. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- El-Ajou, A.; Abu Arqub, O.; Al zhour, Z.; Momani, S. New results on fractional power series: Theories and applications. Entropy 2013, 15, 5305–5323. [Google Scholar] [CrossRef]
- Rudin, W. Principles of Mathematical Analysis, 3rd ed.; China Machine Press: Beijing, China, 2004. [Google Scholar]

| x | Exact Solution | ||
|---|---|---|---|
| 0 | |||
| 2.2 × 10 | |||
| 1.7 × 10 | |||
| 5.8 × 10 | |||
| 1.4 × 10 | |||
| 2.6 × 10 |
| x | Exact Solution | ||
|---|---|---|---|
| 0 | |||
| 1.9 × 10 | |||
| 1.5 × 10 | |||
| 4.9 × 10 | |||
| 1.1 × 10 | |||
| 2.2 × 10 |
| x | Exact Solution | ||
|---|---|---|---|
| 0 | |||
| 1.4 × 10 | |||
| 1.2 × 10 | |||
| 2.0 × 10 | |||
| 2.1 × 10 | |||
| 2.6 × 10 |
| x | Exact Solution | ||
|---|---|---|---|
| 1 | 1 | 0 | |
| 1.01981437 | 1.01981441 | 4.0 × 10 | |
| 1.03931280 | 1.03931294 | 1.4 × 10 | |
| 1.05857420 | 1.05857444 | 2.4 × 10 | |
| 1.07767317 | 1.07767348 | 3.1 × 10 | |
| 1.09668137 | 1.09668171 | 3.4 × 10 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syam, M.I. A Numerical Solution of Fractional Lienard’s Equation by Using the Residual Power Series Method. Mathematics 2018, 6, 1. https://doi.org/10.3390/math6010001
Syam MI. A Numerical Solution of Fractional Lienard’s Equation by Using the Residual Power Series Method. Mathematics. 2018; 6(1):1. https://doi.org/10.3390/math6010001
Chicago/Turabian StyleSyam, Muhammed I. 2018. "A Numerical Solution of Fractional Lienard’s Equation by Using the Residual Power Series Method" Mathematics 6, no. 1: 1. https://doi.org/10.3390/math6010001
APA StyleSyam, M. I. (2018). A Numerical Solution of Fractional Lienard’s Equation by Using the Residual Power Series Method. Mathematics, 6(1), 1. https://doi.org/10.3390/math6010001




