1. Introduction
Let
denote the space of all
n-square matrices over the complex field
and let
be the symmetric group of degree
n. For
, the permanent function is defined as:
The permanent function therefore resembles the determinant, which in turn is given by:
where
denotes the sign function.
Although not as prominent as the determinant, the permanent function is still a well-known matrix function, with many applications in combinatorics and graph theory. However, while the determinant can be easily computed, no efficient algorithm for computing the permanent is known. The difficulty for a direct computation of the permanent leads to the idea of trying to compute it by using determinants. This problem dates back to 1913 in a work by Pólya [
1], and it has been under intensive investigation since then. While it is clear that the permanent of a
matrix:
equals the determinant of the related matrix:
Szegö [
2] proved that for
, there is no way to generalize this procedure. That is, there is no uniform way of changing the signs in the entries of a matrix
in order to obtain a matrix
B satisfying
.
In [
3], Gibson proved that if
A is an
n-square
-matrix, and if the permanent of
A can be converted to a determinant by affixing ± signs to the elements of the matrix, then
A has at most
positive entries.
Later, Little [
4] proved that an
n-square
-matrix can be conveniently represented by means of a bipartite graph and reinterpreted the problem of characterizing convertible matrices as the problem of characterizing bipartite graphs whose 1-factors can be counted by using Pfaffians in the manner suggested by Kasteleyn [
5].
The computational complexity for determining if a
-matrix is convertible was studied by Vazirani and Yannakakis [
6] and Robertson, Seymour, and Thomas [
7], leading the latter authors to design a polynomial-time algorithm capable of determining whether or not the permanent of the matrix is convertible into a determinant.
In this article, we consider mostly
n-square
-matrices with the maximum number of positive entries
. For these cases, we present a procedure to determine whether or not a given matrix is convertible. Compared with previously available algorithms, this method does not rely on the associated bipartite graph, and is more efficient. This result is presented in
Section 4, where we introduce a new concept: the imprint. Before that, in
Section 3, we define Hessenberg-type matrices, generalizing the well-known notion of Hessenberg matrices, and present some preliminary results. Our main results are presented in
Section 5. We extend Fonseca’s result [
8] by presenting an explicit characterization of convertible Hessenberg-type matrices and corresponding subspaces. We conclude that convertible matrices can be reduced to a basic set.
2. Basic Definitions and Preliminary Results
Let us start with a brief summary of definitions and results that are subsequently used throughout the article.
In the present work, we exclusively consider square matrices, so we will drop the qualifier square in what follows. In general, the order n of the considered matrices is arbitrary, except when explicitly stated otherwise.
A matrix
is said to be convertible if there exists a
-matrix
, such that:
where ★ denotes the Hadamard product. As already mentioned in the Introduction, a convertible matrix of order
n has at most
nonzero entries [
3].
For a
-matrix
S of order
n, we define the associated coordinate subspace as:
It is clear that if
S is convertible then every element of
is also convertible, with respect to the same matrix
C; i.e., there exists a
-matrix
such that:
We will also say that is convertible.
A well-known set of convertible matrices is the set of Hessenberg matrices. The matrix
is said to be a lower (upper) Hessenberg matrix if
for
(
). In [
9], Gibson proved that the linear space of lower (or upper) Hessenberg matrices is a convertible subspace of
. In [
8], Fonseca extended Gibson’s result to a broader class of matrices. In the next section we introduce a definition that further extends the class of matrices considered in [
8].
Definition 1. Two matrices A and B are permutation equivalent if there exist permutation matrices P and Q such that . In such a case, we denoted it by .
It is clear that if A is convertible and , then B is also convertible.
Proposition 1. If a matrix is convertible, then it is sufficient to change at most signs in order to convert the permanent into the determinant.
Proof. Trivial by Lemma 3 and by the Theorem in [
3]. ☐
Let . We denote by the submatrix of A obtained after removing rows and columns .
The following result is given in the proof of Lemma 1 of [
3]:
Lemma 1. Let be a convertible -matrix, with , where is a -matrix . If , then is also convertible, with: A subspace version of this lemma follows immediately.
Proposition 2. If is a convertible subspace and , then is also a convertible subspace.
Corollary 1. If is a convertible subspace and are k nonzero elements of S, then is also a convertible subspace.
Proof. Trivial by induction. ☐
3. Hessenberg-Type Matrices
In this section we will extend further the class of matrices considered in [
8]. Throughout what follows, the adjective “lower” for the lower Hessenberg matrices will be dropped, since no ambiguity will appear.
Definition 2. An n-square matrix is a Hessenberg-type matrix if it has at most nonzero entries above the main diagonal. A coordinate subspace V of is said to be a Hessenberg-type subspace if there is a Hessenberg-type -matrix with if , such that: If S has exactly nonzero entries above the main diagonal, we call V a -Hessenberg-type subspace, or simply a -subspace if there is no ambiguity. If , then S is called a full Hessenberg-type matrix and the corresponding subspace is called a full Hessenberg-type subspace.
Note that a full Hessenberg-type -matrix has precisely the maximum allowed number of nonzero entries for convertibility.
Standard Hessenberg matrices are of course special cases of Hessenberg-type matrices. In particular, a matrix in a -subspace, with all nonzero entries located in the second upper diagonal, will be referred to as a full Hessenberg matrix.
Fonseca’s extension result [
8], concerning a particular Hessenberg-type subspace, can be stated as follows:
Theorem 1. [
8]
Let be a full Hessenberg-type -matrix, and , with . If the positions of the nonzero entries, above the main diagonal, satisfy:then is a convertible subspace. The -matrix such that for all satisfies: Example 1. For example, if , , and , then:and the coordinate subspace is convertible. Next, we present some results concerning nonfull Hessenberg-type subspaces.
Proposition 3. The -subspace is convertible.
Proof. Trivial by Theorem 1. ☐
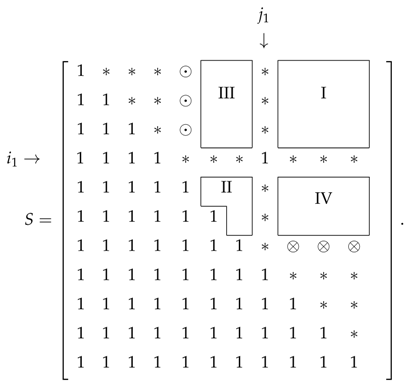
Proposition 4. Let S be a -Hessenberg-type -matrix with a 1 in position , . S is convertible if and only if the position of the second 1 above the main diagonal is not in one of the following regions: Proof. Without loss of generality, let us consider the scheme below. Note that if
, then we only have region I.
Let us first suppose that the second 1 is in region I. Assume, without loss of generality, that the second 1 is in the upper-right corner of
S. If this is not the case, then there exists a submatrix
of
S satisfying this condition, and the non-convertibility of
implies the non-convertibility of
S. Note that
is an
-square matrix with
nonzero entries above the main diagonal—which cannot be convertible because it has more than
nonzero entries [
3]. Then, by Lemma 1, we conclude that
S is not convertible.
The situation where the second 1 is in region II is no different from the previous case, since one can interchange the role of the two 1’s.
Next, let us suppose that the second 1 is in region III. So, we have
and we may assume—without loss of generality—that
and
(an example of a matrix
S of this form is given in Equation (
16) below). If this is not the case, then as we argued for the region I case, there exists a submatrix
of
S satisfying this condition.
Since the number of nonzero entries of S is , it follows that is an -square matrix with nonzero entries, because there are nonzero entries eliminated in S. Since in region III, the number of nonzero entries of this -square matrix is greater than the maximum admissible , and is therefore not convertible. By Corollary 1, this implies that the initial matrix is also nonconvertible.
Finally, if the second 1 is in region IV, one can interchange the role of the 1’s above the main diagonal, thus falling in the previous case.
If the second 1 is not in any of the four regions, then we have three cases:
- •
if and (positions labeled by ⊙), then S is permutation equivalent to a convertible matrix by Theorem 1, permuting columns and .
- •
if and (positions labeled by ⊗), then S is permutation equivalent to a convertible matrix by Theorem 1, permuting rows and .
- •
otherwise (positions labeled by ∗) S is convertible by Theorem 1. ☐
Lemma 2. For , the number of convertible -subspaces with a nonzero entry at a fixed position , , is: Proof. Consider first the case
. By Proposition 4, the number of convertible
-subspaces is given by:
where
is the
nth triangular number.
For
the number of convertible
-subspaces is likewise given by:
☐
Proposition 5. For , the number of convertible -subspaces is .
Proof. The formula clearly holds for
. Let us prove it for general
n by induction. Suppose then that the formula holds for
n. Let
S be an arbitrary
-Hessenberg-type
-matrix. Two cases may occur: apart from the
position, there is either none or at least one nonzero entry in the first row of
S. In the first case, it is clear that the number of convertible subspaces of
coincides with the number of convertible subspaces of
, which is, by hypothesis:
In the second case, one applies Lemma 2 at fixed positions
. For position
the counting is provided by Formula (18), which gives:
For positions
,
, the counting is provided by Formula (
17). Summing over all different possibilities gives:
where the term
takes care of the double counting (since there may be two nonzero entries in the first row, apart from the position
). This sum can be easily performed, yielding:
Finally, summing all contributions (
21), (
22), and (
24) for the number of convertible
-subspaces, we get:
It follows by induction that the number of convertible -subspaces is . ☐
5. Charaterization of Full Hessenberg-Type Subspaces
In this section we consider full Hessenberg-type matrices and the corresponding subspaces. Our aim is to obtain an explicit characterization of convertible full Hessenberg-type subspaces.
Hessenberg-type matrices can be composed to produce new higher-dimensional matrices as follows.
Definition 4. Let and be two Hessenberg-type -matrices with dimensions m and n, respectively, such that the submatrix of formed by the lower-right corner coincides with the submatrix of formed by its upper-left corner. The k-overlap is the -dimensional matrix obtained by superposition of and by their main diagonal, overlapping the coincident submatrix, where the missing entries below and above the main diagonal are 1 and 0, respectively.
Note that the new matrix is not necessarily of the Hessenberg-type, as the following counting of nonzero entries above the main diagonal shows. Let a, b, and c respectively denote the number of 1’s above the main diagonal in , , and the common submatrix. The number of 1’s above the main diagonal in is then . In the least favorable case when both matrices and are full (i.e., and ), it follows that is Hessenberg-type only if .
Example 3. For the two following (full) Hessenberg-type matrices:two examples of overlaps are: In the first case, the matrix is Hessenberg-type, whereas in the second case it is not.
Lemma 4. Let and be two full Hessenberg-type -matrices. is a full Hessenberg-type -matrix if and only if the common matrix is a full Hessenberg-type -matrix.
Proof. If the matrix is full, the conclusion follows trivially from the counting below Definition 4. By the same counting, if is full, we have , and thus the number of nonzero entries above the main diagonal in the matrix is . ☐
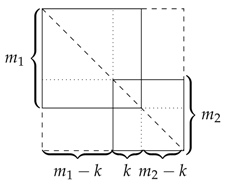
Proposition 7. Let and be two full and convertible Hessenberg-type -matrices. If a k-overlap is a full Hessenberg-type matrix, then it is convertible.
Proof. Let and be two full and convertible Hessenberg-type -matrices of order and , respectively, and S the k-overlap matrix of order n, , which by hypothesis is a full Hessenberg-type matrix. If , then or , and it is therefore convertible.
Suppose that
. Without loss of generality, one can consider the scheme depicted below:
where the
overlap submatrix will be denoted by
. It follows from the previous lemma that
is a full Hessenberg-type matrix. Moreover, it follows from Corollary 1 that
is convertible, since
.
Let us calculate
. For the last
rows of
S, the number of nonzero entries in each row is obtained by adding
to each value of the first row of
,
Since
is a full convertible matrix, we have:
and the contribution of these
k rows to the first row of
is:
which correspond to the last
k values of the first row of
. It follows that the first
values of the first row of
correspond to the first
rows of
, and therefore to the first
rows of
S. Hence, after taking into account the first
values of the first row of
, the first row of
turns out to be:
Since a similar argument is clearly valid for the columns, we get:
and it follows from Proposition 6 that
S is convertible. ☐
We will now show that a small family of matrices generates—by means of the above defined overlap—all possible full convertible Hessenberg-type subspaces.
For
, consider the family of full
n-square Hessenberg-type
-matrices represented below:
where the
nonzero entries above the main diagonal are in the following regions: position
, positions
, …,
in the first line and positions
, …,
in the last column, where the integer
k can take any of the values
. In particular, if
, all the 1’s above the main diagonal are positioned in the first row and if
all the 1’s are positioned in the last column.
We will refer to these matrices as basic, with the understanding that for the (only) basic matrix is the -Hessenberg matrix.
Proposition 8. The basic matrices are convertible.
Proof. The basic matrices are permutation equivalent to the Hessenberg matrix (or coincide with it, for ). ☐
Proposition 9. If a full Hessenberg-type -matrix is convertible, then it is basic or an overlap of two or more basic matrices.
Proof. We will prove it by induction.
For
there are three convertible subspaces
, where:
The first matrix S is a 1-overlap of two 2-square -hessenberg matrices, whereas the last two are basic.
Suppose now that the proposition is valid for n. Note first that validity for n actually guarantees validity for , and therefore for , with , for the following reason. Suppose there is a -square full convertible Hessenberg-type -matrix that is neither basic nor an overlap of basic matrices. The 1-overlap of this matrix (by means of the diagonal position ) with the basic matrix is then a full Hessenberg-type matrix of order n, and is convertible by Proposition 7, but fails to be basic or an overlap of basic matrices, which is a contradiction.
Let then be an -square full convertible Hessenberg-type -matrix. In what follows, we will repeatedly use Proposition 6, which establishes that for all integer , there is exactly one row and one column of S with exactly ℓ nonzero entries. Proposition 2 and Corollary 1 are also used.
Let , be the number of 1’s in the first row of S. It follows that rows 2, 3, …, until row k are fully determined. In particular, for these rows, for . Moreover, all entries in the first row at positions with must be 1’s, for the following reason. Matrices are convertible , and must therefore have less nonzero entries above the diagonal than S. However, for (and ), no 1’s would be removed from S, unless they are at positions . So, , …, in S are necessarily 1’s, with the remaining 1 in the first row appearing in an arbitrary position , (of course, the above constraints are void for ). Note that the column is also completely determined: it is already established that for , and it follows from Proposition 6 that the remaining entries must be 1’s. Now, if , we are done, since S is then seen to be basic (in particular, this includes the case ). Otherwise, we have and let be the square matrix formed by the first m rows and columns of S. This matrix is clearly convertible, by Corollary 1. On the other hand, since the combined number of 1’s above the diagonal in the first row and last column of is clearly , it follows that the maximum number of admissible nonzero entries is saturated, showing that is of the basic type. Furthermore, is certainly Hessenberg-type, convertible, and full, since the number of 1’s above the diagonal in is precisely , given that exactly k nonzero entries above the diagonal are removed from S. It is clear that S is an -overlap of with , thus completing our proof, since is, by hypothesis, basic or an overlap of basic matrices. ☐
We will conclude by counting the number of convertible full Hessenberg-type subspaces of order n, or the corresponding full convertible Hessenberg-type -matrices. Given an -subspace, there are different combinations of distributing the nonzero entries above the diagonal, where is the th triangular number. Of course, not all of them correspond to a convertible subspace. The number of convertible subspaces is established by the following proposition.
Proposition 10. For , there are different full convertible Hessenberg-type -matrices of order n.
Proof. We will prove it by induction. The hypothesis is clearly verified for . Suppose then that the proposition is valid for n and let us consider the case. It follows again from Proposition 6 that full convertible Hessenberg-type -matrices S fall in two classes: there are either two 1’s in the first row, with one of them necessarily at position , or two 1’s in the second row, necessarily at positions and . In the first case, assigning the remaining 1 to the position puts no restriction on the (full convertible n-square Hessenberg-type) matrix , and so there are as many possibilities for S as there are for (i.e., ). Assigning the remaining 1 to one of the positions , , restricts the form of , but one can easily convince oneself that the reunion of all these cases exhausts all possibilities for , so one again gets possibilities. In the second case, it follows from the arguments in the proof of Proposition 9 that there must be a 1 at position . In this case, there is no restriction on the matrix , and one gets again possibilities. So, there are full Hessenberg-type convertible matrices of order , thus completing the proof. ☐