Generalized Langevin Equation and the Prabhakar Derivative
Abstract
:1. Introduction
2. Prabhakar Derivatives
3. Free Particle
4. Tempered Friction
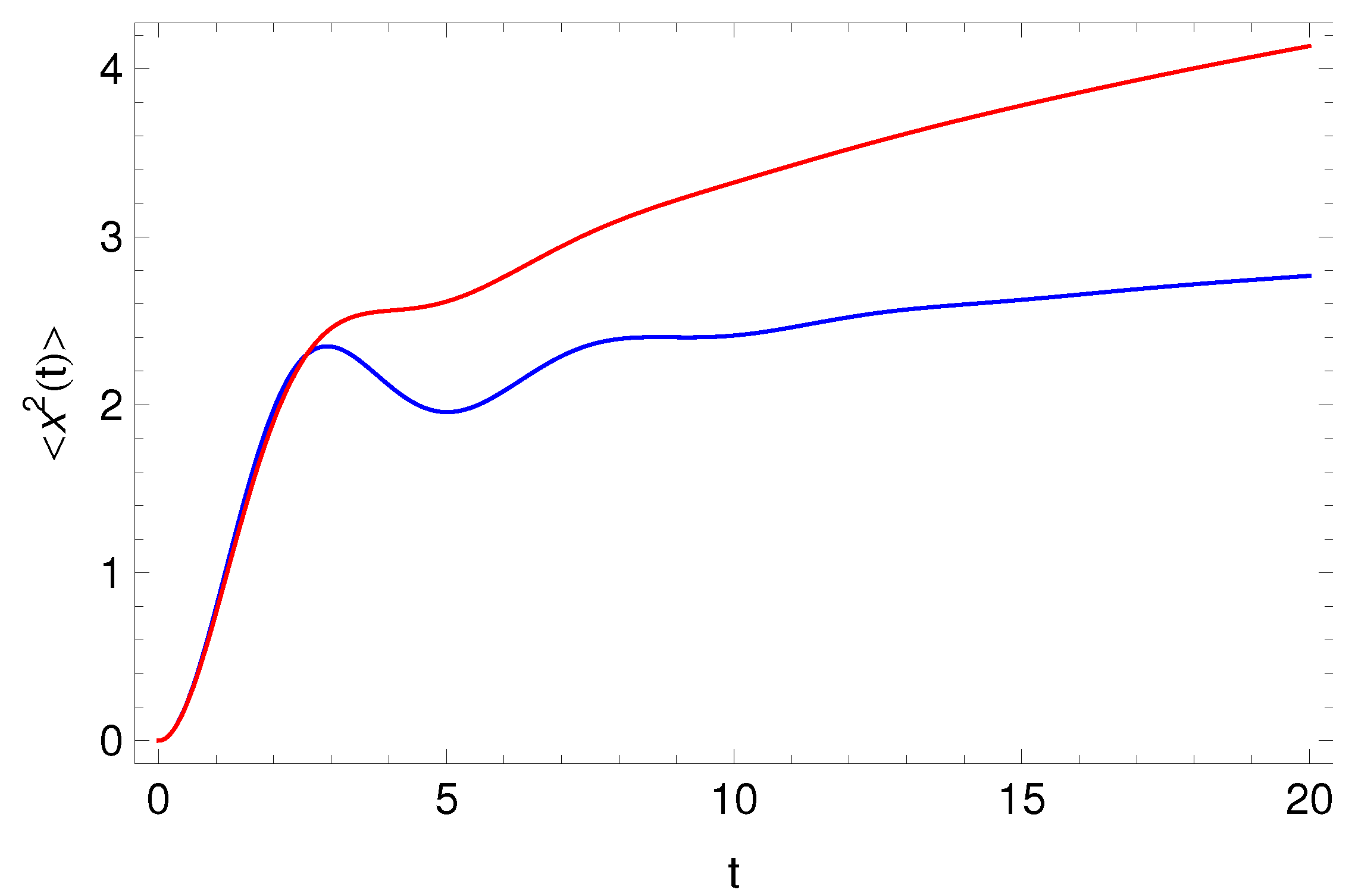
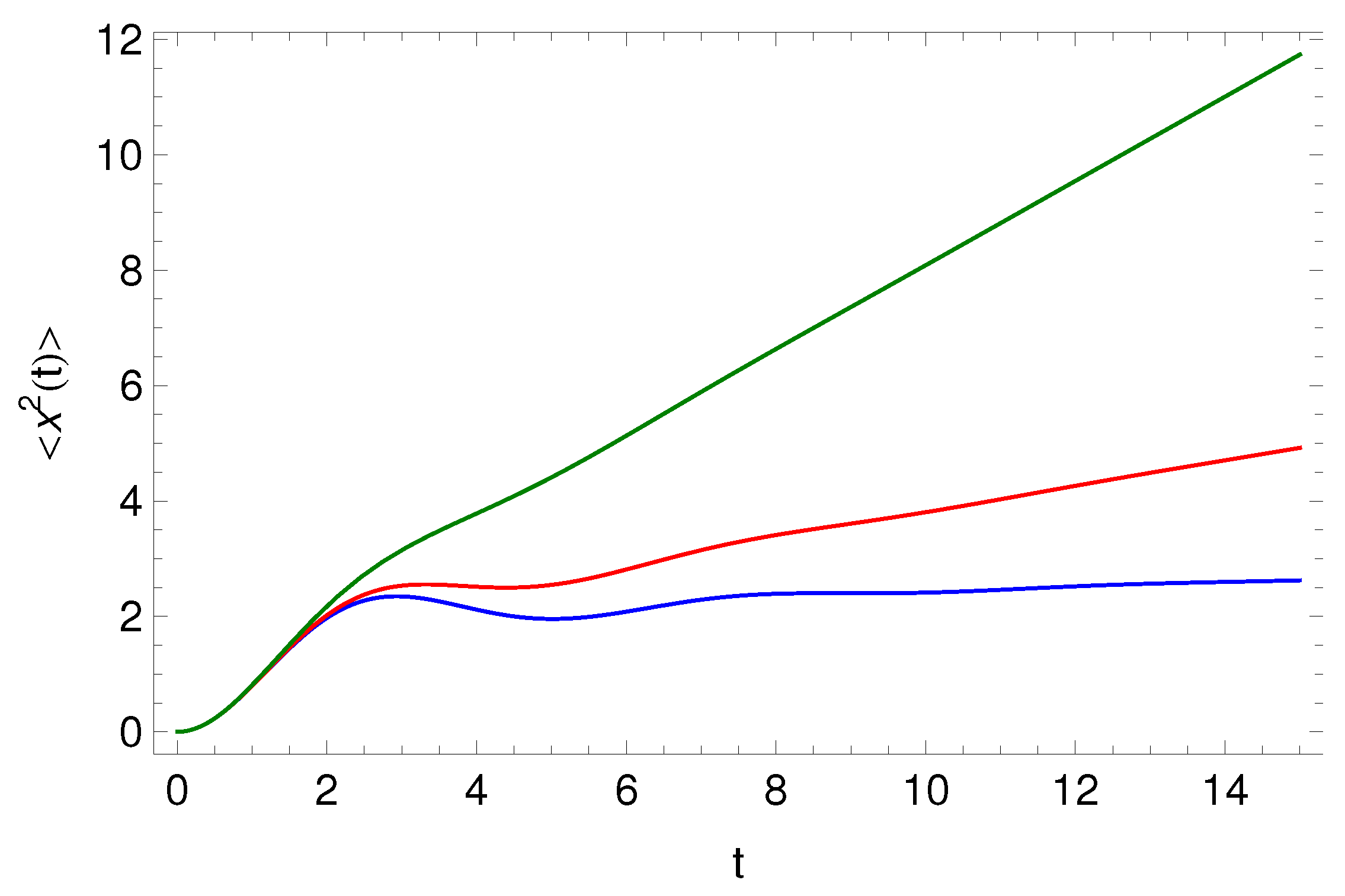
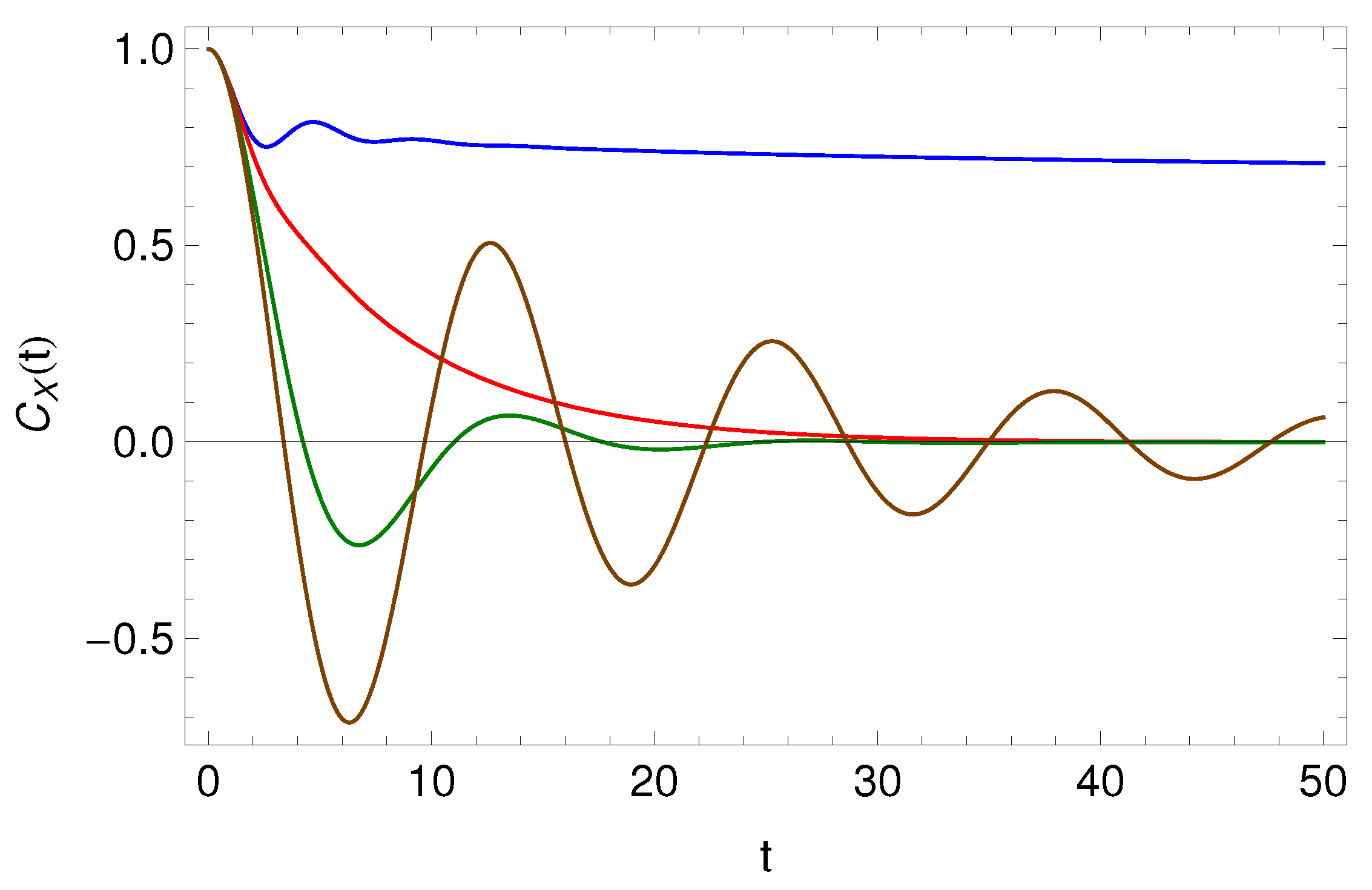
5. Harmonically Bounded Particle in Presence of Prabhakar Friction Term
6. Summary
Acknowledgments
Conflicts of Interest
References
- Coffey, W.T.; Kalmykov, Yu.P.; Waldron, J.T. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering; World Scientific: Singapore, 2012. [Google Scholar]
- Langevin, P. On the theory of Brownian motion. Comptes Rendus 1908, 146, 530–533. [Google Scholar]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Lutz, E. Fractional Langevin equation. Phys. Rev. E 2001, 64, 051106. [Google Scholar] [CrossRef] [PubMed]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelesticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Metzler, R.; Jeon, J.-H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, X.; Deng, W. Localization and ballistic diffusion for the tempered fractional Brownian-Langevin motion. J. Stat. Phys. 2017, 169, 18–37. [Google Scholar] [CrossRef]
- Liemert, A.; Sandev, T.; Kantz, H. Generalized Langevin equation with tempered memory kernel. Physica A 2017, 466, 356–369. [Google Scholar] [CrossRef]
- Sandev, T.; Chechkin, A.; Kantz, H.; Metzler, R. Diffusion and Fokker-Planck-Smoluchowski equations with generalized memory kernel. Fract. Calc. Appl. Anal. 2015, 18, 1006–1038. [Google Scholar] [CrossRef]
- Sandev, T.; Sokolov, I.M.; Metzler, R.; Chechkin, A. Beyond monofractional kinetics. Chaos Solitons Fractals 2017, 102, 210–217. [Google Scholar] [CrossRef]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag-Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, A. Hilfer-Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef]
- Polito, F.; Tomovski, Z. Some properties of Prabhakar-type fractional calculus operators. Fract. Differ. Calc. 2016, 6, 73–94. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transform. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Garrappa, R. Grünwald-Letnikov operators for fractional relaxation in Havriliak-Negami models. Commun. Nonlinear Sci. Numer. Simul. 2016, 38, 178–191. [Google Scholar] [CrossRef]
- Garrappa, R.; Mainardi, F.; Maione, G. Models of dielectric relaxation based on completely monotone functions. Fract. Calc. Appl. Anal. 2016, 19, 1105–1160. [Google Scholar] [CrossRef]
- Giusti, A.; Colombaro, I. Prabhakar-like fractional viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 138–143. [Google Scholar] [CrossRef]
- Bulavatsky, V.M. Mathematical modeling of fractional differential filtration dynamics based on models with Hilfer–Prabhakar derivative. Cybern. Syst. Anal. 2017, 53, 204–216. [Google Scholar] [CrossRef]
- Darani, M.A.; Derakhshan, M.H.; Ansari, A.; Khoshsiar, R. On asymptotic stability of Prabhakar fractional differential systems. Comput. Methods Differ. Equ. 2016, 4, 276–284. [Google Scholar]
- Agarwal, R.; Jain, S.; Agarwal, R.P. Analytic solution of generalized space time fractional reaction diffusion equation. Fract. Differ. Calc. 2017, 7, 169–184. [Google Scholar] [CrossRef]
- Xu, J. Time-fractional particle deposition in porous media. J. Phys. A Math. Theor. 2017, 50, 195002. [Google Scholar] [CrossRef]
- Kochubei, A. General fractional calculus, evolution equations, and renewal processes. Integral Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Luchko, Y.; Yamamoto, M. General time fractional diffusion equation: Some uniqueness and existence results for the initial-boundary-value problems. Fract. Calc. Appl. Anal. 2016, 19, 676–695. [Google Scholar] [CrossRef]
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Hilfer, R. Experimental evidence for fractional time evolution in glass forming materials. Chem. Phys. 2002, 284, 399–408. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Z. Fractional diffusion equation with a generalized Riemann-Liouville time fractional derivative. J. Phys. A Math. Theor. 2011, 44, 255203. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Space-time fractional reaction-diffusion equations associated with a generalized Riemann-Liouville fractional derivative. Axioms 2014, 3, 320–334. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Computational solutions of distributed order reaction-diffusion systems associated with Riemann-Liouville derivatives. Axioms 2015, 4, 120–133. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Analysis of solar neutrino data from Super-Kamiokande I and II. Entropy 2014, 16, 1414–1425. [Google Scholar] [CrossRef]
- Saxena, R.K.; Tomovski, Z.; Sandev, T. Analytical solution of generalized space-time fractional cable equation. Mathematics 2015, 3, 153–170. [Google Scholar] [CrossRef]
- Kubo, R. The Fluctuation-Dissipation Theorem. Rep. Prog. Phys. 1966, 29, 255–284. [Google Scholar] [CrossRef]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag–Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018. [Google Scholar] [CrossRef]
- Despósito, M.A.; Viñales, A.D. Subdiffusive behavior in a trapping potential: Mean square displacement and velocity autocorrelation function. Phys. Rev. E 2009, 80, 021111. [Google Scholar] [CrossRef] [PubMed]
- Mainardi, F.; Pironi, P. The fractional Langevin equation: Brownian motion revisited. Extr. Math. 1996, 10, 140–154. [Google Scholar]
- Pottier, N. Aging properties of an anomalously diffusing particle. Physica A 2003, 317, 371–382. [Google Scholar] [CrossRef]
- Paneva-Konovska, J. Convergence of series in three parametric Mittag-Leffler functions. Math. Slovaca 2014, 64, 73–84. [Google Scholar] [CrossRef]
- Paneva-Konovska, J. From Bessel to Multi-Index Mittag-Leffler Functions: Enumerable Families, Series in Them and Convergence; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Sandev, T.; Tomovski, Z.; Dubbeldam, J.L.A. Generalized Langevin equation with a three parameter Mittag-Leffler noise. Physica A 2011, 390, 3627–3636. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Monne, H.M.-S.; Javanainen, M.; Metzler, R. Anomalous diffusion of phospholipids and cholesterols in a lipid bilayer and its origins. Phys. Rev. Lett. 2012, 109, 188103. [Google Scholar] [CrossRef] [PubMed]
- Min, W.; Luo, G.; Cherayil, B.J.; Kou, S.C.; Xie, X.S. Observation of a power-law memory kernel for fluctuations within a single protein molecule. Phys. Rev. Lett. 2005, 94, 198302. [Google Scholar] [CrossRef] [PubMed]
- Burov, S.; Barkai, E. Fractional Langevin equation: Overdamped, underdamped, and critical behaviors. Phys. Rev. E 2008, 78, 031112. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandev, T. Generalized Langevin Equation and the Prabhakar Derivative. Mathematics 2017, 5, 66. https://doi.org/10.3390/math5040066
Sandev T. Generalized Langevin Equation and the Prabhakar Derivative. Mathematics. 2017; 5(4):66. https://doi.org/10.3390/math5040066
Chicago/Turabian StyleSandev, Trifce. 2017. "Generalized Langevin Equation and the Prabhakar Derivative" Mathematics 5, no. 4: 66. https://doi.org/10.3390/math5040066
APA StyleSandev, T. (2017). Generalized Langevin Equation and the Prabhakar Derivative. Mathematics, 5(4), 66. https://doi.org/10.3390/math5040066




